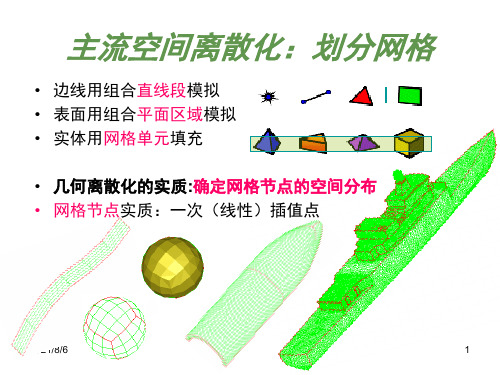
网格划分原理与实例(最终版本)
网格化PPT课件

04 网格化的未来发展
网格化技术的发展趋势
网格化技术将更加智能化
随着人工智能和机器学习技术的不断 发展,网格化技术将更加智能化,能 够更好地实现自动化和智能化管理。
网格化技术将更加精细化
网格化技术将更加融合化
随着各行业的不断融合,网格化技术 将能够更好地实现跨行业的应用,为 各行业提供更加全面和高效的管理和 服务。
THANKS FOR WATCHING
感谢您的观看
大数据技术可以实现对PPT课 件的数据监测和预警,及时发 现和解决潜在的问题。
网格化与人工智能的结合
人工智能技术可以为网格化PPT课件 提供智能化的推荐和匹配服务,根据 用户的需求和行为,推荐更加精准和 个性化的内容。
人工智能技术可以实现对PPT课件的 智能分析和评估,提供更加客观和全 面的评价结果。
随着数据处理和分析技术的不断进步, 网格化技术将能够实现更精细化的管 理和控制,进一步提高管理效率。
网格化在各行业的应用前景
能源行业
网格化技术可以应用于能源行 业的分布式能源管理和智能电 网建设,提高能源利用效率和
能源安ห้องสมุดไป่ตู้。
城市管理
网格化技术可以应用于城市管 理的城市基础设施管理和城市 安全监控,提高城市管理和服 务水平。
制造业
网格化技术可以应用于制造业 的智能制造和工业互联网建设 ,提高生产效率和产品质量。
农业
网格化技术可以应用于农业的 精准农业和智慧农业建设,提 高农业生产效率和农产品质量
。
网格化面临的挑战与解决方案
数据安全问题
网格化技术涉及大量的数据传输 和处理,需要加强数据安全保护 措施,保障数据的安全性和隐私
网格化的优势
第3章网格划分

Main Menu: Preprocessor > Material Properties >Material Models
APDL: mp,1,ex,2e11 mp,1,prxy,0.3 mp,1,dens,7.8e-9 mp,1,mu,0.1 mp,1,kxx ,48
3.2定义单元属性
单元属性是指在划分网格以前必须指定的所分析对象的特征。这些特征 包括: 单元类型 实常数 材料属性 单元坐标系(对各向异性材料) 截面号(对beam44,beam188,beam189单元有效)
第3章 网格划分
单元类型设定 Main Menu: Preprocessor > Element Type > Add/Edit/Delete
✓ 如果多于四条边,可将线合并成Lcomb合并 ✓ 分割面,各面包含3或4条边
第3章 网格划分
3.3.2映射网格 体映射网格(MSHAPE,0,3D $MSHKEY,1)对几何形状要求
外形为块状(六面体)、楔形或棱形(五面体)、四面体 对边必须划分为相同的单元数,或分割符合过渡网格形式 如果体是棱形或四面体,三角形面上的单元分割数必须是 偶数 当需要减少围成体的面数以进行映射网格划分时,可以对 面合并,如果连接边界线为多条,线也必须连接在一起。
第3章 网格划分
网格划分是有限元分析的基础, 所划分的网格形状对计算精度和 计算规模有直接的影响。网格划分还应考虑加载和后处理的要求。
内容包括:
单元属性 网格划分 直接建模法 编号控制
第3章 网格划分
3.1有限元网格划分步骤
(1)定义单元属性 (2)网格生成的控制 (3)生成网格 步骤(2)不是必须的,可以采用默认控制
ICEM---网格划分原理
2021/8/6
28
2021/8/6
29
分析块 ->模仿
1
块
网格
2
2D增 块补
2021/8/6
30
分析块
2021/8/6
31
结构网格的索引与合并->减少总块数,加速求解
关键:统一索引
y/ j
索引
空间
2021/8/6
索引 空间
x /i
32
结构网格的索引与合并
ICEM中 块的合并
2021/8/6
三个块
实体
L_grid
2021/8/6
18
成块与实体:拓扑分析
实体 基本块
衍生块
2021/8/6
19
几何分解_组合块
2021/8/6
20
几何分解_组合块
2021/8/6
此处复制的每块 的节点都是独立的, 要进行节点的合并
21
构思块举例->找到最优块
2D
基
本
O-grid
块
C-grid(二分之一O-grid) L-grid(四分之一O-grrid)
11
块-关联-设置节点数-网格
原理示例_2D(正三角形)
2021/8/6
建块
×
关联
设置 节点数
× L-grid
12
原理示例_球壳
映射
M1 构造块 M2 关联点、线
2021/8/6
映射
13
原理示例_圆柱
O-grid 建块方法
建块
点、线的关联
映射
原始建块方法
2021/8/6
14
原理示例_球
L-grid方法
网格划分实例

Training Manual
3-7
Meshing Methods for 3D Geometries
扫掠方法中膨胀
15. 右击 Sweep Method 并选择 Inflate this Method. 膨胀将作用于三个源面.
16. 对 boundary, 需要选择面的三个外圆边(可 能需要启动Select Edges 触发器来简化这 个操作 ).
影响球的坐标系
23. 右击 Coordinate Systems 并插入一个 坐标系。 设置 Global Coordinates的Define By选项 ,在Origin X, Y,和Z 中分别输入 [0 [m], 0.1 [m], 和 0.08 [m]) 。 关掉 Section Plane, 坐标系如下图所示.
Training Manual
3-22
Meshing Methods for 3D Geometries
面尺寸
Training Manual
22. 重新激活 Section Plane ,并使视图方向平行于三通管的轴。 注意这里只在面尺寸 激活的截面厚度方向有多个单元
3-23
Meshing Methods for 3D Geometries
Training Manual
3-25
Meshing Methods for 3D Geometries
体尺寸
26. 设置 Sphere Radius 为 0.01 [m] 和 Element Size 为 0.005 [m]. 显示的模型会更新以预览影响球的范围.
Training Manual
3-26
Training Manual
网格算法的原理

网格算法的原理
网格算法是一种常用的计算机图形学算法,用于将二维空间划分为规则的网格格点,以实现图形模型的离散化表示和各类计算操作。
其原理是将整个空间划分为一个个小的单元格,每个单元格都具有固定的大小。
网格算法的主要思想是将空间划分为一系列的网格单元,每个单元格代表了一个离散化的小区域。
这些单元格可以用于表示图形对象的形状、位置、颜色等属性。
在网格算法中,常用的单元格形状包括正方形和长方形。
每个单元格可以表示一个像素、一个点或者更大的对象。
其中,最小的单元格称为基本单元。
通过将空间划分为网格单元,可以将图形模型转换为离散化的数据结构。
这样,可以使用一组有限的数据结构来表示整个图形模型,从而简化图形模型的处理和操作。
网格算法的主要应用包括图形渲染、图形碰撞检测、物理模拟等。
在图形渲染中,可以根据每个网格单元的属性来确定其颜色,从而生成图像。
在图形碰撞检测中,可以通过判断不同网格单元是否相交来判断碰撞是否发生。
在物理模拟中,可以根据每个网格单元的属性来计算物理效应,如重力、摩擦力等。
总之,网格算法通过将空间划分为网格单元,将图形模型离散化表示,以实现各种计算操作。
这种离散化的表示方式使得图形计算更加高效和方便。
ANSYS第3章网格划分技术及技巧(完全版)

ANSYS第3章⽹格划分技术及技巧(完全版)ANSYS ⼊门教程 (5) - ⽹格划分技术及技巧之⽹格划分技术及技巧、⽹格划分控制及⽹格划分⾼级技术第 3 章⽹格划分技术及技巧3.1 定义单元属性单元类型 / 实常数 / 材料属性 / 梁截⾯ / 设置⼏何模型的单元属性3.2 ⽹格划分控制单元形状控制及⽹格类型选择 / 单元尺⼨控制 / 部⽹格划分控制 / 划分⽹格3.3 ⽹格划分⾼级技术⾯映射⽹格划分 / 体映射⽹格划分 / 扫掠⽣成体⽹格 / 单元有效性检查 / ⽹格修改3.4 ⽹格划分实例基本模型的⽹格划分 / 复杂⾯模型的⽹格划分 / 复杂体模型的⽹格划分创建⼏何模型后,必须⽣成有限元模型才能分析计算,⽣成有限元模型的⽅法就是对⼏何模型进⾏⽹格划分,⽹格划分主要过程包括三个步骤:⑴定义单元属性单元属性包括:单元类型、实常数、材料特性、单元坐标系和截⾯号等。
⑵定义⽹格控制选项★对⼏何图素边界划分⽹格的⼤⼩和数⽬进⾏设置;★没有固定的⽹格密度可供参考;★可通过评估结果来评价⽹格的密度是否合理。
⑶⽣成⽹格★执⾏⽹格划分,⽣成有限元模型;★可清除已经⽣成的⽹格并重新划分;★局部进⾏细化。
3.1 定义单元属性⼀、定义单元类型1. 定义单元类型命令:ET, ITYPE, Ename, KOP1, KOP2, KOP3, KOP4, KOP5, KOP6, INOPR ITYPE - ⽤户定义的单元类型的参考号。
Ename - ANSYS 单元库中给定的单元名或编号,它由⼀个类别前缀和惟⼀的编号组成,类别前缀可以省略,⽽仅使⽤单元编号。
KOP1~KOP6 - 单元描述选项,此值在单元库中有明确的定义,可参考单元⼿册。
也可通过命令KEYOPT进⾏设置。
INOPR - 如果此值为 1 则不输出该类单元的所有结果。
例如:et,1,link8 ! 定义 LINK8 单元,其参考号为 1;也可⽤ ET,1,8定义et,3,beam4 ! 定义 BEAM4 单元,其参考号为 3;也可⽤ ET,3,4 定义2. 单元类型的 KEYOPT命令:KEYOPT, ITYPE, KNUM, VALUEITYPE - 由ET命令定义的单元类型参考号。
结构有限元分析中的网格划分技术及其应用实例

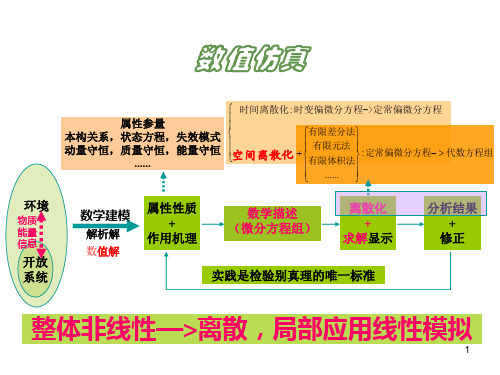
结构有限元分析中的网格划分技术及其应用实例一、前言有限元网格划分是进行有限元数值模拟分析至关重要的一步,它直接影响着后续数值计算分析结果的精确性。
网格划分涉及单元的形状及其拓扑类型、单元类型、网格生成器的选择、网格的密度、单元的编号以及几何体素。
从几何表达上讲,梁和杆是相同的,从物理和数值求解上讲则是有区别的。
同理,平面应力和平面应变情况设计的单元求解方程也不相同。
在有限元数值求解中,单元的等效节点力、刚度矩阵、质量矩阵等均用数值积分生成,连续体单元以及壳、板、梁单元的面内均采用高斯(Gauss)积分,而壳、板、梁单元的厚度方向采用辛普生(Simpson)积分。
辛普生积分点的间隔是一定的,沿厚度分成奇数积分点。
由于不同单元的刚度矩阵不同,采用数值积分的求解方式不同,因此实际应用中,一定要采用合理的单元来模拟求解。
CAD软件中流行的实体建模包括基于特征的参数化建模和空间自由曲面混合造型两种方法。
Pro/E和SoildWorks是特征参数化造型的代表,而CATIA与Unigraphics等则将特征参数化和空间自由曲面混合造型有机的结合起来。
现有CAD软件对表面形态的表示法已经大大超过了CAE软件,因此,在将CAD实体模型导入CAE软件的过程中,必须将CAD模型中其他表示法的表面形态转换到CAE软件的表示法上,转换精度的高低取决于接口程序的好坏。
在转换过程中,程序需要解决好几何图形(曲线与曲面的空间位置)和拓扑关系(各图形数据的逻辑关系)两个关键问题。
其中几何图形的传递相对容易实现,而图形间的拓扑关系容易出现传递失败的情况。
数据传递面临的一个重大挑战是,将导入CAE程序的CAD模型改造成适合有限元分析的网格模型。
在很多情况下,导入CAE程序的模型可能包含许多设计细节,如细小的孔、狭窄的槽,甚至是建模过程中形成的小曲面等。
这些细节往往不是基于结构的考虑,保留这些细节,单元数量势必增加,甚至会掩盖问题的主要矛盾,对分析结果造成负面影响。
ICEM网格划分原理ppt课件
三个块
实体
L_grid
29
成块与实体:拓扑分析
基本块
实体
衍生块
30
几何分解_组合块
31
几何分解_组合块
此处复制的每块 的节点都是独立的, 要进行节点的32合并
构思块举例->找到最优块
2D
基
本
O-grid
块
C-grid(二分之一O-grid) L-grid(四分之一O-grrid)
减少 网格 数量
按Material
AUTODYN不支持ICEM的二维网格,可对ICEM输出的网格 文件info.geo编程修改成.zon的格式再导入。
.geo与.zon文件数据段的差别:同样的数据,不同的顺序
53
ICEM二次开发
Solidworks AutoCAD
ProE UG ……
几何实体
ICEM
网格
Autodyn Ls_dyna
5
认识界面
修 非构 非
改 结造 结
几 构块 构
何网
网
格
格
划
修
分
补
几何显示控制 块显示控制 part显示控制
非结 结构 构网 网格 格输 输出 出
几何体视角控制
块的索引控制
6
ANSYS ICEM CFD
非结构网格(Mesh)
划分步骤
设置参数 选择方法 自动划分 大多需网格修补
7
认识非结构网格
网格单元 2D:三角形
42
43
分析块 ->模仿
1
块
网格
2
2D增 块补
44
分析块
45
结构网格的索引与合并->减少总块数,加速求解
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
d、自由网格对原始几何的填充效果较好,效率高,傻瓜化。但网格
可控性差,精度视计算程序波动较大,且计算工作量大。
e、Hexa网格的网格/节点大致为1:1;Tetra网格/节点大致为5:1 f、 Tetra网格的计算消耗大致为Hexa的0.4倍,因此当模型节点数量
破解影 射路径 是复杂 几何网 格处理 的不二 法则
分块要诀:
a、获得和积分路径大约一致的网格路径,提高积分精度。 b、获得高质量Hexa网格,节省计算成本,满足非线性计算
的网格变形需求。 c、 “分块” 是讲求刀法的。武士的刀法,是用来杀出一条生
路,网格技术的刀法,则是为了砍出完整的sweep路径。
(vertices)。
影射拓补
2.1基于拓扑的分块
分块拓扑的思想即是切分复杂几何的基本拓补体,展露原 始几何的本质拓扑结构。以圆形为简单例子,下图为圆面没有
分块前的映射网格:方形——圆形。
畸变, Jacobian接
近0
进行分块后:
影射路径发生 改变
原始影射路径
影射路径发生 改变
多少个影射路 径呢?
分块网格可 以形成拓补 结构库,不 同几何无需 再次划分网 格,只需把 基本拓补网 格映射到几 何表面即可。
2.2基于几何的分块
和基于拓补分块不同,这种方法完全基于几何。 要领: 1、对复杂几何进行砍伐,直到砍出具备六面体特征
的基本几何体。 2、途径为一系列boolean运算 特点: 1、分块操作复杂,容易出错 2、即使基于低端CAD程序理论上也能做出全结构化
几何成形技术:
1、三维数值拟合成 像技术——计算几何 方法。 2、CT图形扫描点云 成像技术
全结构化六面体网格
拓补结构
网格成形,约21万网格
网格细部
难点: 1、影射路径复杂,且不唯一。 2、几何细部特征复杂,控制边界繁杂,完全捕捉很难。
其他案例—全结构化六面体网格
平键 轴承
难点:轴 向sweep 路径被平 键破坏
计算结构力学问 题对网格的适应 能力更强,即使 网格质量仅仅达 到0.1也能获得好 的断裂计算结果。
案例3——骨头模型
1难度很高的 模型,不具备 明显的几何拓 扑特征。
2代表了生物 力学常用分析 模型的特征。
骨头网格
网格模型(全六面体网 格方案),网格质量0.3,网格总数约9万。
案例4——庖丁“解”人,难度超高!
难点: 1、接触分析中的非连续网格处理技术。 2、实体+板壳网格自由度耦合网格处理技术。
薄钢板踩踏屈曲——断裂、自接触、失稳、
非连续网格
难点: 1、接触分析中的非连续网格处理技术。 2、大变形大应变非线性问题的网格处理技术。
高难度案例——F6短舱CFD模型
共约540万结构化网格,质量0.25
机体
网格是一门艺术,而不仅仅是单纯的技术。
几个思考问题——试试寻找其分块策略
陶叉耳
刹车 鼓盘
液体 料斗
谢谢!
网格划分原理与案例(绪)
By 余志祥
——西南交通大学——
将生活网格化——有序、 紧凑、工作、享受、艺术!
一、网格Grid的基本概念
1、现代CAE学科的基本载体,结合有限元、离散元 技术,适用于CSD和CFD计算,岩土工程的无网格法 也是基于网格概念的发展。
2、结构化网格和非结构化网格;结构化网格针对网 格的序列映射关系,六面体网格不等同于结构化网 格,四面体或者三角形网格也可做出结构化网格。结 构化六面体网格技术代表了网格技术的最高端。
3、网格算法是Computer Graphics和Computer Mathematics结合的产物,和力学无关。
4、网格可以连续,也可以不连续。 5、网格是艺术,不仅仅是技术。
二、网格剖分基本刀法:
1、自由网格剖分——算法复杂
a、现有的CAE软件通常自带自由网格划分功能,以自由网格方案为
空气
拓补结构
混凝土模型网格—岩石节理模型、接触、材
料非线性、微动力阻尼松弛法、实体网格、杆系网格
普通钢筋 砼T joint
高强钢筋 高强砼柱
相关文献 实验结果
计算结果
计算结果
相关文献 实验结果
结束语
网格方案的选取和网格质量是CAE仿真分析的 支点,没有网格就没有数值计算。
网格是一门独立的专业学科,是计算机图形学 和计算数学的拓展外延,网格技术的掌握基于 图形概念和数学概念的掌握。
六面体网格。 本质:等同于全手工网格制作。
案例1——多体组合复杂网格
约8万混合网格,含接触、预紧、非连续网格、材料非线 性和显式破坏。
KT形矩管桁架试件-反力架网格模型
案例2——屠龙刀:3D几何
几何模型
屠龙刀拓补结构
屠龙刀网格
屠龙刀网格模型(全结构化六面体方案)
好刀还需好刀法—— 屠龙也会砍缺!
暖通模具—
五、六面体 难点:影射
混合网格
关系过于复 杂,需要混
合网格减少
网格数量
建筑结构案例——广告牌CFD
约50万结构化网格
难点: 1、Hexa贴体壁面网格捕捉近壁区流场特征。 2、实体+无厚度膜双侧非连续网格技术(inner wall+split)
案例——标准四坡结构CFD 约60万混合网格,包含覆面Grid
基本一致的前提下,两者的计算消耗大致是2:1——影响计算成本的 关键因素既有节点也有网格。
2结构化映射网格 结构化网格,即映射序列网格。
思路:首先将原始几何映射成规则四边形(Quad),生成正
四边形网格,再重新映射(mapping)到原来的几何形状。 关键:要定义映射成正四边形的四条边(edge)以及角点
难点: 1、四面体劈分——棱形贴体壁 面网格,捕捉近壁区流场特征。 2、Hexa+Tetra+Pyramid混合 网格技术
结构案例——CSD混尺度模型 含杆系、板壳、实体、接触、约束方程、动力非线性。
难点: 复杂模型的混尺度网格及其 边界处理技术。
节点模型——断裂、接触、预紧、弥散开裂、
非连续网格
主——适应群体较广,但欠专业,网格工作可控性太差。
b、在面(Surface or Face)网格方案中,多采用全三角形网格或四 边形+少量三角形网格方案。理论上,任意曲面都可以实现结构化四
边形网格。三角形网格对数值积分格式的适应性差,精度低。
c、在体(Body or Solid)网格中,往往采用Tetra网格方案——不是
