三维设计江苏专用2017届高三数学一轮总复习板块命题点专练三基本初等函数Ⅰ及函数与方程理
三维设计江苏专用2017届高三数学一轮总复习第二章函数与基本初等函数Ⅰ第三节函数的奇偶性及周期性课件文

函数f(x)就叫做奇函数
2.函数的周期性 (1)周期函数
对于函数 f(x),如果存在一个非零常数 T,使得当 x 取定义 域内的任何值时,都有_f_(_x_+__T_)_=__f(_x_)_,那么就称函数 f(x) 为周期函数,称 T 为这个函数的周期. (2)最小正周期 如果在周期函数 f(x)的所有周期中存在一个最 ___小_的 __正 ___数_,那 么这个_最__小__的__正__数__就叫做 f(x)的最小正周期.
(3)∵当f(xx<)0的时定,义f(x域)=为x2-R,x,
∴f(则-当x)x=>03-时x-,-3x=x<-0,(3x-3-x)=-f(x), 所以故故f原f((x-函)为x数)=奇是x函偶2+数函x数=..f(x),
[谨记通法] 判定函数奇偶性的 3 种常用方法 (1)定义法:
(2)图象法:
3.函数 f(x)=(2x+2)
22+ -xx的奇偶性为________.
解析:由22+-xx≥0,得函数 f(x)=(2x+2)
22-+xx的定义
域为[-2,2),不关于原点对称,所以函数 f(x)为非奇非偶
函数.
答案:非奇非偶
考点一 函数奇偶性的判断基础送分型考点——自主练透
[题组练透] 判断下列函数的奇偶性: (1)f(x)= 1-x2+ x2-1; (2)f(x)= 3-2x+ 2x-3; (3)f(x)=3x-3-x; (4)f(x)=|x+4-3|-x23; (5)(易错题)f(x)=xx22+-xx,,xx><00,.
(3)性质法: ①设 f(x),g(x)的定义域分别是 D1,D2,那么在它们的 公共定义域上:奇+奇=奇,奇×奇=偶,偶+偶=偶,偶 ×偶=偶,奇×偶=奇. ②复合函数的奇偶性可概括为“同奇则奇,一偶则偶”. [提醒] (1)“性质法”中的结论是在两个函数的公共定 义域内才成立的. (2)判断分段函数的奇偶性应分段分别证明 f(-x)与 f(x) 的关系,只有对各段上的 x 都满足相同的关系时,才能判断 其奇偶性.如“题组练透”第(5)题.
三维设计江苏专用2017届高三数学一轮总复习第八章立体几何第一节空间几何体的结构特征课件理(1)

3.有关不等式的问题常常转化为两个函数图象的上、下关系来解.
[对点训练 1] 已知函数 y=f(x)的图象是圆 x2+y2=2 上的两
段弧,如图 1 所示,则不等式 f(x)>f(-x)-2x 的解集是________.
D [因为 f(x)满足 f(x-4)=-f(x), 所以 f(x-8)=f(x),所以函数 f(x)是以 8 为周期的周期函数,则 f(-25)=f(- 1),f(80)=f(0),f(11)=f(3). 由 f(x)是定义在 R 上的奇函数,且满足 f(x-4)=-f(x),得 f(11)=f(3)=-f(- 1)=f(1). 因为 f(x)在区间[0,2]上是增函数,f(x)在 R 上是奇函数, 所以 f(x)在区间[-2,2]上是增函数, 所以 f(-1)<f(0)<f(1),即 f(-25)<f(80)<f(11).]
☞角度 2 奇偶性与周期性结合
(2017·贵阳适应性考试(二))若函数 f(x)=asin 2x+btan x+1,且 f(- 3)=5,则 f(π+3)=________.
-3 [令 g(x)=asin 2x+btan x,则 g(x)是奇函数,且最小正周期是 π,由 f(- 3)=g(-3)+1=5,得 g(-3)=4,则 g(3)=-g(-3)=-4,则 f(π+3)=g(π+3) +1=g(3)+1=-4+1=-3.]
(2)函数 f(x)=2f-xx--11,,xx≤>00, 的图象如图所示,
当 a<1 时,函数 y=f(x)的图象与函数 f(x)=x+a 的图象有两个交点,即方 程 f(x)=x+a 有且只有两个不相等的实数根.]
三维设计江苏专用高三数学一轮总复习板块命题点专练十立体几何理

三维设计江苏专用高三数学一轮总复习板块命题点专练十立体几何理1.(2015·山东高考改编)已知等腰直角三角形的直角边的长为2,将该三角形绕其斜边所在的直线旋转一周而形成的曲面所围成的几何体的体积为________.解析:绕等腰直角三角形的斜边所在的直线旋转一周形成的曲面围成的几何体为两个底面重合,等体积的圆锥,如图所示.每一个圆锥的底面半径和高都为2,故所求几何体的体积V =2×13×π×()22×2=42π3. 答案:42π32.(2015·江苏高考)现有橡皮泥制作的底面半径为5,高为4的圆锥和底面半径为2,高为8的圆柱各一个,若将它们重新制作成总体积与高均保持不变,但底面半径相同的新的圆锥和圆柱各一个,则新的底面半径为________.解析:设新的底面半径为r ,由题意得13×π×52×4+π×22×8=13×π×r 2×4+π×r 2×8, ∴r 2=7,∴r =7. 答案:73.(2014·江苏高考)设甲、乙两个圆柱的底面积分别为S 1,S 2,体积分别为V 1,V 2,若它们的侧面积相等,且S 1S 2=94,则V 1V 2的值是________.解析:设甲、乙两个圆柱的底面半径分别是r 1,r 2,母线长分别是l 1,l 2.则由S 1S 2=94可得r 1r 2=32.又两个圆柱的侧面积相等,即2πr 1l 1=2πr 2l 2,则l 1l 2=r 2r 1=23,所以V 1V 2=S 1l 1S 2l 2=94×23=32. 答案:324.(2015·安徽高考)如图,三棱锥P ABC 中,PA ⊥平面ABC ,PA =1,AB =1,AC =2,∠BAC =60°.(1)求三棱锥P ABC 的体积;(2)证明:在线段PC 上存在点M ,使得AC ⊥BM ,并求PMMC的值.解:(1)由题设AB =1,AC =2,∠BAC =60°, 可得S △ABC =12·AB ·AC ·sin 60°=32.由PA ⊥平面ABC ,可知PA 是三棱锥P ABC 的高. 又PA =1,所以三棱锥P ABC 的体积V =13·S △ABC ·PA =36.(2)证明:在平面ABC 内,过点B 作BN ⊥AC ,垂足为N .在平面PAC 内,过点N 作MN ∥PA 交PC 于点M ,连结BM .由PA ⊥平面ABC 知PA ⊥AC ,所以MN ⊥AC . 由于BN ∩MN =N ,故AC ⊥平面MBN . 又BM ⊂平面MBN ,所以AC ⊥BM . 在Rt△BAN 中,AN =AB ·cos∠BAC =12,从而NC =AC -AN =32.由MN ∥PA ,得PM MC =AN NC =13.命题点二 组合体的“切”“接”问题 难度: 中命题指数:☆☆☆1.(2015·全国卷Ⅱ改编)已知A ,B 是球O 的球面上两点,∠AOB =90°,C 为该球面上的动点.若三棱锥O ABC 体积的最大值为36,则球O 的表面积为________.解析:如图,设球的半径为R , ∵∠AOB =90°,∴S △AOB =12R 2.∵V O ABC =V C AOB ,而△AOB 面积为定值,∴当点C 到平面AOB 的距离最大时,V O ABC 最大,∴当C 为与球的大圆面AOB 垂直的直径的端点时,体积V O ABC 最大,为13×12R 2×R =36,∴R =6,∴球O 的表面积为4πR 2=4π×62=144π. 答案:144π2.(2014·陕西高考改编)已知底面边长为1,侧棱长为2的正四棱柱的各顶点均在同一个球面上,则该球的体积为________.解析:因为该正四棱柱的外接球的半径是四棱柱体对角线的一半,所以半径r =1212+12+22=1,所以V 球=4π3×13=4π3.答案:4π33.(2013·全国卷Ⅱ)已知正四棱锥O ABCD 的体积为322,底面边长为3,则以O 为球心,OA 为半径的球的表面积为________.解析:过O 作底面ABCD 的垂线段OE ,连结EA ,则E 为正方形ABCD 的中心.由题意可知13×(3)2×OE =322,所以OE =322,故球的半径R =OA =OE 2+EA 2=6,则球的表面积S =4πR 2=24π.答案:24π命题点三 直线、平面平行与垂直的判定与性质 难度: 中命题指数:☆☆☆☆☆1.(2015·四川高考)一个正方体的平面展开图及该正方体的直观图的示意图如图所示.(1)请将字母F ,G ,H 标记在正方体相应的顶点处(不需说明理由); (2)判断平面BEG 与平面ACH 的位置关系,并证明你的结论; (3)证明:直线DF ⊥平面BEG . 解:(1)点F ,G ,H 的位置如图所示. (2)平面BEG ∥平面ACH . 证明如下:因为ABCD EFGH 为正方体, 所以BC ∥FG ,BC =FG . 又FG ∥EH ,FG =EH , 所以BC ∥EH ,BC =EH ,于是四边形BCHE 为平行四边形,所以BE ∥CH . 又CH ⊂平面ACH ,BE ⊄平面ACH ,所以BE ∥平面ACH . 同理BG ∥平面ACH .又BE ∩BG =B ,所以平面BEG ∥平面ACH . (3)证明:连接FH ,与EG 交于点O ,连接BD . 因为ABCD EFGH 为正方体,所以DH ⊥平面EFGH . 因为EG ⊂平面EFGH ,所以DH ⊥EG .又EG ⊥FH ,DH ∩FH =H ,所以EG ⊥平面BFHD . 又DF ⊂平面BFHD ,所以DF ⊥EG .同理DF ⊥BG .又EG ∩BG =G ,所以DF ⊥平面BEG .2.(2015·全国卷Ⅰ)如图,四边形ABCD 为菱形,G 为AC 与BD 的交点,BE ⊥平面ABCD .(1)证明:平面AEC ⊥平面BED ;(2)若∠ABC =120°,AE ⊥EC ,三棱锥E ACD 的体积为63,求该三棱锥的侧面积. 解:(1)证明:因为四边形ABCD 为菱形,所以AC ⊥BD . 因为BE ⊥平面ABCD ,所以AC ⊥BE . 又BD ∩BE =B ,故AC ⊥平面BED . 因为AC ⊂平面AEC , 所以平面AEC ⊥平面BED .(2)设AB =x ,在菱形ABCD 中,由∠ABC =120°,可得AG =GC =32x ,GB =GD =x 2. 因为AE ⊥EC ,所以在Rt △AEC 中,可得EG =32x . 由BE ⊥平面ABCD ,知△EBG 为直角三角形, 可得BE =22x . 由已知得,三棱锥E ACD 的体积V 三棱锥E ACD =13×12·AC ·GD ·BE =624x 3=63, 故x =2.从而可得AE =EC =ED = 6.所以△EAC 的面积为3,△EAD 的面积与△ECD 的面积均为 5.故三棱锥E ACD 的侧面积为3+2 5.3.(2015·北京高考)如图,在三棱锥V ABC 中,平面VAB ⊥平面ABC ,△VAB 为等边三角形,AC ⊥BC 且AC =BC =2,O ,M 分别为AB ,VA 的中点.(1)求证:VB ∥平面MOC ; (2)求证:平面MOC ⊥平面VAB ; (3)求三棱锥V ABC 的体积.解:(1)证明:因为O ,M 分别为AB ,VA 的中点, 所以OM ∥VB .又因为VB ⊄平面MOC ,OM ⊂平面MOC , 所以VB ∥平面MOC .(2)证明:因为AC =BC ,O 为AB 的中点, 所以OC ⊥AB .又因为平面VAB ⊥平面ABC ,且OC ⊂平面ABC , 所以OC ⊥平面VAB .又OC ⊂平面MOC ,所以平面MOC ⊥平面VAB . (3)在等腰直角三角形ACB 中,AC =BC =2, 所以AB =2,OC =1.所以等边三角形VAB 的面积S △VAB = 3. 又因为OC ⊥平面VAB ,所以三棱锥C VAB 的体积等于13OC ·S △VAB =33.又因为三棱锥V ABC 的体积与三棱锥C VAB 的体积相等,所以三棱锥V ABC 的体积为33. 4.(2014·四川高考)在如图所示的多面体中,四边形ABB 1A 1和ACC 1A 1都为矩形.(1)若AC ⊥BC ,证明:直线BC ⊥平面ACC 1A 1;(2)设D ,E 分别是线段BC ,CC 1的中点,在线段AB 上是否存在一点M ,使直线DE ∥平面A 1MC ?请证明你的结论.解:(1)证明:因为四边形ABB 1A 1和ACC 1A 1都是矩形, 所以AA 1⊥AB ,AA 1⊥AC .因为AB ,AC 为平面ABC 内两条相交直线, 所以AA 1⊥平面ABC .因为直线BC ⊂平面ABC ,所以AA 1⊥BC .又由已知,AC ⊥BC ,AA 1,AC 为平面ACC 1A 1内两条相交直线,所以BC ⊥平面ACC 1A 1.(2)取线段AB 的中点M ,连接A 1M ,MC ,A 1C ,AC 1,设O 为A 1C ,AC 1的交点. 由已知,O 为AC 1的中点.连接MD ,OE ,则MD ,OE 分别为△ABC ,△ACC 1的中位线, 所以,MD 綊12AC ,OE 綊12AC ,因此MD 綊OE .连接OM ,从而四边形MDEO 为平行四边形,则DE ∥MO . 因为直线DE ⊄平面A 1MC ,MO ⊂平面A 1MC , 所以直线DE ∥平面A 1MC .即线段AB 上存在一点M (线段AB 的中点),使直线DE ∥平面A 1MC .。
2019-2020年三维设计江苏专用2017届高三数学一轮总复习第二章函数与基本初等函数Ⅰ第五节二次函数与幂函数
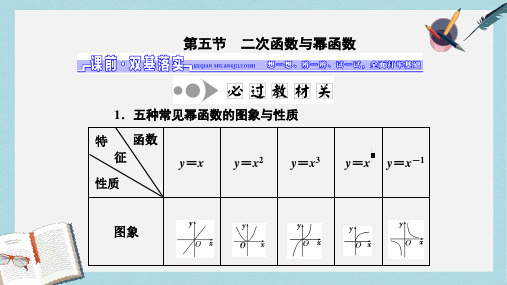
[小题纠偏]
1
1
1.若(m+1) 2 <(3-2m) 2 ,则实数 m 的取值范围为______.
1
解析:∵y=x 2 在定义域[0,+∞)上是单调增函数,
∴ m3-+21m≥≥0, 0, m+1<3-2m,
解得-1≤m<23,
即 m 的取值范围是-1,23. 答案:-1,23
编后语
• 常常可见到这样的同学,他们在下课前几分钟就开始看表、收拾课本文具,下课铃一响,就迫不及待地“逃离”教室。实际上,每节课刚下课时的几分 钟是我们对上课内容查漏补缺的好时机。善于学习的同学往往懂得抓好课后的“黄金两分钟”。那么,课后的“黄金时间”可以用来做什么呢?
• 一、释疑难 • 对课堂上老师讲到的内容自己想不通卡壳的问题,应该在课堂上标出来,下课时,在老师还未离开教室的时候,要主动请老师讲解清楚。如果老师已
角度三:二次函数中恒成立问题 4.已知 a 是实数,函数 f(x)=2ax2+2x-3 在 x∈[-1,1]上恒
小于零,求实数 a 的取值范围.
解:由题意知 2ax2+2x-3<0 在[-1,1]上恒成立. 当 x=0 时,-3<0,适合; 当 x≠0 时,a<321x-132-16, 因为1x∈(-∞,-1]∪[1,+∞), 当 x=1 时,右边取最小值12,所以 a<12. 综上,实数 a 的取值范围是-∞,12.
考点三 二次函数的图象与性质常考常新型考点——多角探明 [命题分析]
高考对二次函数图象与性质的考查.常与一元二次方程、 一元二次不等式等知识交汇命题是高考的热点,考查二次函数 的图象与性质的应用.
常见的命题角度有: (1)二次函数的单调性问题; (2)二次函数的最值问题; (3)二次函数中恒成立问题.
三维设计江苏专用2017届高三数学一轮总复习第二章函数与基本初等函数Ⅰ第六节指数与指数函数课件理

由于 所以
fg(令(xx))g有应(x最有)=大最-值小x值32,--41x,+3,
因 解此 得必a由 在 而=有于 (y1-=,a3g>a2即(a-130,x,)当t4在在+=f(R(∞--x上))有1∞上,单最,单调大-调递值2递减)3上减,时单,,调a 递的增值等,于 1.
∴(a2-a+1)0=1,故②是正确的;
③3
1
x4+y3=(x4+y3) 3 ,故③是错误的;
④∵2x=16,
∴x=4,∵3y=217=3-3, ∴y=-3, ∴x+y=4+(-3)=1, 故④是错误的.故填②. 答案:②
4.如果函数 f(x)=a2x+2ax-1(a>0,a≠1)在[-1,1]上的 最大值为 14,则 a=________.
[即时应用] 1.已知 a>0 且 a≠1,函数 y=|ax-1|与 y=2a 的图象有
两个交点,则 a 的取值范围是________.
解析:①当 0<a<1 时,y=|ax-1|的图象如图 1 所示,
由已知得 0<2a<1,
所以
1 0<a<2.
②当 a>1 时,y=|ax-1|的图象如图 2 所示,
② 根据自己预习时理解过的逻辑结构抓住老师的思路。老师讲课在多数情况下是根据教材本身的知识结构展开的,若把自己预习时所理解过的知识 逻辑结构与老师的讲解过程进行比较,便可以抓住老师的思路。
③ 根据老师的提示抓住老师的思路。老师在教学中经常有一些提示用语,如“请注意”、“我再重复一遍”、“这个问题的关键是····”等等,这些 用语往往体现了老师的思路。来自:学习方法网
3.有下列命题:
3
①当 a<0 时,(a2) 2 =a3;
三维设计江苏专用2017届高三数学一轮总复习第二章函数与基本初等函数Ⅰ第一节函数的概念及其表示课件理

4.若函数 f(x2+1)的定义域为[-1,1],则 f(lg x)的定 V
义域为________. 解析:因为 f(x2+1)的定义域为[-1,1], 则-1≤x≤1,故 0≤x2≤1, 所以 1≤x2+1≤2. 因为 f(x2+1)与 f(lg x)是同一个对应法则, 所以 1≤lg x≤2,即 10≤x≤100, 所以函数 f(lg x)的定义域为[10,100]. 答案:[10,100]
[小题纠偏]
1.函数y=
x 与函数y=
x x
________(填“是”或“不是”)
同一函数.
解析:函数y=
x的定义域为[0,+∞),y=
x 的定 x
义域为(0,+∞).因为两个函数的定义域不同,所以
不表示同一函数.
答案:不是
2.函数f(x)= x-1· x+1的定义域为________. 解析:由题意,得xx-+11≥≥00,, 所以 x≥1,所以函数 f(x) 的定义域是[1,+∞). 答案:[1,+∞)
定义域是________. 解析:令 t=x+1,则由已知函数的定义域为[1,2 016],可知 1≤t≤2 016.要使函数 f(x+1)有意义,则有 1≤x+1≤2 016,解 得 0≤x≤2 015,故函数 f(x+1)的定义域为[0,2 015].所以使 函数 g(x)有意义的条件是0x≤-x1≤≠200,15, 解得 0≤x<1 或 1< x≤2 015.故函数 g(x)的定义域为[0,1)∪(1,2 015] 答案:[0,1)∪(1,2 015]
[题组练透] 角度一:求给定函数解析式的定义域
1.(2016·南师附中月考)y=
x2-x1-log2(4-x2)的定义域
是________.
三维设计江苏专用2017届高三数学一轮总复习板块命题点专练六简单的三角恒等变换及解三角形理

板块命题点专练(六) 简单的三角恒等变换及解三角形1.(2015·重庆高考改编)若tan α=2tan π5,则cos⎝⎛⎭⎫α-3π10sin ⎝⎛⎭⎫α-π5=________. 解析:∵cos ⎝ ⎛⎭⎪⎫α-3π10=cos ⎝ ⎛⎭⎪⎫α+π5-π2=sin ⎝⎛⎭⎪⎫α+π5, ∴原式=sin ⎝⎛⎭⎪⎫α+π5sin ⎝ ⎛⎭⎪⎫α-π5=sin αcos π5+cos αsinπ5sin αcos π5-cos αsin π5=tan α+tanπ5tan α-tanπ5.又∵tan α=2tan π5,∴原式=2tan π5+tanπ52tan π5-tanπ5=3.答案:32.(2015·江苏高考)已知tan α=-2,tan(α+β)=17,则tan β的值为________.解析:tan β=tan[(α+β)-α]=α+β-tan α1+α+βα=17--1+17-=3. 答案:33.(2015·北京高考)已知函数f (x )=2sin x 2cos x2-2sin 2x2.(1)求f (x )的最小正周期;(2)求f (x )在区间[-π,0]上的最小值. 解:(1)由题意得f (x )=22sin x -22(1-cos x )=sin ⎝⎛⎭⎪⎫x +π4-22,所以f (x )的最小正周期为2π.(2)因为-π≤x ≤0,所以-3π4≤x +π4≤π4.当x +π4=-π2,即x =-3π4时,f (x )取得最小值.所以f (x )在区间[-π,0]上的最小值为f ⎝ ⎛⎭⎪⎫-3π4=-1-22. 4.(2015·四川高考)已知A ,B ,C 为△ABC 的内角,tan A ,tan B 是关于x 的方程x 2+3px -p +1=0(p ∈R)的两个实根.(1)求C 的大小;(2)若AB =3,AC =6,求p 的值.解:(1)由已知,方程x 2+3px -p +1=0的判别式 Δ=(3p )2-4(-p +1)=3p 2+4p -4≥0, 所以p ≤-2或p ≥23.由根与系数的关系,有tan A +tan B =-3p ,tan A tan B =1-p , 于是1-tan A tan B =1-(1-p )=p ≠0,从而tan(A +B )=tan A +tan B 1-tan A tan B =-3pp =- 3.所以tan C =-tan(A +B )=3,所以C =60°. (2)由正弦定理,得sin B =AC sin C AB =6sin 60°3=22, 解得B =45°或B =135°(舍去). 于是A =180°-B -C =75°.则tan A =tan 75°=tan(45°+30°) =tan 45°+tan 30°1-tan 45°tan 30°=1+331-33=2+ 3. 所以p =-13(tan A +tan B ) =-13(2+3+1)=-1- 3.________. 解析:∠C =180°-75°-45°=60°,由正弦定理得AB sin C =ACsin B ,即6sin 60°=ACsin 45°,解得AC =2.答案:22.(2015·广东高考改编)设△ABC 的内角A ,B ,C 的对边分别为a ,b ,c .若a =2,c =2 3,cos A =32且b <c ,则b =________. 解析:由a 2=b 2+c 2-2bc cos A ,得4=b 2+12-6b ,解得b =2或4.又b <c ,∴b =2. 答案:23.(2015·北京高考)在△ABC 中,a =3,b =6,∠A =2π3,则∠B =________.解析:在△ABC 中,根据正弦定理asin A =bsin B,有3sin2π3=6sin B ,可得sin B =22. 因为∠A 为钝角,所以∠B =π4. 答案:π44.(2015·福建高考)若△ABC 中,AC =3,A =45°,C =75°,则BC =________. 解析:∠B =180°-75°-45°=60°,由正弦定理,得BC sin A =AC sin B ,即BCsin 45°=3sin 60°,解得BC = 2.答案: 25.(2015·全国卷Ⅰ)已知a ,b ,c 分别为△ABC 内角A ,B ,C 的对边,sin 2B =2sin A sinC .(1)若a =b ,求cos B ;(2)设B =90°,且a =2,求△ABC 的面积. 解:(1)由题设及正弦定理可得b 2=2ac . 又a =b ,可得b =2c ,a =2c .由余弦定理可得cos B =a 2+c 2-b 22ac =14.(2)由(1)知b 2=2ac .因为B =90°,由勾股定理得a 2+c 2=b 2,故a 2+c 2=2ac ,进而可得c =a = 2. 所以△ABC 的面积为12×2×2=1.6.(2015·山东高考)△ABC 中,角A ,B ,C 所对的边分别为a ,b ,c .已知cos B =33,sin(A +B )=69,ac =23,求sin A 和c 的值. 解:在△ABC 中,由cos B =33,得sin B =63, 因为A +B +C =π, 所以sin C =sin(A +B )=69. 因为sin C <sin B ,所以C <B ,可得C 为锐角, 所以cos C =539,因此sin A =sin(B +C )=sin B cos C +cos B sin C =63×539+33×69=223. 由a sin A =csin C, 可得a =c sin Asin C =223c 69=23c .又ac =23,所以c =1.7.(2015·全国卷Ⅱ)△ABC 中,D 是BC 上的点,AD 平分∠BAC ,BD =2DC . (1)求sin B sin C;(2)若∠BAC =60°,求∠B . 解:(1)由正弦定理,得AD sin B =BD sin ∠BAD ,AD sin C =DCsin ∠CAD . 因为AD 平分∠BAC ,BD =2DC , 所以sin B sin C =DC BD =12.(2)因为∠C =180°-(∠BAC +∠B ),∠BAC =60°,所以sin C =sin(∠BAC +∠B )=32cos B +12sin B . 由(1)知2sin B =sin C ,所以tan B =33, 所以∠B =30°8.(2015·浙江高考)在△ABC 中,内角A ,B ,C 所对的边分别为a ,b ,c ,已知tan ⎝ ⎛⎭⎪⎫π4+A =2.(1)求sin 2A sin 2A +cos 2A的值;(2)若B =π4,a =3,求△ABC 的面积.解:(1)由tan ⎝ ⎛⎭⎪⎫π4+A =2,得tan A =13, 所以sin 2A sin 2A +cos 2A =2tan A 2tan A +1=25. (2)由tan A =13,A ∈(0,π),得sin A =1010,cos A =31010. 由a =3,B =π4及正弦定理a sin A =bsin B ,得b =3 5.由sin C =sin(A +B )=sin ⎝ ⎛⎭⎪⎫A +π4,得sin C =255.设△ABC 的面积为S ,则S =12ab sin C =9.9.(2015·江苏高考)在△ABC 中,已知AB =2,AC =3,A =60° (1)求BC 的长; (2)求sin 2C 的值.解:(1)由余弦定理知,BC 2=AB 2+AC 2-2AB ·AC ·cos A =4+9-2×2×3×12=7,所以BC =7.(2)由正弦定理知,AB sin C =BCsin A,所以sin C =AB BC ·sin A =2sin 60°7=217.因为AB <BC ,所以C 为锐角,。
三维设计江苏专用2017届高三数学一轮总复习第四章三角函数解三角形第七节正弦定理和余弦定理课件文

,c2=
b2+c2-a2
a2+c2-b2
a2+b2-c2
___2_b_c____,cos B=____2_a_c___,cos C=____2_a_b____.
3.三角形中常用的面积公式
(1)S=12ah(h表示边a上的高);
1
1
(2)S=12bcsin A=__2_a_c_si_n__B_=__2_a_b_s_i_n_C___;
编后语
老师上课都有一定的思路,抓住老师的思路就能取得良好的学习效果。在上一小节中已经提及听课中要跟随老师的思路,这里再进一步论述听课时如何 抓住老师的思路。
① 根据课堂提问抓住老师的思路。老师在讲课过程中往往会提出一些问题,有的要求回答,有的则是自问自答。一般来说,老师在课堂上提出的问 题都是学习中的关键,若能抓住老师提出的问题深入思考,就可以抓住老师的思路。
=(3 2)2+62-2×3 2×6×cos34π
=18+36-(-36)=90,所以a=3 10.
又由正弦定理得sin
B=bsin∠a BAC=3
3= 10
1100,
由题设知0<B<π4,
所以cos B= 1-sin2B=
1-110=3
10 10 .
在△ABD中,因为AD=BD,所以∠ABD=∠BAD,
[即时应用] (2016·南京师大附中检测)设△ABC的内角A,B,C的对边分 别为a,b,c,且bsin A= 3acos B. (1)求角B的大小; (2)若b=3,sin C=2sin A,求a,c的值.
解:(1)∵bsin A= 3acos B, 由正弦定理得 sin Bsin A= 3sin Acos B. 在△ABC中,sin A≠0, 即得tan B= 3,∴B=π3. (2)∵sin C=2sin A,由正弦定理得c=2a, 由余弦定理b2=a2+c2-2accos B, 即9=a2+4a2-2a·2acosπ3, 解得a= 3, ∴c=2a=2 3.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
板块命题点专练(三) 基本初等函数(Ⅰ)及函数
与方程
1.(2015·山东高考改编)设a=0.60.6,b=0.61.5,c=1.50.6,
则a,b,c的大小关系是________.
解析:因为函数y=0.6x是减函数,0<0.6<1.5,所以1>0.60.6>0.61.5,即b<a<1.因为函数y=x0.6在(0,+∞)上是增函数,1<1.5,所以1.50.6>10.6=1,即c>1.综上,b<a<c.
答案:b<a<c
2.(2015·全国卷Ⅱ改编)设函数f(x)=则f(-2)+f(log212)=________.
解析:∵-2<1,
∴f(-2)=1+log2(2+2)=1+log24=1+2=3.
∵log212>1,∴f(log212)=2==6.
∴f(-2)+f(log212)=3+6=9.
答案:9
3.(2015·陕西高考改编)设f(x)=ln x,0<a<b,若p=f(),q=f,r =(f(a)+f(b)),则p,q,r的大小关系是________.
解析:因为b>a>0,故>.又f(x)=ln x(x>0)为增函数,所以f >f(),即q>p.又r=(f(a)+f(b))=(ln a+ln b)=ln=p,即p=r<q.
答案:p=r<q
4.(2015·山东高考)若函数f(x)=是奇函数,则使f(x)>3成立的x的取值范围为________.
解析:因为函数y=f(x)为奇函数,所以f(-x)=-f(x),即=-.化简可得a=1,则>3,即-3>0,即>0,故不等式可化为<0,即1<2x<2,解得0<x<1.
答案:(0,1)
5.(2015·四川高考改编)设a,b都是不等于1的正数,
则“3a>3b>3”是“log a3<log b3”的________条件(填“充要”“充分不必要”“必要不充分”“既不充分又不必要”).
解析:∵3a>3b>3,∴a>b>1,此时log a3<log b3正确;反之,若
log a3<log b3,则不一定得到3a>3b>3,例如当a=,b=3时,log a3<log b3成立,但推不出a>b>1.故“3a>3b>3”是“log a3<log b3”的充分不必要条件.答案:充分不必要
6.(2015·浙江高考)若a=log43,则2a+2-a=________.
解析:∵a=log43=log23=log2,
∴2a+2-a=2+2=+2=+=.
答案:
7.(2015·山东高考)已知函数f(x)=a x+b(a>0,a≠1)的定义域和值域都是[-1,0],则a+b=________.
解析:当a>1时,函数f(x)=a x+b在上为增函数,由题意得无解.当0<a<1时,函数f(x)=a x+b在[-1,0]上为减函数,由题意得解得所以a +b=-.
答案:-
8.(2015·天津高考)已知a>0,b>0,ab=8,则当a的值为________时,log2a·log2(2b)取得最大值.
解析:由于a>0,b>0,ab=8,所以b=.
所以log2a·log2(2b)=log2a·log2=log2a·(4-log2a)=-(log2a-2)2+4,
当且仅当log2a=2,即a=4时,log2a·log2(2b)取得最大值4.
答案:4
9.(2015·福建高考)若函数f(x)=2|x-a|(a∈R)满足f(1+x)=f(1-x),且f(x)在[m,+∞)上单调递增,则实数m的最小值等于________.解析:因为f(x)=2|x-a|,所以f(x)的图象关于直线x=a对称.又由f(1+x)=f(1-x),知f(x)的图象关于直线x=1对称,故a=1,且f(x)的增区间是,由函数f(x)在上单调递增,知⊆,所以m≥1,故m的最小值为1.
答案:1
1.(2015·湖南高考)已知函数f(x)=若存在实数b,使函数g(x)=f(x)-b有两个零点,则a的取值范围是________.
解析:函数g(x)有两个零点,即方程f(x)-b=0有两个不等实根,则函数y=f(x)和y=b的图象有两个公共点.
①若a<0,则当x≤a时,f(x)=x3,函数单调递增;当x>a时,f(x)
=x2,函数先单调递减后单调递增,f(x)的图象如图(1)实线部分所示,其与直线y=b可能有两个公共点.
②若0≤a≤1,则a3≤a2,函数f(x)在R上单调递增,f(x)的图象如图(2)实线部分所示,其与直线y=b至多有一个公共点.
③若a>1,则a3>a2,函数f(x)在R上不单调,f(x)的图象如图(3)实线部分所示,其与直线y=b可能有两个公共点.
综上,a<0或a>1.
答案:(-∞,0)∪(1,+∞)
2.(2015·湖南高考)若函数f(x)=|2x-2|-b有两个零点,则实数b的
取值范围是________.
解析:由f(x)=|2x-2|-b=0,得|2x-2|=b.
在同一平面直角坐标系中画出y=|2x-2|与y=b的图象,如图所示,则当0<b<2时,两函数图象有两个交点,从而函数f(x)=|2x-2|-b 有两个零点.
答案:(0,2)
3.(2015·湖北高考)函数f(x)=2sin x sin-x2的零点个数为________.
解析:f(x)=2sin x sin-x2=2sin x cos x-x2=sin 2x-x2,由f(x)=0,
得sin 2x=x2.
设y1=sin 2x,y2=x2,在同一平面直角坐标系中画出二者的图象,如图所示.由图象知,两个函数图象有两个交点,故函数f(x)有两个零点.
答案:2
4.(2015·福建高考改编)若a,b是函数f(x)=x2-px+q(p>0,q>0)的两个不同的零点,且a,b,-2这三个数可适当排序后成等差数列,也可适当排序后成等比数列,则p+q的值等于________.
解析:不妨设a>b,由题意得
∴a>0,b>0,
则a,-2,b成等比数列,a,b,-2成等差数列,
∴∴
∴p=5,q=4,∴p+q=9.
答案:9
1.(2015·四川高考)某食品的保鲜时间y(单位:小时)与储藏温度
x(单位:℃)满足函数关系y=e kx+b(e=2.718…为自然对数的底数,k,b 为常数).若该食品在0 ℃的保鲜时间是192小时,在22 ℃的保鲜时间是48小时,则该食品在33 ℃的保鲜时间是________小时.
解析:由已知条件,得192=e b,∴b=ln 192.
又∵48=e22k+b=e22k+ln 192=192e22k=192(e11k)2,
∴e11k===.
设该食品在33 ℃的保鲜时间是t小时,
则t=e33k+ln 192=192e33k=192(e11k)3=192×3=24.
答案:24
2.(2015·江苏高考)某山区外围有两条相互垂直的直线型公路,为
进一步改善山区的交通现状,计划修建一条连接两条公路和山区边界的直线型公路.记两条相互垂直的公路为l1,l2,山区边界曲线为C,计划修建的公路为l.如图所示,M,N为C的两个端点,测得点M到l1,l2的距离分别为5千米和40
千米,点N到l1,l2的距离分别为20千米和2.5千米.以l2,l1所在的直线分别为x,y轴,建立平面直角坐标系xOy.假设曲线C符合函数y=(其中a,b为常数)模型.
(1)求a,b的值.
(2)设公路l与曲线C相切于P点,P的横坐标为t.
①请写出公路l长度的函数解析式f(t),并写出其定义域.
②当t为何值时,公路l的长度最短?求出最短长度.
解:(1)由题意知,点M,N的坐标分别为(5,40),(20,2.5).
将其分别代入y=,得
解得
(2)①由(1)知,y=(5≤x≤20),
则点P的坐标为.
设在点P处的切线l交x,y轴分别于A,B两点,
y′=-,
则l的方程为y-=-(x-t),
由此得A,B.
故f(t)==,t∈[5,20].
②设g(t)=t2+,则g′(t)=2t-.
令g′(t)=0,解得t=10.
当t∈(5,10)时,g′(t)<0,g(t)是减函数;
当t∈(10,20)时,g′(t)>0,g(t)是增函数.
从而,当t=10时,函数g(t)有极小值,也是最小值,
所以g(t)min=300,此时f(t)min=15.
故当t=10时,公路l的长度最短,最短长度为15千米.。
