2014高三数学(文)周练：程序框图

合集下载

高中数学《算法---程序框图》典型例题练习(含答案)

高中数学《算法---程序框图》典型例题练习（含答案）算法与程序框图在高考中常以小题出现，难度不大，主要考察循环结构。

在处理这类问题时关键在于计算的准确。

一、基础知识：读框图时，要抓住“看头，审尾，记过程”这三点1、看头：观察框图中变量的个数，以及赋予的初始值2、审尾：强调细致的“审查”循环结束时，变量所取到的最后一个值，这也是易错点3、记过程：为了保证计算的准确，在读取框图的过程中，可详细记录循环体中每经过一个步骤，变量取值的变化情况，以便于在跳出循环时能快速准确得到输出变量的值二、典型例题：例1：执行下图所示的程序框图，若输入2x =，则输出y 的值为 .思路：通过框图的判断语句可知y 关于x 的函数为：2321,01,012,1x x y x x x x x −<⎧⎪=+≤<⎨⎪+≥⎩，所以当2x =时，322212y =+⋅=答案：12例2：阅读右边的程序框图，运行相应的程序，则输出的值为（）A ．3B ．4C ．5D ．6思路：循环的流程如下：① 1,2i a ==② 2,5i a ==③ 3,16i a ==④ 4,65i a ==i循环终止，所以4i =答案：B例3：某程序框图如图所示，若输出的57S =，则判断框内为（）A. 4?k >B. 5?k >C. 6?k >D. 7?k >思路：循环的流程如下：① 2,4k S ==② 3,11k S ==③ 4,26k S ==④ 5,57k S ==所以应该在此时终止，所以填入4?k >答案：A例4：执行右面的程序框图，如果输入的N 是6，那么输出的p 是（）A. 120B. 720C. 1440D. 5040思路：循环的流程如下：① 1p =② 2,2k p ==③ 3,6k p ==④ 4,24k p ==⑤ 5,120k p ==⑥ 6,720k p ==答案：B例5：右图是一个算法的流程图，则输出S 的值是______ 第4题思路：循环的流程如下： ① 1123S =+=② 22,327n S ==+=③ 33,7215n S ==+=④ 44,15231n S ==+=⑤ 55,31263n S ==+=循环结束，所以63S =答案：63S =例6：执行如图所示的程序框图，若输出i 的值为2，则输入x 的最大值是( )A ．5B ．6C ．22D ．33思路：因为输出的2i =，说明只经过了一次循环。

高三数学算法和程序框图试题

高三数学算法和程序框图试题1.执行下图所示的程序框图，若输入A=2014，B=125，输出的A的值是____ ．【答案】1【解析】：第一次循环：,,第二次循环：，,第三次循环：,,第四次循环：,,否，所以输出【考点】程序框图的循环结构2.某流程图如图所示，现输入如下四个函数，则可以输出的函数是（）A．B．C．D．【答案】C【解析】根据程序框图知输出的函数为奇函数，并且此函数存在零点．经验证：不存在零点；不存在零点；为偶函数，且的定义域为全体实数，且，故此函数为奇函数，且令，得，函数存在零点，答案C 【考点】程序框图、函数的奇偶性、函数零点．3.（5分）（2011•陕西）如图框图，当x1=6，x2=9，p=8.5时，x3等于（）A．7B．8C．10D．11【答案】B的值．【解析】从程序框图中得到求p的解析式；列出方程，求出x3解：∵∴=8解得x3故选B点评：本题考查通过程序框图能判断出框图的功能．4.执行如图所描述的算法程序,记输出的一列的值依次为,其中且.(1)若输入,写出全部输出结果.(2)若输入,记,求与的关系().【答案】(1)输出结果共4个,依次是:.(2).【解析】(1)这是一个循环结构，依次写出每次循环的结果即可.（2）由框图中可得当时，.再由可得.将代入即可得与的关系.(1)这是一个循环结构，前4次输出的为：，第5次循环的结果为，与相等，故结束循环.所以输出的为：.（2）当时，..【考点】1、程序框图；2、递推数列.5.已知一个算法的程序框图如图所示，当输出的结果为0时，输入的值为（）A．或B．或C．或D．或【答案】C【解析】当时，，即；当时，，即，所以输入的x的值为1或-2.【考点】程序框图.6.按照下图的程序图计算，若开始输入的值为3，则最后输出的结果是（）A．6B．21C．5050D．231【答案】D【解析】由程序框图，输入，第次进入循环体，，第次进入循环体，，第次进入循环体，，成立，输出结果，故选．【考点】程序框图.7.给出30个数：1，2,4,7，……其规律是：第1个数是1；第2个数比第1个数大1；第3个数比第2个数大2；第4个数比第3个数大3；……以此类推，要计算这30个数的和，现已给出了该问题的程序框图如图所示，那么框图中判断框①处和执行框②处应分别填入（）A．B．C．D．【答案】【解析】由于要计算30个数的和，故循环要执行30次，由于循环变量的初值为1，步长为1，故终值应为30，即①中应填写；又由第1个数是1；第2个数比第1个数大1；第3个数比第2个数大2；第4个数比第3个数大3；…故②中应填写故选【考点】循环结构.8.阅读如下程序框图，如果输出，那么空白的判断框中应填入的条件是A．B．C．D．【答案】B【解析】由程序框图知前3次运算结果：因此终止条件为,故选B.【考点】本题主要考查算法的基本思想、算法的结构和功能，考查抽象思维能力和逻辑推理能力.9.图中，，，为某次考试三个评阅人对同一道题的独立评分，为该题的最终得分，当，，时，等于（）A．11B．10C．8D．7【答案】C【解析】先读懂右图的逻辑顺序，然后进行计算判断，其中判断条件是否成立是解答本题的关键．，,不成立,即为“否”，所以再输入；由绝对值的意义（一个点到另一个点的距离）和不等式知，点到点的距离小于点到的距离，所以当时，成立，即为“是”，此时，所以，即，解得，不合题意；当时，不成立，即为“否”，此时，所以，即，解得，符合题意，故选C．10.如图所示的程序框图，输出的S的值为()A．B．2C．－1D．－【答案】A【解析】k＝1时，S＝2，k＝2时，S＝，k＝3时，S＝－1，k＝4，S＝2，……所以S是以3为周期的循环．故当k＝2 012时，S＝．11.程序框图（即算法流程图）如下图所示，其输出结果是．【答案】127【解析】运行该程序框图如下故填127【考点】程序框图12.右图是计算值的一个程序框图，其中判断框内应填入的条件是A．B．C．D．【答案】A【解析】判断框内应该填循环终止条件，∵要加到，一共加4次∴k＞5.【考点】程序框图.13.执行如图所示的程序框图，输出的S＝________．【答案】【解析】执行第一次循环时S＝，i＝1；第二次循环S＝，i＝2，此时退出循环．故输出S＝.14.定义某种运算S=a⊗b,运算原理如图所示,则式子: +的值是.【答案】4【解析】2tan ="2,ln" e=1,∵2>1,∴⊗ln e==3;lg 100=2,=3,∵2<3,∴lg 100⊗==1.∴+=4.15.程序框图如图所示，该程序运行后输出的的值是（）A．B．C．D．【解析】由程序框图知：…，可知S出现周期为4，当时，结束循环输出S，,即输出的，故选D.【考点】程序框图.16.执行如图所示的程序框图，若输入，则输出的值为 .【答案】.【解析】满足条件，执行第一次循环，，；满足条件，执行第二次循环，，；满足条件，执行第三次循环，，；不满足条件，跳出循环体，输出的值为.【考点】算法与程序框图17.一个算法的程序框图如图，则其输出结果是（）A．0B．C．D．【解析】由题意可知：.【考点】1.程序框图；2.三角函数的周期性.18.阅读下边的程序框图，如果输出的函数值在区间内，则输入的实数的取值范围是．【答案】【解析】本题程序框图所反映的数学问题就是当函数的值域为时，求定义域.，，.【考点】程序框图与函数的定义域.19.阅读如图所示的程序框图，运行相应的程序．若输入某个正整数n后，输出的S∈(31，72)，则n的值为( )A．5B．6C．7D．8【答案】A【解析】由程序框图可知：运行第一次：运行第二次：运行第三次：运行第四次：运行第五次：运行第六次：因为，所以运行第五次后应结束，则判断框中的条件应为，所以答案应选B.【考点】循环结构.20.执行如图所示的框图，若输出结果为3，则可输入的实数值的个数为（）A．1B．2C．3D．4【答案】C【解析】若输入的时，则，当输出结果是，即，解得；若输入的时，则，当输出结果为，即，解得.则可输入的实数值的个数为3.故选C.【考点】1.程序框图的应用；2.指数与对数的运算.21.某算法的程序框图如图所示，如果输出的结果是26，则判断框内应为A．K>1B．K>2C．K>3D．K>4【答案】C【解析】第一次循环，否，；第二次循环，否，；第三次循环，否，；第四次循环，是，输出，运行结束，故判断框内应为K>3，选C.【考点】算法与程序框图22.已知函数f(x)＝ax3＋x2在x＝－1处取得极大值，记g(x)＝。

2014届高三数学北京各区模拟分类汇编-程序框图(文)

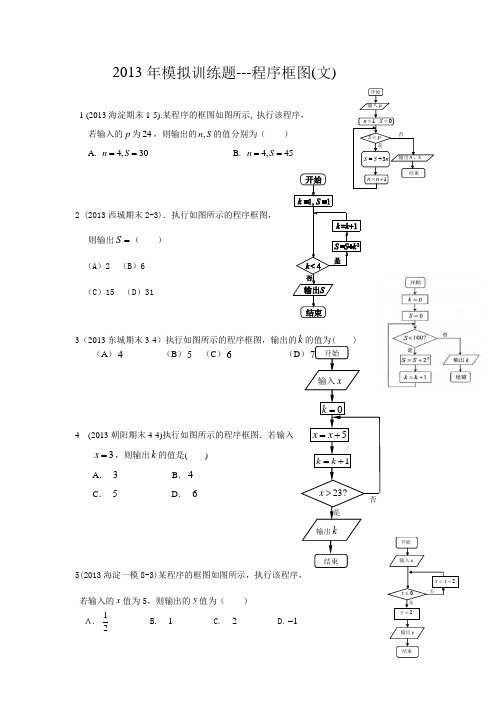
开始10n S ==， S p <是输入p结束输出n ，SnS S 3+=否1n n =+2013年模拟训练题---程序框图(文)1 (2013海淀期末1-5).某程序的框图如图所示, 执行该程序，若输入的p 为24，则输出的,n S 的值分别为（） A. 4,30n S == B. 4,45n S ==2 (2013西城期末2-3)．执行如图所示的程序框图，则输出S =（）（A ）2 （B ）6 （C ）15 （D ）313（2013东城期末3-4）执行如图所示的程序框图，输出的k 的值为( )（A ）4（B ）5 （C ）6（D ）74 (2013朝阳期末4-4)执行如图所示的程序框图．若输入 3x =，则输出k 的值是( )A ． 3B ．4C ． 5D ． 65(2013海淀一模8-3)某程序的框图如图所示，执行该程序，若输入的x 值为5，则输出的y 值为（）Ａ. 12B. 1C. 2D.1-开始0k = 5x x =+1k k =+结束输入x是否输出k23?x >开始输出y结束输入x2-=x x0≤xx y 2=是否6 (2013西城一模10-3)执行如图所示的程序框图．若输出3y =-，则输入角=θ（）（A ）π6 （B ）π6-（C ）π3（D ）π3-7（2013东城一模12-4）执行如图所示的程序框图，输出的结果是56，则判断框内应填入的条件是( ) （A ）5?n ≤ （B ）5?n < （C ）5?n > （D ）5?n ≥8（2013东城二模13-11）阅读程序框图，运行相应的程序，当输入x 的值为25-时，输出x 的值为________．9（2013朝阳一模14-10）执行如图所示的程序框图，输出结果S= .开始 i =0S =0 S =S +2i -1i ≥6? 输出S 结束是 i =i +2否否是结束输出 x x =3x +1x = x 1x >1输入x 开始10（2013朝阳二模15-4）执行如图所示的程序框图，若输出的结果是16，则判断框内的条件是（）A.6n >?B.7n ≥?C.8n >?D.9n >?11（2013丰台期末5-6）．执行如图所示的程序框图，则输出的S 值为（）.(A)3 (B)6 (C) 7 (D) 1012（2013西城二模11-5）．如图所示的程序框图表示求算式“235917⨯⨯⨯⨯” 之值，则判断框内可以填入（）（A ）10k ≤ （B ）16k ≤ （C ）22k ≤ （D ）34k ≤13（2013石景山期末6-6）．执行右面的框图，若输出结果为3，则可输入的实数x 值的个数为（） A ．1 B ．2 C ．3 D ．4否开始S = 0 n = 1 S=S+n 输出S结束是 n=n +2S S n =+开始结束 S =0, n =0输出S n =n +1 n >3? 否是开始输出y 输入x 否是结束>2x2=-1y x 2=log y x是否结束开始s=1,i=1(2)i s s =+-1i i =+输入n输出si n ≤?14（2013石景山一模18-4）．执行右面的框图，输出的结果s 的值为（） A ．-3 B ．2 C ．12-D ．1315（2013昌平期末11）已知某算法的流程图如图所示，则程序运行结束时输出的结果为．16（2013昌平二模23-4）执行如图所示的程序框图，输出的S 值为（）A ．102B ．81C ．39D ．2117（2013大兴一模24-3）执行如图所示的程序框图．若4n =，则输出s 的值是（）（A ）-42 （B ） -21 （C ） 11 （D ） 43开始,1==S n 3n S S n =+⋅4?n <1+=n n输出S结束是否18（2013房山期末10）. 阅读右边的程序框图，运行相应的程序，则输出n 的值为 .19 （2013通州期末6）．执行如图所示的程序框图，输出的S 值为（）（A ）5122- （B ）5022- （C ）5121- （D ）5021-20（2013房山一模3）.执行如图所示的程序框图．若输出15S =，则框图中① 处可以填入（）A. 4n >B. 8n >C. 16n >D. 16n <开始 k =1，S =0 k ≥50S =S +2k 输出S k=k+1 结束是否否1,0==n S 开始结束① 输出S是 n S S += n n 2=21（2013房山二模5).执行如图所示的程序框图．则输出的所有点(,)x y （） A.都在函数1y x =+的图象上 B.都在函数2y x =的图象上 C.都在函数2x y =的图象上 D.都在函数12x y -=的图象上否是开始1,2x y ==4x ≤1,2x x y y =+=结束输出,x y （）。

2014-2015学年高中数学(人教版必修三)课时训练第一章 1.1.2 程序框图与算法的基本逻辑结构

解析：判断框一般有一个进入点、两个退出点．
答案：D

栏目链接

题型一程序框图的画法和基本结构
例1 从下面具体的例子中说明几个基本的程序框和它们各自表示的功能，并把它填在相应的括号内．
栏目链接

解析：
栏目链接
栏目链接
第一步，输入圆的半径R.
第二步，计算L＝2π R. 第三步，计算S＝π R2. 第四步，输出L和S. 程序框图，如右图所示．

题型三含条件结构的程序框图
例3 画出求x的绝对值的程序框图．
解析：程序框图如下：
栏目链接

点评：凡是必须先根据条件作出判断，然后再决定进行哪一个步骤的问题，在画程序框图时，必须引入判断框，采用条件结构．而像本题求分段函数的函数值的程序
然后进行条件的判断，如果条件不满足，继续返回执行循
环体，然后再进行条件的判断，这个过程反复进行，直到某一次条件满足时，不再执行循环体，离开循环结构．直到型循环也称为“后测试型”循环．
栏目链接 A ) A．顺序结构、条件结构、循环结构 B．顺序结构、流程结构、循环结构 C．顺序结构、分支结构、流程结构 D．流程结构、循环结构、分支结构 2．程序框图中表示判断框的是( B ) A．矩形框 B．菱形框 C．圆形框D.椭圆形框

点评：记清各基本程序框的含义，并注意相互间的连接方法，以及程序框图的基本画法规则．
栏目链接

跟踪训练 1．算法共有三种逻辑结构，即顺序逻辑结构、条件逻辑结构和循环逻辑结构，下列说法正确的是( A．一个算法只能含有一种逻辑结构 B．一个算法最多可以包含两种逻辑结构 C．一个算法必须含有上述三种逻辑结构 D．一个算法可以含有上述三种逻辑结构的任意组合 )

高三数学框图试题

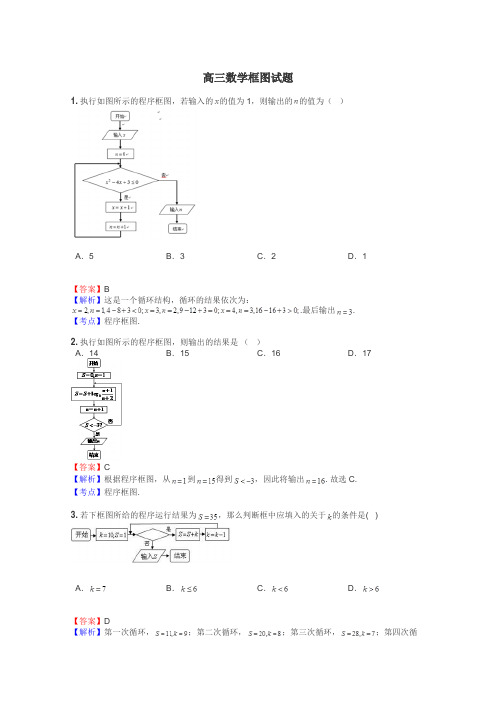
高三数学框图试题1.执行如图所示的程序框图，若输入的的值为1，则输出的的值为（）A．5B．3C．2D．1【答案】B【解析】这是一个循环结构，循环的结果依次为：.最后输出.【考点】程序框图.2.执行如图所示的程序框图，则输出的结果是（）A．14B．15C．16D．17【答案】C【解析】根据程序框图，从到得到，因此将输出. 故选C.【考点】程序框图.3.若下框图所给的程序运行结果为，那么判断框中应填入的关于的条件是( )A．B．C．D．【答案】D【解析】第一次循环，；第二次循环，；第三次循环，；第四次循环，，结束循环，输出，因此【考点】循环结构流程图4.阅读右图的程序框图，则输出S=( )A．14B．20C．30D．55【答案】C【解析】运行程序框图如下:故选C【考点】程序框图5.李强用流程图把早上上班前需要做的事情做了如下几种方案，则所用时间最少的方案是_______【答案】方案三【解析】方案一：所用时间为．方案二：所用时间为．方案三：所用时间为．所以所用时间最少的方案是方案三．【考点】流程图6.阅读右面的程序框图，运行相应的程序，输出的结果为（）A．B．C．D．【答案】C【解析】第一次循环，第二次循环，第三次循环，第四次循环，，因此当时，【考点】循环体流程图7.某程序框图如图所示，现在输入下列四个函数，则可以输出函数是（）A．B．C．D．【答案】B【解析】本题要从程序框图中发现函数的性质，第一个判断框说明是奇函数，第二个判断框说明方程有实解，即函数的图象与轴有交点，因此我们首先判断四个函数的奇偶性，可利用等式来判断，三个函数是奇函数，又，即或，从而，同样，因此两个函数图象与都无交点，只有中，，此函数图象与轴是相交的，因此选B．【考点】函数的奇偶性与函数的值域．8.下图是某算法的流程图，其输出值是 .【答案】.【解析】第一次循环，，不成立，执行第二次循环；，不成立，执行第三次循环；第三次循环，，不成立，执行第四次循环；第四次循环，，成立，跳出循环体，输出的值为.【考点】算法与程序框图9.阅读如图的程序框图，若输出的的值等于，那么在程序框图中判断框内应填写的条件是（）A．？B．？C．？D．？【答案】A【解析】读懂框图可知求满足的值，易得所以．【考点】考查算法与框图．10.阅读程序框图（如图所示），若输入，，,则输出的数是．【答案】【解析】程序框图的功能是：输出中最大的数，∵，，，所以输出的数为.【考点】程序框图.11.某程序框图如图所示，该程序运行后输出的的值是（）A．B．C．D．【答案】A【解析】第一步 ;第二步 ;第三步,第四步【考点】程序框图12.给出下面的程序框图，则输出的结果为_________.【答案】【解析】解：k=1，S=0+=，满足条件k≤5，执行循环，k=2，S=+，满足条件k≤5，执行循环，k=3，S=，满足条件k≤5，执行循环，k=4，S=，满足条件k≤5，执行循环，k=5，S=，满足条件k≤5，执行循环，k=6，S=，不满足条件k≤5，退出循环，输出S=故答案为：【考点】当型循环点评：本题主要考查了循环结构中的当型循环，以及程序框图，解题的关键是弄清循环次数，属于基础题13.如果右边程序框图的输出结果是10，那么在判断框中①表示的“条件”应该是（）A．i≥3B．i≥4C．i≥5D．i≥6【答案】C【解析】第一执行，，第二执行，，第三次执行，，第四次执行，，因为输出结果为10，所以应填.选C.【考点】循环结构点评：本题考查循环结构，已知运算规则与最后运算结果，求运算次数的一个题，是算法中一种常见的题型．14.已知，由如右程序框图输出的为A．B．C．D． 0【答案】B【解析】因为，由程序框图，M<N,S=M=ln2，故选B。

2014年、2013年高考文科数学程序框图(简洁排版)

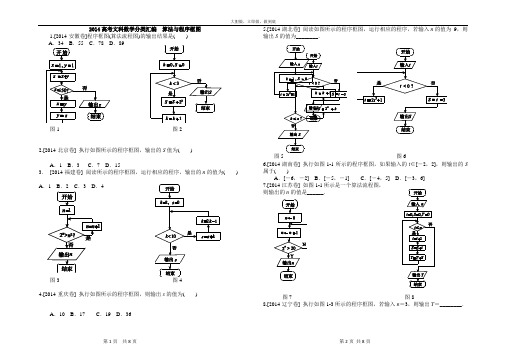
2014高考文科数学分类汇编算法与程序框图1.[2014·安徽卷]程序框图(算法流程图)的输出结果是( ) A ．34 B ．55 C ．78 D ．89图1 图22.[2014·北京卷] 执行如图所示的程序框图，输出的S 值为( )A ．1B ．3C ．7D ．15 3． [2014·福建卷] 阅读所示的程序框图，运行相应的程序，输出的n 的值为( )A ．1B ．2C ．3D ．4图34.[2014·重庆卷] 执行如图所示的程序框图，则输出s 的值为( )A ．10B ．17C ．19D ．365.[2014·湖北卷] 阅读如图所示的程序框图，运行相应的程序，若输入n 的值为 9，则输出S 的值为________．图5 图6 6.[2014·湖南卷] 执行如图1-1所示的程序框图，如果输入的t ∈[－2，2]，则输出的S 属于( )A ．[－6，－2]B ．[－5，－1]C ．[－4，5]D ．[－3，6] 7.[2014·江苏卷] 如图1-1所示是一个算法流程图，则输出的n 的值是______．图7 图88.[2014·辽宁卷] 执行如图1-3所示的程序框图，若输入n ＝3，则输出T ＝________．9.[江西卷]() A．7 B．9 C10.[2014·新课标Ⅱ] 执行如图1-2所示的程序框图，如果输入的x，t均为2，则输出的S＝()A．4 B．5 C．6 D．7图10 图1111.[2014·课标Ⅰ] 执行如图1-1的程序框图，若输入的a，b，k分别为1，2，3，则输出的M＝()A.203 B.72 C.165 D.15812. [2014·山东卷] 执行如图1-3所示的的程序框图，若输入的x的值为1，则输出的n的值为________．图12 图1313.[2014·浙江卷] 若某程序框图如图1-4所示，当输入50时，则该程序运行后输出的结果是________．14.[2014·陕西卷] 根据图1-1所示的框图，对大于2的整数N，输出的数列的通项公式是()A．a n＝2n B．a n＝2(n－1) C．a n＝2n D．a n＝2n－1图14 图1515.[2014·四川卷] 执行如图1-2的程序框图，如果输入的x，y∈R，那么输出的S的最大值为()A．0 B．1 C．2 D．316.[2014·天津卷] 阅读图1-3所示的框图，运行相应的程序，输出S的值为________．图16 图1717.（2011·福建）阅读右图所示的程序框图，运行相应的程序，输出的结果是( ) （A）3 （B）11 （C）38 （D）1232013年全国各地高考文科数学试题分类汇编：<算法初步>1 ．（2013年高考辽宁卷（文））执行如图所示的程序框图,若输入8,n S==则输出的（）A ．49B ．67C ．89D ．10112 ．（2013年高考广东卷（文））执行如图1所示的程序框图,若输入n 的值为3,则输出s 的值是（） A ．1B ．2C ．4D ．73 ．（高考课标Ⅰ卷（文））执行右面的程序框图,如果输入的[1,3]t ∈-,则输出的S 属于（）A ．[3,4]-B ．[5,2]-C ．[4,3]-D ．[2,5]-4 ．（2013年高考陕西卷（文））根据下列算法语句, 当输入x 为60时, 输出y 的值为 A ．25B ．30C ．31D ．615 ．（2013年高考北京卷（文））执行如图所示的程序框图,输出的S 值为（）A ．1B ．23C ．1321D ．6109876 ．（2013年高考福建卷（文））阅读如图所示的程序框图,运行相应的程序,如果输入某个正整数n 后,输出的)20,10(∈S ,那么n 的值为（A ．3B ．4C ．5D ．67．（2013年高考重庆卷（文））执行如题(5)图所示的程序框图,则输出的k 的值是A ．3B ．4C ．5D ．68 ．（2013年高考山东卷（文））执行右边的程序框图,若第一次输入的a 的值为-1.2,第二次输入的a的值为1.2,则第一次、第二次输出的a 的值分别为（） A ．0.2,0.2 B ．0.2,0.8 C ．0.8,0.2 D ．0.8,0.8图 19.【2102高考北京文4】执行如图所示的程序框图，输出S值为（A）2 （B）4 （C）8 （D）1610.阅读如图所示的程序框图，运行相应的程序，输出的结果s=_________。

成都七中2014届高三4月第一次周练数学(文)试题

成都七中2014届高三4月第一次周练数学（文）试题一、选择题(共50分,每题5分)1.数列{}n a 满足:*112,2()n n a a a n N +==+∈,则其前10项的和10S = A.100 B.101 C.110 D.1112.命题甲:2≠x 或3≠y ;命题乙:5≠+y x ,则甲是乙的A.充分非必要条件B.必要非充分条件C.充分必要条件D.既不充分条件也不必要条件 3.程序框图如右图所示,则该程序运行后输出k 的值是 A.3 B.4 C.5 D.64.已知双曲线22221(0,0)x y a b a b-=>>的一条渐近线与x 轴的夹角为060,则此双曲线的离心率为A.2B.3C.2D.35.设0a >且1a ≠.若log sin 2a x x >对(0,)4x π∈恒成立,则a 的取值范围是A.(0,)4πB.(0,]4πC.(,1)(1,)42ππ⋃D.[,1)4π6.在用土计算机进行的数学模拟实验中,一个应用微生物跑步参加化学反应,其物理速度与时间的关系是2()ln (02)6x f x x x =-<<,则A.()f x 有最小值11ln 322-B.()f x 有最大值11ln 322-C.()f x 有最小值3ln 32-D.()f x 有最大值3ln 32-7.定义集合A 与B 的运算“*”为:{A B x x A *=∈或x B ∈,但}x A B ∉I .设X 是偶数集,{1,2,3,4,5}Y =,则()X Y Y **=A.XB.YC.X Y ID.X Y U8.已知三棱柱111ABC A B C -的侧棱1BB 在下底面的射影BD 与AC 平行,若1BB 与底面所成角为30,且160B BC ∠=o ,则ACB ∠的余弦值为9.正项等比数列{}n a 满足:1232a a a +=,若存在n m a a ,,使得2116m n a a a =,则nm 41+的最小值为 A.625 B.134 C.73 D.23 10.已知,x y R ∈且4300x y x y y +≤⎧⎪-≥⎨⎪≥⎩,则存在R θ∈,使得(4)cos sin 0x y θθ-++=的概率为A.4πB.8πC.24π-D.18π-二、填空题(共25分,每题5分)11.将容量为50的样本数据,按从小到大的顺序分成4组如右表,则第3组的频率为____(要求将结果化为最简分数)12.若22i x yi i -=++,其中,,x y R i ∈为虚数单位,则=xy_________. 13.若1(1)(1)2n nM n+--<+对*n N ∈恒成立,则实数M 的取值范围是___________.14.已知(2,0)OB =uu u r ,(2,2)OC =uuu r ,)CA αα=uu r ,则OA uu r 与OB uu u r的夹角的取值范围是______________.15.设,A B 分别为椭圆Γ:22221(0)x y a b a b+=>>的左右顶点,F 为右焦点,l 为Γ在点B 处的切线,P 为Γ上异于,A B 的一点,直线AP 交l 于D ,M 为BD 中点,有如下结论:①FM 平分PFB ∠;②PM 与椭圆Γ相切;③PM 平分FPD ∠;④使得PM =BM 的点P 不存在.其中正确结论的序号是_____________.三、解答题(共75分)16.(12分)有驱虫药1618和1573各3杯,从中随机取出3杯称为一次试验(假定每杯被取到的概率相等),将1618全部取出称为试验成功.(1)求一次试验成功的概率.(2)求恰好在第3次试验成功的概率(要求将结果化为最简分数).17.(12分)已知1)4(cos 2)sin (cos 3)(222++--=πx x x x f 的定义域为[2,0π].(1)求)(x f 的最小值.(2)ABC ∆中, 45=A ,23=b ,边a 的长为6,求角B 大小及ABC ∆的面积.19.(12分)设抛物线1C :24y x =的准线与x 轴交于点1F ,焦点为2F ;椭圆2C 以1F 和2F 为焦点,离心率12e =.设P 是1C 与2C 的一个交点.(1)求椭圆2C 的方程.(2)直线l 过2C 的右焦点2F ,交1C 于12,A A 两点,且12A A 等于12PF F ∆的周长,l 的方程.20.(13分)设2()f x x x =+,用)(n g 表示()f x 当[,1](*)x n n n N ∈+∈时的函数值中整数值的个数. (1)求)(n g 的表达式.(2)设32*23()()n n n a n N g n +=∈,求2121(1)nk n k k S a -==-∑. (3)设12(),2n n n n g n b T b b b ==+++L ,若)(Z l l T n ∈<,求l 的最小值.21.(14分)设函数()(1)f x x α=+的定义域是[1,)-+∞,其中常数0α>.(注: '1()(1)f x x αα-=+ (1)若1α>,求()y f x =的过原点的切线方程.(2)证明当1α>时,对(1,0)x ∈-,恒有1()(1)x f x x αα+<<+.(3)当4α=时,求最大实数A ,使不等式2()1f x x Ax α>++对0x >恒成立.文科参考解答一、CBACD,BACDD10.解.可行域是一个三角形,面积为2;又直线系(4)cos sin 0x y θθ-++=与圆22(4)2x y -+=相切,故该三圆心角为4π的扇形,面积为4π,从而被直线系扫到部分的面积为24π-,故所求概率为18π-.二、11.625 12.34- 13.3[2,)2- 14.]125,12[ππ 15.①② 15.解.由上次中根出的题知①成立;写出椭圆Γ在点P 处的切线知②成立;于是PM 平分F PF '∠,故③不成立;若PA PB ⊥,则PM 为Rt BDP ∆的斜边中线,PM BM =,这样的P 有4个,故④不成立.三、16.解.(1)从6杯中任选3杯,不同选法共有3620C =种,而选到的3杯都是1618的选法只有1种,从而试验一次就成功的概率为120. (2)相当于前两次试验都没成功,第3次才成功,故概率为2191361()20208000P =⋅=.17.解.(1)先化简()f x 的解析式:()2[1cos(2)]12f x x x π=-+++2sin 2x x =+2sin(2)3x π=+由3432320ππππ≤+≤⇒≤≤x x ,得1)22sin(23≤+≤-πx ,所以函数)(x f 的最小值3)23(2-=-=,此时2π=x .(2)ABC ∆中,45=A ,23=b ,6=a ,故21645sin 23sin sin === a Ab B (正弦定理),再由a b <知45=<A B ,故 30=B ,于是 105180=--=B A C ,从而ABC ∆的面积1sin 1)2S ab C ==+.18.解一.连AC 设AC DB O =I ,连1,AO OE . (1)由1A A ⊥面ABCD ,知1BD A A ⊥, 又AC BD ⊥, 故BD ⊥面1ACEA . 再由1A E ⊂面1ACEA 便得E A 1⊥BD . (2)在正1A BD ∆中,1BD AO ⊥,而E A BD 1⊥,又1AO ⊂面OE A 1,⊂E A 1平面OE A 1,且111AO A E A =I ,故BD⊥面OE A 1,于是OE BD ⊥,OE A 1∠为二面角E BD A --1的平面角. 正方体ABCD —1111D C B A 中,设棱长为a 2,且E 为棱1CC 的中点,由平面几何知识易得11,,3EO AO A E a ===,满足22211A E A O EO =+,故1EO C O ⊥. 再由EO BD ⊥知EO ⊥面1A BD ,故1EAO 是直线1A E 与平面1A BD 所成角. 又11sin EO EAO A E ∠==故直线1A E 与平面1A BD .解二.分别以1,,DA DC DD uu u r uuu r uuur为z y x ,,轴正向,建立空间直角坐标系.设正方体棱长为a .(1)易得11(,0,0),(,,0),(0,,0),(,0,),(0,,)A a B a a C a A a a C a a .设(0,,)E a z ,则1(,,)A E a a z a =--uuu r,(,,0)BD a a =--uu u r ,从而1()00A E BD a a a a z a ⋅=-⋅+⋅+-⋅=uuu r uu u r,于是.1BD E A ⊥(2)由题设,(0,,)2a E a ,则1(,,)2a A E a a =--uuu r ,1(,0,),(,,0)DA a a DB a a ==uuur uu u r .设(,,)n x y z =r 是平面1A BD 的一个法向量,则10n DA n DB ⋅=⋅=r uuu r r uu u r,即 0ax az ax ay y z x +=+=⇒==-于是可取(n =-r .易得1132n A E a A E ⋅==r uuu r uuu r ,故若记1A E uuu r 与n r 的夹角为θ,则有11cos n A E n A Eθ⋅==⋅r uuu rr uuu r ,故直线1A E 与平面1A BD .19.解.(1)由条件,12(1,0),(1,0)F F -是椭圆2C 的两焦点,故半焦距为1,再由离心率为12知半长轴长为2,从而2C 的方程为22143x y +=,其右准线方程为4x =.(2)由(1)可知12PF F ∆的周长12126PF PF F F ++=.又1C :24y x =而2(1,0)F .若l 垂直于x 轴,易得124A A =,矛盾,故l 不垂直于x 轴,可设其方程为(1)y k x =-,与1C 方程联立可得2222(24)0k x k x k -++=,从而2124(1)k A k +=, 令126A A =可解出22k =,故l的方程为1)y x =-或1)y x =-.20.解.对*n N ∈,函数x x x f +=2)(在[,1]n n +单增,值域为22[,32]n n n n +++, 故*()23()g n n n N =+∈.(2)322*23()()n n n a n n N g n +==∈,故 21234212()()()n n n S a a a a a a -=-+-++-L222222(12)(34)((21)(2))n n =-+-++--L[37(41)]n =-+++-L 3(21)(1)2n n n n +-=-⋅=-+.(3)由()2n n g n b =得231579212322222n n n n n T -++=+++++L ,且231157212322222n n n n n T +++=++++L 两式相减,得1231523222()()222222n n n n T ++=-++++L 11111(1)52372722()1222212n n n n n -++-++=-+=--于是.2727nn n T +-=故若2772n n n T l +=-<且l Z ∈,则l 的最小值是7.21.解.(1)1()(1)f x x αα-'=+.若切点为原点,由(0)f α'=知切线方程为1y x α=+;若切点不是原点,设切点为000(,(1))(0)P x x x α+≠,由于100()(1)f x x αα-'=+,故由切线过原点知1000(1)(1)x x x ααα-+=+,在(1,)-+∞内有唯一的根011x α=-. 又11()1(1)f ααααα-'=--,故切线方程为1()(1)1y x ααααααα-=+--. 综上所述,所求切线有两条,方程分别为1y x α=+和1()(1)1y x ααααααα-=+--. (2)当1α>时,令()()h x f x x α=-,则1()[(1)1]h x x αα-'=+-,故当(1,0)x ∈-时恒有()0h x '<,即()h x 在[1,0]-单调递减,故(0)()(1)h h x h <<-对(1,0)x ∈-恒成立.又(1),(0)1h h α-==,故1()h x α<<,即1(1)x x ααα<+-<,此即1()(1)x f x x αα+<<+(3)令2()()1g x f x x Ax α=---,则(0)0g =,且3()4(1)42g x x Ax '=+--,显然有(0)0g '=,且()g x '的导函数为22()12(1)212[(1)]6A g x x A x ''=+-=+-若6A ≤,则16A≤,易知2(1)1x +>对0x >恒成立,从而对0x >恒有()0g x ''>,即()g x '在[0,)+∞单调增,从而()(0)0g x g ''>=对0x >恒成立,从而()g x 在[0,)+∞单调增,()(0)0g x g >=对0x >恒成立.若6A >,则16A >,存在00x >,使得2(1)6Ax +<对0(0,)x x ∈恒成立,即()0g x ''<对0(0,)x x ∈恒成立,再由(0)0g '=知存在10x >,使得()0g x '<对1(0,)x x ∈恒成立,再由(0)0g =便知()0g x >不能对0x >恒成立. 综上所述,所求A 的最大值是6.。

安徽省黄山一中2014届高三上文科数学周周练试卷(1)及答案

黄山一中2014届高三文科数学周周练（1）第Ⅰ卷（选择题共50分）一、选择题：本大题共10小题，每小题5分，共50分．在每小题给出的四个选项中，只有一项是符合题目要求的.⒈ 若复数z 满足()112i z i ⋅=-+，则z 的虚部为（）A ．12i -B ．12iC ．12D ．12-⒉ 设x R ∈，则“1x =”是“3x x =”的（）A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件⒊ 已知(){}*30A x N x x =∈-≤，函数ln(1)y x =-的定义域为集合B ，则A B =I （）A . {}1,2,3B . {}2,3C . (]1,3D . []1,3⒋ 已知向量(1,2)=a ，(1,0)=b ，(3,4)=c ．若()λ+⊥b a c ，则实数λ的值为（） A .12 B . 35C . 113-D . 311-⒌ 等差数列{}n a 中的1a 、4025a 是函数321()4613f x x x x =-+-的极值点，则22013log a =（）A . 2B . 3C . 4D . 5⒍ 设变量,x y 满足约束条件3123x y x y x y +≥⎧⎪-≥-⎨⎪-≤⎩，则目标函数23zx y =+的最小值为（）A . 6B . 7C . 8D . 23 ⒎ 某几何体的三视图如图所示，则该几何体的表面积为（）A .B .C .()1π D .()2π⒏ 已知函数 2 0()20x x f x x x +≤⎧=⎨-+>⎩，则不等式2()f x x ≥的解集为（）A . [11]-，B . [22]-，C . [21]-，D . [12]-，⒐ 袋中共有6个除了颜色外完全相同的球，其中有1个红球，2个白球和3个黑球.从袋中任取两球，两球颜色不同．．的概率为（） A .415 B . 13 C . 25 D . 1115⒑ 定义在R 上的偶函数()f x ，满足(3)()f x f x +=，(2)0f =，则函数()y f x =在区间()0,6内零点的个数为（）A ．2个B ．4个C ．6个D ．至少4个第Ⅱ卷（非选择题共100分）二、填空题：本大题共5小题，每小题5分，共25分. 把答案填在答题卡的相应位置.①19211124f π⎛⎫= ⎪⎝⎭；②若12()()f x f x =-，则12x x =-；③()f x 在区间,63ππ⎡⎤-⎢⎥⎣⎦上单调递增； ④将函数()f x的图象向右平移34π个单位可得到1cos22y x =的图象；⑤()f x 的图象关于点,04π⎛⎫- ⎪⎝⎭成中心对称．其中正确说法的序号是 .三、解答题：本大题共6小题，共75分.解答应写出文字说明，演算步骤或证明过程. 解答写在答题卡上的指定区域内. 16.（本小题满分12分）已知函数21()2cos 2f x x x --，x R ∈．（Ⅰ）求函数()f x 的最小值和最小正周期；（Ⅱ）设ABC ∆的内角A 、B 、C 的对边分别为a 、b 、c ，满足c =()0f C =且sin 2sin B A =，求a 、b 的值.17.（本小题满分12分）如图，ABCD 是边长为2的正方形，ED ⊥平面ABCD ,1ED =,EF //BD 且2EF BD =. （Ⅰ）求证：平面EAC ⊥平面BDEF ；（Ⅱ）求几何体ABCDEF 的体积.18.（本小题满分13分）数列{}n a 的前n 项和为n S ，2131(*)22n n S a n n n N +=--+∈．（Ⅰ）设n n b a n =+，证明：数列{}n b 是等比数列；（Ⅱ）求数列{}n nb 的前n 项和n T .19.（本小题满分12分）某校从参加高三模拟考试的学生中随机抽取60名学生，将其数学成绩(均为整数)分成六组[90,100)，[100,110)，…，[140,150)后得到如下部分频率分布直方图．观察图形的信息，回答下列问题．（Ⅰ）求分数在[120,130)内的频率；（Ⅱ）若在同一组数据中，将该组区间的中点值(如：组区间[100,110)的中点值为100＋1102＝105)作为这组数据的平均分，据此估计本次考试的平均分；（Ⅲ）用分层抽样的方法在分数段为[110,130)的学生中抽取一个容量为6的样本，将该样本看成一个总体，从中任取2人，求至多有1人在分数段[120,130)内的概率．20.（本小题满分13分）已知椭圆C ：()222210x y a b a b+=>>的离心率为2，左焦点为)0,2(-F .（Ⅰ）求椭圆C 的方程；（Ⅱ）若直线y x m =+与曲线C 交于不同的A 、B 两点，且线段AB 的中点M 在圆221x y += 上，求m 的值.21.（本小题满分14分）已知函数32()2f x x ax x =--+(a R ∈). （Ⅰ）当1=a 时，求函数)(x f 的极值；（Ⅱ）若对任意x R ∈，不等式4'()||3f x x ≥-恒成立，求实数a 的取值范围．黄山一中2014届高三文科数学周周练（1）答案一、选择题：本大题共10小题，每小题5分，共50分．⒈【解析】由()112i z i ⋅=-+，得111222i z i i +=-=-+，从而虚部12，选C .⒉【解析】因为3x x =，解得0,1,1x =-，显然条件表示的集合小，结论表示的集合大，由集合的包含关系，选A .⒊【解析】化简集合(){}{}{}**30031,2,3A x N x x x N x =∈-≤∈≤≤=，{}{}101B x x x x =->=>，则{}2,3A B =I ，选B ．⒋【解析】∵()λ+⊥b a c ，∴()0λ+⋅=b a c ，即0λ⋅+⋅=b c a c ，∴()3380λ++=，解得311λ=-，选D .⒌【解析】2()86f xx x '=-+.因为1a、4025a是函数321()4613f x x x x =-+-的极值点，所以1a 、4025a 是方程2860x x -+=的两实数根，则140258a a +=.而{}n a 为等差数列，所以140252013828a a a +===，即20134a =，从而22013log 2a =，选A .⒍【解析】由已知作出可行域为一个三角形区域，得到三个交点(21),(12),(45)，，，，当直线032=+y x 平移通过点(21)，时，目标函数值最小，此时21327z =⨯+⨯=. 【考点定位】本试题考查了线性规划的最优解的运用以及作图能力.⒎【解析】由图知，原几何体是两个相同圆锥底面重合的一个组合体，1R =，1h =，l =，则表面积为21S π=⨯⨯=，选B . ⒏【答案】A .⒐【解析】令红球、白球、黑球分别为12123,,,,,A B B C C C ，则从袋中任取两球有()()12,,,A B A B ，()()()123,,,,,A C A C A C ，()()()()11121312,,,,,,,B C B C B C B B ，()()()212223,,,,,B C B C B C ，()()()121323,,,,,C C C C C C 共15种取法，其中两球颜色相同有()12,B B ，()()()121323,,,,,C C C C C C 共4种取法，由古典概型及对立事件的概率公式可得41111515p =-=. ⒑【解析】∵()f x 是定义在R 上的偶函数，且周期是3，(2)0f =，∴(1)0f -=，即(1)0f =.∴520f f ==（）（），410f f ==（）（），所以方程()0f x =在()0,6内，至少有4个解，选D ．二、填空题：本大题共5小题，每小题5分，共25分.⒕【解析】令y=0得x=-1，所以直线x-y+1=0,与x 轴的交点为1,0C -（）.因为直线30x y ++=与圆C 相切，所以圆心1,0C-（）到直线的距离等于半径，即r ==C 的方程为22(1)2x y ++=. ⒖【解析】1()c o ss i n s i n 22f x x x x =⋅=.①正确，192111s i n 1212264f f πππ⎛⎫⎛⎫===⎪ ⎪⎝⎭⎝⎭；②错误：由122()()()f x f x f x =-=-，知122x x k p =-+或122()x x k k Z p p =++ ；③错误：令22222k x k ππππ-+≤≤-+，得()44k x k k Z ππππ-+≤≤+∈，由复合函数性质知()f x 在每一个闭区间(),44k k k Z ππππ⎡⎤-++∈⎢⎥⎣⎦上单调递增，但(),,6344k k k Z ππππππ⎡⎤⎡⎤-⊄-++∈⎢⎥⎢⎥⎣⎦⎣⎦，故函数()f x 在,63ππ⎡⎤-⎢⎥⎣⎦上不是单调函数；④错误：将函数()f x 的图象向右平移34π个单位可得到13131sin 2sin 2cos 224222y x x x ππ⎛⎫⎛⎫=-=-= ⎪⎪⎝⎭⎝⎭；⑤错误：函数的对称中心的横坐标满足02x k π=，解得02k x π=，即对称中心坐标为(),02k k Z π⎛⎫∈ ⎪⎝⎭，则点,04π⎛⎫- ⎪⎝⎭不是其对称中心.三、解答题：本大题共6小题，共75分.解答应写出文字说明，演算步骤或证明过程. 解答写在答题卡上的指定区域内.⒗ （本小题满分12分）【解析】（Ⅰ）1cos 21()2sin(2)12226x f x x x π+=--=--，…………3分则()f x 的最小值是2-，最小正周期是22T ππ==；…………6分（Ⅱ）()sin(2)106f C C π=--=，则sin(2)106C π--=，…………7分0C π<<,022C π<<,所以112666C πππ-<-<，所以262C ππ-=，3C π=，…………9分因为sin 2sin B A =，所以由正弦定理得2b a =，……①…………10分由余弦定理得2222cos3c a b ab π=+-，即2223c a b ab =+-=……②…………11分由①②解得：1a =，2b =．…………12分⒘ （本小题满分12分）【解析】（Ⅰ）∵ ED ⊥平面ABCD ，AC平面ABCD ，∴ ED ⊥AC ．…………2分∵ ABCD 是正方形，∴ BD ⊥AC ， …………4分 ∴ AC ⊥平面BDEF ． …………6分又AC ⊂平面EAC ，故平面EAC ⊥平面BDEF ．（Ⅱ）连结FO ，∵EFDO ，∴ 四边形EFOD 是平行四边形．由ED ⊥平面ABCD 可得ED ⊥DO ， ∴ 四边形EFOD 是矩形．…………8分方法一：∴FO ∥ED ，而ED ⊥平面ABCD ，∴ FO ⊥平面ABCD ． ∵ ABCD 是边长为2的正方形，∴OA OC ==由（Ⅰ）知，点A 、C 到平面BDEF 的距离分别是OA 、OC ，从而2111221122332A EFOD C EFOD F ABC A EFOD F ABC V V V V V V -----=++=+=⨯⨯⨯⨯⨯=；方法二：∵ 平面EAC ⊥平面BDEF ．∴ 点F 到平面ACE 的距离等于就是Rt △EFO 斜边EO 上的高，且高EF FO h OE ⋅===10分 ∴几何体ABCDEF 的体积==2．…………12分 ⒙（本小题满分12分）【解析】（Ⅰ）因为213122n n a S n n +=--+，所以 ① 当1=n 时，121-=a ，则112a =-，………………………………1分 ② 当2n ≥时，21113(1)(1)122n n a S n n --+=----+，……………………2分所以121n n a a n --=--，即12()1n n a n a n -+=+-，……………………4分所以11(2)2n n b b n -=≥，而11112b a =+=，……………………5分所以数列{}n b 是首项为12，公比为12的等比数列，所以12nn b ⎛⎫= ⎪⎝⎭．……………6分（Ⅱ）由（Ⅰ）得2n n nnb =．所以 ①n n n n n T 221..........242322211432+-+++++=-， ②1232221..........24232212--+-+++++=n n n nn T ，……………8分②-①得：n n n nT 221......2121112-++++=-，……………10分 n n n n n n T 2222211211+-=--⎪⎭⎫ ⎝⎛-=.………………12分⒚（本小题满分12分）【解析】（Ⅰ）分数在[120,130)内的频率为1(0.10.150.150.250.05)10.70.3-++++=-=；……………………2分（Ⅱ）估计平均分为950.11050.151150.151250.31350.251450.05121x =⨯+⨯+⨯⨯⨯+⨯=＋＋.…… ………5分（Ⅲ）由题意，[110,120)分数段的人数为60×0.15＝9(人)．[120,130)分数段的人数为60×0.3＝18(人)． ……………………7分 ∵用分层抽样的方法在分数段为[110,130)的学生中抽取一个容量为6的样本，∴需在[110,120)分数段内抽取2人，并分别记为m 、n ； ……………………8分在[120,130)分数段内抽取4人，并分别记为a 、b 、c 、d ； ……………………9分设“从样本中任取2人，至多有1人在分数段[120,130)内”为事件A ，则基本事件共有()m n ，，()()()()()()m a m d n a n d a b c d ⋯⋯⋯，，，，，，，，，，，，，，共15种． ………………10分则事件A 包含的基本事件有()()()()()()()()m n m a m b m c m d n a n b n c ，，，，，，，，，，，，，，，，()n d ，共9种． ……………………11分 ∴()93155P A ==. ……………………12分 ⒛（本小题满分13分）【解析】（Ⅰ）由题意得2c a =，2c =………2分解得⎩⎨⎧==222b a………4分所以椭圆C 的方程为：14822=+y x………6分（Ⅱ）设点A 、B 的坐标分别为),(11y x ，),(22y x ，线段AB 的中点为()00,M x y ，由⎪⎩⎪⎨⎧+==+m x y y x 14822，消去y 得0824322=-++m mx x ………8分 ∵29680m ∆=->，∴m -<………9分 ∴120223x x m x +==-，003my x m =+= ………10分 ∵点 ()00,M x y 在圆122=+y x 上，∴222133m m ⎛⎫⎛⎫-+= ⎪ ⎪⎝⎭⎝⎭，即m =13分21.（本小题满分14分）【解析】（Ⅰ）当1=a 时，32()2f x x x x =--+21'()3213(1)3f x x x x x ⎛⎫=--=-+ ⎪⎝⎭，………………………………………………2分令'()0f x =，解得121,13x x =-=.当'()0f x >时，得1x >或13x <-；当'()0f x <时，得113x -<<.………………………4分当x 变化时，'()f x ，()f x 的变化情况如下表：∴当13x =-时，函数()f x 有极大值，159()=327f x f ⎛⎫-=⎪⎝⎭极大； …………………………5分当1x =时，函数()f x 有极大值，()()=11f x f =极小， …………………………………6分（Ⅱ）∵2'()321f x x ax =--，∴对x R ∀∈，4()3f x x '≥-恒成立，即243213x ax x --≥-对x R ∀∈恒成立， ………………………………………………………………7分①当0x >时，有()212133a x x +≤+，即12133a x x+≤+对0x ∀>恒成立，………………9分∵1323x x +≥=，当且仅当13x =时等号成立， ∴212a +≤，解得12a ≤ ………………………………………………………………11分②当0x <时，有()211233a x x -≤+，即11233a x x -≤+对0x ∀<恒成立，…………12分∵1323x x +≥=，当且仅当13x =-时等号成立， ∴122a -≤，解得12a ≥- ………………………………………………………………13分 ③当0x =时，a R ∈.综上得实数a 的取值范围为11,22⎡⎤-⎢⎥⎣⎦. …………………………………………………………14分。

2014数学高考题型历炼(Word解析版)：1-2 平面向量、复数、程序框图及合情推理

1．(交汇新)已知向量OA →＝(1，－3)，OB →＝(2，－1)，OC →＝(k ＋1，k －2)，若A ，B ，C 三点不能构成三角形，则实数k 应满足的条件是( )A ．k ＝－2B ．k ＝12C ．k ＝1D ．k ＝－12．(背景新)已知x ，y ∈R ，i 为虚数单位，且(x －2)i －y ＝－1＋i ，则(1＋i)x ＋y 的值为( )A ．4B ．－4C ．4＋4iD ．2i3．(定义新)设向量a ＝(a 1，a 2)，b ＝(b 1，b 2)，定义一种向量运算a ⊗b ＝(a 1，a 2)⊗(b 1，b 2)＝(a 1b 1，a 2b 2)．已知m ＝⎝ ⎛⎭⎪⎫2，12，n ＝⎝ ⎛⎭⎪⎫π3，0，点P (x ，y )在y ＝sin x 的图象上运动，点Q 在y ＝f (x )的图象上运动且满足O Q →＝m ⊗OP →＋n (其中O 为坐标原点)，则y ＝f (x )的最大值为( )A ．1B ．3C ．5 D.124．(角度新)已知函数f (x )＝ax 3＋12x 2在x ＝－1处取得极大值，记g (x )＝1f ′(x ).程序框图如图所示，若输出的结果S ＞2 0112 012，则判断框中可以填入的关于n 的判断条件是( )A ．n ≤2 011?B ．n ≤2 012?C ．n ＞2 011?D ．n ＞2 012?[历炼]1．解析：若点A ，B ，C 不能构成三角形，则向量AB →，AC →共线，∵ AB →＝OB →－OA →＝(2，－1)－(1，－3)＝(1,2)，AC →＝OC →－OA →＝(k ＋1，k －2)－(1，－3)＝(k ，k ＋1)，∴ 1×(k ＋1)－2k ＝0，解得k ＝1，故选C .答案：C2．解析：由x －2＝1，y ＝1，得(1＋i )4＝(2i )2＝－4，故选B .答案：B3．解析：OP →＝(x ，y)＝(x ，sin x)，则OQ →＝⎝ ⎛⎭⎪⎫2x ，12sin x ＋⎝ ⎛⎭⎪⎫π3，0 ＝⎝ ⎛⎭⎪⎫2x ＋π3，12sin x .令Q(x 0，y 0)，则⎩⎪⎨⎪⎧ x 0＝2x ＋π3，y 0＝12sin x ，∴ y 0＝12sin ⎝ ⎛⎭⎪⎫12x 0－π6， ∴ f(x)＝12sin ⎝ ⎛⎭⎪⎫12x －π6， ∴ f(x)的最大值为12.故选D .答案：D 4．解析：由题意得f ′(x)＝3ax 2＋x ，由f ′(－1)＝0得a ＝13，∴ f ′(x)＝x 2＋x ，即g(x)＝1x 2＋x ＝1x (x ＋1)＝1x －1x ＋1. 由程序框图可知S ＝0＋g(1)＋g(2)＋…＋g(n)＝0＋1－12＋12－13＋…＋1n －1n ＋1＝1－1n ＋1＞2 0112 012，得n ＞2 011，故选B . 答案：B。

四川省成都七中2014届高三5月第一次周练数学(文)试题 Word版含答案

成都七中2014级考试数学试卷(文科)一、选择题(每小题5分,共50分,在每小题给出的四个选项中,只有一项是符合要求的.) 1.若{1,2,3,4,5,6,7}U =,{3,4,6,7},{3,5,6,7},A B ==则()U C AB =( )(A){1,2,4,5} (B){2,6,8} (C){1,3,5,7} (D){1,2} 2.若βα,表示两个不同的平面,b a ,表示两条不同的直线,则α//a 的一个充分条件是( ) (A) ββα⊥⊥a , (B)b a b //,=βα (C)α//,//b b a (D)ββα⊂a ,// 3.已知等比数列{}n a 的前n 项和215,,5n n S t n N -*=⋅-∈则实数t =( ) (A)4 (B)5 (C)45 (D)154.某几何体的三视图如图所示,则该几何体的体积为( ) (A)6(B) (C)3(D)5.若1cos23θ=,则44sin cos θθ+的值为( ) (A)59 (B)1118 (C)1318(D)16.已知0,0,228,x y x y xy >>++=则2x y +的最小值是( ) (A)3 (B)4 (C)92 (D)1127.若点(,)P x y 满足线性约束条件20220,0x y x y y -≤⎧⎪-+≥⎨⎪≥⎩则4z x y =+的最大值为( )(A)1 (B)2 (C)3 (D)48.若函数3()3f x x x a =-+有3个不同的零点,则实数a 的取值范围是( )(A)(,1)-∞- (B)[2,2]- (C)(2,2)- (D)(1,)+∞9.如图,四边形ABCD 是边长为1的正方形,延长CD 至E ,使得2DE CD =.动点P 从点A 出发,沿正方形的边按逆时针方向运动一周回到A 点, AP AB AE λμ=+.则λμ-的取值范围为( )(A)[1,1]- (B)[1,2]- (C)[2,1]- (D)[0,2]10.从1232,2,2,,2n 这n 个数中取m *(,,2)n m N m n ∈≤≤个数组成递增的等比数列,所有可能的递增等比数列的个数记为(,)n m ϕ,则(100,10)ϕ=( )(A)504 (B)505 (C)506 (D)507二、填空题(每小题5分,共25分.把答案填在题中横线上.) 11.在平面直角坐标系中,点(1,3)A ,(2,)B k -,若0OA AB ⋅=, 则实数k =12.已知12z i =+,则3z =13.阅读右面的程序框图,运行相应的程序,输出的结果为14.设A 、B 、P 是椭圆22221(0)x y a b a b+=>>上不同的三个点,且A 、B 连线经过坐标原点,若直线PA 、PB 的斜率之积为14-,则该椭圆的离心率为15.若ABC ∆的三个内角,,A B C 所对的边,,a b c 满足2a c b +=,则称该三角形为“中庸”三角形.已知ABC ∆为“中庸”三角形,给出下列结论：①1(,2)2a c ∈； ②112a c b+≥； ③3B π≥； ④若2,AB AB AC BA BC CA CB =⋅+⋅+⋅则4sin 5B =.其中正确结论的序号是 .(写出所有正确结论的序号) 三、解答题(本大题共6小题.共75分.1619-题每题12分,20题13分,21题14分,解答应写出文字说明、证明过程或演算步骤.)16.数列{}n a 满足*212(),n n n a a a n N ++=-∈数列{}n b 满足2*12(),n n n b b b n N ++=∈11221, 2.a b a b ====(1)求数列{}n a ,{}n b 的通项公式； (2)设n n n c a b =,求数列{}n c 的前n 项和n T .17.在ABC ∆中,角,,A B C 所对的边分别为,,a b c ,已知222b c a bc +=-.(1)求A 的大小； (2)如果cos B =2b =,求ABC ∆的面积．18.在如图所示的多面体中,四边形ABCD 为正方形,四边形ADPQ 是直角梯形,AD D P ⊥,CD ⊥平面ADPQ ,12AB AQ DP ==． (1)求证：PQ ⊥平面DCQ ；(2)若2AQ =,求四面体C BDQ -的体积．19.高尔顿板是英国生物统计学家高尔顿设计用来研究随机现象的模型.在一块木板上钉着若干排相互平行但相互错开的圆柱形小木块,小木块之间留有适当的空隙作为通道,前面挡有一块玻璃.让一个小球从高尔顿板上方的通道口落下,小球在下落的过程中与层层小木块碰撞,且等可能向左向右滚下,最后掉入编号为1,2,,7的球槽内.某高三同学试验1000次,掉入各球槽的个数统计如下：规定小球掉入2,4,6号球槽中的任何一个即为中奖,其余不中奖. (1)分别求,,x y z 的值. (2)假设中奖的概率为12,现有5位同学依次参加这个高尔顿板游戏,每人玩一次,求中奖不连续发生的概率.A BCD P20.已知椭圆2222:1(0)x y C a b a b +=>>的短轴长为6.若12,l l 是椭圆C 的两条相互垂直的切线,12,l l 的交点为点P .(1)求椭圆C 的方程； (2)求点P 的轨迹方程.21.已知函数2()(),()ln .ln x f x a R g x x x ax x=∈=-+ (1)当0a =时,求()f x 在(1,)+∞上的最小值；(2)若()y f x =与()y g x =的图象恰有三个不同的交点112233(,),(,),(,)A x y B x y C x y (123x x x <<).(i)求实数a 的取值范围； (ii)求证：()22123123()()()f x f x f x x x x =.成都七中2014级考试数学试卷(文科)参考答案11. 4 12. 112 i -- 13. 1 - 14. 15. ②④16.解：(1)212n n n a a a ++=-即122n n n a a a ++=+.所以数列{}n a 是首项为1,公差为1的等差数列,n a n =.212n n n b b b ++=,121,2bb ==, 所以数列{}n b 是首项为1,公比为2的等比数列,12n n b -=.…………………………………6分 (2)12n n n nc a b n -==,则01211222322n n T n -=⋅+⋅+⋅++ 12321222322n n T n =⋅+⋅+⋅++两式相减得: 0121122222n n n T n --=⋅++++-整理得(1)21n n T n =-+.……………………………………………………………………12分17.解(1)因为222b c a bc +=-,所以2221cos 222b c a bc A bc bc +--===-,又因为(0,)A π∈,所以23A π=.……………………………………………………………6分(2)因为cos B =(0,)B π∈,所以sin B ==．由正弦定理sin sin a bA B=,得sin 3sin b A a B ==．因为222b c a bc +=-,所以2250c c +-=,解得1c =-±因为0c >,所以1c ．故ABC ∆的面积1sin 2S bc A ==………………………………………………12分18.解(1)因为CD ⊥平面ADPQ ,所以CD PQ ⊥,作QE DP ⊥,E 为垂足,则四边形ADEQ 是正方形,不妨设1AB =,则1DE =,DQ =又22DP AB==,所以E是DP的中点,1EP=,所以PQ=所以222DQ PQ DP+=,所以DQ PQ⊥．故CD PQ⊥,DQ PQ⊥,又CD DQ D=,所以PQ⊥平面DCQ．………………………6分(2)因为CD⊥平面ADPQ,所以AQ CD⊥又,AQ AD⊥所以AQ⊥平面ABCD,2111422.3323C BDQ Q BCD BCDV V S AQ--∆==⋅=⨯⨯⨯=所以四面体C BDQ-的体积为43.……………………………………………………12分19.解(1)10000.234234,x=⨯=100015952342349217313,y=------=3130.3131000z==.…………………………………………5分(2)中奖的概率为12,中奖与不中奖等可能,中奖用1表示,不中奖用0表示.画树状图.(总的基本事件为5232=,没有画X的表示中奖不连续发生)记中奖不连续发生为事件A,其基本事件有13个.13()32P A=.中奖不连续发生的概率为1332. ……………………………………………………………12分20解(1)26,b=所以3,b=又e=从而2222227.16c a bea a-===2216,9.a b==所以椭圆C的方程为221169x y+=.…………………………………………………………6分(2)①若直线1l 的斜率存在且不为零时,设为k ,设00(,)P x y ,则直线1l 的方程为00()y y k x x -=-. 即00y kx y kx =+-,令00m y kx =-.22222(169)321614401169y kx m k x kmx m x y =+⎧⎪⇒+++-=⎨+=⎪⎩. 直线1l 是椭圆的切线,所以222(32)4(169)(16144)0km k m ∆=-+-=,所以22169m k =+, 坐标原点O 到直线1l的距离1d =所以22212216911m k d k k +==++. 设坐标原点O 到直线2l 的距离为2d ,同理可得222222116()9916111()k k d k k-++==++-. 所以222221222169916||2511k k OP d d k k ++=+=+=++. ②若直线1l 的斜率不存在或为零时,容易验证22212||25.OP d d =+=所以2||25.OP =点P 的轨迹是圆2225.x y +=……………………………………………13分21.解(1)2()ln x f x x =,2(2ln 1)()0(ln )x x f x x -'==,(1,), x x ∈+∞∴所以当0a =时,()f x 在(1,)+∞上的最小值为2.f e =…………………3分(2) (i)2ln (0,ln 0)ln x x x x ax x ax x=->+≠+, 分离参数得ln ln x x a x x x =--,令ln ().ln x xh x x x x =--22221ln 1ln ln (1ln )(2ln )()0(ln )(ln )x x x x x x h x x x x x x x ----'=-==--通过求导分析容易证得2ln (0)x xx x >>>,所以1x =或e .0,()x h x →→+∞,(1)1h =,()11(1)h e e e e e =-=+--,,()1x h x →+∞→. 画ln ()ln x xh x x x x=--的草图,实数a 的取值范围为1(1,1)(1)e e +-.…………………7分注意到ln 0ax x +≠,若00ln 0ax x +=,则00ln x ax =-,00000ln 1(ln 1x x a a x x x a=-=+-+矛盾).所以1(1,1)(1)a e e ∈+-时,三个不同的交点,,A B C 均使得ln 0ax x +≠成立.所以实数a 的取值范围为1(1,1)(1)e e +-.…………………………………………………9分(ii)由(i)知12301x x e x <<<<<,ln 1ln ln 1x x x a x x x x x=-=---,令ln x u x =,则11a u u=--,即2(1)10u a u a +-+-=,121210, 10u u a u u a +=-<=-<,画ln xu x=图象.不妨设12u u <,则111ln x u x =,32223ln ln x x u x x ==,()()22123123233112222123123123()()()()()()ln ln ln ()f x f x f xg x g x g x x x x x x x x x x x x x x x x ---== 22231212312123ln ln ln (1)(1)(1)(1)(1)(1)[(1)(1)]x x x u u u u u x x x =---=---=--221212[1()][1(1)(1)]1u u u u a a =-++=--+-=.………………………………………14分注：(i)也可以按(ii)的思维方式解答。

2014届高考数学一轮复习 12.4 程序框图与算法语句考点及自测理新人教A版

第4讲程序框图与算法语句【2014年高考会这样考】1．考查程序框图的理解与应用(尤其是条件结构与循环结构)．2．考查程序框图的补充与完善．对应学生197考点梳理1．程序框图的结构类型及作用(1)顺序结构①定义：由若干个依次执行的步骤组成的，这是任何一个算法都离不开的基本结构．②结构形式(2)条件结构①定义：算法的流程根据条件是否成立有不同的流向，条件结构就是处理这种过程的结构．②结构形式(3)循环结构①定义：从某处开始，按照一定的条件反复执行某些步骤的情况，这就是循环结构，反复执行的步骤称为循环体．②结构形式2．算法语句的格式与应用(1)输入语句、输出语句和赋值语句①功能：实现条件结构．②条件语句的格式及框图：a．IF－THEN格式IF 条件THEN语句体END IFb．IF－THEN－ELSE格式IF 条件THEN语句体1ELSE语句体2END IF(3)循环语句①功能：实现程序框图中的循环结构．②循环语句的格式及框图：a．UNTIL语句b．WHILE语句DO循环体WHILE 条件LOOP UNTIL 条件循环体WEND【助学·微博】一个共同点一般只有一个入口也只能在一个出口输出，每一个基本逻辑结构的每一部分都有机会被执行到，而且结构内不能有死循环．两种结构特点(1)利用循环结构表示算法，一定要先确定是用当型循环结构，还是用直到型循环结构；当型循环结构的特点是先判断再循环，直到型循环结构的特点是先执行一次循环体，再判断．(2)循环结构中，当型循环又称“前测试型”循环，直到型循环又称“后测试型”循环．三点提醒(1)确定循环变量和初始值；(2)确定算法中反复执行的部分，即循环体；(3)确定循环的终止条件．考点自测1．(2012·)执行如图所示的程序框图，输出的S值为( )．A．2 B．4 C．8 D．16解析当k＝0时，满足k<3，因此S＝1×20＝1；当k＝1时，满足k<3，因此S＝1×21＝2；当k＝2时，满足k<3，因此S＝2×22＝8；当k＝3时，不满足k<3，因此输出S＝8.答案 C2．(2012·某某)阅读右边的程序框图，运行相应的程序，当输入x的值为－25时，输出x的值为( )．A．－1 B．1C．3 D．9解析执行程序框图，x＝－25，|x|＝|－25|>1，x＝|－25|－1＝4，|4|>1，x＝|4|－1＝1,1>1不成立，∴x＝2×1＋1＝3.故选C.答案 C3．(2012·某某)如图所示，程序框图的输出结果是( )．A．3 B．4 C．5 D．8解析当x＝1，y＝1时，满足x≤4，则x＝2，y＝2；当x＝2，y＝2时，满足x≤4，则x＝2×2＝4，y＝2＋1＝3；当x＝4，y＝3时，满足x≤4，则x＝2×4＝8，y＝3＋1＝4；当x＝8，y＝4时，不满足x≤4，则输出y＝4.答案 B4．(2012·某某)下图是用模拟方法估计圆周率π值的程序框图，P表示估计结果，则图中空白框内应填入( )．A ．P ＝N 1 000B ．P ＝4N1 000C ．P ＝M 1 000D ．P ＝4M 1 000解析利用几何概型，构造一个边长为1的正方形及其内一个半径为1、圆心角为90°的扇形，易知扇形的面积S ≈M 1 000，又由面积公式得S ＝14π×12≈M 1 000，解得π≈4M 1 000，所以选D. 答案 D5．(2012·某某)若某程序框图如图所示，则该程序运行后输出的值是________．解析由程序框图可知，当T ＝1，i ＝1时，T ＝Ti＝1，i ＝2，不满足i >5；T ＝T i ＝12，i ＝3，不满足i >5；T ＝T i ＝16，i ＝4，不满足i >5；T ＝T i ＝124，i ＝5，不满足i >5；T ＝T i ＝1120，i ＝6，满足i >5；输出T ＝1120.答案1120对应学生198考向一基本逻辑结构和程序框图的运用【例1】►(2013·某某一模)若执行如图所示的框图，输入x 1＝1，x 2＝2，x 3＝3，x ＝2，则输出的数等于( )． A.13 B.23 C.23D ．1 [审题视点] 这是一个求解方差的问题，共3项，通过一个计数变量用循环结构实现这一算法．解析算法的功能是求解三个数的方差，输出的是S ＝ 1－22＋2－22＋3－223＝23. 答案 C搞清进入或退出循环的条件和功能，循环次数是做对题的关键．【训练1】 (2012·某某三模)阅读如图所示的程序框图，执行相应的程序，则输出的结果是( )．A ．2B ．－2C ．3D ．－3 解析第一次循环，n ＝1，s ＝－1，第二次循环，n ＝2，s ＝－1＋2＝1，第三次循环，n ＝3，s ＝1－3＝－2，第四次循环，n ＝4，s ＝－2＋4＝2，第五次循环，n ＝5，s ＝2－5＝－3，第六次n ＝6不满足条件，输出s ＝－3，选D.答案 D 考向二程序框图的补充与完善【例2】►如图所示的框图，当x 1＝6，x 2＝9，p ＝8.5时，x 3等于( )． A ．7 B ．8 C ．10 D ．11[审题视点] 先读懂图中的逻辑顺序，然后进行计算判断，其中判断条件|x 2－x 1|<|x 3－x 2|是否成立是利用框图知识反推出x 3的值的关键，是完善该框图的任务所在．解析 |x 1－x 2|＝3，|x 2－x 3|＝|x 3－9|，故当|x 1－x 2|＜|x 2－x 3|，即3＜|x 3－9|时，p ＝x 1＋x 22＝152，与p ＝8.5不符；当|x 1－x 2|≥|x 2－x 3|，即3≥|x 3－9|时，p ＝x 2＋x 32＝9＋x 32＝8.5，∴x 3＝8. 答案 B解答这类题目时，一定要理解、悟透各种框图的作用，才能得到正确的结果．特别注重对问题的转化，问题与框图的表示的相互转化、框图与函数的转化等等．【训练2】 (2012·东北三省联考)一个算法的程序框图如图所示，若该程序输出的结果是163，则判断框内应填入的条件是( )．A ．i <4B ．i >4C ．i <5D ．i >5解析初始值i ＝1，T ＝0，P ＝15；第一次循环后i ＝2，T ＝1，P ＝5；第二次循环后i ＝3，T ＝2，P ＝1；第三次循环后i ＝4，T ＝3，P ＝17；第四次循环后i ＝5，T ＝4，P ＝163，因此循环次数应为4次，故i <5可以作为判断循环终止的条件，故选C.答案 C 考向三算法与其他知识的交汇【例3】►(2012·新课标全国)如果执行右面的程序框图，输入正整数N (N ≥2)和实数a 1，a 2，…，a N ，输出A ，B ，则( )． A ．A ＋B 为a 1，a 2，…，a N 的和 B.A ＋B2为a 1，a 2，…，a N 的算术平均数C ．A 和B 分别是a 1，a 2，…，a N 中最大的数和最小的数D．A和B分别是a1，a2，…，a N中最小的数和最大的数[审题视点] 循环结构中满足x>A成立，则A＝x，是说将大数赋值给A；满足x<B成立，则B＝x，是说将小数赋值给B，故这个程序是找最大数A和最小数B.解析随着k的取值不同，x可以取遍实数a1，a2，…，a N，依次与A，B比较，A始终取较大的那个数，B始终取较小的那个数，直到比较完为止，故最终输出的A，B分别是这N 个数中的最大数与最小数，故选C.答案 C对框图的考查常与函数、数列、统计等结合，进一步强化框图问题的实际背景．【训练3】某篮球队6名主力队员在最近三场比赛中投进的三分球个数如下表所示：队员i 12345 6三分球个数a1a2a3a4a5a6如图是统计该6名队员在最近三场比赛中投进的三分球总数的程序框图，则图中判断框应填______，输出的S＝______.解析由题意可知，程序框图是要统计6名队员投进的三分球的总数，由程序框图的循环逻辑知识可知，判断框应填i＜7？或i≤6？，输出的结果就是6名队员投进的三分球的总数，而6名队员投进的三分球数分别为a1，a2，a3，a4，a5，a6，故输出的S＝a1＋a2＋…＋a6.答案i＜7？(i≤6？) a1＋a2＋…＋a6对应学生200热点突破28——破解程序框图中的计算【命题研究】通过近三年的高考试题分析，对程序框图的考查主要是程序框图中的计算和程序框图的完善，常与函数、数列、统计等知识结合，题型为选择题、填空题，难度不大．【真题探究】► (2012·某某)执行如图所示的程序框图，若输入n 的值为8，则输出s 的值为________．[教你审题] 逐步运行程序框图，列出输出的相关数据．解析开始时n ＝8，i ＝2，k ＝1，s ＝1.因i ＝2<8，故s ＝1×(1×2)＝2，i ＝2＋2＝4，k ＝1＋1＝2；因i ＝4<8，故s ＝12×(2×4)＝4，i ＝4＋2＝6，k ＝2＋1＝3；因i ＝6<8，故s ＝13×(4×6)＝8，i ＝6＋2＝8，k ＝3＋1＝4，退出循环．故输出的s 的值为8. 答案 8[反思] (1)运行程序框图时，未注意到条件的应用，导致多运行一次或少运行一次． (2)在循环结构中要注意两个问题，一是执行循环时有的是先判断条件再执行循环，有的是先执行循环再判断条件，二是在结束循环时也有的是条件为真结束循环，有的是条件为假结束循环．【试一试】若某程序框图如图所示，则输出的P 的值是( )．A ．21B ．26C ．30D ．55解析据框图得各次运行结果为n ＝2，P ＝1＋22＝5；n ＝3，P ＝5＋32＝14；n ＝4，P ＝14＋42＝30>20，由判断框知程序结束，故输出P ＝30. 答案 C对应学生351A 级基础演练(时间：25分钟满分：50分)一、选择题(每小题5分，共25分)1．(2012·某某)执行如图所示的程序框图，则输出的S 值是( )．A ．－1 B.23C.32D ．4解析根据程序框图，程序执行的步骤为S ＝4，i ＝1<9；S ＝－1，i ＝2<9；S ＝23，i ＝3<9；S ＝32，i ＝4<9；S ＝4，i ＝5<9；S ＝－1，i ＝6<9，所以S 的周期为4，即i ＝9时S ＝4.答案 D2．(2013·某某二次预测)如图给出的是计算12＋14＋16＋…＋120的值的一个程序框图，其中判断框内应填入的条件是( )．A ．i >10?B ．i <10?C ．i >20?D ．i <20?解析依题意，得12＋14＋16＋…＋120可表示为数列⎩⎨⎧⎭⎬⎫12n 的前10项和，结合题目中的程序框图知，判断框内应填入的条件是“i >10？”，选A. 答案 A3．(2013·某某二模)某客运部门规定甲、乙两地之间旅客托运行李的费用为：不超过25 kg 按0.5元/kg 收费，超过25 kg 的部分按0.8元/kg 收费，计算收费的程序框图如图所示，则①②处应填( )．A ．y ＝0.8xy ＝0.5xB ．y ＝0.5xy ＝0.8xC ．y ＝25×0.5＋(x －25)×0.8 y ＝0.5xD ．y ＝25×0.5＋0.8xy ＝0.8x解析设行李的重量为x kg ，则所需费用为y ＝⎩⎪⎨⎪⎧0.5x ，0<x ≤25，12.5＋0.8x －25，x >25，所以选C. 答案 C4．(2012·某某诊断)阅读如图所示的程序框图，输出的S 值为( )．A ．0B ．1＋ 2C ．1＋22D.2－1 解析程序框图的功能是计算sin π4＋sin 2π4＋sin 3π4＋sin 4π4＋sin 5π4＋sin6π4＋sin7π4＋sin 8π4＋sin 9π4＋sin 10π4＋sin 11π4的值．而sin π4＋sin 2π4＋sin 3π4＋sin 4π4＋sin 5π4＋sin 6π4＋sin 7π4＋sin 8π4＝0，sin 9π4＋sin 10π4＋sin 11π4＝1＋ 2. 答案 B5．(2013·潍坊模拟)运行右图所示的程序框图，若输出结果为137，则判断框中应该填的条件是( )．A ．k >5B ．k >6C ．k >7D ．k >8 解析据题意令S ＝1＋11×2＋12×3＋…＋1k ×k ＋1＝1＋1－12＋12－13＋…＋1k －1k ＋1＝2－1k ＋1，令S ＝2－1k ＋1＝137，解得k ＝6，故判断框应填入k >6. 答案 B二、填空题(每小题5分，共25分)6．(2012·某某)阅读如图所示的程序框图，运行相应的程序，输出的s值等于________．解析第一次循环：s＝1，k＝1<4，s＝2×1－1＝1，k＝1＋1＝2；第二次循环：k＝2<4，s＝2×1－2＝0，k＝2＋1＝3；第三次循环：k＝3<4，s＝2×0－3＝－3，k＝3＋1＝4；当k＝4时，k<4不成立，循环结束，此时s＝－3.答案－37．(2012·某某)阅读如图所示的程序框图，运行相应的程序，输出的结果s＝________.解析按算法框图循环到n＝3时输出结果．当n＝1时，s＝1，a＝3；当n＝2时，s＝1＋3＝4，a＝5；当n＝3时，s＝4＋5＝9，a＝7，所以输出s＝9.答案98．(2012·某某)如果执行如图所示的程序框图，输入x＝－1，n＝3，则输出的数S＝________.解析逐次运算的结果是S＝6×(－1)＋3＝－3，i＝1；S＝(－3)×(－1)＋2＝5，i＝0；S＝－5＋1＝－4，i＝－1，结束循环，故输出的S＝－4.答案－49．(2012·某某)下图是某算法的程序框图，则程序运行后输出的结果是________．解析由题意知，运行一次后T＝1，k＝2，运行两次后T＝1，k＝3，运行三次后T＝1，k ＝4，运行四次后T＝2，k＝5，运行五次后T＝3，k＝6，退出循环，此时T的值为3.答案 310．(2013·某某二模)在数列{a n}中，a1＝1，a n＋1＝a n＋n，要计算此数列前30项的和，现已给出了该问题算法的程序框图(如图所示)，请在图中判断框内(1)处和执行框中的(2)处填上合适的语句，使之能完成该题算法功能．(1)________________；(2)________________．解析因为是求30个数的和，故循环体应执行30次，其中i是计数变量，因此判断框内的条件就是限制计数变量i的，故应为i>30.算法中的变量p实质是表示参与求和的各个数，由于它也是变化的，且满足第i个数比其前一个数大i－1，第i＋1个数比其前一个数大i，故应有p＝p＋i.故(1)处应填i>30；(2)处应填p＝p＋i.答案(1)i>30(2)p＝p＋iB级能力突破(时间：20分钟满分：30分)一、选择题(每小题5分，共15分)1．(2012·某某)执行下面的程序框图，如果输入a＝4，那么输出的n的值为( )．A．2 B．3C．4 D．5解析当a＝4时，第一次P＝0＋40＝1，Q＝3，n＝1，第二次P＝1＋41＝5，Q＝7，n＝2，第三次P＝5＋42＝21，Q＝15，n＝3，此时P≤Q不成立，输出n＝3，选B.答案 B2．(2013·豫西五校联考)执行如图所示的程序框图，则输出的λ是( )．A．－4 B．－2 C．0 D．－2或0解析依题意，若λa＋b与b垂直，则有(λa＋b)·b＝4(λ＋4)－2(－3λ－2)＝0，解得λ＝－2；若λa＋b与b平行，则有－2(λ＋4)＝4(－3λ－2)，解得λ＝0.结合题中的程序框图，输出的λ是－2，选B.答案 B3．(2013·某某质检)按如图所示的算法框图运算，若输出k ＝2，则输入x 的取值X 围是( )．A ．19≤x <200B ．x <19C ．19<x <200D ．x ≥200解析由框图可知，输出k ＝2，需满足⎩⎪⎨⎪⎧10x ＋10<2 010，1010x ＋10＋10≥2 010，解得19≤x <200，故选A. 答案 A二、填空题(每小题5分，共15分)4．(2012·某某)右图是一个算法框图，则输出的k 的值是________．解析由k 2－5k ＋4>0得k <1或k >4，所以k ＝5. 答案 55．(2013·某某模拟)对任意非零实数a ，b ，若a ⊗b 的运算原理如下程序框图所示，则3⊗2＝________.解析∵a ＝3，b ＝2，则a >b ，∴输出a ＋1b ＝3＋12＝2. 答案 26．(2013·揭阳模拟)如图甲是某市有关部门根据对当地干部的月收入情况调查后画出的样本频率分布直方图，已知图甲中从左向右第一组的频数为 4 000.在样本中记月收入在[1 000,1 500)，[1 500,2 000)，[2 000,2 500)，[2 500,3 000)，[3 000,3 500)，[3 500,4 000]的人数依次为A 1、A 2、…、A 6.图乙是统计图甲中月工资收入在一定X 围内的人数的程序框图，则样本的容量n ＝________；图乙输出的S ＝________.(用数字作答)图甲图乙解析∵月收入在[1 000,1 500)的频率为0.000 8×500＝0.4，且有4 000人，∴样本的容量n ＝4 0000.4＝10 000，由题图乙知输出的S ＝A 2＋A 3＋…＋A 6＝10 000－4 000＝6 000. 答案 10 000 6 000。

高中数学必修三同步练习题库：算法与程序框图(填空题：一般)

算法与程序框图（填空题：一般）1、执行如图所示的程序框图，若输入的，值分别为0和9，则输出的值为__________．2、已知流程图如图，则输出的i＝________．3、（2014年苏州B6）若某程序框图如图所示，则该程序运行后输出的值是______．4、如图是一个算法流程图，则输出的的值是__________．5、下图是一个算法流程图，则输出的的值是______．6、已知一个学生的语文成绩为89，数学成绩为96，外语成绩为99．求他的总分和平均成绩的一个算法为：第一步：取A=89，B=96，C=99；第二步：；第三步：；第四步：输出计算的结果．7、写出求1+2+3+4+5+6+…+100的一个算法．可运用公式1+2+3+…+n=直接计算．第一步；第二步；第三步输出计算的结果．8、执行如图所示的程序框图，若输出，则输入的值为 .9、在如图的程序框图中，输出的值为，则， .10、根据如图所示的算法流程图，可知输出的结果S为______．11、执行如图所示的流程图，则输出的值为______．12、如图程序框图的输出结果是_________.13、如果执行下面的程序框图，那么输出的s＝______________.14、执行如图所示的程序框图,则输出的值为_______________.15、执行如图所示的程序框图，输出的________．16、运行如图所示的程序框图，输出的__________．17、我国明朝数学家程大位著的《算法统宗》里有一道闻名世界的题目：“一百馒头一百僧，大僧三个更无争，小僧三人分一个，大小和尚各几丁？”以下程序框图反映了对此题的一个求解算法，则输出的的值为________.18、如图所示的程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”．执行该程序框图，若输入的a，b分别为14,18，则输出的a＝ __________19、如图所示的程序框图（未完成），设当箭头指向①时，输出的结果，当箭头指向②时，输出的结果，则_____.20、执行如图所示的程序框图.若输出，则框图中①处可以填入条件为___________21、执行如图所示的程序框图，若输入的值为3，则输出的的值为_______________.22、如图所示的算法流程图，若输出y的值为，则输入的值为__________．23、如图所示的算法流程图，若输出y的值为，则输入x的值为__________．24、某篮球队6名主力队员在最近三场比赛中投进的三分球个数如下表所示，下图是统计该6名队员在最近三场比赛中投进的三分球总数的程序框图，则图中判断框应填________，输出的________.25、用秦九韶算法求多项式当时的值为____________.26、阅读如图的程序框图，运行相应的程序，输出的结果为__________．27、按右面的程序框图运行后,输出的应为_______．28、执行如图所示的程序框图后，输出的结果是__________．（结果用分数表示）29、如下图是一个算法的伪代码，其输出的结果为__________．30、图中的程序框图的算法思路来源于我国古代数学名著《九章算术》中的“更相减损术”，执行该程序框图，若输入的值分别为，则输出的________.31、执行如图所示的程序框图，输出的值是__________．32、已知函数，右图表示的是给定的值，求其对应的函数值的程序框图，则①处应填写________；②处应填写________．33、执行如图所示的算法框图，若输入的的值为2，则输出的的值为__________．34、下图是一个算法流程图，若输入x的值为，则输出的y的值是_____________35、如图所示，输出的的值为__________．36、如果执行下面的程序框图，那么输出的______．37、下左图是计算某年级500名学生期末考试（满分为100分）及格率的程序框图，则图中空白框内应填入___________38、执行如下图所示的程序框图，若输入的值为6，则输出的值为__________．39、（苏州2010年B8）下面是一个算法的流程图，则输出的结果是____________.40、（2011年苏州B6）如图，程序执行后输出的结果为___________．41、（2012年苏州B8）如图，程序执行后输出的结果为_________．42、（2013年苏州B6）执行下面的流程图，输出的S=43、（2015年苏州B5）如图所示，此程序框图运行后输出的值是________．44、阅读如图所示的程序框图，运行相应的程序，输出的S值为________．45、阅读如图所示的流程图，运行相应的程序，则输出n的值为______．46、执行如图所示的程序框图，当输出的值是4时，输入的整数的最大值是__________．47、图中所示的是一个算法的流程图，其表达式为__________．48、下图是一个算法流程图，则输出的的值是 .49、如图所示的流程图中，输出的为______________50、现有若干（大于20）件某种自然生长的中药材，从中随机抽取20件，其重量都精确到克，规定每件中药材重量不小于15克为优质品，如图所示的程序框图表示统计20个样本中的优质品数，其中表示每件药材的重量，则图中①，②两处依次应该填写的整数分别是________________.51、下边程序框图的算法思路源于数学名著《几何原本》中的“辗转相除法”，执行该程序框图（图中“”表示除以的余数），若输入的分别为495,135，则输出的__________．52、如图是某算法的程序框图，则程序运行后输出的结果是__________．53、执行如图所示的程序框图，则输出的结果是__________．54、执行如图所示的程序框图，若输入的，值分别为0和9，则输出的值为__________．55、《孙子算经》是中国古代重要的数学著作，约成书于四、五世纪，也就是大约一千五百年前，传本的《孙子算经》共三卷.卷中有一问题：“今有方物一束，外周一匝有三十二枚，问积几何？”该著作中提出了一种解决问题的方法：“重置二位，左位减八，余加右位，至尽虚加一，即得.”通过对该题的研究发现，若一束方物外周一匝的枚数是8的整数倍时，均可采用此方法求解.如图，是解决这类问题的程序框图，若输入，则输出的结果为__________．56、程序框图如图所示,若输入,,,则输出的为__________．57、某程序框图如图所示，若运行程序后输出为__________．58、阅读下列算法：第一步，输入x的值；第二步，若x≥0，则y＝x；第三步，否则，；第四步，输出y的值．若输入的，则输出的的取值范围是________．59、下边程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”.执行该程序框图，若输入的分别为14,20，则输出的 .60、某程序的伪代码如下图所示，则程序运行后的输出结果为．61、如图，若时，则输出的结果为 .62、当输入的实数时，执行如图所示的程序框图，则输出的不小于103的概率是__________．63、给出一个如图所示的程序框图，若要使输入的值与输出的值相等，则这样的值得个数是个．64、给出一个如图所示的程序框图，若要使输入的值与输出的值相等，则这样的值的个数是__________个．65、二进制数转换成十进制数是．66、执行如图所示的程序框图,若输入的值为,则输出的值是．67、执行如图所示的程序框图，若输入的值为2，则输出的值为．68、已知程序框图如图所示，其功能是求一个数列的前项和，则数列的一个通项公式，数列的前项和为 .69、执行如图所示的程序框图，若输入 , 则输出．70、下图是某算法的程序框图，则程序运行后输出的结果是．参考答案1、32、93、34、5、6、S=A+B+C；．7、取n=100；计算．8、.9、10、11、412、13、4614、-1015、716、72017、2518、219、2020、21、22、－23、－24、25、26、27、28、29、30、431、32、33、234、35、36、2037、38、1539、3540、6441、42、21043、44、1545、446、2347、48、49、50、14,1951、4552、53、854、355、12156、102457、58、59、260、61、62、63、64、65、66、67、68、，69、270、【解析】1、因为输入的的值分别为和 .第一次执行循环体后：，不满足条件，故；第二次执行循环体后：，不满足条件，故；第三次执行循环体后：，满足条件，故输出的值为，故答案为.【方法点睛】本题主要考查程序框图的循环结构流程图，属于中档题. 解决程序框图问题时一定注意以下几点：(1) 不要混淆处理框和输入框；(2) 注意区分程序框图是条件分支结构还是循环结构；(3) 注意区分当型循环结构和直到型循环结构；(4) 处理循环结构的问题时一定要正确控制循环次数；(5) 要注意各个框的顺序,（6）在给出程序框图求解输出结果的试题中只要按照程序框图规定的运算方法逐次计算，直到达到输出条件即可.2、根据流程图可得：，否，，；否，；否，；否，；是输出，故答案为9.3、第一次执行完循环体后，，，不满足退出循环的条件；再次执行完循环体后，，，，不满足退出循环的条件；第三次执行完循环体后，满足退出循环的条件；故输出的值为3，故答案为3.4、由题设中提供的算法流程图中的算法程序可知当时，；当时，；当时，，此时运算程序结束，输出，应填答案。

2014高中数学 1.1.2 程序框图与算法的基本逻辑结构课件(2)新人教A版必修3

开始
a 2, b 4, h 5
S 1 ( a b) h 2
输出
S
结束
(2)条件结构---在一个算法中,经常会遇到一些条件的判断,算法的流向根据条件是否成立有不同的流向.条件结构就是处理这种过程的结构. 两种常见形式：
否满足条件？是
步骤A
满足条件？
否
是
步骤B
步骤A
特征：两个步骤A，B根据条件选择一个执行
特征：根据条件选择是否执行步骤A
例题剖析1
任意给定3个正实数,设计一个算法,判断分别以这3 个数为三边边长的三角形是否存在.画出这个算法的程序框图. 算法步骤: 第一步:输入3个正实数a,b,c; 第二步:判断a+b>c,a+c>b,b+c>a是否同时成立,若是,则能组成三角形;若否,则组不成三角形.
程序框图:
x 800 0. 8 x , f ( x) 0.9 x, 500 x 800 x, x 500
否是
开始输入x x≥800?
是
否 y=x
x≥500?
y=0.8x y=0.9x 输出y
结束
归纳小结
本节课学习的主要内容： 3.基本逻辑结构：（1）顺序结构：由若干个依次执行的处理步骤组成的.这是任何一个算法都离不开的基本结构。 (2)条件结构---算法的流向根据条件是否成立有不同的流向.
温故知新
1.程序框图的定义:又称流程图,是一种用规定的图形、指向线及文字说明来准确、直观地表示算法的图形. 2.基本程序框图及其功能； 3.基本逻辑结构：（1）顺序结构：由若干个依次执行的处理步骤组成的. 这是任何一个算法都离不开的基本结构。

高三数学程序框图4

最便于初学者掌握。
常用流程图符号
终端框
输入输出框
表示一个算法的起始和结束
表示一个算法输入和输出的信息赋值、计算
处理框
判断框
判断某一条件是否成立，成立时在出口处标明“是”或“Y”；不成立时标明“否”或“N”.
表示流程的路径和方向
流程线
三种基本结构（表示一个良好算法的基本单元） ③循环结构 ①顺序结构 ②条件结构（选择结构）
二、算法的表示
比较自然语言与程序框图表示方法的各自特点
1. 用自然语言表示优点是使用日常用语, 通俗易懂缺点是文字冗长, 容易出现歧义 2. 用程序框图表示: 用图框表示各种操作优点是直观形象, 易于理解
程序框图
程序框图（也称为流程图）是最常用的一
种表示法，它是描述计算机一步一步完成任
务的图表，直观地描述程序执行的控制流程，
While（当型）循环 Until（直到型）循环
③循环结构
A
A P
成立不成立
P
不成立
成立
例3 设计一个计算1+2+3+……+100的值的算法，并画出程序框图。算法分析：需要一个累加变量和一个计数变量，将累加变量的初始值设为0，计数变量的值可以从1到100. 开始
i=1 sum=0 i<=100?
输入a、b、c
a+b>c,a+c>b, b+c>a是否同时成立是存在这样的三角形否
不存在这样的三角形
结束
在一些算法中，从否处开始，按照一定条件，反复执行某一处理步骤的情况，这就是循环结构。反复执行的处理步骤称为循环体。在循环结构中，通常都有一个起到循环计数作用的变量，这个变量的取值一般都含在执行或中止循环体的条件中。

四川省成都七中2014届高三4月第二次周练数学(文)试题

成都七中2014级高三数学测试题（文科）一、选择题（每小题5分，共50分）1.若复数z ，满足：12z z i +=+，则z 的虚部为（） A. 2i B. 1 C. 2 D. i2.设全集U 是实数集R ，{}234M x x x =-≥，13log (2)0N x x ⎧⎫=+≥⎨⎬⎩⎭，则M N ⋂=( )A.32x x ⎧⎫≤-⎨⎬⎩⎭B. {}1x x ≤- C. 312x x ⎧⎫-≤≤-⎨⎬⎩⎭ D. 322x x ⎧⎫-<≤-⎨⎬⎩⎭ 3. 设a R ∈，则“2a =-”是“直线l 1：1:210l ax y +-=与2:(1)20l x a y +++= 直线l 2：x ＋(a ＋1)y ＋4＝0平行”的( )A ．充分不必要条件B ．必要不充分条件C ．充分必要条件D ．既不充分也不必要条件4. 阅读如图所示的程序框图，运行相应的程序，输出的结果k =( ) A.4 B.5 C.6 D.75. 设a 、b 是两条不同的直线，α、β是两个不同的平面，则下列命题正确的是（） A ．若//,//,a b a α则//b αB ．若,//,a αβα⊥则a β⊥C ．若,,a αββ⊥⊥则//a αD ．若,,,a b a b αβ⊥⊥⊥则α⊥6. 已知双曲线22221 (,0)x y a b a b-=>的一条渐近线与圆8)322=+-y x （相交于N M ,两点，且4=MN ，则此双曲线的离心率为（）A B C D ．57. 一个空间几何体的三视图如图所示，则该几何体的表面积为( )A ．48B ．48+8C ．D ．808. 已知锐角βα,满足： 51cos sin =-ββ，3tan tan 3tan tan =⋅++βαβα，则cos α=（）ABCD9.用分期付款方式（贷款的月利率为1%）购买总价为25万元的汽车,购买当天首付15万元,此后可采用以下方式支付贷款:以后每月的这一天都支付相同数目的还款,20个月还完,则每月应还款约（）元（201.01 1.22≈）A ．5545B ．5546C ．5547D ．554810. 已知函数()x f y =是定义在R 上的增函数，函数()1-=x f y 的图象关于点()0,1对称。

【推荐下载】数学2014年高三必修同步训练程序框图

5
[键入文字]
比较频率趋势与概率，可得乙同学所编程序符合算法要求的可能性较大. (3)随机变量ξ可能的取值为 0,1,2,3. P(ξ=0)=C03 乘以 130233=827， P(ξ=1)=C13 乘以 131 乘以 232=49， P(ξ=2)=C23 乘以 132 乘以 231=29， P(ξ=3)=C33 乘以 133 乘以 230=127，故ξ的分布列为 ξ0123 P827 49 29 127 所以 Eξ=0 乘以 827+1 乘以 49+2 乘以 29+3 乘以 127=1.
3
[键入文字]
2 1001 027376697 乙的频数统计表(部分) 运行次数 n 输出 y 为 1 的频数的值输出 y 的值为 2 的频数输出 y 的值为 3 的频数 3012117 2 1001 051696353 当 n=2 100 时，根据表中的数据，分别写出甲、乙所编程序各自输出 y 的值为

[键入文字]
解析：输入ε=0.25 后，程序执行如下： ①ε=0.25，F0=1，F1=2，n=1，②F1=F0+F1=3，F0=F1-F0=2，n=2， 1F1=130.25， ③F1=F0+F1=5，F0=F1-F0=3，n=3，1F1=15≤0.25，此时输出的 n 的值为 3. 答案：3 4.(理科)(2013•四川)某算法的程序框图如图所示，其中输入的变量 x 在 1,2,3，， 24 这 24 个整数中等可能随机产生. (1)分别求出按程序框图正确编程运行时输出 y 的值为 i 的概率 Pi(i=1,2,3); (2)甲、乙两同学依据自己对程序框图的理解，各自编写程序重复运行 n 次后，统计记录了输出 y 的值为 i(i=1,2,3)的频数.以下是甲、乙所作频数统计表的部分数据. 甲的频数统计表(部分) 运行次数 n 输出 y 的值为 1 的频数输出 y 的值为 2 的频数输出 y 的值为 3 的频数 3014610