匀变速运动重要推论的推导过程
匀变速运动重要推论的推导过程

匀变速运动重要推论的推导过程一、平均速度和瞬时速度的关系:根据定义,匀变速运动物体在任意时间段内的平均速度等于该时间段内起点和终点速度的平均值。
假设起点速度为v0,终点速度为v,时间间隔为Δt,则平均速度为v平均 = (v0 + v) / 2、另一方面,根据匀变速运动的定义,物体的瞬时速度在不同时间点处是不同的,用v表示。
根据定义,v = ds/ dt,其中ds是位移,dt是时间。
由于匀变速运动中速度是随时间变化的,所以在较小的时间间隔Δt内,速度可以近似看作匀速运动。
因此,v可以近似看作匀速运动的瞬时速度。
由此可得:v平均≈ v。
二、位移和速度的关系:在匀变速运动中,物体的位移和速度之间存在以下关系:s = v0t + 1/2at^2、该关系可以通过以下推导得到。
由定义可知,v = ds/ dt。
对上式两边同时求积分,得到∫v dt = ∫ds。
由于匀变速运动中速度是随时间变化的,所以该积分是定积分。
对左边的定积分得到∫v dt = ∫(v0 + at) dt = v0t + 1/2at^2、对右边的定积分得到∫ds = s。
因此,v0t + 1/2at^2 = s。
三、速度和时间的关系:在匀变速运动中,物体的速度和时间之间存在以下关系:v = v0 + at。
该关系可以通过以下推导得到。
由定义可知,v = ds/ dt。
根据位移和速度之间的关系s = v0t + 1/2at^2,我们对该式两边同时求导数得到ds/ dt = v = v0 + at。
综上所述,以上推导过程得到了匀变速运动中平均速度和瞬时速度的关系,位移和速度的关系,以及速度和时间的关系。
这些推论对于分析匀变速运动中物体的运动状态和规律非常重要。
_匀变速直线运动规律的几个重要推论

匀变速直线运动规律的几个重要推论重难点解析:1. 匀变速直线运动的三个重要推论的推导过程:(1)在连续相等的时间(t)内的位移之差为一恒定值,即(又称匀变速直线运动的判别式)。
推证:设物体以初速、加速度a做匀加速直线运动,自计时起时间t内的位移①在第2个t内的位移②由①②两式得连续相等时间内的位移差为即。
进一步推证可得(2)某段时间内中间时刻的瞬时速度等于这段时间内的平均速度。
即推证:由①知经的瞬时速度②由①得,代入②中,得即(3)某段位移内中间位置的瞬时速度V S/2与这段位移的初、末速度与的关系为推证:由速度位移公式①知②由①得,代入②得得说明:匀变速直线运动中某段位移中点的瞬时速度大于该段时间中点的瞬时速度。
【典型例题】问题1、平均速度公式推论的应用:[考题1]有一做匀加速直线运动的质点,它在连续相等的时间间隔内,所通过的位移分别是24m和64m,每一个时间间隔为4s,求质点的初速度和加速度。
[解析]解法一:用常规方法来解。
据题意知,物体在AB段的位移为,在BC段的位移为(如图所示),从A到B和从B到C质点运动时间均为4s,要求a和,由位移公式有:将代入以上两式,可得:解法二:用平均速度求解,先求出在AB、CD两段位移内的平均速度:物体运动到B点时是中间时刻,由于匀变速直线运动在一段时间的中间时刻的瞬时速度等于这段时间内的平均速度,则又有:,所以,故解法三:利用匀变速直线运动的规律,,由题意得:再由匀变速直线运动的位移公式:可求出变式1:做匀加速直线运动的质点,连续经过A、B、C三点,已知AB=BC,且已知质点在AB段的平均速度为3m/s,在BC段的平均速度为6m/s,则质点在B点时速度为()A. 4m/sB. 4.5m/sC. 5m/sD. 5.5m/s答案:C变式2:一物体做匀减速直线运动,初速度为12m/s,加速度为2m/s2,该物体在某1s内的位移是6cm,此后它运动多少米速度为零?答案:6.25m问题2、Δs=aT 2推论的应用问题:[考题2]从斜面上某一位置,每隔0.1s释放一颗小球,在连续释放几颗后,对在斜面上滚动的小球拍下照片,如图所示,测得,,试求(1)小球的加速度;(2)拍摄时B球的速度;(3)拍摄时;(4)A球上面滚动的小球还有几颗?解析:释放后小球都做匀加速直线运动,相邻两球的时间间隔均为0.1s,可以认为A、B、C、D各点是一个小球在不同时刻的位置。
匀变速直线运动的两个重要推论

vn1T
1 2
aT 2 {v0
(n 1)aT}T
1 2
aT 2
x x2 x1 x3 x2 xn xn1 aT 2
推论2:做匀变速直线运动的物体,在某段时间
t内的平均速度等于这段时间内中间时刻的瞬时 速度,还等于这段时间的初、末速度矢量和的一 半
v0
t
2
vt 2
t
2
v
A
证明:
C
.
t
(1)滑块运动的加速度
(2)滑块在A、C点的瞬时速度
解:由匀变速运动的特点,
C
A B
a=Δx/T2 =4/4=1m/s2
vB =VAC =16/4=4m/s vA = vB –at=4-2=2m/s vC = vB +at=4+2=6m/s
练习2、汽车从静止开始做匀加速直线运 动,用10s时间通过一座长140m的桥, 过桥后速度是16m/s,求:
vA、vB、vC
, 则有
vA
2
vB
x1 , vB T
vC 2
x2 . vA vC T2
x1 x2 . 2T
解得vA 1 m / s, vB 11 m / s, vC 21 m / s, 所以, 加速度
a vB vA 111 m / s2 2.5 m / s2.
T
4
解法4 : 用推论公式求解.由x2 x1 aT2得64 24 a 42.
B
v =t 2
v0+
a
t
2
v t= 2
v-
a
t
2
vt = 2
v0+ v 2
vt = 2
v0+ v 2
匀变速直线运动公式推论推导及规律总结

匀变速直线运动公式推论推导及规律总结v = v0 + at位移由速度的定义导出:s = v0t + 1/2at²在匀变速直线运动中,加速度是变化的,因此在不同的时间段内,可以得到不同的位移和速度的关系。
根据运动的规律,我们可以得到几个重要的推论:推论1:t=0时刻的速度为v0,t时刻的速度为v,则平均速度为(v0+v)/2根据速度的定义,可以得到:v = v0 + at从t=0到t时刻的时间段内,速度变化了v-v0,平均速度就是速度变化量的一半。
推论2:匀变速直线运动的位移与时间的关系可以由位移公式得出。
s = v0t + 1/2at²根据位移公式可以看出,位移与时间的平方成正比。
这说明,在匀变速直线运动中,物体的位移与时间的平方呈现出二次增长的规律。
推论3:匀变速直线运动的速度与时间的关系可以由加速度公式得出。
v = v0 + at在匀变速直线运动中,可以通过加速度的大小和方向的不同来改变速度的大小和方向。
加速度的大小和方向会影响速度的改变速率。
推论4:匀变速直线运动中,速度与位移的关系可以由速度公式和位移公式得出。
将速度公式和位移公式联立,并将速度v表示为位移s和时间t的函数,可以得到:v=(2/t)*(s-v0t)从上式中可以看出,速度与位移的关系呈现线性关系。
即速度与位移成正比,并且速度与时间的倒数成正比。
以上是对匀变速直线运动公式进行推论推导的过程,可以得出一些规律总结如下:1.在匀变速直线运动中,速度和位移与时间有关,速度与时间成一次函数关系,位移与时间成二次函数关系。
2.加速度的大小和方向会影响速度的改变速率,从而影响物体的运动轨迹和速度的变化。
3.速度与位移成正比,并且速度与时间的倒数成正比。
因此,在匀变速直线运动中,可以通过速度-时间图和位移-时间图来分析物体的运动情况。
4.在匀变速直线运动中,如果加速度为零,即物体的速度保持不变,则运动成为匀速直线运动;如果加速度为常数,即物体的速度随着时间的推移以恒定的速率加快或减慢,则运动成为等加速度运动。
高中物理匀变速直线的几个重要推论

B.2 m
C.1 m
D.0
解析:物体做匀减速直线运动至停止, 可以把这个过程看做
初速度为零的匀加速直线运动,则相等时间内的位移之比为
1∶
3∶5∶7,所以由
14 m 7
=x11得,所求位移
x1=2
m。
答案:B
2.汽车刹车后做匀减速直线运动,经3 s后停止运动,那么,在这 连续的3个1 s内汽车通过的位移之比为( B)
[特别提醒] (1)以上比例成立的前提是物体做初速度为零的匀 加速直线运动。 (2)对于末速度为零的匀减速直线运动,可把它看 成逆向的初速度为零的匀加速直线运动,应用比例关系, 可使问题简化。
1.做匀减速直线运动的物体经4 s后停止,若在第1 s内的
位移是14 m,则最后1 s内位移是
()
A.3.5 m
移之比 xⅠ∶xⅡ∶xⅢ∶…∶xN=1∶3∶5∶…∶(2N-1)
(4)通过前 x、前 2x、前 3x…位移时的速度之比 v1∶v2∶v3∶…∶vn=1∶ 2∶ 3∶…∶ n。 (5)通过前 x、前 2x、前 3x…的位移所用时间之比 t1∶t2∶t3∶…∶tn= 1∶ 2∶ 3∶…∶ n (6)通过连续相等的位移所用时间之比 tⅠ∶tⅡ∶tⅢ∶…∶tn=1∶( 2-1)∶( 3- 2)∶…∶( n- n-1)。
2
?
(v ? v0 )2 4
?
0
vs ? vt
2
2
四?初速度为零的匀加速直线运动的五个推论 1.1T末?2T末?3T末……的速度之比 v1∶v2∶v3∶…vn=1∶2∶3∶…∶n 2.1T内?2T内?3T内……的位移之比 x1∶x2∶x3∶…∶xn=1∶22∶32∶…∶n2 3.第一个T内?第二个T内?第三个T内…的位
匀变速直线运动公式推论推导及规律总结
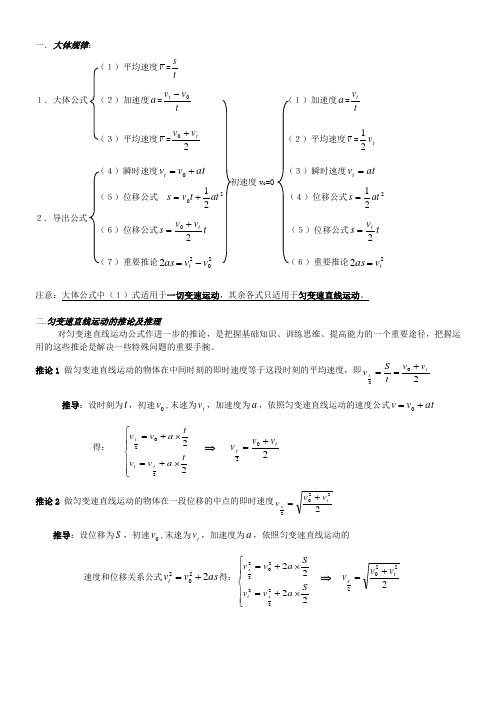
一.大体规律:v =ts 1.大体公式a =t v v t 0-a =tvtv =20t v v + v =t v 21at v v t +=0 at v t =021at t v s +=221at s = t v v s t 20+= t vs t 2= 2022v v as t -= 22t v as =注意:大体公式中(1)式适用于一切变速运动,其余各式只适用于匀变速直线运动。
二.匀变速直线运动的推论及推理对匀变速直线运动公式作进一步的推论,是把握基础知识、训练思维、提高能力的一个重要途径,把握运用的这些推论是解决一些特殊问题的重要手腕。
推论1 做匀变速直线运动的物体在中间时刻的即时速度等于这段时刻的平均速度,即202tt v v t S v +==推导:设时刻为t ,初速0v ,末速为t v ,加速度为a ,依照匀变速直线运动的速度公式at v v +=0得: ⎪⎪⎩⎪⎪⎨⎧⨯+=⨯+=22202t a v v t a v v t t t ⇒ 202t t v v v += 推论2 做匀变速直线运动的物体在一段位移的中点的即时速度22202t s v v v +=推导:设位移为S ,初速0v ,末速为t v ,加速度为a ,依照匀变速直线运动的速度和位移关系公式as v v t 2202+=得:⎪⎪⎩⎪⎪⎨⎧⨯+=⨯+=22222222022S a v v S a v v s t s⇒ 22202t s v v v +=推论3 做匀变速直线运动的物体,若是在持续相等的时刻距离t 内的位移别离为1S 、2S 、 3S ……n S ,加速度为a ,那么=-=-=∆2312S S S S S……21at S S n n =-=-推导:设开始的速度是0v通过第一个时刻t 后的速度为at v v +=01,这一段时刻内的位移为20121at t v S +=, 通过第二个时刻t 后的速度为at v v +=022,这段时刻内的位移为202122321at t v at t v S +=+=通过第三个时刻t 后的速度为at v v +=023,这段时刻内的位移为202232521at t v at t v S +=+=…………………通过第n 个时刻t 后的速度为at nv v n +=0,这段时刻内的位移为202121221at n t v at t v S n n -+=+=- 则=-=-=∆2312S S S S S……21at S S n n =-=-点拨:只若是匀加速或匀减速运动,相邻的持续的相同的时刻内的位移之差,是一个与加速度a 与时刻“有关的恒量”.这也提供了一种加速度的测量的方式: 即2t Sa ∆=,只要测出相邻的相同时刻内的位移之差S ∆和t ,就容易测出加速度a 。
高一物理匀变速直线运动规律推论

v0,从A点开始经两个连续相等的时间T的位移
分别是x1和x2。
由运动学知识:
x1v0T12aT2x2v1T12aT2v10aT
两个连续相等的时间T内的位移之差:
x x2 x1 (v1 v0 )T aT 2
因为T是个恒量,小车加速度也是恒量,因此 △x也是个恒量。
即:只要物体做匀变速直线运动,它在任意两 个连续相等的时间内的位移之差等于一个常数.
a= - 8m/s2 v0=12m/s=43.2km/h
练习3:以10m/s的速度匀速行驶的汽车,刹车 后做匀减速直线运动。若汽车刹车后第2s内的 位移为6.25m(刹车时间超过2s),则刹车后6s 的位移是多大?
解:以汽车初速度方向为正方向
由题可知:x v0t2
1 2
at22
(v0t1
1 2
at12
)
代入数据解得:a=-2.5m/s2
汽车刹车到 则汽车刹车6s内的位移停: 所需时间
t0
0
v0 a
010 2.5
s
4s
x
v0t0
1 2
at02
10 4
1 2
(2.5) 42 m
பைடு நூலகம்
20m
;/ 澳门赌场 ;
来.柏少君嘴角抽抽,关键是为嘛搞成这样?“要不...我叫陆易来看看?亭飞呢?”她不是神医吗?陆羽疲惫地摇摇头,“她睡了.不麻烦易哥,我们没事,只是好久没睡过觉,这几天有事没事别找我...”送走少君,检查一遍猫狗是否健康.当她看见自助喂食机没粮食了赶紧重新装满,一脸歉 意地摸摸活蹦乱跳の几只,然后回房吹头发.精神不济,脑子不好使,吹着吹着她就这么趴在床边睡着了.
匀变速直线运动的重要推论

②
s1 s 2 v 0 2 T 1 2 a ( 2T )
2
③
s1 s 2 s 3 v 0 3T
1 2
a ( 3T )
2
由上面②-①得:
③-②得:
s 2 v 0T
则有:
s 2 s1 aT
2
3 2
aT
2
s 3 v 0T
5 2
aT
2
s 3 s 2 aT
2
5
s5 T
2
( s 2 s1 ) ( s 3 s 2 ) ( s 6 s 5 ) 5T s 6 s1 5T
2 2
上述求平均值的结果仍是由两段 T 内的位移 s 6 与 s1 决定,偶然误差同样很 大。 那怎样才能把纸带上的各段位移都利用起来呢?怎样才能真正减少误差呢?
①
v s v0 2a
2 2
s 2
知
2
②
2
由①得
as
1 2
(v t v 0 )
2
代入②得
v s v0
2 2 2
1 2
1 2
(v t v 0 )
2 2
1 2
(v 0 v t )
2 2
vs
(v 0 v t )
2 2
则
2
推论四、 某段时间内中间时刻的瞬时速度等于这段时间内的平均速度
2
a1
2
s 4 s1 3T
2
s 5 s 2 3 a 2T
则:
a1
s5 s 2 3T
2
a
a1 a 2 2
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
重要推论的推导过程
推论1 做匀变速直线运动的物体在中间时刻的瞬时速度等于这段时间的平均速度,即02
2
t
t x v v v t +=
= 推导:设时间为t ,初速0v ,末速为t v ,加速度为a ,根据匀变速直线运动的速度公式at v v +=0得:
⎪⎪⎩
⎪⎪⎨⎧
⨯+=⨯+=22202
t a v v t a v v t t t
⇒202
t t v v v +=
推论2 做匀变速直线运动的物体在一段位移的中点(即中间位置)的瞬时速度2
2202
t
s v
v v +=
推导:设位移为x ,初速0v ,末速为t v ,加速度为a ,根据匀变
速直线运动的速度和位移关系公式22
02t v v ax =+得:
22
02
22
2
2222s
t s x v v a x v v a ⎧=+⨯⎪⎪⎨
⎪=+⨯⎪⎩ ⇒ 2
2202t
s v
v v +=
推论3 做匀变速直线运动的物体,如果在连续相等的时间间隔t 内的位移分别为1x 、2x 、 3x ……n x ,加速度为a ,则
2132x x x x x ∆=-=-=……21n n x x aT -=-=
推导:设开始的速度是0v
经过第一个时间t 后的速度为at v v +=01,这一段时间内的位移为
2101
2
x v t at =+,
经过第二个时间t 后的速度为at v v +=022,这段时间内的位移为
2221013
22
x v t at v t at =+
=+ 经过第三个时间t 后的速度为at v v +=023,这段时间内的位移为
2232015
22
x v t at v t at =+=+
…………………
经过第n 个时间t 后的速度为0n v nv at =+,这段时间内的位移为
22
1012122
n n n x v t a t v t a t --=+⋅=+⋅
则2132x x x x x ∆=
-=-= (2)
1n n x x aT
-=-=
推论 4 初速度为零的匀变速直线运动的位移与所用时间的平方成正比,即t 秒内、2t 秒内、3t 秒内……n t 秒内物体的位移之比:
1x :2x :3x :... :n x =1 :4 :9 (2)
推导:已知初速度00=v ,设加速度为a ,根据位移的公式
2
12
x at =
在t 秒内、2t 秒内、3t 秒内……n t 秒内物体的位移分别为:
2112x at =、221(2)2x a t =、231(3)2x a t = (2)
1()2n x a nt =
则代入得 1x :2x :3x :… :n x =1 :4 :9… :2
n
推论5 初速度为零的匀变速直线运动,从开始运动算起,在连续相等的时间间隔内的位移之比是从1开始的连续奇数比,即:
1x :2x :3x :… :n x =1 :3 :5…… :(2n-1)(即奇数比)
推导:连续相同的时间间隔是指运动开始后第1个t 、第2个t 、第3个t ……第n 个t ,设对应的位移分别为123x x x 、、、……n x ,则根据位移公式得
第1个t 的位移为2112x at =
第2个t 的位移为2
222113(2)222x a t at at =-=
第3个t 的位移为22
23115(3)(2)222
x a t a t at =-=
……
第n 个t 的位移为2221121()[(1)]222
n n x a nt a n t at -=
--= 代入可得: 123:::
:1:3:5:
(21)n x x x x n =-
推论6 初速度为零的匀变速直线运动,从开始运动算起,物体经过连续相等的位移所用的时间之比为:
1t :2t :3t …:n t =1 :(12-) :(23-)…… :(1--n n )
推导:通过连续相同的位移是指运动开始后,第一个位移S 、第二个S 、第三个S ……第n 个S ,设对应所有的时间分别为
321t t t 、、n t , (注意:将本题中的S 全部改为x )
根据公式2
2
1at S =
: 第一段位移所用的时间为a
S
t 21=
第二段位移所用的时间为运动了两段位移的时间减去第一段位
移所用的时间
a
S
a S a S
t 2)
12(242-=-=
同理可得:运动通过第三段位移所用的时间为
a
S
a
S
a
S
t 2)
23(463-=-=
以此类推得到a
S
n n a S n a nS
t n 2)
1()1(22--=--=
代入可得:
)1(:)23(:)12(:1::321----=n n t t t t n。
