高中必修2数学:3.2 《直线的方程》同步测试
高中数学第三章直线与方程3.2.2直线的两点式方程练习(含解析)新人教A版必修2

第23课时 直线的两点式方程直线的两点式方程A .2 B .-3 C .-27 D .27 答案 D解析 由两点式得直线方程为y -65-6=x +32+3,即x +5y -27=0.令y =0,得x =27.2.已知点P(3,m)在过点M(2,-1)和N(-3,4)的直线上,则m 的值是( ) A .5 B .2 C .-2 D .-6 答案 C解析 由两点式方程,得 直线MN 的方程为y --4--=x -2-3-2,化简,得x +y -1=0. 又点P(3,m)在此直线上,代入得3+m -1=0,解得m =-2.直线的截距式方程A .x 2-y 3=1 B .x 2+y3=1 C .y 3-x 2=1 D .x 2+y3=0 答案 A解析 根据截距式方程x a +yb=1,(其中a ,b 分别为x 轴和y 轴上的截距)得所求直线方程为x 2+y -3=1,即x 2-y3=1,选A .4.过点(5,2),且在y 轴上的截距是在x 轴上截距的2倍的直线方程是( ) A .x 6+y 12=1 B .x 6+y 12=1或y =25x C .x -y 2=1 D .x -y 2=1或y =25x答案 B解析 当直线过原点时满足题意,所求方程为y =25x ;当直线不过原点时,可设其截距式为x a +y 2a =1,由该直线过点(5,2),解得a =6,对应的方程为x 6+y12=1.故选B .直线方程的应用形各边所在的直线方程.解 由题意可知A(-4,0),C(4,0),B(0,-3),D(0,3),由截距式方程可知直线AB 的方程为x -4+y-3=1,即3x +4y +12=0.同理可得直线BC 的方程为3x -4y -12=0, 直线CD 的方程为3x +4y -12=0, 直线AD 的方程为3x -4y +12=0.6.已知线段BC 的中点为D3,32.若线段BC 所在直线在两坐标轴上的截距之和是9,求BC 所在直线的方程.解 由已知得直线BC 的斜率存在且不为0.设直线BC 在x 轴上的截距为a ,在y 轴上的截距为b .则直线BC 的截距式方程为x a +yb =1.由题意得a +b =9, ① 又点D3,32在直线BC 上,∴3a +32b =1,∴6b+3a =2ab , ② 由①②联立得2a 2-21a +54=0,即(2a -9)(a -6)=0,解得a =92或a =6.∴⎩⎪⎨⎪⎧a =92,b =92或⎩⎪⎨⎪⎧a =6,b =3.故直线BC 的方程为2x 9+2y 9=1或x 6+y3=1,即2x +2y -9=0或x +2y -6=0.一、选择题1.有关直线方程的两点式,有如下说法:①直线方程的两点式适用于求与两坐标轴不垂直的直线方程; ②直线方程y -y 1y 2-y 1=x -x 1x 2-x 1也可写成y -y 2y 1-y 2=x -x 2x 1-x 2;③过点P 1(x 1,y 1),P 2(x 2,y 2)的直线可以表示成(x 2-x 1)(y -y 1)=(y 2-y 1)(x -x 1). 其中正确说法的个数为( ) A .0 B .1 C .2 D .3 答案 D解析 ①正确,从两点式方程的形式看,只要x 1≠x 2,y 1≠y 2,就可以用两点式来求解直线的方程.②正确,方程y -y 1y 2-y 1=x -x 1x 2-x 1与y -y 2y 1-y 2=x -x 2x 1-x 2的形式有异,但实质相同,均表示过点(x 1,y 1)和(x 2,y 2)的直线.③显然正确.2.若直线x a +yb =1过第一、二、三象限,则( )A .a>0,b>0B .a>0,b<0C .a<0,b>0D .a<0,b<0 答案 C解析 因为直线过第一、二、三象限,所以结合图形可知a <0,b >0.3.一条光线从A ⎝ ⎛⎭⎪⎫-12,0处射到点B(0,1)后被y 轴反射,则反射光线所在直线的方程为( )A .y =2x +1B .y =-2x +1C .y =12x -12D .y =-12x -12答案 B解析 由光的反射定律可得,点A ⎝ ⎛⎭⎪⎫-12,0关于y 轴的对称点M ⎝ ⎛⎭⎪⎫12,0在反射光线所在的直线上.再由点B(0,1)也在反射光线所在的直线上,用两点式可求得反射光线所在的直线的方程为y -01-0=x -120-12,即y =-2x +1.4.过点P(2,3),并且在两坐标轴上的截距互为相反数的直线l 的方程是( ) A .x -y +1=0B .x -y +1=0或3x -2y =0C .x +y -5=0D .x +y -5=0或3x -2y =0 答案 B解析 若直线l 过原点,则方程为y =32x ,即3x -2y =0;若直线l 不过原点,则设直线方程为x a -ya =1,将(2,3)代入方程,得a =-1,故直线l 的方程为x -y +1=0.所以直线l的方程为3x -2y =0或x -y +1=0.5.若直线过点(1,1)且与两坐标轴所围成的三角形的面积为2,则这样的直线有( ) A .1条 B .2条 C .3条 D .4条 答案 C解析 设直线的方程为x a +yb=1,∵直线经过点(1,1),且与两坐标轴所围成的三角形的面积为2,∴1a +1b =1,12|ab|=2,解得⎩⎪⎨⎪⎧a =2,b =2或⎩⎨⎧a =-22-2,b =22-2或⎩⎨⎧a =22-2,b =-22-2.∴满足条件的直线有3条.二、填空题6.直线l 与两直线y =1,x -y -7=0分别交于P ,Q 两点,线段PQ 的中点是(1,-1),则l 的斜率是________.答案 -23解析 设P(m ,1),由线段PQ 的中点是(1,-1),得Q(2-m ,-3),∴2-m -(-3)-7=0,∴m=-2,∴P(-2,1),∴直线l 的斜率k =1---2-1=-23.7.已知直线l 经过点A(-4,-2),且点A 是直线l 被两坐标轴截得的线段中点,则直线l 的方程为________.答案 x +2y +8=0解析 设直线l 与两坐标轴的交点为(a ,0),(0,b),由题意知a +02=-4,b +02=-2,∴a=-8,b =-4.∴直线l 的方程为x -8+y-4=1,即x +2y +8=0.8.已知A(1,-2),B(5,6),经过线段AB 的中点M ,且在两坐标轴上的截距相等的直线方程为________.答案 2x -3y =0或x +y -5=0解析 点A(1,-2),B(5,6)的中点M 的坐标为(3,2).当直线过原点时,方程为y =23x ,即2x -3y =0;当直线不过原点时,设直线的方程为x +y =m ,把中点M 的坐标(3,2)代入直线的方程,得m =5,故所求直线的方程是x +y -5=0.综上,所求的直线方程为2x -3y =0或x +y -5=0.三、解答题9.已知△ABC 中,A(1,-4),B(6,6),C(-2,0).求:(1)△ABC 中平行于BC 边的中位线所在直线的方程并化为截距式方程; (2)BC 边的中线所在直线的方程并化为截距式方程.解 (1)平行于BC 边的中位线就是AB 、AC 中点的连线.因为线段AB ,AC 中点坐标为⎝ ⎛⎭⎪⎫72,1,⎝ ⎛⎭⎪⎫-12,-2, 所以这条直线的方程为y +21+2=x +1272+12,整理得,6x -8y -13=0,化为截距式方程为x 136+y-138=1.(2)因为BC 边上的中点为(2,3),所以BC 边上的中线所在直线的方程为y +43+4=x -12-1,即7x -y -11=0,化为截距式方程为x 117+y-11=1.10.已知直线l :x m +y4-m=1.(1)若直线l 的斜率等于2,求实数m 的值;(2)若直线l 分别与x 轴、y 轴的正半轴交于A ,B 两点,O 是坐标原点,求△AOB 面积的最大值及此时直线l 的方程.解 (1)直线l 过点(m ,0),(0,4-m), 则k =4-m -m =2,则m =-4.(2)由m >0,4-m >0,得0<m <4, 则S =-2=--2+42,易知当m =2时,S 有最大值2, 此时直线l 的方程为x +y -2=0.。
数学:3.2.3《直线的方程》测试(新人教A版必修2)

直线的方程学习目标:1.明确直线方程一般式的形式特征.2.会根据直线方程的一般式求斜率和截距.3.会把直线方程的点斜式、两点式化为一般式.2、已知直线:0l ax by c ++= 且0,0ab bc <<,则l 不通过的象限是第__ _象限3、求过点(4,-3)且在两坐标轴上截距的绝对值相等的直线的方程。
二、自学,记下重点,并提出问题。
三、提问与答疑四、课堂练习: P 46练习1、2、3补充例题:1、求过点(2,-1),倾斜角是直线4340x y -+=倾斜角的一半的直线方程。
2、直线Ax +By +C =0通过第二、三、四象限,则系数A 、B 、C 需满足条件( )A.A 、B 、C 同号B.AC <0,BC <0C.C =0,AB <0D.A =0,BC <0五、作业布置:★1、求过点P (0,1)且和点A (3,3)B (5,-1)距离相等的直线方程。
3、直线方程Ax +By +C =0的系数A 、B 、C 满足什么关系时,这条直线有以下性质?(1)与两条坐标轴都相交; (2)只与x 轴相交;(3)只与y 轴相交; (4)是x 轴所在的直线;(5)是y 轴所在的直线。
4、证明:三点A(1,3)、B(5,7)、C(10,12)在同一条直线上.5、设点P(x 0,y 0)在直线A+By+C=0上,求证:这条直线的方程可以写成A(x-x 0)+B(y-y 0)=0.★ ★6、直线l 的方程为14)()32(22-=-+-+m y m m x m m①当m=________时,直线l 的倾斜角为045;②当m=________时,直线l 在x 轴的截距为1;③当m=________时,直线l 在y 轴的截距为23-; ④当m=________时,直线l 与x 轴平行;⑤当m=________时,直线l 与y 轴平行;7、设直线l 的方程为y m m x m m )12()32(22-++-- 062=+-m ,试根据下列条件,分别求出m 的值:(1)l 在x 轴上的截距为3-; (2)l 的斜率为1。
人教A版高中数学必修二3.2.3直线方程的一般式 同步训练 (II)卷

人教A版高中数学必修二3.2.3直线方程的一般式同步训练(II)卷姓名:________ 班级:________ 成绩:________一、单选题 (共11题;共22分)1. (2分)已知点A(1,3)、B(-2,-1).若过点P(2,1)的直线l与线段AB相交,则直线l的斜率k的取值范围是()A .B .C . 或D .2. (2分)过两点A(4,y)、B(2,-3)的直线的倾斜角是45°,则y等于()A . -1B . -5C . 1D . 53. (2分)若直线2x+my=2m﹣4与直线mx+2y=m﹣2平行,则m的值为()A . m=﹣2B . m=±2C . m=0D . m=24. (2分)若直线经过点A(m2,0),B(2, ),且倾斜角为60°,则实数m=()B . 2或-2C . 1或-2D . -1或25. (2分)两直线与的位置关系是()A . 相交B . 平行C . 重合D . 平行或重合6. (2分) (2019高二上·兴宁期中) 与直线:平行的直线,在轴上的截距是,则在轴上的截距为()A .B .C .D .7. (2分)直线2x+y+m=0和x+2y+n=0的位置关系是()A . 平行B . 垂直C . 相交但不垂直D . 不能确定8. (2分)过点(-1,3)且平行于直线x-2y+3=0的直线方程为()B . x-2y-5=0C . x-2y+7=0D . 2x+y-5=09. (2分) (2018高二上·南昌期中) 若直线与平行,则的值为()A . -3B . 1C . 0或-D . 1或-310. (2分)过点且在两坐标轴上截距的绝对值相等的直线有()A . 1条B . 2条C . 3条D . 4条11. (2分) (2018高二上·慈溪期中) 若直线过第一、三、四象限,则实数满足()A .B .C .D .二、填空题 (共2题;共2分)12. (1分) (2017高一下·南通期中) 经过点(4,﹣3)且在y轴上截距为2的直线的方程为________.13. (1分)若方程(2m2+m-3)x+(m2-m)y-4m+1=0表示一条直线,则实数m的取值范围是________.三、解答题 (共2题;共15分)14. (10分) (2017高一下·中山期末) 已知:以点为圆心的圆与x轴交于点O,A,与y轴交于点O、B,其中O为原点,(1)求证:△OAB的面积为定值;(2)设直线y=﹣2x+4与圆C交于点M,N,若OM=ON,求圆C的方程.15. (5分) (2018高一上·阜城月考) 已知直线l的斜率与直线3x-2y=6的斜率相等,且直线l在x轴上的截距比在y轴上的截距大1,求直线l的方程.参考答案一、单选题 (共11题;共22分)1-1、2-1、3-1、4-1、5-1、6-1、7-1、8-1、9-1、10-1、11-1、二、填空题 (共2题;共2分)12-1、13-1、三、解答题 (共2题;共15分)14-1、14-2、15-1、。
高中数学人教版必修2 3.2.2直线的两点式方程 作业(系列四)

直线的两点式方程一、选择题(每小题6分,共30分)1.在x轴,y轴上的截距为3,-4的直线方程为()A.y-2=2(x-1)B.y=43x-4C.y2x13(1)12--=---D.x y43+=12.直线l在x轴上的截距为2,且斜率为1,则直线l在y轴上的截距为()A.2B.-2C.2或-2D.以上都不正确3.两条直线x y1m n-=与x y1n m-=的图象是下图中的()4.设全集I={(x,y)|x∈R,y∈R},M={(x,y)|y3x2--=1},N={(x,y)|y≠x+1},则M与N的并集的补集为()A.∅B.{(2,3)}C.(2,3)D.{(x,y)|y=x+1}5.△ABC的三个顶点是A(0,3),B(3,3),C(2,0),直线l:x=a将△ABC分割成面积相等的两部分,则a的值是()二、填空题(每小题8分,共24分)6.(2013·苏州高一检测)过点(2,-3),在两坐标轴上的截距互为相反数的直线方程为.7.过点A(a,0),B(0,b)及C(1,3)三点且a,b均为正整数的直线方程为.8.直线y=12x+k与两坐标轴所围成的三角形面积不大于1,那么k的范围是.三、解答题(9题,10题14分,11题18分)9.(2013·金华高一检测)已知△ABC中,A(4,2),B(1,8),C(-1,8).(1)求AB 边上的高所在的直线方程.(2)直线l ∥AB,与AC,BC 依次交于E,F,S △CEF ∶S △ABC =1∶4,求l 所在的直线方程. 10.求分别满足下列条件的直线l 的方程: (1)斜率是34,且与两坐标轴围成的三角形的面积是6. (2)经过两点A(1,0),B(m,1).11.(能力挑战题)为了绿化城市,拟在矩形区域ABCD 内建一个矩形草坪,另外△AEF 内部有一文物保护区不能占用,经测量AB=100m,BC=80m,AE=30m,AF=20m,应如何设计才能使草坪面积最大?答案解析1.【解析】选B.因为直线在x 轴,y 轴上的截距为3,-4,所以由直线的截距式得方程为x y 134+=-,即y=43x-4,故选B.2.【解析】选B.因为直线的斜率为1,所以直线在x 轴,y 轴上的截距互为相反数,又因为直线l 在x 轴上的截距为2,所以直线l 在y 轴上的截距为-2.【变式训练】若直线y=43x-4被两坐标轴截得的线段长为1c ,则c 的值为( ) A.1 B.15 C.±15D.±1【解析】选B.由直线的方程y=x-4,可得直线与两坐标轴的交点分别为(3,0),(0,-4),因为直线被两坐标轴截得的线段长为,则=,即c=,故选B.3.【解析】选B.由x y 1m n -=得y=n m x-n,由x y 1n m -=得y=mnx-m,即两直线的斜率k 1,k 2同号且互为倒数. 4.【解析】选B.集合M={(x,y)|y 3x 2--=1}={(x,y)|y=x+1,x≠2},又因为N={(x,y)|y≠x+1},所以M ∪N={(x,y)|x ≠2,y≠3},所以M 与N 的并集的补集为 {(2,3)}.5.【解析】选A.如图,由图可知0<a<3,S △ABC =12×3×3=92,若a<2,则x=a 与AC交于(a,3-32a),所以12×32a 2=94,所以若a>2,则x=a 与BC 交于(a,3a-6),所以12×(3-a)×(9-3a)= 94,所以与a>2矛盾,舍去,故选A. 6.【解析】当直线过原点时,设直线方程为y=kx,把点(2,-3)代入得k=32-,所以所求直线的方程为y=32-x;当直线不过原点时,因为在两坐标轴上的截距互为相反数,设直线的方程为x y1a a+=-,把点(2,-3)代入得231a a -+=-,所以a=5,所以所求直线的方程为x y 155+=-,整理得y=x-5. 答案:y=32-x 和y=x-5【举一反三】若将“在两坐标轴上的截距互为相反数”改为“在两坐标轴上的截距相等”,则直线方程为 .【解析】当直线过原点时,设直线方程为y=kx,把点(2,-3)代入得k=32-,所以所求直线的方程为y=32-x;当直线不过原点时,因为在两坐标轴上的截距相等,设直线的方程为x y a a +=1,把点(2,-3)代入得23a a-+=1,所以a=-1,所以所求直线的方程为x y11+--=1,整理得y=-x-1.答案:y=32-x 和y=-x-17.【解析】因为直线过A(a,0),B(0,b)和C(1,3),所以k AB =k BC ,即0b b 3a 001--=--,整理得3a+b=ab,又a,b 均为正整数,所以a=2,b=6或a=4,b=4.所以由两点式可得所求直线的方程为y=-x+4或y=-3x+6. 答案:y=-x+4或y=-3x+68.【解题指南】根据直线在两坐标轴上的截距,利用k 表示出直线y=12x+k 与两坐标轴所围成的三角形面积,从而得出关于k 的不等式,解得k 的取值范围.【解析】令x=0,得y=k,令y=0,得x=-2k,所以三角形的面积S=12|xy|=k 2.因为S≤1,即k 2≤1,所以-1≤k≤1,又因为k=0时不合题意,所以-1≤k≤1,且k≠0. 答案:-1≤k≤1,且k≠09.【解析】(1)由A(4,2),B(1,8),可知k AB =8214--=-2,所以AB 边上的高所在的直线的斜率k=12,又所求直线过C(-1,8),所以由直线的点斜式方程,可知AB 边上的高所在的直线方程为y=117x 22+. (2)因为S △CEF ∶S △ABC =1∶4,所以E,F 分别是AC,BC 的中点,所以E,F 的坐标分别为(3,52),(0,8),由直线方程的两点式,可得直线EF 的方程为y=-2x+8. 10.【解析】(1)设直线l 的方程为y=34x+b.令y=0, 得x=34-b,所以12|b·(34-b)|=6,b=±3.所以直线l 的方程为y=34x±3. (2)当m≠1时,直线l 的方程是y 0x 110m 1--=--,即y=1m 1-(x-1),当m=1时,直线l 的方程是x=1. 【方法锦囊】两点式方程的注意事项两点式方程的使用范围是不能表示平行或重合于坐标轴的直线,但其变形形式(y 2-y 1)(x-x 1)-(x 2-x 1)(y-y 1)=0可以表示过点(x 1,y 1),(x 2,y 2)的所有直线,因此在已知两点求经过两点的直线方程时,可直接利用上式写出方程,也可通过分类讨论的思想分类求解含参数的直线方程,最后总结.11.【解题指南】求出点E,F 的坐标,利用直线方程的两点式,写出直线EF 的方程,在线段EF 上取点P(m,n),利用点P 的坐标表示出草坪的面积,从而得出答案. 【解析】如图建立坐标系,则E(30,0),F(0,20),所以线段EF 所在的直线方程为x y3020+=1(0≤x≤30),在线段EF 上取点P(m,n),作PQ ⊥BC 于点Q,做PR ⊥CD 于点R,设矩形PQCR 的面积为S,则S=|PQ|·|PR|=(100-m)·(80-n),又因为m n3020+=1(0≤x≤30),所以n=20(m 130-), 所以S=(100-m)(28020m 3-+) =23-(m-5)2+18 0503(0≤m≤30), 于是当m=5,即|EP |5|PF |1=时,草坪面积最大.关闭Word 文档返回原板块。
《必修2》第三章“直线与方程”测试题(含答案)

《必修2》第三章“直线与方程”测试题(含答案)《必修2》第三章“直线与方程”测试题一.选择题:1. 在同一直角坐标系中,表示直线y ax =与y x a =+正确的是( )x y O x y O x y O xyOA B C D2.若直线20x ay ++=和2310x y ++=互相垂直,则a =( )A .32-B .32C .23- D .23 3.过11(,)x y 和22(,)x y 两点的直线的方程是( )111121212112211211211211...()()()()0.()()()()0y y x x y y x x A B y y x x y y x x C y y x x x x y y D x x x x y y y y ----==---------=-----=4.直线2350x y +-=关于直线y x =对称的直线方程为( ) A 、3x+2y-5=0 B 、2x-3y-5=0C 、3x+2y+5=0D 、3x-2y-5=05 如果直线l 沿x 轴负方向平移3个单位再沿y 轴正方向平移1个单位后,又回到原来的位置,那么直线l 的斜率是( )23-二.填空题:11. 过点(1,2)且在两坐标轴上的截距相等的直线的方程方程1=+y x 表示的图形所围成的封闭区域的面积为_________13 点(,)P x y 在直线40x y +-=上,则22xy +的最小值是________14 直线10x y -+=上一点P 的横坐标是3,若该直线绕点P 逆时针旋转090得直线l ,则直线l 的方程是15 已知直线,32:1+=x y l若2l 与1l 关于y 轴对称,则2l 的方程为__________;23y x =-+三、解答题16.求过点(5,4)A --的直线l ,使它与两坐标轴相交且与两轴所围成的三角形面积为517. 一直线被两直线0653:,064:21=--=++y x l y x l 截得线段的中点是P 点,当P 点为(0,0)时,求此直线方程18.直线313y x =-+和x 轴,y 轴分别交于点,A B ,在线段AB为边在第一象限内作等边△ABC ,如果在第一象限内有一点1(,)2P m 使得△ABP 和△ABC 的面积相等, 求m 的值19.已知三角形ABC的顶点坐标为A(-1,5)、B (-2,-1)、C(4,3),M是BC边上的中点。
人教A版高中数学必修二3.2.3直线方程的一般式 同步训练 (I)卷

人教A版高中数学必修二3.2.3直线方程的一般式同步训练(I)卷姓名:________ 班级:________ 成绩:________一、单选题 (共11题;共22分)1. (2分)设点P(-4,2),Q(6,-4),R(12,6),S(2,12),则下面四个结论:①PQ∥SR;②PQ⊥PS;③PS∥QS;④RP⊥QS.正确的个数是()A . 1B . 2C . 3D . 42. (2分)设点,直线l过点P(1,1)且与线段AB相交,则l的斜率k的取值范围是()A . 或B .C .D . 或3. (2分)已知直线l经过点P(2,1),且与直线2x﹣y+2=0平行,那么直线l的方程是()A . 2x﹣y﹣3=0B . x+2y﹣4=0C . 2x﹣y﹣4=0D . x﹣2y﹣4=04. (2分)若过两点A(4,y)、B(2,-3)的直线的倾斜角为45°,则y等于()A .B .C . -1D . 15. (2分) (2019高二下·深圳月考) 曲线在处的切线平行于直线,则点的坐标为()A .B .C . 和D . 和6. (2分)直线 + =1在y轴上的截距是()A . |b|B . -b2C . b2D . ±b7. (2分) (2017高二下·嘉兴期末) 在直角坐标系中,直线的倾斜角是()A .B .C .D .8. (2分) (2017高一下·鸡西期末) 过点且平行于直线的直线方程为()A .B .C .D .9. (2分) (2016高二上·怀仁期中) 已知直线l1:x+2ay﹣1=0,l2:(a+1)x﹣ay=0,若l1∥l2 ,则实数a的值为()A .B . 0C . 或0D . 210. (2分)过点且在两坐标轴上截距的绝对值相等的直线有()A . 1条B . 2条C . 3条D . 4条11. (2分)(2019·黄冈模拟) 过点的直线在两坐标轴上的截距相等,则该直线方程为A .B .C . 或D . 或二、填空题 (共2题;共2分)12. (1分) (2018高一上·兰州期末) 经过点,且在轴上的截距等于在轴上的截距的2倍的直线的方程是________.13. (1分)若方程(2m2+m-3)x+(m2-m)y-4m+1=0表示一条直线,则实数m的取值范围是________.三、解答题 (共2题;共20分)14. (10分)已知△ABC中,A(1,-4),B(6,6),C(-2,0).求:(1)△ABC中平行于BC边的中位线所在直线的一般式方程和截距式方程;(2) BC边的中线所在直线的一般式方程,并化为截距式方程.15. (10分) (2018高一下·包头期末) 求满足下列条件的直线的方程:(1)直线经过点,并且它的倾斜角等于直线的倾斜角的2倍,求直线的方程;(2)直线过点,并且在轴上的截距是轴上截距的,求直线的方程.参考答案一、单选题 (共11题;共22分)1-1、2-1、3-1、4-1、5-1、6-1、7-1、8-1、9-1、10-1、11-1、二、填空题 (共2题;共2分)12-1、13-1、三、解答题 (共2题;共20分)14-1、14-2、15-1、15-2、。
人教A版高中数学必修二 3.2.2 直线的两点式方程 检测(教师版)
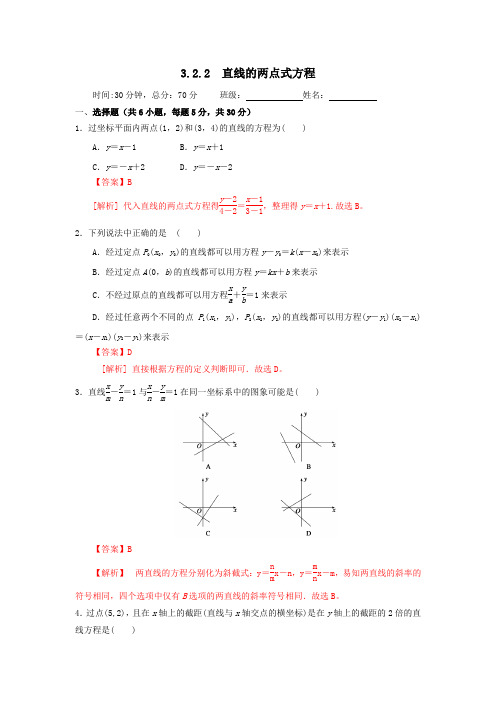
3.2.2 直线的两点式方程时间:30分钟,总分:70分 班级: 姓名:一、选择题(共6小题,每题5分,共30分)1.过坐标平面内两点(1,2)和(3,4)的直线的方程为( )A .y =x -1B .y =x +1C .y =-x +2D .y =-x -2【答案】B[解析] 代入直线的两点式方程得y -24-2=x -13-1,整理得y =x +1.故选B 。
2.下列说法中正确的是 ( )A .经过定点P 0(x 0,y 0)的直线都可以用方程y -y 0=k (x -x 0)来表示B .经过定点A (0,b )的直线都可以用方程y =kx +b 来表示C .不经过原点的直线都可以用方程x a +y b =1来表示D .经过任意两个不同的点P 1(x 1,y 1),P 2(x 2,y 2)的直线都可以用方程(y -y 1)(x 2-x 1)=(x -x 1)(y 2-y 1)来表示【答案】D[解析] 直接根据方程的定义判断即可.故选D 。
3.直线x m -y n =1与x n -y m=1在同一坐标系中的图象可能是( )【答案】B【解析】 两直线的方程分别化为斜截式:y =n m x -n ,y =m nx -m ,易知两直线的斜率的符号相同,四个选项中仅有B 选项的两直线的斜率符号相同.故选B 。
4.过点(5,2),且在x 轴上的截距(直线与x 轴交点的横坐标)是在y 轴上的截距的2倍的直线方程是( )A .2x +y -12=0B .2x +y -12=0或2x -5y =0C .x -2y -1=0D .x +2y -9=0或2x -5y =0【答案】D【解析】当y 轴上截距b =0时,方程设为y =kx ,将(5,2)代入得,y =25x ,即2x -5y =0;当b ≠0时,方程设为x 2b +y b =1,求得b =92,∴选D . 5.过点P (1,3)且在x 轴上的截距和在y 轴上的截距相等的直线方程为( )A .x +y -4=0B .3x -y =0C .x +y -4=0或3x +y =0D .x +y -4=0或3x -y =0【答案】D[解析] 若直线过原点,则设直线方程为y =kx ,把点P (1,3)代入得k =3,此时直线方程为y =3x ,即3x -y =0.若直线不经过原点,则设直线方程为x a +y a =1,即x +y =a ,把点P (1,3)代入得a =4,所以直线方程为x +y =4,即x +y -4=0,所以选D.6.若直线l 经过A (2,1),B (1,-m 2)(m ∈R )两点,则直线l 的倾斜角α的取值范围是( )A .0≤α≤π4 B.π2<α<π C.π4≤α<π2 D.π2<α≤3π4【答案】C [解析] 因为直线l 的斜率k =tan α=1+m 22-1=m 2+1≥1,所以π4≤α<π2. b ≠0时,方程设为x 2b +y b =1,求得b =92,∴选D . 二、填空题(共4小题,每题5分,共20分)7、已知点A (1,2),B (3,1),则线段AB 的垂直平分线的点斜式方式为______________.【答案】y -32=2(x -2) 【解析】 k AB =-12,由k ·k AB =-1得k =2,AB 的中点坐标为⎝ ⎛⎭⎪⎫2,32,点斜式方程为y -32=2(x -2). 8.过点P (6,-2),且在x 轴上的截距比在y 轴上的截距大1的直线方程是________________.【答案】x 3+y 2=1或x 2+y =1 【解析】设直线方程的截距式为x a +1+y a =1,则6a +1+-2a=1,解得a =2或a =1,则直线的方程是x 2+1+y 2=1或x 1+1+y 1=1,即x 3+y 2=1或x 2+y =1. 9、已知直线l 过原点且平分▱ABCD 的面积,若平行四边形的两个顶点分别为B (1,4),D (5,0),则直线l 的方程为________.【答案】y =23x [解析] 若直线l 平分平行四边形ABCD 的面积,则直线l 过BD 的中点(3,2),又因为直线l 过原点,所以直线l 的方程为y =23x . 10.若直线l 在x 轴上的截距比在y 轴上的截距大1,且过定点A (6,-2),则直线l 的方程为________.【答案】x 2+y =1或x 3+y 2=1 [解析] 设直线l 在y 轴上的截距为a (a ≠0),则在x 轴上的截距为a +1.则l 的方程为x a +1+y a =1,代入点A (6,-2)得6a +1-2a=1,即a 2-3a +2=0, ∴a =2或a =1,∴直线l 的方程为x 2+y =1或x 3+y 2=1. 三、解答题(共2小题,每题10分,共20分)11、已知直线l 的斜率为6,且被两坐标轴所截得的线段长为37,求直线l 的方程. 解 方法一 设所求直线l 的方程为y =kx +b .∵k =6,∴方程为y =6x +b .令x =0,∴y =b ,与y 轴的交点为(0,b);令y =0,∴x =-b 6,与x 轴的交点为⎝ ⎛⎭⎪⎫-b 6,0. 根据勾股定理得⎝ ⎛⎭⎪⎫-b 62+b 2=37, ∴b =±6.因此直线l 的方程为y =6x ±6.方法二 设所求直线为x a +y b=1,则与x 轴、y 轴的交点分别为(a,0)、(0,b).由勾股定理知a 2+b 2=37.又k =-b a =6,∴⎩⎪⎨⎪⎧ a 2+b 2=37,-b a=6. 解此方程组可得⎩⎪⎨⎪⎧ a =1,b =-6或⎩⎪⎨⎪⎧ a =-1,b =6.因此所求直线l 的方程为x +y -6=1或-x +y 6=1. 12.设直线l 的方程为(a +1)x +y +2-a =0(a ∈R ).(1)若l 在两坐标轴上的截距相等,求l 的方程;(2)若l 不经过第二象限,求实数a 的取值范围.解:(1)令x =0,得y =a -2,令y =0,得x =a -2a +1(a ≠-1). ∵l 在两坐标轴上的截距相等,∴a -2=a -2a +1,解之,得a =2或a =0, ∴所求的直线l 方程为3x +y =0或x +y +2=0.(2)直线l 的方程可化为y =-(a +1)x +a -2,∵l 不过第二象限, ∴⎩⎪⎨⎪⎧-(a +1)≥0,a -2≤0.∴a ≤-1,∴a 的取值范围为(-∞,-1].。
高中数学人教版必修2 3.2.2直线的两点式方程 作业2

3.2.2 直线的两点式方程一、选择题1.直线x 2-y5=1在x 轴、y 轴上的截距分别为( )A .2,5B .2,-5C .-2,-5D .-2,5[答案] B[解析] 将x 2-y 5=1化成直线截距式的标准形式为x 2+y-5=1,故直线x 2-y5=1在x 轴、y 轴上的截距分别为2,-5.2.如右图所示,直线l 的截距式方程是x a +yb=1,则有( )A .a >0,b >0B .a >0,b <0C .a <0,b >0D .a <0,b <0[答案] B[解析] 很明显M (a,0),N (0,b ),由图知M 在x 轴正半轴上,N 在y 轴负半轴上,则a >0,b <0.3.在y 轴上的截距是-3,且经过A (2,-1),B (6,1)中点的直线方程为( ) A .x 4+y3=1B .x 4-y 3=1C .x 3+y4=1D .x 3-y 6=1[答案] B[解析] A (2,-1),B (6,1)的中点坐标为(4,0),即直线在x 轴上的截距为4,则直线的截距式方程为x 4-y3=1.4.过(x 1,y 1)和(x 2,y 2)两点的直线方程是( ) A .y -y 1y 2-y 1=x -x 1x 2-x 1B .y -y 1y 2-y 1=x -x 2x 1-x 2C .(y 2-y 1)(x -x 1)-(x 2-x 1)(y -y 1)=0D .(x 2-x 1)(x -x 1)-(y 2-y 1)(y -y 1)=0[答案] C5.已知△ABC 三顶点A (1,2),B (3,6),C (5,2),M 为AB 中点,N 为AC 中点,则中位线MN 所在直线方程为( ) A .2x +y -8=0 B .2x -y +8=0 C .2x +y -12=0 D .2x -y -12=0 [答案] A[解析] 点M 的坐标为(2,4),点N 的坐标为(3,2),由两点式方程得y -24-2=x -32-3,即2x +y -8=0.6.过两点(-1,1)和(3,9)的直线在x 轴上的截距为( ) A .-32B .-23C .25D .2[答案] A[解析] 直线方程为y -91-9=x -3-1-3,化为截距式为x -32+y 3=1,则在x 轴上的截距为-32.二、填空题7.已知点P (-1,2m -1)在经过M (2,-1),N (-3,4)两点的直线上,则m =_________. [答案]32[解析] 方法1:MN 的直线方程为:y +14+1=x -2-3-2,即x +y -1=0,代入P (-1,2m -1)得m =32.方法2:M 、N 、P 三点共线, ∴4-2m -1-3+1=4--1-3-2,解得m =32.8.过点(0,3),且在两坐标轴上截距之和等于5的直线方程是_________. [答案] 3x +2y -6=0[解析] 设直线方程为x a +yb =1,则⎩⎨⎧b =3,a +b =5,解得a =2,b =3,则直线方程为x 2+y3=1,即3x +2y -6=0.三、解答题9.已知点A (-1,2),B (3,4),线段AB 的中点为M ,求过点M 且平行于直线x 4-y2=1的直线l 的方程.[解析] 由题意得M (1,3),直线x 4-y 2=1的方程化为斜截式为y =12x -2,其斜率为12,所以直线l 的斜率为12.所以直线l 的方程是y -3=12(x -1),即x -2y +5=0.10.求分别满足下列条件的直线l 的方程:(1)斜率是34,且与两坐标轴围成的三角形的面积是6;(2)经过两点A (1,0),B (m,1);(3)经过点(4,-3),且在两坐标轴上的截距的绝对值相等.[分析] 欲求直线的方程,关键是根据已知条件选择一种最合适的形式. [解析](1)设直线l 的方程为y =34x +b .令y =0,得x =-43b ,∴12|b ·(-43b )|=6,b =±3. ∴直线l 的方程为y =43x ±3.(2)当m ≠1时,直线l 的方程是 y -01-0=x -1m -1,即y =1m -1(x -1)当m =1时,直线l 的方程是x =1. (3)设l 在x 轴、y 轴上的截距分别为a 、b . 当a ≠0,b ≠0时,l 的方程为x a +yb =1;∵直线过P (4,-3),∴4a -3b =1.又∵|a |=|b |,∴⎩⎪⎨⎪⎧4a -3b =1,a =±b .解得⎩⎨⎧ a =1,b =1或⎩⎨⎧a =7,b =-7.当a =b =0时,直线过原点且过(4,-3), ∴l 的方程为y =-34x .综上所述,直线l 的方程为x +y =1或x 7+y -7=1或y =-34x .[点评] 明确直线方程的几种特殊形式的应用条件,如(2)中m 的分类,再如(3)中,直线在两坐标轴上的截距相等包括截距都为零的情况.能力提升一、选择题1.如果直线l 过(-1,-1),(2,5)两点,点(1 008,b )在直线l 上,那么b 的值为( ) A .2 014 B .2 015 C .2 016 D .2 017[答案] D[解析] 根据三点共线,得5--12--1=b -51 008-2,得b =2 017.2.两直线x m -y n =1与x n -ym=1的图像可能是图中的哪一个( )[答案] B3.已知2x 1-3y 1=4,2x 2-3y 2=4,则过点A (x 1,y 1),B (x 2,y 2)的直线l 的方程是( ) A .2x -3y =4 B .2x -3y =0 C .3x -2y =4 D .3x -2y =0[答案] A[解析] ∵(x 1,y 1)满足方程2x 1-3y 1=4,则(x 1,y 1)在直线2x -3y =4上.同理(x 2,y 2)也在直线2x -3y =4上.由两点决定一条直线,故过点A (x 1,y 1),B (x 2,y 2)的直线l 的方程是2x -3y =4.[点评] 利用直线的截距式求直线的方程时,需要考虑截距是否为零. 4.过P (4,-3)且在坐标轴上截距相等的直线有( ) A .1条 B .2条 C .3条 D .4条 [答案] B[解析] 解法一:设直线方程为y +3=k (x -4)(k ≠0). 令y =0得x =3+4kk ,令x =0得y =-4k -3.由题意,3+4k k =-4k -3,解得k =-34或k =-1.因而所求直线有两条,∴应选B .解法二:当直线过原点时显然符合条件,当直线不过原点时,设直线在坐标轴上截距为(a,0),(0,a ),a ≠0,则直线方程为x a +ya =1,把点P (4,-3)的坐标代入方程得a =1.∴所求直线有两条,∴应选B .二、填空题5.直线l 过点P (-1,2),分别与x ,y 轴交于A ,B 两点,若P 为线段AB 的中点,则直线l 的方程为_________. [答案] 2x -y +4=0[解析] 设A (x,0),B (0,y ).由P (-1,2)为AB 的中点,∴⎩⎪⎨⎪⎧x +02=-1,0+y2=2,∴⎩⎨⎧x =-2,y =4由截距式得l 的方程为x -2+y4=1,即2x -y +4=0. 6.若直线l 的方程为2x -13y =-1,则它的截距式方程为_________,斜截式方程为_________,直线l 与x 轴交于点_________,与y 轴交于点_________. [答案]x-12+y 3=1 y =6x +3 (-12,0) (0,3) 三、解答题7.求过点P (6,-2),且在x 轴上的截距比在y 轴上的截距大1的直线方程. [解析] 设直线方程的截距式为x a +1+ya =1.则6a +1+-2a=1,解得a =2或a =1,则直线方程是x 2+1+y 2=1或x 1+1+y1=1,即2x +3y -6=0或x +2y -2=0.8.△ABC 的三个顶点分别为A (0,4),B (-2,6),C (-8,0). (1)分别求边AC 和AB 所在直线的方程; (2)求AC 边上的中线BD 所在直线的方程; (3)求AC 边的中垂线所在直线的方程; (4)求AC 边上的高所在直线的方程; (5)求经过两边AB 和AC 的中点的直线方程.[解析] (1)由A (0,4),C (-8,0)可得直线AC 的截距式方程为x -8+y4=1,即x -2y +8=0.由A (0,4),B (-2,6)可得直线AB 的两点式方程为y -46-4=x -0-2-0,即x +y -4=0.(2)设AC 边的中点为D (x ,y ),由中点坐标公式可得x =-4,y =2, 所以直线BD 的两点式方程为y -62-6=x +2-4+2,即2x -y +10=0.(3)由直线AC 的斜率为k AC =4-00+8=12,故AC 边的中垂线的斜率为k =-2.又AC 的中点D (-4,2),所以AC 边的中垂线方程为y -2=-2(x +4), 即2x +y +6=0.(4)AC 边上的高线的斜率为-2,且过点B (-2,6), 所以其点斜式方程为y -6=-2(x +2),即2x +y -2=0. (5)AB 的中点M (-1,5),AC 的中点D (-4,2),∴直线DM 方程为y -25-2=x --4-1--4,即x -y +6=0.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高考数学精品资料
3. 2 直线的方程 单元测试
1. 下列命题中正确的是: ( )
A 、经过点P 0(x 0, y 0)的直线都可以用方程y -y 0=k (x -x 0)表示
B 、经过定点A (0, b )的直线都可以用方程y =kx +b 表示
C 、经过任意两个不同点P 1(x 1, y 1), P 2(x 2, y 2)的直线都可用方程
(x 2-x 1)(y -y 1)=(y 2-y 1)(x -x 1)表示
D 、不经过原点的直线都可以用方程1=+b
y a x 表示 2. 直线x cosα+y si n α+1=0,α)2
,0(π∈的倾斜角为( ) A α B 2π-α C π-α D 2
π+α 3. 以A(1,3),B(-5,1)为端点的线段的垂直平分线方程是( )
A.3x -y -8=0 B .3x +y +4=0 C. 3x -y +6=0 D. 3x +y +2=0
4.方程012)1(=++--a y x a )(R a ∈表示的直线( )
A.恒过(-2, 3)
B. 恒过(2, 3)
C. 恒过(-2, 3)或(2, 3)
D.都是平行直线
5. 过点M(2, 1)的直线与x 轴,y 轴分别交于P,Q两点,且|MP|=|MQ|,则l 的方程
是( )
A. x -2y +3=0
B. 2x -y -3=0 C .2x +y -5=0 D. x +2y -4=0
6. 直线2x +y +m =0和x +2y +n =0的位置关系是( )
A.平行
B.垂直
C.相交但不垂直
D.不能确定
7.把直线l 1: x +3y -1=0沿y 轴负方向平移1个单位后得到直线l 2,又直线l 与直线l 2关于x
轴对称,那么直线l 的方程是( )
A. x -3y +2=0
B. x -3y -4=0
C. x -3y -2=0
D. x -3y +4=0
8. 如图,直线
ax y 1-
=的图象可能是( )
A B C D
9.设A 、B 两点是x 轴上的点,点P 的横坐标为2,且|PA|=|PB|,若直线PA 的方程为x -
y+1=0,则PB 的方程为 ( )
A .x+y -5=0
B .2x -y -1=0
C .2 y -x -4=0
D .2x +y -7=0
10.过点P (1,-2),且在两坐标轴上截距的绝对值相等的直线有( )
A.4条
B.3条
C.2条
D.1条
11. 直线l 1, l 2在x 轴上的截距都是m ,在y 轴上的截距都是n ,则l 1, l 2满足( )
A .平行
B .重合
C .平行或重合
D .相交或重合
12. 已知直线l 1的方程为y =x ,直线l 2的方程为ax -y =0(a 为实数).当直线l 1与直线l 2的
夹角在(0,12π
)之间变动时,a 的取值范围是( )
, 1)∪) B., ) C.(0,1) D.(1) 13 . 将直线y =x +3-1绕它上面一点(1,3)沿逆时针方向旋转15°,则所得直线方程为 .
14.一直线过点(-3,4),并且在两坐标轴上截距之和为12,这条直线方程是_____ _____.
15. 直线ax -6y -12a =0(a ≠0)在x 轴上的截距是它在y 轴上的截距的3倍,则a 等
于 .
16.原点O在直线l 上的射影为点H(-2, 1),则直线l 的方程为 .
17.若方程02222=++-y x my x 表示两条直线,则m 的取值是 .
18. 不论a , b 为何实数,直线(2a +b )x +(a +b )y +a -b =0均通过一定点,此定点坐标
是 .
19. ①求平行于直线3x +4y -12=0,且与它的距离是7的直线的方程;
②求垂直于直线x +3y -5=0, 且与点P(-1,0)的距离是
105
3的直线的方程.
③求过直线17810l x y --=:
和221790l x y ++=:的交点,且垂直于直线270x y -+=的直线方程.
20. 在直线方程y =kx +b 中,当x ∈[-3,4]时,y ∈[-8,13],求此直线的方程
21. 已知直线l 被两平行直线063=-+y x 033=++y x 和所截得的线段长为3,且直线过点(1,0),求直线l 的方程.
22.过点作一直线l ,使它与两坐标轴相交且与两轴所围成的三角形面积为5.
23. 设不等式2x -1>m (x 2-1)对一切满足|m |≤2的值均成立,求x 的范围.
3.2 直线方程 D 13. y =3 x
14. 或0164=+-y x
15. -2
16. 2x -y +5=0;
17. 1=m
18. (-2, 3)
19. (1)3x +4y +23=0或3x +4y -47=0;(2)3x -y +9=0或3x -y -3=0.
(3)解:由方程组217907810x y x y ++=⎧⎨--=⎩,解得112713
27x y ⎧=-⎪⎪⎨⎪=-⎪⎩
,所以交点坐标为11132727--(,). 又因为直线斜率为12k =-, 所以求得直线方程为27x +54y +37=0.
20. y =-3x +4; y =3x +1
21. x =1或3x -4y -3=0.
22. 分析:直线l 应满足的两个条件是
(1)直线l 过点(-5, -4);(2)直线l 与两坐标轴相交且与两轴所围成的三角形面积为5.
如果设a ,b 分别表示l 在x 轴,y 轴上的截距,则有52
1=⋅b a .
这样就有如下两种不同的解题思路:
第一,利用条件(1)设出直线l 的方程(点斜式),利用条件(2)确定;
第二,利用条件(2)设出直线l 的方程(截距式),结合条件(1)确定a ,b 的值. 解法一:设直线l 的方程为()54+=+x k y 分别令00==x y ,, 得l 在x 轴,y 轴上的截距为:k k a 45+-=
,45-=k b 由条件(2)得()104545±=-⋅+-∴k k
k 得01630252=+-k k 无实数解;或01650252=+-k k ,解得5
25821==k k , 故所求的直线方程为:02058=+-y x 或01052=--y x
解法二:设l 的方程为1=+b y a x ,因为l 经过点()45--,,则有: 145=-+-b a ① 又10±=ab ②
联立①、②,得方程组⎪⎩⎪⎨⎧±==-+-10
15ab b b a 解得⎪⎩⎪⎨⎧=-=425b a 或⎩⎨⎧-==25b a 因此,所求直线方程为:02058=+-y x 或01052=--y x .
23.解析:原不等式变为(x 2-1)m +(1-2x )<0,构造线段f (m )=(x 2-1)m +1-2x ,-2≤m ≤2,则f (-
2)<0,且f (2)<0. 答案:
2
13217+<<-x。
