流体力学习题及答案 第七章
流体力学6,7,8章课后题答案

第六章 6-1解:层流状态下雷诺数Re 2000< 60.1Re 6.710vdv υ-⨯==⨯ ⇒60.120006.710v -⨯<⨯⇒62000 6.710/0.10.134(/)v m s -<⨯⨯= 即max 0.134/v m s =223max max max 0.13.140.1340.00105/ 1.05/44d Q Av v ms L sπ===⨯⨯≈=6-2解:层流状态下雷诺数Re 2000<3Re 20000.910120000.0450.1()vd d m d ρυ-=<⨯⨯⨯⇒<⇒<6-3解:3221.66100.21(/)0.13.1444Q v m s d π-⨯==≈⨯临界状态时Re 2000=52533Re Re0.210.1 1.0510(/)20001.05100.88109.2410()vd vd m s Pa s υυυμυρ---=⇒=⨯⇒==⨯⇒==⨯⨯⨯=⨯⋅ 6-4解:当输送的介质为水时:32210101270131444.(/)..Q v m s d π-⨯===⨯ 612701838632000151910..Re .vd υ-⨯===>⨯水 3015100001501...d -∆⨯== 根据雷诺数和相对粗糙度查莫迪图可知流态为水力粗糙。
当输送的介质为石油时:质量流量与水相等3310101010(/)Q kg s -=⨯⨯=31000118850.(/)Q m s == 2200118150********..(/)..Q v m s d π===⨯ 415030113184200011410..Re .vd υ-⨯===>⨯水3015100001501...d -∆⨯== 根据雷诺数和相对粗糙度查莫迪图可知流态为水力光滑。
6-5解:判断流态需先求出雷诺数()2900036009000088023144./..Re Q v m s Avd υ÷===⨯=冬季:421101./m s υ-⨯=40088021608820001110..Re ..vd υ-⨯===<⨯ ⇒ 流态为层流。
哈工程船舶流体力学答案第七章答案

第七章答案7-1 油在水平圆管内作定常层流运动,d=75mm, Q=7l/s, ρ=800kg/3m , 壁面上τ=48N/2m ,求油的粘性系数。
解:圆管层流,流量44482a p Q Q p l l aπμμπ∆=∆⇒= 管壁上342433444 3.5510/24p Q Q Q a y a a m s l a a a Q μμρυτπτυπππρ-∆=====⇒==⨯ (结论)7-2 Prandtl 混合长度理论的基本思路是什么?答:把湍流中微团的脉动与气体分子的运动相比拟,将Reynolds 应力用混合长度与脉动速度表示。
7-3 无限大倾斜平板上有厚度为h 的一层粘性流体,在重力g 的作用下作定常层流运动,自由面上压力为大气压Pa 且剪切应力为0。
流体密度为ρ ,运动粘性系数为 ν,平板倾斜角为 θ。
求垂直于x 轴的截面上流体的速度分布和压力分布。
解:不可压缩平面流动的Navier-Stokes 方程为:2211x y u u upu v f u t x y xv v v p u v f v tx y yυρυρ∂∂∂∂⎧++=-+∇⎪∂∂∂∂⎪⎨∂∂∂∂⎪++=-+∇⎪∂∂∂∂⎩连续方程为:0u v t t∂∂+=∂∂ 由于流动定常,故Navier-Stokes 方程中0u v t t∂∂==∂∂,则 Navier-Stokes 方程可简化为2211x y u u p u v f u x y x v v p u v f v xy y υρυρ∂∂∂⎧+=-+∇⎪∂∂∂⎪⎨∂∂∂⎪+=-+∇⎪∂∂∂⎩边界条件为:y=0时,u=0 ,v=0y=h 时,v=0,τ=0,p=Pa由上述边界条件知,v 始终为0,故0,0v u x∂∂==∂∂。
则以上Navier-Stokes 方程的第二式可进一步简化为:10y pf yρ∂=-∂1cos cos cos y p pf g g p g y c y yθρθρθρ∂∂⇒==-⇒=-⇒=-+∂∂ 由y=h 时p=Pa 解得:常数cos c Pa g h ρθ=+故cos ()P Pa g h y ρθ=+-以上Navier-Stokes 方程的第一式可进一步简化为:210x pf u xυρ∂=-+∇∂ 因p 为y 的函数,所以上式中p x∂∂=0 上式最终简化为:22222212sin sin sin sin 2x u f g d ug dy d u g dy g y u c y c υθυθρθμρθμ∇=-=-⇒=-⇒=-⇒=-⋅++由边界条件,y=0时,u=0,立即得到2c =0,又由11sin 01sin g h c c g hρτμθμρθμ⎛⎫=-⋅+= ⎪⎝⎭⇒=⋅ 所以21sin sin 2g y u g h y ρθρθμμ=-⋅+⋅⋅2s i n 2y hy γθμ⎛⎫=-+ ⎪⎝⎭(答案)7-4 两块无限长二维平板如图所示,其间充满两种粘性系数分别为1μ、2μ,密度分别为1ρ、2ρ,厚度分别为1h 、2h 。
流体力学课后习题答案

第一章习题答案选择题(单选题)1.1 按连续介质的概念,流体质点是指:(d )(a )流体的分子;(b )流体内的固体颗粒;(c )几何的点;(d )几何尺寸同流动空间相比是极小量,又含有大量分子的微元体。
1.2 作用于流体的质量力包括:(c )(a )压力;(b )摩擦阻力;(c )重力;(d )表面张力。
1.3 单位质量力的国际单位是:(d )(a )N ;(b )Pa ;(c )kg N /;(d )2/s m 。
1.4 与牛顿内摩擦定律直接有关的因素是:(b )(a )剪应力和压强;(b )剪应力和剪应变率;(c )剪应力和剪应变;(d )剪应力和流速。
1.5 水的动力黏度μ随温度的升高:(b )(a )增大;(b )减小;(c )不变;(d )不定。
1.6 流体运动黏度ν的国际单位是:(a )(a )2/s m ;(b )2/m N ;(c )m kg /;(d )2/m s N ⋅。
1.7 无黏性流体的特征是:(c )(a )黏度是常数;(b )不可压缩;(c )无黏性;(d )符合RT p=ρ。
1.8 当水的压强增加1个大气压时,水的密度增大约为:(a )(a )1/20000;(b )1/10000;(c )1/4000;(d )1/2000。
1.9 水的密度为10003kg/m ,2L 水的质量和重量是多少? 解: 10000.0022m V ρ==⨯=(kg )29.80719.614G mg ==⨯=(N )答:2L 水的质量是2 kg ,重量是19.614N 。
1.10 体积为0.53m 的油料,重量为4410N ,试求该油料的密度是多少? 解: 44109.807899.3580.5m G g V V ρ====(kg/m 3) 答:该油料的密度是899.358 kg/m 3。
1.11 某液体的动力黏度为0.005Pa s ⋅,其密度为8503/kg m ,试求其运动黏度。
工程流体力学答案(陈卓如)第七章

[陈书7-6] 烟囱直径m d 1=,烟量h k 69.17g q m =,烟气密度3k 7.0m g =ρ,周围大气密度32.1m Kg a =ρ,烟囱内压强损失gVd h P w 2035.02=∆,V 为烟囱内烟气流动的速度,h 为烟囱高度。
为保证烟囱底部断面1处的负压不小于mm 10水柱,烟囱的高度h 应大于(或小于)多少?[解] 此题用Bernoulli 方程求解。
对1、2断面列出总流的伯努利方程: w h gV gp z gV gp z +++=++222212221111αραρ(1)由质量守恒可知:21V V = 再假定动能修正系数:121==αα 式(1)可简化为: w h gp z g p z ++=+ρρ2211(2)()w h z z g p p --=-2112ρ(3)断面1处的负压:111p p p aV-=,移项可得:Vap p p 111-= 而断面2处的压强为当地的大气压,即: ap p 22= 其中ap 1和ap 2分别为断面1、2处的大气压 将以上各式代入(3)式得:()()w Vaah z z g p p p--=+-21112ρ(4)而:gh p p a aa ρ=-12,h z z =-21代入(4)式得:()gh h h g p a w V ρρ--=1(5)依题意,能量损失:gVd h P h w w 2035.02=∆=代入(5)式:⎥⎦⎤⎢⎣⎡-⎪⎪⎭⎫⎝⎛-=-⎪⎪⎭⎫ ⎝⎛-=a a Vdg V gh gh dgV gh pρρρρ2035.012035.01221移项得:⎥⎦⎤⎢⎣⎡-⎪⎪⎭⎫ ⎝⎛-=a Vdg V g p h ρρ2035.0121(6)令w ρ为水的密度,负压可用h ∆高的水柱表示为:h g p w V∆=ρ1代入(6)得:a w dg V hh ρρρ-⎪⎪⎭⎫ ⎝⎛-∆=2035.012将流速:24dq V mρ=代入上式,得:a m w g d q hh ρρρρ-⎪⎪⎭⎫ ⎝⎛-∆=322216035.01 (7)将:mm h 10=∆、210s m g =、3k 2.1m g a =ρ、3k 7.0m g =ρ、3k 1000m g w =ρ、h k 69.17g q m =和m d 1=代入(7)式得:()m h 20-=因为:h z z =-21,所以:m h z z 2012=-=-【陈书7-10】 将一平板伸入水的自由射流内,垂直于射流的轴线。
流体力学习题及答案-第七章(DOC)

第七章 粘性流体动力学7-1 油在水平圆管内做定常层流运动,已知75=d (mm ),7=Q (litres/s ),800=ρ (kg/m 3),壁面上480=τ(N/m 2),求油的粘性系数ν。
答:根据圆管内定常层流流动的速度分布可得出2081m u λρτ=; 其中:λ是阻力系数,并且Re64=λ; m u 是平均速度,585.1075.014.325.010741232=⨯⨯⨯==-d Qu m π(m/s )。
由于阻力系数208m u ρτλ=,因此0202886464Re τρτρλmm u u ===; 即:28τρνmm u du =;所以油的粘性系数为401055.3585.18008075.0488-⨯=⨯⨯⨯==m u d ρτν(m 2/s )。
7-2 Prandtl 混合长度理论的基本思路是什么?答:把湍流中流体微团的脉动与气体分子的运动相比拟。
7-3无限大倾斜平板上有厚度为h 的一层粘性流体,在重力g 的作用下做定常层流运动,自由液面上的压力为大气压Pa ,且剪切应力为0,流体密度为ρ,运动粘性系数为ν,平板倾斜角为θ。
试求垂直于x 轴的截面上的速度分布和压力分布。
答:首先建立如图所示坐标系。
二维定常N-S 方程为:⎪⎪⎭⎫ ⎝⎛∂∂+∂∂+∂∂-=∂∂+∂∂22221y u x u x pf y u v x u u x νρ ⎪⎪⎭⎫ ⎝⎛∂∂+∂∂+∂∂-=∂∂+∂∂22221y v x v y pf y v v x v u y νρ 对于如图所示的流动,易知()y u u =,()y p p =,0=v ,θsing f x =,θcos g f y -=;即x 方向速度u 和压力p 仅是y 的函数,y 方向速度分量0=v 。
因此上式可改写为:⎪⎪⎭⎫ ⎝⎛∂∂+∂∂+=∂∂2222y u x u f x uu x ν ypf y ∂∂=ρ1 由不可压缩流体的连续方程0=∂∂+∂∂y v x u 可知,由于0=v ,0=∂∂yv,则0=∂∂x u ; 则上式可进一步简化为:022=∂∂+yuf x ν (1)ypf y ∂∂=ρ1 (2) 对于(1)式,将θsin g f x =代入,则有:θνsin 122g y u -=∂∂ 两端同时积分,得到:1sin 1C y g y u +-=∂∂θν由于当h y =时,0=∂∂=yuμτ,即0=∂∂y u ,代入上式有:h g C θνsin 11=因此:y g h g y u θνθνsin 1sin 1-=∂∂ 两端再次同时积分,得到:()22sin 21sin 1C y g hy g y u +-=θνθν由于0=y 时,()00=u ,代入上式,知02=C ;则有:()⎪⎭⎫ ⎝⎛-=221sin 1y hy g y u θν 若将ρμν=代入,则上式成为: ()⎪⎭⎫ ⎝⎛-=221sin y hy g y u θμρ 该式即为流动的速度分布。
流体力学经典习题解答以及经典试卷及详细解答
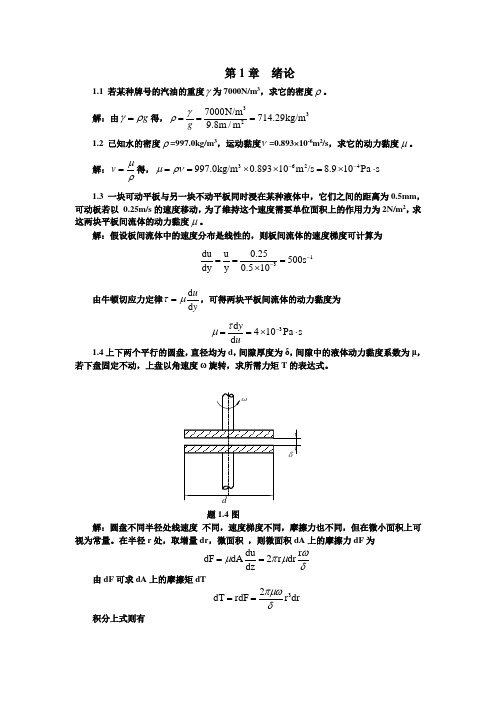
第1章 绪论1.1 若某种牌号的汽油的重度γ为7000N/m 3,求它的密度ρ。
解:由g γρ=得,3327000N/m 714.29kg/m 9.8m /m γρ===g1.2 已知水的密度ρ=997.0kg/m 3,运动黏度ν=0.893×10-6m 2/s ,求它的动力黏度μ。
解:ρμ=v 得,3624997.0kg/m 0.89310m /s 8.910Pa s μρν--==⨯⨯=⨯⋅ 1.3 一块可动平板与另一块不动平板同时浸在某种液体中,它们之间的距离为0.5mm ,可动板若以 0.25m/s 的速度移动,为了维持这个速度需要单位面积上的作用力为2N/m 2,求这两块平板间流体的动力黏度μ。
解:假设板间流体中的速度分布是线性的,则板间流体的速度梯度可计算为13du u 0.25500s dy y 0.510--===⨯ 由牛顿切应力定律d d uyτμ=,可得两块平板间流体的动力黏度为 3d 410Pa s d yuτμ-==⨯⋅1.4上下两个平行的圆盘,直径均为d ,间隙厚度为δ,间隙中的液体动力黏度系数为μ,若下盘固定不动,上盘以角速度ω旋转,求所需力矩T 的表达式。
题1.4图解:圆盘不同半径处线速度 不同,速度梯度不同,摩擦力也不同,但在微小面积上可视为常量。
在半径r 处,取增量dr ,微面积 ,则微面积dA 上的摩擦力dF 为du r dF dA2r dr dz ωμπμδ== 由dF 可求dA 上的摩擦矩dT32dT rdF r dr πμωδ==积分上式则有d 43202d T dT r dr 32πμωπμωδδ===⎰⎰1.5 如下图所示,水流在平板上运动,靠近板壁附近的流速呈抛物线形分布,E 点为抛物线端点,E 点处0d =y u ,水的运动黏度ν=1.0×10-6m 2/s ,试求y =0,2,4cm 处的切应力。
(提示:先设流速分布C By Ay u ++=2,利用给定的条件确定待定常数A 、B 、C )题1.5图解:以D 点为原点建立坐标系,设流速分布C By Ay u ++=2,由已知条件得C=0,A=-625,B=50则2u 625y 50y =-+ 由切应力公式du dy τμ=得du(1250y 50)dyτμρν==-+ y=0cm 时,221510N /m τ-=⨯;y=2cm 时,222 2.510N /m τ-=⨯;y=4cm 时,30τ= 1.6 某流体在圆筒形容器中。
流体力学课后答案第七章

1. 已知平面流场的速度分布为xy x u x +=2,y xy u y 522+=。
求在点(1,-1)处流体微团的线变形速度,角变形速度和旋转角速度。
解:(1)线变形速度:y x xu xx +=∂∂=2θ 54+=∂∂=xy yu y y θ角变形速度:()x y y u x u x y z +=⎪⎪⎭⎫ ⎝⎛∂∂+∂∂=222121ε 旋转角速度:()x y x u x u x y z -=⎪⎪⎭⎫ ⎝⎛∂∂-∂∂=222121ω 将点(1,-1)代入可得流体微团的1=x θ,1=y θ;23/z =ε;21/z =ω2.已知有旋流动的速度场为z y u x 32+=,x z u y 32+=,y x u z 32+=。
试求旋转角速度,角变形速度和涡线方程。
解:旋转角速度:2121=⎪⎪⎭⎫ ⎝⎛∂∂-∂∂=z u y u y z x ω 2121=⎪⎭⎫⎝⎛∂∂-∂∂=x u z u z x y ω2121=⎪⎪⎭⎫⎝⎛∂∂-∂∂=y u x u xyz ω 角变形速度:2521=⎪⎪⎭⎫ ⎝⎛∂∂+∂∂=z u y u y z x ε 2521=⎪⎭⎫⎝⎛∂∂+∂∂=x u z u z x y ε2521=⎪⎪⎭⎫ ⎝⎛∂∂+∂∂=y u x u x y z ε 由zyxdzdydxωωω==积分得涡线的方程为:1c x y +=,2c x z +=3.已知有旋流动的速度场为22z y c u x +=,0=y u ,0=z u ,式中c 为常数,试求流场的涡量及涡线方程。
解:流场的涡量为:0=∂∂-∂∂=zu y u yz x Ω22zy cz xu z u zx y +=∂∂-∂∂=Ω22zy cyy u xu x y z +-=∂∂-∂∂=Ω 旋转角速度分别为:0=x ω222zy cz y +=ω222zy cy z +-=ω则涡线的方程为:c dzdyzy+=⎰⎰ωω即c y dzz dy +-=⎰⎰可得涡线的方程为:c z y =+224.求沿封闭曲线222b yx =+,0=z 的速度环量。
流体力学吴望一教材第七章作业参考答案

第七章作业参考答案12.设复位势为()()()()()2211ln 123ln 4z i z i z z ω=+++-++ 试分析它们是由哪些基本流动组成的?并求沿园周229x y +=的速度环量Γ及通过该圆周的流体体积流量Q .解:()()()()()()()11ln ln 23ln 2ln 2z i z i z i i z i z i zω=+++-+-++-+⎡⎤⎡⎤⎣⎦⎣⎦ =()()()()()()ln ln ln ln 2ln 22ln 2z i z i i z i i z i z i z i ++-+++-+++-()()13ln 23ln 2i z i i z i z-+--+ 它可看成是在()0,1±处强度为2π的点源,在()0,2±处强度为4π的的点源和在()0,1±处强度为2π-的点涡,在()0,2±处强度为6π的点涡,以及在原点强度为2M π=-的偶极子。
所以8πΓ=,12Q π=13.设复位势为()1ln z m z z ω⎛⎫=- ⎪⎝⎭试问它们是由哪些基本流动组成的?求流线和单位时间通过z i =和1/2z =两点连线的流体体积.习题册,习题六(7)题中m 的定义有所不同。
18.证明沿正x 轴的均匀流V 加上在z a =-处强度为2m π的点源和在z a =处强度为2m π点汇组成卵形体的绕流,求驻点及卵形体方程.由题知()()()ln ln z vz m z a m z a ω=++--d m m V V dz z a z aω==+-+-,当0V =时为驻点。
,则驻点位置为z =()()()ln ln z vz m z a m z a ω=++--,z 用x iy +带入,则流线为()2222Im arctan y ay V m x y a ω=++-所以卵形体的方程为: 2222arctan 0y ay V m x y a+=+- 32.设一圆柱半径为a ,在距圆柱中心为()f f a >处分别放置(1)强度为2Q π的点源;(2)强度为2m π的偶极子;(3)强度为2πΓ的点涡.分别计算以上各种情况下圆柱所受的合力,设流体密度为ρ.解:(1)()()22()ln ln ln ln ln a a z Q z f Q f Q z f z z c z f ω⎛⎫⎛⎫⎛⎫=-+-=-+--+ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭根据恰普雷金公式222211122c c i d i Q R dz dz z f z a f z ρωρ⎛⎫⎛⎫==+- ⎪ ⎪--⎝⎭⎝⎭⎰⎰ ()22222a Q f f a πρ=- (2)(3)方法同(1)结果为(2)()223224a m fR f a πρ=-,(3)()22222a R f f a ρπΓ=-。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
7-1油在水平圆管内做定常层流运动,已知d =75 (mm ),Q=7( litres/s ),P =800(kg/m 3),壁面上T o =48 ( N/m 2),求油的粘性系数 V 。
答:根据圆管内定常层流流动的速度分布可得出即卩:Umd _ 8皿m7-2 Prandtl 混合长度理论的基本思路是什么?答:把湍流中流体微团的脉动与气体分子的运动相比拟。
7-3无限大倾斜平板上有厚度为 h 的一层粘性流体,在重力g 的作用下做定常层流运动,自由液面上的压力为大气压 Pa ,且剪切应力为 0,流体密度为P ,运动粘性系数为V ,平板 倾斜角为日。
试求垂直于x 轴的截面上的速度分布和压力分布。
答:首先建立如图所示坐标系。
二维定常N-S 方程为:c u 丄 c u , 1 c p U ——+v ——=f e x c yd v 丄点V 上 u ——+V ——=f ycy甘勺易知 u =u(y ),p = p(y ), V = 0,f^ gsin 日,fy = —gcos9 ;第七章粘性流体动力学其中:A 是阻力系数,并且、64 人-—;ReU ;是平均速度,u m37x10 2 =1.585( m/s )。
1 .20.25x3.14x0.075一兀d由于阻力系数Z,因此64 64 Pu ; 8Pu m所以油的粘性系数为48X0.075 8X800X1.585= 3.55X10^( 2(m /S )。
(-2 -2、c u + C u-2- 2W对于如图所示的流动, r 2列丿两端同时积分,得到:竺--Zgsiney +G c y V由于当y=h 时,— =0,即—=0,代入上式有:列 列1G = — g si n 日hV因此:邑JgsiMh-lgsineyby VV即x 方向速度u 和压力p 仅是y 的函数,y 方向速度分量v = 0。
因此上式可改写为:duu ——=f x +v ,—2次 I 冰c2u1 <P P dy由不可压缩流体的连续方程竺+竺=0可知,由于v = 0,巳=0,则 e x c y色=0 ;e x则上式可进一步简化为:fx +v(1)对于 cu P dy(2)(1 )式,将 f x = g sin 日 代入,则有:=-Igsi n 日V两端再次同时积分,得到:u(y )=lgsin日hy-丄gsin切+C2V 2由于y=0时,u(0)=0,代入上式,知C2 = 0 ;则有:W 丄 cv u ——中V ——<X cyf -2 -2 、 c v ^c v 一 2 IO °y 丿u (y )=1g sin 0 (hy -- y 2V I 2若将-护入,则上式成为: pg 该式即为流动的速度分布。
对于(2)式,将fy = —gcosQ 代入,有:—=-pg COS0 两端同时积分得到: P (y )= -电 cosOy +C 由于当y =h 时,P (h )= P a ,代入上式有: 因此: P(y )= P a + pg cos 日h - pg cos^y = P a + 电 cosT(h -y ) 该式即为流动的压力分布。
7-4两块无限长二维平行平板如图所示,其间充满两种粘性系数分别为 比和卩2,密度分别 为R 和已的液体,厚度分别为 h i 和h 2。
已知上板以等速 v相对于下板向右作平行运动, 整个流场应力相同(不计重力),流动是层流,求流场中速度和切应力的分布。
答:首先建立如图所示的坐标系。
当不计及质量力时,平面定常层流流动的 N-S 方程为: e 丄c u u ——+v —— <x o y / 小f c2■-■21 cp 丄 C u c u =_----- 匚+十|——-+——- P 血■-■2 P cy显然,y 方向的速度分量v=0 ;由不可压缩流体的连续方程可知一+邑=0,可知竺=0,u 仅仅是y 的函数,即e x c y e xU =u (y ),所以上式可重新整理成为:将(1)式分区域写成:分别对两式两端同时积分得到:-h 2兰y 兰0II du II du叫——=^2——,因此有: dy dy(3) ( 4)两式化为:du dy du dy1凹y +C 1e xdy 3y+P i C iex0<y <h0<y <hi d 2y=V dy 2(1)1 e P dy=0由(2)式知道,空=0, 点yP 仅仅是x 的函数p=p (x 卜d 2u dy 2UP 气exd 2u dy 21 cp 卩2 ex-h2 < y < 0卜du2dy由于当y =0时,两种流体界面上的剪切应力相同,即Vdu 1 cp 小上y+G cx=一空y 2+ — C 1 y +C 4 2馬& 巴 4y =0时,两种流体界面上的速度相同,得C^C 4,则:0 < y < h,当y=h i 时,u =V 0,带入到(5)式;当y = -h 2时,u=0,带入到(6)式;得到:(7)1 O2 匕 屛22一严9=0(8)(7)( 8)两式相减,经整理后得到: V 0 1 巴h+A i h 2 02 气(巴h i + A ih2)戲 将G 代入(8)式,经整理后得到: 片 1 cp 2 C 3芯h 2C1 -匾争2叫.f 巴 +1已忙―巴h 2即、=—h 2 ---------- V -十—” --------------------- ”— -4応 V1— ----------------- V042甘%222 气+ 气h2 ) &丿 2^2 血 砧2佝+h2 )生 (巴^+4/2 ) e x将G 和C 3代回到(5)( 6) 两式,则可得到两种流体中的速度分布;将(3)和(4) 两du dy腸y +2C i-h2 < y < 0分别对3) 和(4)两式两端同时积分得到:1IX y29y 9"^10 < y < hl dy 一h2 < y < 0 由于当式两端分别乘以片和卩2,并将C i 代入,可得到应力分布分别为:dy du工2 =贱 ------ 。
dy7-5直径为15mm 的光滑圆管,流体以速度14m/s 在管中流动,是确定流体的状态。
又若要保持为层流,最大允许速度是多少?这些流体分别为((4)空气。
已知 V 润滑油=10x10* m 2/s ,V 汽油=0.884X 10》m 2/s 。
答:对于圆管内的流动,临界雷诺数为 Rec = 2300。
当流速U =14 (m/s )时,各种流体的流动状态如下: (1 )润滑油:J 4".015=210,RecRec=2300,为层流流动。
10x1014 X 0 015 =08跖产 2.376><105,Re >Rec= 2300,为湍流流动。
(3)水:心需T 844"。
5,心R心2300,为湍流流动。
(4)空气:Re =翌=149012= 1.443咒 104,Re 》Rec = 2300,为湍流流动。
V 1.455 咒 10若保持流动为层流状态,则要求 Rec Rec = 2300,各种流体的临界速度分别为:翌 V Rec = 2300V(1 )润滑油:1 )润滑油;(2)汽油;(3)水;D Ud Re =——取水的粘性系数V =1.139X10上(2(m /S )。
取空气的粘性系数 V =1.455X10°( 2(m /S )。
U =2300咒一=2300咒10勺=153.3( m/s);d 0.015(2)汽油:因此雷诺数为:O."0.0254=142.6,流动状态是层流; 5.342x10则阻力系数为:压力降为: l 1 30 1△p =几一一 Pu m =0.449x ----- x_x739.2xo.32 =17640.4(N/m 2);d 2 0.0254 2最大流速:U max =2U m =0.6 ( m/s ); 圆管内沿径向的速度分布为:U =2300 X-=2300 x 0.884^10=0.136 d0.015(m/s );(3)水:U =2300xt =2300咒1.139*10=0.175 d0.015(m/s );(4)空气:U =2300x-=2300丁.455乂10=2.231 d0.015(m/s )。
7-6 粘性系数》=39.49x10-3( m 2/s ), 丫 =7252N/m2的油流过直径为 2.45cm 的光滑圆管;平均流速为0.3m/s 。
试计算30m 长管子上的压力降,并计算管内距管壁 0.6cm 处的流速。
答:雷诺数:Re=U m d,其中:V平均流速:U m =0.3(m/s );流体密度:g 7252=739.2( kg/m 3);9.81运动粘性系数:=卩39.49心0° 739.2 处妙10^ 2(m /s )。
、64A = - Re-6^ =0.449 ;142.6上式中:a =25.4/2=12.7(mm ),则在 r =12.7-6 = 6.7 (mm )处,流动速度为: r r 2r<6.7U =Umax 1— p =0.6 X 1- 1 a丿 1112.7 10.433(m/s )。
J7-7 30 C 的水流过直径为 d=7.62cm 的光滑圆管,每分钟流量为 0.340m 3,求在915m 长度 上的压力降,管壁上的剪应力 T 0及粘性底层的厚度。
当水温下降到5 C 时,情况又如何? 答:(1)当水温为30 C 时,取水的粘性系数为 V =0.8009X 10》(m 2/s )平均流速为: 0.34/60 Um = — = ----- 55’ ~ -- -2 =1 .243 1 .2 0.25X 3.14x0.07622 —ird 4雷诺数为: (m/s );Rx 晋二^^243需"183"05,流动为湍流流动; 查莫迪图谱,得到阻力系数为: A=0.017 ;则压力降为: Id Qd C d A p = A ——P u m =0.017X ------- x -x 1.^10Sc 1.243^ =157698(N/m 2) d 2 0.0762 2=1.58( Pa );管壁上的剪切应力: 10 =1几P u : = l x 0.017X 1.0X103 X1.2432 =3.283 ( N/m 2); 8 8 又由于吩占H 等i.0573,并且宁=5,得到粘性底层厚度为: y 上 尹O.8009"二0.069(mm )。
UT0.05736 2(2)当水温下降为5 C 时,取水的粘性系数为 V =1.517心0(m 2/s)平均流速为:-11-雷诺数为:1.243X 0.0762 . ,_5 、去一卄%沖、音去一卄--------- L = 1.183X 10,流动为湍流流动;1.51^1^6查莫迪图谱,得到阻力系数为:"0.017 ; 则压力降为:l 1 915 1邙尹ao.。
