有多类顾客且转移率与状态相依的排队网络设计
排队模型——精选推荐
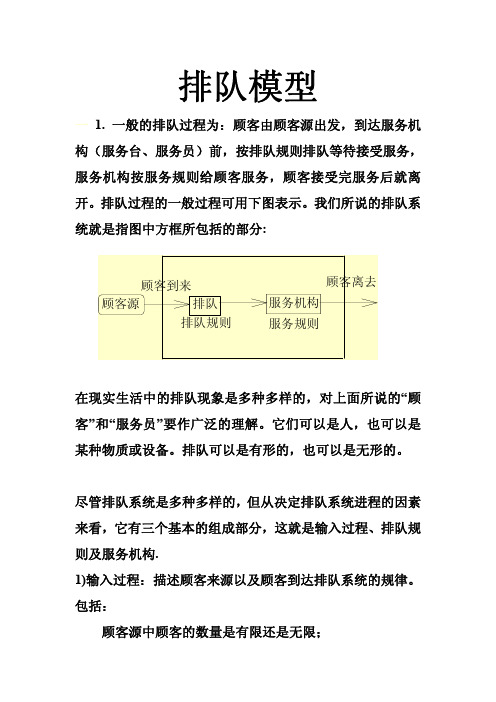
排队模型一 1. 一般的排队过程为:顾客由顾客源出发,到达服务机构(服务台、服务员)前,按排队规则排队等待接受服务,服务机构按服务规则给顾客服务,顾客接受完服务后就离开。
排队过程的一般过程可用下图表示。
我们所说的排队系统就是指图中方框所包括的部分:在现实生活中的排队现象是多种多样的,对上面所说的“顾客”和“服务员”要作广泛的理解。
它们可以是人,也可以是某种物质或设备。
排队可以是有形的,也可以是无形的。
尽管排队系统是多种多样的,但从决定排队系统进程的因素来看,它有三个基本的组成部分,这就是输入过程、排队规则及服务机构.1)输入过程:描述顾客来源以及顾客到达排队系统的规律。
包括:顾客源中顾客的数量是有限还是无限;顾客到达的方式是单个到达还是成批到达;顾客相继到达的间隔时间分布是确定型的还是随机型的,分布参数是什么,是否独立,是否平稳。
2)排队规则:描述顾客排队等待的队列和接受服务的次序。
包括:即时制还是等待制;等待制下队列的情况(是单列还是多列,顾客能不能中途退出,多列时各列间的顾客能不能相互转移);等待制下顾客接受服务的次序(先到先服务,后到先服务,随机服务,有优先权的服务)。
3)服务机构:描述服务台(员)的机构形式和工作情况。
包括:服务台(员)的数目和排列情况;服务台(员)的服务方式;服务时间是确定型的还是随机型的,分布参数是什么,是否独立,是否平稳。
2.到达和服务过程的模型2.1 到达过程的模型用表示第i 个顾客到达的时间,.i t 称为第i 个到达时间间隔.1i i T t t +=−i 我们用的特征来刻画顾客到达过程. 最常见的情况是独立同分布. 用X 表示这样的随机变量.12,,T T 12,,T T 如果X 服从参数为λ的指数分布.这时1()()i E T E X λ==即平均每隔1λ来一个顾客.换句话说,单位时间理平均有λ个顾客到来.称λ为到达速率. 用表示到时刻t 为止到达的顾客总数,则在上面的假设下()N t ()()N t P t λ∼.除了指数分布外,常用的还有爱尔朗分布,其密度函数为1()(), 0.(1)!k RxR Rx e f x x k −−=≥− 这时2(), ()i i k k E T D T R R==. k 叫形状参数, R 叫速率参数.当取λ使得R k λ=, 则爱尔朗分布可以看成是k 个独立的服从参数为λ的指数分布随机变量的和的分布.2.2服务过程的模型一般总是认为不同顾客接受服务占用的时间长短是相互独立的. 用Y表示一个客户接受服务的时间长短, 它是一个随机变量.若Y的分布是参数为μ的指数分布, 意味着一个顾客的服务时间平均为1μ. 单位时间里可以完成的平均顾客数为μ.若Y服从形状参数为k, 速率参数为R kμ=的爱尔朗分布, 则平均服务时间为1μ, 根据爱尔朗分布的性质, 可以将Y看作是k个相继子服务的总时间, 每个子服务都服从参数为1kμ的指数分布且相互独立.在排队论中,我们常用如下字母表示特定的到达时间间隔或服务时间分布:M: i.i.d. 指数分布D: i.i.d. 的确定分布E k: i.i.d. 的形参为k的爱尔朗分布GI: 到达时间间隔是i.i.d. 的某种一般分布G: 服务时间是i.i.d. 的某种一般分布在处理实际排队系统时,需要把有关的原始资料进行统计,确定顾客到达间隔和服务时间的经验分布,然后按照统计学的方法确定符合哪种理论分布。
客户排队方案

客户排队方案在各种类型的服务场所,诸如餐馆、医院、银行、超市、机场等,经常会出现客户排队等候的情况。
这时,客户排队的方案就变得极为重要。
因为这不仅关系到客户的体验和感受,而且还关系到机构的服务效率和形象。
因此,如何制定合理的客户排队方案,成为了需要着重思考和优化的问题。
客户排队方案设计的原则1.公平性原则:所有客户应该平等地被服务,无论其先后到达时间或VIP等级。
2.优化客户等待时间原则:尽可能减少客户等待的时间,使客户有更好的体验。
3.灵活性原则:应该以灵活的方式应对突发事件,如客户突然增加或网络异常等。
4.操作简单易行原则:方案设计应尽量做到简单易懂、易实施,避免因操作复杂而影响服务效率。
5.可变性原则:方案应能够应对长期和短期等不同的情况,以适应不同场景的需要。
1.系统排队方案:这种方案需要使用排队系统,公平性更高,但需要投入大量资金建设。
一般来说,在人员多、人流量大的机构,这种方案更加适用。
2.同时取号方案:此方案需要设置取号机。
客户到达机构后,首先在取号机上取号,并排队等候。
该方案具有操作逻辑简单,成本较低的特点,但等待时间较长,不太适合客户需求较高的场所。
3.预约服务方案:预约服务方案通过预约的方式为客户提供服务,如加号、网上预约等。
此方案消除了等待的过程,更加注重客户对服务体验的感受。
该方案的缺点是操作复杂,且与预约时间不符的客户需要重新排队,会造成一定的浪费。
4.分批服务方案:此方案是根据客户到达的时间将客户分批次服务的方案。
一般适用于批量、大型的机构。
该方案可更好地控制人流,让客户在等待期间更有顺畅感。
5.转移等待方案:当突然出现大量客户需要服务时,发现当前排队方案无法满足时间需求,机构可选择转移等待。
将部分服务放到其他场地进行,或将一些客户引入其他场地,以缓解等待的效果。
以医院为例,医院的客户通常需要排队候诊。
对于医院而言,应根据医院的特点,量身定制合适的排队方案。
以下列举几个实例:1.取号排队法及分批服务法:该法针对医院门诊业务,可使用取号机为客户排队,同时将客户分批服务,使等待时间更加合理,减少等待过程。
排队网智慧餐饮系统设计方案

排队网智慧餐饮系统设计方案智慧餐饮系统是一种通过科技手段来提升餐饮业务流程和用户体验的系统。
排队网智慧餐饮系统旨在解决传统餐饮行业中存在的排队问题,通过预约和排队管理等功能,提高顾客的用餐效率和满意度。
下面是排队网智慧餐饮系统的设计方案。
一、系统功能1. 预约功能:顾客可以通过手机APP或网站预约座位或取餐时间,提前安排用餐计划。
2. 取号功能:顾客到达餐厅后,在系统上取号,避免长时间排队等待。
3. 排队监控功能:餐厅工作人员可以通过系统监控当前排队情况,及时调整服务资源,提高服务效率。
4. 短信提醒功能:系统会根据预约或取号的顺序,自动发送短信提醒顾客取餐或就座。
5. 餐桌管理功能:系统可以实时监控餐桌使用情况,自动安排就座,避免顾客争抢座位。
6. 线上支付功能:顾客可以通过系统线上支付,提高收款效率和安全性。
7. 数据分析功能: 系统可以对顾客就餐数据进行分析,如顾客流量、用餐时长等,为餐厅管理者提供数据决策支持。
二、系统架构排队网智慧餐饮系统采用分布式架构,主要包括前端、后端和数据库三个层次。
前端:包括手机APP和网站,提供顾客预约、取号、支付等功能的界面和交互逻辑。
后端:包括管理系统和服务系统,负责接收顾客的请求,并进行相应的逻辑处理。
管理系统提供对系统参数的设定和监控功能;服务系统负责处理顾客的预约、取号、支付等请求。
数据库:存储系统运行过程中产生的各种数据,包括顾客信息、餐厅设备信息、预约记录等。
三、系统流程1. 顾客预约流程:顾客使用手机APP或网站选择餐厅、日期、时间等信息,并预约座位或取餐时间。
系统将预约信息存储在数据库中,并发送短信提醒顾客预约成功。
2. 顾客到达餐厅流程:顾客到达餐厅后,在系统上使用手机扫描二维码或输入预约信息取号。
系统将顾客信息记录在数据库中,并显示顾客取号的顺序。
同时,系统发送短信提醒顾客取餐或就座。
3. 顾客用餐流程:当餐桌空闲时,系统根据取号顺序自动安排就座。
排队叫号系统的分析和设计PPT课件

1. 课程设计需求分析 1.2 需求分析
排队叫号模拟系统 应用场景:某营业厅配一台叫号机,设置6个业务窗口,每个业务窗口均 可办理指定类型客户的业务。根据业务流量,1-4号窗口暂定为普通窗口,5号 窗口暂定为特殊窗口,6号窗口暂定为VIP窗口。
3
1. 关于课程设计 1.2 需求分析
4
1. 课程设计需求分析 1.3 其它要求 ❖ 业务办理信息:今天累计接待客户×××人,其中普通客户×人,特殊客 户×人,VIP客户×人。 ❖ 数据归档要求:每天办理的窗口编号、窗口名称、用户号码、接待时间等 信息保存到一个文本文件中。 ❖ 语音播报叫号信息。
17
知识准备 数据归档的实现-Log4j 在Java Project中应用Log4j的步骤如下: ❖ 将log4j-2.13.jar复制到项目文件夹中并添加到BuildPath。 ❖ 在项目文件夹src中建立log4j.properties。 ❖ 在编程中使用Log4j。
18
知识准备 文本转语音组件
13
知识准备 可调度线程池
这里,我们要模拟普通客户、特殊客户、VIP客户的比例大约为:6:3:1 ,就要用到 可 调 度 线 程 池 : 可以指定每隔n秒启动一个相应类型的客户线程。 示例程序如下:
14
知识准备
JList应用示例
JList是一个遵循MVC模式设计和实现的列表组件。 JList类的构造方法如下: ❖ JList():构造一个具有空的、只读模型的JList。 ❖ JList(Vector<?> listData):构造一个JList,使其显示指定Vector中的 元素。适用于选项数目变化不定的应用场合。 JList常用方法如下: ❖ public void setListData(Vector<?> listData) ❖ public void setSelectedIndex(int index)
排队解决方案

排队解决方案引言随着人口的增长和城市化的推进,生活中排队现象越来越普遍。
无论是排队购买电影票、餐厅用餐还是办理业务,排队现象都在我们生活的各个方面出现。
然而,长时间等待在排队中无疑是一种浪费时间和资源的现象。
为了提高效率和减少排队带来的负面影响,各个领域都在积极寻求解决方案来改善排队问题。
本文将介绍几种常见的排队解决方案,从传统的手工排队方式到现代的智能化排队系统,以期为读者提供一些参考和启示。
传统排队解决方案基于人工管理的排队方式人工排队方式是最传统的一种排队方式,它通常适用于小型场所或需求量不大的场合。
在人工排队方式中,一般会有工作人员负责管理排队顺序,例如超市的收银员、餐厅的服务员等。
这种排队方式的优点是操作简单,成本低廉,并且可以灵活地根据需求进行调整。
然而,它的缺点也非常明显,包括容易发生人为错误、排队效率低下等。
叫号排队方式叫号排队方式是另一种常见的传统排队方式。
顾客在到达现场后,会从一个叫号机或者工作人员手中领取一个号码。
然后,系统根据号码的先后顺序来安排服务顺序。
这种排队方式的优点是能够确保公平性,避免优先级的问题,并且能够减少人为错误。
然而,对于顾客而言,等待时间仍然是一个存在的问题。
现代排队解决方案网上预约排队随着互联网的发展,网上预约排队逐渐成为一种流行的解决方案。
在网上预约排队中,顾客可以通过手机或者电脑提前预约,选择合适的时间段进行预约。
这种方式的优点是减少了排队的等待时间,提高了效率,并且可以提前安排自己的时间。
不过,这种方法也有一些问题,比如预约系统可能会出现故障,或者一些顾客可能会预约多个时间段而导致资源浪费。
可视化排队系统可视化排队系统是一种利用技术手段来管理排队的方式。
它通常会在现场的墙或者屏幕上展示当前的排队情况,包括当前等待人数、平均等待时间等信息。
通过这种方式,顾客可以直观地了解到自己的等待时间和位置,从而更好地安排自己的时间。
这种排队方式的优点是能够提供实时的信息,并且可以减少对工作人员的依赖。
排队论大学课件9-多服务窗排队模型

10
2 多服务窗等待制排队模型M/M/n
E {0,1, 2,...}
k
k k n k n k n
4 多服务窗闭合式排队模型M/M/n/m/m
外线利用率
L服 n
外线损失系数,(空闲、浪费系数)
q ( n) 1
L服 n
1
28
5 M/M…排队系统的输出过程
输出是与输入同强度的泊松流 设排队系统为M/M/n/m(1nm ),设到 达的顾客流是参数为的泊松流(在等待制 时,进入系统的流是参数为的泊松流;在 混合制与损失制时,进入系统的流是参数 为(1-pm)的泊松流),如果把混合制与损 失制时的损失流也看作系统的输出,则系 统的输出是参数为的泊松流。 证明略
29
队长分布与顾客到达时刻看到的队长分布 的关系
设统计平衡条件下,顾客到达时看到的队长为ls(不包括到达的这个顾客), ls-与平稳队长ls的 分布相同吗?
排队系统
平稳分布记做: pn P (ls n)
pn P (ls n)
30
队长分布与顾客到达时刻看到的队长分布 的关系
k 0
k!
称为爱尔兰损失公式,又称爱尔兰B公式,欧洲人称 为爱尔兰第一公式
6
1 多服务窗损失制排队模型M/M/n/n
爱尔兰B公式的广泛性:
我们把一个具有泊松输入的损失制排队系统称为 爱尔兰损失制系统,这种损失制系统对于任何服 务时间分布,它在统计平衡条件下的状态概率都 相同与M/M/n/n相同。 即M/M/n/n排队系统的平稳分布=M/G/n/n排队系 统的平稳分布
多服务台指数分布排队系统

• 引言 • 引言 • 引言 • 多服务台指数分布排队系统概述 • 多服务台指数分布排队系统的性能指
标
• 多服务台指数分布排队系统的优化设 计
• 多服务台指数分布排队系统的应用实 例
• 结论与展望
01
引言
平均等待时间
• 平均等待时间表示顾客在进入系统后等待接受服务的平均 时间。
系统参数的优化调整
等待时间
过长可能导致客户不满,过短可能造成资源浪 费。
忙期持续时间
过长可能导致服务台超负荷运行,过短可能造 成资源闲置。
优化建议
通过实时监控和数据分析,调整系统参数,以实现服务质量和经济效益的平衡。
05
多服务台指数分布排队系统的应用实
例
银行服务排队系统
总结词
适用于银行服务的多服务台指数分布排队系统能够有效地解决客户等待时间过长的问题, 提高服务效率。
详细描述
在机场安检过程中,乘客需要经过多个环节的检查才能进入候机区。为了提高安检效率,机场通常会设置多个安 检通道,并采用多服务台指数分布排队系统来分配乘客到各个通道。该系统能够根据乘客到达时间和安检流程的 复杂程度,动态调整每个通道的服务速率,使得乘客能够快速、有序地完成安检。
医院挂号排队系统
要点一
04
本文还探讨了系统在不同负载情况下的性能表现,发 现系统在高负载下容易出现性能瓶颈,因此需要合理 设计系统以应对高负载情况。
研究展望
未来研究可以进一步探讨多服务台指 数分布排队系统在不同类型任务和复 杂环境下的性能表现,以更好地适应 实际应用需求。
此外,可以考虑将多服务台指数分布 排队系统与其他排队模型进行比较研 究,以进一步了解其优势和局限性。
排队系统方案

排队系统方案第1篇排队系统方案一、背景随着社会经济的发展和人们生活水平的提高,公共服务领域对排队系统的需求日益增长。
高效、公平、透明的排队系统不仅能够提升服务质量和效率,还能增强顾客的满意度和信任度。
本方案旨在为某服务机构设计一套合法合规的排队系统,确保服务流程顺畅,提高服务水平和客户体验。
二、目标1. 提高排队效率,缩短顾客等待时间。
2. 确保公平公正,消除人为干预。
3. 提升服务质量,增强顾客满意度。
4. 合法合规,遵循相关法律法规。
三、核心设计原则1. 公平性:确保每位顾客都能按照到达时间顺序接受服务。
2. 透明性:让顾客了解排队进度,提高信任度。
3. 灵活性:适应不同场景和业务需求,易于调整。
4. 安全性:遵循国家法律法规,保护顾客隐私。
四、方案设计1. 取号系统- 顾客到达服务机构后,通过自助取号机获取排队号码,号码具有唯一性,不可替代。
- 取号机支持身份验证功能,确保每位顾客只能取一个号码。
- 取号机界面友好,支持多种语言,方便不同顾客操作。
2. 排队管理系统- 系统根据取号时间自动生成排队序列,遵循先来先服务的原则。
- 顾客可通过现场显示屏或手机端实时查看排队进度,了解等待时间。
- 排队管理系统具备异常处理机制,如号码丢失、重复等,确保公平公正。
3. 业务办理流程- 工作人员根据排队序列逐个呼叫顾客,确保服务顺序与排队顺序一致。
- 顾客在办理业务时,工作人员需进行身份核验,确保信息一致。
- 业务办理过程中,工作人员应遵循服务规范,提高服务质量和效率。
4. 数据安全与隐私保护- 排队系统遵循国家相关法律法规,确保数据安全和顾客隐私。
- 对顾客个人信息进行加密存储,防止泄露。
- 定期对系统进行安全检查,确保系统稳定可靠。
5. 顾客满意度调查- 通过现场反馈、在线调查等方式收集顾客意见,了解排队系统运行情况。
- 定期分析调查结果,针对问题进行优化调整,提高顾客满意度。
五、实施与评估1. 实施步骤- 系统设计:根据本方案设计排队系统,确保合法合规。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
中图分类 号 : 3 1 TP 1
文 献标 志码 : A
文 章 编 号 :6 3 8 8 2 1 ) 3 0 1 5 1 7 - ̄ o ( 0 1 0 -0 7 -0
0 引言
对 于排 队 网络 的研 究 , 们 已经给 出 了一 些结 果 , 国 内大 部分 研究 集 中于 网络 的逼 近 , 对 于定量 人 但 而 分析 , 即给 出具 体 的队长 稳态 分布 , 果很少 . 结 国外 , 自从 Jcsn 用拟 可逆 性方 法 , 出乘积形 式 稳态解 ako 利 给 之 后 ,el Kl y等人 做 了进 一步 扩展 . ho Pnd (9 3引入 了含 多类顾 客 与消极 信号 的排 队网络 , 出了 C a 和 ieo 19 ) 给 乘 积形 式解 . 之后 , yzw Mi a a和 C a 19 ) 只有 一类顾 客 的 网络 结果 下 , 究 了状 态 相依 网络 , 出 了 a ho(9 6 在 研 给
到达 k , 处 以概率 ,作为消极信号到达 k , 以概率 , 处 或 。 离开系统. : 设
令:
凡 ( l 2… ,N , 中 r ( jn , , ) = n , , n )其 n t n ,j … n 。 j 1 2 = N
为稳态下 处 u 类顾客数 ,
设 c 1为 j I 置顾 客类 , j) 处 位 ( 引入 另一状 态 为 : c ( c, , )其 中 G (j ) … ,j j) = c,2… c , = c 1 , c n) ( (
顾客到达 j , 处 也以概率 (吩 1 占据 1 f+) J 位置 , 1 而 位置的顾客服务率占总服务率的比率也 ( )则 由 f , [] 1中结 果 , 网络 的稳态分 布是 : 此
.
刀 c N ( ()
一
)j n
∽
其 中
, 喜, :
() 1 . 1
,、
平衡 的方 法是很 经 典 的排 队论方法 , cos 而 rs 部分 平衡 是 一种新 的平衡 , 更能 体 现 网络 性质 , 以很好 地 用 可
于验证非线性排队网络的稳态分布 , 同时对于一些网络 , 以由其构建 出整体平衡式 , 可 本文所研究网络即 是关于 c s部分平衡具体见文献 [ ] rs o 1.
1 模型假 设
先给 出到达与服务率与状态独立 , 且含多类顾客和消极信号 的排队网络的一些假设及结论. 设网络有
N个节点 ,类顾 客 ,一 类 消极信 号记 为 CM类顾 客 与信号从 外 界分别 以 A _ 率 的 Pi o I , Ai 速 o sn过程 到达节 s
点j , u 处 且 类顾客在 j 处接受指数服务 , 服务率龇 类顾 客在. , “ 『 处服务完成 , 以概率 ,作为 类顾客
[ 稿 日期 ]00 1 - 4 收 2 1- 1 2
[ 作者简介 ] 王
晓(9 0 , 山西榆次人 , 18 一) 男, 太原理 工大学计算机科学与技术学院 , 硕士 , 中学院计算机科 学与技术学院 , 晋
助教 , 研究方向: 计算机应 用.
・
7l ・
王 晓
有 多类顾客且转移率与状态相依的排队网络设计
的 转 移 率 , 建 了新 的 模 型 , 通 过 两 类 平 衡 : 体 平衡 和 co s 分 平 衡 , 证 了新 网络 的 稳 构 并 整 rs 部 验
态 分 布 具 有 新 形 式 的 乘 积 解 , 且 说 明 了 cos 分 平 衡 如 何 构 建 出 整 体 平 衡 式 . 并 rs部
∥ , ( ) :。l , , , , =o , Ⅳ ) , , ,…
(. 1 2J
且 %, 为下 列方程 的解 :
- -
-
2十 ∑∑
JI“l
= ∑∑ 一 . + P,, . 一
此 结果 可见 [ ] 1. 利 用下述 方法 , 正此 网络 , 修 使其具 有状态 相关 的转移 率 :
g , jC{ j : ,j)i C  ̄l e1 )
第 2 卷第 3期 8
2 1 年 6月 01
晋
中
学
院
学
报
Vo _8 No3 l 2 .
J u nl o Jn h n Unv ri o r a f iz o g iest y
J n 2 1 u. 01
有 多类顾 客且 转移 率与 状 态 相依 的排 队 网络设 计
王 晓 ,
到达和服务率与状态相关情形下 , 网络的另一种乘积形式解 , 同时也揭示与状态独立网络的稳态解的关系. 本 文 将在 此基 础 上 , 进一 步 研究 含有 多 类顾 客 与消 极信 号 , 且状 态 相依 的排 队 网络 , 用 服务 率 与状 利 态独 立 网络 的稳 态 结果 , 通过 整 体平衡 和 cos rs 部分 平衡 , 两种方 法 验证 了新 网络 的稳 态分 布 , 中整 体 用 其
(. 1太原理 工大学 计算机科 学与技术学院 , 山西 太原 00 2 ;. 中学院 计算机科 学与技术学院 , 30 4 2 晋 山西 晋 中 00 0 ) 3 60 摘 要 : 含 有 多类 顾 客 和 消 极 信 号 的 经 典 J c sn网 络 模 型 基 础 上 , 在 ak o 引入 了 与 状 态 相 关
且1 p 一 e ) ,, ) :c c ∈ ( ) ( , 1 父 , : c c = (n , ( , = ,, +) (,O f,p , , ) , g 【c,O 'f ̄7 :f Je) l 1,, ) ( c ) J j(( y) 月 c 即c 类信号到达J . 处以概率 ( ) 1 f 使 位置的顾客离开 , , 且设此顾 客将永远离开网络; 同时一个 “ 类
