英文版大学物理功和能共44页
合集下载
大学物理第四章--功和能
a
a
l
xdx
2l
前已得出：
Af
mg(l a)2
2l
mg(l 2 a2 ) mg(l a)2 1 mv2
2l
2l
2
得v
g l
1
(l 2 a 2 ) (l a)2 2
§3 保守力的功与势能 一、 保守力
rB
B
两个质点之间的引力
B
第四章 功和能
§4.1 功 §4.2 动能定理 §4.3 保守力功与势能 §4.4 功能原理机械能守恒定律
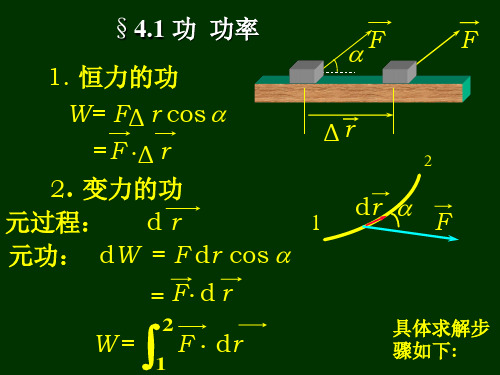
§1 功和功率
一、恒力做功 直线运动
A=Fcos S
记作A F S F r
F
F
M
M
S
位移无限小时：
dA
F
dr
dA称为元功
功等于质点受的力和它的位移的点积(标积)
例１一水平放置的弹簧，其一端固定，另一端系一小球，求小
球的位置由A到B的过程中弹力对它所做的功。（在O处弹簧无 形变）
解：根据胡克定律 F F kx
W F dr
xB Fdx
xA
xB xA
kxdx
O
1 2
A
k xB2
B
xA2
1 2
k xA2
作用在质点
上．在该质点从坐标原点运动到(0，2R)位
置过程中，力
F
对它所作的功为多少？
y
b
b
A a F.dr a (Fxdx Fydy)
R
x O
例4 如图，水平桌面上有质点 m ，桌面的摩 擦系数为μ 求：两种情况下摩擦力作的功
a
l
xdx
2l
前已得出：
Af
mg(l a)2
2l
mg(l 2 a2 ) mg(l a)2 1 mv2
2l
2l
2
得v
g l
1
(l 2 a 2 ) (l a)2 2
§3 保守力的功与势能 一、 保守力
rB
B
两个质点之间的引力
B
第四章 功和能
§4.1 功 §4.2 动能定理 §4.3 保守力功与势能 §4.4 功能原理机械能守恒定律
§1 功和功率
一、恒力做功 直线运动
A=Fcos S
记作A F S F r
F
F
M
M
S
位移无限小时：
dA
F
dr
dA称为元功
功等于质点受的力和它的位移的点积(标积)
例１一水平放置的弹簧，其一端固定，另一端系一小球，求小
球的位置由A到B的过程中弹力对它所做的功。（在O处弹簧无 形变）
解：根据胡克定律 F F kx
W F dr
xB Fdx
xA
xB xA
kxdx
O
1 2
A
k xB2
B
xA2
1 2
k xA2
作用在质点
上．在该质点从坐标原点运动到(0，2R)位
置过程中，力
F
对它所作的功为多少？
y
b
b
A a F.dr a (Fxdx Fydy)
R
x O
例4 如图，水平桌面上有质点 m ，桌面的摩 擦系数为μ 求：两种情况下摩擦力作的功
英文版物理功和能
Calculate the work by the force when the particle moves from x1=2(m) to x2=3(m) in the following cases: 1. The trajectory is a parabola
Example
x 4y
2
2. The trajectory is a straight line 4 y x 6
Work is a scalar, no direction. π positive work; 0 d W 0 ,
π 2 π 2 π 2 dW 0 , d W 0,
Constant Force (including its direction)
A
rA
o
s
(2) Work done by a varying force: When a particle moves from A to B along a curve path, the total work ds done by the force equals the integral of F from A to B: A
7-1 Work and Power (P147-)
1. Work
研究力和运动的空间过程关系。
The work done by a force F in displacing a s body s as the scalar product of F and s.
W F r cos F r
1
2
O
3 X
A1
( Fx dx Fy dy ) 2 ydx 4dy
Example
x 4y
2
2. The trajectory is a straight line 4 y x 6
Work is a scalar, no direction. π positive work; 0 d W 0 ,
π 2 π 2 π 2 dW 0 , d W 0,
Constant Force (including its direction)
A
rA
o
s
(2) Work done by a varying force: When a particle moves from A to B along a curve path, the total work ds done by the force equals the integral of F from A to B: A
7-1 Work and Power (P147-)
1. Work
研究力和运动的空间过程关系。
The work done by a force F in displacing a s body s as the scalar product of F and s.
W F r cos F r
1
2
O
3 X
A1
( Fx dx Fy dy ) 2 ydx 4dy
大学物理《功和能》课件
A
L A L B
L
L
B
L
B
A
B f dr f dr 0
L
A
§4.3 保守力与势能
2.势能
A引 Gm 1 m 2 rB Gm 1 m 2 rA
A弹 1 2 ks
2 A
1 2
ks B
2
A引
Gm 1 m 2 r B r rA
B f dr k (r
A
r k ( r r0 ) A r 1 1 2 2 k ( r A r0 ) k ( rB r0 ) 2 2
O rA r r0 ) d r r r d r k ( r r0 ) d r r
第4章 功 和 能
Work and Energy
第4章
功和能
质点受力的作用时，如果持续一段时间，质点的动量会 改变；如果质点由空间位置的变化，则力对位移的累积（功） 会使质点的能量（动能和势能）发生变化。对功和能的研究， 是经典力学中重要的组成部分。 与机械运动相联系的能量守恒定律（机械能守恒定律）， 是普遍的能量守恒定律的一种特殊形式。
一般引力势能的零点取质点相距无穷远，E
r
一般弹性势能的零点取弹簧无伸缩状态，Ep
0 ， 0 C
s 0
A点势能可表为 E p ( A )
Ep 0 A
f保 dr
§4.4 引力势能与弹性势能
2.势能曲线
Ep
Ep
Gm1m2 r
Gm1m2 r0
引力势能曲线
引力势能是空间变量
动量动量角动量角动量能量能量守恒量对称性时空性质空间平移空间平移空间转动空间转动时间平移时间平移空间均匀性空间均匀性空间各向同性空间各向同性时间均匀性时间均匀性守称守恒守恒空间反演对称性空间反演对称性安保是指为了达到安全的目的而进行的对人或物的保护活动安保工作是指为集体或个人的安全而进行保卫的各种活动
L A L B
L
L
B
L
B
A
B f dr f dr 0
L
A
§4.3 保守力与势能
2.势能
A引 Gm 1 m 2 rB Gm 1 m 2 rA
A弹 1 2 ks
2 A
1 2
ks B
2
A引
Gm 1 m 2 r B r rA
B f dr k (r
A
r k ( r r0 ) A r 1 1 2 2 k ( r A r0 ) k ( rB r0 ) 2 2
O rA r r0 ) d r r r d r k ( r r0 ) d r r
第4章 功 和 能
Work and Energy
第4章
功和能
质点受力的作用时，如果持续一段时间，质点的动量会 改变；如果质点由空间位置的变化，则力对位移的累积（功） 会使质点的能量（动能和势能）发生变化。对功和能的研究， 是经典力学中重要的组成部分。 与机械运动相联系的能量守恒定律（机械能守恒定律）， 是普遍的能量守恒定律的一种特殊形式。
一般引力势能的零点取质点相距无穷远，E
r
一般弹性势能的零点取弹簧无伸缩状态，Ep
0 ， 0 C
s 0
A点势能可表为 E p ( A )
Ep 0 A
f保 dr
§4.4 引力势能与弹性势能
2.势能曲线
Ep
Ep
Gm1m2 r
Gm1m2 r0
引力势能曲线
引力势能是空间变量
动量动量角动量角动量能量能量守恒量对称性时空性质空间平移空间平移空间转动空间转动时间平移时间平移空间均匀性空间均匀性空间各向同性空间各向同性时间均匀性时间均匀性守称守恒守恒空间反演对称性空间反演对称性安保是指为了达到安全的目的而进行的对人或物的保护活动安保工作是指为集体或个人的安全而进行保卫的各种活动
大学物理课件第4章-功和能
如图,求船从离岸 x1处移到 x2 处的 过程中,力 F 对船所作的功.
F
解:判别F 是否为变力作功(大小不变,方
向变元),功属于dW变力作F功.建dx立坐F标,取dx元过co程sa
h
o x2
a
dx x x1 x
cosa x
x2 h2 x
dW F dx
x2 h2
功在数值上等于示功图
F
曲线下的面积。
3. 功率
0 x1
x2 x
dx
平均功率: P =ΔΔWt
瞬时功率:
P
= lim
Δt 0
Δ Δ
Wt =
dW dt
=
F
. dr
dt
= F .v
[ 例1 ] 有一单摆，用一水平力作用于m
使其极其缓慢上升。当θ 由 0 增大到 0 时，
求: 此力的功。
{
F T sinθ T cosθ mg
两边平方
v 2 v12
由动量守恒
2v1
v2
v 22
v
v1
v2
由机械能守 恒（ 势能无变化）
v2
v12
v
2 2
v1 v2 0 两球速度总互相垂直
例8：已知半圆柱形光滑木凹槽，放在光滑桌面上，
如图，求质点下滑至最低点时给木块的压力.
解：
mv MV 0
•2.碰撞分类
正碰 斜碰
（从碰撞前后两球中心连线角度分类 ）
弹性碰撞 非弹性碰撞 完全非弹性碰撞
一般非弹性碰撞
（从碰撞能量损失角度分类）
例7：在平面上两相同的球做完全弹性碰撞，其中一球开始时处于
英文版大学物理 第三章
r r r W = F cos θ ∆r = F ∆r
Bead a Wire
θ
F
b
x
Signs for work θ < 90o, W > 0; θ > 90o, W < 0; θ = 90o, W = 0.
r r ∆r = ∆xi
Units for Work 1 N·m= 1 J
Work done by a variable constant force The work done on the particle in moving through r the small displacement dr due to the force is
Chapter 3 Work and Energy
3-1 Work and Power 3-2 Work−Kinetic Energy Theorem − 3-3 Conservative Force 3-4 Potential Energy 3-5 Calculating the Conservative Force from the Potential 3-6 Conservation of Mechanical Energy 3-7 Conservation of Energy
3-1 Work and Power Work done by a constant force Suppose that a bead can slide along a frictionless wire. r A constant force F directed at an angle θ to the wire, r r causes the bead to move a displacement ∆r = ∆xi The work done by the force is defined to be the product of the magnitude of the displacement and the r component of force that is parallel to the displacement.
Bead a Wire
θ
F
b
x
Signs for work θ < 90o, W > 0; θ > 90o, W < 0; θ = 90o, W = 0.
r r ∆r = ∆xi
Units for Work 1 N·m= 1 J
Work done by a variable constant force The work done on the particle in moving through r the small displacement dr due to the force is
Chapter 3 Work and Energy
3-1 Work and Power 3-2 Work−Kinetic Energy Theorem − 3-3 Conservative Force 3-4 Potential Energy 3-5 Calculating the Conservative Force from the Potential 3-6 Conservation of Mechanical Energy 3-7 Conservation of Energy
3-1 Work and Power Work done by a constant force Suppose that a bead can slide along a frictionless wire. r A constant force F directed at an angle θ to the wire, r r causes the bead to move a displacement ∆r = ∆xi The work done by the force is defined to be the product of the magnitude of the displacement and the r component of force that is parallel to the displacement.
(英文版)大学物理-力学
26
Dep. physics
1.NEWTON’S LAW
Newton’s First Law
An object at rest remains at rest, and an object in motion continues in motion with constant velocity (that is, constant speed in a straight line) unless it experiences a net external force.
v v u
t t
•Acceleration commutation
a a
y S u y S
r
P
r
O
R uti
O
x x
t t z
z
Dep. physics
v
x
vx
u
v
y
vy
v
z
vz
t t
ax a x ay a y az az
t t
S
F
ma
S
F
ma
动画
22
Summarizing:
Dep. physics
7
a
dv
dt
d 2r dt 2
a
dvx dt
i
dv y dt
j
dvz dt
k
d2 dt
x
2
i
d2y dt 2
j
d 2z dt 2
k
axi ay j azk
a a
ax2
a
2 y
az2
Dep. physics
cos ax a
cos ay a
Dep. physics
1.NEWTON’S LAW
Newton’s First Law
An object at rest remains at rest, and an object in motion continues in motion with constant velocity (that is, constant speed in a straight line) unless it experiences a net external force.
v v u
t t
•Acceleration commutation
a a
y S u y S
r
P
r
O
R uti
O
x x
t t z
z
Dep. physics
v
x
vx
u
v
y
vy
v
z
vz
t t
ax a x ay a y az az
t t
S
F
ma
S
F
ma
动画
22
Summarizing:
Dep. physics
7
a
dv
dt
d 2r dt 2
a
dvx dt
i
dv y dt
j
dvz dt
k
d2 dt
x
2
i
d2y dt 2
j
d 2z dt 2
k
axi ay j azk
a a
ax2
a
2 y
az2
Dep. physics
cos ax a
cos ay a
大学物理第4章 功与能work and energy(1)
2.动能的性质: 瞬时性;相对性
问题：
铅直下落的冰雹，质量为 m，某时刻的速率为v，试问从地 面上以速率v水平运动的车上观察，该冰雹的动能是多少？
（答案:mv2）
3.动能与动量的关系:
v v
v v
u
二 、动能定理 1. 质点的动能定理
合外力对质点所作的功, 等于质点动能的增量 .
质点运动的动能定理 合外力对质点所做的功等于质点动能的增量
典型的保守力： 重力、万有引力、弹性力 与保守力相对应的是非保守力，如摩擦力。
若质点沿任意闭合路径运动一周，保守力 对质点所做的功为零。
A保
Fdr l
Fdr ACB
F dr
BDA
F d r F d r
ACB
ADB
A C
解：（1）选择地球惯性系建立坐标系； （2）确定研究对象： 链条 设经时间 t 秒，链条下落 x （3）分析所受的力；重力和摩擦力 摩擦力:
f LL-- ax o
xa
（4）链条离开桌面过程中摩擦力所做的功
X
（5）下落过程重力做的功： （6）应用动能原理列方程解方程
链条刚刚离开桌面时的速率：
f L- x o x
例 一轻弹簧, 其一端 系在铅直放置的圆环的顶 点P，另一端系一质量为m 的小球, 小球穿过圆环并在 环上运动(μ =0)．开始球 静止于点 A, 弹簧处于自然 状态，其长为环半径R; 当球运动到环的底端点B时，球对环没有压 力．求弹簧的劲度系数．
解 以弹簧、小球和 地球为一系统
只有保守内力做功 系统
P.229 4.15
一质量为 m 的物体，从质量为M的圆弧形槽顶由静止滑下， 圆弧形槽的半径为R，张角为 900 。如果所有摩擦可以忽略。
大学物理 功和能汇总
0 1
2 动能定理： A 1 2 mv 0
2A v 4 m s m
[思考] 在 x =0 至 x =1m 过程中， F 的冲量？
10
§4.3 质点系的动能定理
Theorem of Kinetic Energy for a system of Particle
对第 i 质点 求和
O 张力不做功，重力做功： 用动能变化定理解：
l
m
T
A mg dl mg dl cos
mgl cos d mgl sin 0 1 2 mgl sin mv 2
ˆn e
v
mg
ˆt e
比直接解牛顿方程简单，但仍作积分运算。
13
§4.4 *柯尼希定理
i
14
一对力 的功
内力总是成对出现 dr1 两质点间的内力 f ij 和 f ji ,
B1
B2
dr2
f 12
称为一对力 f ij f ji
m1
r21
f 21
m2
A1
A2
一对力做的功之和
dA = f12 dr1 + f21 dr2
f 21 dr2 dr1 f 21 dr21
mi ac dri
m i ac
z
y
mi
= ac mi dri
ri
ac
C 质心 O
12
= ac d mi ri = 0 A i
B
x
=
0
【例】柔软细绳长为l，小球质量为m，求摆下至 角时小球的速度和绳的张力。
2 动能定理： A 1 2 mv 0
2A v 4 m s m
[思考] 在 x =0 至 x =1m 过程中， F 的冲量？
10
§4.3 质点系的动能定理
Theorem of Kinetic Energy for a system of Particle
对第 i 质点 求和
O 张力不做功，重力做功： 用动能变化定理解：
l
m
T
A mg dl mg dl cos
mgl cos d mgl sin 0 1 2 mgl sin mv 2
ˆn e
v
mg
ˆt e
比直接解牛顿方程简单，但仍作积分运算。
13
§4.4 *柯尼希定理
i
14
一对力 的功
内力总是成对出现 dr1 两质点间的内力 f ij 和 f ji ,
B1
B2
dr2
f 12
称为一对力 f ij f ji
m1
r21
f 21
m2
A1
A2
一对力做的功之和
dA = f12 dr1 + f21 dr2
f 21 dr2 dr1 f 21 dr21
mi ac dri
m i ac
z
y
mi
= ac mi dri
ri
ac
C 质心 O
12
= ac d mi ri = 0 A i
B
x
=
0
【例】柔软细绳长为l，小球质量为m，求摆下至 角时小球的速度和绳的张力。