大学物理功和能
大学物理第四章--功和能

a
l
xdx
2l
前已得出:
Af
mg(l a)2
2l
mg(l 2 a2 ) mg(l a)2 1 mv2
2l
2l
2
得v
g l
1
(l 2 a 2 ) (l a)2 2
§3 保守力的功与势能 一、 保守力
rB
B
两个质点之间的引力
B
第四章 功和能
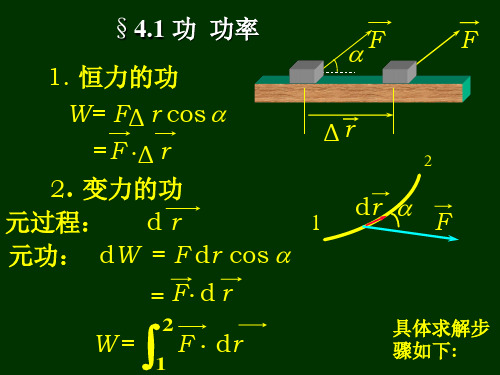
§4.1 功 §4.2 动能定理 §4.3 保守力功与势能 §4.4 功能原理机械能守恒定律
§1 功和功率
一、恒力做功 直线运动
A=Fcos S
记作A F S F r
F
F
M
M
S
位移无限小时:
dA
F
dr
dA称为元功
功等于质点受的力和它的位移的点积(标积)
例1一水平放置的弹簧,其一端固定,另一端系一小球,求小
球的位置由A到B的过程中弹力对它所做的功。(在O处弹簧无 形变)
解:根据胡克定律 F F kx
W F dr
xB Fdx
xA
xB xA
kxdx
O
1 2
A
k xB2
B
xA2
1 2
k xA2
作用在质点
上.在该质点从坐标原点运动到(0,2R)位
置过程中,力
F
对它所作的功为多少?
y
b
b
A a F.dr a (Fxdx Fydy)
R
x O
例4 如图,水平桌面上有质点 m ,桌面的摩 擦系数为μ 求:两种情况下摩擦力作的功
大学物理第04章_功和能

Ek
1 2
mv2
单位:(J)
设质点m在力的作用下沿 曲线从a点移动到b点
dr
b
元功:
F
dW F dr F cosds a
F cos
ma
m dv dt
dW
F
cosds m
dv ds dt
mvdv
总功:
W
dW
v2 v1
mvdv
1 2
m(v22
v12 )
质点的动能定理:
合外力对质点所做的功等于质点动能的增量。
对系统内所有质点求和
i
n
n
n
n
Wi内 Wi外 Ek2i Ek1i
fi
i 1
i 1
i 1
i 1
W内 W外 Ek 2 Ek1
质点系的动能定理:
质点系动能的增量等于作用于系统的所有外力和 内力作功之代数和。
值得注意:
内力做功可以改变系统 的总动能。
例3 如图所示,用质量为M的铁锤把质量为m 的钉子 敲入木板。设木板对钉子的阻力与钉子进入木板的深 度成正比。在铁锤敲打第一次时,能够把钉子敲入 1cm深,若铁锤第二次敲钉子的速度情况与第一次完 全相同,问第二次能把钉子敲入多深?
dxi dyj dzk
bx ax
Fxdx
by ay
Fydy
bz az
Fzdz
在自然坐标系中
F F e Fnen dr dse
W
b
F dr
a
b
a F e
Fnen
dse
s1 s0
F
ds
附:功率的定义:
功率是反映作功快慢程度的物理量。
功率: 单位时间内所作的功。
大学物理-力学中的功和能1

dh
drv
ϕ
mg
水平方向无外力,水平方向系统 动量守恒。
mv + MV = 0
V = − mv M
W重力
+ W内力
=
1 2
MV
2
+
1 2
mv
2
V = − mv M
对M,内力 N ’ 所做的功, 由质点的动能定理可得:
WN′
=
1 2
MV
2
=
m2v 2 2M
mN
M N’
对m,内力 N 所做的功
x1
y24dy
y1
∫ ∫ =
3 −2
x2 2
dx
+
9 4 4dy
1
4y = x+6
y
2.25
a 1
−2 O
= 10.8 J
x2 = 4y
b
3x
若质点沿直线运动
∫ ∫ ∫ W2 =
b a
(Fxdx
+
Fydy)
=
2 x2 ydx +
x1
y24dy
y1
∫ ∫ =
3 −2
1 2
(
x
+
6)d
x
+
9 4 4dy
Q2
?
例:有一面为 1/4 凹圆柱面(半径 R,质量 M),放置在 光滑水 平面上。一小球(质量 m),从静止开始沿圆柱面从顶端无摩擦 下落(如图),最终从水平方向以速度 v 飞离物体 ,求:1)此 过程中重力所做的功;2)内力所做的功。
m M
解:重力只对小球做功
R dW重力 = mg drv cosϕ = mgdh
大学物理ch3 功和能

= mg tanθ cosθ ds
= mgL tan θ cos θdθ
0 θ0
= mgL(1 − cos θ0 )
2
2016/3/3
书中例题3.2 (p.98)(重点) 一条长L,质量M的均匀柔绳,A端挂在天花板上,自然下垂,将 B端沿铅直方向提高到与A端同高处。 求:该过程中重力所作的功。 解:提升高度y时,提的链长y/2 提起部分的质量
力与位移的夹角在变的例子
求 θ = θ0 时,F 作的功。
解
例 已知用力 F 缓慢拉质量为m 的小球,F 保持方向不变
3.2 几种常见力的功
一.重力的功
重力mg 在曲线路径 M1M2 上的功为
z
Z2
M1
②
F − T sin θ = 0
T cosθ − mg = 0
F = mg tanθ A = F ⋅ dr = F cosθ ds
m1
Ai = Ai外 + Ai内
i i i
讨论 (1) 内力和为零,内力功的和 是否为零? 不一定为零
v m2 2 v4 m3 v3
f1
B A S
v1 m4
∵功是标量,其和为代数和。 内力总是成对出现的,按照牛顿第三定律,这一对力 的矢量和为0,但这一对力所作的功的和不一定为0。
f2
b0 =
μ0 l 1 + μ0
1 1 1 ρg (l 2 − b 2 ) − μρg (l − b) 2 = ρlv 2 − 0 2 2 2
v=
当 y >b0 ,拉力大于最大静摩擦力时,链条将开始滑动。
g 2 2 μg (l − b ) − (l − b) 2 l l
大学物理课件第4章-功和能
如图,求船从离岸 x1处移到 x2 处的 过程中,力 F 对船所作的功.
F
解:判别F 是否为变力作功(大小不变,方
向变元),功属于dW变力作F功.建dx立坐F标,取dx元过co程sa
h
o x2
a
dx x x1 x
cosa x
x2 h2 x
dW F dx
x2 h2
功在数值上等于示功图
F
曲线下的面积。
3. 功率
0 x1
x2 x
dx
平均功率: P =ΔΔWt
瞬时功率:
P
= lim
Δt 0
Δ Δ
Wt =
dW dt
=
F
. dr
dt
= F .v
[ 例1 ] 有一单摆,用一水平力作用于m
使其极其缓慢上升。当θ 由 0 增大到 0 时,
求: 此力的功。
{
F T sinθ T cosθ mg
两边平方
v 2 v12
由动量守恒
2v1
v2
v 22
v
v1
v2
由机械能守 恒( 势能无变化)
v2
v12
v
2 2
v1 v2 0 两球速度总互相垂直
例8:已知半圆柱形光滑木凹槽,放在光滑桌面上,
如图,求质点下滑至最低点时给木块的压力.
解:
mv MV 0
•2.碰撞分类
正碰 斜碰
(从碰撞前后两球中心连线角度分类 )
弹性碰撞 非弹性碰撞 完全非弹性碰撞
一般非弹性碰撞
(从碰撞能量损失角度分类)
例7:在平面上两相同的球做完全弹性碰撞,其中一球开始时处于
大学物理之功、能、能量守恒定律

大学物理之功、能、能量守恒定律
功
1、恒力做功(矢量的标积)。
2、变力做功(微分形式、矢量的标积)。
3、功率。
动能
1、公式及动能定理。
2、刚体的动能及其动能定理(转动的问题)。
势能
1、重力势能公式、重力的功等于重力势能增量的负值。
2、弹性势能公式、弹性力的功等于弹性势能增量的负值。
3、引力势能公式、万有引力的功等于引力势能增量的负值。
保守力和非保守力
保守力做功只与物体的始末位置有关和路径无关。
保守力做正功,系统的势能减少。
保守力做负功,系统的势能增加。
物体沿闭合路径绕行一周,保守力的功等于零。
非保守力如摩擦力,做功与路径有关。
能量守恒定律(机械能、非机械能)(保守力、非保守力)
1、一孤立系统的各种形式的能量保持不变,成为能俩功能守恒。
2、孤立系统中,机械能增加或减少时就有等量的非机械能减少或增加,从而保持机械能和非机械能之和不变。
3、孤立系统内只有保守力做功时,机械能保持不变。
4、外力和系统内非保守力所做功的总和,等于系统机械能的增量,称为系统的功能原理。
多做题,多分析,多复习。
大学物理功和能课件讲义

解: 以雪橇、冰道和地球为一系统,由功能原理得
Af E2 E1
E2 E1 mgh
Af mg cos s' mgs mg(s's)
mg(s's) mgh
代入已知数据有 s h s' 500m
例4.5 一半径为 R的四分之一圆弧垂直固定于地面上,
止,距离为a. 在万有引力作用下,
两者距离变为b. 在此过程中,万有引
力做的功A=.
解: A Epa Epb
( Gm2 ) ( Gm2 )
a
b
Gm2 (a b)
ab
[思考]两者距离为b时的速率?
[例4-8] 质量为m的质点在指向圆心的力
F=k/r2 的作用下,作半径为r的
圆周运动,若取Ep=0,则系统的机
2. 力学中常见的势能函数
(1) 万有引力势能
由
Aab
(
Gm1m2 ra
) (
Gm1m2 rb
)
=
EPa-EPb
以r→∞时为万有引力势能零点,即令 EPy 0
由任一状态势能值的定义,可得 两物体相距r时的万有引力势能
EP引
EP引
Gm1m2 dr Gm1m2
r
r2
r
O
r
E
P引
G m1m 2 r
一、保守力的定义
1.万有引力的功 —与路径无关 rb
dr
dA以MF处G Md为rm原点rG,Mr2m
r0
dr
r2
dr r
M
r
ra m
(r0
r) r
GMm
r 2 dr
rb
A
rb
ra
大学物理-力学中的功和能1

§1 功 Work
一、功的概念
功的两要素
力 在力的方向上的位移
二、恒力的功
v
W W
= F ∆rv cosθ
= Fv ⋅ ∆rv
=
Fr
∆rv
讨论: 功是标量,但有正负
Fn
F
θ
∆rv
Fr
0≤θ
<
π 2
,W
>0
π 2
<
θ
≤
π,
W
<0
θ
=
π 2
,W
=0
三、变力的功
元功
dW
=
v F
⋅ drv
b
质点从 a → b 的功 A
W=
b
∫
Fv
⋅
drv
=
b
∫
F
drv
cosθ
b
= ∫ F cosθ ds
a( L)
a( L)
a( L)
drv θ
v F
a (L)
直角坐标系中
v F
=
v Fxi
+
F
y
v j
+
v Fz k
drv = dxiv + dyvj + dzkv
∫ ( ) ∫ W =
Fydy)
=
2 x2 ydx +
x1
y24dy
y1
∫ ∫ =
3 −2
1 2
(
x
+
6)d
x
+
9 4 4dy
1
= 21.25 J
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第四章 功和能
P88-92习题:3、4、5、12、13、14、19、23、27、30、36、
一. 选择题:
3.如图4-18所示,一质点在如图所示的坐标平面内作圆周运动,有一力
0()+F =F i j x y 作用在质点上.在该质点从坐标原点运动到(0,2R )位置过程中,力F 对它所作的功为( )。
(A) 20R F . (B) 2
02R F .
(C) 2
03R F . (D) 2
04R F .
[ ]
4.如图4-19所示,,木块m 沿固定的光滑斜面下滑,当下降h 高度时,重力作功的瞬时功率是( )。
(A)2
1)
2(gh mg . (B)2
1)
2(cos gh mg θ.
(C)1()21/2
mgsin θgh (D) (2)1/2mgsin θgh
[ ]
5.质量为m =0.5 kg 的质点,在Oxy 坐标平面内运动,其运动方程为x =5t ,y =0.5t 2(SI ),从t =2 s 到t =4 s 这段时间内,外力对质点作的功为( )。
(A) 1.5 J . (B) 3 J .
(C) 4.5 J .
(D) -1.5 J .
[ ]
二. 填空题:
12 .已知地球质量为M ,半径为R .一质量为m 的火箭从地面上升到距地面高度为2R 处.在此过程中,地球引力对火箭作的功为_____________________.
13.某质点在力F =(4+5x )i (SI)的作用下沿x 轴作直线运动,在从x =0移动到x =10 m 的过程中,力F 所做的功为__________.
图4-18 习题4-3图 图4-19 习题4-4图
14.二质点的质量各为m 1,m 2.当它们之间的距离由a 缩短到b 时,它们之间万有引力所做的功为_ __.
19.如图4-24所示,劲度系数为k 的弹簧,一端固定在墙壁上,另一端连一质量
为m 的物体,物体在坐标原点O 时弹簧长度为原长.物体与桌面间的摩擦系数为μ.若物体在不变的外力F 作用下向右移动,则物体到达最远位置时系统的弹性势能E P =_____.
23.如图4-27所示,劲度系数为k 的弹簧,上端固定,下端悬挂重物.当弹簧伸长x 0,
重物在O 处达到平衡,现取重物在O 处时各种势能均为零,则当弹簧长度为原长时,系统的重力势能为_ ____;系统的弹性势能为 ;系统的总势能为 . (答案用k 和x 0表示)
三. 计算题:
27.如图4-28所示,质量m 为 0.1 kg 的木块,在一个水平面上和一个劲度系数k 为20 N/m 的轻弹簧碰撞,木块将弹簧由原长压缩了x = 0.4 m .假设木块与水平面间的滑动摩擦系数μ k 为0.25,
问在将要发生碰撞时木块的速率v 为多少?
图4-27 习题4-23图
图4-28 习题4-27图
30.质量分别为m和M的两个粒子,最初处在静止状态,并且彼此相距无穷远.以后,由于万有引力的作用,它们彼此接近.求:当它们之间的距离为d时,它们的相对速度多大?
36.在一光滑水平面上,有一轻弹簧,一端固定,一端连接一质量m = 1 kg 的Array滑块,如图4-35所示.弹簧自然长度l0= 0.2 m,劲度系数k =100 N·m-1. 设t =
0时,弹簧长度为l0,滑块速度v0 = 5 m·s-1,方向与弹簧垂直.以后某一时刻,
弹簧长度l =0.5 m.求该时刻滑块速度v的大小和夹角θ .
图4-35 习题4-36。
