(完整版)布尔函数参考答案
具有K阶代数免疫的布尔函数

( o eeo t mac , hn zo nvri , hnzo 5 0 1C ia C l g f l Ma e ts Z e ghuU iesy Z egh u40 0 , hn ) h i t
Abta t: g bac i sr c Ale ri mmu i sa otn d xt auetea it eitag b acatc .I oe nfn t n h salw g — nt i li y l mp r tn e me s r bfyt rss le ri t k faBo la u ci a o a e a i o h i o a o l baci ri mmu i nt y.i c n t eitteag  ̄acatc .Ac odn oteag baci t a o ss e i t k n r h l a c rig t h le ri mmu ed ge faBo la u cinwi 一fr l e r n e reo oe nf n t t 1 om i a o h n
定义 3 若,为 n元布尔 函数 ,
.
.
.
是 它 的
处的 wl ah循环谱定义为: ∽ ):2 s s( ∑
( ) 一1 一。
收 稿 日期 :0 0 0 — 5; 回 日期 :00 0 一 8 2 1— 6 2 修 2 1 — 9 I
作者简介 : 张毛优 (9 5 , , 18 一) 女 硕士研究 生, 研究 方向为布尔 函数 、
记 为 n() 其 中 z 所有 的线 性 函 数 。 l , f 为
定 义 2若 E F , 中 1 ; 的个 数 称 为 的重 量 , 记 为 z ) c 。 , (
数字逻辑电路 第三章 布尔代数与逻辑函数化简(52P)

例4 F=AD+AD+AB+AC+BD+ACEG+BEG+DEGH 解: 原式=A+AB+AC+BD+ACEG+BEG+DEGH (吸收律1)
=A+AC+BD+BEG+DEGH (吸收律2)
=A+C+BD+BEG+DEGH(吸收律3) =A+C+BD+BEG (多余项定律)
例5
F=AB+BC+BC+AB F=AB+BC+BC(A+A)+AB(C+C) (互补律A+A=1) =AB+BC+ABC+ABC+ABC+ABC (分配律) =AB+BC+ABC+ABC+ABC(吸收律2: AB+ABC=AB) =AB+BC+ABC+ABC (吸收律2: BC+ABC=BC) =AB+BC+AC(吸收律1:ABC+ABC=AC)
反函数
③ 反演法则
例:求F A B C D E的反函数F
F A B C D E A B C D E A BC D E A BC DE
上述过程要反复应用求反律。而利用反演法则直接写出结果。
F A B C D E
3.1.3 基本公式应用
5.交换律
6.结合律 7.分配律 8.吸收律1
A· B= B· A
A· (B· C)= (A· B)· C A(B+C)=AB+AC (A+B)(A+B)=A
数字逻辑随堂练习答案

*数字逻辑o第一章进位计数制o第二章、布尔代数▪第一节、“与”“或”“非”逻辑运算的基本定义▪第二节、布尔代数的基本公式及规则▪第三节、逻辑函数的代数化简法▪第四节、逻辑函数的图解化简法▪第五节、逻辑函数的列表化简法o第三章组合逻辑电路的设计▪第一节、常用门电路▪第二节、半加器和全加器的分析▪第三节译码器的分析▪第四节、其它常用电路分析o第四章组合逻辑函数的设计▪第一节、采用门电路实现组合逻辑电路的设计▪第二节、转化成“与非”“或非”“与或非”形式▪第三节、组合电路设计中几个问题的考虑▪第四节、组合逻辑电路设计举例o第五章大规模集成电路▪第一节、由中规模器件构成的组合逻辑电路▪第二节、由中规模器件构成的组合逻辑电路设计▪第三节、采用只读存贮器实现组合逻辑电路设计▪第四节、组合逻辑电路中的竞争与险象*o第六章时序电路的分析▪第一节、同步时序电路▪第二节、触发器的逻辑符号及外部特性▪第三节、时序电路的状态表和状态图▪第四节、同步时序电路的分析方法o第七章同步时序电路的设计▪第一节、概述▪第二节、形成原始状态表的方法▪第三节、状态化简▪第四节、同步时序电路设计举例▪第五节、状态编码*o第八章异步时序电路的分析和设计▪第一节、脉冲异步电路的分析和设计▪第二节、电平异步电路概述▪第三节、电平异步电路分析▪第四节、电平异步电路的设计▪第五节、时序电路中的竞争与险象*o第九章数字逻辑计算机辅助设计方法▪3 / 205 / 207 / 209 / 2011 / 20A. B. C. D. 参考答案:D13 / 2015 / 2017 / 20。
布尔函数a (b∧c)

布尔函数a (b∧c)布尔函数是一种逻辑函数,它将一个或多个二进制变量映射到一个二进制输出变量。
其中,布尔代数是一种基于逻辑运算的代数,由这些逻辑运算构成。
其中的一个经典的布尔函数是“a (b∧c)”,它是针对三个输入变量a、b、c的值进行的逻辑运算,并输出布尔值的函数。
下面将对这个经典的布尔函数进行详细的分析:第一步:研究布尔函数的表达式“a (b∧c)”是这个布尔函数的一个基本表达式,意思是当变量b和c都为1时,如果a也为1,则该函数输出1,否则输出0。
因此,我们可以检查该函数表的输出结果,如下所示:a b c a(b∧c)0 0 0 00 0 1 00 1 0 00 1 1 01 0 0 01 0 1 01 1 0 01 1 1 1这张表中包含了该布尔函数的所有输入和输出的组合,我们可以根据这张表来检验该布尔函数的正确性。
第二步:分离布尔函数的各个部分针对布尔函数“a (b∧c)”,我们可以将它分解为两个子函数,即“b∧c”和“a (b∧c)”。
其中,“b∧c”函数意思是当输入变量b 和c都为1时,输出1,否则输出0,也被称为“与门”。
而“a(b∧c)”是由布尔乘积和逻辑运算符组成的一个短语,其中的逻辑运算符是“或门”,其意思是当输入变量a或者子函数“b∧c”中的一个或多个变量为1时,输出1,否则输出0。
第三步:实现布尔函数的计算为了计算“a (b∧c)”这个布尔函数,我们需要使用基本的逻辑运算,例如布尔乘积和逻辑或运算。
针对“b∧c”,我们可以将它表示为“NOT (NOT b OR NOT c)”的形式。
接着,我们将其代入“a(b∧c)”表示式中,得到以下形式:a (b∧c) = a AND (NOT (NOTb OR NOT c))接着,我们可以使用计算机程序来计算这个布尔函数的逻辑结果。
下面是Python代码实现该布尔函数的计算:def boolFuncA(a, b, c):return a and (not (not b or not c))boolFuncA(0, 0, 0) # 0boolFuncA(0, 0, 1) # 0boolFuncA(0, 1, 0) # 0boolFuncA(0, 1, 1) # 0boolFuncA(1, 0, 0) # 0boolFuncA(1, 0, 1) # 0boolFuncA(1, 1, 0) # 0boolFuncA(1, 1, 1) # 1这段代码首先定义了一个名为“boolFuncA”的函数,在函数体内实现了该布尔函数的计算。
函数习题及答案精选全文完整版

可编辑修改精选全文完整版函数习题一.选择题1.以下正确的说法是 B 。
A)用户若需要调用标准库函数,调用前必须重新定义B)用户可以重新定义标准库函数,如若此,该函数将失去原有定义C)系统不允许用户重新定义标准库函数D)用户若需要使用标准库函数,调用前不必使用预处理命令将该函数所在的头文件包含编译,系统会自动调用。
2.以下正确的函数定义是 D 。
A)double fun(int x, int y) B)double fun(int x,y){ z=x+y ; return z ; } { int z ; return z ;}C)fun (x,y) D)double fun (int x, int y){ int x, y ; double z ; { double z ;z=x+y ; return z ; } return z ; }3.以下正确的说法是 D 。
A)实参和与其对应的形参各占用独立的存储单元B)实参和与其对应的形参共占用一个存储单元C)只有当实参和与其对应的形参同名时才共占用相同的存储单元D)形参时虚拟的,不占用存储单元4.以下正确的函数声明是 C 。
A)double fun(int x , int y) B)double fun(int x ; int y)C)double fun(int x , int y) ; D)double fun(int x,y)5.若调用一个函数,且此函数中没有return语句,则正确的说法是 D 。
A)该函数没有返回值B)该函数返回若干个系统默认值C)能返回一个用户所希望的函数值D)返回一个不确定的值6.以下不正确的说法是 B 。
A)实参可以是常量,变量或表达式B)形参可以是常量,变量或表达式C)实参可以为任意类型D)如果形参和实参的类型不一致,以形参类型为准7.C语言规定,简单变量做实参时,它和对应的形参之间的数据传递方式是 B 。
A)地址传递B)值传递C)有实参传给形参,再由形参传给实参D)由用户指定传递方式8.C语言规定,函数返回值的类型是由 D 决定的。
第三章:布尔代数分析与数字电路逻辑化简表示(不同的展开方式)
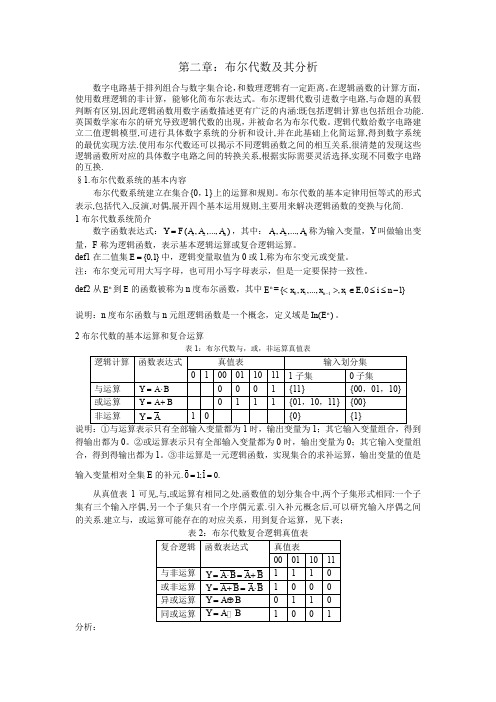
第二章:布尔代数及其分析数字电路基于排列组合与数字集合论,和数理逻辑有一定距离。
在逻辑函数的计算方面,使用数理逻辑的非计算,能够化简布尔表达式。
布尔逻辑代数引进数字电路,与命题的真假判断有区别,因此逻辑函数用数字函数描述更有广泛的内涵:既包括逻辑计算也包括组合功能.英国数学家布尔的研究导致逻辑代数的出现,并被命名为布尔代数。
逻辑代数给数字电路建立二值逻辑模型,可进行具体数字系统的分析和设计,并在此基础上化简运算,得到数字系统的最优实现方法.使用布尔代数还可以揭示不同逻辑函数之间的相互关系,很清楚的发现这些逻辑函数所对应的具体数字电路之间的转换关系,根据实际需要灵活选择,实现不同数字电路的互换.§1.布尔代数系统的基本内容布尔代数系统建立在集合{0,1}上的运算和规则。
布尔代数的基本定律用恒等式的形式表示,包括代入,反演,对偶,展开四个基本运用规则,主要用来解决逻辑函数的变换与化简. 1布尔代数系统简介数字函数表达式:12(,,...,)n Y F A A A =,其中:12,,...,n A A A 称为输入变量,Y 叫做输出变量,F 称为逻辑函数,表示基本逻辑运算或复合逻辑运算。
def1在二值集{0,1}E =中,逻辑变量取值为0或1,称为布尔变元或变量。
注:布尔变元可用大写字母,也可用小写字母表示,但是一定要保持一致性。
def2从n E 到E 的函数被称为n 度布尔函数,其中n E =011{,,...,,,01}n i x x x x E i n -<>∈≤≤- 说明:n 度布尔函数与n 元组逻辑函数是一个概念,定义域是()n In E 。
2布尔代数的基本运算和复合运算表1:布尔代数与,或,非运算真值表说明:①与运算表示只有全部输入变量都为1时,输出变量为1;其它输入变量组合,得到得输出都为0。
②或运算表示只有全部输入变量都为0时,输出变量为0;其它输入变量组合,得到得输出都为1。
《编译原理》课后习题答案第二章

4、试为文法G[P]:
P∷=begin S end S∷=A|C
A∷=V:=E C∷=if E then S
E∷=V E∷=E+V V∷=i
采用某种程序设计语言构造递归下降识别程序。
解:由于文法存在左递归,进行文法等价变换,得到等价文法G′[P]:
步骤三检查可得f的值与原有的优先矩阵一致所以上表函数即为所求优先函数bell有向图法形式化步骤一构造布尔矩阵b步骤二使用warshall算法构造布尔矩阵b1521步骤三则优先函数为
第二章
习题1
6.答:省略表示法:{1.3,1.33,1.333…};描述表示法:{1.3i|i=1,2,3…}
7.答:x+={0,12,123,1234…};
最小化:
(2)由e构造转换系统:
去ε弧及无用状态和死状态:
因为现在只有一个状态,所以无需再最小化,此时就是最小化.
13.解:建立方程组如下:
W=Ua+Vb ①
U=Va+c ②
V=Ub+c ③
把③代入②得,U=(Ub+c)a+c
=Uba+ca+c
把它改写成U=(ca+c){ba},因此U=(ca|c){ba} ④
follow(E)={#,)}
follow(E′)={#,)}
follow(T)={#,),+,-}
follow(T′)={#,),+,-}
follow(F)={*,/,#,),+,-}
识别输入符号串i*i-(i+i)/i,则识别过程
步骤 栈 输入 输出
0 #E i*i-(i+i)/i# E∷=TE′
《数字电子技术(第三版)》3布尔代数与逻辑函数化简

《数字电子技术(第三版)》3布尔代数与逻辑函数化简数字电子技术第3章布而代数与逻辑函数化简学习要点:学习要点:三种基本运算,基本公式、定理和规则。
逻辑函数及其表示方法。
逻辑函数的公式化简法与卡诺图化简法。
无关项及其在逻辑函数化简中的应用。
3.1基本公式和规则3.1.1逻辑代数的公式和定理(1)常量之间的关系与运算:00=001=010=011=1或运算:0+0=0非运算:1=00+1=10=11+0=11+1=1(2)基本公式A+0=A0-1律:A1=A互补律:A+A=1A+1=1A0=0AA=0双重否定律:A=A等幂律:A+A=A(3)基本定理AB=BA交换律:A+B=B+A(AB)C=A(BC)结合律:(A+B)+C=A+(B+C)A00A(B+C)=AB+AC1分配律:A+BC=(A+B)(A+C)1BA.BB.A000100000111A.B=A+B反演律(摩根定律):A+B=AB证明分配率:A+BC=(A+B)(A+C)证明:证明:(A+B)(A+C)=AA+AB+AC+BC=A+AB+AC+BC=A(1+B+C)+BC=A+BC分配率A(B+C)=AB+AC等幂率AA=A等幂率AA=A分配率A(B+C)=AB+AC0-1率A+1=1(4)常用公式AB+AB=A还原律:(A+B)(A+B)=AA+AB=A吸收率:A(A+B)=AA(A+B)=ABA+AB=A+B证:A+AB=(A+A)(A+B)明分配率A+BC=(A+B)(A+C)互补率A+A=1互补率A+A=10-1率A·1=11=1 =1(A+B)=A+B冗余律:AB+AC+BC=AB+AC证明:AB+AC+BC=AB+AC+(A+A)BC=AB+AC+ABC+ABC互补率A+A=1互补率A+A=1分配率A(B+C)=AB+AC0-1率A+1=1=AB(1+C)+AC(1+B)3.1.2逻辑代数运算的基本法则(1)代入法则:任何一个含有变量A的等式,如果将所有出现A的位置都用同一个逻辑函数代替,则等式仍然成立。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
湖北大学研究生课程考试参考答案及评分标准
一、概念题参考答案及评分标准:
1.设是二元有限域,n 为正整数,是上的n 维向量空间,从到的2F n F 22F n F 22F 映射:称为n 元布尔函数.
22:F F f n →一个n 元布尔函数可以表示为上的含n 个变元的多项式:
f 2F ∑∈++++++=
2
)
1()1)(1)(,,(),,(22112
1
21F a n n n
n i a x a x a x
a a a f x x x f .
n i a
n a
a
F a n x x x a a a f 212
2121),,(∑
∈=
这里表示中的加法运算,即模2的加法运算.形如上式的表示
()1
1n
i i i x a =++∏2F 称为布尔函数的小项表示.若将小项表示展开并合并同类项,则会得到如下形f 式的一个多项式:
n
n n
j i i i i i n
j i j i
j i n
i i i n x x a x x a
x x a
x a a x x x f d d
1,11,1,102111),,(++++
+=∑∑∑≤<<≤≤<≤=这里系数.
∈j i a ,2F 评分标准:答出n 元布尔函数的定义得5分,答出其多项式表示得5分.
2布尔函数的安全性指标主要有:平衡性、代数次数、差分均匀度、非线性度、相关免疫阶、弹性阶和代数免疫度等等.
平衡性:一个n 元布尔函数是平衡的,当且仅当其真值表中0和1的个数相同,也就是该布尔函数的Hamming 重量为.
12n -代数次数:密码体制中使用的布尔函数通常具有高的代数次数.差分均匀度:设是一个n 元布尔函数,其差分均匀度定义为
.
2
220max max {|()()}n n f F a F x F f x a f x βδβ∈≠∈=∈+-=非线性度:的非线性度定义为和所有仿射函数的最小Hamming 距离:
f ()NL f f .
()min (,)min ()n
n
l A l A NL f d f l wt f l ∈∈==-相关免疫阶:设是一个n 元布尔函数,其中是上独立且均匀分布的随机变量,如果与中任意个变元统计独立,则称是m 阶相关免疫函数。
评分标准:每个指标2分,答出其中5个得10分.
3.(10分)设,,.线性空间中的子集合
1m ≥2m n =0r m ≤≤2n F 2(,){|,deg }
n f m RM r m c F f B f r =∈∈≤叫做r 阶的二元Reed-Muller 码其中为全体布尔函数的集合
m B 二、证明题答题要点及评分标准:
1.(1)(10分)根据循环Walsh 谱的定义,得到
2()()(1)
n
f x x f x F W ω
ω+∈=
-∑A 22{|()}{|()}
n n x F f x x x F f x x ωω=∈=-∈≠A A 22()
n t f x ωω=-+A (2)(10分)根据循环Walsh 谱的定义,得到
22()n
f
F W
ωω∈∑222()()(1)
(1)
n n
n
f x x f y y F x F y F ω
ω
ω++∈∈∈=
--∑∑∑A A 222()()
()
(1)
(1)n n
n
f x f y x y x F y F F ωω++∈∈∈⎛⎫=
-- ⎪ ⎪⎝⎭
∑∑∑A 2222n
n n
x y F =∈=
=∑
倒数第二个等号成立是因为仅当时取值,其他时候取值均为
2(1)n
x
F ω
ω∈-∑A 0x =2n 0.
2.证明:定义的对偶函数如下:()f x ()f
x ()()()220,2;1,2,
n
f x n f x W f x W ⎧
=⎪=⎨⎪=-⎩
运用Walsh 变换的性质得出,即也是Bent 函数.(4分)()2
2n f W a =± ()f x 再证明n 元布尔函数是Bent 函数当且仅当矩阵
()f x ()()222
,,,[2]n
n n f f u v F u v F B h u v W u v -∈∈'==+⎢⎥⎣⎦是一个的Hadamard 矩阵.(6分)n n 22⨯最后证明原命题:
(必要性)是Bent 函数则也是Bent 函数.()f x ()f x 通过,得出矩阵
()()
2
21n
u v
f W u v -++=- ()()
()
()2
2
22
,,,,[1][2]n n n n
f u v f f u v F u v F u v F H h u v W u v B -
+∈∈∈==-=+=⎢⎥⎣⎦
是Hadamard 矩阵;(5分)
(充分性)由.
()()()
2
2,,,[1]n n f x y x y F u v F H h x y +∈∈==-⎢⎥⎣⎦得出
()
()
()
()
212n f x f x y n x F y δ++∈-=∑将上式两边同时乘以,并对求和得到即,则
()1y u
⋅-y ()22
n
f
W
u =()2
2n f W u =±是Bent 函数. (5分)
()f x 3.证明:先利用McEliece 定理,证明若是相关免疫函数,,则
()f x 1m n ≤- ,对任意.(5分)
()110
mod 2
n m m d f W a --⎢⎥++⎢⎥
⎣⎦
≡2n a F ∈于是
()2
1
max 2n
m f a F W a +∈≥再结合即得()2
11
()2max 2n
n f a F NL f W a -∈=-
.(5分)
1()22n m NL f -≤-类似的,若是m 阶弹性函数
()f x ,对任意.(5分)
()220
mod 2
n m m d f W a --⎢⎥++⎢⎣⎦
≡2n a F ∈再结合即得()211
()2max 2n
n f a F NL f W a -∈=-.(5分)
11()22n m NL f -+≤-4. 证明:记为所有代数次数不超过的n 元单项式构成的集合;
T 2n ⎡⎤
⎢⎥⎢⎥
令,则
{}|Tf fX X T =∈,
(5分)222n n i n T Tf i ⎡⎤⎢⎥⎢⎥
⎛⎫
+=> ⎪⎝⎭
∑注意到T 中所有元素线性无关,从而
,
0X
Y X T
Y T
a
X a fY ∈∈+=∑∑其中,,且存在某个.令
X a 2Y a F ∈0Y a ≠,,
X
X T
h a
X ∈=
∑Y Y T
g a Y ∈=∑则
,(5分)
0f gh +=其中.
0,deg ,deg 2n g g h ⎡⎤
≠≤⎢⎥⎢⎥
于是,若,则,否则,所以
0h =0fg =()10f h +=(5分).
()2n AI f ⎡⎤
≤⎢⎥⎢⎥
因为是到的映射,总有,于是
f 2n F 2F ()10f f +=(5分)
()deg AI f f ≤。
