剪力弯矩计算.ppt
合集下载
剪力和弯矩计算
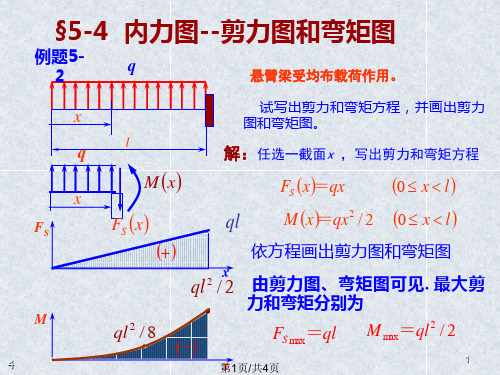
力和弯矩分别为
ql 2 / 8
FS max＝ql
第x 1页/共4页
M max＝ql 2 / 2
1
例题5-3
F
a
b
A
C
x1 x2
FAY
l
FS Fb / l
Fa / l
Fab/ l
M
图示简支梁C点受集中力作用。
试写出剪力和弯矩方程，并 B 画出剪力图和弯矩图。
解：1．确定约束力
FBY
M A＝0， MB＝0
FAy＝Fb/l FBy＝Fa/l
2．写出剪力和弯矩方程
x AC
FS x1＝Fb / l 0 x1 a
M x1＝Fbx1 / l 0 x1 a
CB FS x2 ＝ Fa / l a x2 l
M x2 ＝Fal x2 / l a x2 l
3x. 依方程画出剪力图和弯矩图2
第2页/共4页
FAy＝ FBy＝ ql/2
2．写出剪力和弯矩方程
x
ql / 2
FS x＝ql / 2 qx
0 x l
ql 2 / 8
M 3ql2 / 32
3ql2 / 32
Mx＝qlx / 2 qx2 / 2 0 x l
3. 依方程画出剪力图和弯矩
x 图。
4
第4页/共4页
Mb / l
CB FS x2 ＝M / l 0 x2 b
M x2 ＝ Mx2 / l 0 x2 b
3. 依方程画出剪力图和弯矩图
3
第3页/共4页
Байду номын сангаас题5-5
简支梁受均布载荷作用
y
q
A xC
FAY
l
试写出剪力和弯矩方程
剪力与弯矩的计算方法
§7-2剪力与弯矩一、剪力和弯矩根据作用在梁上的已知载荷，求出静定梁的支座反力以后，梁横截面上的内力可利用前面讲过的“截面法”来求解，如图7-8a 所示简支梁在外力作用下处于平衡状态，现在讨论距A 支座距离为x 的m m -截面上的内力。
图7-8简支梁指定截面的剪力、弯矩计算根据截面法计算内力的基本步骤“切、代、平”，计算梁的内力的步骤为：①、首先根据静力平衡方程求支座反力Ay F 和By F ，为推导计算的一般过程，暂且用Ay F 和By F 代替。
②、用截面假想沿m m -处把梁切开为左、右两段，如图7-8b、7-8c 所示，取左段梁为脱离体，因梁原来处于平衡状态，所以被截取的左段梁也同样保持平衡状态。
从图7-8b 中可看到，左段梁上有一向上的支座反力Ay F 、向下的已知力1P 作用，要使左段梁不发生竖向移动，则在m m -截面上必定存在一个竖直方向的内力S F 与之平衡；同时，Ay F 、1P 对m m -截面形心O 点有一个力矩，会引起左段梁转动，为了使其不发生转动，在m m -截面上必须有一个力偶矩M 与之平衡，才能保持左段梁的平衡。
S F 和M 即为梁横截面上的内力，其中内力S F 使横截面有被剪开的趋势，称为剪力；力偶矩M 将使梁发生弯曲变形，称为弯矩。
由于外载荷的作用线垂直于梁的轴线，所以轴力为零，通常不予考虑。
剪力S F 和弯矩M 的大小可由左段梁的静力平衡方程来求解。
由0=∑Y 得：10Ay S F P F --=，得1S Ay F F P =-由0o M =∑得：()01=+-+-M a x P x F Ay 得()a x P x F M Ay --=1如图7-8c 所示，如果取右段梁为脱离体，同样可求得m m -截面的剪力S F 和弯矩M 。
根据作用力与反作用力原理，右段梁在m m -截面上的剪力S F 和弯矩M 与左段梁在m m -截面上的剪力S F 和弯矩M 应大小相等，方向相反。
梁的剪力图与弯矩
梁的剪力图与弯矩
目录 CONTENT
• 梁的剪力与弯矩的基本概念 • 梁的剪力图 • 梁的弯矩图 • 剪力与弯矩的关系 • 梁的剪力与弯矩的实例分析
01
梁的剪力与弯矩的基本概 念
剪力与弯矩的定义
剪力
剪力是作用在梁上的垂直力，它 使梁产生剪切变形。剪力通常用 Q表示，单位为牛顿或千牛顿。
弯矩
弯矩是作用在梁上的力矩，它使 梁产生弯曲变形。弯矩通常用M 表示，单位为牛顿米或千牛顿米 。
在梁的跨中位置，剪力图的峰值最大，而在梁的 支座位置，剪力图的谷值最小。
随着梁上载荷的增加，剪力图的峰值逐渐增大， 谷值逐渐减小。
03
梁的弯矩图
弯矩图的绘制方法
1 2
截面法
通过分析梁在不同截面上的弯矩值，绘制出弯矩 图。
叠加法
将多个弯矩值叠加起来，绘制出弯矩图。
3
微分法
利用弯矩函数的微分性质，绘制出弯矩图。
剪力与弯矩的符号规定
剪力的正负号规定
在截面左侧上作用的剪力为正，反之 为负。
弯矩的正负号规定
在截面左侧上作用的弯矩为正，反之 为负。
剪力与弯矩的计算公式
剪力计算公式
Q = F * sinθ（F为作用在梁上的外力，θ为外力与梁轴线的夹角）。
弯矩计算公式
M = F * d / 2（F为作用在梁上的外力，d为梁的跨度）。
考察，从而为实际工程设计提供依据。
梁的剪力与弯矩的模拟计算
01
模拟计算是利用计算机软件对梁的剪力和弯矩进行数值模拟分 析的方法。通过模拟计算，可以快速得到梁在不同载荷条件下
的剪力和弯矩分布情况。
02
模拟计算可以采用不同的计算方法，如有限元法、有限差分法 和边界元法等。其中，有限元法是最常用的一种方法，能够考
目录 CONTENT
• 梁的剪力与弯矩的基本概念 • 梁的剪力图 • 梁的弯矩图 • 剪力与弯矩的关系 • 梁的剪力与弯矩的实例分析
01
梁的剪力与弯矩的基本概 念
剪力与弯矩的定义
剪力
剪力是作用在梁上的垂直力，它 使梁产生剪切变形。剪力通常用 Q表示，单位为牛顿或千牛顿。
弯矩
弯矩是作用在梁上的力矩，它使 梁产生弯曲变形。弯矩通常用M 表示，单位为牛顿米或千牛顿米 。
在梁的跨中位置，剪力图的峰值最大，而在梁的 支座位置，剪力图的谷值最小。
随着梁上载荷的增加，剪力图的峰值逐渐增大， 谷值逐渐减小。
03
梁的弯矩图
弯矩图的绘制方法
1 2
截面法
通过分析梁在不同截面上的弯矩值，绘制出弯矩 图。
叠加法
将多个弯矩值叠加起来，绘制出弯矩图。
3
微分法
利用弯矩函数的微分性质，绘制出弯矩图。
剪力与弯矩的符号规定
剪力的正负号规定
在截面左侧上作用的剪力为正，反之 为负。
弯矩的正负号规定
在截面左侧上作用的弯矩为正，反之 为负。
剪力与弯矩的计算公式
剪力计算公式
Q = F * sinθ（F为作用在梁上的外力，θ为外力与梁轴线的夹角）。
弯矩计算公式
M = F * d / 2（F为作用在梁上的外力，d为梁的跨度）。
考察，从而为实际工程设计提供依据。
梁的剪力与弯矩的模拟计算
01
模拟计算是利用计算机软件对梁的剪力和弯矩进行数值模拟分 析的方法。通过模拟计算，可以快速得到梁在不同载荷条件下
的剪力和弯矩分布情况。
02
模拟计算可以采用不同的计算方法，如有限元法、有限差分法 和边界元法等。其中，有限元法是最常用的一种方法，能够考
剪力、弯矩方程与剪力、弯矩图
截面位置对剪力和弯矩的影响
总结词
截面位置对剪力和弯矩具有显著影响。不同的截面位置会导致剪力和弯矩的大小和方向发生变化。
详细描述
在结构分析中，截面位置是影响剪力和弯矩的重要因素之一。不同的截面位置会导致剪力和弯矩的大小和方向发 生变化，从而影响结构的整体受力性能。例如，在梁中选取不同的截面位置进行支撑或固定，会对梁的剪力和弯 矩产生显著影响。
05 剪力、弯矩与材料力学性 能的关系
材料弹性对剪力和弯矩的影响
弹性材料在剪力和弯矩作用下会发生弹性变形，变形量与外力成正比，当外力去 除后，材料能够恢复原状。
弹性材料的剪切模量和弯曲刚度决定了剪力和弯矩的大小，剪切模量越大，材料 抵抗剪切变形的能力越强；弯曲刚度越大，材料抵抗弯曲变形的能力越强。
根据绕顺时针方向观察确定，使上侧 纤维受拉时为正。
02 剪力方程与弯矩方程
剪力图与弯矩图的绘制
1
剪力图和弯矩图是表示梁上剪力和弯矩随截面位 置变化的图形。
2
这些图的绘制基于剪力方程和弯矩方程的计算结 果，通过将计算得到的剪力和弯矩值标在图中相 应的位置上，并连接成线。
3
剪力图和弯矩图的绘制有助于直观地了解梁在不 同截面位置的受力状态和应力分布情况。
弯矩
在梁或结构中，由于弯曲而产生 的力矩，表示弯曲变形的大小。
剪力与弯矩在力学中的作用
剪力
主要影响结构的剪切变形，对梁的剪切承载能力有重要影响 。
弯矩
主要影响结构的弯曲变形，对梁的弯曲承载能力有重要影响 。
剪力与弯矩的符号规定
剪力正方向
根据右手定则确定，从杆件的受压一 侧指向受拉一侧。
弯矩正方向
02
材料强度越高，抵抗剪力和弯矩等外力的能力越强， 所能承受的剪力和弯矩越大。
剪力弯矩计算
2
2
M(x)为x得二次函数,M图为抛物线;
x 0, M (0) 0; x l, M (l) 0; x l , M ( l ) 1 ql 2; 作
2 28
结论:当梁段上有均布荷载q作用时,Q图为斜直线,M图 为二次抛物线。
返回 下一张 上一张 小结
例3-6 作图示简支梁得内力图。
解:1、列内力方程: 求支座反力:由
dQ(x) q(x)......(a) dx
MO 0, (Mo—矩心O取在右侧截面d得x 形心。)
[M (x) dM (x)] M (x) Q(x)dx q(x)dx 0; 2
dM (x) Q(x)......(b) dx
将(b)代入(a),
d
2M (x) dx 2
q( x)......(c)
返回 下一张 上一张 小结
结论:在集中力P作用截面,Q图发生 突变,突变值等于该集中力P得大小;M图 有尖角,尖角得指向与集中力P相同。
内力函数得不连续就是由于将集中力 得作用范围简化为一个点得结果。若考虑 集中力为微梁段上得均布荷载,则C截面得 Q图与M图应为斜直线与抛物线。
因此,当谈到集中力作用出得剪力时,
( x1 )
m l
(l
x1 ); (a
x1
l)
m
m
Q(x2 ) l , M (x2 ) l x2;(0 x2 b)
2、 作内力图:
AC段:
x
0
:ቤተ መጻሕፍቲ ባይዱ
Q(0)
m l
,
M
(0)
0;
x a : Q(a) m , M (a) ma ;
l
l
CB段:
x1
a
剪力图和弯矩图(史上最全面)解析
三、 叠加原理： 多个载荷同时作用于结构而引起的内力等于每个载荷单
独作用于结构而引起的内力的代数和。
Q(P1P2 Pn) Q1(P1) Q2(P2) Qn(Pn)
M(P1P2 Pn) M1(P1) M2(P2) Mn(Pn)
M (P1P2 Pn) M1(P1) M2(P2) Mn(Pn)
适用条件：所求参数（内力、应力、位移）必然与荷载满 足线性关系。即在弹性限度内满足虎克定律。
27
二、材料力学构件小变形、线性范围内必遵守此原理 ——叠加方法
步骤： ①分别作出各项荷载单独作用下梁的弯矩图； ②将其相应的纵坐标叠加即可（注意：不是图形的简单
四、对称性与反对称性的应用： 对称结构在对称载荷作用下，Q图反对称，M图对称；对称
结构在反对称载荷作用下，Q图对称，M图反对称。
M 的驻点： Q 0 ; M 3 qa2 2
x
右端点： Q 0; M 3 qa2 2
22
[例5] 用简易作图法画下列各图示梁的内力图。AB=BC=CD=a
q AB
RA qa Q qa/2
+ – qa/2
qa2 CD
RD
– qa/2
M
qa2/2
+
–
3qa2/8 qa2/2
qa2/2
RB
Pa l
Y
0,
YA
P(l a) l
XA A YA
P B
P B
RB
11
②求内力——截面法
Y
0,
Q YA
P(l a) l
mC 0 , M YA x
m XA A
剪力图和弯矩图例题弯矩图例题(共15张PPT)
3.作剪应力图和弯矩图
最大剪力发生在梁端，其值为
F 1ql 2 Qmax
最大弯矩发生在跨中，它的数值为Mmax
1 ql 2 8
例题3 简支梁受集中作用如图示，作此梁的剪力图和弯矩图。
解：1.求约束反力
FAyFl b,FByFl a
2.列剪力方程和弯矩方程 AC段：
FQ(x)
FAy
Fb l
〔0<x<a 〕
• 口诀表述：剪力图 力偶荷载无影响。
•
弯矩图 力偶荷载有突变。
二、根据内力图规律做图
１.剪力图与荷载的关系
〔１〕在均布荷载作用段， FQ图是斜直线，倾斜方向与荷载指向相同
(2)无荷载作用区段，即q(x)=0，FQ图为平行x轴的直线。
(3)在集中力作用处，FQ图有突变，突变方向与外力一致，且突变的数值等于该集
例7 外伸梁如下图，试画出该梁的内力图。
m=3.6kNm
P＝3kN
x
AD
C
RA
a=0.6m a=0.6m
q=10kN/m
B E
2a=1。2m
RB
解：
〔1〕求梁的支座反力
由 mA0
P 5 aR3 am 1q2 a20
B
2
解得
R BP2q a R A5kN
由 Y 0
P R AR B 2 q a 0
解得
M(x)FAyxFl b (0≤x≤a)
CB段：
F Q(x)F Ay FF l bFF l a(a<x<l)
Fa M (x)F Ax yF (xa )l (lx)
(0≤x≤l)
3.作剪力图和弯矩图
Q图 M图
图三
梁的剪力和弯矩.剪力图和弯矩图
M2 M1
F x2
x1 S
x dx
q
A
C
D
B
FA
a
c
l
FA
b
FB
FB
FAa
FBb
突 变 规 律(从左向右画)
1、集中力作用处，FS图突变，方
向、大小与力同；M图斜率突 变，突变成的尖角与集中力F的 箭头是同向。
2、集中力偶作用处，M图发生
突变，顺下逆上，大小与M 同，FS图不发生变化。
0
dM dx
FS
d 2M dx2 q
dFs q dx
dM dx
FS
d 2M dx2
q
dFs 0
FS C 剪力图是水平直线.
dx
dM C 弯矩图是斜直线.
C0
C0
dx
dM 0
M C 弯矩图是水平直线.
dx
dFs q dx
剪力图是斜直线. 弯矩图是二次抛物线.
截开后取右边为示力对象：
向上的外力引起负剪力，向下的外力引起正剪力； 向上的外力引起正弯矩，向下的外力引起负弯矩； 顺时针引起负弯矩，逆时针引起正弯矩。
4.3 求图示外伸梁中的A、B、C、D、E、
例题
F、G各截面上的内力。
3kN
C A
2kN m
1kN m
6kN m
D EF BG
FA
FB
1m 1m 1m 1m 1m 1m 1m 1m
MB
q
MA
B
l
B
+ MA
+
M0
+ MA M0
例题 4.15
建筑力学弯矩图、剪力图课件
BC：
QCD QDC 5
QBC 20 q 2 10 QCB＝5-P=-10
剪力图如图所示。 在已荷点和所有反应力的情况下，可以 取分段分离体求剪力控制截面值，但如 果 M 图已知，不求约束反力也可确定分 段杆端的剪力控制截面值。
D 5kN 10kN + C 10kN B
+
A
几种常见简支梁M、Q图的记忆
P L/2 M P/2 Q L/2 q L M PL/4 + P/2 Q qL/2 + + qL2/8 qL/2
+
几种常见简支梁M、Q图的记忆
P m b L M + Pb/L Q + Pa/L Pab/4 Q M/2 M + m/L M/2 + -
a
L/2
L/2
（四）叠加法作弯矩图与剪力图
10kNm D
C B 10kNm M图 A
轴力为零不考虑。 杆端作用剪力、弯矩与相应简支梁两端 作用弯矩受力情况完全相同，即对应。 所以任意分段均可同叠加法作M图。
（3）画剪力图：取控制截面如图。 计算剪力：取分离体如图。 AB：QAB=0（自由端） QBA q 2 10 CD： QDC 5
l
或由
0 A
M0 BA来自01 0 QBA ( M A M B m A l
M , M ，分别为荷载对杆端 A ， B 之矩的代数和。
MA
P
MB
QAB
QBA
例6－10 外伸梁如图所示，已知，试画出该梁的 内力图。本例同例6-10反向
QCD QDC 5
QBC 20 q 2 10 QCB＝5-P=-10
剪力图如图所示。 在已荷点和所有反应力的情况下，可以 取分段分离体求剪力控制截面值，但如 果 M 图已知，不求约束反力也可确定分 段杆端的剪力控制截面值。
D 5kN 10kN + C 10kN B
+
A
几种常见简支梁M、Q图的记忆
P L/2 M P/2 Q L/2 q L M PL/4 + P/2 Q qL/2 + + qL2/8 qL/2
+
几种常见简支梁M、Q图的记忆
P m b L M + Pb/L Q + Pa/L Pab/4 Q M/2 M + m/L M/2 + -
a
L/2
L/2
（四）叠加法作弯矩图与剪力图
10kNm D
C B 10kNm M图 A
轴力为零不考虑。 杆端作用剪力、弯矩与相应简支梁两端 作用弯矩受力情况完全相同，即对应。 所以任意分段均可同叠加法作M图。
（3）画剪力图：取控制截面如图。 计算剪力：取分离体如图。 AB：QAB=0（自由端） QBA q 2 10 CD： QDC 5
l
或由
0 A
M0 BA来自01 0 QBA ( M A M B m A l
M , M ，分别为荷载对杆端 A ， B 之矩的代数和。
MA
P
MB
QAB
QBA
例6－10 外伸梁如图所示，已知，试画出该梁的 内力图。本例同例6-10反向
梁的剪力和弯矩剪力图和弯矩图
2m
120
40
kN
190 160
kNm
210 340
. 280
q
q A
B
a
a
qa 2
C
qa
qa 2
1 qa 2 2
.
q
q
A
C
B
a
qa
a
qa
qa
qa 1 qa 2 2
.
q
A
B
qa
结构对称， 2 a
q
qa
a
2
载荷反对称，
则FS图对称，
qa 2
M图反对称
a2
qa 2
qa
2
a2
qa 2
8
.
qa 2
8
F
AD段：q<0， FS 图为向下斜直线，
.
M图为下凸抛物线。
例题 4.9 4.10
F
Fa
a
a
F
5
kN
4
Fa
.
kNm
2kN m 4m 3k N
kN
3
2.25
kNm
例题
4.11
作图示梁的内力图
3k N 4.5kN m
2kNm
D A C BE
FA 10kN
1m 2m
2m
FB 2kN 1m
7
kN
3
x1.56 2
一、梁平面弯曲的概念
1、平面弯曲的概念
弯曲变形：作用于杆件上的外力垂直于杆件的轴线，使 杆的轴线由直线变为曲线。
.
平面弯曲：梁的外载荷都作用在纵向对称面内时，则梁的轴 线在纵向对称面内弯曲成一条平面曲线。
《弯矩分配法》课件
《弯矩分配法》PPT 课件
REPORTING
• 引言 • 弯矩分配法的基本原理 • 弯矩分配法的实际应用 • 弯矩分配法的优缺点分析 • 弯矩分配法的未来发展 • 总结与展望
目录
PART 01
引言
REPORTING
什么是弯矩分配法
01
弯矩分配法是一种用于计算结 构内力的方法，特别适用于分 析具有多跨连续梁和刚架结构 的体系。
实际应用
通过实际工程案例的实 践和应用，不断总结经 验，优化和完善弯矩分 配法的应用技巧和方法 。
弯矩分配法与其他方法的结合应用
01
与有限元法结合
将弯矩分配法与有限元法相结合，发挥各自的优势，提高结构分析的精
度和效率。
02
与优化算法结合
将弯矩分配法与优化算法相结合，实现结构的优化设计和性能提升。
03
02
它通过将结构的弯矩进行分配 ，并利用结构的节点平衡条件 ，求解出各杆件的弯矩和剪力 。
03
弯矩分配法基于弯矩与剪力之 间的相互影响关系，将结构的 弯矩分布状态作为计算的基础 。
弯矩分配法的重要性
01
弯矩分配法在结构分析中具有广泛的应用，尤其在桥梁、建筑 和机械等领域。
02
它能够快速准确地计算出结构的内力分布，为结构设计提供重
步骤三
根据相对刚度的大小，将节点 弯矩分配到各个杆件上。
步骤五
根据计算结果进行结构分析和 设计。
弯矩分配法的应用范围
1
弯矩分配法适用于分析连续梁和刚架等结构形式 ，特别适用于分析具有多个节点和复杂受力情况 的结构。
2
在实际工程中，弯矩分配法广泛应用于桥梁、房 屋、工业厂房等建筑结构的分析和设计中。
弯矩分配法的核心思想是将复杂的结构简化为简单的基本单元，通过分析基本单元 的受力特性，推导出整个结构的内力分布。
REPORTING
• 引言 • 弯矩分配法的基本原理 • 弯矩分配法的实际应用 • 弯矩分配法的优缺点分析 • 弯矩分配法的未来发展 • 总结与展望
目录
PART 01
引言
REPORTING
什么是弯矩分配法
01
弯矩分配法是一种用于计算结 构内力的方法，特别适用于分 析具有多跨连续梁和刚架结构 的体系。
实际应用
通过实际工程案例的实 践和应用，不断总结经 验，优化和完善弯矩分 配法的应用技巧和方法 。
弯矩分配法与其他方法的结合应用
01
与有限元法结合
将弯矩分配法与有限元法相结合，发挥各自的优势，提高结构分析的精
度和效率。
02
与优化算法结合
将弯矩分配法与优化算法相结合，实现结构的优化设计和性能提升。
03
02
它通过将结构的弯矩进行分配 ，并利用结构的节点平衡条件 ，求解出各杆件的弯矩和剪力 。
03
弯矩分配法基于弯矩与剪力之 间的相互影响关系，将结构的 弯矩分布状态作为计算的基础 。
弯矩分配法的重要性
01
弯矩分配法在结构分析中具有广泛的应用，尤其在桥梁、建筑 和机械等领域。
02
它能够快速准确地计算出结构的内力分布，为结构设计提供重
步骤三
根据相对刚度的大小，将节点 弯矩分配到各个杆件上。
步骤五
根据计算结果进行结构分析和 设计。
弯矩分配法的应用范围
1
弯矩分配法适用于分析连续梁和刚架等结构形式 ，特别适用于分析具有多个节点和复杂受力情况 的结构。
2
在实际工程中，弯矩分配法广泛应用于桥梁、房 屋、工业厂房等建筑结构的分析和设计中。
弯矩分配法的核心思想是将复杂的结构简化为简单的基本单元，通过分析基本单元 的受力特性，推导出整个结构的内力分布。
剪力与弯矩的计算方法
FAy 3.5 kN
②、求 1-1 截面上的内力 在 1-1 截面处将梁切开成左右两段， 取左段为脱离体， 受力图如图 7-10b 所示，
FS 1
Y 0 ，
、弯矩 M 1 的方向都按规定的正方向标出。根据脱离体的平衡方程得：
FAy FS 1 0
，得
FS 1 FAy 3.5
01
kN
由所有外力对 1-1 截面的形心取矩
FAy 1 M 1 0
，得
M 1 FAy 1 3.5 kN .m
M
0
：
求得 1-1 截面的剪力 S 1 及弯矩 M 1 均为正值， 表示所假设的 S 1 及 M 1 的方向 与实际方向相同，在脱离体上，剪力和弯矩的方向一律设为正向，计算结果为正则 内力就为正，计算结果为负则内力就为负。 ③、求 2-2 截面上的内力 在 2-2 截面处将梁切开成左右两段， 取左段为脱离体， 受力图如图 7-10c 所示， 将剪力 由
F
FS
Y 0 得： M 0 由 得：
o
和弯矩 M 的大小可由左段梁的静力平衡方程来求解。
FAy P 1 FS 0
FAy x P1 x a M 0
，
得 得
FS FAy P 1 M FAy x P1 x a FS 和弯矩 M 。
FS
如果取右段进行分析时，则有： S ， （也即 S ） ； 当取左段（或右段）进行分析时，任意截面的弯矩等于所有产生向上的线位移的力对该 点之矩减去所有产生向下的线位移的力对该点之矩，即：
F
F
（7-1）
M
利用式 、 可以直接写出指定截面的剪力和弯矩。 四、计算剪力、弯矩的简便方法 利用上面的关系，可以直接根据作用在梁上的外力计算出任意截面的剪力、弯矩，从而 省去取脱离体列平衡方程的步骤，使计算过程简化。 例 7-2 计算图 7-11 所示梁 1-1 和 2-2 截上的内力。 解：①、求支座反力由梁的整体平衡方程:
工学土木力学剪力弯矩的计算
第7页/共47页
4.求截面3-3的内力
Fy
0 : FQ3
FBy
0得FQ3
FBy
F 4
M 3
0
:
M3
Me
2FByl
0得M 3
Fl
2
F 4
l
3 2
Fl
5.求截面4-4的内力
Fy
0 : FQ4
FBy
0得FQ4
FBy
F 4
M 4
0 : M4
FBy
2l
0得M 4
2FByl
1 2
Fl
比较截面1-1和2-2的内力发现说在集中力的两侧 截面剪力发生了突变，突变值等该集中力的值。
第15页/共47页
例题9.3 图所示，悬臂梁受集中力F作用，试作 此梁的剪力图和弯矩图 解： 1.列剪力方程和弯矩方程
FQ (x) F (0＜x＜l )
M (x) Fx (0≤x＜l)
2.作剪力图和弯矩图 由剪力图和弯矩图可知：
FQ max F M Fl
max
第16页/共47页
例题9.4 简支梁受均布荷载作用，如图示， 作此梁的剪力图和弯矩图。
第37页/共47页
主应力、主平面： 在三对相互垂直的相对面上剪应力等于零，
第8页/共47页
比较截面3-3和4-4的内力在集中力偶两侧横截面 上剪力相同，而弯矩突变值就等于集中力偶矩。
梁的内力计算的两个规律：
（1）梁横截面上的剪力FQ，在数值上等于该截面 一侧（左侧或右侧）所有外力在与截面平行方向
投影的代数和。即：
FQ
F yi
若外力使选取研究对象绕所求截面产生顺时针方
截面B左、B右：取右侧梁计算，得：
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
2、剪力和弯矩的符号规定
1）剪力Q：截面上的剪力Q使 所取脱离体产生顺时针转动趋势 时（或者左上右下）为正，反之 为负。
2）弯矩M：截面上的弯矩M使 所取脱离体产生下边凸出的变形 时（或者左顺右逆）为正，反之 为负。
为避免符号出错,要求： 未知内力均按符号规定的正向
假设。
返回 下一张 上一张 小结
2-2截面：
Q2
VA
P 6
3-3截面：
Q3
VA
P 6
4-4截面:
Q4
VB
7P 6
M2
VA
L 3
m
p 6
L 3
PL 2
4PL 9
M3
VA
(
L 3
L) 3
m
P 6
2L 3
PL 2
7PL 18
M4
VB
L 3
7P 6
L 3
7PL 18
返回 下一张 上一张 小结
第二节 梁的内力图及其绘制
一、剪力图和弯矩图的概念
（1）梁任一横截面上的剪力在数值上等于该截面一侧（左侧或 右侧）所有外力沿截面方向投影的代数和；
Q PiQ
符号规定：外力使截面产生顺时针转 动趋势时（或左上右下）该截面剪力为正， 否则为负； （2）梁任一横截面上的弯矩在数值上等于该截面一侧（左侧或 右侧）所有外力对截面形心力矩的代数和；
M Mo (PiQ )
符号规定：外力使梁段产生上凹下凸 变形时（或左顺右逆）该截面弯矩为正， 否则为负；
计算时可按二看一定的顺序进行：一看截面一侧有几个力， 二看各力使梁段产生的变形，最后确定该截面内力的数值。
返回 下一张 上一张 小结
例3-3：简支梁如图所示。试计算1-1、2-2、
3-3、4-4 截面上的剪力和弯矩。
返回 下一张 上一张 小结
二、梁的内力及其求法
内力—外力引起的受力构件内相邻部分之间相互作用力的改变量。
杆件横截面上的内力有：轴力，剪力，弯矩，扭矩等。
1、剪力和弯矩的概念 图示简支梁在荷载及支座反
力共同作用下处于平衡状态。
求距支座A为x的横截面m-m. 上的内力。用截面法求内力。
步骤：1)截开 2)代替
2）求2-2截面上的内力
Y 0
P ql Q2 0
Q2 P ql
M0 0
l P l (ql) 2 M 2 0
M2
Pl
1 2
ql 2
求得的 Q2 、M2 均为负值,说明内力实际方向与假设 方向相反。矩心 O1是2-2截面的形心。
返回 下一张 上一张 小结
例3-2 外伸梁如图，试求1-1，2-2截面上的剪力和弯矩。
变形特点：杆轴由直变弯。 平面弯曲—荷载与反力均作用
在梁的纵向对称平面内，梁轴线也 在该平面内弯成一条曲线。
单跨静缩— 杆（纵向力作用） 受力特点：外力与杆轴线方向重合； 变形特点：杆轴沿外力方向伸长或缩短。 3、扭转—轴（外力偶作用） 受力特点：外力偶作用在垂直杆轴平面内； 变形特点：截面绕杆轴相对旋转。 4、组合变形—两种或两种以上基本变形的组合。
解：1、求支座反力：由整体平衡
MB 0, P1 8 P2 3YA 6 0 YA 14kN
MA 0, P1 2 P2 3YB 6 0 YB 9kN
校核： Y YA YB P1 P2 149320 0 反力无误。
2、求1-1截面上的内力：取左半段研究
Y 0,YA P1 Q1 0 Q1 YA P1 14 3 11kN
梁各截面的内力随截面位置而变化，其函数关系式
Qx=Q(x), Mx=M(x) 称作剪力方程和弯矩方程。
列内力方程即求任意截面的内力。
Q(x) P qx (0 x l)
M (x) Px 1 qx2 (0 x l) 2
反映剪力（弯矩）随截面位置变化 规律的曲线，称作剪力（弯矩）图。
二、剪力图和弯矩图的作法： 取平行梁轴的轴线表示截面位置，规定
例3-1：悬臂梁如图所示。求1-1截面和2-2截 面上的剪力和弯矩。
解：1）求1-1截面上的内力
Y 0
P
1 2
ql
Q1
0
Q1
P
1 2
ql
M0 0
l1 l
P
2
( 2
ql)
4
M1
0
M1
1 2
Pl
1 8
ql 2
求得的 Q1 、M1 均为负值,说明内力实际方 向与假设方向相反。矩心 O 是1-1截面的形心。
剪力Q——限制梁段上下移动的内力; 弯矩M——限制梁段转动的内力偶。
单位：剪力Q KN, N；弯矩M KN.m ， N.m
3)平衡 Y 0 RA Q 0 Q RA
Mo 0 Mo RAx 0
M o RAx
若取右半段梁为研究对象,可得： Q' Q Mo ' Mo
返回 下一张 上一张 小结
正值的剪力画轴上侧，正值的弯矩画轴下侧； 可先列内力方程再作其函数曲线图。
Pl 1 ql2 2
Mo 0, P1 3YA 1 M1 0 矩心o—1-1截面形心
M1 YA 1 P1 3 5kN m
3、求2-2截面上的内力：取右半段研究
Y 0,Q2 YB 0 Q2 YB 9kN
Mo' 0,YB 1.5 M2 0 矩心o’—2-2截面形心
M 2 1.5YB 13.5kN m 若取左半段梁研究，则
Y 0,YA P1 P2 Q2' 0 Q2 ' YA P1 P2 14 3 20 9kN
Mo' 0,YA 4.5 P1 6.5 P2 1.5 M2' 0
M 2 ' YA 4.5 P1 6.5 P2 1.5 13.5kN m
返回 下一张 上一张 小结
3、直接法求梁的内力：（由外力直接求梁横截面上的内力）
第一节 杆件的内力及其求法 第二节 梁的内力图及其绘制 第三节 弯矩、剪力、荷载集度 间的关系 第四节 叠加法作剪力图和弯矩图 第五节 其它杆件的内力计算方法 小结
返回
第一节 杆件的内力及其求法
一、杆件的外力与变形特点 1.弯曲—梁（横向力作用）
受力特点：垂直杆轴方向作用外力， 或杆轴平面内作用外力偶；
解：1）求支座反力
pL 2L
M A 0 2 P 3 VB L 0
7P VB 6 ()
MB 0
PL L 2 P 3 VA L 0
校核
VA
P 6
()
P 7P
Y VA P VB 6 P 6 0
反力无误。
2）计算截面内力
6
1-1截面： Q1 VA P
3 18 M1 VA L PL