巧用补形法解决立体几何问题
立体几何中的割补法解题技巧

⽴体⼏何中的割补法解题技巧
⽴体⼏何中的割补法解题技巧
※⾼考提⽰
⽴体⼏何中常⽤割补法解题.特别是⾼考中的⽴体⼏何题很多可⽤割补法解,有时解起来还⽐较容易.
[规律⼩结]
割补法是割分形法即割法与补加形法即补法的总称。
补法是把不熟悉的或复杂的⼏何体延伸或补加成熟悉的或简单的⼏何体,把不完整的图形补成完整的图形。
割法是把复杂的或不熟悉的⼏何体,割分为简单的或熟悉的⼏何体。
这样对此解起题来就有好处。
割补法中的割与补是⼀个问题中的相反两个⽅⾯,是对⽴统⼀的⼀对⽭盾。
解决⼀个问题,是割是补?这要看问题的性质,宜补就补,宜割就割,不可割补就不割补,就是宜割补,也要讲究如何割补,不要盲⽬⾏动,否则就会导致⿇烦,使问题复杂化,使得其反,甚⾄问题还不能解决。
⽴体⼏何中需得三棱柱补成平⾏六⾯体,将三棱维补成三棱柱,将三棱柱割分为三棱维等等这些我们很熟悉,其实,割补法不仅仅使⽤于⽴体⼏何,将上述概念中的⼏何体或图形改为代数式,那么在数学的其它⽅⾯使割补法也就很多了,⽐如运算中的添项减项,重新组合另⾏考虑,考虑问题的对⽴⾯等等均可视为割补法,因此,割补法不只是⼀种⽅法,可把它上升为⼀种思想——⼀种数学思想。
关于我们:。
补形巧解立体几何题

AD
=
1 2
,求面
SCD
与面
SAB
所成二面角的正切值.
解析 如图 13,延长 BA、CD 交于 E,连结 SE.
因为 AD
=
1 2
BC,且 AD ∥ BC,所以 EA
= AB
= SA
= 1,SE ⊥ SB.
又因为 SA ⊥ 面 ABCD,所以面 SEB ⊥ 面 ABCD,
因为 BC ⊥ EB,所以 BC ⊥ 面 SEB,BC ⊥ SE,
所以 SE ⊥ 面 SBC,SE ⊥ SC,∠BSC 是所求二面
角的平面角,又因为 SB = 2 ,BC = 1,所以 tan∠BSC
=
2 2.
10 把长( 正) 方体补成长( 正) 方体
图 13 图 14
例 12 如图 14,在长方体 ABCD—A1B1C1D1 中, 已知 AB = 4,AD = 3,AA1 = 2,E、F 分别是线段 AB、BC 上的点,且 EB = FB = 1,求 EC1 与 FD1 所成角的余弦 值.
=
22 5
.
图 11 图 12
例 10 在正三棱柱 ABC—A1B1C1 中, 若 AB = 2 BB1,则 AB1 与 C1B 所成角的大小为( ).
A.60° B.90° C.30° D.45°
中学数学杂志 2014 年第 11 期 ZHONGXUESHUXUEZAZHI
例 1 一个四面体的棱长都为 2 ,四个顶点都 在同一球面上,则球的表面积为( ).
A.3π B.4π C.3 3 π D.6π 解析 如图 1,把四面体补成一个棱长为 1 的 正方体,则正方体的对角线就是球的直径.因为 2R = 3 ,所以 S球表面积 = 4πR2 = 3π,故应选 A.
巧借“补形”思维,妙解立体几何问题

ʏ孙海鹰利用 补形 思维这一桥梁,可以使数学的思维方法更加活跃㊁简捷,应用起来更加灵活㊁多样,能有效培养同学们思维的灵活性㊁独创性㊂利用 补形 思维可以把空间立体几何中的一些不规则形体㊁不熟悉形体㊁残缺形体补成相应的规则形体㊁熟悉形体㊁完整形体等,对解决问题起到化繁为简㊁一目了然的作用,使得数学思维更加灵活,数学知识结构更加完整㊁充实,数学思想方法更加完美㊂一㊁还原补形法例1为了给数学家帕西奥利的‘神圣的比例“画插图,列奥纳多㊃达㊃芬奇绘制了一些多面体,图1所示的多面体就是其中之一㊂它是由一个正方体沿着各棱的中点截去八个三棱锥后剩下的部分,这个多面体的各棱长均为2,则该多面体外接球的体积为()㊂图1A.16πB.8πC.16π3D.32π3分析:对于此类空间立体几何中的不规则形体 多面体,直接处理起来有较大的难度,可借助空间几何体的还原补形法,把该多面体进行还原补形为正方体,结合补形前后对应图形中相关元素的位置关系与变化情况,进行合理分析与运算㊂解:结合图1,把该多面体进行还原补形为正方体,如图2所示㊂图2由所给多面体的棱长为2,可得正方体的棱长为22,那么正方体的中心即为多面体的外接球的球心,所以球心到多面体顶点的距离为(2)2+(2)2=2,即多面体外接球的半径R=2㊂故该多面体外接球的体积V=43πR3=32π3㊂应选D㊂还原是回归问题本质的一种逻辑推理方式㊂在解决一些空间几何体问题中,合理回归,完整地进行还原与补形是解题的关键㊂在处理空间几何体的还原补形时,要注意回归的简单几何体与 补 上去的小几何体之间要素的联系与图形之间的变化,正确构建相互之间的关系,不要出现添加或遗漏㊂二㊁联系补形法例2已知正三棱锥P-A B C,点P,A, B,C都在半径为3的球面上,若P A,P B, P C两两相互垂直,则球心到截面A B C的距离为㊂分析:此类不同空间几何体间(正三棱锥与球)的联系问题,需要进行合理补形,将正三棱锥与球这两种不同的空间几何体联系在一起,使得问题的处理直观易懂,从而便于分析与计算㊂解:由于正三棱锥的侧棱P A,P B,P C5知识结构与拓展高一数学2023年4月Copyright©博看网. All Rights Reserved.两两互相垂直,故以P A ,P B ,P C 为棱补成正方体,如图3所示㊂图3球心O 为正方体的体对角线P D 的中点,且P O =3,则正方体的棱长为2㊂设点P 到平面A B C 的距离为h ㊂根据正三棱锥的体积,借助等体积法得13ˑ34ˑ(22)2㊃h =13ˑ12ˑ2ˑ2ˑ2,解得h =233,所以所求球心到截面AB C 的距离为3-233=33㊂寻找联系是构建不同数学元素之间的桥梁㊂在空间立体几何问题中,抓住不同空间几何体之间的联系,合理补形(如三条侧棱两两互相垂直,可补形为正方体或长方体),使得问题更加直观易求㊂三㊁对称补形法 图4例3 如图4所示,在斜截圆柱中,已知圆柱的底面直径为40c m ,母线最短与最长的分别为50c m ,80c m ,则该斜截圆柱的体积V =㊂分析:此类空间几何体中的残缺形体,属于不太规则的空间几何体,直接求解无从下手,可借助空间几何体的几何特征进行合理的对称补形,将题设条件中的斜截圆柱按斜截面吻合对接,补全为一个完整的圆柱,再利用圆柱的体积公式求解㊂解:将题设条件中的斜截圆柱按斜截面吻合对接,补全为一个完整的圆柱(即斜截圆柱进行翻转对接)㊂由题意知所求体积V =12ˑ(πˑ202)ˑ(50+80)=26000π(c m 3)㊂对称是数学中的一种重要关系,也是充分展示数学美的一种表现形式㊂在解决空间几何体问题时,对于一些特殊的残缺形体,要善于发现图形中的对称关系与几何特征,借助相同图形之间的对称补形法进行化归与转化,对空间想象能力的提升很有帮助㊂编者的话: 补形 思维解决立体几何问题,是整体思想的一种具体体现,可将不规则的㊁陌生的㊁复杂的几何体补成规则的㊁熟悉的㊁简单的几何体(如常见的长方体㊁正方体㊁平行六面体㊁圆柱等),在所补成的空间几何体中研究原几何体的有关元素的位置关系㊁空间角或空间距离的计算等,从而实现问题的顺利解决㊂这类问题,能全面考查数学基础知识㊁基本技能㊁基本思想㊁基本活动经验这 四基 的落实情况,以及发现问题㊁提出问题㊁分析问题和解决问题能力的培养与提升㊂若三棱锥P -A B C 中最长的棱P A =2,且各面均为直角三角形,则此三棱锥外接球的体积是㊂图5提示:根据题意,可把该三棱锥补成长方体,如图5所示,则该三棱锥的外接球即为该长方体的外接球㊂易得外接球的半径R =12P A =1,所以该三棱锥外接球的体积V =43ˑπˑ13=43π㊂作者单位:江苏省江阴中等专业学校高新区校区(责任编辑 郭正华)6知识结构与拓展 高一数学 2023年4月Copyright ©博看网. All Rights Reserved.。
空间几何体中几种常见的补形法

s△^船 ·AA =丁1×24×8=96 .
【小结 】比较 上述 两种 方 法 ,补 形
图3
法显 然 比分割法要简 洁得 多 ,计算 量也很 小 ,但 要抓 住 图形
的对 称性 ,巧妙的补成熟悉的几何 体 ,并找到 原几何 体 与补
形后 的几何体 的关 系 ,实现化繁为 简的奇效.
了一种构造思 想 ,同时也反 映了对 立统一的辩证思想 .
利用补形 法解决立体几何 问题 的基本 步骤是 :
第一步 :把不熟悉 的或 复杂 的几 何体 延 伸或 补加 成 熟
悉的或简单 的几何 体 ,把不完整 的图形 补成完整 的图形 ;
第二 步 :运用常见几何体 的知识 等计算结果 ;
第三 步 :得 出结论.
以外接球直径 2R= ,所 以 R= ,所 以外接 球 的表 面积
s球=挚.
方 法 二 联 系补 形 例 2 已知 三棱 锥 P—ABC,PA=BC=5,朋 :AC= 4,PC:AB= l,求三棱 锥的体积. 【思路 】如按常规求法 ,需求三棱锥 的底 面积和 高 ,而高 很 难求 出.由已知三组相对棱相 等这一 特点 ,联想长 方体对 面不平行 的对 角线恰 好组 成对 棱相 等 的三棱 锥 ,因此 可把 三棱锥 P—ABC补成长方体 ,再将长方体 分割成三棱锥 P— ABC和 四个相 同体积 的三棱锥.
在高考 中 ,补形法既可 以在选 择填空 题 中体 现 ,也 可以
在解答题 中体 现 ,常见的补形法 有对称 补形 、联系补 形 和还
原补形 ,还原补形主要涉及 台体 中“还台为锥 ”.下 面结合 实
例进行剖析 :
方法一 对称补形
巧用补形法,妙解立体几何题

则G ()m =e m -ma ()m -1<e 2-e 2=0,而G ()m G ()2<0,所以存在零点x 0∈()1,2使G ()x =0,即F ()x 有唯一极值点且为极小值x 0∈()1,2,因为F ()x 0=ae x 0x 0-ln x0,G ()x 0=e x 0-x 0a ()x 0-1=0,e x=x 0a ()x 0-1,所以F ()x 0=1x 0-1-ln x 0,因为F '()x 0=-1()x 0-12-1x 0<0,所以F ()x 0=1x 0-1-ln x 0在()1,2上单调递减,故F ()x 0>F ()2=1-ln 2>0,所以F ()x >0,综上可知,当a >2e 2时,总有f ()x >0.该不等式中含有多项式,于是通过移项、作差,将不等式变形,以便构造出新函数F ()x =ae xx-ln x ,再利用导数法证明函数F ()x 的极小值大于0,从而达到证明不等式的目的.对于含有指数、对数式的不等式恒成立问题,在构造出新函数后,通常需借助导数法,对函数求导,研究导函数与函数单调性之间的关系,根据函数单调性求得函数的最值.由此可见,解答不等式恒成立问题,关键在于将不等式与函数关联起来,利用函数、导函数的性质来解题.这就需将不等式进行合适的变形,如分离参数、构造出函数,以将问题转化为函数最值问题来求解.(作者单位:江苏省南京市第一中学)有些立体几何问题较为复杂,或几何图形不规则,我们采用常规方法很难求得问题的答案.此时,可巧用补形法,根据已知条件和图形,添加合适的辅助线,将不规则的、陌生的、不易计算边角的几何图形割补为规则的、熟悉的、易计算边角的图形,取得化难为易的效果.而运用补形法求解立体几何问题,关键在于如何巧妙地割补图形,主要有以下几种思路.一、将棱锥补成棱柱棱锥是常见的几何体,如三棱锥、四棱锥、五棱锥等.有些棱锥的高很难找到或求得,此时我们可以将棱锥补成棱柱,如将正三棱锥补为正方体,将对棱的长相等的三棱锥补为长方体,再根据正方体、长方体的性质,便能快速求得三棱锥的边、角的大小,从而使问题顺利获解.例1.如图1所示,三棱锥S-ABCD 的所有棱长都为2,四个顶点在同一球面上,则球的表面积为().图1A.3πB.4πC.33πD.6π解:如图2,将正三棱锥补为正方体,并使正方体的棱长为1,图2解题宝典42则正方体的对角线长为1+1+1=3,故球的半径为r =,所以球的表面积为4π×èø2=3π,因此正确选项为A .我们仅根据三棱锥的特征,很难确定其外接球的球心,为了便于计算,需采用补形法,将正三棱锥补形为正方体,那么正方体的中心即为三棱锥外接球的球心,即正方体的对角线就是球的直径,据此建立关系式,即可快速求得球的半径和表面积.二、将斜三棱柱补成四棱柱对于正三棱锥,一般很容易确定其高,但对于斜三棱柱,我们却很难确定其高.此时可采用补形法,将斜三棱柱补形为四棱柱,这样根据四棱柱的特点,可快速确定其高,求得顶点与底面之间、点与点之间的距离.例2.已知斜三棱柱的侧面A 1ACC 1与平面ABC 垂直,∠ABC =90°,BC =2,AC =23,且AA 1⊥A 1C ,AA 1=A 1C ,求点C 到侧面A 1ABB 1的距离.图3解:如图3所示,将斜三棱柱ABC -A 1B 1C 1补为四棱柱,设点C 到侧面A 1ABB 1的距离为d ,由四棱柱的上下底面平行的性质可知,d 也是平面ABB 1A 1与平面CMM 1C 1的距离,作A 1D ⊥AC 于点D ,作A 1E ⊥AB 于点E ,∵AA 1=A 1C ,AC =23,AA 1⊥A 1C ,∴A 1D =3,∵∠ABC =90°,BC =2,∴AB =22,∵侧面A 1ACC 1与平面ABC 垂直,A 1D ⊥AC 于点D ,∴A 1D ⊥AB ,A 1E ⊥AB ,∴AB ⊥面A 1ED ,∴AB ⊥ED ,即∠ABC =90°,∴DE ∥BC ,D 为AC 中点,且DE =12BC =1,∴A 1E =A 1D 2+DE 2=2,而V 四棱柱=S ABMC ∙A 1D =S A 1ABB 1∙d ,∴d =S ABMC ∙A 1D S A 1ABB 1==3.为了便于计算,将斜三棱柱补为四棱柱,从而将线面距离转化为面面距离,再利用等体积变换法使问题得解.三、将棱台补为棱锥棱台较为特殊,它的上下底面平行,且成比例,但侧棱相交于一点.为了便于计算,我们可采用补形法,将棱台补形为棱锥,这样便可构造出几组相似的三角形、多边形,借助相似图形的性质建立关系式,便可顺利求得棱台的边、高的长度.例3.如图4所示,平面EB 1C 1F 将三棱柱ABC -A 1B 1C 1分成体积为V 1,V 2两部分,其中AB ,AC 的中点分别是E ,F ,则V 1:V 2为______.图4解:延长A 1A 到A 2,B 1B 到B 2,C 1C 到C 2,使得A 1A =AA 2,B 1B =BB 2,C 1C =CC 2,并延长B 1E ,C 1F ,可知V ABC -A 2B 2C 2=V ABC -A 1B 1C 1,∵A 2A :A 2A 1=1:2,∴V A 2-AEF=18V A 2-A 1B 1C 1,∵V A2-AEF=14V A2-ABC=14×13V ABC -A 2B 2C 2=112×V ABC -A 1B 1C 1,∴V AEF -A 1B 1C 1=7V A 2-AEF =712V ABC -A 1B 1C 1,∴V 1:V 2=7:5.将棱台补成棱锥,利用棱锥A 2-AEF 的性质以及相似三角形的性质求得各条棱的长和各个三棱锥的体积,再借助棱台ABC -A 1B 1C 1与棱柱ABC -A 2B 2C 2之间的位置关系进行转换,即可顺利解题.由上述分析可以看出,对于一些较为复杂的立体图形、立体几何问题,采用补形法求解,能使问题快速获解.因此,在解答立体几何问题时,同学们要学会联想,根据几何体的结构特征合理添加辅助线,将棱锥补成棱柱,将斜三棱柱补成四棱柱,将棱台补为棱锥,以便根据棱柱、四棱柱、棱锥的性质来解题.(作者单位:江苏省如皋市第二中学)解题宝典43。
立体几何微专题3: 补成长(正)方体的几何体的内切与外接球问题
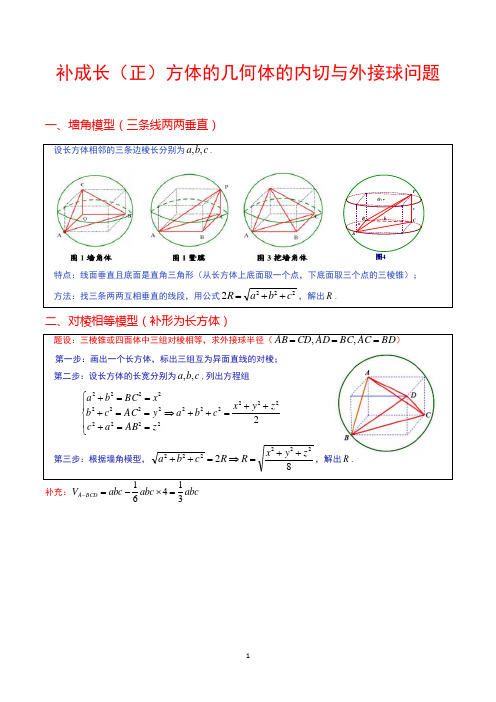
补成长(正)方体的几何体的内切与外接球问题一、墙角模型(三条线两两垂直)设长方体相邻的三条边棱长分别为c b a ,,.特点:线面垂直且底面是直角三角形(从长方体上底面取一个点,下底面取三个点的三棱锥); 方法:找三条两两互相垂直的线段,用公式2222c b a R ++=,解出R .二、对棱相等模型(补形为长方体)题设:三棱锥或四面体中三组对棱相等,求外接球半径(BD AC BC AD CD AB ===,,) 第一步:画出一个长方体,标出三组互为异面直线的对棱; 第二步:设长方体的长宽分别为c b a ,,,列出方程组2222222222222222222z y x c b a z AB a c y AC c b x BC b a ++=++⇒⎪⎩⎪⎨⎧==+==+==+第三步:根据墙角模型,82222222z y x R R c b a ++=⇒=++,解出R .补充:abc abc abc V BCD A 346=⨯-=-a bc图4PCO 2B A【精炼】1、已知三棱锥P ABC 的三条侧棱两两互相垂直,且AB =5,BC =7,AC =2,则此三棱锥的外接球的体积为( )A.83πB.823πC.163πD.323π 2、在三棱锥BCD A -中,侧棱AD AC AB ,,两两垂直,ADB ACD ABC ∆∆∆,,的面积分别为26,23,22,则三棱锥BCD A -的外接球的体积为( )3、在三棱锥P-ABC 中侧棱PA ,PB ,PC 两两垂直,Q 为底面△ABC 内一点,若点Q 到三个侧面的距离分别为3,4,5,则过点P 和Q 的所有球中,表面积最小的球的表面积为 . 4、已知正三棱锥ABC P -,点P,A,B,C,若PA,PB,PC 两两互相垂直,则球心到截面ABC 的距离为____________.5、已知边长为2的等边三角形ABC ,D 为BC 的中点,沿AD 进行折叠,使折叠后的∠BDC =π2,则过A ,B ,C ,D 四点的球的表面积为( )A .3πB .4πC .5πD .6π6、已知S A B C ,,,都是球O 表面上的点,SA ⊥平面ABC ,AB BC ⊥,2SA =,3AB =,4BC =,则球O 的表面积等于______.7、(2019·全国卷Ⅰ)已知三棱锥P ABC 的四个顶点在球O 的球面上,PA =PB =PC ,△ABC 是边长为2的正三角形,E ,F 分别是PA ,AB 的中点,∠CEF =90°, 则球O 的体积为( )A .86πB .46πC .26π D.6π 8、在平行四边形中,,,且,以为折痕,将折起,使点到达点处,且满足,则三棱锥的外接球的表面积为_________.9、三棱锥中S ABC ,SA =BC =13,SB =AC =5,SC =AB =10.则三棱锥的外接球的表面积为________.10、已知直三棱柱111ABC A B C -的6个顶点都在球O 的球面上,若3AB =,4AC =,AB AC ⊥,112AA =,则球O 的半径为( ) A B .C .132D .11 )A .3πB .4πC .D .6πABCD AB =3BC =cos A =BD BDC C E AE AD =E ABD -1、【解析】:∵AB=5,BC=7,AC=2,∴PA=1,PC=3,PB=2.以PA,PB,PC为过同一顶点的三条棱,作长方体如图所示,则长方体的外接球同时也是三棱锥PABC的外接球.∵长方体的对角线长为1+3+4=22,∴球的直径为22,半径R=2,因此,三棱锥PABC外接球的体积是43πR3=43π×(2)3=823π.故选B.2、【解析】:因为3212,2,2SacSbcSab===1322321223122,2,2SSScSSSbSSSa===⇒,222cbaR++=26434241=++=,πππ626343433=⎪⎪⎭⎫⎝⎛==RV,故选A.3、【解析】:根据题意:点Q到三个侧面的垂线与侧棱PA、PB、PC围成一个棱长为3、4、5的长方体,则其外接球的直径即为PQ且为长方体的体对角线.过点P和Q的所有球中,以PQ为直径的球的表面积最小,2r=22234552++=∴r=522,由球的表面积公式得:ππ5042==rS.4、【解析】:因为正三棱锥ABC,PA,PB,PC两两互相垂直,所以我们可以把正三棱锥ABC,放到正方体中,P、A、B、C为正方体的顶点,则正三棱锥ABCP-的外接球的球心为正方体体对角线的交点,在正方体ABCD-A1B1C1D1中,面A1BD和面CB1D1把体对角线三等分,所以球心到截面ABC的距离为33. 5、【解析】:连接BC(图略),由题知几何体ABCD为三棱锥,BD=CD=1,AD=3,BD⊥AD,CD⊥AD,BD⊥CD,将折叠后的图形补成一个长、宽、高分别是3,1,1的长方体,其体对角线长为1+1+3=5,故该三棱锥外接球的半径是52,其表面积为5π.6、【解析】:因为SA⊥平面ABC,AB BC⊥,所以四面体S ABC-的外接球半径等于以长、宽、高分别为,,SA AB BC三边长的长方体的外接球的半径.因为2SA=,3AB=,4BC=,所以2R=222SA AB BC++=29,所以表面积为ππ2942=R.7、【解析】:因为点E,F分别为PA,AB的中点,所以EF∥PB,因为∠CEF=90°,所以EF⊥CE,所以PB⊥CE.取AC的中点D,连接BD,PD,易证AC⊥平面BDP,所以PB⊥AC,又AC∩CE=C,AC,CE⊂平面PAC,所以PB⊥平面PAC,所以PB⊥PA,PB⊥PC,因为PA=PB=PC,△ABC为正三角形,所以PA⊥PC,即PA,PB,PC两两垂直,将三棱锥PABC放在正方体中.因为AB=2,所以该正方体的棱长为2,所以该正方体的体对角线长为6,所以三棱锥PABC的外接球的半径R=62,所以球O的体积πππ626343433=⎪⎪⎭⎫⎝⎛==RV,故选D.P-P-8、【解析】:在中,,,且, 由余弦定理,得即:,解得: 在四面体中,,,三组对棱长相等,可将四面体放在长方体中设长方体的相邻三棱长分别为,,,设外接球半径为则,,,则,即,所以 所以,四面体外接球的表面积为: 9、【解析】:如图,在长方体中,设AE =a ,BE =b ,CE =c.则SC =AB =a 2+b 2=10,SA =BC =b 2+c 2=13,SB =AC =a 2+c 2= 5.从而a 2+b 2+c 2=14=(2R)2,可得S =4πR 2=14π. 故所求三棱锥的外接球的表面积为14π.10、【解析】∵AB AC ⊥,∴直三棱柱111ABC A B C -的底面ABC 为直角三角形,把直三棱柱111ABC A B C -补成长方体,则长方体的体对角线就是球O 的直径,即球O 的半径为22234121322++=. 11、【解析】如图,将四面体补成正方体,则正方体的棱长是1,正方体的体对角线长为3,即此球的半径3R =,故球的表面积24π3πS R ==.ABD △22AB =3BC =2cos 3A =2222cos BD AB AD AB AD A =+-⋅()222222322239BD =+-⨯⨯⨯=3BD =ABED 3AE BD ==3AD BE ==22AB ED ==ABED x y z R 229x y +=229y z +=228z x +=22213x y z ++=213R =13R =E ABD -2134413π4R ππ=⨯=。
巧用补形法研究四面体问题

数学教学通讯投稿由0 箱:**********>解広集锦巧用补形法研究四面体问题重庆市巴蜀中学400023[摘要]殳体几何问题中,有一类问题可以通过补形法,得到一个常见的几何体,使复杂的线面关系变得清晰明了.文章从一道例题出发分析解决这类问题的方法,并在竝基础上总结规律,归纳常见的一些 四面体的补形方法.[关键词]立体几何;四面体;补形教学中,遇到这样一个问题:已知 在半径为2的球面上有4,B,C,D 四点, 若4 B=CD=2侧四面体4 BCD 的体积最大 值为多少?这是某年数学全国卷的第12题,主 要考查几何体的体积的计算、球的性 质、异面直线间的距离,通过球这个载 体考查学生的空间想象能力和推理计 算能力.解答是这样的:过CD 作平面PCD,使 4B 垂直于平面PCD,KAB 于R 设点P 到 CD 的距离为/1,则有V HW =yXyX2x/t X 2=却,当直径通过AB 与CD 中点时,饥…= 2V2M j=2VT ,故卩甜乂各本小题这个解答当中,学生比较疑 惑的有两点:(1)为什么可以过CD 作平 面PCD ,使AB 垂直于平面PCD ,能这样作 的前提是AB 和CZ )要垂直,那为什么认定 体积最大时4B 和CD 要垂直?(2)为什么 直径通过AB 与CD 中点时,距离人最大?要解释清楚这两个疑点,首先需要 补充说明一个公式.四面体体积公式:如果一个四面体 的两条相对棱的长分别是a, 6,它们的距 离为d,所成的角为0,那么它的体积为 %畴=丄岛dsin&(证明见后).6根据这个公式,我们首先得到结论: 仙和(?。
必须垂直,即sin&=90。
时才能得 到最大的体积.其次,由于AB=CD=R (球的半径),所以连结球心0和四个顶点,则容易知道 △ 04 B 和△ OCD 都是正三角形.设AB 的中点为E,CD 的中点为F,则0E 丄 A B,0F 丄 CD.设AB 与CD 间的距离为d,有dWEFW OE+OF.(异面直线间公垂线段最短)因此,0E/洪线时,四面体的体积可 以达到最大值,因为oe =of =a /T,故 昨 3这样解决一个选择题比较花费时 间,而且在高中数学教学中,不涉及四 面体的体积公式,异面直线的距离即公 垂线段的长度在教学中也仅仅要求了解.下面我们用补形的思路来解决这个 问题因为题目当中两条线段长度一样, 所以考虑把这个四面体补形成一个长 方体:图1则四面体的外接球即是长方体的外接球,四面体的体积是长方体的体积 减去四个全等的小三棱锥的体积.设长方体的边长为a,b,c,体对角线 即为外接球的宜径,得到:d+Ppjp,&2^2=22,所以a =2VT ,80 > 2020年九冃(下旬)作者简介:曾睿(1982-),本科学历,中学一级教师,从事高中数学教学.得教学通讯g•>解注集锦则V四面休"长方体一4V三棱锥=必-4x1,1,iVTbcx—abc=—abc=-------------.233又沪+c~22,所以j=2Vp>c wv^L(i2+c2)=£\£L33当且仅当b=c=V2时,等号成立.从等号成立的条件可以比较容易地看出是在AB和CD垂宜时,四面体的体积取到了最大值.我们会发现,使用补形,一下子把陌生的几何体变得熟悉了,原本错综复杂的线面关系也变得清晰起来.利用这一方法解决某些几何问题,思路清晰明朗,较其他方法简洁明了.比如刚才提到的四面体的体积公式也可以用补形法得到.一个四面体的两条相对棱的长分别是a,&,它们的距离为d,所成的角为0,将四面体补形成平行六面体(因为相对棱的长度不确定,相等的时候才能补成长方体).那么该平行六面体的底面积%s= -^-absinO,平行六面体的体积为卩六同*=丄abdsinO.同样,该平行六面体由原四面2体和四个全等的三棱锥构成.三棱锥与平行六面体的高相等,底面积为平行六面体的一半,x x<^>sin0= ^absind.所以F hw=V aw-4x7=w=—absinO.6一起来看一下常见的几种四面体补形方式:一、把四面体的四个面各补上一个三棱锥,最后形成一个平行六面体.其中正四面体是最特殊的形式,可以补成正方体.而对棱相等的四面体则可以补形成一个长方体.例1:正四面体棱长为°,求外接球的半径R.正四面体补形为一个正方体,正四面体的外接球即为正方体的外接球.如图3:图3正方体的面对角线是正四面体的棱长,体对角线为外接球的直径.设正方体边长为&,则a=V2b,2R=b,所以R=-^-^—a.4例2:在三棱锥A-BCD中,AB=CD=3,AD=BC=4,AC=BD=5,求三棱锥A_BCD外接球的半径.因为有三组对棱相等,把四面体补成一个长方形,如图4:图4长方体的三个面的面对角线是三棱锥的棱长,体对角线是外接球的直径.设长方体的棱长为°,6,c,外接球的半径为R,a^+b2=32,则■fe^cM2,(2R)2=<z2+62+c2,所以t^+c^S2,R丄.2二、把四面体的一个角作为平行六面体的一个角补形成平行六面体.例3:四面体ABCD,侧棱AB,AC,40两两垂宜,AB=2,AC=3,AD=4,求四面体的外接球的半径R.因为四面体的侧棱两两垂直,所以可以把这个角看作长方体的一个角,把四面体补形成一个长方体,则四面体的外接球就是长方体的外接球图5四面体的三条侧棱就是长方体的长、宽、高,外接球的宜径就是长方体的体对角线,则(2R)2=AB2+A(?+402=29,所以R=^_.2例4:若三棱锥S-ABC的所有顶点都在球0的球面上,SA丄平面ABC,SA=2VT,AB=1,A C=2,厶BA C=60°,求球0的半径R.根据已知条件可以得到AABC是宜角三角形,把四面体补成一个长方体,则四面体的外接球就是长方体的外接球,外接球的直径就是长方体的体对角线.如图6:图6则(2R)2=SA2+A CM6,所以R=2.例5:已知四面体PABC的侧面刃C与平面4BC垂直,Z j4BC=90°,BC=2VT,AB=2,且PA±PC,PA=PC,求异面直线PC与4B所成角的余弦值解答:把四面体补成如图所示平行六面体,异面直线PC与4B所成角即为PC与CD所成角的补角的余孩值.取AC中点M,PA=PC,则PMLAC,又因为平面E4C与平面ABC垂直,所以PM丄平面ABC.A A BC中,AABC=90°,AB=2,BC=2020年14冃(下旬)<81数学教学通讯投稿由0 箱:**********>解広集锦2VT ,所以乙4 CB=30° ,A C=4.APAC 中,E4 丄PC,PA=PC 9AC=4, 所以P M=2,PC=2VT.底面四边形ABDC 中i DM * 12=DC 2 +芯仏p),因Ji 匕只要证血1+血2 (f f )<1 眄-1%2仏一方2) , f2-----------In ------------, ln^-lni 2 ln^-lnf 2只要证ln£+l%<21n —戈一,1 2 ln^-lnt,只要证石<,"[(对数平均不 ln^-hi^2等式).C4^-2DC-CM-cosl20°,得到RtAPMD 中,加二 4.△PCD 中,cos 厶P CD 二 M+C 乎-PD2 二 2PC-CD V24 •所以异面直线PC 与AB 所成角的 余弦值为匹.4此题也可以用空间向量法解答,用 补形能更好地体现线面关系.三、把四面体补形成三棱柱例6:已知某几何体底面ABC 是棱 长为1的等边三角形,刃丄平面ABC, PA =3,求该几何体的外接球的半径.解答:将该四面体补形成一个三棱柱四面体的外接球就是三棱柱的外接球.先求三棱柱底面三角形外接圆半 径r=A. VT = VT.3 2 3又因为刃丄平面ABC,B4=3,所以三棱柱的外接球半径为R =四面体的问题可以通过补形变成 正方体、长方体乃至平行六面体的问题.尤其在正方体和长方体中,点线面的关系是我们所熟悉的.一些几何题的证明和求解,由原几何图形分析探究会比较 烦琐,通过补形填补成一个新的几何图形,能使原问题的本质得到充分的体现,解决起来比较容易.本文着重讨论四面 体的补形问题,希望窥一斑而知全豹, 探究立体几何中补形法这一重要的转化策略.(上接第74页)-771=0,证法4:由题意得 所以ln(x 1+m)-m%1=0,ln(%2+7?l ) -77U ;2=O.^x l +m=t l ,x 2+m=t 2,^ix l =t l -m 所以两式相减得]nt 2-m (£2-7n ) =0,1叫一1皿2,所 以?n=-----------方1-方21 ln^-ln^ / ln^-ln^鸟,所以|2=a 勾芯 ,、t r t 2ln^-lnt / 1叫 一1叫 ]叫--------XL+ ----------两式相加得lrUj+ln^- x (i !+力1一力22=0,t 2)+2'1%-1%,lnL-lni 2所以----------X (£ 1 +匚)=lni ] +lni 2+f 2I lm-liu 2 u'E 丿,~ ln/^lnL ln/^lnL所以鼻+%-2><_ =—_ («!-t x -t 2(2)-7 1要证衍+%2<0,只要证% i +%2<—In —, m m 只要证t 1+t 2-2m<—In 丄,m mlnL-lnt, InL-liU.又?n=-----------+£2-2x ----------------=右-方2 NF ln^+lnij U1 2令卩(")=u-21mz -----,贝U0(«)=1-----+u u丄二(弘1) >0,所以卩(訪)在"e (1,+qo ) u 2 u 2上单调递增,所以卩@)>卩(1)二0,所以21n “-丄>0,所以X1+x 2<0,所以*匕题得证.U卩形成结论极值点偏移问题中的南辕北辙现象,是由基函数极值点偏移方向不符题 意要求引起的.要避免这种现象的发生,应使基函数极值点偏移方向与题意 要求一致.82 > 2020年九冃(下旬)。
求几何体外接球半径的两种思路

有关几何体外接球的半径问题是各类试题中经常出现的题目.此类问题重点考查同学们的空间想象能力和抽象思维能力,也是很多同学感到头疼的问题.这里介绍两种求几何体外接球半径的方法,以帮助同学们拓展解答该类问题的思路.一、补形法所谓补形法,即把几何体补形成规则的、简单的几何体,利用新几何体的性质和边角关系求得几何体外接球的半径的方法.在求几何体外接球的半径时,常将几何体补形为长方体、正棱柱等,使其顶点与原几何体的若干个顶点重合,这样,两个几何体的外接球半径就会相等,求得新几何体的半径,便可求得原几何体的半径.例1.已知在四面体P -ABC 中,PA =PB =4,PC=2,AC =25,PB ⊥平面PAC ,则四面体P -ABC 外接球的半径为____.解:由PA =4,PC =2,AC =25可得PA 2+PC 2=AC 2,即PA ⊥PC∵PB ⊥平面PAC ,PA 、PC ⊂平面PAC ,∴PB ⊥PA ,PB ⊥PC ,如图1,以PA 、PB 、PC 为长、宽、高作长方体,则该长方体的外接球就是四面体P -ABC 的外接球,∵该长方体的对角线为42+42+22=6,∴该四面体P -ABC 外接球的半径3.若已知三个平面两两垂直或能根据条件推断出三个平面两两垂直,可运用补形法,将其补形为长方体,利用长方体的对角线求几何体外接球的半径.运用补形法求几何体外接球的半径较为便捷,能有效降低问题的难度、简化计算的过程.二、转化法转化法是将复杂的立体几何外接球的半径问题转化为简单的平面几何问题来求解的方法.在求几何体外接球的半径时,可根据几何体的特点添加适当的辅助线,构造出三角形,利用正、余弦定理、勾股定理等平面几何知识求出几何体外接球的半径.例2.如图2,在直三棱柱ABC -A 1B 1C 1中,AB =4,AC =6,角A 为π3,AA 1=4,则直三棱柱ABC -A 1B 1C 1外接球的半径为____.解:设O 1、O 2分别是△ABC 和△A 1B 1C 1外接圆的圆心,由直三棱柱的性质可知ABC -A 1B 1C 1外接球的球心O 是O 1O 2连线的中点,连接O 1A 、OA ,在△ABC 中,AB =4,AC =6,A =π3,∴BC 2=AC 2+AB 2-2AB ×AC cos A=42+62-2×4×6cos π3=27,∵O 1是△ABC ∴BC sin A =2O 1A ,即O1A π3,在Rt△OO 1A 中,OO 1=12O 1O 2=12AA 1=2,O 1A =,∴OA =OO 12+O 1A 2=,即直三棱柱ABC -A 1B 1C 1外接球的半径为.这里首先添加辅助线,构造Rt△OO 1A ,根据直三棱柱的性质将求几何体外接球的半径问题转化为求Rt△OO 1A 中OA 的长,利用正余弦定理以及勾股定理求得直三棱柱ABC -A 1B 1C 1外接球的半径.相比较而言,补形法较为简单、直接,但同学们在解题时要注意联想、类比,才能顺利将几何体补形;转化法较为复杂,但是一种常用的方法.同学们只有熟练掌握这两种求几何体外接球半径的方法,才能有效地提升解题的效率.(作者单位:甘肃省陇南市宕昌县第一中学)李甲银图1图246。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
体或置于一个更熟悉的几何体中,巧妙地破解空间几何体的体积等问
题,常见的补形法有对称补形、联系补形与还原补形,对于还原补形,
主要涉及台体中“还台为锥”.
(2)补形法的应用条件:当某些空间几何体是某一个几何体的一部分, 且求解的问题直接求解较难入手时,常用该法.
【类题试解】如图所示,在等腰梯形ABCD中,AB=2DC=2,∠DAB=60°,E
3 2 6 AH= 3 ,在△AFG和△AHO中,根据三角形相似可知 1-( ) , 3 3 3 3 3 AG AH 6 外接球的表面积S球= 4( 6 ) 2 3 . 2 3 OA . 4 2 AF 4 6 3 答案: 3 2
2
【巧妙解法】由已知条件知,平面图形中AE=EB=BC=CD=DA=DE=EC=1.
折叠后得到一个正四面体.如图所示,把正四面体放在
正方体中,显然,正四面体的外接球就是正方体的外接 球.因为正四面体的棱长为1,所以正方体的棱长为 2 , 所以外接球直径2R= 3 2 ,所以R= 6 ,
4 所以外接球的表面积S球= 4( 6 )2 3 . 4 2 答案: 3 2 2 2
所以V几何体=V三棱柱+V四棱锥.
由题知三棱柱ABC-NDM的体积为
V1= 1 ×8×6×3=72.
2
四棱锥D-MNEF的体积为:
1 1 1 V2 S梯形MNEF DN 1 2 6 8 24, 3 3 2
则几何体的体积为:V=V1+V2=72+24=96.
答案:96
【巧妙解法】用“补形法”把原几何体补成一个直三 棱柱,使AA′=BB′=CC′=8, 所以V几何体= 1 V三棱柱= 1 ×S△ABC·AA′=
2 2 1 24×8=96. × 2
ห้องสมุดไป่ตู้
答案:96
【方法指导】(1)补形法的应用思路:“补形法”是立体几何中一种常
见的重要方法,在解题时,把几何体通过“补形”补成一个完整的几何
为AB的中点,将△ADE与△BEC分别沿ED,EC向上折起,使A,B重合,则形
成的三棱锥的外接球的表面积为 .
【常规解法】由已知条件知,平面图形中AE=EB=BC=CD=DA=DE=EC=1.
折叠后得到一个正四面体.作AF⊥平面DEC,垂足为F,F即为△DEC的中
心.
取EC的中点G,连接DG,AG,过球心O作OH⊥平面AEC,则垂足H为△AEC的 中心.所以外接球半径可利用△OHA∽△GFA求得.因为AG= 3 ,AF=
巧用补形法解决立体几何问题
【典例】(2015·唐山模拟)如图:△ABC中,AB=8,BC=10,
AC=6,DB⊥平面ABC,且AE∥FC∥BD,BD=3,FC=4,AE=5.则
此几何体的体积为 .
【常规解法】如图,取CM=AN=BD,连接DM,MN,DN,用“分割法”把原几
何体分割成一个直三棱柱和一个四棱锥.
