数字逻辑电路第2版刘常澍天津大学高等教育出版社习题解答 (1)
数字逻辑电路第二版刘常澍习题解答

P3-21(c)
⑷Y ABC (AB AB BC)题解图P3-21(c)
解:先变换逻辑式为与-或式,用两次取非法变换为与非-与非式,再用与非门实现,如题解图
P3-21(d)
试分析题图P3-15所示电路的逻辑功能。
Y ABC ABC ABC ABC当ABC为全0或全1时,
Y为1。
题图P3-15
逻辑电路如题图P3-16所示,试分析其逻辑功能。
该
Y A B C A B C
A A B C
实质
(A B C)( A B C
A)(A
B C
个三
A(A B C)( A B C B)( A B C C)
(c) *
2-19现有四2输入与非门CC4011和四2输入或非门CC4001各一块,题图(d)
图。试问实现Y1=ABCD和丫2=A+B + C+D。
P2-19是它们的封装引脚示意
题图P2-19
解:
Y ABCD AB CD
D (A B) (C D)
3-15
解:
3-16
连线图如下图所示。
第5次:第3章:3-15、3-16
1-31用K图完成下列函数运算(3)丫(AC ABC ABC) (ABC ABC ABC ABC)
解:(a)Y,AB C
解:设M AC ABC ABC,N
ABC ABC ABC ABC,贝U Y M
(b
Y
逻辑图如题解图
题解图
题图P2-13所示各电
解:£AB,
Y3A B,
F1
-
—
&
1
r
(c)
P2-12所示。
2-13根据输入
数字逻辑电路__刘常澍主编____第二章习题答案

第2章 习题答案2-1 二极管、三极管用于数字电路中与用于模拟电路有什么不同?答:二极管和三极管在数字电路中主要用作开关,工作于大信号状态,即二极管工作在正向导通和反向截止两个状态,三极管工作在饱和于截止两个状态; 模拟电路中二极管一般工作在小信号状态或反向击穿状态,三极管一般工作在放大状态。
2-2 有两个二极管A 和B ,在相同条件下测得A 管的I F =10mA ,I R =2mA ;B 管的I F=30mA ,I R =0.5μA ;比较而言,哪个性能更好?答:B 管更好,因为其反向漏电流较小而正向允许电流大。
2-3 三极管工作在截止、饱和、放大状态的外部条件各是什么?答:截止时,使发射结反偏即v BE ≤0;饱和时,使基极电流等于或大于基极饱和电流,即i B ≥I BS =V CC /βR C ;放大时,使发射结正偏,而i B <I BS =V CC /βR C 。
2-4 MOS 管工作在截止、恒流、可变电阻区的外部条件各是什么? 答:对于常用的增强型NMOS 管,截止时,使栅源电压小于开启电压V T 即v GS >V GS(th)N ;工作于恒流区时,使v DS >v GS - V GS(th)N ;工作于可变电阻区时,使v DS <v GS - V GS(th)N2-5 二极管电路如图P2-5所示。
v I =5sin ωt (V ),假设二极管是理想二极管,试画出输出 v O 的波形。
若考虑二极管的导通压降V D =0.7V ,画出输出v O 的波形。
解:输出波形如图解P2-5所示。
(a)为输入波形, D 为理想二极管时输出波形为(b), 考虑D 导通压降为0.7伏时输出波形为(c)。
2-6 二极管开关电路如图P2-6所示。
二极管导通电压为0.7V ,试分析输入端A 、B 分别为0V 和5V 时管子的工作状态,输出电压v O =?解:v A =5V ,v B =0V 时,D 2、D 1均导通 v O =–0.7V ; v A =5V ,v B =5V 时, D 2、D 1均导通 v O =4.3V ; v A =0V ,v B =5V 时,D 1 导通、D 2截止 v O =4.3V ; v A =5V, v B =0V 时, D 1截止、D 2导通 v O =4.3V 。
数字逻辑电路第二版刘常澍 习题解答

数字逻辑电路第二版刘常澍 习题解答第1次: 1-14:(3)、(4);1-15:(3)、(4);1-18:(1); 1-22:(3);1-23:(2)1-14 将下列带符号数分别表示成原码、反码和补码形式。
(3) (-1111111)2 (4) , (-0000001)2 ;解: (3) (-1111111)2 =(11111111)原= (10000000)反= (10000001)补(4) (-0000001)2 =(10000001)原= (11111110)反= (11111111)补1-15 将下列反码和补码形式的二进制数变成带符号的十进制数(3) (10000000)补; (4) (11100101)补解: (3) (10000000)补=(-128) 10 (4) (11100101)补=(-27) 101-18列出下述问题的真值表,并写出逻辑式。
(1)有A 、B 、C 三个输入信号,如果三个输入信号均为0或其中一个为1时,输出信号Y =1,其余情况下,输出Y =0。
解:逻辑式:CB AC B A C B A C B A Y +++=1-22 求下列逻辑函数的反函数(3)C A C BCD A Y ⋅+=)(CA D C CB D A Y ++++++=())((1-23 求下列逻辑函数的对偶式(2)DBC B A D B A BC Y ⋅++++=)(])()([)(*D C A B A D B A C B Y ++⋅+⋅++=第2次:1-21(5)(8)1-21 用代数法将下列函数化简为最简与-或式。
(5) (8)第3次:第1章:26(4)、28(4)、27(3)(4)、30(3)、31(3)1-26用K 图化简法将下列逻辑函数化为最简与-或式(4)∏=)12,11,10,8,5,4,3,2,1,0(),,,(M D C B A Y (1) 真值表:A B CY 00010011010101101001101011001110ABCBC A ABC AB BC A C B A AB BC A C AB ABBC A C AB ABBC A C AB Y =+=+++=⋅+⋅=⋅++=⋅++=)())(()(ABCACD ABC CD B A ACD BC ACD B A BC AD C B A BC AD C B A B A AB BC AD C B A C B A B A Y +=+++=+⋅+=+⋅⋅+=+⋅⋅++=++⋅+=0)()()()()(())((1-28 用K 图化简法将下列逻辑函数化为最简与-或-非式(4)∏=)151412108765420()(,,,,,,,,,,M D ,C ,B ,A Y1-27 用K 图化简法将下列逻辑函数化为最简或-与式(3)(4)∑=11,14),6,8,9,10,(0,1,2,3,4)(m D ,C ,B ,A Y=)151413111098632()(,,,,,,,,,M D ,C ,B ,A Y1-30 用K 图将下列具有约束条件的逻辑函数化为最简“与-或”逻辑式。
数字逻辑电路第二版刘常澍习题解答

数字逻辑电路第二版刘常澍 习题解答第1次: 1-14:(3)、(4);1-15:(3)、(4);1-18:(1); 1-22:(3);1-23:(2) 1-14 将下列带符号数分别表示成原码、反码和补码形式。
(3) (1111111)2 (4) , (0000001)2 ; 解: (3) (1111111)2 =()原= ()反= ()补(4) (0000001)2 =()原= ()反= ()补1-15 将下列反码和补码形式的二进制数变成带符号的十进制数补; 补解: (3) 补=(-128) 10 (4) 补=(-27) 10 1-18列出下述问题的真值表,并写出逻辑式。
(1)有A 、B 、C 三个输入信号,如果三个输入信号均为0或其中一个为1时,输出信号Y =1,其余情况下,输出Y =0。
解:式:C B A C B A C B A C B A Y +++=逻辑逻辑函数的反函数(3)C A D C BC D A Y ⋅+=)( 1-22 求下列逻辑函数的对偶式(2)D BC B A D B A BC Y ⋅++++=)(1-23 求下列第2次:1-21(5)(8)1-21 用代数法将下列函数化简为最简与-或式。
(5)(8) 第3次:第1章:26(4)、28(4)、27(3)(4)、30(3)、31(3) 1-26用K 图化简法将下列逻辑函数化为最简与-或式(4)∏=)12,11,10,8,5,4,3,2,1,0(),,,(M D C B A Y1-28 用K 图化简法将下列逻辑函数化为最简与-或-非式(4)∏=)151412108765420()(,,,,,,,,,,M D ,C ,B ,A Y 1-27 用K 图化简法将下列逻辑函数化为最简或-与式(3)∑=11,14),6,8,9,10,(0,1,2,3,4)(m D ,C ,B ,A Y (4)∏=)151413111098632()(,,,,,,,,,M D ,C ,B ,A Y 用K 图将下列具有约束条件的逻辑函数化为1-30 最简“与-或”逻辑式。
数字逻辑(第2版)习题答案

毛法尧第二版习题一1.1 把下列不同进制数写成按权展开式:⑴(4517.239)10= 4×103+5×102+1×101+7×100+2×10-1+3×10-2+9×10-3⑵(10110.0101)2=1×24+0×23+1×22+1×21+0×20+0×2-1+1×2-2+0×2-3+1×2-4⑶(325.744)8=3×82+2×81+5×80+7×8-1+4×8-2+4×8-3⑷(785.4AF)16=7×162+8×161+5×160+4×16-1+A×16-2+F×16-31.2 完成下列二进制表达式的运算:1.3 将下列二进制数转换成十进制数、八进制数和十六进制数:⑴(1110101)2=(165)8=(75)16=7×16+5=(117)10⑵(0.110101)2=(0.65)8=(0.D4)16=13×16-1+4×16-2=(0.828125)10⑶(10111.01)2=(27.2)8=(17.4)16=1×16+7+4×16-1=(23.25)101.4 将下列十进制数转换成二进制数、八进制数和十六进制数,精确到小数点后5位:⑴(29)10=(1D)16=(11101)2=(35)8⑵(0.207)10=(0.34FDF)16=(0.00111)2=(0.15176)8采用0舍1入规则⑶(33.333)10=(21.553F7)16=(100001.01011)2=(41.25237)81.5 如何判断一个二进制正整数B=b6b5b4b3b2b1b0能否被(4)10整除?解: 一个二进制正整数被(2)10除时,小数点向左移动一位, 被(4)10除时,小数点向左移动两位,能被整除时,应无余数,故当b1=0和b0=0时, 二进制正整数B=b6b5b4b3b2b1b0能被(4)10整除.1.6 写出下列各数的原码、反码和补码:⑴0.1011[0.1011]原=0.1011; [0.1011]反=0.1011; [0.1011]补=0.1011⑵0.0000[0.000]原=0.0000; [0.0000]反=0.0000; [0.0000]补=0.0000⑶-10110[-10110]原=110110; [-10110]反=101001; [-10110]补=1010101.7 已知[N]补=1.0110,求[N]原,[N]反和N.解:由[N]补=1.0110得: [N]反=[N]补-1=1.0101, [N]原=1.1010,N=-0.10101.8 用原码、反码和补码完成如下运算:⑴0000101-0011010[0000101-0011010]原=10010101;∴0000101-0011010=-0010101。
数字逻辑电路课后答案综述

数字逻辑电路 刘常澍课后习题答案1-14 将下列带符号数分别表示成原码、反码和补码形式。
(3) (-1111111)2 (4) , (-0000001)2 ;解:(3) (-1111111)2 =(11111111)原= (10000000)反= (10000001)补(4) (-0000001)2 =(10000001)原= (11111110)反= (11111111)补1-15 将下列反码和补码形式的二进制数变成带符号的十进制数(3) (10000000)补;(4) (11100101)补解:(3) (10000000)补=(-127) 10 (4) (11100101)补=(-27) 101-18列出下述问题的真值表,并写出逻辑式。
(1)有A 、B 、C 三个输入信号,如果三个输入信号均为0或其中一个为1时,输出信号Y =1,其余情况下,输出Y =0。
解: 逻辑式:C B A C B A B A C B A Y +++=1-22 求下列逻辑函数的反函数(3)A D BC A Y ⋅+=)(C AD C C D A Y ++++++=)())(B (1-23 求下列逻辑函数的对偶式(2)D BC B A D B A BC Y ⋅++++=)(])()([)(*D C A B A D C A C B Y ++⋅+⋅++=1-21 用代数法将下列函数化简为最简与-或式。
(5) (8)ABBC A C AB AB AB Y ⋅++=⋅+=BC AD C B A BC AD C B A B A AB BC AD C B A C B A B A Y +⋅⋅+=+⋅⋅++=++⋅+=)()()()())((1-26 用K 图化简法将下列逻辑函数化为最简与-或式(4)∏=)12,11,9,8,5,4,2,1,0(),,,(M D C B A Y1-28 用K 图化简法将下列逻辑函数化为最简与-或-非式 (4)∏=)15,13,12,10,9,7,6,5,4,2,1(),,,(M D C B A Y1-27 用K 图化简法将下列逻辑函数化为最简或-与式(3)∑=,15),8,9,10,11(0,1,3,4,6),,,(m D C B A Y (4)∏=)151413111098632()(,,,,,,,,,M D ,C ,B ,A Y1-30 用K 图将下列具有约束条件的逻辑函数化为最简“与-或”逻辑式。
[数字电子技术及应用(第2版)习题答案第1单元习题答案

自我检测题:一、填空题1-1 (1001010)2 =( 112 )8 =( 4A )16 =( 74 )10 1-2 (37.375)10 =( 100101.011 )2 =( 45.3 )8 =( 25.6 )161-3 (CE)16=( 11001110 )2 =( 316 )8 =( 206 )10 =( 001000000110 )8421BCD 1-4在逻辑代数运算的基本公式中,利用分配律可得A (B +C )= AB+AC ,A +BC = (A+B)(A+C) ,利用反演律可得ABC = C B A ++ ,C B A ++ = C B A 。
1-5在数字电路中,半导体三极管多数主要工作在 截止 区和 饱和 区。
1-6 COMS 逻辑门是 单 极型门电路,而TTL 逻辑门是 双 极型门电路。
1-7 COMS 集成逻辑器件在 功耗 、 抗干扰 方面优于TTL 电路,同时还具有结构相对简单,便于大规模集成、制造费用较低等特点。
1-8 CT74 、 CT74H 、 CT74S 、 CT74LS 四个系列的 TTL 集成电路,其中功耗最小的为 CT74LS ;速度最快的为 CT74S ;综合性能指标最好的为 CT74LS 。
二、选择题1-9指出下列各式中哪个是四变量A、B、C、D的最小项( C )。
A 、ABC B 、A+B+C+D C 、ABCD D 、AC 1-10逻辑项D BC A 的逻辑相邻项为( A )。
A 、ABCD —B 、ABCDC 、AB —CD D 、ABC —D1-11当利用三输入的逻辑或门实现两变量的逻辑或关系时,应将或门的第三个引脚( B )。
A 、接高电平B 、接低电平C 、悬空1-12当输入变量A 、B 全为1时,输出为0,则输入与输出的逻辑关系有可能为( A )。
A 、异或 B 、同或 C 、与 D 、或1-13TTL 门电路输入端悬空时应视为( A )电平,若用万用表测量其电压,读数约为( D )。
第四章 《数字逻辑》(第二版)习题答案
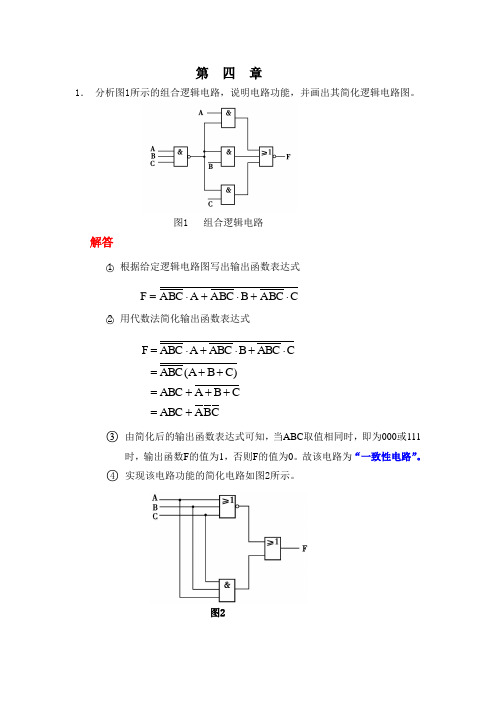
第四章1.分析图1所示的组合逻辑电路,说明电路功能,并画出其简化逻辑电路图。
图1 组合逻辑电路解答○1根据给定逻辑电路图写出输出函数表达式CABCBABCAABCF⋅+⋅+⋅=○2用代数法简化输出函数表达式CBA ABC CBA ABC C)B(A ABCCABCBABCAABCF+ =+ ++ =+ +=⋅+⋅+⋅=○3由简化后的输出函数表达式可知,当ABC取值相同时,即为000或111时,输出函数F的值为1,否则F的值为0。
故该电路为“一致性电路”。
○4实现该电路功能的简化电路如图2所示。
图22. 分析图3所示的逻辑电路,要求:(1) 指出在哪些输入取值下,输出F 的值为1。
(2) 改用异或门实现该电路的逻辑功能。
图3 组合逻辑电路解答分析给定逻辑电路,可求出输出函数最简表达式为 C B A C B A F ⊕⊕=⊕⊕=○1 当ABC 取值000、011、101、110时,输出函数F 的值为1; ○2 用异或门实现该电路功能的逻辑电路图如图4所示。
图43.析图5所示组合逻辑电路,列出真值表,并说明该电路的逻辑功能。
图5 组合逻辑电路= 1 = 1 = 1 A W B C D X Y Z . . .解答○1 写出电路输出函数表达式如下: D C Z C,B Y B,A X A,W ⊕=⊕=⊕==○2 列出真值表如表1所示。
表1ABCD WXYZ ABCD WXYZ 0000 0001 0010 0011 0100 0101 0110 0111 0000 0001 0011 0010 0110 0111 0101 0100 1000 1001 1010 1011 1100 1101 1110 1111 1100 1101 1111 1110 1010 1011 1001 1000○3 由真值表可知,该电路的功能是将四位二进制码转换成Gray 码。
4.设计一个组合电路,该电路输入端接收两个2位二进制数A=A 2A 1,B=B 2B 1。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Y ABC A BC ABC A B C A BC ABC AB C ABC A B A C B C ABC A B A C B C ABC
4
题解图 P3-21(c)
(4) Y A BC ( AB A B BC ) 解:先变换逻辑式为与-或式,用两次取非法变换为与非-与非式,再用与非门实现,如 题解图 P3-21(d)。
Y ABC A BC AB ABC A BC AB ABC ( A BC ) AB ( A B C )( A BC ) AB ABC ( A BC ) ABC
( AB A B A B ) C ( AD BC ) ( A B ) C ( AD BC ) ( A B ) ( ACD BC ) ACD A BCD ABC 0 ACD ABC
1
第 3 次:第 1 章:26(4) 、28(4) 、27(3) (4) 、30(3) 、31(3) 1-26 用 K 图化简法将下列逻辑函数化为最简与-或式 (4) 1-28 用 (4)
Y ( A, B, C , D) M (0,1,2,3,4,5,8,10,11,12)
K 图化简法将下列逻辑函数化为最简与-或-非式
题解图 P3-30(c)
题解图 P3-30(d)
第 8 次作业: 第 4 章 4-8、4-9、4-11、4-12 4-8 图 P3-8 是主从 RS 触发器的符号。已知初 始状态 Q=0,输入信号 S 和 R 的波形,试画出 输出端 Q 的波形。 解:输出端 Q 的波形画于题图 P4-8 中。
题图 4-8
Y ( A, B ,C , D) M (0,2 ,4 ,5,6,7 ,8,10,12,14,15)
1-27 用 K 图化简法将下列逻辑函数化为最简或-与式 (3)Y ( A, B ,C , D) m(0,1,2,3,4,6,8,9,10,11,14) (4)Y ( A, B ,C , D) M (2,3,6 ,8,9 ,10,11,13,14,15)
Y2 A B C D ( A B) (C D)
第 5 次:第 3 章:3-15、3-16 3-15 试分析题图 P3-15 所示电路的逻辑功能。
解: Y ABC A B C ABC A B C 当 ABC 为全 0 或全 1 时,Y 为 1。 3-16 逻辑电路如题图 P3-16 所示,试分析其逻辑功能。 解:
Y ( A C )( A B C )( B C ) AC A B C B C
(3)
Y ( ABC BC ) D A BD
解:先将逻辑式变换为与-或式,再用 K 图将逻辑式变换为或-与式,进而变换为或非或非式,用或非门实现,如题解图 P3-22(c)。
1-30 用 K 图将下列具有约束条件的逻辑函数化为最简“与-或”逻辑式。 (3)
Y ( A, B, C , D ) m(0,1,3,5,8,9) d (10,11,12,13,14,15)
解:
(3) Y B C CD BD
1-31 用 K 图完成下列函数运算
(3) Y ( AC ABC ABC) ( ABC ABC ABC A B C)
题图 4-13
4-9 图 P4-9 是主从 JK 触发器符号。 已知输入信号 J 和 K 的波形,初始状态 Q=0,试画出输出端 Q 的 波形。 解:输出端 Q 的波形画于题图 P4-9 中。
题图 4-9
6
4-11 试画出题图 P4-11 所示 D 触发器输出端 Q 的电压波形,已知输入信号的波形如图所 示。 解:输出端 Q 的波形画于题图 P4-11 中。
题图 4-11
4-12 题图 P4-12 给出了集成 D 触发器 CC4013 的逻辑符 号和输入信号的电压波形,试画出输出端 Q 的波形。 解:输出端 Q 的波形画于题图 P4-12 中。
题图 4-12
第 9 次作业: 第 4 章 4-20、4-21 4-13 图 P4-21 是 D 触发器 74LS74 的符号。已知输入信号波形如图所示,试画出输出端 Q 和的电压波形。 解:输出端 Q 的波形画于题图 P4-13 中。
Y ( A D )( B C ) ( C D ) A C
1-23 求下列逻辑函数的对偶式(2) Y BC ( A B D ) AB BC D
Y * ( B C ABD) [( A B) ( A C ) D]
第 2 次:1-21(5) (8) 1-21 用代数法将下列函数化简为最简与-或式。 (5) (8) Y ( A B AB C A BC )( AD BC )
数字逻辑电路 第二版 天津大学 刘常澍 高等教育出版社 习题解答
请各位同学不要抄答案,答案是用来核对与复习的! ! !
学长上传习题解答是为了让你们数电学得更好!
第 1 次: 1-14: (3) 、 (4) ;1-15: (3) 、 (4) ;1-18: (1) ; 1-22: (3) ;1-23: (2) 1-14 将下列带符号数分别表示成原码、反码和补码形式。 (3) (1111111)2 (4) , (0000001)2 ; 解: (3) (1111111)2 =(11111111)原= (10000000)反= (10000001)补 (4) (0000001)2 =(10000001)原= (11111110)反= (11111111)补 1-15 将下列反码和补码形式的二进制数变成带符号的十进制数 (3) (10000000)补; (4) (11100101)补 解: (3) (10000000)补=(-128) 10 (4) (11100101)补=(-27) 10 1-18 列出下述问题的真值表,并写出逻辑式。 (1)有 A、B、C 三个输入信号,如果三个输入信号均为 0 或其中一个为 1 时,输出 信号 Y=1,其余情况下,输出 Y=0。 解:
解:设 M AC ABC ABC , N ABC A BC ABC A B C ,则 Y M N
M AC ABC ABC
N ABC ABC ABC A B C
Y BC
第 4 次:第 2 章:2-12、2-13、2-18、2-19 2-12 设开关闭合为 1,断开为 0,灯亮为 1,灯灭为 0,用逻辑式表示题图 P2-12 所示开关 电路的逻辑关系,并用逻辑符号画出逻辑图。
题图 P2-12
2
解: (a) Y1 AB C 逻辑图如题解 图 P2-12 所示。
题解图 P2-12
(b) Y1 ( A B )C
(c)
Y1 AB CD
2-13 根据输入信号波形,画出题图:
Y1 AB
,
Y2 A B
,
Y3 A B ,
Y ABC ( AB A B BC ) A( B C ) ( AB ) ( A B ) ( B C ) AB AC AB AC
题解图 P3-21(d)
3-22 试画出用“或非”门和反相器实现下列逻辑函数的逻辑图。 (2) Y ( A C )( A B C )( A B C ) 解:
(1) 真值表: A 0 0 0 0 1 1 1 1 B 0 0 1 1 0 0 1 1 C 0 1 0 1 0 1 0 1 Y 1 1 1 0 1 0 0 0 逻辑式: Y A B C A BC ABC AB C
1-22 求下列逻辑函数的反函数(3) Y ( A D BC ) C D A C
Y ( ABC BC ) D A BD ( A B C )( B C ) D A BD ABD A CD B CD BCD A BD AD B C D BCD Y D ( A B C )( A B C ) D A B C A B C
题图 P3-16
题图 P3-15
该电路实质是一个三输入与门 第 6 次作业: 第 3 章 3-21(3) 、 (4) ;3-22(2) 、 (3) 3-21 试画出用“与非”门和反相器实现下列逻辑函数的逻辑图。 (3) Y ABC A BC ABC 解:所给原式非号下的与-或式是原函数的反函数,原函数(不带非号)和反函数的最 小项编号是错开的,根据反函数即可直接写出原函数的最小项式,进而化简逻辑式为与-或 式,用两次取非法变换为与非-与非式,再用与非门实现,如题解图 P3-21(c)。
题解图 P2-18
对应输入波形各输出波形如题解图 P2-18 所示。 2-19 现有四 2 输入与非门 CC4011 和四 2 输入或非门 CC4001 各一块,题图 P2-19 是它们 的封装引脚示意图。试问实现 Y1=ABCD 和 Y2=A+B+C+D。
3
题图 P2-19
解: Y1 ABCD AB CD , 连线图如下图所示。
Y4 A B A B ,输出波形图如下。
2-18 写出题图 P2-18 各电路的逻辑表达式,并对应图题图 P2-18(d)输入波形画出各输 出波形。
题图 P2-18
解:(a) Y1 AB C ; (b) (c)
AB(C 0) ; Y2 0(C 1) A B(C 1) 。 Y3 Z (C 0)
C 0 1 0 1 0 1 0 1
R 0 0 1 1 0 1 1 1
G 0 1 0 1 0 1 1 1
Y 0 0 0 1 1 1 1 1
3-30 试用八选一数据选择器 CT74151 实现下列函数 (3) F3 ( A, B ,C , D) m(0,3,6 ,7 ,10,13,14) 解:所用 K 图及逻辑图如题解图 P3-30(c) 所示。逻辑图如解图 P3-30(d)所示
