15 平面体系的几何组成分析1
合集下载
哈工大结构力学题库一章
第一章平面体系的几何组成分析一判断题1. 图示体系是几何不变体系。
（）题1图题2图题3图题4图2. 图示体系为几何可变体系。
（）3. 图示体系是几何不变体系。
（）4. 图示体系是几何不变体系。
（）5. 图示体系是几何不变体系。
（）题5图题6图题19图题20图6. 图示体系为几何不变有多余约束。
（）7. 几何瞬变体系产生的运动非常微小并很快就转变成几何不变体系，因而可以用作工程结构。
（）8. 两刚片或三刚片组成几何不变体系的规则中，不仅指明了必需的约束数目，而且指明了这些约束必需满足的条件。
（）9. 在任意荷载下，仅用静力平衡方程即可确定全不反力和内力的体系是几何不变体系。
（）10. 计算自由度W小于等于零是体系几何不变的充要条件。
( )11. 几何可变体系在任何荷载作用下都不能平衡。
( )12. 三个刚片由三个铰相联的体系一定是静定结构。
( )13. 有多余约束的体系一定是超静定结构。
( )14. 有些体系为几何可变体系但却有多余约束存在。
（）15. 平面几何不变体系的三个基本组成规则是可以相互沟通的。
（）16. 三刚片由三个单铰或任意六根链杆两两相联，体系必为几何不变。
（）17. 两刚片用汇交于一点的三根链杆相联，可组成几何不变体系。
（）18. 若体系计算自由度W<0，则它一定是几何可变体系。
（）19. 在图示体系中，去掉其中任意两根支座链杆后，所余下都是几何不变的。
（）20. 图示体系按三刚片法则分析，三铰共线，故为几何瞬变体系。
（）21. 有多余约束的体系一定是几何不变体系。
（）22. 几何不变体系的计算自由度一定等于零。
（）23. 几何瞬变体系的计算自由度一定等于零。
（）24. 图中链杆1和2的交点O可视为虚铰。
（）题24图二选择题1. 图示体系为：（）A．几何不变无多余约束 B．几何不变有多余约束 C．几何常变 D．几何瞬变题1图题2图题3图2. 图示体系为：（）A．几何不变无多余约束 B．几何不变有多余约束 C．几何常变 D．几何瞬变3. 图示体系虽有三个多余约束，但为保证其几何不变，哪两根链杆是不能同时去掉的。
平面体系的几何组成分析
建筑力学
Architectural Mechanics
主 讲：杜留记
河南城建学院土木工程系力学教研室
第五章 平面体系的几何组成分析
5.1 几何不变与几何可变体系的概念 5.2 刚片·自由度·联系的概念 5.3 几何不变体系的组成规则 5.4 静定结构和超静定结构·常见的结构形式
§5-1 几何不变与几何可变体系的概念
几何不变体系(geometrically unchangeable system) ： 在不考虑材料应变的条件下，体系的位置和形状不能改变。 几何可变体系(geometrically changeable system)： 在不考虑材料应变的条件下，体系的位置和形状可以改变。
几何可变体系又可分为两种
§5-2 刚片·自由度·联系的概念
◆单刚结点：将两刚片联结成一个整体的结点 图示两刚片有六个自由度, 加刚联结后有三个自由度
一个单刚结点可减少三个自由度相当于三个 约束。
刚结点将刚片连成整体（新刚片）。若是发散的，无多余约束,若是闭合的，则 每个无铰封闭框都有三个多余约束。
三个多余约束
两个多余约束 一个多余约束
W=（各部件自由度总数）－（全部约束总数） 如刚片数m，单铰数h，支座链杆数r，则
W=3m－2h－r
§5-2 刚片·自由度·联系的概念 注意：
1、复连接要换算成单连接。
连四刚片h=3
连三刚片h=2
连两刚片h=1
2、刚接在一起的各刚片作为一大刚片。如带 有a个无铰封闭框，约束数应加3a个。
3、铰支座、定向支座相当于两个支承链杆， 固定端相三于个支承链杆。
§5-4 静定结构和超静定结构·常见的结构形式
结构类型：框筒结构 高 度：138m 层数：38 建筑面积：67750m2 开工日期：1993.01 竣工日期：1996.06
Architectural Mechanics
主 讲：杜留记
河南城建学院土木工程系力学教研室
第五章 平面体系的几何组成分析
5.1 几何不变与几何可变体系的概念 5.2 刚片·自由度·联系的概念 5.3 几何不变体系的组成规则 5.4 静定结构和超静定结构·常见的结构形式
§5-1 几何不变与几何可变体系的概念
几何不变体系(geometrically unchangeable system) ： 在不考虑材料应变的条件下，体系的位置和形状不能改变。 几何可变体系(geometrically changeable system)： 在不考虑材料应变的条件下，体系的位置和形状可以改变。
几何可变体系又可分为两种
§5-2 刚片·自由度·联系的概念
◆单刚结点：将两刚片联结成一个整体的结点 图示两刚片有六个自由度, 加刚联结后有三个自由度
一个单刚结点可减少三个自由度相当于三个 约束。
刚结点将刚片连成整体（新刚片）。若是发散的，无多余约束,若是闭合的，则 每个无铰封闭框都有三个多余约束。
三个多余约束
两个多余约束 一个多余约束
W=（各部件自由度总数）－（全部约束总数） 如刚片数m，单铰数h，支座链杆数r，则
W=3m－2h－r
§5-2 刚片·自由度·联系的概念 注意：
1、复连接要换算成单连接。
连四刚片h=3
连三刚片h=2
连两刚片h=1
2、刚接在一起的各刚片作为一大刚片。如带 有a个无铰封闭框，约束数应加3a个。
3、铰支座、定向支座相当于两个支承链杆， 固定端相三于个支承链杆。
§5-4 静定结构和超静定结构·常见的结构形式
结构类型：框筒结构 高 度：138m 层数：38 建筑面积：67750m2 开工日期：1993.01 竣工日期：1996.06
[精品]平面体系的几何组成分析
![[精品]平面体系的几何组成分析](https://img.taocdn.com/s3/m/dfa18f6dbf1e650e52ea551810a6f524ccbfcb80.png)
三、点、刚片、结构的自由度
四、约束（联系）
1、约束：凡能减少自由度的装置。
2、一根链杆相当于一个约束(图3）。
y
o
x
（图3）
y
o
x
x
y
3、一个简单铰相当于两个约束(图4）。
y
o
x
（图4）
y
o
x
x
y
4、联结n个刚片的复铰相当于(n-1)个简单铰，减少(n-1)×2个约束（图5）。
（图5）
F
A
B
C
实饺：几何可变
虚饺：几何瞬变
2、三根链杆相互平行
实饺
虚饺
三饺共线（瞬变）
三个刚片上用不在同一直线上的三个铰两两相联结，形成无多余约束的几何不变体系。
三、三个刚片间的联结（规则三）：
第四节 几何组成分析的方法、步骤和举例
一、方法 一般先考察体系的计算自由度，若W0，则体系为几何可变，不必进行 几何组成分析；若W0，则应进行几何组成分析。
三、举例
例题1
结论: 无多余约束几何不变体系
第五节 体系几何组成与静定性的关系
一、几何可变体系 一般无静力解答。
二、无多余联系的几何不变体系 静力解答唯一确定。
三、几何瞬变体系 其平衡方程或者没有有限值解答，或在特殊情况下，解答不确定。
四、具有多余联系的几何不变体系 静力解答有无穷多组解。
二、两个刚片之间的联结（规则二）：
两个刚片上用一个铰和一根不通过此铰的一根链杆相连结，形成无多余约束的几何不变体系（或：两个刚片上用三根不交于一点、也不全平行的三根链杆相连结 ，形成无多余约束的几何不变体系）。
特殊情况： 1、三根链杆交于一点
四、约束（联系）
1、约束：凡能减少自由度的装置。
2、一根链杆相当于一个约束(图3）。
y
o
x
（图3）
y
o
x
x
y
3、一个简单铰相当于两个约束(图4）。
y
o
x
（图4）
y
o
x
x
y
4、联结n个刚片的复铰相当于(n-1)个简单铰，减少(n-1)×2个约束（图5）。
（图5）
F
A
B
C
实饺：几何可变
虚饺：几何瞬变
2、三根链杆相互平行
实饺
虚饺
三饺共线（瞬变）
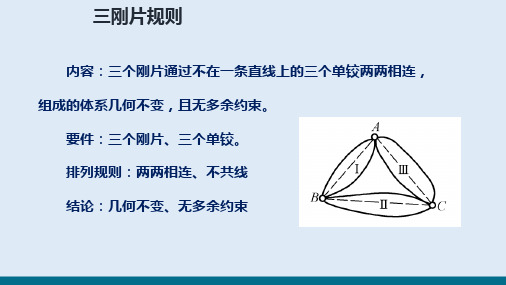
三个刚片上用不在同一直线上的三个铰两两相联结，形成无多余约束的几何不变体系。
三、三个刚片间的联结（规则三）：
第四节 几何组成分析的方法、步骤和举例
一、方法 一般先考察体系的计算自由度，若W0，则体系为几何可变，不必进行 几何组成分析；若W0，则应进行几何组成分析。
三、举例
例题1
结论: 无多余约束几何不变体系
第五节 体系几何组成与静定性的关系
一、几何可变体系 一般无静力解答。
二、无多余联系的几何不变体系 静力解答唯一确定。
三、几何瞬变体系 其平衡方程或者没有有限值解答，或在特殊情况下，解答不确定。
四、具有多余联系的几何不变体系 静力解答有无穷多组解。
二、两个刚片之间的联结（规则二）：
两个刚片上用一个铰和一根不通过此铰的一根链杆相连结，形成无多余约束的几何不变体系（或：两个刚片上用三根不交于一点、也不全平行的三根链杆相连结 ，形成无多余约束的几何不变体系）。
特殊情况： 1、三根链杆交于一点
平面体系几何组成分析的方法(静定的概念)(建筑力学)
当使用判定规则进行判定时，可以使用如下技巧，使问题简化： ①去二元体； ②地基可以当作特殊的刚片； ③扩大刚片法：将整个体系的几何不变部分看作刚片，并考察其与周 围部分的连接方式，逐步扩大刚片，减少杆件数目； ④刚片与链杆灵活转换：根据需要可以将链杆当作刚片使用，也可以 将刚片（包括地基）或几何不变部分当作链杆使用； ⑤巧用虚铰：链杆数目较多时，使用虚铰可以使体系简化。
例题分析
例1.分析图示体系的几何构造性。 解析：（1）计算自由度
W 4244 0
自由度为0，说明体系具有成为几何不变体系的最少约束数目。 进一步判断，依次去掉二元体DFE、BDC、BEC、BCA后，整个体系只剩下 地基了，为几何不变体系。由于去掉二元体并不改变原体系的几何构造性，因此 原体系也是几何不变体系。
二元体规则是非常好用的规则，特别是去二元体，可以大大简化体系 构件数目，使判断简化，其主要有以下几个技巧：
（1）根据需要进行链杆与刚片之间的转化，巧妙使用二元体； （2）当体系比较复杂时，可以先考虑其中的一个它部分之间的连接关系， 判定整个体系的几何构造性。
例题分析
例2.分析图示体系的几何构造性。 解析：（1）计算自由度
W 72 113 0
自由度为0，说明体系具有成为几何不变体系的最少约束数目。 体系没有二元体，但体系本身是有二元体的，去掉所有二元体，只剩下一个 杆件，所以体系本身几何不变，再考虑其与地基的连接方式，判定体系几何不变。
总结与技巧
示例
例1.分析图示体系的几何构造性。
解析：（1）计算自由度
W 7277 0
体系具有成为几何不变体系的最少约束数目，需进一步判断。 （2）依次去掉二元体FAB、IED、FBJ、IDC如图所示。 （3）三角形GCH看作刚片Ⅰ，地基看作特殊刚片Ⅱ。 （4）刚片Ⅰ、Ⅱ之间通过三根链杆相连，三链杆汇交
例题分析
例1.分析图示体系的几何构造性。 解析：（1）计算自由度
W 4244 0
自由度为0，说明体系具有成为几何不变体系的最少约束数目。 进一步判断，依次去掉二元体DFE、BDC、BEC、BCA后，整个体系只剩下 地基了，为几何不变体系。由于去掉二元体并不改变原体系的几何构造性，因此 原体系也是几何不变体系。
二元体规则是非常好用的规则，特别是去二元体，可以大大简化体系 构件数目，使判断简化，其主要有以下几个技巧：
（1）根据需要进行链杆与刚片之间的转化，巧妙使用二元体； （2）当体系比较复杂时，可以先考虑其中的一个它部分之间的连接关系， 判定整个体系的几何构造性。
例题分析
例2.分析图示体系的几何构造性。 解析：（1）计算自由度
W 72 113 0
自由度为0，说明体系具有成为几何不变体系的最少约束数目。 体系没有二元体，但体系本身是有二元体的，去掉所有二元体，只剩下一个 杆件，所以体系本身几何不变，再考虑其与地基的连接方式，判定体系几何不变。
总结与技巧
示例
例1.分析图示体系的几何构造性。
解析：（1）计算自由度
W 7277 0
体系具有成为几何不变体系的最少约束数目，需进一步判断。 （2）依次去掉二元体FAB、IED、FBJ、IDC如图所示。 （3）三角形GCH看作刚片Ⅰ，地基看作特殊刚片Ⅱ。 （4）刚片Ⅰ、Ⅱ之间通过三根链杆相连，三链杆汇交
建筑力学第五章 平面体系的几何组成分析(00001)[精]
![建筑力学第五章 平面体系的几何组成分析(00001)[精]](https://img.taocdn.com/s3/m/c22cc24a31b765ce05081475.png)
建筑力学电子教案
第五章 平面体系的几何组成分析
§5–2 刚片、自由度、联系的概念
1、刚片：在平面体系中将刚体称为刚片。 2、自由度：确定体系位置时所需要的独立参数（坐标）的数目。
⑴ 平面上的点有两个自由度
y
x
o
A
y x
独立变化的几何参
数为：x、y。
建筑力学电子教案
第五章 平面体系的几何组成分析
Ⅱ Ⅰ
建筑力学电子教案
第五章 平面体系的几何组成分析
瞬变体系：原为几何可变体系，但经过微小位移后转化为 几何不变体系。
瞬变体系特点：瞬变体系承受荷载后，构件将产生很大的
内力，故不能用作建筑结构。属于几何可
变体系范畴。
例如:
o.
上述情况为瞬变体系。
建筑力学电子教案
第五章 平面体系的几何组成分析
小结
建筑力学电子教案
第五章 平面体系的几何组成分析
例8: 对图示体系作几何组成分析
例6
解： 此体系的
支座连杆只有 三根，且不完 全平行也不交 于一点，故可 只分析体系本 身。
第五章 平面体系的几何组成分析
当拆到结点６时，二元体的两杆共线，故此体系为瞬变体系， 不能作为结构。
. 建筑力学电子教案
第五章 平面体系的几何组成分析
.
例7
O1
O2
解：
Ⅰ
ⅡⅡ
Ⅲ
ADCF和BECG这两部分都是几何不变的，作为刚片Ⅰ、Ⅱ， 地基为刚片Ⅲ。而联结三刚片的O1、 O2、C不共线，故为几何不 变体系，且无多余联系。
建筑力学电子教案
第五章 平面体系的几何组成分析
5、计算自由度的讨论:
任何平面体系的计算自由度，其计算结果将有以下三种情 况：
结构力学之平面体系的几何组成分析
二、二刚片规则： 两个刚片用既不全平行也不全交于一点的 三根链杆相联，所组成的体系是几何不变 体系，且无多余约束。
O
ΙΙ
ΙΙΙ
推论： 两个刚片由一个铰和一根轴线不通过该铰的 链杆相联，所组成的体系是几何不变体系， 且无多余约束。
ΙΙ
C
A
B
例三、
C
A
分析图示体系的几何构造：
D
解法一： 1、找刚片：
依据材料概括晚清中国交通方式的特点，并分析其成因。
提示：特点：新旧交通工具并存(或：传统的帆船、独轮车， 近代的小火轮、火车同时使用)。 原因：近代西方列强的侵略加剧了中国的贫困，阻碍社会发 展；西方工业文明的冲击与示范；中国民族工业的兴起与发展；
政府及各阶层人士的提倡与推动。
[串点成面· 握全局]
（二）二元体规则：
增加或去掉二元体不改变原体系的几何
组成性质。
C
A
B
例五、 分析图示体系的几何构造：
解：
A
D
E
基本铰结三角形ABC符合 三刚片规则，是无多余约
B
束的几何不变体系；依次
C
F
G
在其上增加二元体A-D-C、
C-E-D、C-F-E、E-G-F后， 体系仍为几何不变体，且 无多余约束。
一、几何构造特性：
（一）无多余联系的几何不变体系称为静定 结构。
静定结构几何组成的特点是：
任意取消一个约束，体系就变成了
几何可变体系。
（二）有多余联系的几何不变体系称为超静 定结构。
特点： 某些约束撤除以后，剩余体系仍
为几何不变体系。
二、静力特性：
（一）静定结构： 在荷载作用下，可以依据
结构力学前半部分重点复习
M F Q F N — 单位力作用下结构产生的弯矩
剪力、轴力
(1)梁和刚架，轴向变形和剪切变形的影响甚小，主要
考虑弯曲变形的影响，位移公式： MMP dx EI (2)桁架，只考虑轴向变形的影响，且每根杆件的内力 及截面都沿杆长不变，故位移公式： F N FNP F N FNP l dx EA EA
结点法和截面法联合运用： 有的杆件用结点法求，有的杆件用截
面法求。
判断零杆：桁架中的某些杆件可能是零杆，计算前 应先进行零杆的判断，这样可以简化计算。零杆判 断的方法：
FN1
不共线的两杆结点，当无 ▲ 两杆节点：
荷载作用时，则两杆内力为FN1=FN2=0。 由三杆构成的结点，有两杆 ▲ 三杆节点：
平面体系的几何组成分析
1. 基本概念： 几何不变体系、几何可变体系、瞬变体系、自由度、 约束 2. 几何不变体系的组成规律 3.灵活运用组成规律分析体系的几何不变性
几何不变体系：不考虑材料的应变，在任意荷
载作用下，几何形状和位置保持不变的体系。 几何可变体系： 不考虑材料的应变，在微小荷 载作用下，不能保持原有几何形状和位置的体 系。
规律 2
三刚片的组成规则：
将链杆看 成刚片
规律 3
三刚片用不在同一直线上的三个铰两两相联， 则组成的体系是几何不变体系且无多余约束。
两根链杆组成 的虚铰替换铰
二元体规则：
二元体的概念：由两根不共线的链杆联结一 个新结点的装置称为二元体。
二元体
去掉二元体 增加二元体
规律 4
在一个体系上，增加或去掉二元体，体系的 几何组成不变。
FP3
f
B
xk
L1 L
第二章_平面体系的几何组成分析
三、三刚片组成规则
规则三：三个刚片用不在同一直线上的三个 铰两两相联，则组成没有多余约束的几何不 变体系。如图所示。
A
A
O2 O1 O2 O3O1
O3
B
B
C
C
第二章 平面结构的几何构造分析
现在来讨论三刚片联结的特殊情况。如果两个刚
片之间是通过平行链杆联结，则其形成的虚铰将在无 穷远处。三个刚片之间的联结包括一对、两对和三对 平行链杆的情况。
合理，因B而不能限制瞬时运动B 的情况。 C
C
A
B
A'
第二章 平面结构的几何构造分析
二、两刚片组成规则
规则二：两个刚片用一个铰和不通过该铰 的一根链杆或用不交于一点也不互相平行 的三根链杆相联结，则组成没有多余约束 的几何不变体系。如图所示。
O
几何可变体系
O
R P
几何不变体系
A
C
A CE
B
D
变，实际上就是判别该体系 是否存在刚体运动的自由度。 y
所谓体系的自由度，是指体
系运动时可以独立变化的几
何参数的数目，也就是确定
xA
物体位置所需的独立坐标数
目。例如一个点在平面内自 由运动时，其位置要用两个 o
y x
坐标和来确定（右图），所
以一个点的自由度等于2。
第二章 平面结构的几何构造分析
如一个刚片在平面
1
2
A
1
3
2
第二章 平面结构的几何构造分析
体系中的约束有的对组成几何不变体 系来说是必须的，这种约束称为必要约束， 而必要约束之外的约束称之为多余约束。 每一个必要约束都可以使体系的自由度减 少1个，而多余约束并不减少体系的自由 度。
规则三：三个刚片用不在同一直线上的三个 铰两两相联，则组成没有多余约束的几何不 变体系。如图所示。
A
A
O2 O1 O2 O3O1
O3
B
B
C
C
第二章 平面结构的几何构造分析
现在来讨论三刚片联结的特殊情况。如果两个刚
片之间是通过平行链杆联结，则其形成的虚铰将在无 穷远处。三个刚片之间的联结包括一对、两对和三对 平行链杆的情况。
合理，因B而不能限制瞬时运动B 的情况。 C
C
A
B
A'
第二章 平面结构的几何构造分析
二、两刚片组成规则
规则二：两个刚片用一个铰和不通过该铰 的一根链杆或用不交于一点也不互相平行 的三根链杆相联结，则组成没有多余约束 的几何不变体系。如图所示。
O
几何可变体系
O
R P
几何不变体系
A
C
A CE
B
D
变，实际上就是判别该体系 是否存在刚体运动的自由度。 y
所谓体系的自由度，是指体
系运动时可以独立变化的几
何参数的数目，也就是确定
xA
物体位置所需的独立坐标数
目。例如一个点在平面内自 由运动时，其位置要用两个 o
y x
坐标和来确定（右图），所
以一个点的自由度等于2。
第二章 平面结构的几何构造分析
如一个刚片在平面
1
2
A
1
3
2
第二章 平面结构的几何构造分析
体系中的约束有的对组成几何不变体 系来说是必须的，这种约束称为必要约束， 而必要约束之外的约束称之为多余约束。 每一个必要约束都可以使体系的自由度减 少1个，而多余约束并不减少体系的自由 度。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
结
m
r1 r2 r3
3m (r1 2r2 3r3 )
3.3平面体系的几何组成分析
——基本概念
3.3.1几何组成分析的目的
工程中的结构
几何可变体系
几何不变体系
1、判断体系是否为几何不变体系 2、正确区分静定结构和超静定结构 3、明确体系的几何组成顺序
3.3.2 几何不变体系的组成分析
几个基本概念 刚片
一个几何不变的部分
在几何组成分析中不考虑材料的应变。
一根梁
一 个链杆
一根柱
自由度
一个体系运动时，用来确定其位置所需要的独
立坐标（或参数变量）数目ω
ω>0,体系几何可变 ω=0，体系几何不变，静定 工程上可用 ω<0,体系几何不变，超静定
y C A B
1、一个点的自由度ω=2 2、刚片的自由度ω=3 3、地基的自由度ω=0
O
φ
x
约束
能减少自由度的装置，也称联系。
减少一个自由度的装置为一个约束。
1、链杆约束：一个约束来自单铰：2个约束 2、铰链约束 复铰：2(n-1)个约束
y
O
x
3、简单刚性联结： 3个约束
多余约束 在一个体系中增加一个约束而自由度并不减少， 则此约束为多余约束
虚铰
o点称为转动瞬心，即虚铰，其位
o
o'
置随着两刚片的转动而改变
小
刚片 自由度 约束 多余约束 虚铰