新北师大版数学七下3.1《认识三角形》word练习题

合集下载

北师大版数学七年级下1.认识三角形(一).doc

初中数学试卷鼎尚图文**整理制作1.认识三角形（一）一、判断题1.三条线段组成一个三角形.（）2.连接三个点就能得到一个三角形.（）3.有一个角是锐角的三角形叫锐角三角形.（）4.三角形的三边越长它的内角和越大.（）5.三角形中两个角互余，那么这个三角形是一个直角三角形.（）二、填空题1.一个三角形中至少有_______个锐角，至多有_______个直角或钝角.2.在△ABC中，∠A=10°，∠B=30°，则∠C=_________.3.在△ABC中，∠A=90°，∠B=∠C，则∠B=_________..4.图1中共有_________个三角形图15.三条线段分别是5 cm，6 cm，12 cm，则这三条线段_________（填“能”或“不能”）组成三角形.三、选择题1.图2中，共有（）个不同的三角形.（）D.10A.4B.6C.8图22.一个三角形的内角中，至少有一个角的度数不会大于（）A.60°B.90°C.120°D.150°3.一个三角形的三个内角互不相等，则它的最大角不小于（）A.45°B.60°C.90°D.120°4.△ABC的边BA延长得∠1.若∠2＞∠1，则△ABC的形状为（）如图3.（）图3A.锐角三角形B.直角三角形C.钝角三角形D.无法确定5.三角形三边之比为3∶4∶5，则这个三角形三边关系（）A.三边相等B.有两边相等C.三边都不相等D.非以上答案四、解答题1.一个三角形中，一个角等于另外两个角的差，试判断三角形的形状.2.如图4，三角形ABC，两边长AB=12，AC=2，且周长为奇数，求第三边BC的长.图4参考答案1.认识三角形（一）一、1.× 2.× 3.× 4.× 5.√二、1.2 1 2.140° 3.45° 4.3 5.不能三、1.C 2.A 3.B 4.C 5.C四、1.设三角分别为∠A、∠B、∠C.2.∵10＜BC＜14，周长为奇数∴BC为奇数，∴BC=11或13。

七年级数学下册《3.1 认识三角形》习题1(无答案)(新版)北师大版

《3.1 认识三角形》1．下面各组线段中，能组成三角形的是（）A．5，6，11 B．8，8，16 C．4，5，10 D．6，9，142．已知的三边长，化简的结果是（）A． B． C． D．3．两根木棒长分别为5cm和7cm，要选择第三根，将它们钉成一个三角形，如果第三根木棒长为偶数，则组成方法有（）A．3种 B．4种 C．5种 D．6种4．已知三角形两边长分别为4和9，则此三角形的周长L的取值范围是（）A．5<L<13 B．4<L<9 C．18<L<26 D．14<L<225．在△ABC中，∠A=39°，∠B=41°，则∠C的外角度数为（）A．80° B．100° C．90° D．70°6．下列说法正确的是（）A．三角形的角平分线是射线．B．三角形三条高都在三角形内．C．三角形的三条角平分线有可能在三角形内，也可能在三角形外．D．三角形三条中线相交于一点．7．如图，在建筑工地我们经常看见用木条EF固定矩形门框ABCD的情形，这种做法根据（）A．两点之间线段最短 B．两点确定一条直线C．三角形的稳定性 D．矩形的四个角都是直角8．如图，绕点逆时针旋转到的位置，已知，则等于（）A．B． C．D．9．如图所示，把一个长方形纸片沿EF折叠后，使D、C分别落在G、H 的位置，若∠EFB=650，则∠AEG等于（）A．70° B．65° C．50° D．25°1．如图所示，以点A为顶点的三角形有_____个，它们分别是________.2．若一个三角形的两边长是2和9，则第三边长a的取值范围是_______.3．四条线段的长度分别为5cm，6cm，8cm，13cm，以其中任意三条为边可构成_____个三角形，它们的边长分别是_____________.4．用10根火柴摆一个三角形，能摆出_____种.5．已知等腰三角形的一边长为4cm，另一边长为7cm，求三角形的周长是______.6．如图所示，图中共有个三角形，其中以AB为一边的三角形有个，以∠C 为一个内角的三角形有个.7．在一个三角形的内角中，最多有个钝角，至少有个锐角.8．如图，D是AB边上的中点，将沿过D的直线折叠，使点A落在BC上F处，若，则__________度.9．某市政府为使四个小区（用A，B，C，D表示）（如图所示）的孩子能就近上学，想在附近修建一所小学校P．问P建在何处才能使四个小区的孩子上学走的路的总和最小？10.小聪画了一个△ABC，用尺量得三边的长之后，他发现△ABC的周长是偶数，且AB-AC=2，AB：AC=3：2，你能猜出小聪量得的第三边BC的长吗？中国书法艺术说课教案今天我要说课的题目是中国书法艺术，下面我将从教材分析、教学方法、教学过程、课堂评价四个方面对这堂课进行设计。

北师大版七年级数学下册4.1：认识三角形练习(word无答案)

4.1认识三角形练习一、选择题1．一定在△ABC内部的线段是（）A．锐角三角形的三条高、三条角平分线、三条中线B．钝角三角形的三条高、三条中线、一条角平分线C．任意三角形的一条中线、二条角平分线、三条高D．直角三角形的三条高、三条角平分线、三条中线2．以下列各组长度的线段为边能组成一个三角形的是（）A．3，5，8 B．8，8，18 C．3，4，8 D．2，3，4 3．若三角形两边长分别为6cm，2cm，第三边长为偶数，则第三边长为（）A．2cm B．4cm C．6cm D．8cm4．现有两根木棒分别长40cm和50cm，要从下列长度的木棒中选出一条，与前面两根木棒钉成一个三角架（木棒不能余），则可选出（）①5cm②10cm③40cm④45cm⑤80cm⑥90cm．A．3条B．4条C．5条D．6条5．△ABC中，∠ABC与∠ACB的平分线相交于I，且∠BIC＝130°，则∠A的度数是（）A．40°B．50°C．65°D．80°6．以下是四位同学在钝角三角形ABC中画BC边上的高，其中画法正确的是（）A．B．C．D．7．至少有两边相等的三角形是（）A．等边三角形B．等腰三角形C．等腰直角三角形D．锐角三角形8．如图，虚线部分是小刚作的辅助线，你认为线段CD（）A．是AC边上的高B．是BC边上的高C．是AB边上的高D．不是△ABC的高9．如图，△ABC中，∠A＝30°，∠B＝40°，则∠ACD＝（）A．30°B．40°C．70°D．110°10．如图，在△ABC中，∠B、∠C的平分线BE，CD相交于点F，∠ABC＝42°，∠A＝60°，则∠BFC＝（）A．118°B．119°C．120°D．121°11．如图，在△ABC中，BC边上的高是、在△BCE中，BE边上的高、在△ACD中，AC边上的高分别是（）A．AF、CD、CE B．AF、CE、CD C．AC、CE、CD D．AF、CD、CE 二、填空题12．在△ABC中，∠BAC＝3∠B，∠ABC﹣∠C＝30°，则∠BAC＝，∠B＝，∠C＝．13．如图，△ABC三边的中线AD、BE、CF的公共点为G，若S△ABC＝12，则图中阴影部分的面积是．14．在△ABC中，高AD与BE所在直线相交于点H，且BH＝AC，则∠ABC＝．15．如图，△ABC中，点E是BC上的一点，EC＝2BE，点D是AC的中点．若△ABC的面积S△ABC＝12，则S△ADF﹣S△BEF＝．三、解答题16．如图，△ABC中，∠B＝50°，AD平分∠BAC，∠ADC＝80°．求∠C的度数．17．如图，在△ABC中，AE是中线，AD是角平分线，AF是高，则：（1）∵AE是△ABC的中线，∴BE＝＝；（2）∵AD是△ABC的角平分线，∴∠BAD＝＝；（3）∵AF是△ABC的高，∴∠AFB＝＝90°；（4）∵AE是△ABC的中线，∴BE＝CE，又∵S△ABE＝，S△AEC＝，∴S△ABE＝S△ACE＝．18．如图所示，直线AD和BC相交于O，AB∥CD，∠AOC＝95°，∠B＝50°，求∠A和∠D．。

(完整word版)北师大版数学七年级下三角形练习题含答案(20200805113345)

10.如图，ZU 〃C 啊 ZACH = 90° ,把「沿JCH 折180S 便点〃落在 F 的位置，则关于线段才「的性质中”准确的说法是 < 人扎是边/?捋上的中线B*是边刖上的裔11三角形练习題（三）一、选择題I.如图，^AOB^LCOD f 若= AD = \O. AB"则CD 的长为© \2,如图.己知Z1二Z2,要说明△ AfiD^/\ACI ）,连需从下列条件中选个.错谋的选法是（）.乳如图，生祜中.我们经常会看到在电线杆上拉两条钢来加固电线杆*这是利用了二角形的（）oA.稳定性&全等性C*灵活件 D.对称杵4.如图，平行四边宠冲RCD 対幷线叔儿RJJ 交丁o 过0的但线J^^ADf-E,交BC 卜F *则图中全等三曲形共有（）.A. 7X 寸B. 6^jC. § 对D, 4 对,如果•个三角形两边上的烏的交点在三角形的内部，那么这个三対仍是（人 A.锐角三角形B.戌角三弟形C.钝角三肃形6任卓三角形6.在中’如®Z^-ZB = 90% 那么氐ABC 是（）.A.瓦角三角脱B.钝角=角形C.锐饰三角形（X 锐角三和彤或钝角=角形A. 10B. 8C. 5D.不能跚定C. DB 二 DCO. AB = AC阳题1, 若「的三边长分别为鞭数.周长曲lb 且有一垃为叭则腔个三角形的绘大边长为（A. 7B. 6C* 5D. 4•如图” 厶二32心，ZZ? = 45% ZC = 38°> W ZDEb' J ( A, 120°B. 115°C* 110° D. 105°9.下列说法正说的迪（>c扎有-迪和两角刈应相導的两个三角他全等 B. 仃两边和-角对应相弄时两个三角形全等 C-二个怖对应相等的两牛三布形个零 D.曲枳相習、且肓-边相等的两个二竹形金等A. £ADB = ZAIX!氐 ZB = ZC第IM第4题1«.用直尺和岡规作一个外等十已知角的示意图如图所》总则说明/AO^ = ZAOB 的依据是三、解答题 19.如图丫中，0在川*上，S.^CAD^^CHE 都是等边三角形。

北师大版七年级下册4.1认识三角形同步练习题(word无答案)

4.1认识三角形同步练习一、选择题1．试通过画图来判定，下列说法正确的是（）A．一个直角三角形一定不是等腰三角形B．一个等腰三角形一定不是锐角三角形C．一个钝角三角形一定不是等腰三角形D．一个等边三角形一定不是钝角三角形2．已知三角形ABC三边a、b、c满足（a﹣b）2+|b﹣c|＝0，则△ABC的形状是（）A．钝角三角形B．直角三角形C．等边三角形D．以上都不对3．现有若干个三角形，在所有的内角中，有5个直角，3个钝角，25个锐角，则在这些三角形中锐角三角形的个数是（）A．3 B．4或5 C．6或7 D．84．在下列各图的△ABC中，正确画出AC边上的高的图形是（）A．B．C．D．5．下列说法错误的是（）A．三角形的角平分线能把三角形分成面积相等的两部分B．三角形的三条中线，角平分线都相交于一点C．直角三角形三条高交于三角形的一个顶点D．钝角三角形的三条高所在直线的交点在三角形的外部6．如图，△ABC的两条中线AM、BN相交于点O，已知△ABO的面积为4，△BOM的面积为2，则四边形MCNO的面积为（）A．4 B．3 C．4.5 D．3.57．如图所示，在△ABC中，已知点D、E、F分别为边BC、AD、CE的中点，且△ABC的面积是4cm2，则阴影部分面积等于（）A．2cm2B．1cm2C．0.25cm2D．0.5cm28．在△ABC中，已知点D、E、F分别是边BC、AD、CE上的中点，且S△ABC＝4cm2，则S △BEF的值为（）A．2cm2B．1cm2C．0.5cm2D．0.25cm2 9．a，b，c，d四根竹签的长度分别为2cm，3cm，4cm，6cm，若从中任意选取三根首尾依次相接围成不同的三角形，则围成的三角形共有（）A．1个B．2个C．3个D．4个10．如图，在△ABC中，∠A＝52°，∠ABC与∠ACB的角平分线交于D1，∠ABD1与∠ACD1的角平分线交于点D2，依此类推，∠ABD4与∠ACD4的角平分线交于点D5，则∠BD5C 的度数是（）A．56°B．60°C．68°D．94°二、填空题11．如图，在△ABC中，AD⊥BC，AE平分∠BAC，若∠1＝30°，∠2＝20°，则∠B＝．12．如图，已知△ABC的周长为27cm，AC＝9cm，BC边上中线AD＝6cm，△ABD周长为19cm，AB＝．13．如图，在△ABC中，AD，BE是两条中线，则S△EDC：S△ABC＝．14．在Rt△ABC中，AD是斜边BC边上的中线，G是△ABC重心，如果BC＝6，那么线段AG的长为．三、解答题15．已知，如图，在△ABC中，∠B＜∠C，AD，AE分别是△ABC的高和角平分线，（1）若∠B＝30°，∠C＝50°．则∠DAE的度数是．写出∠DAE、∠B、∠C的数量关系：，并证明你的结论．16．如图，在△BCD中，BC＝4，BD＝5，（1）求CD的取值范围；（2）若AE∥BD，∠A＝55°，∠BDE＝125°，求∠C的度数．。

(完整word版)北师大版七年级下三角形练习题

北师大版七年级下册数学三角形单元检测一、选择题1．以以下各组长度的线段为边，能构成三角形的是(A ． 6 cm,8 cm,15 cmB ． 7 cm,5 cm,12 cmC．4 cm,6 cm,5 cm D ．8 cm,4 cm,3 cm)．2．如图，△AOB≌△ COD ， A 和 C， B 和 D 是对应极点，若BO＝ 6， AO＝3， AB＝ 5，则 CD 的长为 ()．A ． 10 C．5B ． 8D ．不可以确立3．如图，已知∠选法是 ()．1＝∠ 2，要说明△ABD ≌△ ACD ，还需从以下条件中选一个，错误的A ．∠ ADB ＝∠ ADC B ．∠ B＝∠ CC．DB ＝ DC D ．AB＝AC4．要使五边形木架不变形，则起码要钉上( )根木条．A ． 1B ． 2 C． 3 D． 45．以下语句：①面积相等的两个三角形全等；②两个等边三角形必定是全等图形；③假如两个三角形全等，它们的形状和大小必定都同样；④边数同样的图形必定能相互重合．此中错误的说法有( )．A ． 4 个B ． 3 个C． 2 个D． 1 个6．假如一个三角形的三条高所在直线的交点在三角形外面，那么这个三角形是()．A ．锐角三角形B ．直角三角形C．钝角三角形 D ．等边三角形7．图中全等的三角形是( ) ．A ．Ⅰ和ⅡB ．Ⅱ和ⅣC．Ⅱ和Ⅲ D ．Ⅰ和Ⅲ8．如图，△ ABC 中，∠ ACB＝90°，把△ ABC 沿 AC 翻折 180 °，使点 B 落在 B′的地点，则对于线段 AC 的性质中，正确的说法是 ( )．A ．是边C．是∠BB′上的中线BAB′的均分线B ．是边 BB′上的高D ．以上三种性质都有二、填空题9．在△ ABC 中，若∠ A∶∠ B∶∠ C＝ 1∶ 3∶ 5，这个三角形为__________ 三角形． (按角的分类 )10．一木匠师傅有两根长分别为一个三角形框架，现有长分别为5 cm,8 cm 的木条，他要找第三根木条，将它们3 cm,10 cm,20 cm 的三根木条，他能够选择长为钉成__________cm 的木条．11．如图，假如AD＝ BC，∠ 1＝∠ 2，那么△ ABC≌△ CDA，依据是 __________．12．如图，已知∠ABC＝∠ DCB，现要说明△ABC≌△ DCB ，则还要补加一个条件是______．13．如图，△ABC 中， AB＝ AC， AD 是∠ BAC 的均分线，则∠ABD __________ ∠ACD (填“＞”“＜”或“＝”)．14．如图，长方形ABCD 中( AD＞ AB)， M 为 CD 上一点，若沿着AM 折叠，点N 恰落在BC 上，则∠ ANB＋∠ MNC ＝ __________度．三、解答题15．如图，在△ ABC 中，∠ BAC 是钝角，达成以下绘图，并用适合的符号在图中表示AC 边上的高．16．已知：如图，在△ABC 中，∠ BAC＝80°， AD ⊥ BC 于 D ，AE 均分∠ DAC ，∠ B＝60°，求∠ AEC 的度数．17．如图，已知AB＝AC， BD ＝ CE，请说明△ ABE≌△ ACD .18．请你找一张长方形的纸片，按以下步骤进行着手操作：PM 和 PN，如步骤一：在CD 上取一点P，将角 D 和角 C 向上翻折，这样将形成折痕图①所示；步骤二：翻折后，使点 D， C 落在原长方形所在的平面内，即点 D′和 C′，仔细调整折痕PN， PM 的地点，使 PD′， PC′重合，如图②，设折角∠ MPD ′＝∠ α，∠ NPC ′＝∠β.(1)猜想∠ MPN 的度数；(2)若重复上边的操作过程，并改变∠α的大小，猜想：跟着∠α的大小变化，∠ MPN 的度数如何变化？参照答案1． C 点拨：本题考察了三角形的三边关系． A.6 ＋ 8＜ 15，不可以构成三角形； B.7 ＋ 5 ＝12，不可以构成三角形； C.4 ＋ 5＞ 6，能够构成三角形； D.4 ＋ 3＜ 8，不可以构成三角形．2． C 点拨：由于△AOB≌△COD，A和C，B和D是对应极点，因此AB＝CD.由于AB＝5，因此 CD＝5.3． C 点拨：本题要点考察了三角形全等的判断定理，一般两个三角形全等共有四个定理，即 AAS， ASA， SAS， SSS，而“ SSA”没法证明三角形全等．4． B5． B 点拨：错误的说法有①②④，共 3 个．6． C 点拨：经过三角形的形状能够判断三角形高线的地点，反之，经过三条高线交点的地点能够判断三角形的形状．7． D 点拨： A 选项中条件不知足“ SAS”，不可以判断两三角形全等； B 选项中条件对应边不相等，不可以判断两三角形全等； C 选项中条件不知足“ SAS”，不可以判断两三角形全等； D选项中条件知足“ SAS”，能判断两三角形全等．8． D 点拨：本题考察的是图形的翻折变换及全等三角形的性质，熟知图形翻折变换的性质是解答本题的要点．9．钝角点拨：由于∠∶∠ ∶∠＝ 1∶ 3∶ 5，∠ ＋∠ ＋∠ ＝180°，因此∠＝A B C ABC A 20°，∠B＝60°，∠C＝100°. 由于∠C＞90°，因此这个三角形是钝角三角形．10． 10 点拨：已知三角形的两边长分别是 5 cm 和 8 cm，则第三边长必定大于 3 cm 且小于 13 cm. 故他能够选择此中长为10 cm 的木条．11． SAS 点拨：由于 AD＝BC，∠1＝∠2， AC＝ CA，因此△ ABC≌△ CDA(SAS)．12．∠＝∠D 或＝或∠＝∠A AB CD ACB DBC13．＝点拨：由于△ ABC中， AB＝AC， AD是∠ BAC的均分线，因此∠BAD＝∠ CAD.又由于 AD＝ AD，因此△ ABD≌△ ACD(SAS)．因此∠ ABD＝∠ ACD.14． 90 点拨：依据折叠的性质，有∠ANM＝∠ ADM＝90°，故∠ ANB＋∠ MNC＝180°－∠ANM＝90°.15．解：如图，BE即为AC边上的高．16．解：由于AD⊥BC，∠B＝60°，∠BAC＝80°，因此∠ BAD＝30°，∠ DAC＝50°，∠ C＝40°.由于 AE均分∠ DAC，因此∠ DAE＝∠ EAC＝25°，因此∠ AEC＝180°－∠ C－∠ EAC＝180°－25°－40°＝115°.17．解：由于AB＝AC，BD＝CE，因此 AD＝ AE.又由于∠ A＝∠ A，因此△ ABE≌△ ACD(SAS)．18．解： (1) 由于∠α＝∠MPD，∠β＝∠NPC，又由于∠α＋∠β＋∠MPD＋∠NPC＝180°，因此∠α＋∠β＝90°，即∠MPN＝90°.(2) ∠MPN的度数不变，仍为90°.银川十八中。

七年级数学下册《认识三角形》练习题及答案解析(北师大版)

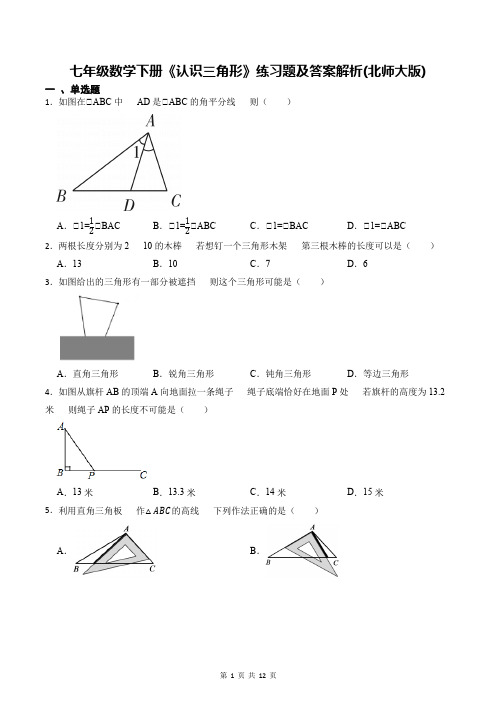
七年级数学下册《认识三角形》练习题及答案解析(北师大版) 一、单选题1．如图在△ABC中AD是△ABC的角平分线则（）A．△1=12△BAC B．△1=12△ABC C．△1=△BAC D．△1=△ABC2．两根长度分别为2 10的木棒若想钉一个三角形木架第三根木棒的长度可以是（）A．13B．10C．7D．63．如图给出的三角形有一部分被遮挡则这个三角形可能是（）A．直角三角形B．锐角三角形C．钝角三角形D．等边三角形4．如图从旗杆AB的顶端A向地面拉一条绳子绳子底端恰好在地面P处若旗杆的高度为13.2米则绳子AP的长度不可能是（）A．13米B．13.3米C．14米D．15米5．利用直角三角板作△ABC的高线下列作法正确的是（）A．B．C．D．6．若一个直角三角形其中一个锐角为40° 则该直角三角形的另一个锐角是（）A．60°B．50°C．40°D．30°7．如图AD BE CF是△ABC的三条中线则下列结论正确的是（）A．BC=2AD B．AB=2AF C．AD=CD D．BE=CF8．如图用四个螺丝将四条不可弯曲的木条围成一个木框（形状不限）不计螺丝大小其中相邻两螺丝的距离依次为3 4 5 7 且相邻两木条的夹角均可调整．若调整木条的夹角时不破坏此木框则任意两个螺丝间的距离的最大值为（）A．9B．8C．7D．69．将一个三角形纸片剪开分成两个三角形这两个三角形不可能()A．都是直角三角形B．都是钝角三角形C．都是锐角三角形D．是一个直角三角形和一个钝角三角形10．如图若△ABC的三条内角平分线相交于点I 过I作DE△AI分别交AB AC于点D E 则图中与△ICE一定相等的角（不包括它本身）有（）个．A．1B．2C．3D．4二、填空题11．如图AD AE分别是△ABC的角平分线和高∠B=50°∠C=70°则∠BAD=度∠EAD=度.12．已知三角形三边长分别为2 x 13 若x为正整数则这样的三角形有个．13．已知△ABC中△A=12△B=13△C 则△ABC是三角形．14．同一平面内有A B C三点A B两点之间的距离为5cm点C到直线AB 的距离为2cm且△ABC为直角三角形则满足上述条件的点C有个.三、作图题15．用圆规和直尺作图：已知△AOB（如图）求作：△AOB的平分线OC．（要求保留作图痕迹不写作法和证明过程）．四解答题16．如图AD是△BAC的平分线CE是△ADC边AD上的高若△BAC＝80° △ECD＝25° 求△ACB的度数．17．已知a b c是△ABC的三边长若b=2a−1c=a+5且△ABC的周长不超过20cm 求a范围．18．如图在△ABC中AD△BC 垂直为D △1=△B △C=67° 求△BAC的度数19．如图所示图中共有多少个三角形？请写出这些三角形并指出所有以E为顶点的角．20．如图在△ABC中CE BF是两条高若△A＝70° △BCE＝30° 求△EBF与△FBC的度数．21．如图求△A+△B+△C+△D+△E的大小．22．如图1 AB与CD相交于点O 若△D=38° △B=28° △DAB和△BCD的平分线AP和CP 相交于点P 并且与CD AB分别相交于M N．试求：（1）△P 的度数；（2）设△D=α △B=β △DAP= 13 △DAB △DCP= 13 △DCB 其他条件不变如图2 试问△P 与△D △B 之间存在着怎样的数量关系（用α β表示△P ）直接写出结论．参考答案1．【答案】A【解析】【解答】解：∵AD 是△ABC 的角平分线 ∴△1=12△BAC故答案为：A.【分析】根据角平分线的定义求解即可.2．【答案】B【解析】【解答】解：设第三边的长度为x则10−2<x <10+2 即8<x <12 则x =10符合题意故答案为：B.【分析】设第三边的长度为x 根据三角形中任意两边之和大于第三边任意两边之差小于第三边列出不等式组求解可得x 的取值范围从而一一判断即可得出答案.3．【答案】B【解析】【解答】解：由图形可得：该三角形为锐角三角形.故答案为：B.【分析】观察图形可知：图中的三角形有两个锐角且第三个角也小于90° 据此可判断出三角形的形状.4．【答案】A【解析】【解答】解：∵旗杆的高度为AB =13.2米又∵AP ＞AB∴绳子AP 的长度不可能是：13米. 故答案为：A.【分析】直角三角形的性质：斜边大于直角边据此解答即可.5．【答案】C【解析】【解答】解：由三角形的高线的定义可知：A 作法不符合题意不符合题意；B 作法不符合题意不符合题意；C 作法符合题意符合题意；D 作法不符合题意不符合题意；故答案为：C ．【分析】根据高线的定义逐项判断即可。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

辅导内容：3.1 认识三角形时间：2013-4-14上午
一、本节知识点
知识点1：三角形的概念详见课本P62
【易错点津】三角形必须同时满足三个条件：①三条线段；②不在同一直线上；③首位顺次相接的封闭图形。

【例1】如图1，图中有多少个三角形？把它们用符号分别表示
出来。

【针对性训练1】如图2所示，共有三角形（）个
A.5个
B.6个
C.7个
D.8个
知识点2 三角形的三边关系
【知识拓展】图 1 图2
（1）得出三角形任意两边之和大于第三边的依据是：两点之间，线段最短；
（2）三角形两边之差小于第三边可由三角形两边之和大于第三边移项得出；
（3）三角形的三边存在不等关系，这种关系反映了三角形自身存在的限制条件。

【易错点津】“两边”是指三角形中的任意两边。

【例2】以下列各组长度的线段为边，能组成三角形的是（）
A、2cm ,4cm,10㎝
B、1cm ,2cm,3㎝ C 、4cm ,7cm,10㎝D、2cm ,5cm,2㎝
判断的简便方法：只要将两条较短的线段相加，和最长的线段相比较即可。

【针对性训练2】（2012 义乌）如果三角形的两边长分别为3和5，第三边长是偶数，则第三边的长可以是（）
A.2
B.3
C.4
D.8
知识点3 三角形内角和定理
【知识拓展】
（1）三角形内角和定理的证明思路：设法将三个内角拼成一个平角
（2）在直角三角形中，两锐角互余；
（3）三角形内角和定理的作用：①在三角形中已知两角可求第三角，或已知各角之间的关系求各角；
②求一个三角形中个角之间的关系。

【例2】在⊿ABC中，已知∠A+∠B=80°，∠C=2∠B，试求∠A、∠B和∠C的度数。

【针对性训练3】
（2012•云南）如图3，在△ABC中，∠B=67°，∠C=33°，AD是△ABC的
角平分线，则∠CAD的度数为（）
A．40°B．45°C．50°D．55°
知识点4 三角形按角分类
图
3
【易错点津】在任意一个三角形中，最多有3个锐角，最少有两个锐角，最多有1个钝角，最多有1个直角。

【例4】适合下列条件的△ABC是锐角三角形？直角三角形？还是钝角三角形？
（1）∠A=20°，∠B=75°（2）∠A:∠B:∠C=2：3：4(可用方程思想)
【针对性训练4】
一个三角形的三个内角的度数之比为2：3：7，则这个三角形一定是（）
A.等腰三角形
B.直角三角形
C.锐角三角形
D.钝角三角形
知识点5 三角形的三条重要线段
【例5】如图所示，△ABC中，∠ABC=40°，∠C=60°，A D⊥BC于D，AE是△ABC的角平分线。

（1）求∠DAE的度数；
（2）指出AD是那几个三角形的高。

【针对性训练5】如图4所示，A C⊥BC，CD⊥AB，DE⊥AC，DF⊥BC，则下列说法错误的是（）
A．△ABC中，BC是AB边上的高； B.△ABC中，CD是AB边上的高；
C.△BCD中，DF是BC边上的高；
D.△ABE中，DE是AE边上的高；
图4 图5 图6
【例6】如图5所示，CD是△ABC的AB边上的中线，△BCD的周长比△ACD的周长大3㎝，BC=8㎝，求边AC的长。

【针对性训练6】如图6所示，△ABC中，BD是△ABC的角平分线，已知∠ABC=80°，则∠DBC=
二、多维解题方略
★综合应用
【例1】若a ，b ，c 为△ABC 的三边长，化简 ∣a+b+c ∣+ ∣a-c-b ∣
【例2】有一块三角形的优良品种实验土地，由于引进四个进行对比试验，需将这块分成面积相等四块，请你制定出两种以上的划分方案供选择（画图说明）．
★ 探索创新
【例3】如上右图所示,第二次龟兔赛跑时,聪明的乌龟设计的是从A 到B 点,因A,B 直间有猎人的陷阱，乌龟让兔子沿A--B--C ，而它沿路线A －D-E-B ，乌龟告诉兔子，兔子只跑三角形的两边（AC+BC ）而它要跑四边形的三边（AD+DE+EB ），这样跑的路程比兔子多，请用所学知识说明它们到底谁跑的路程多。

★ 教材习题拓广【例4】 P68问题解决2
【变式】若等腰三角形两边长分别为3和5，则它的周长是 3、规律方法突破
如图所示，已知△ABC 中，BD 、CE 是△ABC 的两条角平分线，且相交于点O. （1）当∠ABC=60°，∠ACB=80°时，∠ABC+∠ACB= ，2
1
（∠ABC+∠ACB ）= ， ∠BOC=
（2）当∠A=40°时，∠ABC+∠ACB= ，2
1（∠ABC+∠ACB ）= ，∠BOC= （3）当∠A=m 时，
2
1
（∠ABC+∠ACB ）= ，∠BOC= (4)从以上计算过程中，我们能得到∠BOC 与∠A 的关系式为∠BOC= ，若∠A=100°时，应用上述公式可知∠BOC= ，若∠BOC=120°，则可求出∠A=。