2018年秋九年级数学下册 第27章 圆 27.4 正多边形和圆练习 (新版)华东师大版
华东师大版初中九年级下册数学同步练习 第27章 圆 27.4 正多边形和圆 2

27.4正多边形和圆同步练习-华东师大版数学九年级下册学校:___________姓名:___________班级:___________考号:___________一、单选题2.如图,O是正六边形ABCDEF的外接圆,P为CAD上除C,D外的任意13.如图,四边形ABCD内接于O,延长DC至点E,连接BE.若四边形ABED 是菱形,80∠的度数为是( )∠=︒,则EBCDABA.20︒B.25︒C.30︒D.35︒4.如图,A、B、C、D为一个正多边形的顶点,O为正多边形的中心,若∠=︒,则这个正多边形的边数为()18ADBA.8 B.9 C.10 D.115.如图,A,B是⊙O上的两点,C是⊙O上不与A,B重合的任意一点. 如果∠AOB=140°,那么∠ACB的度数为()A.70°B.110°C.140°D.70°或110°6.如图,正五边形ABCDE内接于O,点F是DE上的动点,则AFC∠的度数为()A.60°B.72°C.144°D.随着点F的变化而变化7.在矩形ABCD中,AB=6,BC=4,有一个半径为1的硬币与边AB、AD相切,硬币从如图所示的位置开始,在矩形内沿着边AB、BC、CD、DA滚动到开始的位置为止,硬币自身滚动的圈数大约是A.1圈B.2圈C.3圈D.4圈8.由四个图1所示的四边形和四个图2所示的菱形拼成一个正八边形(如9.如图,面积为18的正方形ABCD内接于⊙O,则AB的长度为()910.如图,正六边形ABCDEF内接于⊙O,连接BD.则∠CBD的度数是()A.30°B.45°C.60°D.90°二、填空题11.如图,ABC中,90,3,4,ACB AC BC CD∠=︒==是边E上的高,,E F分别是,ACD BCD的内切圆,则E与F的面积比为.12.正六边形的边长为2,则其外接圆的半径为,正六边形的面积为.13.半径为1的圆的内接正三角形的边长为.14.如图,多边形ABCDE是⊙O的内接正五边形,则∠ACD等于°.内接于O,取次对剩余五段弧取中点可得一个圆内接正十二边形,,正六边形的面积为218.如图,正六边形ABCDEF内接于O,正六边形的周长是24,则O的半径是.19.若正六边形的周长为6,则它的面积为.20.如图,A、B、C、P是⊙O上的四个点,∠ACB=60°,且PC平分∠APB,则△ABC的形状是.参考答案:。
2018华师大版数学九年级下册27.4《正多边形和圆》练习题(无答案)

2018华师大版数学九年级下册27.4《正多边形和圆》练习题一、选择题(共12小题;每小题3分,共36分)1.下列说法正确的是()A.平分弦的直径垂直于弦B.三点确定一个圆C.相等的圆心角所对弦相等D.直径为圆中最长的弦2. 已知圆的半径是)A.B.C.D.3. 如图,以点O为圆心的两个圆中,大圆的弦AB切小圆于点C,OA交小圆于点D,若OD=2,tan∠OAB=,则AB的长是()A. 4B. 2C. 8D. 44. 如图,⊙O是正五边形ABCDE的外接圆,这个正五边形的边长为a,半径为R,边心距为r,则下列关系式错误的是()A.R2﹣r2=a2B.a=2Rsin36°C.a=2r tan36°D.r=Rcos36°5.如果一个扇形的弧长等于它的半径,那么此扇形称为“等边扇形”.则半径为2的“等边扇形”的面积为()A. πB. 1C. 2D.6.如图,△ABC内接于⊙O,D为线段AB的中点,延长OD交⊙O于点E,连接AE,BE,则下列五个结论①AB⊥DE,②AE=BE ,③OD=DE,④∠AEO=∠C,⑤弧AE=弧AEB,正确结论的个数是()A. 2B. 3C. 4D. 57. 一张圆心角为45°的扇形纸板和圆形纸板按如图方式剪得一个正方形,边长都为2,则扇形纸板和圆形纸板的面积比是()A.5:4 B.5:2 C. 2 D.8.如图,在平面直角坐标系中,⊙A与y轴相切于原点O,平行于x轴的直线交⊙A于M、N两点,若点M 的坐标是(-4,-2),则点N的坐标为()A. (1,-2)B. (-1,-2)C. (-1.5,-2)D. (1.5,-2)9. 若正多边形的一个外角为60°,则这个正多边形的中心角的度数是()A.30°B.60°C.90°D.120°A. 65°B. 50°C. 80°D. 100°10.已知⊙O半径为3,M为直线AB上一点,若MO=3,则直线AB与⊙O的位置关系为()A. 相切B. 相交C. 相切或相离D. 相切或相交11. 正八边形的中心角是()A.45°B.135°C.360°D.1080°12.如图,A,B是⊙O的直径,C、D在⊙O上,,若∠DAB=58°,则∠CAB=()A. 20°B. 22°C. 24°D. 26°二、填空题(共10题;30分)13.如图,扇形OAB的圆心角为120°,半径为3cm,则该扇形的弧长为________ cm,面积为________ cm2.(结果保留π)cm,则正六边形的半径为cm.14.已知正六边形ABCDEF15.如图,四边形ABCD是⊙O的外切四边形,且AB=10,CD=12,则四边形ABCD的周长为________.16.半径为5cm的圆中有两条平行弦,长度分别为6cm和8cm,则这两条弦的距离为________ 。
九年级数学下册第27章圆27.4正多边形和圆同步练习2含解析新版华东师大版

一.选择题1.若正多边形的中心角为72°,则该正多边形的边数为()A.8B.7C.6D.52.如图,六边形ABCDEF是正六边形,点P是边AF的中点,PC,PD分别与BE交于点M,N,则S△PBM:S四边形MCDN的值为()A.B.C.D.3.如图,在正五边形ABCDE中,连结AC,以点A为圆心,AB为半径画圆弧交AC于点F,连接DF.则∠FDC的度数是()A.18°B.30°C.36°D.40°4.如图,五边形ABCDE是⊙O的内接正五边形,AF是⊙O的直径,则∠BDF的度数是()A.18°B.36°C.54°D.72°5.如图,矩形HGML四个顶点在正六边形ABCDEF的边上,且GM∥EF.若图中4块阴影的面积相等,则该矩形的长与宽之比()A.3:5B.2:C.4:3D.5:46.如图,在正八边形ABCDEFGH中,连结AC,AE,则的值是()A.B.C.D.7.如图,在面积为135cm2的正六边形ABCDEF中有两个等边三角形组成的菱形AMDN.则剪掉这个菱形后剩余部分的面积为()A.75cm2B.70cm2C.65cm2D.60cm28.如图,在圆内接正六边形ABCDEF中,BF,BD分别交AC于点G,H.若该圆的半径为15厘米,则线段GH的长为()A.厘米B.5厘米C.3厘米D.10厘米9.如图,在由边长相同的7个正六边形组成的网格中,点A,B在格点上.再选择一个格点C,使△ABC是以AB为腰的等腰三角形,符合点C条件的格点个数是()A.1B.2C.3D.410.如图,正五边形ABCDE与正三角形AMN都是⊙O的内接多边形,若连接BM,则∠MBC的度数是()A.12°B.15°C.30°D.48°二.填空题11.如图,将边长相等的正六边形ABCDEF和正五边形ABGHK的AB边重合叠放在一起,则∠GBC的度数是.12.如图,五边形ABCDE为⊙O的内接正五边形,则∠CAD=.13.把边长相等的正六边形ABCDEF和正五边形GHCDL的CD边重合,按照如图所示的方式叠放在一起,延长LG交AF于点P,则∠APG=.14.如图,点O为正五边形的中心,⊙O与正五边形的每条边都相交,则∠1=.15.如图,点O是正六边形ABCDEF的中心,OG⊥CD于G,H为OG的中点,连结HA,HB,HC,则S△HCB:S△HBA等于.三.解答题16.如图,在正六边形ABCDEF中,对角线AE与BF相交于点M,BD与CE相交于点N.(1)求证:AE=FB;(2)在不添加任何辅助线的情况下,请直接写出所有与△ABM全等的三角形.17.如图,正六边形ABCDEF的边长为2,点P为六边形内任一点.则点P到各边距离之和是多少?18.如图,AG是正八边形ABCDEFGH的一条对角线.(1)在剩余的顶点B、C、D、E、F、H中,连接两个顶点,使连接的线段与AG平行,并说明理由;(2)两边延长AB、CD、EF、GH,使延长线分别交于点P、Q、M、N,若AB=2,求四边形PQMN的面积.参考答案一.选择题1.解:由题意,=72°,∴n=5,故选:D.2.解:设正六边形的边长为a.则S△PCD=2×a2=a2,S四边形BCDE=3×a2=a2,由题意MN是△PCD的中位线,∴S△PMN=S△PCD=a2,∴S四边形MNDC=a2﹣a2=a2,∴S△BMC=S△DNE=(a2﹣a2)=a2,∵PM=CM,∴S△PBM=S△BMC=a2,∴S△PBM:S四边形MCDN=a2:a2=1:2,故选:A.3.解:∵五边形ABCDE是正五边形,∴∠AED=∠EAB=∠ABC=108°,∵BA=BC,∴∠BAC=∠BCA=36°,∴∠EAC=72°,∴∠AED+∠EAC=180°,∴DE∥AF,∵AE=AF=DE,∴四边形AEDF是菱形,∴∠EDF=∠EAF=72°,∵∠EDC=108°,∴∠FDC=36°,故选:C.4.解:∵AF是⊙O的直径,五边形ABCDE是⊙O的内接正五边形,∴,,∠BAE=108°,∴,∴∠BAF=∠BAE=54°,∴∠BDF=∠BAF=54°,故选:C.5.解:连接BF,AD交于Q,BF交GM于P,则BF⊥AD,∵正六边形ABCDEF中,∠BAF=120°,AB=AF,∴∠AGH=∠AFQ=30°,设正六边形ABCDEF的边长为2a,FP=x,∴PG=x,AQ=a,∴GM=2a+,HG=2a﹣2x,∵若图中4块阴影的面积相等,∴×(2a﹣2x)×(a﹣x)=(2a++2a)x,解得:x=a,GH=2a﹣a=a,GM=2a+a=a,∴该矩形的长与宽之比为=3:5,故选:A.6.解:连接AG、GE、EC,如图所示:在正八边形ABCDEFGH中,AB=BC=AH=HG,∠B=∠H=135°,∴△ABC≌△AHG(SAS),∴AC=AG,同法可得AC=CE=EG,∴AC=CE=EG=AG,∴四边形ACEG是菱形,∵∠BAC=∠GAH°,∠BAH=135°,∴∠CAG=135°﹣°﹣°=90°,∴四边形ACEG为正方形,∴∠CAE=45°,∴=sin45°=,故选:A.7.解:连接AD,设AD=2h,则正六边形ABCDEF是有六个边长为h的等边三角形组成,∴边长为h的正△BOC的面积为h2,∴S正六边形=6×h2=135,∴h2=30,设菱形的边长AM=a,则h=a,∴a2=h2,∴菱形AMDN的面积=2×a2=×h2=××30=60(cm2),∴剪掉这个菱形后剩余部分的面积为135﹣60=75(cm2).故选:A.8.解:∵在圆内接正六边形ABCDEF中,AB=AF=BC=CD,∠BAF=∠ABC=∠BCD=120°,∴∠AFB=∠ABF=∠BAC=∠ACB=∠CBD=∠BDC=30°,∴AG=BG,BH=CH,∵∠GBH=∠BGH=∠BHG=60°,∴AG=GH=BG=BH=CH,连接OA,OB交AC于N,则OB⊥AC,∠AOB=60°,∵OA=15cm,∴AN=OA=(cm),∴AC=2AN=15(cm),∴GH=AC=5(cm),故选:B.9.解:AB的长等于六边形的边长+最长对角线的长,据此可以确定共有2个点C,位置如图,故选:B.10.解:连接OA、OC.∵五边形ABCDE是正五边形,∴∠AOB==72°,∴∠AOC=72°×2=144°,∵△AMN是正三角形,∴∠AOM==120°,∴∠=∠AOC﹣∠AOM=144°﹣120°=24°,∴∠MBC=∠=×24°=12°.故选:A.二.填空题11.解:∵在正六边形ABCDEF和正五边形ABGHK中,∠ABG==108°,∠ABC==120°,∴∠GBC=∠ABC﹣∠ABG=120°﹣108°=12°,故答案为:12°.12.解:∵五边形ABCDE是⊙O的内接正五边形,∴AB=BC,∠B=∠BAE==108°,∴∠ACB=∠BAC=36°,同理∠EAD=36°,∴∠CAD=108°﹣36°﹣36°=36°,故答案为:36°.13.解:∵六边形ABCDEF,∴∠A=∠B=∠BCD=,∵五边形GHCDL是正五边形,∴∠CDL=∠L=,∵∠A+∠B+∠BCD+∠CDL+∠L+∠APG=(6﹣2)×180°=720°,∴∠APG=720°﹣120°×3﹣108°×2=144°,故答案为:144°.14.解:设AB与CD交于点P,连接OA、OB、OC、OD、OE、BC,如图所示:∵正五边形的中心与⊙O的圆心重合,∴图形是轴对称图形,∴∠AOC=∠COB=∠BOE=∠EOD=∠AOD==72°,∵∠ABC=∠AOC=×72°=36°,∠BOD=∠BOE+∠EOD=72°+72°=144°,∠BCD=∠BOD=×144°=72°,∴∠APC=∠PBC+∠BCP=36°+72°=108°,即∠1=108°,故答案为:108°.15.解:如图,连接CF、HD、HE,过H作直线PQ⊥AB,由于正六边形的对角线必过圆心,所以C、O、F共线,由于AB∥DE∥CF,则PQ⊥DE,PQ⊥CF,P、K、Q都是垂足,∵点O是正六边形ABCDEF的中心,OG⊥CD,∴点C和点D,点E和点B关于直线OG对称,∴DH=CH,BH=EH,∵DE=BC,∴△BCH≌△EDH(SSS),∴PK=KQ=OG=2OH,又因为∠HOK=∠COG=30°,KH=OH,令KH=1,∴OH=2,OG=4,∴PK=4,∴PH=PK+KH=5,HQ=KQ﹣KH=3,∴S△HCB:S△HBA=PH:HQ=3:5.故答案为:3:5.三.解答题16.证明:(1)∵正六边形ABCDEF,∴AF=EF=AB,∠AFE=∠FAB,在△AFE与△BAF中,,∴△AFE≌△BAF(SAS),∴AE=FB;(2)与△ABM全等的三角形有△DEN,△FEM,△CBN;∵六边形ABCDEF是正六边形,∴AB=DE,∠BAF=120°,∴∠ABM=30°,∴∠BAM=90°,同理∠DEN=30°,∠EDN=90°,∴∠ABM=∠DEN,∠BAM=∠EDN,在△ABM和△DEN中,,∴△ABM≌△DEN(ASA).同理利用ASA证明△FEM≌△ABM,△CBN≌△ABM.17.解:过P作AB的垂线,分别交AB、DE于H、K,连接BD,作CG⊥BD于G∵六边形ABCDEF是正六边形∴AB∥DE,AF∥CD,BC∥EF,且P到AF与CD的距离之和,及P到EF、BC的距离之和均为HK的长,∵BC=CD,∠BCD=∠ABC=∠CDE=120°,∴∠CBD=∠BDC=30°,∴BD∥HK,且BD=HK,∵CG⊥BD,∴BD=2BG=2×BC×cos∠CBD=2×2×=6,∴点P到各边距离之和=3BD=3×6=18.18.解:(1)连接BF,则有BF∥AG.理由如下:∵ABCDEFGH是正八边形,∴它的内角都为135°.又∵HA=HG,∴∠°,从而∠2=135°﹣∠°.由于正八边形ABCDEFGH关于直线BF对称,∴即∠2+∠3=180°,故BF∥AG.(2)根据题设可知∠PHA=∠PAH=45°,∴∠P=90°,同理可得∠Q=∠M=90°,∴四边形PQMN是矩形.又∵∠PHA=∠PAH=∠QBC=∠QCB=∠MDE=∠MED=45°,AH=BC=DE,∴△PAH≌△QCB≌△MDE,∴PA=QB=QC=MD.即PQ=QM,故四边形PQMN是正方形.在Rt△PAB中,∵∠PAH=45°,AB=2,∴,∴.故.。
九年级数学下册 27.4 正多边形和圆同步练习题 (新版)华东师大版

27.4 正多边形和圆1.下列说法:①各边相等的圆内接多边形是正多边形;②各角相等的圆内接多边形是正多边形;③既是轴对称图形又是中心对称图形的多边形是正多边形.正确的个数是( )A .0个B .1个C .2个D .3个2.如图所示,正六边形ABCDEF 内接于⊙O ,则∠ADB 的度数是( )A .60°B .45°C .30°D .22.5°3.如图所示,△PQR 是⊙O 的内接正三角形,四边形ABCD 是⊙O 的内接正方形,BC ∥QR ,则∠AOQ =( )A .60°B .65°C .72°D .75°4.如图,有一圆内接正八边形ABCDEFGH ,若△ADE 的面积为10,则正八边形ABCDEFGH 的面积为( )A .40B .50C .60D .805.已知⊙O 的面积为2π,则其内接正三角形的面积为( )A .3 3B .3 6 C. 32 3 D. 326 6.正三角形的高、外接圆半径、边心距之比为( )A .3∶2∶1B .4∶3∶2C .4∶2∶1D .6∶4∶37.有一边长为4的正n 边形,它的一个内角为120°,则其外接圆的半径为( )A .3B .4C .33D .4 28.圆内接正五边形ABCDE 中,对角线AC 和BD 相交于点P ,则∠APB 的度数是( )A .36°B .72°C .54°D .60°9.如图,正三角形ABC 内接于⊙O ,AD 是⊙O 的内接正十二边形的一边,连结CD ,若CD =12,则⊙O 的半径为__.10.如图,将边长为3的正六边形铁丝框ABCDEF 变形为以点A 为圆心,AB 为半径的扇形(忽略铁丝的粗细),则所得扇形AFB(阴影部分)的面积为____.11.如图,正六边形ABCDEF 的边长为6 cm .(1)求作该正六边形的外接圆;(要求不写作法,保留作图痕迹)(2)求这个正六边形的半径R、边心距、面积.12. 如图,圆O的半径为R,T1,T2分别为圆O的内接正六边形和外切正六边形.(1)求T1与T2的周长比;(2)求图中阴影部分的面积.(用含R的式子表示)13.已知⊙O和⊙O上的一点A(如图所示).(1)作⊙O的内接正方形ABCD和内接正六边形AEFCGH;(2)在(1)题的作图中,如果点E在弧AD上,求证:DE是⊙O的内接正十二边形的一边.14.如图①有一个宝塔,它的地基边缘是周长为26 m的正五边形ABCDE(如图②),点O为中心.(下列各题结果精确到0.1 m)(1)求地基的中心到边缘的距离;(2)已知塔的墙体宽为1 m,现要在塔的底层中心建一圆形底座的塑像,并且留出最窄处为1.6 m的观光通道,问塑像底座的半径最大是多少?15.如图,(1)、(2)、(3)……,点M,N分别是⊙O的内接正三角形ABC,正方形ABCD,正五边形ABCDE,…正n边形的边AB,BC上的点,且BM=CN,连结OM,ON.(1)求图(1)中∠MON 的度数;(2)图(2)中∠MON 的度数为______,图(3)中∠MON 的度数为______;(3)试探索∠MON 的度数与正n 边形数n 的关系(直接写出答案).答案:1---8 BCDAC ABB 9. 6 210. 1811. 解:(1) 略 (2) 6 cm ,3 3 cm ,54 3 cm 212. 解:(1) 3∶2 (2) 32R 2 13. 解:(1)作法:①作直径AC ;②作直径BD ⊥AC ;③依次连结A ,B ,C ,D 四点,四边形ABCD 即为⊙O 的内接正方形;④分别以A ,C 为圆心,OA 长为半径作弧,交⊙O 于E ,H ,F ,G ;⑤顺次连结A ,E ,F ,C ,G ,H 各点.六边形AEFCGH 即为⊙O 的内接正六边形.作图略 (2)连结OE ,DE ,∵∠AOD =360°4=90°,∠AOE =360°6=60°,∴∠DOE =∠AOD -∠AOE =30°,∴DE 为⊙O 的内接正十二边形的一边 14. 解:(1)作OM ⊥AB 于点M ,连结OA ,OB ,则OM 为边心距,∠AOB 是中心角,由正五边形性质得:∠AOB =360°÷5=72°,又AB =15×26=5.2,∴AM =2.6,∠AOM =36°,在Rt △AMO 中,边心距OM =AM tan36°= 2.6tan36°≈3.6(m) (2)3.6-1-1.6=1(m),答:地基的中心到边缘的距离约为3.6 m ,塑像底座的半径最大约为1 m15. 解:(1)120° (2)90° 72° (3)∠MON =360°n。
九年级数学下册 第27章 圆 27.4 正多边形和圆同步练习1(含解析)(新版)华东师大版
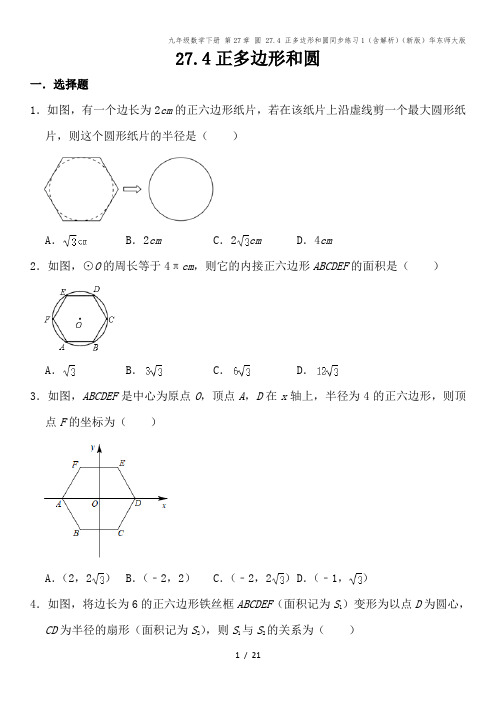
27.4正多边形和圆一.选择题1.如图,有一个边长为2cm的正六边形纸片,若在该纸片上沿虚线剪一个最大圆形纸片,则这个圆形纸片的半径是()A.B.2cm C.2cm D.4cm2.如图,⊙O的周长等于4πcm,则它的内接正六边形ABCDEF的面积是()A.B.C.D.3.如图,ABCDEF是中心为原点O,顶点A,D在x轴上,半径为4的正六边形,则顶点F的坐标为()A.(2,2)B.(﹣2,2)C.(﹣2,2)D.(﹣1,)4.如图,将边长为6的正六边形铁丝框ABCDEF(面积记为S1)变形为以点D为圆心,CD为半径的扇形(面积记为S2),则S1与S2的关系为()A.S1=S2B.S1<S2C.S1=S2D.S1>S25.如图,AB,AC分别为⊙O的内接正三角形和内接正四边形的一边,若BC恰好是同圆的一个内接正n边形的一边,则n的值为()A.8 B.10 C.12 D.156.如图,⊙O与正六边形OABCDE的边OA,OE分别交于点F,G,点M为劣弧FG的中点.若FM=4.则点O到FM的距离是()A.4 B.C.D.7.如图,⊙O与正五边形ABCDE的边AB,DE分别相切于点B,D,则劣弧BD所对的圆心角∠BOD的大小为()A.108°B.118°C.144°D.120°8.下列圆的内接正多边形中,中心角最大的图形是()A.正三角形B.正方形C.正五边形D.正六边形9.如图,正五边形ABCDE内接于⊙O,过点A作⊙O的切线交对角线DB的延长线于点F,则下列结论不成立的是()A.AE∥BF B.AF∥CD C.DF=AF D.AB=BF10.如图,A、B、C、D、E是⊙O上的5等分点,连接AC、CE、EB、BD、DA,得到一个五角星图形和五边形MNFGH.有下列3个结论:①AO⊥BE,②∠CGD=∠COD+∠CAD,③BM=MN=NE.其中正确的结论是()A.①②B.①③C.②③D.①②③二.填空题11.以半径为2的圆的内接正三角形、正方形、正六边形的边心距为三边作三角形,则该三角形的面积是.12.刘徽是我国魏晋时期卓越的数学家,他在《九章算术》中提出了“割圆术”,利用圆的内接正多边形逐步逼近圆来近似计算圆的面积,如图所示,若用圆的内接正十二边形的面积S1来近似估计⊙O的面积S,设⊙O的半径为1,则S﹣S1=.(π取3.14,结果精确到0.01)13.如图,点O为正五边形的中心,⊙O与正五边形的每条边都相交,则∠1=.14.如图,点O是正六边形ABCDEF的中心,OG⊥CD于G,H为OG的中点,连结HA,HB,HC,则S△HCB:S△HBA等于.15.如图,△PQR是⊙O的内接正三角形,四边形ABCD是⊙O的内接正方形,BC∥QR,则∠BOQ=.三.解答题16.(1)已知:如图1,△ABC是⊙O的内接正三角形,点P为劣弧BC上一动点.求证:PA=PB+PC;(2)已知:如图2,四边形ABCD是⊙O的内接正方形,点P为劣弧BC上一动点.求证:PA=PC+PB.17.如图,AG是正八边形ABCDEFGH的一条对角线.(1)在剩余的顶点B、C、D、E、F、H中,连接两个顶点,使连接的线段与AG平行,并说明理由;(2)两边延长AB、CD、EF、GH,使延长线分别交于点P、Q、M、N,若AB=2,求四边形PQMN的面积.18.如图,O是正六边形ABCDEF的中心,连接BD、DF、FB,(1)设△BDF的面积为S1,正六边形ABCDEF的面积为S2,则S1与S2的数量关系是;(2)△ABF通过旋转可与△CBD重合,请指出旋转中心和最小旋转角的度数.参考答案一.选择题1.解:如图所示,连接OB、OC,过点O作OG⊥BC于点G,正六边形的边长为2cm,OG ⊥BC,∵六边形ABCDEF是正六边形,∴∠BOC=360°÷6=60°,∵OB=OC,OG⊥BC,∴∠BOG=∠BOC=×60°=30°,∵OG⊥BC,OB=OC,BC=2cm,∴BG=BC=×2=1cm,∴OB==2cm,∴OG===,∴圆形纸片的半径为cm,故选:A.2.解:如图,连接OA、OB,作OG⊥AB于点G,∵⊙O的周长等于4πcm,∴⊙O的半径为:=2,∵ABCDEF是⊙O的内接正六边形,∴OA=OB=AB=2,∵OG⊥AB,∴AG=BG=AB=1,∴OG=,∴S△AOB=AB•OG=2×=.∴它的内接正六边形ABCDEF的面积是6S△AOB=6(cm2).故选:C.3.解:连接OF.∵∠AOF==60°,OA=OF,∴△AOF是等边三角形,∴OA=OF=4.设EF交y轴于G,则∠GOF=30°.在Rt△GOF中,∵∠GOF=30°,OF=4,∴GF=2,OG=2.∴F(﹣2,2).故选:C.4.解:由题意:的长度=24,∴S2=×24×6=72=18×4=18,∵S1=×6×3×6=54=18×3=18,∴S1>S2,故选:D.5.解:连接OA、OB、OC,如图,∵AB,AC分别为⊙O的内接正四边形与内接正三角形的一边,∴∠AOC==90°,∠AOB==120°,∴∠BOC=∠AOB﹣∠AOC=30°,∴n==12,即BC恰好是同圆内接一个正十二边形的一边.故选:C.6.解:连接ON,过O作OH⊥FM于H,∵正六边形OABCDE,∴∠FOG=120°,∵点M为劣弧FG的中点,∴∠FOM=60°,∵OH⊥FM,OF=OM,∴∠OFH=60°,∠OHF=90°,FH=FM=2,∴OH=FH=2,故选:C.7.解:∵五边形ABCDE是正五边形,∴∠E=∠A=180°﹣=108°.∵AB、DE与⊙O相切,∴∠OBA=∠ODE=90°,∴∠BOD=(5﹣2)×180°﹣90°﹣108°﹣108°﹣90°=144°,故选:C.8.解:∵正三角形一条边所对的圆心角是360°÷3=120°,正方形一条边所对的圆心角是360°÷4=90°,正五边形一条边所对的圆心角是360°÷5=72°,正六边形一条边所对的圆心角是360°÷6=60°,∴一条边所对的圆心角最大的图形是正三角形,故选:A.9.解:∵五边形ABCDE是正五边形,∴∠BAE=∠ABC=∠C=∠EDC=∠E==108°,BC=CD,∴∠CBD=∠CDB=×(180°﹣∠C)=36°,∴∠ABD=108°﹣36°=72°,∴∠EAB+∠ABD=180°,∴AE∥BF,故本选项不符合题意;B、∵∠F=∠CDB=36°,∴AF∥CD,故本选项不符合题意;C、连接AD,过A作AH⊥DF于H,则∠AHF=∠AHD=90°,∵∠EDC=108°,∠CDB=∠EDA=36°,∴∠ADF=108°﹣36°﹣36°=36°=∠F,∴AD=AF,∴FH=DH,当∠F=30°时,AF=2AH,FH=DH=AH,此时DF=AF,∴此时∠F=36°时,DF≠AF,故本选项符合题意;D、连接OA、OB,∵五边形ABCDE是正五边形,∴∠AOB==72°,∵OA=OB,∴∠OAB=∠OBA=(180°﹣72°)=54°,∵FA切⊙O于A,∴∠OAF=90°,∴∠FAB=90°﹣54°=36°,∵∠ABD=72°,∴∠F=72°﹣36°=36°=∠FAB,∴AB=BF,故本选项不符合题意;故选:C.10.解:∵A、B、C、D、E是⊙O上的5等分点,∴=,∴AO⊥BE,故①正确;∵A、B、C、D、E是⊙O上的5等分点,∴的度数==72°∴∠COD=72°∵∠COD=2∠CAD∴∠CAD=36°;连接CD∵A、B、C、D、E是⊙O上的5等分点,∴===,∴∠BDC=∠DCE=∠CAD=36°,∴∠CGD=108°,∴∠CGD=∠COD+∠CAD,故②正确;连接AB,AE,则∠BAM=∠ABM=∠EAN=∠AEN=36°,∵AB=AE,∴△ABM≌△AEN(ASA),∴BM=EN=AM=AN,∵∠MAN=36°,∴AM≠MN,③错误.故选:A.二.填空题11.解:如图1,∵OC=2,∴OD=OC=1;如图2,∵OB=2,∴OE=BE,∴OE2+BE2=2OE2=OB2=4,∴OE=;如图3,∵OA=2,∴AD=OA=1,∴OD==,则该三角形的三边分别为:1,,,∵(1)2+()2=()2,∴该三角形是直角三角形,∴该三角形的面积是:×1×=,故答案为:A.12.解:∵⊙O的半径为1,∴⊙O的面积S=π,∴圆的内接正十二边形的中心角为=30°,∴过A作AC⊥OB,∴AC=OA=,∴圆的内接正十二边形的面积S1=12××1×=3,∴则S﹣S1=π﹣3≈0.14,故答案为:0.14.13.解:设AB与CD交于点P,连接OA、OB、OC、OD、OE、BC,如图所示:∵正五边形的中心与⊙O的圆心重合,∴图形是轴对称图形,∴∠AOC=∠COB=∠BOE=∠EOD=∠AOD==72°,∵∠ABC=∠AOC=×72°=36°,∠BOD=∠BOE+∠EOD=72°+72°=144°,∠BCD=∠BOD=×144°=72°,∴∠APC=∠PBC+∠BCP=36°+72°=108°,即∠1=108°,故答案为:108°.14.解:如图,连接CF、HD、HE,过H作直线PQ⊥AB,由于正六边形的对角线必过圆心,所以C、O、F共线,由于AB∥DE∥CF,则PQ⊥DE,PQ⊥CF,P、K、Q都是垂足,∵点O是正六边形ABCDEF的中心,OG⊥CD,∴点C和点D,点E和点B关于直线OG对称,∴DH=CH,BH=EH,∵DE=BC,∴△BCH≌△EDH(SSS),∴PK=KQ=OG=2OH,又因为∠HOK=∠COG=30°,KH=OH,令KH=1,∴OH=2,OG=4,∴PK=4,∴PH=PK+KH=5,HQ=KQ﹣KH=3,∴S△HCB:S△HBA=PH:HQ=3:5.故答案为:3:5.15.解:连结OA,OD,∵△PQR是⊙O的内接正三角形,∴PQ=PR=QR,∴∠POQ=×360°=120°,∵BC∥QR,OP⊥QR,∵BC∥QR,∴OP⊥BC,∵四边形ABCD是⊙O的内接正方形,∴OP⊥AD,∠AOD=90°,∴=,∴∠AOP=∠DOP,∴∠AOP=×90°=45°,∴∠AOQ=∠POQ﹣∠AOP=75°.∵∠AOB=90°,∴∠QOB=15°,故答案为:15°.三.解答题16.证明:(1)延长BP至E,使PE=PC,连接CE,如图1,∵A、B、P、C四点共圆,∴∠BAC+∠BPC=180°,∵∠BPC+∠EPC=180°,∴∠BAC=∠CPE=60°,∵PE=PC,∴△PCE是等边三角形,∴CE=PC,∠E=60°;又∵∠BCE=60°+∠BCP,∠ACP=60°+∠BCP,∴∠BCE=∠ACP,∵△ABC、△ECP为等边三角形,∴CE=PC,AC=BC,在△BEC和△APC中,,∴△BEC≌△APC(SAS),∴PA=BE=PB+PC;(2)过点B作BE⊥PB交PA于E,连接OA,OB.如图2,∵∠1+∠2=∠2+∠3=90°∴∠1=∠3,∵∠APB=∠AOB=45°,∴BP=BE,∴PE=PB,在△ABE和△CBP中,,∴△ABE≌△CBP(SAS),∴PC=AE,∴PA=AE+PE=PC+PB;17.解:(1)连接BF,则有BF∥AG.理由如下:∵ABCDEFGH是正八边形,∴它的内角都为135°.又∵HA=HG,∴∠1=22.5°,从而∠2=135°﹣∠1=112.5°.由于正八边形ABCDEFGH关于直线BF对称,∴即∠2+∠3=180°,故BF∥AG.(2)根据题设可知∠PHA=∠PAH=45°,∴∠P=90°,同理可得∠Q=∠M=90°,∴四边形PQMN是矩形.又∵∠PHA=∠PAH=∠QBC=∠QCB=∠MDE=∠MED=45°,AH=BC=DE,∴△PAH≌△QCB≌△MDE,∴PA=QB=QC=MD.即PQ=QM,故四边形PQMN是正方形.在Rt△PAB中,∵∠PAH=45°,AB=2,∴,∴.故.18.解:(1)S2=2S1,如右图所示,连接OD、OF、OB,∵六边形ABCDEF是正六边形,∴△BDF是正三角形,∴△ABF、△BDC、△DEF、△DOF、△BOF、△BOD都是全等的,∴S2=2S1;(2)旋转中心是O,最小旋转角是120°,由于正n边形关于对称中心O旋转与自身重合,而通过观察可知△ABF必须逆时针旋转才可以与△CBD重合,故旋转的角度==120°.九年级数学下册第27章圆 27.4 正多边形和圆同步练习1(含解析)(新版)华东师大版21 / 21。
2018九年级数学下册27.4正多边形和圆习题课件新版华东师大版

解:(1)连接 CO,交 DB 于 E,∴∠O=2∠D=60°.又∵∠OBE = 30 ° , ∴∠ BEO = 180 °- 60 °- 30 °= 90 ° . ∵ AC ∥ BD , ∴∠ ACO=∠BEO=90°,∴AC 是⊙O 的切线. (2)∵OE⊥DB,∴EB 1 = DB=3 3.在 Rt△EOB 中,∵EB=3 3,由勾股定理可得 OB=6, 2 又 ∵∠D = ∠DBO , DE = BE , ∠ CED = ∠OEB , ∴ △ CDE ≌ △ 60 OBE,∴S△CDE=S△OBE,S 阴影=S 扇形 OCB= π·62=6π(cm2) 360
5.如图所示,已知:AB是⊙O的直径,点C,D在⊙O上,∠ABC=50°, 则∠D为( C ) A.50° B.45° C.40° D.30°
第6题图 6. 如图所示 ,点A, B, C,D 分别是⊙O 上四点 ,∠ ABD= 20 ° ,BD 是直径,则∠ACB=__70°__.
第5题图
7.如图所示,在△ABC中,BC=3,以BC为直径的⊙O交AC于点D, 若D是AC的中点,∠ABC=120°. (1)求∠ACB的大小; (2)求点A到直线BC的距离.
正多边形的有关概念Байду номын сангаас
1.(3 分)下列说法不正确的是( A.正多边形一定有一个外接圆 B.各边相等且各角相等的多边形一定是正多边形 C.正多边形的内切圆和外接圆是同心圆 D.正多边形既是轴对称图形又是中心对称图形 2.(3 分)下列说法正确的有( C ) ①各边相等的圆内接多边形是正多边形;②圆内接菱形是正多边 形;③各角相等的圆内接多边形是正多边形;④正多边形都是中心对 称图形. A.0 个 B.1 个 C.2 个 D.3 个 D )
九年级数学下册 第27章 圆 27.4 正多边形和圆同步练习 (新版)华东师大版

27.4 正多边形和圆一、选择题1.2018·益阳如图K -22-1,正方形ABCD 内接于⊙O ,AB =4,则图中阴影部分的面积是( )图K -22-1A .4π-16B .8π-16C .16π-32D .32π-162.在正三角形、正五边形、正十边形和正十五边形中,既是轴对称图形又是中心对称图形的有( ) 链接听课例2归纳总结 A .1个 B .2个 C .3个 D .4个3.一个正n 边形的中心角是它的一个内角的15,则n 的值为( )A .12B .11C .10D .84.如图K -22-2所示,在⊙O 中,OA =AB ,OC ⊥AB ,则下列结论错误的是( )图K -22-2A .弦AB 的长等于圆内接正六边形的边长 B .弦AC 的长等于圆内接正十二边形的边长 C.AC ︵=BC ︵D.∠BAC=30°5.如图K-22-3,正六边形ABCDEF内接于⊙O,若直线PA与⊙O相切于点A,则∠PAB的度数为( )图K-22-3A.30° B.35° C.40° D.60°6.正六边形的边心距与边长之比为( )A.3∶3B.3∶2 C.1∶2 D.2∶27.圆内接正五边形ABCDE中,对角线AC和BD相交于点P,则∠APB的度数是( )链接听课例3归纳总结A.36° B.60° C.72° D.108°8.若正多边形的内切圆与外接圆的周长之比为3∶2,则这个正多边形为( )A.正十二边形 B.正六边形C.正方形 D.正三角形9.如图K-22-4所示,△PQR是⊙O的内接正三角形,四边形ABCD是⊙O的内接正方形,BC∥QR,则∠AOQ的度数为( )图K-22-4A.60° B.65° C.72° D.75°二、填空题10.已知正六边形的边长为a,则它的内切圆的面积为________.11.如图K -22-5,将边长为3的正六边形铁丝框ABCDEF 变形为以点A 为圆心,AB 长为半径的扇形(忽略铁丝的粗细),则所得扇形AFB (阴影部分)的面积为________.图K -22-512.如图K -22-6,在⊙O 的内接四边形ABCD 中,AB =AD ,∠C =120°,点E 在AD ︵上.若AE 恰好为⊙O 的内接正十边形的一边,∠DAE 的度数为________.图K -22-6三、解答题13.如图K -22-7所示,⊙O 中,AB ︵=BC ︵=CD ︵=DE ︵=EF ︵=FA ︵.求证:六边形ABCDEF 是正六边形.图K -22-714.如图K-22-8所示,已知等边三角形ABC的外接圆⊙O的半径为R,求△ABC的边长a,周长P,边心距r及面积S.链接听课例3归纳总结图K-22-815.如图K-22-9,在正五边形ABCDE中,连结AC,AD,CE,CE交AD于点F,连结BF.小颖得出了下列四个结论:(1)△CDF的周长等于AD+CD;(2)FC平分∠BFD;(3)AC2+BF2=4CD2;(4)DE2=EF·CE.你认为这四个结论正确吗?请说明理由.图K-22-916.如图K -22-10,已知⊙O 和⊙O 上的一点A . (1)作⊙O 的内接正方形ABCD 和内接正六边形AEFCGH ;(2)在(1)题的作图中,如果点E 在AD ︵上,求证:DE 是⊙O 的内接正十二边形的一边. 链接听课例4归纳总结图K -22-10阅读探究阅读材料并解答问题:与正三角形各边都相切的圆叫做正三角形的内切圆,与正四边形各边都相切的圆叫做正四边形的内切圆,…,与正n (n ≥3)边形各边都相切的圆叫做正n 边形的内切圆.设正n 边形的面积为S 正n 边形,其内切圆的半径为r ,试探索正n 边形的面积.图K -22-11(1)如图K -22-11所示,当n =3时,设AB 切⊙O 于点C ,连结OC ,OA ,OB , 则OC ⊥AB ,OA =OB , ∴∠AOC =12∠AOB ,AB =2AC .在Rt △AOC 中,∵∠AOC =12×360°3=60°,OC =r ,∴AC =r ·tan60°,AB =2r ·tan60°, ∴S △OAB =12·r ·2r ·tan60°=r 2tan60°,∴S 正三角形=3S △OAB =3r 2tan60°.(2)如图K -22-12①,当n =4时,仿照(1)中的方法和过程可求得:S 正四边形=4S △OAB =__________;(3)如图②,当n =5时,仿照(1)中的方法和过程求S 正五边形; (4)如图③,根据以上探索过程,请直接写出S 正n 边形=________.图K -22-12教师详解详析[课堂达标] 1.[解析] B 连结OA ,OB ,如图.∵四边形ABCD 为正方形,∴∠AOB =90°. 设OA =OB =r ,则r 2+r 2=42,解得r =2 2. ∴S 阴影=S ⊙O -S 正方形ABCD =π×(2 2)2-42=8π-16. 故选B . 2.[答案] A 3.[答案] A4.[解析] D 因为OA =OB =AB ,所以△OAB 是等边三角形.又因为OC⊥AB,所以∠AOC=∠BOC =30°,所以∠BAC=15°,AC ︵=BC ︵,所以A ,B ,C 正确,D 不正确. 5.[答案] A6.[解析] B 如图,设正六边形的边长是a ,则其半径长也是a.过正六边形的中心O 作边AB 的垂线段OC ,连结OA ,OB ,则AC =12AB =12a ,∴OC =OA 2-AC 2=32a , ∴正六边形的边心距与边长之比为32a∶a=3∶2.故选B .7.[答案] C8.[解析] B 正多边形的内切圆与外接圆的周长之比为3∶2,则半径之比为3∶2. 如图,设AB 是正多边形的一边,O 为正多边形内切圆与外接圆的圆心,OC ⊥AB 于点C ,OC =3k ,则OA =OB =2k ,在Rt △AOC 中,cos ∠AOC =OC AC =32, ∴∠AOC =30°, ∴∠AOB =60°,则正多边形的边数是360°60°=6.故选B .9.[解析] D 因为圆心角与它所对弧的度数相等,所以求出AQ ︵的度数就求出了∠AOQ 的大小,而AQ ︵=PQ ︵-AP ︵.根据题意,得PQ ︵所对的圆心角为120°,AP ︵所对的圆心角为18×360°=45°,所以AQ ︵所对的圆心角为120°-45°=75°,所以∠AOQ=75°. 10.[答案] 3πa2411.[答案] 18[解析] 由题意可得,正六边形的边长AB 就是扇形的半径,正六边形的边长BC ,CD ,DE ,EF 的和就是扇形的弧长,所以扇形AFB 的半径AB =3,弧BDF 的长为12, 所以扇形AFB(阴影部分)的面积为S =12rl =12×3×12=18.故答案为18.12.[答案] 42°[解析] 连结BD ,OA ,OE ,OD ,如图所示.∵四边形ABCD 是⊙O 的内接四边形, ∴∠BAD +∠C=180°. ∵∠C =120°,∴∠BAD =60°. 又∵AB=AD ,∴△ABD 是等边三角形, ∴∠ABD =60°,∴∠AOD =2∠ABD=120°. ∵AE 恰好为⊙O 的内接正十边形的一边, ∴∠AOE =360°÷10=36°,∴∠DOE =120°-36°=84°,∴∠DAE =42°.13.[解析] 由弧相等得到弦相等,从而证得该六边形的六条边相等,由弧相等也可以证得该六边形的六个内角相等.证明:∵AB ︵=BC ︵=CD ︵=DE ︵=EF ︵=FA ︵,∴AB =BC =CD =DE =EF =FA(等弧所对的弦相等). ∵BCF ︵=CEA ︵=BED ︵=CAE ︵=DAF ︵=ACE ︵,∴∠A =∠B=∠C=∠D=∠E=∠F(等弧所对的圆周角相等), ∴六边形ABCDEF 是正六边形.14.解:如图,连结OB ,OC ,过点O 作OD⊥BC 于点D ,则OB =R ,∠OBD =12∠ABC=30°,∴OD =12OB =12R ,∴a =2·R 2-⎝ ⎛⎭⎪⎫12R 2=2·32R =3R ,P =3a =33R ,r =OD =12R , S =3·12ar =3×12×3R×12R =334R 2. 15.解:结论(2)错误,其他三个结论都正确.理由:正五边形的每一个内角均为108°,由AE =DE ,可求得∠EAD=∠EDA=36°,同理可得∠ECD=36°.又因为∠FED=∠DEC,所以△EFD∽△EDC,可得DE 2=EF·CE;由角的关系可得AF =CF ,所以△CDF 的周长=CF +DF +CD =AF +DF +CD =AD +CD.所以(1)和(4)正确.易知∠AFB=∠BFC=54°,而∠CFD=72°,所以(2)是错误的.由条件可得AB =BC =AF =CF ,所以四边形ABCF 是菱形,则AC 垂直平分BF ,设AC 与BF 交于点M ,由勾股定理可得CM 2+MF 2=CF 2,从而可得AC 2+BF 2=4CD 2,所以(3)正确.16.解:(1)作法:①作⊙O 的直径AC ;②作直径BD⊥AC;③依次连结A ,B ,C ,D 四点,则四边形ABCD 即为⊙O 的内接正方形;④分别以A ,C 为圆心,OA 长为半径作弧,交⊙O 于点E ,H 和F ,G ;⑤顺次连结AE ,EF ,FC ,CG ,GH ,HA ,则六边形AEFCGH 即为⊙O 的内接正六边形.(2)证明:如图,连结OE ,DE.∵∠AOD =360°4=90°, ∠AOE =360°6=60°, ∴∠DOE =∠AOD-∠AOE=90°-60°=30°,∴DE 为⊙O 的内接正十二边形的一边.[素养提升]解:(2)4r 2tan 45°(3)如图,当n =5时,设AB 切⊙O 于点C ,连结OC ,OA ,OB ,则OC⊥AB,OA =OB ,∴∠AOC=12∠AOB=12×360°5=36°,AB =2AC. ∵OC =r ,∴AC =r ·tan 36°,AB =2r·tan 36°,S △OAB =12·r ·2r ·tan 36°=r 2tan 36°, ∴S 正五边形=5S △OAB =5r 2tan 36°.(4)nr 2tan 180°n。
2018-2019学年九年级数学下册 第27章 圆 27.4 正多边形和圆同步练习 (新版)华东师大版

圆27.4 正多边形和圆知|识|目|标1.了解正多边形的概念,而且知道正多边形与圆的关系.2.在理解正多边形与圆的关系的基础上,通过例题和练习的学习,能够进行正多边形的有关计算.3.通过阅读教材,能借助等分圆周的方法画圆内接正多边形和圆外切正多边形.目标一了解正多边形的概念例1 教材补充例题已知:如图27-4-1所示,正方形ABCD的四个顶点都在大⊙O上,连结AC和BD,那么OA,OB,OC,OD都是大⊙O的________,∠AOB=∠BOC=∠COD=∠DOA=________°,以点O为圆心,作小⊙O与AB相切,那么AD,DC,AB和BC都与小⊙O________,四边形ABCD是小⊙O的____________.图27-4-1例2 教材补充例题下列结论中正确的有( )(1)各边都相等的多边形是正多边形;(2)各角都相等的多边形是正多边形;(3)正七边形有7条对称轴;(4)任何正多边形只有一个外接圆和一个内切圆;(5)一个圆有无数个内接正多边形和外切正多边形;(6)边数为奇数的正多边形一定是轴对称图形;(7)如果一个正多边形的每个外角都等于36°,那么它是正十边形;(8)若正方形的边长为6,则其内切圆的半径为3.A.5个 B.6个 C.7个 D.8个【归纳总结】各边相等、各角相等是正多边形的两个基本特征,边数为n(n>3)的多边形必须同时满足这两个特征才是正多边形,否则就不一定是正多边形.目标二能进行正多边形的有关计算例3 教材补充例题如图27-4-2,已知△ABC是⊙O的内接等腰三角形,顶角∠A=36°,弦BE,CD分别平分∠ABC,∠ACB.(1)求证:五边形ADBCE是正五边形;(2)指出正五边形的中心;(3)求正五边形的中心角;(4)如果正五边形的半径是r,边长是a,求正五边形的边心距d、周长P和面积S.图27-4-2【归纳总结】正多边形的有关计算:(1)正多边形满足以下两个条件:各边相等、各角相等.(2)正多边形中各元素间的关系:设正n (n ≥3,且n 为整数)边形的边长为a n ,半径为R ,边心距为r n ,中心角为αn ,周长为C n ,面积为S n ,则R 2=r n 2+⎝ ⎛⎭⎪⎫a n 22,αn =360°n ,C n =na n ,S n =12nr n a n =12C n r n . 从以上关系式可以看出,正多边形的有关计算都可以转化到由半径、中心到边的垂线段和边长的一半组成的直角三角形中解决.(3)正三角形中,边心距∶半径∶高=1∶2∶3;正方形中,正方形的对角线长等于其半径的2倍,边心距等于其边长的一半;正六边形中,正六边形的边长等于其半径.目标三 会画正多边形例4 教材例题针对训练 如图27-4-3,已知A ,B ,C ,D ,E 是⊙O 的五等分点,过点A 画出⊙O 的内接正五边形和外切正五边形.图27-4-3【归纳总结】等分圆周画圆内接正多边形的工具和方法:(1)只用量角器:用量角器把360°的圆心角n (n >2,且n 为整数)等分,相应圆周也被n 等分,顺次连结各分点即可得到圆内接正n 边形.(2)用量角器和圆规:先用量角器画出360°圆心角的1n (n >2,且n 为整数),相应地可得到圆周的1n;再用圆规顺次截取,便得到圆周的n 等分点,顺次连结各分点即可得到圆内接正n 边形.(3)用圆规和直尺:用尺规等分圆周,可以作正六边形、正方形等特殊的圆内接正多边形.知识点一 正多边形与圆的关系正多边形:____________、____________的多边形叫做正多边形.任何一个正多边形都有一个________和一个________,并且这两个圆是同心圆.知识点二 正多边形的有关概念正多边形的中心:正多边形的________(或内切圆)的圆心叫做正多边形的中心.正多边形的半径:外接圆的________叫做正多边形的半径.正多边形的边心距:________的半径叫做正多边形的边心距.正多边形的中心角:正多边形每一条边所对的外接圆的圆心角都相等,叫做正多边形的中心角.正n (n ≥3,且n 为整数)边形的每个中心角都等于________.知识点三 正多边形的画法基本原理:由于在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦相等,因此可以用等分圆心角的方法来等分圆周,从而画正多边形.把圆分成n (n ≥3,且n 为整数)等份,依次连结各分点所得的多边形是这个圆的一个内接________;经过各分点作圆的切线,以相邻切线的交点为顶点的多边形是这个圆的外切________.等分圆周的常用方法:(1)用________等分;(2)用________等分.知识点四 正多边形与圆的有关计算解决正多边形的相关计算问题,关键在于添加辅助线,将其转化为直角三角形,然后运用勾股定理来解决.学习了正多边形与圆后,三名同学有下列结论:张东:正多边形内切圆的半径与正多边形的半径相等;李艳:边数相同的正多边形都相似;刘浩:正多边形既是轴对称图形,也是中心对称图形.他们的说法正确吗?教师详解详析【目标突破】例1 [答案] 半径 90 相切 外切正四边形例2 [解析] B 菱形的四条边都相等,但它不是正四边形,所以(1)不正确;矩形的四个角都相等,但它不是正四边形,所以(2)不正确;其余六个结论都正确.例3 [解析] (1)要证明五边形ADBCE 是正五边形,只需要证明AD ︵=DB ︵=BC ︵=CE ︵=EA ︵即可;(2)正多边形的中心就是其外接圆的圆心;(3)正n 边形的中心角为360°n; (4)连结OB ,OC ,过点O 作BC 的垂线,垂线段的长度就是边心距,根据勾股定理即可求出.解:(1)证明:∵△ABC 是等腰三角形,且∠BAC =36°,∴∠ABC =∠ACB =72°.又∵BE 平分∠ABC ,CD 平分∠ACB ,∴∠ABE =∠EBC =∠ACD =∠DCB =36°,即∠ABE =∠EBC =∠ACD =∠DCB =∠BAC ,∴AE ︵=EC ︵=AD ︵=DB ︵=BC ︵,∴A ,D ,B ,C ,E 是⊙O 的五等分点,∴五边形ADBCE 是正五边形.(2)∵正多边形的中心是其外接圆的圆心,∴正五边形的中心是点O.(3)∵AD ︵=DB ︵=BC ︵=EC ︵=AE ︵,∴正五边形的中心角是360°5=72°. (4)如图,连结OB ,OC ,过点O 作OF ⊥BC 于点F.∵OB =r ,BF =12BC =12a , ∴正五边形的边心距d =OB 2-BF 2=r 2-a 24; 正五边形的周长P =5a ;正五边形的面积S =5S △OBC =5×12ad =5a 2 r 2-a 24. 例4 [解析] 依次连结圆的五等分点,所得的五边形是圆内接正五边形;经过圆的五等分点作圆的切线,相邻切线相交成的五边形是圆外切正五边形.解:(1)如图,依次连结AB ,BC ,CD ,DE ,EA ,就得到⊙O 的内接正五边形ABCDE.(2)如图,分别过点A ,B ,C ,D ,E 作⊙O 的切线,所得的五边形FGHMN 是⊙O 的外切正五边形.【总结反思】[小结] 知识点一各条边相等各个角也相等外接圆内切圆知识点二外接圆半径内切圆360°n知识点三正n边形正n边形量角器圆规[反思] 正多边形内切圆的半径与正多边形的边心距相等,所以张东的说法不正确;根据相似形的定义可知边数相同的正多边形都相似,所以李艳的说法正确.正多边形都是轴对称图形,但不一定是中心对称图形,比如正五边形不是中心对称图形,所以刘浩的说法不正确.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第27章 圆
7.4 多边形和圆
1.如果一个正多边形的中心角是36°,那么这个正多边形的边数是( ) A .10 B .8 C .6 D .5
2.如图所示,在⊙O 中,OA =AB =OB ,OC ⊥AB ,则下列结论错误的是( )
A .弦A
B 的长等于圆的内接正六边形的边长 B .弦A
C 的长等于圆内接正十二边形的边长 C.AC ︵=BC ︵
D .∠BAC =30°
3.[2018·德阳]已知圆内接正三角形的面积为3,则该圆的内接正六边形的边心距是( )
A .2
B .1 C. 3 D.
32
4.半径为2的圆内接正三角形、正四边形、正六边形的边心距之比为_______________________.
5.有一个亭子,它的地基是边心距为2 m 的正六边形,求地基的周长和面积(结果保留根号).
一,他在《九章算术》中提出了“割圆术”,即用内接或外切正多边形逐步逼近圆来近似计算圆的面积.设圆O 的半径为1,若用圆O 的外切正六边形的面积来近似估计圆O 的面积,S = ______.(结果保留根号)
7.如图所示,边长为a 的正六边形内有两个三角形(数据如图),则阴影部分的面积是空白面积的多少倍?
8.小刚现有一边长为a m 的正方形花布,准备做一个形状为正八边形的风筝,参加全校组织的风筝比赛,那么在这样的花布上怎样裁剪,才能得到一个面积最大的风筝?
参考答案
【分层作业】
1.A 2.D 3.B 4.1∶2∶ 3
5.解:如答图所示,∵六边形ABCDEF 是正六边形,
答图
∴∠BOC =1
6×360°=60°.
又∵OB =OC ,OP ⊥BC ,
∴△OBC 是等边三角形,∠BOP =∠COP =30°,∴BC =OB ,cos 30°=OP OB
.而OP =23,∴BC =OB =4,
∴该地基的周长=4×6=24(m), 面积=6×12×4×23=243(m 2
).
6.23 【解析】如答图.
答图
根据题意可知OH =1,∠BOC =60°,∴△OBC 为等边三角形,∴BH
OH
=tan ∠BOH ,∴BH =
33,∴S =12×33×1×1
2
=2 3.
7.
答图
解:如答图,∵三角形的斜边长为a , ∴两条直线边长分别为12a ,3
2a ,
∴S 空白=12a ·32a =34a 2
.
∵AB =a ,∴OC =
3
2
a , ∴S 正六边形=6×12a ·32a =332
a 2
,
∴S 阴影=S 正六边形-S 空白=332a 2-34a 2=534a 2
,
∴
S 阴影
S 空白
=5. 8. 解:如答图所示,在正方形ABCD 中,△DEF ,△CGH ,△BOP ,△AMN 为全等的等腰直角
三角形,八边形EMNOPHGF 为正八边形.
答图
设直角边DE =DF =CG =CH =x .在Rt △DEF 中,EF =2x .∵EF =FG ,且DC =DF +FG +CG ,∴x +x +2x =a ,解得x =2-22a ≈0.3a ,因此,从四个角上各剪去一个直角边长约为0.3a
m 的等腰直角三角形,即可得到一个面积最大的正八边形风筝.。
