【解析版】小专题(六) 构造全等三角形的方法技巧
构造全等三角形的方法技巧

方法1 角形
利用“角平分线”构造全等三ห้องสมุดไป่ตู้
【方法归纳】 因角平分线本身已经具备 全等的三个条件中的两个(角相等和公共 边相等),故在处理角平分线问题时,常 作以下辅助线构造全等三角形: (1)在角的两边截取两条相等的线段; (2)过角平分线上一点作角两边的垂线.
思1.如图,AB∥CD,BE平分 ∠ABC,CE平分∠BCD,点E在AD 上,求证:BC=AB+CD. 考
2.如图,已知∠AOB=90°,OM是 ∠AOB的平分线,三角尺的直角顶点 P在射线OM上滑动,两直角边分别与 OA,OB交于点C,D,求证:PC= PD.
方法2 利用“截长补短法”构造全等 三角形
【方法归纳】 截长补短法的具体做法 :在某一条线段上截取一条线段与特定 线段相等,或将某条线段延长,使之与 特定线段相等,再利用三角形全等的有 关性质加以说明.这种方法适用于证明 线段的和、差、倍、分等类的题目.
3.如图,在△ABC中,AD平分 ∠BAC,∠C=2∠B,试判断AB, AC,CD三者之间的数量关系,并 说明理由.(想一想,你会几种方法)
方法3 利用“倍长中线法”构造全 等三角形
【方法归纳】 将中点处的线段延长 一倍,然后利用SAS证三角形全等.
6.已知:如图,AD,AE分别是 △ABC和△ABD的中线,且BA= BD.求证:AE=AC.
6 探索全等三角形的条件(1)-边角边(SAS)(拓展提高)(解析版)

专题1.6 探索全等三角形的条件(1)-边角边(SAS )(拓展提高)一、单选题1.如图所示,在△ABC 中,∠ACB =90°,CD 平分∠ACB ,在BC 边上取点E ,使EC =AC ,连接DE ,若∠A =50°,则∠BDE 的度数是( )A .10°B .20°C .30°D .40°【答案】A 【分析】先由直角三角形的性质得∠B =90°﹣∠A =40°,再证△CDE ≌△CDA (S A S ),得∠CED =∠A =50°,然后由三角形的外角性质即可得出答案.【详解】∵∠ACB =90°,∠A =50°,∴∠B =90°﹣∠A =40°,∵CD 平分∠ACB ,∴∠ECD =∠ACD ,在△CDE 和△CDA 中,EC AC ECD ACD CD CD =⎧⎪∠=∠⎨⎪=⎩,∴△CDE ≌△CDA (S A S ),∴∠CED =∠A =50°,又∵∠CED =∠B +∠BDE ,∴∠BDE =∠CED ﹣∠B =50°﹣40°=10°,故选:A .【点睛】本题考查了全等三角形的判定与性质.2.如图所示,AD 是ABC ∆的边BC 上的中线,5AB =cm ,4=AD cm ,则边AC 的长度可能是( )A .3cmB .5cmC .14cmD .13cm【答案】B 【分析】延长AD 至M 使DM =AD ,连接CM ,根据SAS 得出≅ADB MDC ,得出AB =CM =4cm ,再根据三角形的三边关系得出AC 的范围,从而得出结论;【详解】解:延长AD 至M 使DM =AD ,连接CM ,∵AD 是ABC ∆的边BC 上的中线,∴BD =CD ,∵∠ADB =∠CDM ,∴≅ADB MDC ,∴MC =AB =5cm ,AD =DM =4cm ,在AMC 中,3<AC <13,故选:B【点睛】本题考查了全等三角形的判定与性质以及三角形的三边关系,根据三角形的三边关系找出AC 长度的取值范围是解题的关键.3.如图,已知AB AD =,BC DE =,且10CAD ∠=︒,25B D ∠=∠=︒,120EAB ∠=︒,则EGF ∠的度数为( )A .120︒B .135︒C .115︒D .125︒【答案】C 【分析】由已知可得△ABC ≌△ADE ,故有∠BAC =∠DAE ,由∠EAB =120°及∠CAD =10°可求得∠AFB 的度数,进而得∠GFD 的度数,在△FGD 中,由三角形的外角等于不相邻的两个内角的和即可求得∠EGF 的度数.【详解】在△ABC 和△ADE 中AB AD B D BC DE =⎧⎪∠=∠⎨⎪=⎩∴ △ABC ≌△ADE (SAS )∴∠BAC =∠DAE∵∠EAB =∠BAC +∠DAE +∠CAD =120°∴∠BAC =∠DAE ()112010552=⨯︒-︒=︒ ∴∠BAF =∠BAC +∠CAD =65°∴在△AFB 中,∠AFB =180°-∠B -∠BAF =90°∴∠GFD =90°在△FGD 中,∠EGF =∠D +∠GFD =115°故选:C【点睛】本题考查了三角形全等的判定和性质、三角形内角和定理,关键求得∠BAC 的度数.4.如图,AD 是ABC 的中线,E ,F 分别是AD 和AD 延长线上的点,且DE DF =,连接BF ,CE ,下列说法:①ABD △和ACD △面积相等; ②BAD CAD ∠=∠; ③BDF ≌CDE △;④//BF CE ;⑤CE AE =.其中正确的是( )A.①②B.①③C.①③④D.①④⑤【答案】C【分析】根据三角形中线的定义可得BD=CD,根据等底等高的三角形的面积相等判断出①正确,然后利用“边角边”证明△BDF和△CDE全等,根据全等三角形对应边相等可得CE=BF,全等三角形对应角相等可得∠F=∠CED,再根据内错角相等,两直线平行可得BF∥CE.【详解】解:∵AD是△ABC的中线,∴BD=CD,∴△ABD和△ACD面积相等,故①正确;∵AD为△ABC的中线,∴BD=CD,∠BAD和∠CAD不一定相等,故②错误;在△BDF和△CDE中,BD CDBDF CDE DF DE=⎧⎪∠=∠⎨⎪=⎩,∴△BDF≌△CDE(SAS),故③正确;∴∠F=∠DEC,∴BF∥CE,故④正确;∵△BDF≌△CDE,∴CE=BF,故⑤错误,正确的结论为:①③④,故选:C.【点睛】本题考查了全等三角形的判定与性质,等底等高的三角形的面积相等,熟练掌握三角形全等的判定方法并准确识图是解题的关键.5.如图已知ABC ∆中,12AB AC cm ==,B C ∠=∠,8BC cm =,点D 为AB 的中点.如果点P 在线段BC 上以2/cm s 的速度由B 点向C 点运动,同时,点Q 在线段CA 上由C 点向A 点运动.若点Q 的运动速度为v ,则当BPD ∆与CQP ∆全等时,v 的值为( )A .1B .3C .1或3D .2或3【答案】D 【分析】设运动时间为t 秒,由题目条件求出BD=12AB=6,由题意得BP=2t ,则CP=8-2t ,CQ=vt ,然后结合全等三角形的判定方法,分两种情况列方程求解.【详解】解:设运动时间为t 秒,∵12AB AC cm ==,点D 为AB 的中点.∴BD=12AB=6, 由题意得BP=2t ,则CP=8-2t ,CQ=vt ,又∵∠B=∠C∴①当BP=CQ ,BD=CP 时,BPD ∆≌CQP ∆∴2t=vt ,解得:v=2②当BP=CP ,BD=CQ 时,BPD ∆≌CPQ ∆∴8-2t=2t ,解得:t=2将t=2代入vt=6,解得:v=3综上,当v=2或3时,BPD ∆与CQP ∆全等故选:D【点睛】本题主要考查了全等三角形全等的判定、熟练掌握全等三角形的判定方法是解题的关键,学会用分类讨论的思想思考问题,属于中考常考题型.6.如图1,已知AB AC =,D 为BAC ∠的角平分线上面一点,连接BD ,CD ;如图2,已知AB AC =,D 、E 为BAC ∠的角平分线上面两点,连接BD ,CD ,BE ,CE ;如图3,已知AB AC =,D 、E 、F 为BAC ∠的角平分线上面三点,连接BD ,CD ,BE ,CE ,BF ,CF ;…,依次规律,第n 个图形中有全等三角形的对数是( ).A .nB .21n -C .(1)2n n +D .3(1)n +【答案】C 【分析】根据条件可得图1中△ABD ≌△ACD 有1对三角形全等;图2中可证出△ABD ≌△ACD ,△BDE ≌△CDE ,△ABE ≌△ACE 有3对三角形全等;图3中有6对三角形全等,根据数据可分析出第n 个图形中全等三角形的对数.【详解】解:∵AD 是∠BAC 的平分线,∴∠BAD=∠CAD .在△ABD 与△ACD 中,AB=AC ,∠BAD=∠CAD ,∴△ABD≌△ACD.∴图1中有1对三角形全等;同理图2中,△ABE≌△ACE,∴BE=EC,∵△ABD≌△ACD.∴BD=CD,又DE=DE,∴△BDE≌△CDE,∴图2中有3对三角形全等;同理:图3中有6对三角形全等;由此发现:第n个图形中全等三角形的对数是()12n n+.故选:C.【点睛】此题主要考查了三角形全等的判定以及规律的归纳,解题的关键是根据条件证出图形中有几对三角形全等,然后寻找规律.二、填空题7.如图所示,点O为AC的中点,也是BD的中点,那么AB与CD的关系是________.【答案】平行且相等【分析】只需要证明△AOB≌△COD,根据全等三角形的性质和平行线的判定定理即可得出结论.【详解】解:∵点O为AC的中点,也是BD的中点,∴AO=OC,BO=OD,又∵∠AOB=∠DOC,∴△AOB≌△COD(SAS)∴AB=CD,∠A=∠C,即AB 与CD 的关系是平行且相等,故答案为:平行且相等.【点睛】本题考查全等三角形的性质和判定,平行线的判定定理.掌握全等三角形的判定定理是解题关键.8.在ABC ∆中,AD 是BC 边上的中线,若7,5AB AC ==,则AD 长的取值范围是_________.【答案】16AD <<【分析】利用中线的性质,作辅助线AD=DE ,构造全等三角形()ADB EDC SAS ≅,再有全等三角形对应边相等的性质,解得7CE AB ==,最后由三角形三边关系解题即可.【详解】如图,AD 为BC 边上的中线,延长AD 至点E ,使得AD=DE在△ADB 和△EDC 中BD DC ADB CDE AD DE =⎧⎪∠=∠⎨⎪=⎩()ADB EDC SAS ∴≅7CE AB ∴==CE AC AE AC CE -<<+75275AD ∴-<<+16AD ∴<<故答案为:16AD <<.【点睛】本题考查三角形三边的关系,其中涉及全等三角形的判定与性质等知识,是重要考点,掌握相关知识、正确作出辅助线是解题的关键.9.如图,在ABC 中,,90AC BC ACB =∠=︒,点D 是BC 上的一点,过点B 作//BE AC ,使BE CD =,连接CE 与AD 相交于点G ,则AD 与CE 的关系是_______________.【答案】AD ⊥CE ,AD =CE【分析】证明△ACD ≌△CBE ,得到∠CAD =∠BCE ,AD =CE ,结合∠ACB =90°,可得∠CGD =90°,从而可得结果.【详解】解:由题意可知:∵∠ACB =90°,BE ∥AC ,∴∠ACB =∠EBC =90°,在Rt △ACD 和Rt △CBE 中,AC CB ACD CBE CD BE =⎧⎪∠=∠⎨⎪=⎩,∴△ACD ≌△CBE (SAS ),∴∠CAD =∠BCE ,AD =CE ,∵∠CAD +∠CDA =90°,∴∠CDA +∠BCE =90°,∴∠CGD =180°-(∠CDA +∠BCE )=90°,∴AD ⊥CE ,综上:AD ⊥CE ,AD =CE ,故答案为:AD ⊥CE ,AD =CE .【点睛】本题考查了全等三角形的判定和性质,解题的关键是证明△ACD ≌△CBE ,得到角和线段之间的相等关系.10.如图,在ABC 中,90B ∠>︒,CD 为ACB ∠的角平分线,在AC 边上取点E ,使DE DB =,且90AED ∠>︒,若A x ∠=︒,ACB y ∠=︒,则AED =∠_______.(用x 、y 的代数式表示)【答案】180°-x°-y° 【分析】在AC 上截取CF =BC ,根据全等三角形的性质可得BD =DF =DE ,可得∠AED =∠ABC ,根据三角形的内角和可求解.【详解】解:如图,在AC 上截取CF =BC ,∵CD 为∠ACB 的角平分线,∴∠ACD =∠BCD ,∵CF =BC ,∠ACD =∠BCD ,CD =CD ,∴△BDC ≌△FDC (SAS ),∴∠ABC =∠CFD ,DF =BD ,∵BD =DE ,∴DE =DF ,∴∠DEF =∠DFE ,∴∠AED =∠CFD ,∵∠A =x°,∠ACB =y°,∴∠ABC =180°-∠A -∠ACB =180°-x°-y°,∴∠AED =∠DBC =180°-x°-y°,故答案为:180°-x°-y°.【点睛】本题考查了全等三角形的判定和性质,三角形内角和定理,添加恰当辅助线构造全等三角形是解本题的关键.11.如图,在ABC 中,90,,,ACB AC BC CE BE CE ∠=︒=⊥与AB 相交于点F ,且CD BE =,则ACD CBA DAF ∠∠∠、、之间的数量关系是_____________.【答案】=ACD CBA DAF ∠∠∠+【分析】先利用同角的余角相等得到ACD ∠=CBE ∠,再通过证ACD CBE ≌,得到==90ADC CEB ∠︒∠即==90ADF CEB ∠︒∠,再 利用三角形内角和得=AFD ADF EFB FEB ︒--︒-∠-180∠∠180∠可得=DAF EBF ∠∠,最后利用角的和差即可得到答案,ACD ∠==++CBE CBA EFB CBA DAF ∠∠∠=∠∠.【详解】证明:∵90ACB ∠=︒,CE BE ⊥∴+90ACD ECB ∠=︒∠,+90CBE ECB ∠=︒∠∴ACD ∠=CBE ∠又∵AC BC =,CD BE =∴ACD CBE ≌∴==90ADC CEB ∠︒∠即==90ADF CEB ∠︒∠∵=AFD EFB ∠∠∴=AFD ADF EFB FEB ︒--︒-∠-180∠∠180∠即=DAF EBF ∠∠∴ACD ∠==++CBE CBA EFB CBA DAF ∠∠∠=∠∠故答案为:=ACD CBA DAF ∠∠∠+.【点睛】本题考查了直角三角形的性质、内角和定理以及全等三角形的判定和性质,能通过性质找到角与角之间的关系是解答此题的关键.12.如图所示的是一张直角ABC 纸片(90C ∠=︒),其中30BAC ∠=︒,如果用两张完全相同的这种纸片恰好能拼成如图2所示的ABD △,若2BC =,则ABD △的周长为______.【答案】12【分析】根据题意证明三角形全等即可得解;【详解】如图所示,由题可知ABC ADC ≅△△,∴30BAC DAC ∠=∠=︒,90ACB ACD ∠=∠=︒,2BC BD ==,∴60BAD ∠=︒,180BCD ∠=︒,∴B ,C ,D 在一条直线上,∵60B D ∠=∠=︒,∴△ABD 是等边三角形,∴△ABD 的周长()3312BD BC CD==+=;故答案是12.【点睛】本题主要考查了全等三角形的判定与性质,结合等边三角形的性质计算是解题的关键. 13.已知:如图,在长方形ABCD 中,AB =4,AD =6.延长BC 到点E ,使CE =2,连接DE ,动点P 从点B 出发,以每秒2个单位的速度沿BC ﹣CD ﹣DA 向终点A 运动,设点P 的运动时间为t 秒,当t 的值为__秒时,△ABP 和△DCE 全等.【答案】1或7【分析】分两种情况进行讨论,根据题意得出BP=2t=2或AP=16-2t=2即可求得结果.【详解】因为AB=CD,若∠ABP=∠DCE=90°,BP=CE=2,根据SAS证得△ABP≌△DCE,由题意得:BP=2t=2,所以t=1,因为AB=CD,若∠BAP=∠DCE=90°,AP=CE=2,根据SAS证得△BAP≌△DCE,由题意得:AP=16﹣2t=2,解得t=7.所以,当t的值为1或7秒时.△ABP和△DCE全等.故答案为:1或7.【点睛】本题考查了全等三角形的判定,要注意分类讨论.14.如图,△P AB与△PCD均为等腰直角三角形,点C在PB上,若△ABC与△BCD的面积之和为10,则△P AB与△PCD的面积之差为_____.【答案】10【分析】由“SAS”可证△APC≌△BPD,可得S△APC=S△BPD,由面积和差关系可求解.【详解】解:∵△P AB与△PCD均为等腰直角三角形,∴PC=PD,∠APB=∠CPD=90°,AP=BP,∴△APC≌△BPD(SAS),∴S△APC=S△BPD,∵S△APB﹣S△PCD=S△APC+S△ABC﹣(S△BPD﹣S△BCD),∴S△APB﹣S△PCD=S△BCD+S△ABC=10,故答案为:10.【点睛】本题考查了全等三角形的判定和性质,等腰直角三角形的性质,证明△APC≌△BPD是本题的关键.三、解答题15.如图所示,AC BC ⊥,DC EC ⊥,垂足均为点C ,且AC BC =,EC DC =.求证:AE BD =.【答案】见解析【分析】根据SAS 证明ACE BCD △≌△即可.【详解】证明:∵AC BC ⊥,DC EC ⊥,∴90ACB ECD ∠=∠=︒∴ACB BCE ECD BCE ∠+∠=∠+∠即ACE BCD ∠=∠在ACE 和BCD △中AC BC ACE BCD EC DC =⎧⎪∠=∠⎨⎪=⎩∴()SAS ACE BCD ≌△△ ∴AE BD =【点睛】此题主要考查了全等三角形的判定与性质,证明ACE BCD ∠=∠是解答此题的关键. 16.如图,点B ,E ,C ,F 在一条直线上,//,,AB DE AB DE BE CF ==.求证:A D ∠=∠.【答案】证明见解析【分析】根据平行得出B DEF ∠=∠,然后用“边角边”证明ABC DEF △≌△即可.【详解】证明:∵//AB DE ,∴B DEF ∠=∠.∵BE CF =,∴BE EC CF EC +=+.∴BC EF =.在ABC 和DEF 中,,,,AB DE B DEF BC EF =⎧⎪∠=∠⎨⎪=⎩∴ABC DEF △≌△.∴A D ∠=∠.【点睛】本题考查了全等三角形的判定与性质,解题关键是熟练运用已知条件,推导证明出全等三角形判定所需条件,运用全等三角形判定定理证明.17.如图,四边形ABCD 的对角线交于点O ,点E 、F 在AC 上,//DF BE ,且DF BE =,AE CF =.求证:AB CD =,且//AB CD .【答案】见解析【分析】根据已知条件可证得ABE CDF △≌△,从而由全等三角形的性质可得要证的结论.【详解】//DF BEBEO DFO ∴∠=∠AEB CFD ∴∠=∠又DF BE =∵,AE CF =ABE CDF ∴△≌△AB CD ∴=,BAE DCF ∠=∠//AB CD ∴【点睛】本题考查了三角形全等的的判定的性质,关键是得出AEB CFD ∠=∠.18.如图,BD ,CE 分别是ABC 的边AC 和AB 边上的高,点P 在BD 的延长线上,点Q 在CE 上,BP AC =,CQ AB =,请说明AQ 与AP 的关系.【答案】AP =AQ 且AP ⊥AQ【分析】由于BD AC ⊥,CE AB ⊥,可得ABD ACE ∠=∠,又由对应边的关系,进而得出ABP QCA ∆≅∆,即可得出AQ=AP .在此基础上,可证明90PAQ ∠=︒.【详解】解:证明:BD AC ⊥,CE AB ⊥(已知),90BEC BDC ∴∠=∠=︒,90ABD BAC ∴∠+∠=︒,90ACE BAC ∠+∠=︒(直角三角形两个锐角互余),ABD ACE ∴∠=∠(等角的余角相等),在ABP ∆和QCA ∆中,BP AC ABD ACE CQ AB =⎧⎪∠=∠⎨⎪=⎩()ABP QCA SAS ∴∆≅∆,∴=AP AQ .ABP QCA ∆≅∆,CAQ P ∴∠=∠,BD AC ⊥,即90P CAP ∠+∠=︒,90CAQ CAP ∴∠+∠=︒,即90QAP ∠=︒,AP AQ ∴⊥.【点睛】本题主要考查了全等三角形的判定及性质问题,能够熟练掌握并运用.19.平面上有ACD △与,BCE AD 与BE 相交于点,P AC 与BE 相交于点,M AD 与CE 相交于点N ,若,,AC BC CD CE ECD ACB ==∠=∠.(1)求证:≌ACD BCE ;(2)55,145ACE BCD ∠=︒∠=︒,求BPD ∠的度数.【答案】(1)证明见解析;(2)∠BPD =140°.【分析】(1)利用SAS 证明△ACD ≌△BCE 即可;(2)由全等三角形的性质可知:∠A =∠B ,再根据已知条件和四边形的内角和为360°,即可求出∠BPD 的度数.【详解】解:(1)证明:∵∠ACB =∠ECD ,∠ACE =∠ACE ,∴∠BCE =∠ACD ,在△ACD 和△BCE 中,AC BC BCE ACD CD CE =⎧⎪∠=∠⎨⎪=⎩,∴△ACD ≌△BCE (SAS );(2)∵△ACD ≌△BCE ,∴∠A =∠B ,∠BCE =∠ACD ,∴∠BCA =∠ECD ,∵∠ACE =55°,∠BCD =155°,∴∠BCA +∠ECD =100°,∴∠BCA =∠ECD =50°,∵∠ACE =55°,∴∠ACD =105°∴∠A +∠D =75°,∴∠B +∠D =75°,∵∠BCD =145°,∴∠BPD =360°-75°-145°=140°.【点睛】本题考查了全等三角形的判定和性质、三角形的内角和定理以及四边形的内角和定理,解题的关键是利用整体的数学思想求出∠B+∠D=75°.20.(1)如图1,一扇窗户打开后,用窗钩AB将其固定,这里所运用的几何原理是:;(2)如图2,小河的旁边有一个甲村庄所示,现计划在河岸AB上建一个泵站,向甲村供水,使得所铺设的供水管道最短,请在上图中画出铺设的管道,这里所运用的几何原理是:(3)如图3,在新修的小区中,有一条“Z”字形长廊ABCD,其中AB∥CD,在AB,BC,CD三段长廊上各修一小凉亭E,M,F,且BE=CF,点M是BC的中点,在凉亭M与F之间有一池塘,不能直接到达,要想知道M与F之间的距离,只需要测出线段ME的长度(用两个字母表示线段).这样做合适吗?请说出理由.【答案】(1)三角形具有稳定性;(2)见解析,垂线段最短;(3)合理,见解析【分析】(1)根据三角形的稳定性解答;(2)根据垂线段最短解答;(3)首先证明△MEB≌△MFC,根据全等三角形的性质可得ME=MF.【详解】解:(1)一扇窗户打开后,用窗钩AB要将其固定,这里所运用的几何原理是三角形具有稳定性;故答案为:三角形具有稳定性;(2)过甲向AB作垂线,如图2所示;运用的原理是:垂线段最短;故答案为:垂线段最短;(3)合理,∵AB ∥CD ,∴∠B =∠C ,∵点M 是BC 的中点,∴MB =MC ,在△MCF 和△MBE 中BE CF B C BM CM =⎧⎪∠=∠⎨⎪=⎩,∴△MEB ≌△MFC (SAS ),∴ME =MF ,∴想知道M 与F 之间的距离,只需要测出线段ME 的长度.【点睛】此题主要考查了垂线段的性质,三角形的稳定性,以及全等三角形的应用,关键是掌握全等三角形判定定理,会用它证明对应边相等.。
[数学]-必考点06 添加辅助线构造全等三角形的技巧-【题型·技巧培优系列】2022-2023学年八
![[数学]-必考点06 添加辅助线构造全等三角形的技巧-【题型·技巧培优系列】2022-2023学年八](https://img.taocdn.com/s3/m/612e7ba6112de2bd960590c69ec3d5bbfd0ada34.png)
必考点06 添加辅助线构造全等三角形的技巧●题型一添加公共边构造全等三角形【例题1】如图,AB=AC,BD=CD.(1)求证:∠B=∠C(2)若∠A=2∠B,求证:∠BDC=4∠C.【例题2】如图,已知CA=CB,AD=BD,M,N分别是CB,CA的中点,求证:DN=DM.【例题3】(2022秋•韩城市月考)如图,在Rt△ABC和Rt△ADE中,∠ABC=∠ADE=90°,BC与DE 相交于点F,且AB=AD,AC=AE,连接CD,EB.(1)求证:∠CAD=∠EAB;(2)试判断CF与EF的数量关系,并说明理由.【解题技巧提炼】当图形中直接证明全等条件不够时,有时可以连接公共边构造全等三角形,再利用全等三角形的判定与性质解决问题.●题型二巧用角平分线构造全等三角形【例题4】如图,AD∥BC,∠DAB的平分线与∠CBA的平分线交于点P,过点P的直线垂直于AD,垂足为D,交BC于点C.试问:点P是线段CD的中点吗?为什么?【例题5】(2021春•酒泉期末)如图所示,在△ABC中,D为BC的中点,DE⊥BC,交∠BAC的平分线AE于点E,EF⊥AB于点F,EG⊥AC交AC延长线于点G.求证:BF=CG.【例题6】感知:如图①,AD平分∠BAC,∠B+∠C=180°,∠B=90°,易知:DB=DC.探究:如图②,AD平分∠BAC,∠ABD+∠ACD=180°,∠ABD<90°,求证:DB=DC.应用:如图③,四边形ABCD中,∠B=60°,∠C=120°,DB=DC=a,求AB﹣AC的值(用含a的代数式表示)【解题技巧提炼】当题中出现角平分线的条件或结论时,常向角的两边作垂线段,构造全等三角形,在利用全等三角形的判定和性质解决问题.●题型三“倍长中线法”构造全等三角形【例题7】数学兴趣小组在活动时,老师提出了这样一个问题:如图1,在△ABC中,AB=8,AC=6,D 是BC的中点,求BC边上的中线AD的取值范围.小明在组内经过合作交流,得到了如下的解决方法:延长AD到E,使DE=AD,请补充完整证明“△ADC≌△EDB”的推理过程.(1)求证:△ADC≌△EDB证明:∵延长AD到点E,使DE=AD在△ADC和△EDB中AD=ED(已作)∠ADC=∠EDB()CD=BD(中点定义)∴△ADC≌△EDB()(2)探究得出AD的取值范围是;【感悟】解题时,条件中若出现“中点”“中线”等字样,可以考虑延长中线构造全等三角形,把分散的已知条件和所求证的结论集合到同一个三角形中.【问题解决】(3)如图2,△ABC中,∠B=90°,AB=2,AD是△ABC的中线,CE⊥BC,CE=4,且∠ADE=90°,求AE的长.【例题8】(2022春•碑林区校级期末)问题提出:(1)如图①,在Rt△ABC中,∠ACB=90°,点D为AB的中点,连接CD并延长至E,使得DE=CD,连接EB,根据SAS可证△CDA≌△EDB,从而得到∠A=∠EBD,进而得到AC∥EB,再由∠ACB=90°,得到∠EBC=90°,再根据SAS可证△ABC≌△ECB,从而得到AB与CD之间的数量关系为.问题解决(2)如图②,在△ABC中,过点C作CA'⊥CA,CB'⊥CB,使得CA'=CA,CB'=CB,连接A'B',E为A'B'的中点.连接CE,求证:CE=12AB;【解题技巧提炼】当三角形中有中点或中线时,常倍长中线,构造全等三角形,转换边、角条件,从而将分散的边、角集中在一个图形中,使问题得到解决.●题型四利用“截长补短法”构造全等三角形【例题9】(2021秋•五峰县期中)在“教、学、练、评一体化”学习活动手册中,全等三角形专题复习课,学习过七种作辅助线的方法,其中有“截长补短”作辅助线的方法.截长法:在较长的线段上截取一条线段等于较短线段;补短法:延长较短线段和较长线段相等.这两种方法统称截长补短法.请用这两种方法分别解决下列问题:已知,如图,在△ABC中,AB>AC,∠1=∠2,P为AD上任一点,求证:AB﹣AC>PB﹣PC.【例题10】(2021秋•泊头市期中)[阅读]在证明线段和差问题时,经常采用截长补短法,再利用全等图形求线段的数量关系,截长法:将较长的线段截取为两段,证明截取的两段分别与给出的两段相等.补短法:延长较短两条线段中的一条,使得与较长线段相等,证明延长的那一段与另一条较短线段相等.[应用]把两个全等的直角三角形的斜边重合,∠CAD=∠CBD=90°,组成一个四边形ACBD,以D为顶点作∠MDN,交边AC、BC于M、N.(1)若∠ACD=30°,∠MDN=60°,证明:AM+BN=MN;经过思考,小红得到了这样的解题思路:利用补短法,延长CB到点E,使BE=AM,连接DE,先证明△DAM≌△DBE,再证明△MDN≌△EDN,即可求得结论.按照小红的思路,请写出完整的证明过程;(2)当∠ACD+∠MDN=90°时,AM、MN、BN三条线段之间有何数量关系?(直接写出你的结论,不用证明)(3)如图③,在(2)的条件下,若将M、N改在CA、BC的延长线上,完成图③,其余条件不变,则AM、MN、BN之间有何数量关系?证明你的结论.【解题技巧提炼】在证明线段和差问题时,经常采用截长补短法,再利用全等图形求线段的数量关系,截长法:将较长的线段截取为两段,证明截取的两段分别与给出的两段相等.补短法:延长较短两条线段中的一条,使得与较长线段相等,证明延长的那一段与另一条较短线段相等.●题型五利用“一线三等角模型”构造全等三角形【例题11】如图,在△ACB中,∠ACB=90°,AC=BC,点C的坐标为(﹣2,0),点B的坐标为(1,6),求点A的坐标.【例题12】已知C,D过∠BCA顶点的一条直线,CA=CB,E,F是直线CD上的两点,且∠BEC=∠CF A.(1)如图(1),若∠BCA=90°,∠BEC=∠CF A=90°,则BE=CF(填“>”、“<”或“=”)(2)如图(2),∠BCA+∠BEC=180°,则(1)中的结论是否成立?为什么?(3)如图(3),若∠BEC=∠CF A=∠BCA,则线段EF,BE,AF之间有何数量关系?说明理由.【解题技巧提炼】“一线三等角”指的是有三个等角的顶点在同一条直线上构成的全等图形,这个角可以是直角也可以是锐角或钝角,有些时候我们也称之为“M型”“三垂直”等.“一线三等角”----三垂直全等模型辅助线如何构造: 图形中存在“一线二等角”,补上“一等角”构造模型解题.◆◆题型一添加公共边构造全等三角形1.如图:已知AD、BC相交于O,且AB=CD,AD=CB.求证:∠B=∠D.2.如图,在四边形ABCD中,已知AB=CD,AD=BC,则∠A=∠C,请说明理由;AB与CD相互平行吗?为什么?3.如图,在Rt△ACB和Rt△AED中,已知AB=AD,∠1=∠2,求证:EG=CG.◆◆题型二巧用角平分线构造全等三角形4.已知:如图,点B、C、E三点在同一条直线上,CD平分∠ACE,DB=DA,DM⊥BE于M.(1)求证:AC=BM+CM;(2)若AC=10,BC=6,求CM的长.5.(2021秋•东莞市校级期末)如图,∠B=90°,∠C=90°,E为BC中点,DE平分∠ADC.(1)求证:AE平分∠DAB;(2)求证:AE⊥DE;(3)求证:DC+AB=AD.◆◆题型三“倍长中线法”构造全等三角形6.如图,△ABC中,E,F分别在AB,AC上,DE⊥DF,D是中点,试比较BE+CF与EF的大小.7.如图,AD是△ABC的边BC上的中线,CD=AB,AE是△ABD的边BD上的中线.求证:AC=2AE.◆◆题型四利用“截长补短法”构造全等三角形8.(1)如图1,在四边形ABCD中,AB=AD,∠B=∠D=90°,E、F分别是边BC、CD上的点,若EF=BE+FD.求证:∠EAF=12∠BAD(2)如图2,在四边形ABCD中,AB=AD,∠B+∠ADC=180°,E、F分别是边BC、CD延长线上的点,且∠EAF=12∠BAD,试探究线段EF、BE、FD之间的数量关系,证明你的结论.◆◆题型五利用“一线三等角模型”构造全等三角形9.(2022•南京模拟)如图,在Rt△ABC中,∠ABC=90°点D在BC的延长线上,且BD=AB.过点B 作BE⊥AC,与BD的垂线DE交于点E.(1)求证:△ABC≌△BDE;(2)请找出线段AB、DE、CD之间的数量关系,并说明理由.10.如图,已知AB⊥BC,AE⊥BE,CD⊥BE,垂足分别为B,E,D,AB=BC.求证:(1)△ABE≌△BCD;(2)DE=CD﹣AE.11.在平面直角坐标系中,点A在x轴的负半轴上,且OA=3.(1)如图①,OB=5,以A为直角顶点,在第三象限内作等腰Rt△ABC,求点C的坐标.(2)如图②,以y轴负半轴一点P,作等腰直角三角形Rt△APD,其中∠APD=90°,过点D作DE⊥x 轴于点E,求OP﹣DE的值.1.如图所示,D是四边形AEBC内一点,联结AD,BD,已知CA=CB,DA=DB,EA=EB,请问C,D,E三点在一条直线上吗?为什么?2.如图所示,在四边形ABCD中,已知AB=CD,AD=BC,DE=BF,且点E、F分别在AD、CB的延长线上.求证:BE=DF.3.如图,在△ABC中,BE是∠ABC的平分线,AD⊥BE,垂足为D,求证:∠2=∠1+∠C.4.(2021秋•惠阳区校级月考)如图①所示,在△ABC中,∠ACB=90°,AC=BC,过点C在△ABC外作直线MN,AM⊥MN于点M,BN⊥MN于点N.(1)求证:MN=AM+BN;(2)如图②,若过点C作直线MN与线段AB相交,AM⊥MN于点M,BN⊥MN于点N,(1)中的结论是否仍然成立?请说明理由.5.如图,P为定角∠AOB平分线上的一个定点,且∠MPN与∠AOB互补,若∠MPN在绕点P转动的过程中,其两边分别与OA,OB相交于M,N两点,求证:PM=PN.【拓展1】OM+ON的值是否为定值?请说明理由.【拓展2】四边形PMON的面积是否为定值?请说明理由.6.(2022春•丰城市校级期末)如图,∠BAD=∠CAE=90°,AB=AD,AE=AC,AF⊥CB,垂足为F.(1)求证:△ABC≌△ADE;(2)求证:CD=2BF+DE.7.(2022秋•如皋市校级月考)已知在平面直角坐标系中A(0,2),P(3,3),且P A⊥PB.(1)如图1,求点B的坐标;(2)如图2,若A点运动到A1位置,B点运动到B1位置,仍保持P A1⊥PB1,求OB1﹣OA1的值.8.(2022春•富平县期末)问题情境:(1)如图1,∠AOB=90,OC平分∠AOB,把三角尺的直角顶点落在OC的任意一点P上,并使三角尺的两条直角边分别与OA、OB相交于点E、F,过点P作PN⊥OA于点N,作PM⊥OB于点M,请写出PE与PF的数量关系;变式拓展:(2)如图2,已知OC平分∠AOB,P是OC上一点,过点P作PM⊥OB于M,PN⊥OA于N,PE边与OA边相交于点E,PF边与射线OB的反向延长线相交于点F,∠MPN=∠EPF.试解决下列问题:①PE与PF之间的数量关系还成立吗?为什么?②若OP=2OM,试判断OE、OF、OP三条线段之间的数量关系,并说明理由.9.已知在△ABC中,∠BAC=90°,AB=AC,将△ABC放在平面直角坐标系中,如图所示.(1)如图1,若A(1,0),B(0,3),求C点坐标;(2)如图2,若A(1,3),B(﹣1,0),求C点坐标;(3)如图3,若B(﹣4,0),C(0,﹣1),求A点坐标.10.(2021秋•铁锋区期末)【问题背景】如图1:在四边形ABCD中,AB=AD,∠BAD=120°,∠B=∠ADC=90°,E、F分别是BC、CD上的点,且∠EAF=60°,试探究图中线段BE、EF、FD之间的数量关系.小王同学探究此问题的方法是:延长FD到点G,使DG=BE,连接AG,先证明△ABE≌△ADG,再证明△AEF≌△AGF,可得出结论,他的结论应是.【探索延伸】如图2,若在四边形ABCD中,AB=AD,∠B+∠D=180°,E、F分别是BC,CD上的点,且∠EAF=12∠BAD,上述结论是否仍然成立,并说明理由.【学以致用】如图3,四边形ABCD是边长为5的正方形,∠EBF=45°,直接写出△DEF的周长.11.(2022秋•南关区校级月考)通过对如图数学模型的研究学习,解决下列问题:[模型呈现]如图1,∠BAD=90°,AB=AD,过点B作BC⊥AC于点C,过点D作DE⊥AC于点E.由∠1+∠2=∠2+∠D=90°,得∠1=∠D.又∠ACB=∠AED=90°,可以推理得到△ABC≌△DAE.进而得到AC =,BC=AE.我们把这个数学模型称为“K字”模型或“一线三等角”模型;[模型应用]如图2,AE⊥AB且AE=AB,BC⊥CD且BC=CD,请按照图中所标注的数据,计算图中实线所围成的图形的面积为.A.50B.62C.65D.68[深入探究]如图3,∠BAD=∠CAE=90°,AB=AD,AC=AE,连接BC,DE,且BC⊥AF于点F,DE与直线AF 交于点G.求证:点G是DE的中点;。
专题03 全等三角形的六种模型全梳理(解析版)-2024年常考压轴题攻略(8年级上册人教版)

专题03全等三角形的六种模型全梳理几何探究类问题一直属于考试压轴题范围,在三角形这一章,压轴题主要考查是证明三角形各种模型,或证明线段数量关系等,接来下我们针对其做出详细分析与梳理。
类型一、倍长中线模型目的:①构造出一组全等三角形;②构造出一组平行线。
将分散的条件集中到一个三角形中。
如图1,ABC 中,若86AB AC ==,,求BC 边上的中线小明在组内经过合作交流,得到了如下的解决方法:如图连接BE .请根据小明的方法思考:(1)如图2,由已知和作图能得到ADC EDB ≌△△A .SSS B .SAS C .AAS D .ASA(2)如图2,AD 长的取值范围是.(2)根据全等三角形的性质得到6AC BE ==,由三角形三边关系得到AB BE AE AB BE -<<+,即可求出17AD <<;(3)延长AD 到点M ,使AD DM =,连接BM ,证明ADC MDB △△≌,得到BM AC CAD M =∠=∠,,由AE EF =得到CAD AFE ∠=∠,进而推出BF BM =,即可证明AC BF =.【详解】解:(1)如图2,延长AD 到点E ,使DE AD =,连接BE .∵AD 为BC 的中线,∴BD CD =,又∵AD DE ADC BDE =∠=∠,,∴()SAS ADC EDB ≌△△,故答案为:B ;(2)解:∵ADC EDB ≌△△,∴6AC BE ==,在ABE 中,AB BE AE AB BE -<<+,∴86286AD -<<+,∴17AD <<,故答案为:C ;(3)证明:延长AD 到点M ,使AD DM =,连接BM ,∵AD 是ABC 中线,∴CD BD =,∵在ADC △和MDB △中,DC DB ADC MDB AD HD =⎧⎪∠=∠⎨⎪=⎩,∴()SAS ADC MDB ≌△△,∴BM AC CAD M =∠=∠,,∵AE EF =,(1)如图1,求证:12BF AD =;(2)将DCE △绕C 点旋转到如图2所示的位置,连接,AE BD ,过C 点作CM ⊥①探究AE 和BD 的关系,并说明理由;②连接FC ,求证:F ,C ,M 三点共线.【答案】(1)见解析(2)①,AE BD AE BD =⊥,理由见解析②见解析【分析】(1)证明≌ACD BCE V V ,得到AD BE =,再根据点F 为BE 中点,即可得证;则:AGB CBD BHG ∠=∠+∠=∠∵CBD EAC ∠=∠,∴90BHG ACB ∠=∠=︒,∴AE BD ⊥,综上:,AE BD AE BD =⊥;②延长CF 至点P ,使PF CF =∵F 为BE 中点,∴BF FE =,∴()SAS BFP EFC ≌,∴,BP CE BPF ECF =∠=∠,∴CE BP ,∴180CBP BCE ∠+∠=︒,∵360180BCE ACD ACB DCE ∠+∠=︒-∠-∠=︒,∴CBP ACD ∠=∠,又,CE CD BP AC BC ===,∴()SAS PBC DCA ≌,∴BCP CAD ∠=∠,延长FC 交AD 于点N ,则:18090BCP ACN ACB ∠+∠=︒-∠=︒,∴90CAD ACN ∠+∠=︒,∴90ANC ∠=︒,∴CN AD ⊥,∵CM AD ⊥,∴点,M N 重合,即:F ,C ,M 三点共线.【点睛】本题考查全等三角形的判定和性质,等腰三角形判定和性质.熟练掌握手拉手全等模型,倍长中线法构造全等三角形,是解题的关键.【变式训练1】如图,ABC 中,BD DC AC ==,E 是DC 的中点,求证:2AB AE =.【答案】见解析【分析】利用中线加倍证DEF CEA △≌△(SAS ),可得DF AC BD ==,FDE C ∠=∠,由DC AC =,可得ADC CAD ∠=∠进而可证ADF ADB ∠=∠.,再证ADB ADF △≌△(SAS )即可.【详解】证明:延长AE 到F ,使EF AE =,连结DF ,∵E 是DC 中点,∴DE CE =,∴在DEF 和CEA 中,DE CE DEF CEA EF EA =⎧⎪∠=∠⎨⎪=⎩,∴DEF CEA △≌△(SAS ),∴DF AC BD ==,FDE C ∠=∠,∵DC AC =,∴ADC CAD ∠=∠,又∵ADB C CAD ∠=∠+∠,ADF FDE ADC ∠=∠+∠,∴ADF ADB ∠=∠,在ADB 和ADF △中,AD AD ADB ADF DB DF =⎧⎪∠=∠⎨⎪=⎩,∴ADB ADF △≌△(SAS ),∴2AB AF AE ==.【点睛】本题考查中线加倍构图,三角形全等判定与性质,等腰三角形性质,掌握中线加倍构图,三角形全等判定与性质,等腰三角形性质是解题关键.【变式训练2】(1)如图1,已知ABC 中,AD 是中线,求证:2AB AC AD +>;(2)如图2,在ABC 中,D ,E 是BC 的三等分点,求证:AB AC AD AE +>+;(3)如图3,在ABC 中,D ,E 在边BC 上,且BD CE =.求证:AB AC AD AE +>+.【答案】(1)见解析;(2)见解析;(3)见解析【分析】(1)利用“倍长中线”法,延长AD ,然后通过全等以及三角形的三边关系证明即可;(2)取DE 中点H ,连接AH 并延长至Q 点,使得AH =QH ,连接QE 和QC ,通过“倍长中线”思想全等证明,进而得到AB =CQ ,AD =EQ ,然后结合三角形的三边关系建立不等式证明即可得出结论;(3)同(2)处理方式一样,取DE 中点M ,连接AM 并延长至N 点,使得AM =NM ,连接NE ,CE ,结合“倍长中线”思想证明全等后,结合三角形的三边关系建立不等式证明即可得出结论.【详解】证:(1)如图所示,延长AD 至P 点,使得AD =PD ,连接CP ,∵AD 是△ABC 的中线,∴D 为BC 的中点,BD =CD ,在△ABD 与△PCD 中,BD CD ADB PDC AD PD =⎧⎪∠=∠⎨⎪=⎩∴△ABD ≌△PCD (SAS ),∴AB =CP ,在△APC 中,由三边关系可得AC +PC >AP ,∴2AB AC AD +>;(2)如图所示,取DE 中点H ,连接AH 并延长至Q 点,使得AH =QH ,连接QE 和QC ,∵H 为DE 中点,D 、E 为BC 三等分点,∴DH =EH ,BD =DE =CE ,∴DH =CH ,在△ABH 和△QCH 中,BH CH BHA CHQ AH QH =⎧⎪∠=∠⎨⎪=⎩,∴△ABH ≌△QCH (SAS ),同理可得:△ADH ≌△QEH ,∴AB =CQ ,AD =EQ ,此时,延长AE ,交CQ 于K 点,∵AC +CQ =AC +CK +QK ,AC +CK >AK ,∴AC +CQ >AK +QK ,又∵AK +QK =AE +EK +QK ,EK +QK >QE ,∴AK +QK >AE +QE ,∴AC +CQ >AK +QK >AE +QE ,∵AB =CQ ,AD =EQ ,∴AB AC AD AE +>+;(3)如图所示,取DE 中点M ,连接AM 并延长至N 点,使得AM =NM ,连接NE ,CE ,∵M 为DE 中点,∴DM =EM ,∵BD =CE ,∴BM =CM ,在△ABM 和△NCM 中,BM CM BMA CMN AM NM =⎧⎪∠=∠⎨⎪=⎩∴△ABM ≌△NCM (SAS ),同理可证△ADM ≌△NEM ,∴AB =NC ,AD =NE ,此时,延长AE ,交CN 于T 点,∵AC +CN =AC +CT +NT ,AC +CT >AT ,∴AC +CN >AT +NT ,又∵AT +NT =AE +ET +NT ,ET +NT >NE ,∴AT +NT >AE +NE ,∴AC +CN >AT +NT >AE +NE ,∵AB =NC ,AD =NE ,∴AB AC AD AE +>+.【点睛】本题考查全等三角形证明问题中辅助线的添加,掌握“倍长中线”的基本思想,以及熟练运用三角形的三边关系是解题关键.【答案】(1)1.5 6.5AE <<;(2)见解析;(3)BE DF EF +=,理由见解析【分析】(1)如图①:将ACD △绕着点D 逆时针旋转180 得到EBD △可得BDE ≅ 得出5BE AC ==,然后根据三角形的三边关系求出AE 的取值范围,进而求得AD 范围;(2)如图②:FDC △绕着点D 旋转180︒得到NDB 可得BND CFD ≅ ,得出BN∴1.5 6.5AD <<;故答案为1.5 6.5AD <<;(2)证明:如图②:FDC △绕着点D 旋转180︒得到NDB∴BND CFD ≅ (SAS ),∴BN CF =,DN DF=∵DE DF⊥∴EN EF =,在BNE 中,由三角形的三边关系得:BE BN EN +>,∴BE CF EF +>;(3)BE DF EF +=,理由如下:如图③,将DCF 绕着点C 按逆时针方向旋转100︒∴△DCF ≌△BCH ,∴100CH CF DCB FCH ∠∠=︒=,=∴HBC D DF BH∠∠==,∵180ABC D ∠+∠︒=∴180HBC ABC ∠+∠︒=,∴点A 、B 、H 三点共线∵100FCH ∠=︒,50FCE ∠=︒,∴50ECH ∠=︒∴FCE ECH ∠∠=,在HCE 和FCE △中,===CF CH ECF ECH CE CE ∠∠⎧⎪⎨⎪⎩,∴HCE FCE ≌ (SAS )∴EH EF =,∵BE BH EH DF BH+==,∴BE DF EF +=.【点睛】本题属于三角形综合题,主要考查对全等三角形的性质和判定、三角形的三边关系定理、旋转的性质等知识点,通过旋转得到构造全等三角形是解答本题的关键.类型二、截长补短模型截长补短法使用范围:线段和差的证明(往往需证2次全等)(1)求证:CD BC DE=+;(2)若75B∠=︒,求E∠的度数.【答案】(1)见解析(2)105︒【分析】(1)在CD上截取CF∵CA平分BCD∠,∴BCA FCA∠=∠.在BCAV和FCA△中,⎧⎪∠⎨⎪⎩,∠=︒BAC60【答案】(1)5.8;(2)4.3【分析】(1)由已知条件和辅助线的作法,证得△ACD≌△ECD,得到由于∠A=2∠B,推出∠DEC=2∠B,等量代换得到∠B=∠EDB形,得出AC =CE =3.6,DE =BE =2.2,相加可得BC 的长;(2)在BA 边上取点E ,使BE =BC =2,连接DE ,得到△DEB ≌△DBC (SAS ),在DA 边上取点F ,使DF =DB ,连接FE ,得到△BDE ≌△FDE ,即可推出结论.【详解】解:(1)如图2,在BC 边上取点E ,使EC =AC ,连接DE .在△ACD 与△ECD 中,AC CE ACD ECD CD CD =⎧⎪∠=∠⎨⎪=⎩,∴△ACD ≌△ECD (SAS ),∴AD =DE ,∠A =∠DEC ,∵∠A =2∠B ,∴∠DEC =2∠B ,∴∠B =∠EDB ,∴△BDE 是等腰三角形;∴BE =DE =AD =2.2,AC =EC =3.6,∴BC 的长为5.8;(2)∵△ABC 中,AB =AC ,∠A =20°,∴∠ABC =∠C =80°,∵BD 平分∠B ,∴∠1=∠2=40°,∠BDC =60°,在BA 边上取点E ,使BE =BC =2,连接DE ,在△DEB 和△DBC 中,12BE BC BD BD =⎧⎪∠=∠⎨⎪=⎩,∴△DEB ≌△DBC (SAS ),∴∠BED =∠C =80°,∴∠4=60°,∴∠3=60°,在DA 边上取点F ,使DF =DB ,连接FE ,同理可得△BDE ≌△FDE ,∴∠5=∠1=40°,BE =EF =2,∵∠A =20°,∴∠6=20°,∴AF =EF =2,∵BD =DF =2.3,∴AD =BD +BC =4.3.【点睛】本题考查了全等三角形的性质与判定,等腰三角形的性质,熟悉这些定理是解决本题的关键.类型三、一线三等角模型应用:①通过证明全等实现边角关系的转化,便于解决对应的几何问题;②与函数综合应用中有利于点的坐标的求解。
全等三角形的构造技巧(2020版)

全等三角形的构造技巧一、利用角平分线,构造全等三角形【方法剖析】因为角平分线本身已经具备全等的三个条件中的两个(角相等和公共边相等),故在处理角平分线问题时,常作以下辅助线构造全等三角形:(1)在角的两边截取两条相等的线段;(2)过角平分线上一点作角两边的垂线;(3)延长角平分线的垂线.(一)在角两边截取相等线段例1.如图,AB ∥CD ,BE 平分∠ABC ,CE 平分∠BCD ,点E 在AD 上,求证:BC =AB +CD.证明:在BC 上截取BF =AB ,连接EF.∵∠ABC 、∠BCD 的平分线交AD 于点E ,∴∠ABE =∠FBE ,∠BCE =∠DCE ,在△ABE 和△FBE 中,⎩⎪⎨⎪⎧AB =FB ,∠ABE =∠FBE ,BE =BE ,∴△ABE ≌△FBE.∴∠BAE =∠BFE.∵AB ∥CD ,∴∠BAE +∠CDE =180°.∴∠BFE +∠CDE =180°.∵∠BFE +∠CFE =180°,∴∠CFE =∠CDE.在△FCE 和△DCE 中,⎩⎪⎨⎪⎧∠CFE =∠CDE ,∠FCE =∠DCE ,CE =CE ,∴△FCE ≌△DCE.∴CF =CD.∴BC =BF +CF =AB +CD.练习:1.如图,BC >AB,BD 平分∠ABC 且AD=DC,求证: ∠A+∠C=1800. 分析:在边BC 上截取AB=BE,连接DE,则△BAD ≌△BED,这样,AD 转移到了DE 的位置,∠A 与∠C 就建立了联系。
也可看成 △BAD 翻折到了△BED 的位置。
(二)利用角平分线的性质,过角平分线上一点作角两边的垂线例1.如图,∠AOB =90°,将三角尺的直角顶点落在∠AOB 的平分线上的任意一点P ,使三角尺的两条直角边与∠AOB 的两边分别相交于点E 、F ,试证PE =PF.图1 图2分析:如图1,因为OC 是角平分线,所以本题可以过P 点作PM ⊥OA 于M ,PN ⊥OB 于N ,不难发现只要证明△PME ≌△PNF ,即可得到PE =PF ,根据∠PME =∠PNF =90°、PM =PN(角平 B A M N E F O P BA E F O P G AB C E DA B C E F D 分线性质)、∠MPE =∠NPF 这三个条件,利用ASA 可以证明△PME ≌△PNF 。
2022年人教版八年级上册数学同步培优小专题(六) 全等三角形中的“一线三等角”模型

小专题(六) 全等三角形中的“一线三等角”模型
变式3 钝角型(△APC≌△BDP)
● 模型展示
-8-
小专题(六) 全等三角形中的“一线三等角”模型
3.如图,已知B,C,D三点共线,∠ABC=∠ACE=∠CDE,AC= CE. 求证:BD=AB+DE.
-9-
小专题(六) 全等三角形中的“一线三等角”模型
-5-
小专题(六) 全等三角形中的“一线三等角”模型
变式2 直角型(△ABC≌△CDE)
● 模型展示
-6-
小专题(六) 全等三角形中的“一线三等角”模型
2.如图,∠ACB=90°,AC=BC,AE⊥CE于点E,BD⊥CE于点D. 若AE=5 cm,BD=2 cm,则DE的长是( C ) A.8 cm B.5 cm C.3 cm D.2 cm
-4-
小专题(六) 全等三角形中的“一线三等角”模型
解:由题可知∠1=∠2=∠BAC=50°, ∴∠BAD+∠CAE=50°,∠BAD+∠ABD=50°, ∴∠CAE=∠ABD.又 ∵∠ADB=∠AEC,AB=AC, ∴△ACE≌△BAD(AAS),∴S△ACE=S△BAD, ∴S△ACE+S△BDF=S△BAD+S△BDF=S△ABF. ∵CF=2BF,∴S△ABF=13S△ABC=5, ∴S△ACE+S△BDF=5.
证明:∵∠BCE是△CDE的外角, ∴∠BCE=∠CDE+∠CED, 即∠ACB+∠ACE=∠CDE+∠CED. 又∵∠ACE=∠CDE,∴∠ACB=∠CED. ∵AC=CE,∴△ABC≌△CDE(AAS), ∴AB=CD,BC=DE, ∴BD=BC+CD=AB+DE.
-10-
变式1 锐角型(△APC≌△BDP)
● 模型线三等角”模型
三角形全等、相似及综合应用模型-2024年中考数学答题技巧与模板构建(解析版)

三角形全等、相似及综合应用模型题型解读|模型构建|通关试练三角形的相关知识是解决后续很多几何问题的基础,所以是中考考试的必考知识点。
在考察题型上,三角形基础知识部分多以选择或者填空题形式,考察其三边关系、内角和/外角和定理、“三线”基本性质等。
特殊三角形的性质与判定也是考查重点,年年都会考查,最为经典的“手拉手”模型就是以等腰三角形为特征总结的,且等腰三角形单独出题的可能性还是比较大。
直角三角形的出题类型可以是选择填空题这类小题,也可以是各类解答题,以及融合在综合压轴题中,作为问题的几何背景进行拓展延伸。
模型01与三角形有关的线段应用高(AD )中线(AD )角平分线(AD )中位线(DE )∠ADB =∠ADC =90°BD =CDS △ABD =S △ADCC ∆ACD -C ∆ABD =AC -AB ∠BAD =∠DAC =12∠BAC AD =DB AE =EC DE =12BC DE ∥BC 模型02与三角形有关的角的应用(1)三角形的内角:(1)三角形内角的概念:三角形内角是三角形三边的夹角.每个三角形都有三个内角,且每个内角均大于0°且小于180°.(2)三角形内角和定理:三角形内角和是180°.(3)三角形内角和定理的证明证明方法,不唯一,但其思路都是设法将三角形的三个内角移到一起,组合成一个平角.在转化中借助平行线.(4)三角形内角和定理的应用主要用在求三角形中角的度数.①直接根据两已知角求第三个角;②依据三角形中角的关系,用代数方法求三个角;③在直角三角形中,已知一锐角可利用两锐角互余求另一锐角.(2)三角形的外角:(1)三角形外角的定义:三角形的一边与另一边的延长线组成的角,叫做三角形的外角.三角形共有六个外角,其中有公共顶点的两个相等,因此共有三对.(2)三角形的外角性质:①三角形的外角和为360°.②三角形的一个外角等于和它不相邻的两个内角的和.③三角形的一个外角大于和它不相邻的任何一个内角.(3)若研究的角比较多,要设法利用三角形的外角性质②将它们转化到一个三角形中去.(4)探究角度之间的不等关系,多用外角的性质③,先从最大角开始,观察它是哪个三角形的外角.模型03三角形全等的判定及应用(1)全等三角形的定义:全等的图形必须满足:(1)形状相同;(2)大小相等能够完全重合的两个三角形叫做全等三角形。
三角形全等的判定(6种题型)-2023年新八年级数学核心知识点与常见题型(浙教版)(解析版)
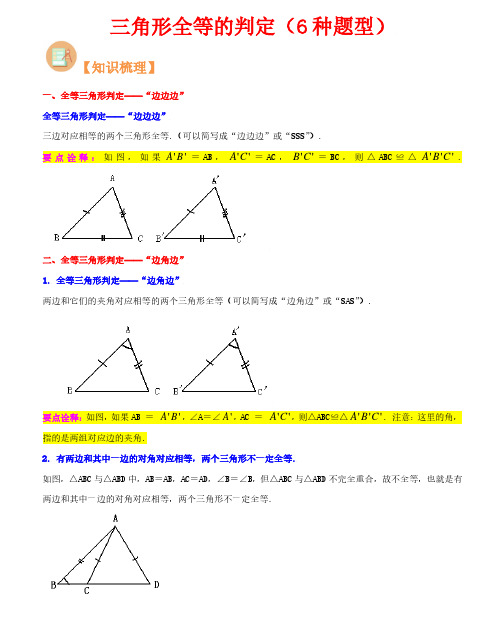
三角形全等的判定(6种题型)【知识梳理】一、全等三角形判定——“边边边”全等三角形判定——“边边边”三边对应相等的两个三角形全等.(可以简写成“边边边”或“SSS ”).要点诠释:如图,如果''A B =AB ,''A C =AC ,''B C =BC ,则△ABC ≌△'''A B C .二、全等三角形判定——“边角边”1. 全等三角形判定——“边角边”两边和它们的夹角对应相等的两个三角形全等(可以简写成“边角边”或“SAS ”).要点诠释:如图,如果AB = ''A B ,∠A =∠'A ,AC = ''A C ,则△ABC ≌△'''A B C . 注意:这里的角,指的是两组对应边的夹角.2. 有两边和其中一边的对角对应相等,两个三角形不一定全等.如图,△ABC 与△ABD 中,AB =AB ,AC =AD ,∠B =∠B ,但△ABC 与△ABD 不完全重合,故不全等,也就是有两边和其中一边的对角对应相等,两个三角形不一定全等.三、垂直平分线:1.定义:垂直于一条线段,并且平分这条线段的直线叫做这条线段的垂直平分线,简称中垂线.2.性质定理:线段垂直平分线上的点到线段两端的距离相等四、全等三角形判定——“角边角”全等三角形判定——“角边角”两角和它们的夹边对应相等的两个三角形全等(可以简写成“角边角”或“ASA ”).要点诠释:如图,如果∠A =∠'A ,AB =''A B ,∠B =∠'B ,则△ABC ≌△'''A B C .五、全等三角形判定——“角角边” 1.全等三角形判定——“角角边”两个角和其中一个角的对边对应相等的两个三角形全等(可以简写成“角角边”或“AAS ”)要点诠释:由三角形的内角和等于180°可得两个三角形的第三对角对应相等.这样就可由“角边角”判定两个三角形全等,也就是说,用角边角条件可以证明角角边条件,后者是前者的推论.2.三个角对应相等的两个三角形不一定全等.如图,在△ABC 和△ADE 中,如果BC ,那么∠ADE =∠B ,∠AED =∠C ,又∠A =∠A ,但△ABC 和△ADE 不全等.这说明,三个角对应相等的两个三角形不一定全等.六、角平分线的性质定理:角平分线上的点到角两边的距离相等.【考点剖析】题型一、全等三角形的判定——“边边边”例1、已知:如图,△RPQ 中,RP =RQ ,M 为PQ 的中点.求证:RM 平分∠PRQ .【思路点拨】由中点的定义得PM =QM ,RM 为公共边,则可由SSS 定理证明全等.【答案与解析】证明:∵M 为PQ 的中点(已知),∴PM =QM在△RPM 和△RQM 中,()(),,RP RQ PM QM RM RM ⎧=⎪=⎨⎪=⎩已知公共边 ∴△RPM ≌△RQM (SSS ).∴ ∠PRM =∠QRM (全等三角形对应角相等).即RM 平分∠PRQ.【总结升华】在寻找三角形全等的条件时有的可以从图中直接找到,如:公共边、公共角、对顶角等条件隐含在题目或图形之中. 用全等三角形的性质和判定.【变式】已知:如图,AD =BC ,AC =BD.试证明:∠CAD =∠DBC.【答案】证明:连接DC ,在△ACD 与△BDC 中()AD BC AC BDCD DC ⎧=⎪=⎨⎪=⎩公共边 ∴△ACD≌△BDC(SSS )∴∠CAD =∠DBC (全等三角形对应角相等)【变式2】、如图,在△ABC 和△ADE 中,AB =AC ,AD =AE ,BD =CE ,求证:∠BAD =∠CAE.【答案与解析】证明:在△ABD 和△ACE 中,AB AC AD AE BD CE =⎧⎪=⎨⎪=⎩∴△ABD ≌△ACE (SSS )∴∠BAD =∠CAE (全等三角形对应角相等).【总结升华】把证明一对角或线段相等的问题,转化为证明它们所在的两个三角形全等,综合应用全等三角形的判定和性质. 要证∠BAD =∠CAE ,先找出这两个角所在的三角形分别是△BDA 和△CAE ,然后证这两个三角形全等.题型二、全等三角形的判定——“边角边”例2、已知:如图,AB =AD ,AC =AE ,∠1=∠2.求证:BC =DE .【思路点拨】由条件AB =AD ,AC =AE ,需要找夹角∠BAC 与∠DAE ,夹角可由等量代换证得相等.【答案与解析】证明: ∵∠1=∠2∴∠1+∠CAD =∠2+∠CAD ,即∠BAC =∠DAE在△ABC 和△ADE 中AB AD BAC DAE AC AE =⎧⎪∠=∠⎨⎪=⎩∴△ABC ≌△ADE (SAS )∴BC =DE (全等三角形对应边相等)【总结升华】证明角等的方法之一:利用等式的性质,等量加等量,还是等量.【变式】如图,将两个一大、一小的等腰直角三角尺拼接 (A 、B 、D 三点共线,AB =CB ,EB =DB ,∠ABC =∠EBD =90°),连接AE 、CD ,试确定AE 与CD 的位置与数量关系,并证明你的结论.【答案】AE =CD ,并且AE ⊥CD证明:延长AE 交CD 于F ,∵△ABC 和△DBE 是等腰直角三角形∴AB =BC ,BD =BE在△ABE 和△CBD 中90AB BC ABE CBD BE BD =⎧⎪∠=∠=︒⎨⎪=⎩∴△ABE ≌△CBD (SAS )∴AE =CD ,∠1=∠2又∵∠1+∠3=90°,∠3=∠4(对顶角相等)∴∠2+∠4=90°,即∠AFC =90°∴AE ⊥CD例3、如图,AD 是△ABC 的中线,求证:AB +AC >2AD .【思路点拨】延长AD 到点E ,使AD =DE ,连接CE .通过证全等将AB 转化到△CEA 中,同时也构造出了2AD .利用三角形两边之和大于第三边解决问题.【答案与解析】证明:如图,延长AD 到点E ,使AD =DE ,连接CE .在△ABD 和△ECD 中,AD DE ADB EDC BD CD ⎧⎪∠∠⎨⎪⎩===.∴△ABD ≌△ECD (SAS ).∴AB =CE .∵AC +CE >AE ,∴AC +AB >AE =2AD .即AC +AB >.【总结升华】证明边的大小关系主要有两个思路:(1)两点之间线段最短;(2)三角形的两边之和大于第三边.要证明AB +AC >2AD ,如果归到一个三角形中,边的大小关系就是显然的,因此需要转移线段,构造全等三角形是转化线段的重要手段.可利用旋转变换,把△ABD 绕点D 逆时针旋转180°得到△CED ,也就把AB 转化到△CEA 中,同时也构造出了2AD .若题目中有中线,倍长中线,利用旋转变换构造全等三角形是一种重要方法.例4、已知,如图:在△ABC 中,∠B =2∠C ,AD ⊥BC ,求证:AB =CD -BD .【思路点拨】在DC 上取一点E ,使BD =DE ,则△ABD ≌△AED ,所以AB =AE ,只要再证出EC =AE 即可.【答案与解析】证明:在DC 上取一点E ,使BD =DE∵ AD ⊥BC ,∴∠ADB =∠ADE在△ABD 和△AED 中,BD DE ADB=ADE AD AD ⎧⎪⎨⎪⎩=∠∠=∴△ABD ≌△AED (SAS ).∴AB =AE ,∠B =∠AED .又∵∠B =2∠C =∠AED =∠C +∠EAC .∴∠C =∠EAC .∴AE =EC .∴AB =AE =EC =CD —DE =CD —BD .【总结升华】此题采用截长或补短方法.上升到解题思想,就是利用翻折变换,构造的全等三角形,把条件集中在基本图形里面,从而使问题加以解决.如图,要证明AB =CD -BD ,把CD -BD 转化为一条线段,可利用翻折变换,把△ABD 沿AD 翻折,使线段BD 运动到DC 上,从而构造出CD -BD ,并且也把∠B 转化为∠AEB ,从而拉近了与∠C 的关系.【变式】已知,如图,在四边形ABCD 中,AC 平分∠BAD ,CE ⊥AB 于E ,并且AE =12(AB +AD ), 求证:∠B +∠D =180°. AE D CB【答案】证明:在线段AE 上,截取EF =EB ,连接FC ,∵CE ⊥AB ,∴∠CEB =∠CEF =90°在△CBE 和△CFE 中,CEB CEF EC =EC EB EF =⎧⎪∠=∠⎨⎪⎩∴△CBE 和△CFE (SAS )∴∠B =∠CFE∵AE =12(AB +AD ),∴2AE = AB +AD ∴AD =2AE -AB∵AE =AF +EF ,∴AD =2(AF +EF )-AB =2AF +2EF -AB =AF +AF +EF +EB -AB =AF +AB -AB ,即AD =AF在△AFC 和△ADC 中(AF AD FAC DAC AC AC =⎧⎪∠=∠⎨⎪=⎩角平分线定义)∴△AFC ≌△ADC (SAS )∴∠AFC =∠D∵∠AFC +∠CFE =180°,∠B =∠CFE.∴∠AFC +∠B =180°,∠B +∠D =180°.题型三、全等三角形的判定——“角边角”例5、已知:如图,E ,F 在AC 上,AD ∥CB 且AD =CB ,∠D =∠B .求证:AE =CF .【答案与解析】证明:∵AD ∥CB∴∠A =∠C在△ADF 与△CBE 中A C AD CB D B ∠=∠⎧⎪=⎨⎪∠=∠⎩∴△ADF ≌△CBE (ASA )∴AF =CE ,AF +EF =CE +EF故得:AE =CF【总结升华】利用全等三角形证明线段(角)相等的一般方法和步骤如下:(1)找到以待证角(线段)为内角(边)的两个三角形;(2)证明这两个三角形全等;(3)由全等三角形的性质得出所要证的角(线段)相等.【变式】(2022•长安区一模)已知:点B 、E 、C 、F 在一条直线上,AB ∥DE ,AC ∥DF ,BE =CF .求证:△ABC ≌△DEF .【分析】先利用平行线的性质得到∠B=∠DEF,∠ACB=∠F,再证明BC=EF,然后根据“ASA”可判断△ABC≌△DEF.【解答】证明:∵AB∥DE,∴∠B=∠DEF,∵AC∥DF,∴∠ACB=∠F,∵BE=CF,∴BE+EC=CF+EC,即BC=EF,在△ABC和△DEF中,{∠B=∠DEF BC=EF∠ACB=∠F,∴△ABC≌△DEF(ASA).5种判定方法是解决问题的关键.选用哪一种判定方法,取决于题目中的已知条件.例6、如图,G是线段AB上一点,AC和DG相交于点E.请先作出∠ABC的平分线BF,交AC于点F;然后证明:当AD∥BC,AD=BC,∠ABC=2∠ADG时,DE=BF.【思路点拨】通过已知条件证明∠DAC=∠C,∠CBF=∠ADG,则可证△DAE≌△BCF【答案与解析】证明:∵AD∥BC,∴∠DAC=∠C∵BF平分∠ABC∴∠ABC=2∠CBF∵∠ABC=2∠ADG∴∠CBF=∠ADG在△DAE 与△BCF 中⎪⎩⎪⎨⎧∠=∠=∠=∠C DAC BCAD CBF ADG ∴△DAE≌△BCF(ASA )∴DE=BF【总结升华】利用全等三角形证明线段(角)相等的一般方法和步骤如下:(1)找到以待证角(线段)为内角(边)的两个三角形;(2)证明这两个三角形全等;(3)由全等三角形的性质得出所要证的角(线段)相等.【变式】已知:如图,在△MPN 中,H 是高MQ 和NR 的交点,且MQ =NQ .求证:HN =PM.【答案】证明:∵MQ 和NR 是△MPN 的高,∴∠MQN =∠MRN =90°,又∵∠1+∠3=∠2+∠4=90°,∠3=∠4∴∠1=∠2在△MPQ 和△NHQ 中,12MQ NQ MQP NQH ∠=∠⎧⎪=⎨⎪∠=∠⎩∴△MPQ ≌△NHQ (ASA )∴PM =HN题型四、全等三角形的判定——“角角边”例7.(2021秋•苏州期末)如图,在四边形ABCD 中,E 是对角线AC 上一点,AD ∥BC ,∠ADC =∠ACD ,∠CED +∠B =180°.求证:△ADE ≌△CAB .【分析】由等角对等边可得AC=AD,再由平行线的性质可得∠DAE=∠ACB,由∠CED+∠B=180°,∠CED+∠AED=180°,得∠AED=∠B,从而利用AAS可判定△ADE≌△CAB.【解答】证明:∵∠ADC=∠ACD,∴AD=AC,∵AD∥BC,∴∠DAE=∠ACB,∵∠CED+∠B=180°,∠CED+∠AED=180°,∴∠AED=∠B,在△ADE与△CAB中,{∠DAE=∠ACB ∠AED=∠BAD=AC,∴△ADE≌△CAB(AAS).【点评】本题主要考查全等三角形的判定,解答的关键是由已知条件得出相应的角或边的关系.例8、已知:如图,AB⊥AE,AD⊥,∠E=∠B,DE=CB.求证:AD=AC.【思路点拨】要证AC=AD,就是证含有这两个线段的三角形△BAC≌△EAD.【答案与解析】证明:∵AB⊥AE,AD⊥AC,∴∠CAD=∠BAE=90°∴∠CAD+∠DAB=∠BAE+∠DAB ,即∠BAC=∠EAD在△BAC和△EAD中BAC EAD B E CB=DE ∠=∠⎧⎪∠=∠⎨⎪⎩∴△BAC ≌△EAD (AAS )∴AC =AD【总结升华】我们要善于把证明一对角或线段相等的问题,转化为证明它们所在的两个三角形全等. 题型五:线段的垂直平分线 例9.(2023秋·浙江杭州·八年级校考开学考试)如图所示,在ABC 中,8AC =,5BC =,AB 的垂直平分线DE 交AB 于点D ,交AC 于点E ,则BCE 的周长为( )A .13B .18C .10.5D .21【答案】A 【分析】根据线段垂直平分线的性质得到AE BE =,再将BCE 的周长转化为AC BC +的长,即可求解.【详解】解:DE 是AB 的垂直平分线,∴AE BE =,∴BCE 的周长为BE EC BC AE EC BC AC BC ++=++=+,8AC =,5BC =,∴BCE 的周长为8513AC BC +=+=,故选:A .【点睛】本题主要考查的是线段垂直平分线的性质,掌握线段垂直平分线的性质是解题的关键.【变式1】(2022秋·浙江温州·八年级校考期中)如图,点D 是ABC 边AC 的中点,过点D 作AC 的垂线交BC 于点E ,已知6AC =,ABC 的周长为14,则ABE 的周长是( )A .6B .14C .8D .20【答案】C 【分析】由题意可知:ED 垂直平分AC ,故EA EC =,结合6AC =,ABC 的周长为14,即可得出答案.【详解】解:∵点D 是ABC 边AC 的中点, ED AC ⊥,∴ED 垂直平分AC ,∴EA EC =,∵6AC =,ABC 的周长为14,∴1468AB BC +=−=,∴8AB BC AB BE EC AB BE AE +=++=++=,∴ABE 的周长是8.故选:C .【点睛】此题考查了垂直平分线的性质和判定,掌握垂直平分线的性质和判定是解题的关键.【答案】C 【分析】根据垂直平分线的性质可知,到A ,B ,C 表示三个居民小区距离相等的点,是AC ,BC 两边垂直平分线的交点,由此即可求解.【详解】解:如图所示,分别作AC ,BC 两边垂直平分线MN ,PQ 交于点O ,连接OA,OB,OC,∵MN,PQ是AC,BC两边垂直平分线,==,∴OA OB OC∴点O是到三个小区的距离相等的点,即点O是AC,BC两边垂直平分线的交点,故选:C.【点睛】本题主要考查垂直平分线的性质,掌握垂直平分线的性质是解题的关键.八年级专题练习)如图,在ABC中,是ABC外的一点,且【分析】根据到线段两端距离相等的点在线段的垂直平分线上,即可证明A、D都在BC的垂直平分线上,由此即可证明结论.AB AC,【详解】证明:∵=∴点A在BC的垂直平分线上,BD CD,∵=∴点D在BC的垂直平分线上,∴A、D都在BC的垂直平分线上,∴AD垂直平分BC.【点睛】本题主要考查了线段垂直平分线的判定,熟知线段垂直平分线的判定条件是解题的关键.【变式】.(2022秋·浙江·八年级专题练习)如图,点E是△ABC的边AB的延长线上一点,∠BCE=∠A+∠ACB,求证:点E在BC的垂直平分线上.【分析】由三角形的外角性质得到∠EBC=∠A+∠ACB,结合已知推出∠BCE=∠EBC,得到BE=CE,即可得到结论.【详解】证明:∵∠BCE=∠A+∠ACB,∠EBC=∠A+∠ACB,∴∠BCE=∠EBC,∴BE=CE,∴点E在BC的垂直平分线上.【点睛】本题考查了三角形的外角性质,线段垂直平分线的判定,用到的知识点:到线段两端点的距离相等的点在线段的垂直平分线上.题型六:角平分线【答案】A【分析】根据角平分线上的点到两边的距离相等即可解答.【详解】根据题意要使集贸市场到三条公路的距离相等即集贸市场应建在三个角的角平分线的交点.故本题选A .【点睛】本题考查了角平分线的性质,熟记角平分线的性质是解答本题的关键. 的中点,ABC ,则BED 的面积为( 【答案】C【分析】作DF AC ⊥于F ,DM AB ⊥于点M ,根据角平分线的性质求出DM ,根据三角形的面积公式计算即可.【详解】解:作DF AC ⊥于F ,DM AB ⊥于点MAD 是ABC 的角平分线DF AC ⊥于F ,DM AB ⊥,112122AC DF AB DM ∴⋅+⋅=,112122AC DM AB DM ⋅+⋅=∴即:3421DM DM +=得3DM =8AB =, E 是AB 的中点,142BE AB ∴== 1143622BEDS BE DM ∴=⋅=⨯⨯= 故选:C .【点睛】本题考查了角平分线上的点到角的两边距离相等的性质,三角形的面积,熟记性质并利用三角形的面积列出方程是解题的关键. 例12.(2022秋·浙江·八年级专题练习)已知:如图,90B C ∠=∠=,M 是BC 的中点,DM 平分ADC ∠.(1)若连接AM ,则AM 是否平分BAD ∠?请你证明你的结论;(2)线段DM 与AM 有怎样的位置关系?请说明理由.【答案】(1)AM 平分BAD ∠,证明见解析(2)DM AM ⊥,理由见解析【分析】(1)过点M 作ME AD ⊥,垂足为E ,证明ME MC MB ==即可得证.(2)利用两直线平行,同旁内角互补,证明1390∠+∠=.【详解】(1)AM 平分BAD ∠,理由为:证明:过点M 作ME AD ⊥,垂足为E ,∵DM 平分ADC ∠,∴12∠=∠,∵ME AD ⊥,MC CD ⊥∴MC ME =(角平分线上的点到角两边的距离相等),又∵MC MB =,∴ME MB =,∵MB AB ⊥,ME AD ⊥,∴AM 平分BAD ∠(到角的两边距离相等的点在这个角的平分线上).(2)DM AM ⊥,理由如下:∵90B C ∠=∠=,∴,DC CB AB CB ⊥⊥,∴DC AB ∥(垂直于同一条直线的两条直线平行),∴180DAB CDA ∠+∠=(两直线平行,同旁内角互补)又∵111,322CDA DAB ∠=∠∠=∠(角平分线定义) ∴2123180∠+∠=,∴1390∠+∠=,∴90AMD ∠=.即DM AM ⊥.【点睛】本题考查了角平分线的性质定理和判定定理,平行线的性质,熟练掌握以上的知识是解题的关键. 【变式1】(2023秋·浙江台州·八年级统考期末)如图 90B C ∠=∠=︒,E 为BC 上一点,AE 平分BAD ∠,DE 平分CDA ∠.(1)求AED ∠的度数;(2)求证:E 是BC 的中点.【答案】(1)90︒(2)见解析.【分析】(1)利用已知条件可以得到180BAD CDA ∠+∠=︒,想要求AED ∠的度数,只需要根据三角形内角和定理和角平分线的性质即可得到结论.(2)过点E 做EF AD ⊥,根据角平分线上的点到角的两边距离相等即可得结论.【详解】(1)解:∵90B C ∠=∠=︒,∴DC AB ∥,∴180BAD CDA ∠+∠=︒,∵AE 平分BAD ∠,DE 平分CDA ∠, ∴12EAD BAD ∠=∠,12EDA CDA ∠=∠, ∴1()902EAD EDA BAD CDA ∠+∠=∠+∠=︒,∴180()90AED EAD EDA ∠=︒−∠+∠=︒;(2)证明:过点E 作EF AD ⊥于点F ,∵AE 平分BAD ∠,90B Ð=°,EF AD ⊥,∴EF EB =.∵DE 平分CDA ∠,90C ∠=︒,EF AD ⊥,∴EF EC =.∴EB EC =,即E 是BC 的中点.【点睛】本题考查了平行线的判定与性质,以及角平分线上的点到角两边距离相等的性质,熟记性质和定理并做出辅助线是解题的关键.【变式2】.(2022秋·浙江杭州·八年级校考期中)如图,在ABC 外作两个大小不同的等腰直角三角形,其中90DAB CAE ∠=∠=︒,AB AD =,AC AE =.连接DC 、BE 交于F 点.(1)求证:DAC BAE ≌△△; (2)直线DC 、BE 是否互相垂直,试说明理由;(3)求证:AF 平分DFE ∠.【答案】(1)见解析(2)DC BE ⊥,理由见解析(3)见解析【分析】(1)由题意可得AD AB =,AC AE =,由90DAB CAE ∠=∠=︒,可得到DAC BAE ∠=∠,从而可证DAC BAE ≌△△;(2)由(1)可得ACD AEB ∠=∠,再利用直角三角形的性质及等量代换即可得到结论;(3)作AM DC ⊥于M ,AN BE ⊥于N ,利用全等三角形的面积相等及角平分线的判定即可证得结论.【详解】(1)证明:∵90DAB CAE ∠=∠=︒,∴DAB BAC CAE BAC ∠+∠=∠+∠,即DAC BAE ∠=∠,又∵AD AB =,AC AE =,∴()SAS DAC BAE ≌△△;(2)解:DC BE ⊥,理由如下;∵DAC BAE ≌△△, ∴ACD AEB ∠=∠,∵90AEB AOE ∠+∠= ,AOE FOC ∠=∠,∴90FOC ACD ∠+∠=,∴90EFC ∠=,∴DC BE ⊥;(3)证明:作AM DC ⊥于M ,AN BE ⊥于N ,∵DAC BAE ≌△△, ∴DAC BAE S S ∆∆=,DC BE =, ∴1122DC AM BE AN ⋅=⋅,∴AM AN =,∴AF 平分DFE ∠.【点睛】本题主要考查全等三角形的判定和性质,及直角三角形的性质,角平分线的判定,熟练掌握判定和性质是解决本题的关键.【变式3】(2023春·浙江金华·八年级浙江省义乌市后宅中学校考阶段练习)已知:OP 平分MON ∠,点A ,B 分别在边OM ,ON 上,且180OAP OBP ∠∠+=︒.(1)如图1,当90OAP ∠=︒时,求证:OA OB =;(2)如图2,当90OAP ∠<︒时,作PC OM ⊥于点C .求证:①PA PB =;②请直接写出OA ,OB ,AC 之间的数量关系 .【答案】(1)见解析(2)①见解析;②2OA OB AC −=【分析】(1)证明()AAS OPA OPB ≌,即可得证;(2)①作PD ON ⊥于点D ,证明()AAS PAC PBD ≌,即可得证; ②证明()AAS OCP ODP ≌,得出OD =,根据AC BD =,即可得证.【详解】(1)证明:180OAP OBP ∠∠+=︒,且90OAP ∠=︒,90OAP OBP ∠∠∴==︒,OP 平分MON ∠,POA POB ∠∠∴=,OP OP =,()AAS OPA OPB ∴≌,OA OB ∴=;(2)证明:①如图2,作PD ON ⊥于点D ,PC OM ⊥于点C ,PC PD ∴=,90PCA PDB OCP ∠∠∠===︒,180OAP OBP ∠∠+=︒,180DBP OBP ∠∠+=︒,OAP DBP ∠∠∴=,在PAC 和PBD 中,CAP DBP PCA PDBPC PD ∠=∠⎧⎪∠=∠⎨⎪=⎩, ()AAS PAC PBD ∴≌, PA PB ∴=;②结论:2OA OB AC −=.理由:在OCP 和ODP 中,OCP ODP COP DOP OP OP ∠=∠⎧⎪∠=∠⎨⎪=⎩,()AAS OCP ODP ∴≌,OC OD ∴=,OA AC OB BD ∴−=+,AC BD =,2OA OB AC BD AC ∴−=+=.故答案为:2OA OB AC −=.【点睛】本题考查了角平分线的性质,全等三角形的性质与判定,掌握全等三角形的性质与判定是解题的关键.【过关检测】一、单选题 1.(2022秋·浙江·八年级专题练习)如图,在ABC 中,90A ∠=︒,点D 是边AC 上一点,3DA =,若点D 到BC 的距离为3,则下列关于点D 的位置描述正确的是( )A .点D 是AC 的中点B .点D 是B ∠平分线与AC 的交点 C .点D 是BC 垂直平分线与AC 的交点D .点D 与点B 的距离为5【答案】B 【分析】作DE BC ⊥于E ,连接BD ,利用角平分线的判定定理可证明BD 是ABC ∠的角平分线,即可作答.【详解】解:如图所示:作DE BC ⊥于E ,连接BD ,∵3DA =,点D 到BC 的距离为3,∴=AD DE ,∵90A ∠=︒,∴DA BA ⊥,∵DE BC ⊥,∴BD 是ABC ∠的角平分线,即点D 是ABC ∠的角平分线与AC 的交点,故B 项正确;其余选项,利用现有条件均无法得出,故选:B .【点睛】本题主要考查了角平分线的判定定理,作出辅助线,证明BD 是ABC ∠的角平分线,是解答本题的关键. 2.(2023·浙江·九年级专题练习)如图,已知BF DE =,AB ∥DC ,要使ABF CDE ≅△△,添加的条件可以是( )A.BE DF =B .AF CE =C .AB CD = D .B D ∠=∠【答案】C 【分析】根据AB ∥DC ,可得B D ∠=∠,又BF DE =,所以添加AB CD =,根据SAS 可证ABF CDE ≅△△.【详解】解:应添加AB DC =,理由如下:AB ∥DC ,B D ∴∠=∠.在ABF △和CDE 中,AB CD B DBF DE =⎧⎪∠=∠⎨⎪=⎩,(SAS)ABF CDE ∴≅,故选:C .【点睛】本题主要考查了平行线的性质以及全等三角形的判定,熟练掌握全等三角形的判定是解题的关键.3.(2023·浙江金华·统考二模)如图,ABC 和DEF 中,AB DE ∥,A D ∠=∠,点B ,E ,C ,F 共线,添加一个条件,不能判断ABC DEF ≌△△的是( )A .AB DE =B .ACB F ∠=∠C .BE CF =D .AC DF =【答案】B 【分析】根据AB DE ∥可得B DEF ∠=∠,加上A D ∠=∠,可知ABC 和DEF 中两组对角相等,因此一组对边相等时,即可判断ABC DEF ≌△△. 【详解】解:AB DE ∥,∴B DEF ∠=∠, 又A D ∠=∠,∴ABC 和DEF 中两组对角相等,当AB DE =时,根据ASA 可证ABC DEF ≌△△,故A 选项不合题意; 当ACB F ∠=∠时,ABC 和DEF 中,三组对角相等,不能判断ABC DEF ≌△△,故B 选项符合题意; 当BE CF =时,BC EF =,根据AAS 可证ABC DEF ≌△△,故C 选项不合题意; 当AC DF =时,根据AAS 可证ABC DEF ≌△△,故D 选项不合题意; 故选B .【点睛】本题考查添加条件使三角形全等,解题的关键是熟练掌握全等三角形的各种判定方法..ABC 的三条中线的交点.ABC 三边的垂直平分线的交点.ABC 三条角平分线的交点.ABC 三条高所在直线的交点【答案】C【分析】角平分线上的点到角的两边的距离相等,由此可解.【详解】解:要使凉亭到草坪三条边的距离相等,∴凉亭应在ABC 三条角平分线的交点处.故选C .【点睛】本题考查了角平分线的性质,解题的关键是注意区分三角形中线的交点、高的交点、垂直平分线的交点以及角平分线的交点之间的区别. 5.(2020秋·浙江·八年级期末)如图,AD 是ABC 中BAC ∠的平分线,DE AB ⊥交AB 于点E ,DF AC ⊥交AC 于点F ,若7ABC S =△,2DE =,4AB =,则AC 的长为( )A .3B .4C .5D .6【答案】A 【分析】先根据角平分线的性质得到2DF DE ==,再利用三角形面积公式得到11242722AC ⨯⨯+⨯⨯=,然后解关于AC 的方程即可.【详解】解:∵AD 是BAC ∠的平分线,DE AB ⊥,DF AC ⊥,2DE =,∴2DF DE ==,∵7ABC S =△,4AB =,又∵ABD ACD ABC S S S +=△△△,∴111124272222AB DE DF AC AC ⋅+⋅=⨯⨯+⨯⨯=,∴3AC =.故选:A .【点睛】本题考查角平分线的性质:角的平分线上的点到角的两边的距离相等.理解和掌握角平分线的性质是解题的关键.本题也考查了三角形的面积及等积变换.6.(2022秋·浙江·八年级专题练习)如图,用B C ∠=∠,12∠=∠,直接判定ABD ACD ≌△△的理由是( )A .AASB .SSSC .ASAD .SAS【答案】A 【分析】根据三角形全等的判定方法判定即可.【详解】解:在ABD △和ACD 中,12B CAD AD ∠=∠⎧⎪∠=∠⎨⎪=⎩, ∴()AAS ABD ACD ≌,故A 正确. 故选:A .【点睛】本题主要考查三角形全等的判定,解题的关键是掌握证明全等三角形的几种证明方法:AAS 、ASA 、SSS 、SAS 、HL .A .2B .【答案】C 【分析】由FC AB ∥,得F ADE ∠=∠,FCE A ∠=∠,即可根据全等三角形的判定定理“AAS”证明CFE ADE ≅,则4CF AD AB BD ==−=.【详解】解:FC AB ∥,F ADE ∴∠=∠,FCE A ∠=∠,在CFE 和ADE V 中,F ADE FCE AFE DE ∠=∠⎧⎪∠=∠⎨⎪=⎩,()AAS CFE ADE ∴≅, CF AD ∴=,5AB =,1BD =,514AD AB BD ∴=−=−=,4CF ∴=,CF ∴的长度为4.故选:C .【点睛】此题重点考查平行线的性质、全等三角形的判定与性质等知识,正确地找到全等三角形的对应边和对应角并且证明CFE ADE ≅是解题的关键.A .SSS【答案】B 【分析】根据已知条件两边,及两边的夹角是对顶角解答.【详解】解:在AOB 和COD △中,OA OC AOB COD OB OD =⎧⎪∠=∠⎨⎪=⎩,()AOB COD SAS ∴≌. 故选:B .【点睛】本题考查了全等三角形的应用,准确识图判断出两组对应边的夹角是对顶角是解题的关键. 9.(2022秋·浙江嘉兴·九年级校考期中)在联欢会上,有A 、B 、C 三名选手站在一个三角形的三个顶点位置上,他们在玩“抢凳子”游戏,要求在他们中间放一个木凳,谁先抢到凳子谁获胜,为使游戏公平,则凳子应放在ABC 的( )A .三边垂直平分线的交点B .三杂中线的交点C .三条角平分线的交点D .三条高所在直线的交点【答案】A【分析】根据题意可知,当木凳所在位置到A 、B 、C 三个顶点的距离相等时,游戏公平,再由线段垂直平分线的性质即可求解.【详解】解:由题意可得:当木凳所在位置到A 、B 、C 三个顶点的距离相等时,游戏公平,∵线段垂直平分线上的点到线段两端的距离相等,∴木凳应放的最适当的位置是在ABC 的三边垂直平分线的交点,故选:A .【点睛】本题考查线段垂直平分线的性质的应用,掌握线段垂直平分线的性质是解题的关键. )可说明ABC 与△ 【答案】A 【分析】先根据垂直的定义可得90ACB ADB ∠=∠=︒,再根据角平分线的定义可得CAB DAB ∠=∠,然后根据AAS 定理即可得.【详解】解:,BC AC BD AD ⊥⊥,90ACB ADB ∴∠=∠=︒,AB 平分CAD ∠,CAB DAB ∴∠=∠,在ABC 和ABD △中,90ACB ADB CAB DABAB AB ∠=∠=︒⎧⎪∠=∠⎨⎪=⎩,()AAS ABC ABD ∴≌,故选:A . 【点睛】本题主要考查了三角形全等的判定,熟练掌握三角形全等的判定方法是解题关键.二、填空题【答案】CA FD =,B E ∠=∠,A D ∠=∠,AB DE ∥等【分析】可选择CA FD =添加条件后,能用SAS 进行全等的判;也可选择B E ∠=∠添加条件后,能用ASA 进行全等的判定;也可选择A D ∠=∠添加条件后,能用AAS 进行全等的判定;也可选择AB DE ∥添加条件后,能用ASA 进行全等的判定即可;【详解】解:添加CA FD =,∵12∠=∠,BC EF =,∴()SAS ABC DEF ≌△△,故答案为:CA FD =;或者添加B E ∠=∠,∵BC EF =,12∠=∠,∴()ASA ABC DEF ≌△△,故答案为:B E ∠=∠;或者添加A D ∠=∠,∵12∠=∠,BC EF =,∴()AAS ABC DEF ≌△△,故答案为:A D ∠=∠;或者添加AB DE ∥,∵AB DE ∥,∴B E ∠=∠,∵12∠=∠,BC EF =,∴()AAS ABC DEF ≌△△,故答案为:AB DE ∥.【点睛】本题考查了全等三角形的判定,解答本题关键是掌握全等三角形的判定定理,本题答案不唯一.【答案】AB DC =【分析】添加条件AB DC =,利用SAS 证明ABC DCB △≌△即可.【详解】解:添加条件AB DC =,理由如下:在ABC 和DCB △中,AB DC ABC DCBBC CB =⎧⎪∠=∠⎨⎪=⎩, ∴()SAS ABC DCB △≌△, 故答案为:AB DC =.【点睛】本题主要考查了全等三角形的判定,熟知全等三角形的判定定理是解题的关键,全等三角形的判定定理有SSS SAS AAS ASA HL ,,,,. 13.(2023秋·浙江湖州·八年级统考期末)如图,已知AC DB =,要使得ABC DCB ≅,根据“SSS”的判定方法,需要再添加的一个条件是_______.【答案】ABDC =【分析】要使ABC DCB ≅,由于BC 是公共边,若补充一组边相等,则可用SSS 判定其全等.【详解】解:添加AB DC =.在ABC 和DCB △中AB DC BC CB AC BD =⎧⎪=⎨⎪=⎩, ∴()ABC DCB SSS ≅△△, 故答案为:AB DC =.【点睛】本题考查三角形全等的判定方法;判定两个三角形全等的一般方法有:SSS 、SAS 、ASA 、AAS 、HL .添加时注意:AAA 、SSA 不能判定两个三角形全等,不能添加,根据已知结合图形及判定方法选择添加的条件是正确解答本题的关键.14.(2022秋·浙江丽水·八年级统考期末)如图,在ABC 中,CD 是边AB 上的高,BE 平分ABC ∠,交CD 于点E ,6BC =,若BCE 的面积为9,则DE 的长为______.【答案】3【分析】过E 作EF BC ⊥于F ,根据角平分线性质求出EF DE =,根据三角形面积公式求出即可.【详解】解:过E 作EF BC ⊥于F ,CD 是AB 边上的高,BE 平分ABC ∠,交CD 于点E ,DE EF ∴=,192BCE S BC EF =⋅=,1692EF ∴⨯⨯=,3EF DE ∴==,故答案为:3.【点睛】本题考查了角平分线性质的应用,能根据角平分线性质求出3EF DE ==是解此题的关键,注意:在角的内部,角平分线上的点到角的两边的距离相等. 八年级期末)如图,在ABC 中, 【答案】4【分析】根据线段垂直平分线的性质得到2AD BD ==,则4CD AC AD =−=.【详解】解:∵AB 的垂直平分线交AB 于点E ,交AC 于点D ,∴2AD BD ==,∵6AC =,∴4CD AC AD =−=,故答案为:4.【点睛】本题主要考查了线段垂直平分线的性质,熟知线段垂直平分线上的点到线段两端的距离相等是解题的关键. 16.(2022秋·浙江温州·八年级校联考期中)如图,在ABC 中,DE 是AC 的中垂线,分别交AC ,AB 于点D ,E .已知BCE 的周长为9,4BC =,则AB 的长为______.【答案】5【分析】先利用三角形周长得到5CE BE +=,再根据线段垂直平分线的性质得到EC EA =,然后利用等线段代换得到AB 的长.【详解】解:∵BCE 的周长为9,9CE BE BC ∴++=,又4BC =,5CE BE ∴+=,又DE 是AC 的中垂线,EC EA ∴=,5AB AE BE CE BE ∴=+=+=;故答案为:5.【点睛】本题考查了垂直平分线的性质:垂直平分线上任意一点,到线段两端点的距离相等.17.(2023秋·浙江杭州·八年级校考开学考试)如图,已知12∠=∠,要说明ABC BAD ≌,(1)若以“SAS ”为依据,则需添加一个条件是__________;(2)若以“ASA ”为依据,则需添加一个条件是__________.【答案】 BC AD = BAC ABD ∠=∠【分析】(1)根据SAS 可添加一组角相等,故可判定全等;(2)根据ASA 可添加一组角相等,故可判定全等;【详解】解:(1)已知一组角相等和一个公共边,以“SAS ”为依据,则需添加一组角,即BC AD =故答案为:BC AD =;(2)已知一组角相等,和一个公共边,以“ASA ”为依据,则需添加一组角,即BAC ABD ∠=∠. 故答案为:BAC ABD ∠=∠.【点睛】本题主要考查三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS SAS ASA AAS HL 、、、、.添加时注意:AAA SSA 、不能判定两个三角形全等. 18.(2019秋·浙江嘉兴·八年级校考阶段练习)如图,点B 、E 、C 、F 在一条直线上,AB ∥DE ,AB=DE ,BE=CF ,AC=6,则DF=________【答案】6.【分析】根据题中条件由SAS 可得△ABC ≌△DEF ,根据全等三角形的性质可得AC=DF=6.【详解】∵AB ∥DE ,∴∠B=∠DEF∵BE=CF ,∴BC=EF ,在△ABC 和△DEF 中,AB DE B DEFBC EF =⎧⎪∠=∠⎨⎪=⎩,∴△ABC ≌△DEF (SAS ),∴AC=DF=6.考点:全等三角形的判定与性质.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
小专题(六) 构造全等三角形的方法技巧
方法1 利用“角平分线”构造全等三角形
【方法归纳】 因角平分线本身已经具备全等的三个条件中的两个(角相等和公共边相等),故在处理角平分线问题时,常作以下辅助线构造全等三角形:
(1)在角的两边截取两条相等的线段;
(2)过角平分线上一点作角两边的垂线.
1.如图,AB ∥CD,BE 平分∠ABC,CE 平分∠BCD,点E 在AD 上,求证:BC =AB +CD.
证明:在BC 上截取BF =AB,连接EF.
∵∠ABC 、∠BCD 的平分线交AD 于点E,
∴∠ABE =∠FBE,∠BCE =∠DCE,
在△ABE 和△FBE 中,
⎩⎪⎨⎪⎧AB =FB ,∠ABE =∠FBE ,BE =BE ,
∴△ABE ≌△FBE.
∴∠BAE =∠BFE.
∵AB ∥CD,
∴∠BAE +∠CDE =180°.
∴∠BFE +∠CDE =180°.
∵∠BFE +∠CFE =180°,
∴∠CFE =∠CDE.
在△FCE 和△DCE 中,
⎩⎪⎨⎪⎧∠CFE =∠CDE ,∠FCE =∠DCE ,CE =CE ,
∴△FCE ≌△DCE.
∴CF =CD.
∴BC =BF +CF =AB +CD.
2.如图,已知∠AOB =90°,OM 是∠AOB 的平分线,三角尺的直角顶点P 在射线OM 上滑动,两直角边分别与OA,OB 交于点C,D,求证:PC =PD.
证明:过点P 作PE ⊥OA 于点E,
PF ⊥OB 于点F.
∴∠PEC =∠PFD =90°.
∵OM 是∠AOB 的平分线.
∴PE =PF.
∵∠AOB =90°,∠CPD =90°,
∴∠PCE +∠PDO =360°-90°-90°=180°.
而∠PDO +∠PDF =180°,
∴∠PCE =∠PDF.
在△PCE 和△PDF 中,
⎩⎪⎨⎪⎧∠PCE =∠PDF ,∠PEC =∠PFD ,PE =PF.
∴△PCE ≌△PDF(AAS ).
∴PC =PD.
方法2 利用“截长补短法”构造全等三角形
【方法归纳】 截长补短法的具体做法:在某一条线段上截取一条线段与特定线段相等,或将某条线段延长,使之与特定线段相等,再利用三角形全等的有关性质加以说明.这种方法适用于证明线段的和、差、倍、分等类的题目.
3.如图,在△ABC 中,AD 平分∠BAC,∠C =2∠B,试判断AB,AC,CD 三者之间的数量关系,并说明理由.(想一想,你会几种方法)
解:AB =AC +CD.理由:
易证△AED≌△ACD(SAS),
∴ED=CD,∠AED=∠C.
∵∠AED=∠B+∠EDB,
∴∠C=∠AED=∠B+∠EDB.
又∵∠C=2∠B,
∴∠B=∠EDB.
∴BE=DE.
∴AB=AE+BE=AC+DE=AC+CD.
方法2:延长AC到点F,使CF=CD,连接DF.
∵CF=CD,
∴∠CDF=∠F.
∵∠ACB=∠CDF+∠F,
∴∠ACB=2∠F.
又∵∠ACB=2∠B,
∴∠B=∠F.
又∵∠BAD=∠FAD,AD=AD,
∴△ABD≌△AFD(AAS).
∴AB=AF=AC+CF=AC+CD.
4.如图,在△ABC中,∠A=60°,BD,CE分别平分∠ABC和∠ACB,BD,CE交于点O,试判断BE,CD,BC的数量关系,并加以证明.
解:BC=BE+CD.
∵BD 平分∠ABC,
∴∠EBO =∠FBO.
又∵OB =OB,
∴△EBO ≌△FBO.
∴∠EOB =∠FOB.
∵∠A =60°,BD,CE 分别平分∠ABC 和∠ACB,
∴∠BOC =180°-∠OBC -∠OCB =180°-12∠ABC -12∠ACB =180°-12
(180°-∠A)=120°. ∴∠EOB =∠DOC =60°.
∴∠BOF =60°,∠FOC =∠DOC =60°.
∵CE 平分∠DCB,
∴∠DCO =∠FCO.
又∵OC =OC,
∴△DCO ≌△FCO.
∴CD =CF.
∴BC =BF +CF =BE +CD.
5.如图,AD ∥BC,DC ⊥AD,AE 平分∠BAD,E 是DC 的中点.问:AD,BC,AB 之间有何关系?并说明理由.
解:AB =AD +BC.
理由:作EF ⊥AB 于F,连接BE.
∵AE 平分∠BAD,DC ⊥AD,EF ⊥AB,AD ∥BC,
∴EF =DE,DC ⊥BC.
∵DE =CE,
∴EC =EF.
∴Rt △BFE ≌Rt △BCE(HL ).
∴BF =BC.
同理可证:AF =AD.
∴AD +BC =AF +BF =AB,
即AB =AD +BC.
方法3 利用“倍长中线法”构造全等三角形
【方法归纳】 将中点处的线段延长一倍,然后利用SAS 证三角形全等.
6.已知:如图,AD,AE 分别是△ABC 和△ABD 的中线,且BA =BD.求证:AE =12
AC.
证明:延长AE 至F,使EF =AE,连接DF.
∵AE 是△ABD 的中线,
∴BE =DE.
∵∠AEB =∠FED,
∴△ABE ≌△FDE.
∴∠B =∠BDF,AB =DF.
∵BA =BD,
∴∠BAD =∠BDA,BD =DF.
∵∠ADF =∠BDA +∠BDF,∠ADC =∠BAD +∠B,
∴∠ADF =∠ADC.
∵AD 是△ABC 的中线,
∴BD =CD.
∴DF =CD.
又∵AD =AD,
∴△ADF ≌△ADC(SAS ).
∴AC =AF =2AE,即AE =12
AC. 7.如图,AB =AE,AB ⊥AE,AD =AC,AD ⊥AC,点M 为BC 的中点,求证:DE =2AM.
证明:延长AM至N,使MN=AM,连接BN.
∵点M为BC的中点,
∴BM=CM.
又∵∠BMN=∠CMA,
∴△AMC≌△NMB(SAS).
∴AC=BN,∠C=∠NBM,∠ABN=∠ABC+∠C=180°-∠BAC=∠EAD. 又∵BN=AC=AD,AB=EA,
∴△ABN≌△EAD(SAS).
∴DE=NA.
∴DE=2AM.。
