安徽省六安市2016年高一数学(理)暑假作业 第十一天 Word版含答案
安徽省六安市2016年高一数学(文)暑假作业 第十一天
第十一天 完成日期 月 日学法指导：1.理解三角函数的相关概念，同角三角函数的基本关系。
一、选择题（在每小题给出的四个选项中只有一项是符合题目要求的） 1. 已知扇形的周长为6cm ，面积为2cm 2，则扇形的中心角的弧度 （ ） A . 1 B. 4 C. 1或4 D. 2或4 2. 已知弧度数为2的圆心角所对的弦长也是2，则这个圆心角所对的弧长是 （ ） A. 2B.2sin1C. 2sin1D. sin23. 已知α和β的终边关于轴对称，则下列各式中正确的是（ ）A. βαsin sin = B ．βαπsin )2sin(=- C ．βαcos cos = D ．βαπcos )2cos(-=-4. α是第二象限角，(P x 为其终边上一点，且cos 4x a =，则sinα的值为（ ）A ．4B ．4 C ．4D ．45.若tan 0θ>，则( )A ． sin 0θ>B ．cos 0θ>C ．sin 20θ>D ．cos20θ>6．已知3sin 5m m θ-=+，42cos 5m m θ-=+， 其中2πθπ<<，则tan θ＝（ ）A.125- C.-2 D.512- 7. 若βαtan ,tan 是关于x 的方程20x px q -+=的两个实根，βαtan 1,tan 1是关于方程20x rx s -+=的两个实根，那么rs=（ ） A pqB1pqC2pqD 2q p8. 函数)421sin(2π+=x y 的周期，振幅，初相分别是（ ） A.424ππ，，B.424ππ--，，C.424ππ，，，D.4,2,2ππ二.填空题 9. cos π7 ＋cos 2π7 ＋cos 3π7 ＋cos 4π7 ＋cos 5π7 ＋cos 6π7= ；10．已知sin 200a =，则tan160等于11.若()π,0∈A ,且137cos sin =+A A ,则=-+AA A A cos 7sin 15cos 4sin 5__________. 12.设)cos()sin()(21απαπ+++=x n x m x f ，其中m 、n 、1α、2α都是非零实数，若(2015)1f =则(2016)f = .三.解答题（应写出文字说明、证明过程或演算步骤） 13.求函数2sin cos 1,[,]22y x x x ππ=++∈-的最大值、最小值，以及取得最大、最小值时x 的取值的集合。
安徽省六安市2016年高一数学理暑假作业第十三天Word版含答案
第十三天 完成日期 月 日 礼拜学法指导：灵活应用三角函数知识进行有关三角函数的求值等。
一、选择题（在每小题给出的四个选项中只有一项是符合题目要求的） 1.若21cos -=α，23sin -=β，),2(ππα∈，)2,23(ππβ∈，则=+)sin(βα （ ）A ．23B ．23-C ．1-D ．02.已知πβπα<<<<20,3sin5,54)cos(-=+βα,则=βsin（ ）A ．0B ．0或2425C ．2425D ．24253.12cos312sinππ-的值是（ ）A ．0B ．2 C D ．24.函数)(),6cos()3sin(2R x x x y ∈+--=π的最小值等于 （ ）A. 3-B.2-C.1-D.5-5.函数]),0[)(26sin(2ππ∈-=x x y 为增函数的区间是 （ ）A. ]3,0[πB. ]127,12[ππC. ]65,3[ππD. ],65[ππ 6.锐角三角形的内角A 、B 知足B AA tan 2sin 1tan =-，则有 （ ）A.0cos 2sin =-B AB.0cos 2sin =+B AC.0sin 2sin =-B AD.0sin 2sin =+B A7.函数44sin cos y x x =+的值域是（ ）A.[]0,1B. []1,1-C.13,22⎡⎤⎢⎥⎣⎦D.1,12⎡⎤⎢⎥⎣⎦8.已知1cos sin 21cos sin x xx x -+=-++，则tan x 的值为（ ）A.34B. 34- C. 43D.43-二.填空题 9.=-3512cos 342π . 10. 函数22sin cos 1sin x xyx的值域是 .11. =+++87cos 85cos 83cos 8cos 4444ππππ.12. 若θθcos sin 3=，则θθ2sin 2cos +的值等于 .三、解答题（应写出文字说明、证明进程或演算步骤） 13. 求[]0200080sin 2)10tan 31(10sin 50sin 2⋅++的值.14. 若55sin =A ,1010sin =B ,且B A ,均为钝角,求B A +的值.15. 已知αtan 、βtan 是方程0242=--x x 的两个实根，求)(sin 3)cos()sin(2)(cos 22βαβαβαβα+-++++的值.【链接高考】16. 【2015高考上海】已知函数()sin f x x =．若存在1x ，2x ，⋅⋅⋅，m x 知足120x x ≤<<⋅⋅⋅6m x π<≤，且()()()()()()1223112n n f x f x f x f x f x f x --+-+⋅⋅⋅+-=，（2m ≥，m *∈N ），则m 的最小值为 ．第十三天9.10. (14,2⎤-⎥⎦； 11. 2312. 7513. 14.47π15. 35-．。
安徽省六安市2016年高一数学(理)暑假作业 第二十六天 Word版含答案
第二十六天 完成日期 月 日 星期学法指导：1. 理解二次函数、一元二次方程与一元二次不等式解集的关系。
2. 掌握一元二次不等式、分式不等式的解法。
一、选择题（在每小题给出的四个选项中只有一项是符合题目要求的） 1．设0a b >>，则下列不等式成立的是（ ）A. ||1b a -≥B.22a b< C.lg0ab< D. 01ab<< 2．设{||1|2}A x x =-<，2{|0}x B x x-=>，则A B ⋂=（ ）A ．{|13}x x -<<B ．{|0x x <或2}x >C ．{|10}x x -<<D ．{|10x x -<<或23}x <<3．设1a >，m = 1+a +a ，n =2+a +1-a ,则m 、n 的大小关系（ ）A ．m n <B ．m n >C ．m n ≤D ．m n ≥ 4．不等式|1|-x x ≥的解集为（ ）A. [21，+∞） B.（－∞，21] C.（－∞，1] D.（－∞，21） 5．若01a <<，则不等式1()()0x a x a-->的解集为（ ）A ．1a x a<<B ．1x x a a ><或C ． 1x a a<< D ．1x x a a<>或 6．函数⎩⎨⎧≤->=1,11,)(x x x x f ，则不等式()2xf x x -≤的解集为（ ）A.［-2，2］B.［-1，2C.［1，2D.［-2，-1］∪［1，2］7．若关于x 的不等式220x ax +->在区间[]1,5上有解，则实数a 的取值范围为（ ）A ．),523(+∞-B ．]1,523[-C ．(1,+∞)D ．)1,(--∞8．若关于x 的方程112545x x m -+-+-⨯=有实数根，则实数m 的取值范围是（ ）A ．0m <B ．4m >-C ．40m -≤<D ．30m -≤<二、填空题9．已知不等式20x ax b --<的解集是{|23}x x <<，则不等式210bx ax -->的解集为 10．若不等式220x ax a -+>对x R ∈恒成立，则关于t 的不等式22123t t t aa++-<的解集为11．设函数()21,01,0x x f x x ⎧+=⎨<⎩≥，则满足不等式()()212f x f x ->的x 的取值范围是 .12．若关于x 的方程0422=+-ax x 在区间(]21，上有且仅有一个根，则实数a 的取值范围是 .三、解答题 （应写出文字说明、证明过程或演算步骤） 13．解关于x 的不等式：22120()x ax a a R --<∈.14. 当k 为何值时，不等式0＜16322+-++x x kx x 6≤对任意实数x 恒成立.15、已知21,x x 是关于x 的一元二次方程20++=ax bx c 的两根，若121<<x x ，求2221212()++x x x x 的取值范围.【链接高考】16. 【2015高考四川理】如果函数()()()()21281002f x m x n x m n =-+-+≥≥，在区间122⎡⎤⎢⎥⎣⎦，上单调递减，求mn 的最大值。
安徽省六安市舒城中学2016年高一数学(理)暑假作业 第十一天
第十一天 完成日期 月 日星期学法指导：理解三角函数的相关概念，同角三角函数的基本关系。
一、选择题（在每小题给出的四个选项中只有一项是符合题目要求的）1. 将表的分针拨慢10分钟，则分针转过的角的弧度数是 （ ） A.3πB.6π C.-3π D.-6π 2. 已知扇形的周长是6cm ，面积是22cm ，则扇形的圆心角的弧度数是（ ）A.1B.4C.1或4D.2或43. 已知角α终边上一点P 的坐标是（2sin 2,2cos 2-)，则αsin 等于 （ ）A.2sinB.2sin -C.2cosD. 2cos -4. α是第二象限角，(P x 为其终边上一点，且cos 4x a =，则αsin 的值为 （ ）A B C D 5. 若α为第二象限角，则下列各式恒小于零的是（ ）A ．ααcos sin +B ．ααsin tan +C ．1cos tan a a- D ．ααtan sin - 6. 已知αsin =55，则αα44cos sin -的值为（ ）A.53- B.51- C.51 D.537. 若βαtan ,tan 是关于x 的方程20x px q -+=的两个实根，βαtan 1,tan 1是关于方程02=+-s rx x 的两个实根，那么=rs（ ）A ．pqB ．1pqC ．2p qD ．2q p8. 若5sin 2cos -=+αα,则αtan 等于（ ） A.21B. 2C.21- D.-2二.填空题9. 已知tan 2θ=，则22sin sin cos 2cos θθθθ+-= .10．已知角α的终边落在直线)0(3<-=x x y 上，则=-ααααcos cos sin sin .11．若()π,0∈A ,且137cos sin =+A A ,则=-+AA A A cos 7sin 15cos 4sin 5 . 12.)2sin()2(sin )tan()2cos()cos()(sin 32πααπαππααππα--∙+∙+--∙+∙+= ．三.解答题（应写出文字说明、证明过程或演算步骤） 13. 已知a a +-=11sin θ,aa +-=113cos θ,若θ是第二象限角，求实数a 的值.14.已知31sin sin =+y x ，求x y 2cos sin -的最大值.15.设函数)(x f 满足)2|(|,cos sin 4)(sin 3)sin (π≤=+-x x x x f x f .（1）求函数)(x f 的解析式； （2）求)(x f 的值域；（3）设函数2()2cos sin g x x x m =++,对任意R x ∈0,有0()()g x f x <恒成立,试求实数m 的取值范围.【链接高考】16. 【2015高考重庆】若tan 2tan 5πα=，则3cos()10sin()5παπα-=-（ ）A 、1B 、2C 、3D 、4第十一天1.A2.C3.D4.A5.B6.A7.C8.B9. 45 10．2. 11.438. 12.1 13 . 9114 .9415 （1）()2f x =[1,1]x ∈- （2）[1,1]- （3）3m <- 16.C。
安徽省六安市2016年高一数学理暑假作业第四天Word版含答案
第四天 完成日期 月 日 星期学法指导：1.理解和掌握指数函数概念及其单调性等性质。
2.会应用指数函数知识解决复合函数（与指数函数复合）的定义域，值域，单调性等问题。
一、选择题（在每小题给出的四个选项中只有一项是符合题目要求的） 1.下列等式能够成立的是（ ） A ．1)3(0=-x ，x R ∈ B ．331x x-=-， x R ∈C ．43433)(y x y x +=+ ，,x y R ∈78a =，0a ≥ 2.函数x a a a y ⋅+-=)33(2是指数函数，则有（ ）A.21==a a 或 B .1=aC. 2=aD.10≠>a a 且3.函数f (x )的图象向右平移一个单位长度，所得图象与y =e x 关于y 轴对称，则f (x )=（ ） A .1ex +B . 1e x -C . 1e x -+ D . 1e x --4.函数x x f 1)21()(= 的定义域，值域依次是（ ）A ．R ，RB ．R ，+RC ．{}{}1,0≠∈≠∈y R y x R xD ．{}{}1,0≠∈≠∈+y R y x R x 5.函数2=y 2x -12-+x 的单调递减区间是（ ） A ．（-∞，+∞） B ．［1，+∞） C ．（-∞，0］ D ．［0，+∞）6.右图为函数xxxxd y c y b y a y ====,,,在同一坐标系中的图象，其中d c b a ,,,都是不等于1的正数，则d c b a ,,,的大小顺序是（ ）A ．c d a b <<<B ．c d b a <<<C ．d c b a <<<D ．d c a b <<<7.已知10,1<<>>x b a ，以下结论中成立的是 ( )A ．x x ba )1()1(>B ．b a x x >C.b a x x log log >D ．log log a b x x >8.函数c bx x x f +-=2)(满足)1()1(x f x f -=+且3)0(=f ,则)(x b f 与)(x c f 的大小关系是（ ）A. )()(xxc f b f > B. )()(xxc f b f < C. )()(xxc f b f ≥ D. )()(xxc f b f ≤ 二、填空题9.当[]1,1-∈x 时，函数23)(-=x x f 的值域为 ． 10. 若4log 3a =，则22aa-+= ．11. 已知函数3,[0,1]()93,(1,3]22x x f x x x ⎧∈⎪=⎨-∈⎪⎩，当[0,1]t ∈时，(())[0,1]f f t ∈，则实数t 的取值范围是 ．12. 若存在正数x ，使24x x a +>成立，则实数a 的取值范围是 . 三、解答题（应写出文字说明、证明过程或演算步骤） 13.设+∈R z y x ,,，且z y x 643==. (1) 求证：yx z 2111=-； (2) 比较x 3，y 4，z 6的大小.14.求函数11()()142x xy =-+在[]3,2x ∈-上的值域．15.设()212xx af x =+-(a 为实数). （1）x R ∈,试讨论()f x 的单调性；（2）当0=a 时，若函数)(x g y =的图象与)(x f y =的图象关于直线1=x 对称，求函数()x g y =的解析式。
安徽省六安市2016年高一数学理暑假作业第二天Word版含答案
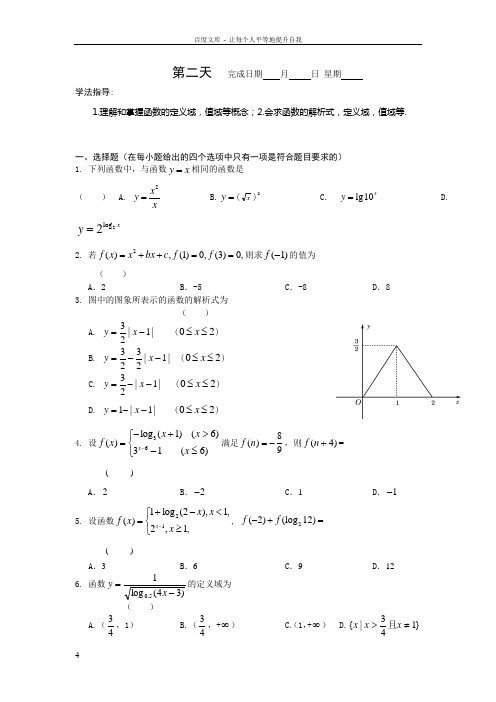
第二天 完成日期 月 日 星期学法指导:1.理解和掌握函数的定义域，值域等概念；2.会求函数的解析式，定义域，值域等.一、选择题（在每小题给出的四个选项中只有一项是符合题目要求的）1. 下列函数中，与函数x y =相同的函数是（ ） A. 2x y x= B.=y (x)2C.lg10xy =D.2log 2x y =2. 若2(),(1)0,(3)0,f x x bx c f f =++==则求(1)f -的值为（ ）A ．2B ．-5C ．-8D ．8 3. 图中的图象所表示的函数的解析式为 （ ）A. |1|23-=x y (20≤≤x ) B. |1|2323--=x y (20≤≤x )C. |1|23--=x y (20≤≤x )D. |1|1--=x y (20≤≤x )4. 设36log (1)(6)()31(6)x x x f x x --+>⎧=⎨-≤⎩满足8()9f n =-，则(4)f n +=( )A ．2B ．2-C ．1D ．1- 5. 设函数211log (2),1,()2,1,x x x f x x -+-<⎧=⎨≥⎩, 2(2)(log 12)f f -+=( )A ．3B ．6C ．9D ．12 6. 函数)34(log 15.0-=x y 的定义域为（ ）A.（43，1） B.（43，+∞） C.（1，+∞） D.}143|{≠>x x x 且7. 已知221)1(x x x x f +=-,则=)(x f（ ）A. x x 22-B. x x 22+C. 22+xD. 22-x8. 用{}c b a ,,min 表示c b a ,,三个数中的最小值，设{}x x x f x-+=10,2,2m in )(（0x ≥）,则()f x 的最大值为（ ）A.7B.6C.5D. 4二、填空题9.已知函数ϕ(x )=)()(x g x f +,其中)(x f 是正比例函数,)(x g 是反比例函数，且ϕ(31)=16, ϕ(1)=8,则ϕ(x )=10.定义在R 上的函数)(x f 满足xy y f x f y x f 2)()()(++=+,2)1(=f ,则)3(-f = 11.若函数)1(+x f 的定义域为[0,1]，则)22(-x f 的定义域为12.设函数1()702()0xx <f x x ⎧⎪= ≥-，若1)(<a f ，则实数a 的取值范围是三、解答题（应写出文字说明、证明过程或演算步骤）13. 已知()f x 是一次函数，且满足3(1)2(1)217f x f x x +--=+，求()f x 的解析式；14.求下列函数的解析式：（1）设(cos )cos 2f x x =，求()f x 的解析式； （2）已知2(1)lg ,f x x+=求()f x 的解析式.ODCB A15. 如图，等腰梯形ABCD 内接于一个半径为r 的圆，且下底r AD 2=，如图，记腰AB 长为x ，梯形周长()y f x =.求()f x 的解析式、定义域和最大值.【链接高考】16.【2015年安徽高考】函数()()2ax bf x x c +=+的图象如图所示，则下列结论成立的是（ ）（A ）0a >，0b >，0c < （B ）0a <，0b >，0c > （C ）0a <，0b >，0c < （D ）0a <，0b <，0c <第二天1.C2.D3. B4.B5.C6.A7.C8. B9. 3x +x5; 10. 6;11.]2,3[log 2;12. (-3,1). 13. ()27f x x =+14. (1)2()21,[1,1]f x x x =-∈-; ；)1(12lg)()2(>-=x x x f 15. 21()()5f x x r r r=--+，定义域为2)r ,x r =时有最大值5r16.C。
安徽省六安市2016年高一数学文暑假作业第六天Word版含答案-精品
安徽省六安市2016年高一数学文暑假作业第六天Word 版含答案-精品学法指导：1.会利用幂函数与二次函数的定义和性质解题。
2.会利用单调性的定义证明函数的单调性。
一、选择题（在每小题给出的四个选项中只有一项是符合题目要求的）1. 设α∈{－1,1，12，3}，则使幂函数y ＝x α的定义域为R 且为奇函数的所有α的值为（ ） A ．1,3 B ．－1,1 C ．－1,3 D ．－1,1,3 2. 已知p >q >1,0<a <1,则下列各式中正确的是 （ ） A.q pa a>B.a a q p <C.q pa a-->D.a a q p -->3. 二次函数c bx ax y ++=2的图象如图所示，则下列关系式不正确 （ ）4. 在下列图象中，二次函数y =ax 2＋bx ＋c 与函数y =(ab )x的图象可能是5.若函数)2(log )(2x x x f a -=）且1,0(≠>a a 在区间⎪⎭⎫⎝⎛1,21内恒有0)(>x f ，则函数)(x f 的单调递增区间是（ ）A ．()0，∞-B ．⎪⎭⎫ ⎝⎛∞-41，C ．⎪⎭⎫ ⎝⎛+∞,21D ．⎪⎭⎫⎝⎛∞+，416. 已知212x x >，则x 的取值范围是（ ） A.R B. x <1 C. x >0D. x >17. 已知函数()3223f x x ax x =--，当()0,x ∈+∞时，()f x ax ≥恒成立，则实数a 的取值范围是（ ）A. 3a ≥-B. 3a ≤-C. 2a ≤-D. 2a ≥-8. 设 f (x )=a x ，g (x )=x 31，h (x )=log a x ，a 满足log a (1－a 2)＞0，那么当x ＞1时必有（ ）A ．h (x )＜g (x )＜f (x )B ．h (x )＜f (x )＜g (x )C ．f(x )＜g (x )＜h (x )D ．f (x )＜h (x )＜..g (x )二、填空题 9.322--=a a xy 是偶函数，且在),0(+∞是减函数，则整数a 的值是 。
安徽省六安市2016年高一数学(理)暑假作业 第一天
第一天 完成日期 月 日 星期学法指导：1.理解集合的概念，元素与集合的关系。
2.识别集合之间的基本关系，并能用venn 图来描述相关基本运算。
一、选择题（在每小题给出的四个选项中只有一项是符合题目要求的） 1.设{}A C ,31|N {A },31|N S 则<<∈=≤≤∈=x x x x S 为（ ） A.∅B.{}3,1C.{}3,1==x xD.{}3,2,1 2.集合2{03},{9}P x Z x M x Z x =∈≤<=∈≤，则P M ⋂=（ ）A ．{}2,1 B.{}2,10，C ．{}30<≤x x D.{}30≤≤x x3.设集合{|(1)(2)0}A x x x =+-<，集合{|13}B x x =<<，则A B =（ ）.{|13}A x x -<< .{|11}B x x -<< .{|12}C x x <<.{|23}D x x <<4.设集合⎭⎬⎫⎩⎨⎧∈+==⎭⎬⎫⎩⎨⎧∈+==Z k k x x N Z k k x x M ,214,,412,则（ ） A ． M=NB.M NC. M ND . M N ⋂=∅5.设全集U=R,集合(2){|21},{|ln(1)}x x A x B x y x -=<==-，则图中阴影部分所表示的集合为（ ）A. {}1≥x xB. {}1≤x xC. {}21<≤x xD.{}10≤<x x6.设集合},01|{<<-=m m P }044|{2恒成立对任意的实数x mx mx m Q <-+=则下列关系中成立的是（ ）≠⊂ ≠⊃A. P ⊆QB. Q ⊆PC. P=QD. P ⊄Q7.{|,},()().M N M N x x M x N M N M N N M -=∈∉⊕=-⋃-对于集合、，定义且2{|3,},{|2,}.x A y y x x x R B y y x R A B ==-∈==-∈⊕=设则（ ） A.]0,49(-B.)0[)49,(∞+⋃--∞， C.)0,49[- D.)0()49,(∞+⋃--∞，8.已知{=P ︳=(1,0)+m (0,1),}R m ∈,{=Q ︳=(1,1)+n (-1,1),}R n ∈是两个向量集合，则P ⋂Q=( )A.(){}11，B. (){}1,1-C.(){}01，D.(){}10，二、填空题9.已知集合,1},02|{2A a x x x A ∉>+-=且则实数a 的取值范围是 . 10.若集合},4,3,2,1{},,,{=d c b a 且下列四个关系：①1=a ；②1≠b ；③2=c ；④4≠d 有且只有一个是正确的，则符合条件的有序数组),,,(d c b a 的个数是_________. 11. 设,a b R ∈，集合{}1,,0,,a a b b a b ⎧⎫+=⎨⎬⎩⎭，则a b -= . 12. 设{}{}260,10,P x x x Q x mx m R =+-==+=∈，若Q P P ⋃=，则实数m 取值的集合是 .三、解答题（应写出文字说明、证明过程或演算步骤） 13.含有三个实数的集合可表示为⎭⎬⎫⎩⎨⎧1,,a b a ，也可表示为{}0,,2b a a +， 求20162016a b +的值．14．已知R x ∈，集合{}0232=+-=x x x A ，{}022=+-=mx x x B ，若B B A =⋂，求实数m 的取值范围．15.设集合{}260P x x x =--<，{}0Q x x a =-≥（1）若P Q ⋂=∅，求实数a 的取值范围. （2）若P Q ⊆，求实数a 的取值范围.【链接高考】16.【2010湖南】若规定E={}1210,,,a a a …的子集{}12nk k k a a a ，，…，为E 的第k 个子集，其中12111222n k k k k ---=+++… ，则（1）{}1,3,a a 是E 的第 个子集； （2）E 的第211个子集是 .第一天1.B2.B3.A4.B5.C6.A7.B8.A9. 1a ≤; 10.6; 11.2;12. 0m =或13或12- 13. -1; 14.3m m -<<=或 15.(1) 3a ≥; (2) 2a ≤-. 16. 5，{}12578,a a a a a ，，，。
安徽省六安市2016年高一数学理暑假作业第十八天Word版含答案
第十八天 完成日期 月 日 礼拜学法指导：把握等差数列，等比数列的通项公式，前n 项和公式。
一、选择题（在每小题给出的四个选项中只有一项是符合题目要求的）1. 已知等差数列{}n a ，n S 为其前n 项和，若20100S =，且1234a a a ++=，则181920a a a ++=（ ） A.20B.24C.26D.302. 等差数列{}n a 的前m 项的和为30，前2m 项的和为100，则它的前3m 项的和为( )A.130 B ． 170 C.210 D ． 2603. 在等差数列{}n a 和{}n b 中，125a =，175b =，100100100a b +=，则数列{}n n a b +的前100项和为（ ）A. 0 B ． 100 C. 1000 D ． 100004. 已知等差数列{}n a 的前n 项和为n S ，47109,a a a ++=14377S S -=,则使n S 取得最小值时n 的值为( )A ．4 B.5 5. 等比数列{}n a 中,37a =,前三项和321S =,则公比q 的值为（ ）B ．12-或12- D ．1-或12 6. 数列2211,12,122,...,122...2,...n -+++++++的前99项和为（ ）A.1002101- B ． 992101- C. 100299- D ． 99299-7. 已知等比数列{}n a 的前n 项和为n S ，且1352a a +=，2454a a +=，则n n S a =（ ）A ．14n - B ．41n - C ．12n - D ．21n -8. 数列{}n a 的首项为3,{}n b 为等差数列且n n n a a b -=+1，若23-=b ,1210=b ，则8a = ( )A ．0B ．3C ．8D ．11二.填空题：9. 数列{}n a 知足1a ,21a a -,32a a -,…, 1n n a a --，…是以1为首项，13为公比的等比数列，则{}n a 的通项公式n a = .10. 已知数列{}n a 知足 331log 1log ()n n a a n N *++=∈，且 2469a a a ++=，则3579log ()a a a ++的值是 .11. 若数列{}n a 的前n 项和2133n n S a =+,则4a = . 12. 记数列{}n a 的前n 和为n s ，若n n s a ⎧⎫⎨⎬⎩⎭是公差为d 的等差数列，则{}n a 为等差数列时,d 的值为 .三. 解答题（应写出文字说明、证明进程或演算步骤）13．在等比数列{}n a 中，5162a =，公比3q =，前n 项和242n S =，求首项1a 和项数n ．14．已知等差数列{n a }中，4a =14，前10项和18510=S ． （1）求n a ；（2）将{n a }中的第2项，第4项，…，第n2项按原先的顺序排成一个新数列，求此数列的前n 项和n G ．15. 已知数列{}n a 中，11a =，前n 项和为*131,()2n n n S S S n N +=+∈且 （1）求数列{}n a 的通项公式； （2）设数列1{}na 的前n 项和为n T ，求知足不等式212+>n n S T 的n 值。
安徽省六安市2016年高一年级数学文暑假作业1-12天12份Word版含答案
第一天 完成日期 月 日学法指导：1.理解集合的概念，元素与集合的关系。
2.识别集合之间的基本关系，并能用venn 图来描述相关基本运算。
一、选择题（在每小题给出的四个选项中只有一项是符合题目要求的） 1．已知集合{}0,1,2A =，{}|,,B z z x y x A y A ==+∈∈，则B =（ ）A ．{}0,1,2,3,4B ．{}0,1,2C ．{}0,2,4D ．{}1,2 2. 已知集合M={},N x 8|N x ∈-∈则M 中元素的个数是（ ） A. 10B. 9C.8D.73. 已知集合{|},{|12},()R A x x a B x x A C B R =<=<<=U ，则实数a 的取值范围是 （ ）A.2a ≥B.2a >C.D.1a < 4．下列各组两个集合A 和B 表示同一集合的是（ ）A ．{}{}, 3.14159AB π== B ．{}(){}2,3,2,3A B ==C ．{}{}3,,,1,3A B ππ==D ．{}{}|11,,1A x x x N B =-<≤∈=5. 设全集U=R,集合)}1ln(|{},12|{)2(x y x B x A x x -==<=-，则图中阴影部分表示的集合为( ) A. {}1x |x ≥ B.{}1x |x ≤ U ABC. {}2x 1|x <≤D. {}1x 0|x ≤<6. 设集合},01|{<<-=m m P }044|{2恒成立对任意的实数x mx mx m Q <-+=则下列关系中成立的是（ ） A. P ⊆Q B. Q ⊆PC. P=QD. P ⊄Q27. {|,},()().{|3,},{|2,}.x M N M N x x M x N M N M N N M A y y x x x R B y y x R A B -=∈∉⊕=-⋃-==-∈==-∈⊕=对于集合、，定义且 设则（ ） A.]0,49(-B.)0[)49,(∞+⋃--∞，C.)0,49[-D.)0()49,(∞+⋃--∞，8. 设S 是至少含有两个元素的集合，在S 上定义了一个二元运算“*”（即对任意的,a b S ∈，对于有序元素对（a ，b ），在S 中有唯一确定的元素a*b 与之对应）．若对任意的,a b S ∈，有(*)a b a b *=，则对任意的,a b S ∈，下列等式中不恒成立的是 （ ） A ．(*)*a b a a =B ．*(*)b b b b =C ．[*(*)]*(*)a b a a b a =D ．(*)*[*(*)]a b b a b b =二、填空题9. 已知集合,1},02|{2A a x x x A ∉>+-=且则实数a 的取值范围是 10.若全集{}{}0,1,2,32U U C A ==且，则集合A 的真子集共有 个 11．已知集合{}24A x y x ==-，{}1B x a x a =≤≤+，若A B A =U ，则实数a 的取值范围为12. 设P 是一个数集，且至少含有两个数，若对任意a 、b ∈P ，都有a+b 、a-b 、ab 、ba∈P （除数b ≠0）,则称P 是一个数域.例如有理数集Q 是数域;数集F={a+b 2|a,b ∈Q}也是数域.有下列命题:①整数集是数域; ②若有理数集Q ⊆M,则数集M 必为数域; ③数域必为无限集; ④存在无穷多个数域.其中正确的命题的序号是 三、解答题（应写出文字说明、证明过程或演算步骤）13. 含有三个实数的集合可表示为{a,}1,ab，也可表示为{},0,b a ,a 2+求20162016a b +的值． 14．已知x ∈R ，集合A ＝｛023|2=+-x xx ｝，B ＝｛02|2=+-mx x x ｝，若A∩B ＝B ，求实数m 的取值范围．15．设全集U R =，已知函数()1f x x =-的定义域为集合A ，函数()()1,102xg x x ⎛⎫=-≤≤ ⎪⎝⎭的值域为集合B .（1）求()U C A B I ；（2）若{}|21C x a x a =≤≤-且B C ⊆,求实数a 的取值范围.（1）当21=a 时，求(R B)⋂A; （2）若B A ⊆,求实数a 的取值范围。
安徽省六安市2016年高一数学(理)暑假作业 第二十三天 Word版含答案
第二十三天 完成日期 月 日 星期学法指导：理解递推公式与数列通项公式关系一、选择题（在每小题给出的四个选项中只有一项是符合题目要求的）1．已知数列{}n a 满足*111,2()n n n a a a n N +=⋅=∈，则10a =（ ） A ．64B ．32C ．16D ．82. 已知数列{}n a 满足：22111, 0, 1(*)n n n a a a a n +=>-=∈N ，那么使5n a <成立的n 的最大值为（ ）A.4B.5C.24D.25 3. 已知1112,1()n na a n N a *+==-∈，记数列{}n a 的前n 项之积为n T ，则2015T 的值为( )A ．－12B ．－1 C.12 D ．24. 在数列{}n a 中，12a =， 11ln(1)n n a a n+=++，则n a =( )A ．2ln n +B ．2(1)ln n n +-C ．2ln n n +D ．1ln n n ++ 5. 如果数列{}n a 满足122,1a a ==且1111++---=-n n n n n n n n a a a a a a a a (n ≥2),则此数列的第10项为( ) A.1021 B.921 C.101D.516. 已知数列{}n a 满足：11a =，12n n n a a a +=+，（*n N ∈），则数列{}n a 的通项公式为（ ）A ．21n n a =-B ．1122n n a -=-C.121n n a =-D.132n na =- 7. 已知数列{}n a满足112n a +=且112a =,则该数列的前 2 010项的和等于（ ） A.20153B.3 015C.1 005D.2 0108．满足*12121,log log 1()n n a a a n +==+∈N ，它的前n 项和为n S ，则满足1025n S >的最小n 值是（ ）A ．9B ．10C ．11D ．12二、填空题9．在数列{}n a 中，11a =，且对于任意自然数n ，都有1n n a a n +=+，则100a ＝ 10．在数列}{n a 中，已知11=a ，且满足11++=+n a a a nn n ，则n a =____________ 11．在数列}{n a 中，311=a ，n S 为数列}{n a 的前项和且n n a n n S )12(-=，则=n S ; 12．已知数列{}n a 满足：m a =1（m 为正整数），1,231,nn n n n a a a a a +⎧⎪=⎨⎪+⎩当为偶数时，当为奇数时。
安徽省六安市2016年高一数学理暑假作业第一天Word版含答案
第一天 完成日期 月 日 星期学法指导：1.理解集合的概念，元素与集合的关系。
2.识别集合之间的基本关系，并能用venn 图来描述相关基本运算。
一、选择题（在每小题给出的四个选项中只有一项是符合题目要求的） 1.设{}A C ,31|N {A },31|N S 则<<∈=≤≤∈=x x x x S 为（ ） A.∅B.{}3,1C.{}3,1==x xD.{}3,2,1 2.集合2{03},{9}P x Z x M x Z x =∈≤<=∈≤，则P M ⋂=（ ）A ．{}2,1 B.{}2,10，C ．{}30<≤x x D.{}30≤≤x x3.设集合{|(1)(2)0}A x x x =+-<，集合{|13}B x x =<<，则AB（ ）.{|13}A x x -<< .{|11}B x x -<< .{|12}C x x <<.{|23}D x x <<4.设集合⎭⎬⎫⎩⎨⎧∈+==⎭⎬⎫⎩⎨⎧∈+==Z k k x x N Z k k x x M ,214,,412,则（ ） A ． M=NNC. M ND . M N ⋂=∅5.设全集U=R,集合(2){|21},{|ln(1)}x x A x B x y x -=<==-，则图中阴影部分所表示的集合为（ ）A. {}1≥x xB. {}1≤x xC. {}21<≤x xD.{}10≤<x x6.设集合},01|{<<-=m m P }044|{2恒成立对任意的实数x mx mx m Q <-+=则下列关系中成立的是（ ） ≠⊂ ≠⊃A. P ⊆QB. Q ⊆PC. P=QD. P ⊄Q7.{|,},()().M N M N x x M x N M N M N N M -=∈∉⊕=-⋃-对于集合、，定义且2{|3,},{|2,}.x A y y x x x R B y y x R A B ==-∈==-∈⊕=设则（ ） A.]0,49(-B.)0[)49,(∞+⋃--∞， C.)0,49[- D.)0()49,(∞+⋃--∞，8.已知{=P ︳=(1,0)+m (0,1),}R m ∈,{=Q ︳=(1,1)+n (-1,1),}R n ∈是两个向量集合，则P ⋂Q=( )A.(){}11，B. (){}1,1-C.(){}01，D.(){}10，二、填空题9.已知集合,1},02|{2A a x x x A ∉>+-=且则实数a 的取值范围是 . 10.若集合},4,3,2,1{},,,{=d c b a 且下列四个关系：①1=a ；②1≠b ；③2=c ；④4≠d 有且只有一个是正确的，则符合条件的有序数组),,,(d c b a 的个数是_________. 11. 设,a b R ∈，集合{}1,,0,,a a b b a b ⎧⎫+=⎨⎬⎩⎭，则a b -= . 12. 设{}{}260,10,P x x x Q x mx m R =+-==+=∈，若Q P P ⋃=，则实数m 取值的集合是 .三、解答题（应写出文字说明、证明过程或演算步骤） 13.含有三个实数的集合可表示为⎭⎬⎫⎩⎨⎧1,,a b a ，也可表示为{}0,,2b a a +， 求20162016a b +的值．14．已知R x ∈，集合{}0232=+-=x x x A ，{}022=+-=mx x x B ，若B B A =⋂，求实数m 的取值范围．15.设集合{}260P x x x =--<，{}0Q x x a =-≥ （1）若P Q ⋂=∅，求实数a 的取值范围. （2）若P Q ⊆，求实数a 的取值范围.【链接高考】16.【2010湖南】若规定E={}1210,,,a a a …的子集{}12nk k k a a a ，，…，为E 的第k 个子集，其中12111222n k k k k ---=+++… ，则（1）{}1,3,a a 是E 的第 个子集； （2）E 的第211个子集是 .第一天9. 1a ≤; ; ;12. 0m =或13或12- 13. -1; 14.3m m -<<=或 15.(1) 3a ≥; (2) 2a ≤-. 16. 5，{}12578,a a a a a ，，，。
安徽省六安市2016年高一数学(理)暑假作业 第十九天 Word版含答案
第十九天 完成日期 月 日 星期学法指导：掌握等差数列定义、公式及性质一、选择题(在每小题给出的四个选项中只有一项是符合题目要求的） 1. 等差数列{}n a 中564a a +=，则310122log (2222)a a aa ⋅⋅⋅⋅=…（ ）A ．10B ．20 C ．40D ．22log 5+2. 已知等差数列{}n a 的前n 项和为n S ，且415a =，555S =，则数列{}n a 的公差是（ ）A ．14B ．4C ．4-D ．3-3. 设n S 是等差数列{}n a 的前n 项和，若3163=S S ，则 =126S S（ ） A ．310B ．13 C ．18D ．194. 在等差数列{}n a 中，912162a a =+，则数列{}n a 的前11项和S 11等于（ ） A.24B.48C.66D .1325．在等差数列{}n a 中31140a a +=，则45678910a a a a a a a -+++-+的值为（ ）A.84B.72C. 60D. 48 6. 已知n S 是等差数列{n a }的前n 项和，且83S S =，k S S =7，则k 的值为（ ）A.3B.4C.5D.67．等差数列{}n a 中,n S 是其前n 和,12013a =-,20132010320132010S S -=,则2013S =( ) A.2012-B. 2012C.2013-D. 20138. 记数列{}n a 的前n 项和为n S ，若不等式 22212n nS a ma n+≥对任意等差数列{}n a 及任意正整数n都成立，则实数m 的最大值为（ ）A ．12 B ．13 C ．14 D ．15二．填空题9.等差数列{}n a 中，若58215a a a -=+，则5a 等于10.等差数列{}n a 的前n 项和是n S ，若125a a +=，349a a +=，则10S 的值为 11．有两个等差数列2,6,10，…，190及2,8,14，…，200，由这两个等差数列的公共项按从小到大的顺序组成一个新数列，则这个新数列}{n a 的通项公式=na12. 数列}{n a 满足11=a ，且11+=-+n a a n n ，则数列}1{na 的前10项和为 .三．解答题（应写出文字说明、证明过程或演算步骤） 13．已知数列{}n a 中，1131,25n n a a a -==-(+∈≥N n n ,2)，且11n n b a =- (+∈N n )．（1）求证：数列{}n b 是等差数列；（2）求数列{}n a 中的最大项和最小项，并说明理由．14．在各项均为正数的等比数列{}n a 中，21=a ，且12a ，3a ，23a 成等差数列．(1) 求等比数列{}n a 的通项公式； (2) 若数列{}n b 满足n n a b 2log 211-=，求数列{}n b 的前n 项和n T 的最大值.15．设等差数列{}n a 的前n 项和为n S ，已知0,0,1212123<>=S S a .（1）求公差d 的取值范围；（2）指出1221,,,S S S 中，哪一个最大，并说明理由．【链接高考】16. 【2015高考新课标1】n S 为数列{n a }的前n 项和.已知n a ＞0，2n n a a +=43n S +.（Ⅰ）求{n a }的通项公式； （Ⅱ）设11n n n b a a +=,求数列{n b }的前n 项和.第19天1. B2.B3.A4.D 5C 6.B 7.C 8.D9、 5 10、65 11、12n －10 12、201113、当n ＝3时，n a 取得最小值－1，当n ＝4时，a n 取得最大值3. 14、 (1)nn a 2=；(2)25 15、（1）－247<<d －3.（2）前6项和S 6最大 16.（1）21n +（2）11646n -+。
高一暑假作业答案,高一暑假作业参考答案
高一暑假作业答案,高一暑假作业参考答案下面是整理的高一暑假作业答案，仅供参考。
语文数学英语第一模块作业(一)一、单项填空1～5BCDAC二、完形填空1～5ABCCB 6～10ADDBC 11～15DABDA三、单词填空 1. geography 2. information 3. move 4. disappears 5. previous四、句型转换1. didn’t; until 2. twice as 3. most interested 4. It’s;that5. my/me going第一模块作业(二)一、单项填空1～5BACDD二、阅读理解1～3BACD三、单词填空 1. embarrassed 2. enthusiastic 3. encouragement 4. interested5. after-class四、阅读表达1. Teaching in the US2. Explanations, preparations, using good examples, answering questions and organization of classes.3. Yes. If they don’t read books before classes (或Without reading books before classes), they will find it very difficult to understand the classes.4. 学生应该把他们所学到的知识应用到学习上去。
5. Seminars are proper for him because this kind of class emphasizes discussions and presentation by the students.一、单项填空1～5BDCAB二、完形填空1～5ACCBD 6～10AABCD 11～15BACAD 16～20BCCBD三、单词填空1.energetic 2. immediately 3. headmistress 4. nervous5. organis/zed四、句型转换1. pass; unless 2. as a result 3. so; that 4. will win5. than watch第二模块作业(二)一、单项填空1～5DBACD二、阅读理解1～3DCB三、单词填空1. relationship 2. scientific 3. appreciate 4. impression 5. admitted四、阅读表达1. The Fairy Lilies.2. The noise came from the fairy babies and the fairy mothers.3. Because she wanted to protect the lily flowers and keep the fairy mothers and babies untroubled.4. If we give love to others, we will get love in return.5. 但那个老妇人的坟墓却因为有美丽的歌声所笼罩而变得美丽葱绿，在坟墓及其周围开满了百合、郁金香等，还有其他美丽的春之花。
安徽省六安市2016年高一数学(理)暑假作业 第十二天
第十二天 完成日期 月 日星期学法指导：1.能画出正弦，余弦，正切函数图像，了解三角函数的周期性。
2.理解正弦，余弦，正切函数在一个周期上的性质（如单调性，最值，对称轴和对称中心）一、选择题（在每小题给出的四个选项中只有一项是符合题目要求的） 1．要得到函数⎪⎭⎫⎝⎛-=62sin πx y 的图象，可以将函数x y 2cos =的图象（ ）A ．向右平移6πB ．向右平移3π C ．向左平移6π D ．向左平移3π2①在⎪⎭⎫ ⎝⎛20π，上递减；②以π2为周期；③是奇函数.（ ） A.x y tan = B.x y cos =C.x y sin -=D.xx y cos sin =3. 下列四个函数x y 2tan =，x y 2cos =，x y 4sin =, 其中以点)0,4(π为中心对称的三角函数有（ ）个 A ．1B ．2C ．3 D. 04. 设函数cos y a x b =+（,a b 为常数)的最大值是1，最小值是-7，那么函数cos sin y a x b x =+的最大值是（ ） A.1B.4C.5D.75．函数x y sin =的一个单调增区间是（ ）A.)4,4(ππ- B.)43,4(ππ C.)23,(ππ D. )2,23(ππ6. 已知⎪⎭⎫⎝⎛∈ππβα,2,且0sin cos >+βα下列各式中成立的是（ ）A.πβα<+B.23πβα>+ C.23πβα=+ D.23πβα<+ 7．ω是正实数，函数x x f ωsin 2)(=在]4,3[ππ-上是增函数，那么（ ）A ．230≤<ω B ．20≤<ωC ．7240≤<ω D ．2≥ω8. 已知函数)2,0,0)(sin()(πϕωϕω≤>>+=A x A x f 的部分图象如图所示，则ϕ=（ ）A ．6π B ．3πC ．6π-D ．3π-二、填空题9．若,(0,)2παβ∈，cos()2βα-=1sin()22αβ-=-，则cos()αβ+的值等于 10. 设常数a 使方程 a x x =+cos 3sin 在闭区间]2,0[π上恰有三个解321,,x x x ，则=++321x x x11．函数1cos sin -=x x y 的最小正周期与最大值的和为 ． 12．设当θ=x 时，函数x x x f cos 2sin )(-=取得最大值，则=θcos . 三、解答题（应写出文字说明、证明过程或演算步骤） 13．求=)(x f )2cos(21x --π的定义域和值域.14．已知函数a x x x f ++-=sin sin )(2. （1）当0)(=x f 有实数解时，求a 的取值范围；（2）若R x ∈，有417)(1≤≤x f ，求a 的取值范围。
安徽省六安市2016年高一物理暑假作业第11天Word版含答案
第十一天运动的合成与分解1．如图所示，一块橡皮用细线悬挂于O点，现用一支铅笔贴着细线的左侧水平向右以速度v匀速移动，运动进程中维持铅笔的高度不变，悬挂橡皮的那段细线维持竖直，则在铅笔未碰着橡皮前，橡皮的运动情形是()A．橡皮在水平方向上做匀速运动B．橡皮在竖直方向上做匀加速运动C．橡皮的运动轨迹是一条直线D．橡皮在图示虚线位置时的速度大小为v2cos1θ+2．在无风的情形下，跳伞运动员从水平飞行的飞机上跳伞，下落进程中受到空气阻力，已知物体速度越大受到的空气阻力越大，下列描述下落速度的水平分量大小v x、竖直分量大小v y与时刻t的图象，可能正确的是()3．如图所示，一块橡皮用细线悬挂于O点，用钉子靠着线的左侧，沿与水平方向成30°角的斜面向右以速度v匀速运动，运动中始终维持悬线竖直，下列说法正确的是()A．橡皮的速度大小为2vB．橡皮的速度大小为3vC．橡皮的速度与水平方向成30°角D．橡皮的速度与水平方向成45°角4．如图所示，人沿平直的河岸以速度v行走，且通过不可伸长的绳拖船，船沿绳的方向行进，此进程中绳始终与水面平行．当绳与河岸的夹角为α时，船的速度大小为（）A．v sin αB．vsin αC．v cos αD．vcos α5．如图所示，甲、乙两同窗从河中O点起身，别离沿直线游到A点和B点后，当即沿原线路返回到O点，OA、OB别离与水流方向平行和垂直，且OA＝OB.若水流速度不变，两人在静水中游速相等，则他们所历时刻t甲、t乙的大小关系为（）A．t甲<t乙B．t甲＝t乙C．t甲>t乙D．无法确信6．如图，沿竖直杆以速度v匀速下滑的物体A通太轻质细绳拉滑腻水平面上的物体B，细绳与竖直杆间的夹角为θ，则以下说法正确的是（）A．物体B向右匀速运动B．物体B向右匀加速运动C．细绳对A的拉力慢慢变小D．细绳对B的拉力慢慢变大7. 质量为m=4 kg 的物体在滑腻的水平面上运动,在水平面上成立x0y坐标系,t=0时,物体位于坐标系的原点0.物体在x轴和y轴方向上的分速度v x、v y随时刻t转变的图象如图甲、乙所示.求:(1)t = s时,物体受到的合力的大小和方向;(2)t = s时,物体速度的大小和方向;(3)t = s时,物体的位置(用位置坐标x、y表示)8．如图，一条小船位于200 m 宽的河正中A 点处，从那个地址向下游m 3100处有一危险区，那时水流速度为4 m ／s ，为了使小船躲开危险区沿直线抵达对岸，小船在静水中的速度至少是多大？9．如图，重物A 、B 由刚性绳拴接，跨过定滑轮处于图中实线位置，此刻绳恰好拉紧，重物静止在水平面上，用外力水平向左推A ，当A 的水平速度为v A 时，如图中虚线所示，求此刻B 的速度v B10．一小船渡河，河宽d ＝180 m ，水流速度v 1＝2.5 m/s.若船在静水中的速度为v 2＝5 m/s ，求：(1)欲使船在最短的时刻内渡河，船头应朝什么方向？用多长时刻？位移是多少？(2)欲使船渡河的航程最短，船头应朝什么方向？用多长时刻？位移是多少？第11天 1． A 2． B 3．B 4．C 5．C 6．D 7. (1) 2 N ， 方向沿y 轴正方向；(2) 5 m/s,与x 轴正方向夹角α=34arctan (3) x = 24 m ， y =16 m 8．2m/s 9．A v 3 10．(1)船头垂直于河岸 36 s 905m (2)船头向上游偏30° 243s 180 m。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
第十一天 完成日期 月 日星期
学法指导：理解三角函数的相关概念，同角三角函数的基本关系。
一、选择题（在每小题给出的四个选项中只有一项是符合题目要求的）
1. 将表的分针拨慢10分钟，则分针转过的角的弧度数是
（ ）
A.
3
π
B.
6
π
C.-
3
π
D.-
6
π 2. 已知扇形的周长是6cm ，面积是22
cm ，则扇形的圆心角的弧度数是
（ ）
A.1
B.4
C.1或4
D.2或4 3. 已知角α终边上一点P 的坐标是（2sin 2,2cos 2-)，则αsin 等于 （ ）
A.2sin
B.2sin -
C.2cos
D. 2cos -
4. α是第二象限角，(P x 为其终边上一点，且cos 4
x a =，则αsin 的值为
（ ）
A ．
4B ．4C ．4
D ．4
5. 若α为第二象限角，则下列各式恒小于零的是
（ ） A ．αα
cos sin + B ．ααsin tan +
C ．1
cos tan a
a
-
D ．ααtan sin - 6. 已知αsin =5
5，则αα44
cos sin -的值为
（ ） A.5
3
-
B.51
-
C.5
1 D.5
3
7. 若βαtan ,tan 是关于x 的方程2
0x px q -+=的两个实根，
β
αtan 1,tan 1是关于方程02=+-s rx x 的两个实根，那么=rs
（ ） A ．pq B ．1
pq C ．
2
p q
D ．2q p 8. 若5sin 2cos -=+αα,则αtan 等于
（ ）
A.2
1 B.
2 C.2
1
-
D.-2
二.填空题
9. 已知tan 2θ=，则22
sin sin cos 2cos θθθθ+-= .
10．已知角α的终边落在直线)0(3<-=x x y 上，则
=-
α
αα
αcos cos sin sin .
11．若()π,0∈A ,且137cos sin =+A A ,则=-+A
A A A cos 7sin 15cos 4sin 5 . 12.
)
2sin()2
(
sin )tan()2cos()cos()(sin 3
2πααπ
αππααππα--∙+∙+--∙+∙+= ．
三.解答题（应写出文字说明、证明过程或演算步骤） 13. 已知a a +-=11sin θ,a
a +-=11
3cos θ,若θ是第二象限角，求实数a 的值.
14.已知3
1sin sin =+y x ，求x y 2
cos sin -的最大值.
15.设函数
)(x f 满足)2
|(|,cos sin 4)(sin 3)sin (π
≤
=+-x x x x f x f .
（1）求函数
)(x f 的解析式；
（2）求)(x f 的值域；
（3）设函数2
()2cos sin g x x x m =++,对任意R x ∈0,有0()()g x f x <恒成立,试求实数m
的取值范围.
【链接高考】
16. 【2015高考重庆】若tan 2tan 5
πα=，则
3cos()
10sin()
5παπα-
=-
（ ）
A 、1
B 、2
C 、3
D 、4
第十一天
1.A
2.C
3.D
4.A
5.B
6.A
7.C
8.B
9. 45 10．2. 11.43
8
. 12.1 13 . 9
1
14 .94
15 （1
）()2f x =[1,1]x ∈- （2）[1,1]- （3）3m <- 16.C。