实验18用亥姆霍兹线圈测磁场空白表格
亥姆霍兹线圈磁场的测量实验报告
亥姆霍兹线圈磁场的测量实验报告
亥姆霍兹线圈是- -对相同的、共轴的、彼此平行的各有N匝的圆环电流。
当它们的间距正好等于其圆环半径R时，称这对圆线圈为亥姆霍兹线圈。
在亥姆霍兹线圈的两个圆电流之间的磁场比较均匀。
在生产和科研中经常要把样品放在均匀磁场中作测试，利用亥姆霍兹线圈是获得-种均匀磁场的比较方便的方法。
一、实验目的
1.熟悉霍尔效应法测量磁场的原理。
2.学会亥姆霍兹磁场实验仪的使用方法。
3.测量圆线圈和亥姆霍兹线圈上的磁场分布，并验证磁场的叠加原理
二、实验原理
同学们注意，根据自己的理解，适当增减，不要太多，有了重点就可以了。
1.霍尔器件测量磁场的原理
如图3- -8--1 所示，有一N型半导体材料制成的霍尔传感器，长为L，宽为b，厚为d,其四个侧面各焊有-一个电极1、2、3、4。
将其放在如图所示的垂直磁场中，沿3、4两个侧面通以电流I，电流密度为J，则电子将沿负J方向以速度ve运动，此电子将受到垂直方向磁场B的洛仑兹力=ev。
B作用，造成电子在半导体薄片的1
测积累过量的负电荷，2侧积累过量的正电荷。
因此在薄片中产生了由2侧指向1侧的电场g，该电场对电子的
作用力F。
=eEx与序=evgB反向，当两种力相平衡时，便出现稳定状态，1、2两侧面将建立起稳定的电压Uz，此种效应为霍尔效应，由此而产生的电压Uz叫霍尔电压，1、2端输出的霍尔电压可由数显电压表测量并显示出来。
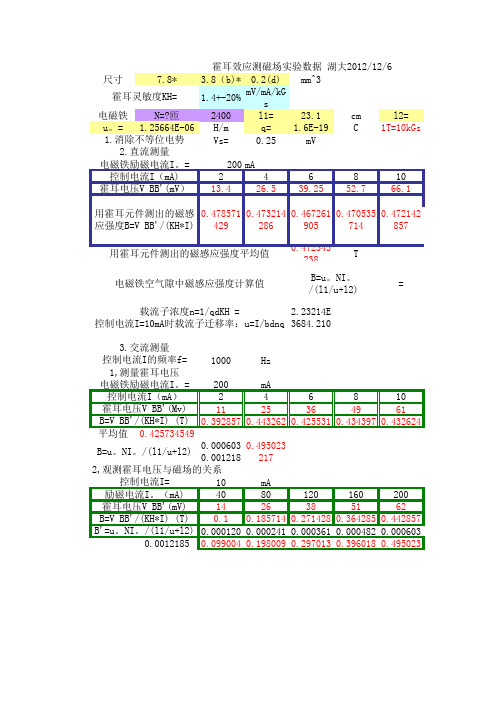
霍耳效应测磁场 实验数据
0.472345238
T =
B=u。NI。 /(l1/u+l2)
2.23214E+19 3684.210526
1000 200 2 11
Hz mA 4 25
6 36
8 49
10 61
0.392857143 0.443262411 0.425531915 0.434397163 0.432624113 0.000603186
2/6
0.118
cmΒιβλιοθήκη u=60000.000603186
0.0012185
0.495023217
T
0.478571429 0.473214286 0.467261905 0.470535714 0.472142857
用霍耳元件测出的磁感应强度平均值 电磁铁空气隙中磁感应强度计算值 载流子浓度n=1/qdKH = 控制电流I=10mA时载流子迁移率：u=I/bdnq 3.交流测量 控制电流I的频率f= 1,测量霍耳电压 电磁铁励磁电流I。= 控制电流I（mA） 霍耳电压V BB'(Mv) B=V BB'/(KH*I) (T) 平均值 0.425734549 B=u。NI。/(l1/u+l2)
霍耳效应测磁场实验数据 湖大2012/12/6 尺寸 7.8* 3.8（b)* 0.2(d) mm^3 霍耳灵敏度KH= 1.4+-20% mV/mA/kGs 电磁铁 N=?匝 2400 l1= 23.1 cm l2= u。= 1.25664E-06 H/m q= 1.6E-19 C 1T=10kGs 1.消除不等位电势 Vs= 0.25 mV 2.直流测量 电磁铁励磁电流I。= 200 mA 控制电流I（mA) 2 4 6 8 10 霍耳电压V BB'(mV） 13.4 26.5 39.25 52.7 66.1 用霍耳元件测出的磁感 应强度B=V BB'/(KH*I)
亥姆霍兹线圈磁场实验
亥姆霍兹线圈磁场实验课次班号:日期:实验室名称:试验人:指导老师:实验目的（1）学习感应法测量磁场的原理和方法;（2）研究研究亥姆霍兹线圈周线上的磁场分布.主要仪器磁场测试仪、亥姆霍兹线圈架和亥姆霍兹磁场实验控制箱.工作温度10～35℃，相对湿度25%～75%.两个励磁线圈各500匝，圆线圈的平均半径105R =mm,两线圈中心间距105mm.感应线圈距离分辨率0.5mm.实验原理一、载流圆线圈与亥姆霍兹线圈1、载流圆线圈磁场半径为R 通以电流为I 的圆线圈，周线上磁场的公式为)(22223200X R RN I B +=μ式中0N 为线圈的匝数；x 为轴上某一点到圆心O 的距离；710410H m μπ-=⨯⋅.本次实验取I=200mA.2、亥姆霍兹线圈两个相同线圈彼此靠近，使线圈上通以同向电流理论计算证明：线圈间距a 等于线圈半径R 时，两线圈合场在轴附近较大范围内是均匀的.这时线圈称为亥姆霍兹线圈，如图所示.二、电磁感应法测磁场1.电磁感应法测磁场的原理设由交流信号驱动的交变磁场的强度sin m B B t ω=，设有一个探测线圈放在这个磁场中，通过这个探测线圈的有效磁通量为cos sin m NSB tθωΦ=式中，N 为探测线圈的匝数，S 为线圈的截面积；θ为B 与线圈法线夹角.线圈产生的感应电动势为d cos cos cos d m m NS B t t tεωθωεωΦ=-==-当0θ=时，max m NS B εω=.用数字式毫伏表测量此时线圈的电动势，则其示值max U 应为，则max maxmax 2U B NS NS εεω==（1）由（1）式可以计算出m B .实验内容1.测量亥姆霍兹线圈周线上的磁场分布2.验证公式cos m m NS B εωθ=3.*研究励磁电流频率改变对磁场强度的影响数据记录与处理：表1载流圆线圈轴线上的磁场分布轴向距L（mm）100-10-20-30-40-50实测磁场B（mT）0.3450.3870.4260.4660.50.5250.534轴向距L（mm）-60-70-80-90-100-110实测磁场B（mT）0.5320.5160.4910.4550.4140.372作出B——L 图象：亥姆霍兹线圈轴上磁场分布注意事项1、开机后应至少预热10分钟才可进行试验.2、更换测量位置时，应切断励磁线圈的电流后将将感应电动势调零；之后再通电测量读数.这时为了抵消地磁场的影响及对其他不稳定因素的补偿.试验建议HD4501型亥姆霍兹磁场试验仪使用螺旋转轴的旋转来控制探测线圈的移动.螺纹的螺距较小，这样可以提高调节的精度；但也使较大距离的移动很不方便.如果如果再次制造该类型的仪器，可以考虑使用较大螺距的螺纹.本实验使用的装置可谓“一体化”，这使操作很方便；但这也使主要实验误差来源于仪器本身，限制了实验可能达到的精度.实验数据：。
亥姆霍兹线圈磁场测定实验报告模板
B(x) x O图3.3.1 载流线圈轴线上磁场B(x) xO 图3.2.2 亥姆霍兹线圈轴线上磁场实验预习部分 一、实验目的：1.测亥姆霍兹线圈在轴线上的磁场分布。
2.测载流圆线圈在轴线上的磁场分布，验证磁场叠加原理。
3.比较两载流圆线圈距离不同时轴线上磁场分布情况。
二、实验仪器设备：FD-HM-І型磁场测定仪由圆线圈和亥姆霍兹线圈实验平台（包括两个圆线圈、固定夹、不锈钢直尺、铝尺）、高灵敏度毫特计和数字式直流稳流电源等组成。
三、实验原理一、圆线圈载流圆线圈在轴线（通过圆心并与线圈平面垂直的直线）上磁场情况如图1。
根据毕奥萨伐尔定律，轴线上某点的磁感应强度B 为I N x R R B ⋅+⋅=2/32220)(2μ （3.3.1）式中I 为通过线圈的电流强度，N为线圈匝数，R 线圈平均半径，x 为圆心到该点的距离，0μ为真空磁导率。
而圆心处的磁感应强度0B 为I N R B ⋅=200μ（3.3.2）轴线外的磁场分布情况较复杂，这里简略。
二、亥姆霍兹线圈亥姆霍兹线圈是一对彼此平行且连通的共轴圆形线圈，每一线圈N 匝，两线圈内的电流方向一致，大小相同，线圈之间距离d 正好等于圆形线圈的平均半径R 。
其轴线上磁场分布情况如图3.3.2所示，虚线为单线圈在轴线上的磁场分布情况。
这种线圈的特点是能在其公共轴线中点附近产生较广的均匀磁场区，故在生产和科研中有较大的实用价值，也常用于弱磁场的计量标准。
设x 为亥姆霍兹线圈中轴线上某点离中心点O 处的距离，则亥姆霍兹线圈轴xB (x )OB (x )x O实验预习部分线上任一点的磁感应强度大小B '为3/23/22222201222R R B N I R R x R x μ--⎧⎫⎡⎤⎡⎤⎛⎫⎛⎫⎪⎪'=⋅⋅⋅++++-⎢⎥⎢⎥⎨⎬ ⎪ ⎪⎝⎭⎝⎭⎢⎥⎢⎥⎪⎪⎣⎦⎣⎦⎩⎭（3.3.3）而在亥姆霍兹线圈轴线上中心O 处磁感应强度大小'0B 为003/285N IB Rμ⋅⋅'= （3.3.4）三、双线圈若线圈间距d 不等于R 。
亥姆霍兹线圈磁场测定-实验报告
亥姆霍兹线圈磁场测定-实验报告实验目的：1. 掌握亥姆霍兹线圈原理及其构造；2. 熟悉磁场测定的基本方法；3. 使用亥姆霍兹线圈测定磁场的强度，了解其精度；4. 熟悉使用万用表和数字万用表进行电量测量。
实验原理：亥姆霍兹线圈是一种特殊的线圈结构，由两个同轴的环形线圈组成，两个线圈的半径相等，通电方向相反，电流强度相等，在同一轴向上构成匀强磁场。
如果通过两线圈流同向电流，其磁场强度将会倍增。
由于外界物体的磁场强度对线圈的磁场有一定的影响，因此在实验过程中，需要先测定环境中的磁场强度，再将线圈放置于恒定的磁场中，通过测量线圈中的磁场强度差，求得外磁场的强度。
实验器材：亥姆霍兹线圈、数字万用表、长板子、短板子、直流电源等。
实验步骤：1. 将亥姆霍兹线圈放置于平稳的桌面上，用数字万用表测定环境中的磁场强度，记录下读数。
2. 在同一位置，保持线圈不动，通过调节直流电源输出电压，使亥姆霍兹线圈中的磁场强度降低至为0。
记录下此时的电压值，并将其记作$U_0$。
5. 测量亥姆霍兹线圈本身的参数：使用数字万用表测量亥姆霍兹线圈中圈数，环半径等参数。
6. 计算环境中的磁场强度B0：根据数字万用表测量得到的环境磁场强度读数，使用其对应的磁场表值作为环境磁场强度B0。
7. 计算磁场强度B：由均匀磁场的定义，设线圈中磁场$B_1$和$B_2$分别为直流电源输出电压为$U_1$和$U_2$时线圈中磁场的强度，则有$B=\frac{1}{2}(B_1+B_2)$。
8. 计算外界磁场的强度B': 由于亥姆霍兹线圈内自带磁场，需要在计算磁场强度B 时，减去线圈的自感磁场强度$B_{self}$。
因此，有$B'=B-B_{self}$。
9. 计算磁场强度的不确定度：需考虑设备测量误差和环境影响因素的影响，根据不确定度的综合误差计算公式$U=\sqrt {\sum_{i=1}^n u_i}$，其中n为误差项的数目，$u_i$为每一误差项的保守评估。
亥姆霍兹线圈的测量磁场
B
=
1 2
μ 0 NIR 2 ⎪⎨⎧⎢⎡R 2 ⎪⎩⎢⎣
+ ⎜⎛ ⎝
R 2
+
z
⎟⎞
2
⎤ ⎥
−
3
2
⎠ ⎥⎦
+
⎡ ⎢R2 ⎢⎣
+
⎜⎛ ⎝
R 2
−
z
⎟⎞
2
⎤ ⎥
−
3 2
⎠ ⎥⎦
⎫ ⎪ ⎬ ⎪⎭
而在亥姆霍兹线圈轴线上中心 O 处磁感应强度 B0 为
B = μ0 N0 I × 16 = 1.43×1.431 = 2.05mT 2R 53/2
假定选择励磁线圈(左)为实验对象。将测量仪面板上的偏置电压与测试架的偏置电压相 连，霍尔电压与霍尔电压相连。
将测试架励磁线圈(左)的两端与测量仪上的励磁电流两端相连。红接线柱与红接线柱相 连，黑接线柱与黑接线柱相连。
调节励磁电流为零，将磁感应强度清零。 调节磁场测量仪的励磁电流调节电位器，使表头显示值为 500mA，此时毫特计表头应显 示一对应的磁感应强度 B 值。 以圆电流线圈中心为坐标原点，每隔 10.O mm 测一磁感应强度 B 的值，测量过程中注意 保持励磁电流值不变。 选做内容：在实验过程中可以将励磁电流反接，即测量仪上励磁电流的两端子的连线对 调。再重复上述过程，可以测得一组负的磁感应强度 B 值。即此时的磁感应强度方向已反向。 （2）测量亥姆霍兹线圈轴线上磁场的分布 按图 7 接线，然后在励磁电流为零的情况下将磁感应强度清零。 调节磁场测量仪的励磁电流调节电位器，使表头显示值为 500mA，此时毫特计表头应显 示一对应的磁感应强度 B 值。 以亥姆霍兹线圈中心为坐标原点，每隔 10.O mm 测一磁感应强度 B 的值，测量过程中注 意保持励磁电流值不变。 选做内容：在实验过程中同样可以将励磁电流反接，即测量仪上励磁电流的两端子的连 线对调。再重复上述过程，可以测得一组负的磁感应强度值 B。即此时的磁感应强度方向已 反向。注意：由于显示位数的限制，当测量的 B 值达到或大于一 2.000mT 时，负号标记将闪 烁，表示测量的 B 值为负。 （3）励磁电流大小对磁场强度的影响 此时可以选择单线圈或者亥姆霍兹线圈磁场分布测量的连线方法之一进行连线，仍然在 励磁电流为零的情况下将磁感应强度清零。 调节磁场测量仪的励磁电流调节电位器，使表头显示值为 100mA，将霍尔化感器的位置 调节到以圆电流线圈中心位置或者亥姆霍兹线圈中心位置。 调节节励磁电流调节电位器，每增加 lOOmA 记下一磁感应强度 B 的值，直到励磁电流显 示为 500mA 记下一磁感应强度 B 值为止。 2.测试数据处理 （1）将圆电流线圈轴线上磁场分布的测最数据记录于表 l(注意坐标原点设在圆心处。表格 中包括测点位置，磁感应强度 B 值(从数字式毫特表上读取)，在同一坐标纸上画出实验曲线
实验报告磁场的研究
实验题目： 磁场的研究1.实验目的：1、研究载流圆线圈轴线上各点的磁感应强度，把测量的磁感应强度与理论计算值比较， 加深对毕奥-萨伐尔定律的理解;2、在固定电流下，分别测量单个线圈（线圈a 和线圈b ）在轴线上产生的磁感应强度B （a ）和B(b)，与亥姆霍兹线圈产生的磁场B(a+b ）进行比较，3、测量亥姆霍兹线圈在间距d=R ／2、 d=R 和d=2R, （R 为线圈半径），轴线上的磁场的分布，并进行比较，进一步证明磁场的叠加原理；4、描绘载流圆线圈及亥姆霍兹线圈的磁场分布。
2.实验仪器：(1)圆线圈和亥姆霍兹线圈实验平台，台面上有等距离1.0cm 间隔的网格线；(2)高灵敏度三位半数字式毫特斯拉计、三位半数字式电流表及直流稳流电源组合仪一台；(3)传感器探头是由2只配对的95A 型集成霍尔传感器(传感器面积4mmx 3mmx 2mm)与探头盒(与台面接触面积为20mmx 20mm)组成。
3.实验原理：（1)根据毕奥一萨伐尔定律，载流线圈在轴线(通过圆心并与线圈平面垂直的直线)上某点的磁感应强度为：232220)(2x R NR I B +=μ （5-1)式中μ0为真空磁导率，R 为线圈的平均半径，x 为圆心O A 到该点的距离，N 为线圈匝数，I 为通过线圈的电流强度。
因此，圆心处的磁感应强度B 0 为：R INB 20μ= （5-2）轴线外的磁场分布计算公式较为复杂，这里简略。
(2)亥姆霍兹线圈是一对彼此平行且连通的共轴圆形线圈，两线圈内的电流方向一致，大小相同，线圈之间的距离d 正好等于圆形线圈的半径R 。
这种线圈的特点是能在其公共轴线中点附近产生较广的均匀磁场区，所以在生产和科研中有较大的使用价值，也常用于弱磁场的计量标准。
设：z 为亥姆霍兹线圈中轴线上某点离中心点O 处的距离，则亥姆霍兹线圈轴线上任意一点的磁感应强度为 ：⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫ ⎝⎛-++⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫ ⎝⎛++='--23222322202221z R R z R R NIR B μ（5-3） 而在亥姆霍兹线圈上中心O 处的磁感应强度B 0′为RNI B 02/3058μ=' （5-4）4.数据记录2、 对载流圆线圈通过电流I=120mA 时轴线上各点磁感应强度的测量。
亥姆霍兹线圈磁场测定
实验数据处理嘉应学院物理学院普通物理实验实验报告实验项目：实验地点：班级：姓名：座号：实验时间： 年 月 日一、实验目的：二、实验仪器和用具：（1）圆线圈和亥姆霍兹线圈实验平台，台面上有等距离cm 0.1间隔的网格线； （2）高灵敏度三位半数字毫特斯拉计、三位半数字电流表及直流稳流电源组合仪一台；（3）传感器探头是由2只配对的95A 型集成霍耳传感器（传感器面积4mm ×3mm ×2mm ）与探头盒。
（与台面接触面积为20mm ×20mm ）三、实验原理：(1)根据毕奥—萨伐尔定律，载流线圈在轴线（通过圆心并与线圈平面垂直的直线）上某点的磁感应强度为：I N x R R B ⋅+⋅=2/32220)(2μ （1） 式中0μ为真空磁导率，R 为线圈的平均半径，x 为圆心到该点的距离，N 为线圈匝数，I 为通过线圈的电流强度。
因此，圆心处的磁感应强度0B 为：I N RB ⋅=200μ（2）轴线外的磁场分布计算公式较为复杂，这里简略。
(2)亥姆霍兹线圈是一对彼此平行且连通的共轴圆形线圈，两线圈内的电流方向一致，大小相同,线圈之间的距离d 正好等于圆形线圈的半径R 。
这种线圈的特点是能在其公共轴线中点附近产生较广的均匀磁场区，所以在生产和科研中有较大的使用价值，也常用于弱磁场的计量标准。
设z 为亥姆霍兹线圈中轴线上某点离中心点O 处的距离，则亥姆霍兹线圈轴线上任意一点的磁感应强度为：⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫ ⎝⎛-++⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫ ⎝⎛++⋅⋅⋅='-222/322202221z R R z R R R I N B μ （3）而在亥姆霍兹线圈上中心O 处的磁感应强度'0B 为： R I N B ⋅⋅='02/3058μ四、实验步骤：（1）必做内容：载流圆线圈和亥姆霍兹线圈轴线上各点磁感应强度的测量。
1）按图1接线，直流稳流电源中数字电流表已串接在电源的一个输出端，测量电流mA I 100=时，单线圈a 轴线上各点磁感应强度)(a B ，每隔cm 00.1测一个数据。
实验报告-霍耳效应与亥姆霍兹线圈磁场测量
实用文档
【实验题目】【实验题目】 霍尔效应与亥姆霍兹线圈磁场测量
【实验记录】
1．实验仪器
2霍尔片工作电流I S ＝ , 零位霍尔电势 V 01＝ , V 02＝
不等位电阻R 01＝
S 01I V ＝ ， R 02＝S
02I V
＝ 3． 测量霍尔电压V H 与工作电流Is 的关系
计算霍尔元件的霍尔灵敏度（要求去除零位霍尔电势对实验结果的影响）
参考公式：'
010H H V V V I I -= 或 '
020
H H V V V I I -=
实用文档
4．亥姆霍兹线圈轴线上的磁感应强度测量
I S = I M =
5．亥姆霍兹线圈其中一个线圈的正负极交换成反接，测量轴线上的磁感应强度
I S = I M =
实用文档
【数据处理】
在同一坐标系中作出轴线上的磁感应强度曲线；定性分析零位霍尔电势对磁场测量结果的影响。
实用文档
【总结与讨论】
【复习思考题】
1．使用霍尔效应实验仪器要注意什么？
2．简述霍尔效应的应用，并针对某一应用简述其工作原理。
报告成绩（满分30分）：⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽指导教师签名：⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽日期：⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽。
电子版报告模版-亥姆霍兹线圈磁场测定
预约开放性实验实验报告——专业姓名学号实验时间实验地点物理实验中心2608亥姆霍兹线圈磁场测定亥姆霍兹线圈是一对相同的、共轴的、彼此平行的各有N匝的圆环电流。
当它们的间距正好等于其圆环半径R时，称这对圆线圈为亥姆霍兹线圈。
在亥姆霍兹线圈的两个圆电流之间的磁场比较均匀。
在生产和科研中经常要把样品放在均匀磁场中作测试，利用亥姆霍兹线圈是获得一种均匀磁场的比较方便的方法。
一、实验目的1. 熟悉霍尔效应法测量磁场的原理。
2. 学会亥姆霍兹磁场实验仪的使用方法。
3. 测量圆线圈和亥姆霍兹线圈上的磁场分布，并验证磁场的叠加原理二、实验原理同学们注意，根据自己的理解，适当增减，不要太多，有了重点就可以了,注意公式和图排序。
1.用霍尔原件测量磁场的原理图1 霍尔效应原理ss如图1所示，将n 型半导体(载流子为电子)加工成宽为a ，高为b 的长方形薄片，当从左向右通以电流I ，且在垂直方向加上方向向上的磁场B ，此时将在里外两侧面PQ 间产生电势差U H ,这种现象即为霍尔效应，电势差称为霍尔电压。
设薄片中的电子带电量为e , 运动方向与电流I S 方向相反, 平均漂移速率为v , 由于该薄片处在外磁场B 中, 且运动方向与磁场方向垂直，故电子受洛仑兹力为F m = evB （1）方向指向Q 侧。
因此, 将在Q 侧积累负电荷, 而在P 侧积累正电荷, 于是在P 、Q 两个侧面之间产生了由P 指向Q 的电场H (称为霍尔电场)。
产生的电场又给载流子一个与m F 反向的电场力e F ，当e m F F >时，H E 将随着P 、Q 两侧电荷的积累而继续增强。
当H E 增强到使电子受到的电场力F e (= eE H )与它受到的洛仑兹力F m (= evB )相等, 即E H = vB 时, 就达到了动态平衡, P 、Q 两侧的电荷不再增加。
这时在P 、Q 两侧之间产生了一个恒定的电势差, 即霍尔电压U H 。
亥姆霍兹线圈磁场实验报告
亥姆霍兹线圈磁场实验报告1. 背景亥姆霍兹线圈是一种用于产生均匀磁场的装置，由两个相同半径和间距的同轴圆线圈组成。
在实验中，我们将使用亥姆霍兹线圈来测量其产生的磁场强度与电流的关系，并验证其是否为均匀磁场。
2. 实验目的1.理解亥姆霍兹线圈的结构和原理；2.掌握使用亥姆霍兹线圈测量磁场强度的方法；3.验证亥姆霍兹线圈产生的磁场是否为均匀磁场；4.分析实验结果，得出结论并提出建议。
3. 实验装置和方法3.1 实验装置•亥姆霍兹线圈（包括两个同轴圆线圈、电源和电流控制器）•磁场计•电流表•直流电源•连接线3.2 实验方法1.将亥姆霍兹线圈放置在水平桌面上，调整线圈间距与半径，使其符合实验要求。
2.将直流电源和电流控制器连接到亥姆霍兹线圈上，将电流表连接到电流控制器上，确保电路连接正确。
3.打开直流电源，调节电流控制器使得电流稳定在设定值，记录电流强度。
4.将磁场计垂直放置于亥姆霍兹线圈的中心位置，记录磁场强度值。
5.调节直流电源的电流值，重复步骤3和4，记录一系列不同电流强度下的磁场强度值。
4. 分析与结果4.1 实验数据我们采集了一系列不同电流强度下的磁场强度值，并绘制了磁场强度与电流强度的关系图：电流强度（A）磁场强度（T）0.1 0.0250.2 0.0500.3 0.0750.4 0.1000.5 0.1254.2 数据处理根据测得的磁场强度值和电流强度值，我们可以绘制磁场强度与电流强度的关系图。
在这个图中，我们可以观察到一个线性关系，并计算出磁场强度与电流强度之间的比例系数。
根据电流对磁场产生的影响可以得到以下关系式：B=μ0⋅I⋅N 2⋅R其中，B为磁场强度，μ0为真空介质中磁导率，I为电流强度，N为线圈匝数，R为线圈半径。
通过线性拟合，我们可以得到磁场强度与电流强度之间的比例系数k。
4.3 结果分析通过拟合得到的结果，我们得到了磁场强度与电流强度之间的线性关系，证明亥姆霍兹线圈可以产生均匀的磁场。
亥姆霍兹线圈磁场实验
亥姆霍兹线圈磁场实验实验名称：亥姆霍兹日期：_ 专业班级：环境工程163班试验人：李璐驿学号：000 指导老师：钟双英实验目的（1）学习感应法测量磁场的原理和方法；（2）研究研究亥姆霍兹线圈周线上的磁场分布主要仪器磁场测试仪、亥姆霍兹线圈架和亥姆霍兹磁场实验控制箱•工作温度10〜35 C,相对湿度25%〜75%.两个励磁线圈各500匝，圆线圈的平均半径R 105mm两线圈中心间距105mm感应线圈距离分辨率•实验原理一、载流圆线圈与亥姆霍兹线圈1、载流圆线圈磁场半径为R通以电流为I的圆线圈，周线上磁场的公式为. 2B 0N01R 32（R2 x2r式中N。
为线圈的匝数；x为轴上某一点到圆心O的距离；° 4 107H m 1.本次实验取l=200mA.2、亥姆霍兹线圈两个相同线圈彼此靠近，使线圈上通以同向电流理论计算证明：线圈间距a等于线圈半径R时，两线圈合场在轴附近较大范围内是均匀的•这时线圈称为亥姆霍兹线圈，如图所示.实验内容1.测量亥姆霍兹线圈周线上的磁场分布2.验证公式m NS B m cos3.*研究励磁电流频率改变对磁场强度的影响数据记录与处理：表1B/mTX/mm -50 -45 -40 -35 -30 -25 -20 X/mm -15 -10 -5 0 5 10 15B/mTX/mm 20 25 30 35 40 45 50B/mT单義圈0.700O.K>CD.4G00.3000.200 0.1000.000■ 50 -45 网 司5 *30 '25-109510 15 20 25 30 35 40 45 50表二X/mm-100-90-80-70-60-50-40B/mTX/mm-30-20-10102030B/mTX/mm 40 50 60 70 80 90 100B/mT注意事项1、开机后应至少预热10分钟才可进行试验•2、更换测量位置时，应切断励磁线圈的电流后将将感应电动势调零；之后再通电测量读数.这时为了抵消地磁场的影响及对其他不稳定因素的补偿试验建议HD4501型亥姆霍兹磁场试验仪使用螺旋转轴的旋转来控制探测线圈的移动.螺纹的螺距较小，这样可以提高调节的精度；但也使较大距离的移动很不方便•如果如果再次制造该类型的仪器，可以考虑使用较大螺距的螺纹本实验使用的装置可谓“一体化”，这使操作很方便；但这也使主要实验误差来源于仪器本身，限制了实验可能达到的精度。
指导书-18用亥姆霍兹线圈测磁场
用亥姆霍兹线圈测磁场所谓亥姆霍兹线圈为两个相同线圈彼此平行且共轴，使线圈上通以同方向电流Ｉ，理论计算证明：线圈间距a 等于线圈半径R 时，两线圈合磁场在轴上（两线圈圆心连线）附近较大范围内是均匀的，如图5所示。
这种均匀磁场在工程运用和科学实验中应用十分广泛。
【实验目的】1、了解亥姆霍兹线圈的结构和工作原理；2、掌握载流圆线圈轴线上磁场的测量方法；3、掌握和亥姆霍兹线圈轴线上磁场的测量方法。
【实验仪器】亥姆霍兹线圈磁场实验仪。
实验仪由二部分组成，它们分别为励磁线圈架和磁场测量仪（见图 3，上部为励磁线圈架，下部为磁场测量仪），亥姆霍兹线圈架部分有一传感器盒，盒中装有用于测量磁场的感应线圈。
仪器参数：二个励磁线圈有效半径为105mm ，单个线圈匝数400匝，二线圈中心间距为105mm ；传感器盒横向移动范围250mm ，纵向移动范围70mm ，距离分辨率1mm ；传感器盒中探测线圈匝数为1000匝，旋转角度360o ； 【实验原理】一、载流圆线圈与亥姆霍兹线圈的磁场 1、 单个载流圆线圈磁场一半径为Ｒ，通以电流Ｉ的圆线圈，轴线上磁感应强度的计算公式为2/322200)(2X R IRN B +=μ （1）式中0N 为圆线圈的匝数，X 为轴上某一点到圆心O 的距离。
m H /10470-⨯=πμ。
轴线上磁场的分布如图2所示。
本实验取Ｎ０＝400匝，Ｒ＝105mm 。
当f=120Hz ，Ｉ＝60m Ａ（有效值）时，在圆心O 处x ＝0，可算得单个线圈的磁感应强度为：B=0.144mT 2、亥姆霍兹线圈设X 为亥姆霍兹线圈中轴线上某点离中心点O 处的距离，则亥姆霍兹线圈轴线上该点的磁感应强度为：}])2([])2({[212/3222/322200'---++++=X RR X R R IR N B μ （2） 而在亥姆霍兹线圈轴线上中心O 处，X =0，磁感应强度为：RIN RIN B O 002/300'7155.058μμ=⨯=（3）图1亥姆霍兹线圈磁场实验仪及接线方法架圈线仪量测图 2 单个圆环线圈磁场分布 图 3亥姆霍兹线圈磁场分布当实验取Ｎ０＝400匝，Ｒ＝105mm 。
亥姆霍兹线圈磁场测定
实验数据处理嘉应学院物理学院普通物理实验实验报告实验项目：实验地点：班级：姓名：座号：实验时间： 年 月 日一、实验目的：二、实验仪器和用具：（1）圆线圈和亥姆霍兹线圈实验平台，台面上有等距离cm 0.1间隔的网格线； （2）高灵敏度三位半数字毫特斯拉计、三位半数字电流表及直流稳流电源组合仪一台；（3）传感器探头是由2只配对的95A 型集成霍耳传感器（传感器面积4mm ×3mm ×2mm ）与探头盒。
（与台面接触面积为20mm ×20mm ）三、实验原理：(1)根据毕奥—萨伐尔定律，载流线圈在轴线（通过圆心并与线圈平面垂直的直线）上某点的磁感应强度为：I N x R R B ⋅+⋅=2/32220)(2μ （1） 式中0μ为真空磁导率，R 为线圈的平均半径，x 为圆心到该点的距离，N 为线圈匝数，I 为通过线圈的电流强度。
因此，圆心处的磁感应强度0B 为：I N RB ⋅=200μ（2）轴线外的磁场分布计算公式较为复杂，这里简略。
(2)亥姆霍兹线圈是一对彼此平行且连通的共轴圆形线圈，两线圈内的电流方向一致，大小相同,线圈之间的距离d 正好等于圆形线圈的半径R 。
这种线圈的特点是能在其公共轴线中点附近产生较广的均匀磁场区，所以在生产和科研中有较大的使用价值，也常用于弱磁场的计量标准。
设z 为亥姆霍兹线圈中轴线上某点离中心点O 处的距离，则亥姆霍兹线圈轴线上任意一点的磁感应强度为：⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫ ⎝⎛-++⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫ ⎝⎛++⋅⋅⋅='-222/322202221z R R z R R R I N B μ （3）而在亥姆霍兹线圈上中心O 处的磁感应强度'0B 为： R I N B ⋅⋅='02/3058μ四、实验步骤：（1）必做内容：载流圆线圈和亥姆霍兹线圈轴线上各点磁感应强度的测量。
1）按图1接线，直流稳流电源中数字电流表已串接在电源的一个输出端，测量电流mA I 100=时，单线圈a 轴线上各点磁感应强度)(a B ，每隔cm 00.1测一个数据。
霍尔法测量圆线圈和亥姆霍兹线圈的磁场
1.了解霍尔法测量磁场的基本原理。 2.掌握仪器使用方法。 3.熟练掌握霍尔法测量亥姆霍兹线圈磁场的
方法
实验原理
一.载流圆线圈与亥姆霍兹线圈的磁场
ቤተ መጻሕፍቲ ባይዱ
1.1载流圆线圈磁场
一半径为Ｒ，通以电流Ｉ的圆线圈，轴线上磁场的
公式为：
B
2(
0
R2
N
0 IR X2
2
)
3
/
2（1）
式中N0为圆线圈的匝数，X为轴上某一点到圆心O 的距离。 0 4 10 7 H / m
本实验取Ｎ０＝500匝，Ｉ＝500mＡ，
Ｒ＝110mm，圆心O处x ＝0，可算得圆电流线圈磁 感应强度B=1.43mT。它的分布图如下图1所示。
1.2亥姆霍兹线圈
1）所谓亥姆霍兹线圈为两个相同线圈彼此平行 且共轴，使线圈上通以同方向电流I 。
2）理论计算证明：线圈间距a等于线圈半径R时， 两线圈合磁场在轴上（两线圈圆心连线）附近较 大范围内是均匀的 。
2、测量亥姆霍兹线圈轴线上磁场的分布
按图接线，然后在励磁电流为零的情况下将磁 感应强度清零。 ▪ 调节磁场测量仪的励磁电流调节电位器，使表头 显示值为500mＡ,此时毫特计表头应显示一对应 的磁感应强度B值。 ▪ 以亥姆霍兹线圈中心为坐标原点，每隔10.0 mm 测一磁感应强度B的值，测量过程中注意保持励 磁电流值不变。
3）本实验亥姆霍兹线圈中心磁感应强度
B
0 N0 I
2R
16 3
52
=1.43×1.431mT =2.05mT
它的分布图如下图2所示
图1 单个圆环线圈磁场分布
图2 亥姆霍兹线圈磁场分布
二、霍尔效应法测磁场
亥姆霍兹线圈磁场测定-实验报告
开放性实验实验报告——亥姆霍兹线圈磁场测定姓名学号班级亥姆霍兹线圈是一对相同的、共轴的、彼此平行的各有N匝的圆环电流。
当它们的间距正好等于其圆环半径R时，称这对圆线圈为亥姆霍兹线圈。
在亥姆霍兹线圈的两个圆电流之间的磁场比较均匀。
在生产和科研中经常要把样品放在均匀磁场中作测试，利用亥姆霍兹线圈是获得一种均匀磁场的比较方便的方法。
一、实验目的1. 熟悉霍尔效应法测量磁场的原理。
2. 学会亥姆霍兹磁场实验仪的使用方法。
3. 测量圆线圈和亥姆霍兹线圈上的磁场分布，并验证磁场的叠加原理二、实验原理同学们注意，根据自己的理解，适当增减，不要太多，有了重点就可以了。
1．霍尔器件测量磁场的原理图3—8—1 霍尔效应原理如图3—8—1所示，有－N型半导体材料制成的霍尔传感器，长为L，宽为b，厚为d，其四个侧面各焊有一个电极1、2、3、4。
将其放在如图所示的垂直磁场中，沿3、4两个侧面通以电流I，电流密度为J，则电子将沿负J方向以速度运动，此电子将受到垂直方向磁场B的洛仑兹力作用，造成电子在半导体薄片的1测积累过量的负电荷，2侧积累过量的正电荷。
因此在薄片中产生了由2侧指向1侧的电场，该电场对电子的作用力，与反向，当两种力相平衡时，便出现稳定状态，1、2两侧面将建立起稳定的电压，此种效应为霍尔效应，由此而产生的电压叫霍尔电压，1、2端输出的霍尔电压可由数显电压表测量并显示出来。
如果半导体中电流I是稳定而均匀的，则电流密度J的大小为（3—8—1）式中b为矩形导体的宽，d为其厚度，则bd为半导体垂直于电流方向的截面积。
如果半导体所在范围内，磁场B也是均匀的，则霍耳电场也是均匀的，大小为（3—8—2）霍耳电场使电子受到一与洛仑兹力F m相反的电场力F e，将阻止电子继续迁移，随着电荷积累的增加，霍耳电场的电场力也增大，当达到一定程度时，F m与F e大小相等，电荷积累达到动态平衡，形成稳定的霍耳电压，这时根据F m=F e有（3—8—3）将（3—8—2）式代入（3—8—3）式得（3—8—4）式中、容易测量，但电子速度难测，为此将变成与I有关的参数。
亥姆赫兹实验报告模板
2.思考题
1.单线圈轴线上磁场分布成正态分布， 轴心磁感应强度最强， 距离轴心越远磁感应强度越小，
两边对称减小；亥姆线圈是有两个相同且平行共轴的线圈组成，并且通以同向电流；其基本 条件为两线圈相同且平行共轴， 通过的电流同向； 其分布规律为两线圈圆心连线范围内磁感 应强度相同且最强，两线两侧磁感应强度均匀减小。 2.分析霍尔效应测量磁场时当流过线圈的电流为零时， 显示的磁场值不为零是因为有地磁场 及各种通讯仪的电磁波的干扰。 3..理论值与测量值的误差原因：由于人眼测量，指针无法准确指在相应示数上，导致每次 移动的实际距离不为 10mm,因此会造成一定的误差，这次可能大于 10mm，使得测量值小于 理论值；实验过程中，老师用扩音器讲课及随身所带的手机所发出的电磁波干扰到所测的 磁场，使有效电流时有波动，对实验结果造成了误差；由于实验室内各个实验仪距离比较 近通电时会对彼此造成一定的干扰，相反方向的磁场会相互消磁，致使测量值比理论值小。
4.集成霍尔元件与显示模块联调，直接显示磁场强度，即直接得出数据。 四． 实验仪器
亥姆赫兹线圈实验仪（励磁线圈架和磁场测量仪）
五． 实验内容及步骤
1.测量圆电流线圈轴线上磁场的分布：先开机预热五分钟，接好电路调零；调节有效电流 为 200mA；调节传感器位置致游标示数-10mm 处开始测量。每隔 10mm 测一次 B 值，直 到 110mm；记录数据作图。 2.测亥姆赫兹轴线上磁场的分布：关闭电源，将两组线圈串联，调零，将有效电流调至
x
-11 0
0.5 13
-10 0
0.5 73
-90
0.6 33
-80
0.6 86
-70
0.7 30
-60
0.7 60