2018年北京高三模拟题分类汇编之立体几何大题
北京市城六区2018届高三一模文科数学试题汇编之解析几何

北京市城六区2018届高三一模文科数学试题汇编之
解析几何
学校_________ 班级__________ 姓名__________ 学号__________
一、解答题
1. 已知椭圆的两个焦点为,离心率为.
(1)求椭圆的方程;
(2)设点是椭圆的右顶点,过点的直线与椭圆交于,两点,直线
,与直线分别交于,两点.求证:点在以为直径的圆上.
2. 已知椭圆的离心率为,以椭圆的任意三个顶点为顶点的三角形的面积是.
(1)求椭圆的方程;
(2)设是椭圆的右顶点,点在轴上.若椭圆上存在点,使得,求点横坐标的取值范围.
3. 已知椭圆的离心率为,长轴长为.
(1)求椭圆的方程;
(2)点是以长轴为直径的圆上一点,圆在点处的切线交直线于点,求证:过点且垂直于直线的直线过椭圆的右焦点.
4. 已知椭圆的离心率为,且过点.
(1)求椭圆的方程;
(2)过椭圆左焦点的直线与椭圆交于两点,直线过坐标原点且直线与的斜率互为相反数,直线与椭圆交于两点且均不与点重合,设直线的斜率为,直线的斜率为.证明:为定值.
5. 已知椭圆:的一个焦点为,点在椭圆上.
(Ⅰ)求椭圆的方程与离心率;
(Ⅱ)设椭圆上不与点重合的两点,关于原点对称,直线,
分别交轴于,两点.求证:以为直径的圆被轴截得的弦长是定值.。
2018年高考数学立体几何试题汇编

2018 年全国一卷(文科):9.某圆柱的高为2,底面周长为16,其三视图如右图.圆柱表面上的点M 在正视图上的对应点为A,圆柱表面上的点N 在左视图上的对应点为 B ,则在此圆柱侧面上,从M 到N 的路径中,最短路径的长度为A.2 17 B.2 5 C.3 D.218.如图,在平行四边形ABCM 中,AB AC 3 ,∠ACM 90 ,以AC 为折痕将△ACM 折起,使点M 到达点D 的位置,且AB⊥DA .(1)证明:平面ACD ⊥平面ABC ;(2)Q 为线段AD 上一点,P为线段BC 上一点,且2BP DQ DA ,求三棱锥Q ABP 的体积.3全国1 卷理科理科第7 小题同文科第9 小题18. 如图,四边形为正方形,分别为的中点,以为折痕把折起,使点到达点ABCD E, F AD ,BC DF △DFC C P 的位置,且PF BF .(1)证明:平面PEF 平面ABFD ;(2)求DP 与平面ABFD 所成角的正弦值.全国 2 卷理科:9.在长方体ABCD A1B1C1D1 中,AB BC 1 ,AA1 3 ,则异面直线A D 与DB1 所成角的余弦值为1A.15B.56C.55D.2220.如图,在三棱锥P ABC 中,AB BC 2 2 ,PA PB PC AC 4 ,O 为AC 的中点.(1)证明:PO 平面ABC ;(2)若点M 在棱BC 上,且二面角M PA C 为30 ,求PC 与平面PAM 所成角的正弦值.全国3 卷理科3.中国古建筑借助榫卯将木构件连接起来,构件的凸出部分叫榫头,凹进部分叫卯眼,图中木构件右边的小长方体是榫头.若如图摆放的木构件与某一带卯眼的木构件咬合成长方体,则咬合时带卯眼的木构件的俯视图可以是19.(12 分)如图,边长为 2 的正方形所在的平面与半圆弧所在平面垂直,是上异于,的点.ABCD CD M CD C D (1)证明:平面AMD⊥平面BMC ;(2)当三棱锥M ABC 体积最大时,求面MAB 与面MCD 所成二面角的正弦值.2018 年江苏理科:10.如图所示,正方体的棱长为2,以其所有面的中心为顶点的多面体的体积为▲.15.(本小题满分14 分)在平行六面体A BCD A B C D 中,AA1 AB, AB1 B1C1.1 1 1 1求证:(1)A B∥平面A B C ;1 1(2)ABB A A BC平面平面.1 1 12018 年北京:(5)某四棱锥的三视图如图所示,在此四棱锥的侧面中,直角三角形的个数为(A)1 (B)2 (C)3 (D)4(16)(本小题14 分)如图,在三棱柱ABC - A1 B1 C1 中,C C 平面ABC,D,E,F,G 分别为1 AA ,AC,1AC ,1 1BB中点,AB=BC = 5 ,AC= AA =2.1(Ⅰ)求证:AC⊥平面BEF;(Ⅱ)求二面角B-CD -C1 的余弦值;(Ⅲ)证明:直线FG 与平面BCD 相交.2018 年浙江:3)是3.某几何体的三视图如图所示(单位:cm),则该几何体的体积(单位:cmA .2 B.4 C.6 D.819.(本题满分15 分)如图,已知多面体ABCA1B1C1,A1A,B1B,C1C 均垂直于平面ABC,∠ABC=120°,A1A=4,C1C=1,AB =BC =B1B=2.(Ⅰ)证明:AB1⊥平面A1B1C1;(Ⅱ)求直线AC1 与平面ABB1 所成的角的正弦值.2018 年上海19.已知圆锥的顶点为P , 底面圆心为O, 半轻为 21. 设圆锥的母线长为 4 , 求圆锥的体积o2. 设PO 4, OA,OB 是底面半径, 且AOB 90 , M 为线段AB 的中点, 如图, 求异面直线PM 与OB 所成的角的大小。
北京高考真题之立体几何

一.1. 已知正三棱锥P ABC−的六条棱长均为6,S是ABC△及其内部的点构成的集合,设集合{5}T Q S PQ=∈,则T表示的区域的面积为(A)34π(B)π(C)2π(D)3π2. 某四面体的三视图如图所示,该四面体的表面积为()A. B. 4 C. 3+ D. 23. 某三棱柱的底面为正三角形,其三视图如图所示,该三棱柱的表面积为().A. 6+B. 6+C. 12+D. 12+4. 某四棱锥的三视图如图所示,在此四棱锥的侧面中,直角三角形的个数为()A.1B.2C.3D.45. 某四棱锥的三视图如图所示,则该四棱锥的最长棱的长度为()A.3B.2C.2D.26. 某三棱锥的三视图如图所示,则该三棱锥的体积为()A.60 B.30 C.20 D.107. 某三棱锥的三视图如图所示,则该三棱锥的体积为()A.B.C.D.18. (5分)已知l,m是平面α外的两条不同直线.给出下列三个论断:①l⊥m;②m∥α;③l⊥α.以其中的两个论断作为条件,余下的一个论断作为结论,写出一个正确的命题:.二.1. (2019文)如图,在四棱锥P﹣ABCD中,P A⊥平面ABCD,底面ABCD为菱形,E为CD的中点.(Ⅰ)求证:BD⊥平面P AC;(Ⅱ)若∠ABC=60°,求证:平面P AB⊥平面P AE;(Ⅲ)棱PB上是否存在点F,使得CF∥平面P AE?说明理由.2. 如图,在四棱锥P﹣ABCD中,底面ABCD为正方形,平面PAD⊥平面ABCD,点M在线段PB上,PD∥平面MAC,PA=PD=,AB=4.(1)求证:M为PB的中点;(2)求二面角B﹣PD﹣A的大小;(3)求直线MC与平面BDP所成角的正弦值.3. (2020) 如图,在正方体1111ABCD A B C D −中,E 为1BB 的中点.(Ⅰ)求证:1//BC 平面1AD E ;(Ⅱ)求直线1AA 与平面1AD E 所成角的正弦值.5. (2022·)如图,在三棱柱111ABC A B C 中,侧面11BCC B 为正方形,平面11BCC B ⊥平面11ABB A ,2AB BC ==,M ,N分别为11A B ,AC 的中点.(1)求证:MN ∥平面11BCC B ;(2)再从条件①、条件②这两个条件中选择一个作为已知,求直线AB 与平面BMN 所成角的正弦值. 条件①:AB MN ⊥; 条件②:BM MN =.注:如果选择条件①和条件②分别解答,按第一个解答计分.7. (2019理)如图,在四棱锥P﹣ABCD中,P A⊥平面ABCD,AD⊥CD,AD∥BC,P A=AD=CD=2,BC=3.E为PD的中点,点F在PC上,且=.(Ⅰ)求证:CD⊥平面P AD;(Ⅱ)求二面角F﹣AE﹣P的余弦值;(Ⅲ)设点G在PB上,且=.判断直线AG是否在平面AEF内,说明理由.8. (14分)如图,在三棱柱ABC﹣A1B1C1中,CC1⊥平面ABC,D,E,F,G分别为AA1,AC,A1C1,BB1的中点,AB=BC=,AC=AA1=2.(Ⅰ)求证:AC⊥平面BEF;(Ⅱ)求二面角B﹣CD﹣C1的余弦值;(Ⅲ)证明:直线FG与平面BCD相交.9. 如图,在四棱锥P﹣ABCD中,平面PAD⊥平面ABCD,PA⊥PD,PA=PD,AB⊥AD,AB=1,AD=2,AC=CD=.(Ⅰ)求证:PD⊥平面PAB;(Ⅱ)求直线PB与平面PCD所成角的正弦值;(Ⅲ)在棱PA上是否存在点M,使得BM∥平面PCD?若存在,求的值,若不存在,说明理由.答案2. 二面角B﹣PD﹣A的大小为60°;直线MC与平面BDP所成角的正弦值为|cos<>|=||=||=3. (Ⅰ)证明见解析;(Ⅱ)2 3.所以PAB为直角三角形,又因为PB=2PB BC+,则PBC为直角三角形,故又因为BC PA⊥PA PB P=,平面PAB,又x轴,过A所以(0,0,1),(1,1,0),(0,1,0),(1,1,AP AC BC PC ====−设平面PAC 的法向量为()111,,m x y z =,则00m AP m AC ⎧⋅=⎪⎨⋅=⎪⎩,即1=,则11y =−,所以(1,1,0)m =−,的法向量为(22,,x n y =00BC PC ⎧⋅=⋅=,即,所以(1,0,1)n =,11,222m n m n m n⋅===⨯,又因为二面角A PC B −−为锐二面角,所以二面角A PC B −−的大小为π系,利用空间向量可求线面角的正弦值. 【详解】(1)取AB 的中点为K ,连接,MK NK , 由三棱柱111ABC A B C 可得四边形11ABB A 为平行四边形, 而11,B M MA BK KA ==,则1//MK BB ,而MK ⊄平面11BCC B ,1BB ⊂平面11BCC B ,故//MK 平面11BCC B , 而,CN NA BK KA ==,则//NK BC ,同理可得//NK 平面11BCC B , 而,,NK MK K NK MK =⊂平面MKN ,故平面//MKN 平面11BCC B ,而MN ⊂平面MKN ,故//MN 平面11BCC B , (2)因为侧面11BCC B 为正方形,故1CB BB ⊥, 而CB ⊂平面11BCC B ,平面11CBB C ⊥平面11ABB A , 平面11CBB C ⋂平面111ABB A BB =,故CB ⊥平面11ABB A , 因为//NK BC ,故NK ⊥平面11ABB A , 因为AB ⊂平面11ABB A ,故NK AB ⊥,若选①,则AB MN ⊥,而NK AB ⊥,NK MN N =, 故AB ⊥平面MNK ,而MK ⊂平面MNK ,故AB MK ⊥, 所以1AB BB ⊥,而1CB BB ⊥,CB AB B ⋂=,故1BB ⊥平面ABC ,故可建立如所示的空间直角坐标系,则()()()()0,0,0,0,2,0,1,1,0,0,1,2B A N M , 故()()()0,2,0,1,1,0,0,1,2BA BN BM ===, 设平面BNM 的法向量为(),,n x y z =, 则00n BN n BM ⎧⋅=⎨⋅=⎩,从而020x y y z +=⎧⎨+=⎩,取1z =−,则()2,2,1n =−−,设直线AB 与平面BNM 所成的角为θ,则4,2n AB =⨯,故1BB M MKN ≅, 111A B BB ⊥, 1BB ⊥平面ABC ,故可建立如所示的空间直角坐标系,则()0,0,0,B 故()()(0,2,0,1,1,0,0,1,2BA BN BM ===设平面BNM 的法向量为(),,n x y z =,00n BN n BM ⎧⋅=⎨⋅=⎩,从而020x y y z +=⎧⎨+=⎩,取,则(2,2,n =−−设直线AB 与平面所成的角为42cos ,233n AB ==⨯6.7. 证明:(Ⅰ)∵P A ⊥平面ABCD ,∴P A ⊥CD , ∵AD ⊥CD ,P A ∩AD =A , ∴CD ⊥平面P AD .解:(Ⅱ)以A 为原点,在平面ABCD 内过A 作CD 的平行线为x 轴, AD 为y 轴,AP 为z 轴,建立空间直角坐标系, A (0,0,0),E (0,1,1),F (,,),P(0,0,2),B(2,﹣1,0),=(0,1,1),=(),平面AEP的法向量=(1,0,0),设平面AEF的法向量=(x,y,z),则,取x=1,得=(1,1,﹣1),设二面角F﹣AE﹣P的平面角为θ,则cosθ===.∴二面角F﹣AE﹣P的余弦值为.(Ⅲ)直线AG在平面AEF内,理由如下:∵点G在PB上,且=.∴G(,﹣,),∴=(,﹣,),∵平面AEF的法向量=(1,1,﹣1),=﹣=0,故直线AG在平面AEF内.8.二面角B﹣CD﹣C1的余弦值为﹣.(III)证明:F(0,0,2),(2,0,1),∴=(2,0,﹣1),∴•=2+0﹣4=﹣2≠0, ∴与不垂直,∴FG 与平面BCD 不平行,又FG ⊄平面BCD , ∴FG 与平面BCD 相交.9. ;.。
2018年高三最新 北京四中立体几何训练题 精品

北京四中立体几何训练题A组1.平面α内有一个半径为a的圆O,OP⊥α且OP=a, PA为α的一条斜线,PA=2a(A∈α),B为圆O上的任意一点,则PA在α内的射影与AB所成角中的最大角的正弦值为______.2.在直四棱柱A1B1C1D1-ABCD中,当底面ABCD满足条件_______时,有A1C⊥B1D1.3.O是正△ABC的中心,PO⊥平面ABC.若PO=AB=a,则PA与平面ABC所成的角为_______;P到直线BC 的距离为_______.4.如图,S是四边形ABCD所在平面外一点,为了推出AB⊥BC,还需要从下述条件中选出一些条件来.①SB⊥平面ABCD;②SC⊥CD;③CD∥AB;④CD∥平面SAB;⑤BC⊥CD;⑥CD⊥平面SBC;⑦AB⊥平面SBC;⑧SB⊥CD.比如,选⑦为条件,有⑦AB⊥BC;又如选③,⑤为条件,有(写③⑤AB⊥BC.现要求推理至少用到两条定理,推理的格式为:_________.出两个正确的推理过程)5.正方体ABCD-A1B1C1D1中,AD1与DB1、DC1、CC1所成的角分别为α、β、γ,则α+β+γ的值是________.6.下图中,不是正四面体的表面展开图的是_______.7.已知甲烷的分子结构是:中心为一个碳原子,外围有4个氢原子,则碳原子与氢原子之间的键角的余弦为_______.8.在任意四面体ABCD内部的任一点P,若P到四面体的各个面BCD、ACD、ABD、ABC的距离顺次为a′、b′、c′、d′,而各顶点A、B、C、D到各个面BCD、ACD、ABD、ABC的距离顺次为a、b、c、d,则(a′/a)+(b′/b)+(c′/c)+(d′/d)为一个常数k,则k为_______.9.连接一体积为72的正四面体的两个面的重心是E、F,则线段EF的长度是__________.10.三棱锥P-ABC中,若棱PA=x,其余各棱长均为1,则x的范围是__________;三棱锥P-ABC的体积的最大值为__________.11.在长方体AC1中,已知顶点A上三条棱长分别是、、2,如果对角线AC1与过点A的相邻三个面所成的角分别是α、β、γ,那么cos2α+cos2β+cos2γ=_________.12.如图,侧棱长为2 的正三棱锥V-ABC中,∠AVB=∠BVC=∠CVA=40°.过A作截面AEF与VB、VC 分别交于E、F点,则截面△AEF的最小周长为_________.13.一个大木球放在水平的地面上,球在太阳下的影子伸到距球与地面接触点的10米远处;同一时刻,一根高1米的垂直立于水平地面上的尺子的影子的长度是2米,则球的半径为_________.B组1.已知长方体的表面积为32cm2,体积为8cm3,其长、宽、高成等比数列,则长方体所有棱长之和为_________.2.如图,在透明塑料制成的长方体ABCD-A1B1C1D1容器内灌进一些水,固定容器底面一边BC于地面上,再将容器倾斜,随着倾斜度的不同,则下列四个命题:①水的部分始终呈棱柱形;②水面四边形EFGH的面积不改变;③棱A1D1始终与水面EFGH平行;④当容器倾斜如图所示时,BF·BE是定值.其中所有正确命题的序号是_______.3.表面积为Q的多面体的每一个面,都外切于表面积为36π的一个球,则这个多面体的体积为_________.4.已知三棱锥A-BCD的体积为V,棱BC的长为a,面ABC和面DBC的面积分别为S1和S2.设面ABC和面DBC所成二面角为α,则sinα=_____________.5.一个底面直径是32cm的圆柱形水箱装入水,然后放入一个铁球,该球被水淹没,水面升高9cm,则球的表面积是_____________.6.如图所示,屋檐的倾斜角α是_________时,雨水在屋顶停留的时间最短.7.在直角坐标系中,已知A(2,3),B(-2,-3),沿x轴把坐标平面折成平面角为θ的二面角AO-x-B,使∠AOB=90°,则cosθ的值是_______.8.在三棱锥P-ABC中,PC⊥底面ABC,∠ACB=90°,AC>BC,D、E分别是AB、BC的中点.设PA与DE所成的角为α,PD与平面ABC所成的角为β,二面角P-AB-C的大小为γ,则α、β、γ的大小关系是____-. 9.如左图,一张正方形纸片ABCD中,有(AE/EB)=(AF/FD)=(CH/HB)=(CG/GD)=(1/2),沿BD折起,使△ABD与△BCD所成的二面角为θ.若EFGH折起后恰成正方形(如右图),则cosθ等于______.10.若一个二面角的一个面α内有一点A,它到棱的距离是它到另一个面β的距离的2倍,则这个二面角的度数是________.11.已知三棱锥D-ABC的三个侧面与底面全等,且AB=AC=,BC=2,则以BC为棱,以面BCD与面BCA为面的二面角的大小是________.12.△ABC 的一边BC 在平面α内,顶点A 在平面α外,∠ABC =60°,△ABC 所在的平面与平面α成30°的二面角,则AB 所在的直线与平面α所成的角的正弦值是________.13.三个12cm ×12cm 的正方形都被连接两条邻边的中点的直线分为A、B两片(如左图),把六片粘在一个正六边形的外围(如中图),然后折成多面体(如右图),则此多面体的体积为_____.A1./3 2.AC ⊥BD 3. 60°(/6)a 4. ⇒⇒①②⑤④③}AB⊥BC 或 ⇒③⑥⑦AB⊥BC 5. 195°6. ④⑥ 7. -(1/3) 8. 1 9.0<x <10.(1/8)11.2 12.613.10-20. B 1.32cm 2. ①③④ 3. Q 4.(3a V)/(2S1S2)5. 576πcm 26. 45°7. -(4/9)8. α<β<γ 9.0.5 10. 30°或150°11. 90° 12.( /4) 13. 864cm 3。
2018北京各区数学一模试题分类汇编——立体几何 精品
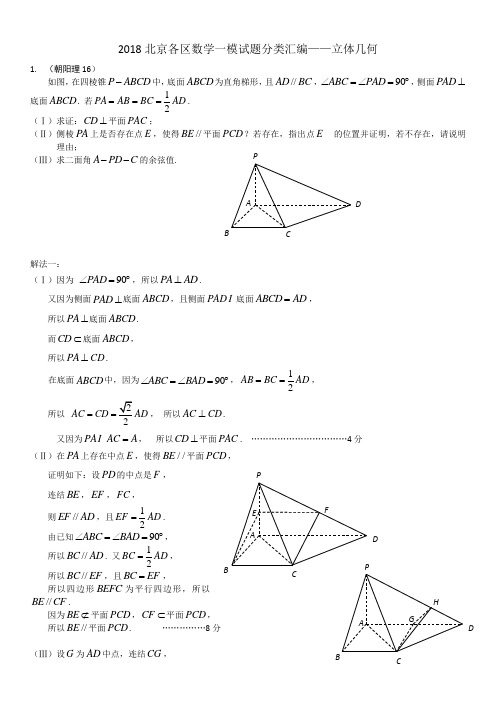
2018北京各区数学一模试题分类汇编——立体几何1. (朝阳理16)如图,在四棱锥P ABCD -中,底面ABCD 为直角梯形,且//AD BC ,90ABC PAD ∠=∠=︒,侧面PAD ⊥底面ABCD . 若12PA AB BC AD ===. (Ⅰ)求证:CD ⊥平面PAC ;(Ⅱ)侧棱PA 上是否存在点E ,使得//BE 平面PCD ?若存在,指出点E 的位置并证明,若不存在,请说明理由;(Ⅲ)求二面角A PD C --的余弦值.解法一:(Ⅰ)因为 90PAD ∠=︒,所以PA AD ⊥.又因为侧面PAD ⊥底面ABCD ,且侧面PAD 底面ABCD AD =, 所以PA ⊥底面ABCD . 而CD ⊂底面ABCD , 所以PA ⊥CD .在底面ABCD 中,因为90ABC BAD ∠=∠=︒,12AB BC AD ==, 所以2AC CD AD ==, 所以AC ⊥CD . 又因为PA AC A = , 所以CD ⊥平面PAC . ……………………………4分 (Ⅱ)在PA 上存在中点E ,使得//BE 平面PCD ,证明如下:设PD 的中点是F , 连结BE ,EF ,FC ,则//EF AD ,且12EF AD =.由已知90ABC BAD ∠=∠=︒,所以//BC AD . 又12BC AD =,所以//BC EF ,且BC EF =,所以四边形BEFC 为平行四边形,所以//BE CF .因为BE ⊄平面PCD ,CF ⊂平面PCD所以//BE 平面PCD . (8)(Ⅲ)设G 为AD 中点,连结CG ,则 CG ⊥AD .又因为平面ABCD ⊥平面PAD , 所以 CG ⊥平面PAD . 过G 作GH PD ⊥于H ,连结CH ,由三垂线定理可知CH PD ⊥. 所以GHC ∠是二面角A PD C --的平面角.设2AD =,则1PA AB CG DG ====, DP =. 在PAD ∆中,GH DG PA DP =,所以GH =. 所以tan CG GHC GH ∠==,cos GHC ∠=. 即二面角A PD C --………………………………13分解法二:因为 90PAD ∠=︒, 所以PA AD ⊥.又因为侧面PAD ⊥底面ABCD , 且侧面PAD 底面ABCD AD =, 所以 PA ⊥底面ABCD . 又因为90BAD ∠=︒,所以AB ,AD ,AP 两两垂直. 分别以AB ,AD ,AP 为x 轴, y 轴,z 轴建立空间直角坐标系,如图.设2AD =,则(0,0,0)A ,(1,0,0)B ,(1,1,0)C ,(0,2,0)D ,(0,0,1)P .(Ⅰ)(0,0,1)AP = ,(1,1,0)AC = ,(1,1,0)CD =-,所以 0AP CD ⋅= ,0AC CD ⋅=,所以AP ⊥CD ,AC ⊥CD .又因为AP AC A = , 所以CD ⊥平面PAC . ………………………………4分(Ⅱ)设侧棱PA 的中点是E , 则1(0, 0, )2E ,1(1, 0, )2BE =- .设平面PCD 的一个法向量是(,,)x y z =n ,则0,0.CD PD ⎧⋅=⎪⎨⋅=⎪⎩n n 因为(1, 1, 0)CD =- ,(0, 2,1)PD =-,所以0,20.x y y z -+=⎧⎨-=⎩ 取1x =,则(1, 1, 2)=n .所以1(1, 1, 2)(1, 0, )02BE ⋅=⋅-= n , 所以BE ⊥ n .因为BE ⊄平面PCD ,所以BE 平面PCD . ………………………………8分(Ⅲ)由已知,AB ⊥平面PAD ,所以(1, 0, 0)AB =为平面PAD 的一个法向量.由(Ⅱ)知,(1, 1, 2)=n 为平面PCD 的一个法向量. 设二面角A PD C --的大小为θ,由图可知,θ为锐角,所以cos AB ABθ⋅===n n . 即二面角A PD C --的余弦值为6………………………………13分2. (朝阳文17)如图,在四棱锥P ABCD -中,底面ABCD 为直角梯形,且//AD BC ,90ABC ∠=︒,侧面PAD ⊥底面ABCD ,90PAD ∠=︒. 若12AB BC AD ==. (Ⅰ)求证:CD ⊥平面PAC ;(Ⅱ)设侧棱PA 的中点是E ,求证:BE 平面PCD .解:(Ⅰ)因为 90PAD ∠=︒, 所以PA AD ⊥.又因为侧面PAD ⊥底面ABCD , 且侧面PAD 底面ABCD AD =, 所以PA ⊥底面ABCD . 而CD ⊂底面ABCD , 所以PA ⊥CD . 在底面ABCD 中,因为90ABC BAD ∠=∠=︒,12AB BC AD ==, 所以AC CD AD ==, 所以AC ⊥CD . 又因为PA AC A = , 所以CD ⊥平面PAC . ……………………………6分PA B CD QM(Ⅱ)设侧棱PD 的中点为F ,连结BE ,EF ,FC ,则EF AD ,且12EF AD =. 由已知90ABC BAD ∠=∠=︒,所以BC AD . 又12BC AD =,所以BC EF . 且BC EF =.所以四边形BEFC 为平行四边形,所以BE CF . 因为BE ⊄平面PCD ,CF ⊂平面PCD ,所以BE 平面PCD . ………………………………………………………13分3. (丰台理16)如图,在四棱锥P -ABCD 中,底面ABCD 为直角梯形,AD //BC ,∠ADC =90°,平面PAD ⊥底面ABCD ,Q 为AD 的中点,M 是棱PC 上的点,PA =PD =2,BC =12AD =1,CD (Ⅰ)若点M 是棱PC 的中点,求证:PA // 平面BMQ ; (Ⅱ)求证:平面PQB ⊥平面PAD ;(Ⅲ)若二面角M -BQ -C 为30°,设PM =tMC ,试确定t 的值 .证明:(Ⅰ)连接AC ,交BQ 于N ,连接MN .∵BC ∥AD 且BC =12AD ,∴四边形BCQA 为平行四边形,且N 为AC 中点, 又∵点M 在是棱PC 的中点,∴ MN // PA ∵ MN ⊂平面MQB ,PA ⊄平面MQB , ∴ PA // 平面MBQ . (Ⅱ)∵AD // BC ,BC =12AD ,Q 为AD 的中点, ∴四边形BCDQ 为平行四边形,∴CD // BQ . ∵∠ADC =90° ∴∠AQB =90° 即QB ⊥AD . 又∵平面PAD ⊥平面ABCD 且平面PAD ∩平面ABCD=AD , ∴BQ ⊥平面PAD .∵BQ ⊂平面PQB ,∴平面PQB ⊥平面PAD . …………………9分 另证:AD // BC ,BC =12AD ,Q 为AD 的中点, ∴ 四边形BCDQ 为平行四边形,∴CD //∵ ∠ADC =90° ∴∠AQB =90°. ∵ PA =PD , ∴PQ ⊥AD .∵ PQ ∩BQ =Q , ∴AD ⊥平面PBQ . ∵ AD ⊂平面PAD ,∴平面PQB PAD .……9分(Ⅲ)∵PA =PD ,Q 为AD 的中点, ∴PQ ⊥AD .∵平面PAD ⊥平面ABCD ,且平面PAD ∩平面ABCD=AD , PA BCDQM∴PQ ⊥平面ABCD .如图,以Q 为原点建立空间直角坐标系.则平面BQC 的法向量为(0,0,1)n =;(0,0,0)Q,P ,B,(1C -.设(,,)M x y z,则(,,PM x y z =,(1,)MC x y z =---, ∵PM tMC = ,∴(1))(x t x y t y z t z =--⎧⎪=⎨⎪=-⎩), ∴11t x t y t z ⎧=-⎪+⎪⎪=⎨+⎪⎪=⎪⎩ …………………12分在平面MBQ中,QB =,(1t QM t =-+ ,∴ 平面MBQ法向量为)m t =.∵二面角M -BQ -C 为30°,c o s 30n m n m ︒⋅===∴ 3t =. ……………………14分4. (丰台文16)如图,在四棱锥P ABCD -中,底面ABCD 为直角梯形,AD //BC ,∠ADC =90°,BC =12AD ,PA =PD ,Q 为AD 的中点.(Ⅰ)求证:AD ⊥平面PBQ ;(Ⅱ)若点M 在棱PC 上,设PM =tMC ,试确定t 的值,使得PA //平面BMQ .证明:(Ⅰ)AD // BC ,BC =12AD ,Q 为AD 的中点, ∴ 四边形BCDQ 为平行四边形, ∴CD // BQ . ∵ ∠ADC =90° ∴∠AQB =90° 即QB ⊥AD . ∵ PA =PD ,Q 为AD 的中点, ∴PQ ⊥AD . ∵ PQ ∩BQ =Q ,∴AD ⊥平面PBQ . ……………………6分C(Ⅱ)当1t =时,PA //平面BMQ .连接AC ,交BQ 于N ,连接MN . ∵BC //12DQ , ∴四边形BCQA 为平行四边形,且N 为AC 中点, ∵点M 是线段PC 的中点, ∴ MN // PA .∵ MN ⊂平面BMQ ,PA ⊄平面BMQ ,∴ PA // 平面BMQ . ……………………13分5. (门头沟理16)已知四棱锥P ABCD -的底面ABCD 为菱形,且060,ABC ∠=2PB PD AB ===,PA PC =,AC 与BD 相交于点O .(Ⅰ)求证:⊥PO 底面ABCD ;(Ⅱ)求直线PB 与平面PCD 所成角的正弦值; (Ⅲ)若M 是PB 上的一点,且PB CM ⊥,求PM MB的值.(Ⅰ)证明:因为ABCD 为菱形,所以O 为,AC BD 的中点……………………………1分 因为,PB PD PA PC ==,所以,PO BD PO AC ⊥⊥所以⊥PO 底面 ABCD …………3分 (Ⅱ)因为ABCD 为菱形,所以AC BD ⊥建立如图所示空间直角坐标系 又060,2ABC PB AB ∠===得1,1OA OB OP === ……………………………4分所以(0,0,1),(0,(1,0,0),P B C D(0,1)PB =- ,(1,0,1)PC =-,1)PD =-……………………5分 设平面PCD 的法向量(,,)m x y z =APDCOB有00m PC m PD ⎧=⎪⎨=⎪⎩所以00x z z -=⎧⎪-=解得x z y z =⎧⎪⎨=⎪⎩所以m =……………………………8分cos ,m PB m PB m PB =cos ,7m PB ==- ……………………………9分 PB 与平面PCD…………………10分 (Ⅲ)因为点M 在PB 上,所以(0,1)PM PB λλ==-所以(0,,1)M λ-+, (1,,1)CM λ=--+因为PB CM ⊥所以 0CM PB = , 得310λλ+-= 解得14λ=所以13PMMB = ……………………………14分6. (门头沟文16)如图所示,PA 垂直矩形ABCD 所在的平面, F E 、分别为PC AB 、的中点。
北京各区2018年高中高三一模解析几何汇编

.【海淀一模】(19) (本小题14分)x 2 y 2 1 (ab 0)的离心率为 3 ,且点T(2,1)在椭圆C 上,设 已知椭圆C :2 b 2 2 a与OT 平行的直线l 与椭圆C 订交于P ,Q 两点,直线TP ,TQ 分别与x 轴正半轴交于M ,两点.求椭圆C 的标准方程; (Ⅱ)判断OM ON 的值能否为定值,并证明你的结论. (19)(本小题 14分) 4 11 a2b 2(Ⅰ)由题意a 2b 2c 2,c 3e2a解得:a 22,b2,c6 故椭圆C 的标准方程为 x 2 y 21·······························5分8 2(Ⅱ)假定直线 TP 或TQ 的斜率不存在,则P 点或Q 点的坐标为(2,-1),直线l 的方程为112(x2),即y 2x2.y1x 2 y 218 2联立方程,得x 2 4x40,y1 2x2此时,直线 l 与椭圆C 相切,不合题意 .故直线TP 和TQ 的斜率存在.方法1:设P(x 1,y 1),Q(x 2,y 2),则直线TP:y1y 1 1(x2),x 1 2直线TQ:y1y 2 1(x2)x 2 2x 12x 2 2故|OM|2,|ON|21y 11 y 2;...由直线OT:y1x ,设直线PQ:y1x t (t 0)22x 2 y 2 182x 22tx 2t 24 0联立方程,1xy t2当0时,x 1 x 22t ,x 1x 22t 24|OM||ON|4(x12x 2 2)y 11 y2 14 (x 1 2x 2 21x)1xt1 t12 12 24x 1x 2 (t 2)(x 1 x 2) 4(t1)1124 x 1x 2 2 (t1)(x 1x 2)(t1)42t 2 4 (t2)(2t) 4(t1)1(t1)(1(2t 24)2t)(t1)242···································14分方法2:设P(x 1,y 1),Q(x 2,y 2),直线 TP 和TQ的斜率分别为k1和k2由OT:y1x ,设直线PQ:y1x t (t 0)22x 2 y 218222联立方程,x 2tx 2t 401xy t2当0时,x 1 x 22t ,x 1x 22t 24k 1 k 2y 1 1 y 2 1x 1 2x 2 21x 1 t 1 1x 2 t 12 2 x 1 2x 2 2x 1x 2 (t2)(x 1 x 2) 4(t 1)(x 1 2)(x 22);...2t 24 (t 2)(2t) 4(t 1)(x 1 2)(x 2 2)故直线TP 和直线TQ 的斜率和为零故 TMN TNM故TMTN故T 在线段MN 的中垂线上,即MN 的中点横坐标为2故|OM| |ON| 4···································14分【东城一模】(18)(本小题13分)已知椭圆C :x 2y 21(ab0)的离心率为3,且过点A(2,0).a 2b 22(Ⅰ)求椭圆C 的方程;(II )设M,N 是椭圆C 上不一样于点A 的两点,且直线AM ,AN 斜率之积等于1 ,试问直4线MN 能否过定点?假如,求出该点的坐标;若不是,请说明原因.(19)(本小题14分)411a 2b 2(Ⅰ)由题意a 2b 2c 2 ,ec 3a2解得:a2 2,b2,c6故椭圆C 的标准方程为x 2 y 2 1·······························5分8 2(Ⅱ)假定直线 TP 或TQ 的斜率不存在,则 P 点或Q 点的坐标为(2,-1),直线l 的方程为y11(x2),即y1x2 .22x 2 y 218 2联立方程,得x 24x40,y 1x 22此时,直线 l 与椭圆C 相切,不合题意 .故直线TP 和TQ 的斜率存在.;...方法1:设P(x1,y1),Q(x2,y2),则直线TP:y1y11(x2),x12直线TQ:y1y21 (x2)x22故|OM|2x12,|ON|2x22 y11y21由直线OT:y 1x,设直线PQ:y1x t(t0)22x2y218222联立方程,x2tx2t401xy t2当0时,x1x22t,x1x22t24|OM||ON|4(x12x22)y11y214(x12x221x2) 1x1t1t1 224x1x2(t2)(x1x2)4(t1) 1xx1(t1)(x x)(t1)2 41221242t24(t2)(2t)4(t1) 1(2t24)1(t1)(2t)(t1)2 42···································14分方法2:设P(x1,y1),Q(x2,y2),直线TP和TQ的斜率分别为k1和k2由OT:y 1x,设直线PQ:y1x t(t0)22x2y218222联立方程,x2tx2t401xy t2;..当0时,x1x22t,x1x22t24k1k2y11y21x12x221x1t11x2t122x12x22x1x2(t2)(x1x2)4(t1)(x12)(x22)2t24(t2)(2t)4(t1)(x12)(x22)故直线TP和直线TQ的斜率和为零故TMN TNM故TMTN故T在线段MN的中垂线上,即MN的中点横坐标为2故|OM| |ON|4···································14分【西城一模】19.(本小题满分14分)已知圆O:x2y24和椭圆C:x22y24,F是椭圆C的左焦点.(Ⅰ)求椭圆C的离心率和点F的坐标;(Ⅱ)点P在椭圆C上,过P作x轴的垂线,交圆O于点Q(P,Q不重合),l是过点Q的圆O的切线.圆F的圆心为点F,半径长为|PF|.试判断直线l与圆F的地点关系,并证明你的结论.解:(Ⅰ)由题意,椭圆C的标准方程为x2y21.[1分] 42所以a24,b22,进而c2a2b22.所以a2,c2.故椭圆C的离心率e c2.[3分]a2椭圆C的左焦点F的坐标为(2,0).[4分](Ⅱ)直线l与圆F相切.证明以下:[5分]设P(x0,y0),此中2x02,则x022y024,[6分] ;..依题意可设Q(x 0,y 1),则x 02y 124.[7 分]直线l的方程为y y 1x 0(x x 0),y 1整理为 x 0xy 1y 4 0.[ 9分]所以圆F 的圆心F 到直线l的距离d| 2x 04| | 2x 2|.[11分]x 02 y 122由于|PF|2(x2)2y2(x2)21(4x2) 1x 2 22x4.[13分]0 022所以|PF|2 d 2,即|PF|d ,所以 直线l 与圆F 相切.[14分]【旭日一模】19.(本小题满分 14分)222,且过点(1,已知椭圆C:x2y 2 1(a b 0)的离心率为2 ).ab22(Ⅰ)求椭圆C 的方程;(Ⅱ)过椭圆C 的左焦点的直线l 1 与椭圆C 交于A,B 两点,直线l 2 过坐标原点且与直线l 1的斜率互为相反数.若直线l 2 与椭圆交于E,F 两点且均不与点A,B 重合,设直线AE 与x 轴所成的锐角为 1,直线BF 与x 轴所成的锐角为2,判断1与2大小关系并加以证明.19.(本小题满分 14分)c2,a2解:(Ⅰ)由题意得a 2b 2 2 ,解得a 2, b1 ,c.c 11 1 1.a22b22故椭圆C 的方程为xy 2 1...5分2(Ⅱ)1=2.证明以下:由题意可设直线 l 1的方程为yk(x 1),直线l 2 的方程为y kx ,设点A(x 1,y 1),;..B(x 2,y 2) ,E(x 3,y 3), F(x 3, y 3).要证1=2,即证直线 AE 与直线BF 的斜率之和为零,即k AE k BF 0.由于k AEkBFy 1 y 3 y 2 y 3x 1 x 3 x 2x 3k(x 1 1)kx 3k(x 2 1)kx 3x 1 x 3 x 2 x 3k[2xx(xx) 2x 2]12 12x 3)3.(x 1 x 3)(x 2yk(x1),由x 2y2得(1 2k 2 )x 24k 2 x 2k 22 0 ,1,222所以x 1x 21 4k ,x 1x 22k2 .2k 2 1 2k 2ykx,2由 x 2得(1 2k 2)x 22,所以 22.y2 1,x 31 2k2所以2x 1x 2(x 1 2 4k 244k 24.x 2)2x 3 121 2k 21202k2kkAEkBFk[2x 1x 2 (x 1 x 2) 2x 32]0 .(x 1 x 3)(x 2 x 3)所以1=2...14分【丰台一模】(19)(本小题共 14分)3x 2 y 21(ab0)上,F(1,0)是椭圆的一个焦点.已知点P(1,)在椭圆C :b 2 2a 2(Ⅰ)求椭圆C 的方程;(Ⅱ)椭圆C 上不与P 点重合的两点D ,E 对于原点O 对称,直线PD ,PE 分别交y 轴于M ,N 两点.求证:以MN 为直径的圆被直线 y3 截得的弦长是定值.2(19)(本小题共14分)解:(Ⅰ)依题意,椭圆的另一个焦点为F(1,0),且c1.1分由于2a22(3)22(3)24,22;..所以a 2,ba 2 c 23,⋯⋯⋯⋯⋯⋯⋯⋯3分所以C 的方程x 2y 2 1.⋯⋯⋯⋯⋯⋯⋯⋯4分4 3(Ⅱ)明:由意可知D ,E 两点与点P 不重合.因D ,E 两点对于原点称,所以D(m,n),E( m, n),(m1).⋯⋯⋯⋯⋯⋯⋯⋯5分以MN 直径的与直y3 交于G(t,3),H(t,3)(t0)两点,所以GM GN .222⋯⋯⋯⋯⋯⋯⋯⋯6分3n直PD :y32(x1).2m1当x 0,y3 直PE :y2n33 n 32 ,所以M(0, 2 m 1 2 m 1n 32 (x1). m13).⋯⋯⋯⋯⋯⋯7分2 n 33n当x0,y2 m 13,所以N(0,22m13).⋯⋯⋯⋯⋯⋯⋯⋯8分2n33n所以GM (t,2),m1GN(t,2),m 1⋯⋯⋯⋯⋯⋯⋯⋯ 9分因GMGN ,所以GMGN0,⋯⋯⋯⋯⋯⋯⋯⋯10分2所以GM GNt 24n 2 9 0. ⋯⋯⋯⋯⋯⋯⋯⋯11分4(m 1)因m 2n 2 1,即3m 2 4n 212,4n 2 93 3m 2,⋯⋯⋯⋯⋯⋯12分43所以t23 0,所以t3⋯⋯⋯⋯⋯⋯⋯⋯13分4.2所以G(3,3),H(3,3),所以GH3.2 2 2 2所以以MN 直径的被直y3 3.⋯⋯⋯⋯14分截得的弦是定2【石景山一模】18.(本小共 13分);...在平面直角坐标系xOy中,动点E到定点(1,0)的距离与它到直线x1的距离相等.(Ⅰ)求动点E的轨迹C的方程;(Ⅱ)设动直线 l:y kx b与曲线C相切于点P,与直线x1订交于点Q.证明:以PQ为直径的圆恒过x轴上某定点.18.(本小题共13分)(Ⅰ)解:设动点E的坐标为(x,y),由抛物线定义知,动点E的轨迹是以(1,0)为焦点,x1为准线的抛物线,所以动点E的轨迹C的方程为y24x.5分y kxb4y4b0.(Ⅱ)证明:由,消去x得:ky2y24x由于直线l与抛物线相切,所以16-16kb0,即b 1.8分k所以直线l的方程为y kx 1.k令x1,得y k1.k所以Q1,k1.10分k设切点坐标P(x0,y0),则ky024y0+40,k12解得:P( , ),11分设M(m,0),MQMP 1m(1m)21)2m1 k2k(k=m m2k2k所以当m2m2=0,即m1时,MQMP0m-10所以MQ MP所以以PQ为直径的圆恒过x轴上定点M(1,0).13分;..。
2018北京六区高三一模数学(理)解答题分类汇编--立体几何

ቤተ መጻሕፍቲ ባይዱ2y
2z
0,
y 2z 0.
n A1 D 0,
令 x 1,则 y 2 , z 1 ,所以 n (1,2, 1) . [7 分 ]
设直线 A1C 和平面 A1BD 所成的角为 ,
则 sin
| cos n, A1C | | n A1C | | n || A1C |
2 2. 3
所以 直线 A1C 和平面 A1 BD 所成角的正弦值为
(Ⅲ)在线段 A C 上是否存在点 P ,使得 OP // 平面 A DE ? 若存在,求出 A P 的值;若不存在,请说明理由. AC
A
E
D
O
A
E D
O
B
C
B
C
图
图
1
2
证明:(Ⅰ)由已知 AB AE 2 ,
因为 O 为 BE 中点,所以 A O BE . 因为平面 A BE 平面 BCDE ,且平面 A BE 平面 BCDE
所以 DE // BC , AD AE .
所以 A1D A1E ,又 O 为 DE 的中点, 所以 A1O DE . [1 分 ] 因为平面 A1DE 平面 BCED ,且 A1O 平面 A1DE , 所以 A1O 平面 BCED , [3 分] 所以 A1O BD . [ 4 分 ] (Ⅱ)取 BC 的中点 G ,连接 OG ,所以 OE OG . 由(Ⅰ)得 A1O OE , A1O OG . 如图建立空间直角坐标系 O - xyz . [5 分]
由题意得, A1 (0,0,2) , B(2, 2,0) , C (2,2,0) , D(0, 1,0) .
1 / 11
所以 A1B (2, 2, 2) , A1D (0, 1, 2) , A1C (2,2, 2) . 设平面 A1BD 的法向量为 n (x , y , z) ,
2018年全国各地高考数学模拟试题立体几何解答题试题汇编(含答案解析)

2018年全国各地高考数学模拟试题立体几何解答题汇编(含答案解析)1.(2018•广陵区校级四模)如图,四棱锥P﹣ABCD中,底面ABCD为菱形,PA ⊥平面ABCD,BD交AC于点E,F是线段PC中点,G为线段EC中点.(Ⅰ)求证:FG∥平面PBD;(Ⅱ)求证:BD⊥FG.2.(2018•黑龙江模拟)在三棱柱ABC﹣A1B l C1中,已知侧棱与底面垂直,∠CAB=90°,且AC=1,AB=2,E为BB1的中点,M为AC上一点,AM=AC.(I)若三棱锥A1﹣C1ME的体积为,求AA1的长;(Ⅱ)证明:CB1∥平面A1EM.3.(2018•黄州区校级三模)如图,在矩形ABCD中,AD=2AB=4,E为BC的中点,现将△BAE与△DCE折起,使得平面BAE⊥平面ADE,平面DCE⊥平面ADE.(Ⅰ)求证:BC∥平面ADE;(Ⅱ)求二面角A﹣BE﹣C的余弦值.4.(2018•焦作四模)如图,梯形ABCD与矩形CC1D1D所在平面相互垂直,AD ∥BC,BA⊥AD,AD=4,AB=BC=CC1=1.(Ⅰ)求证:AD1∥平面BCC1;(Ⅱ)求四棱锥C1﹣ABCD的侧面积.5.(2018•南海区模拟)如图,在四棱锥P﹣ABCD中,底面ABCD为平行四形,AB=2AD=2,∠DAB=60°,PD=BD,且PD⊥底面ABCD.(Ⅰ)证明:BC⊥平面PBD;(Ⅱ)若Q为PC的中点,求三棱锥A﹣PBQ的体积.6.(2018•大武口区校级三模)将棱长为a的正方体截去一半(如图1所示)得到如图2所示的几何体,点E,F分别是BC,DC的中点.(Ⅰ)证明:AF⊥平面DD1E;(Ⅱ)求点E到平面AFD1的距离.7.(2018•郴州二模)如图,在长方形ABCD中,AB=4,BC=2,现将△ACD沿AC折起,使D折到P的位置且P在面ABC的射影E恰好在线段AB上.(Ⅰ)证明:AP⊥PB;(Ⅱ)求三棱锥P﹣EBC的表面积.8.(2018•晋城二模)如图,在几何体ABCDEF中,底面CDEF是平行四边形,AB ∥CD,AB=1,CD=2,DE=2,DF=4,DB=2,DB⊥平面CDEF,CE与DF交于点O.(Ⅰ)求证:OB∥平面ACF;(Ⅱ)求三棱锥B﹣DEF的表面积.9.(2018•香坊区校级三模)如图,在三棱柱ABC﹣A1B1C1中,,C1在线段AB1上的射影为H,H是正方形AA1B1B的中心,.(1)求证:平面C1AB1⊥平面AA1B1B;(2)求二面角C﹣BC1﹣A1的余弦值.10.(2018•石嘴山一模)如图,在直三棱柱ABC﹣A1B1C1中,底面△ABC是边长为2的等边三角形,D为BC的中点,侧棱AA1=3,点E在BB1上,点F在CC1上,且BE=1,CF=2.(Ⅰ)证明:CE⊥平面ADF;(Ⅱ)求二面角F﹣AD﹣E的余弦值.11.(2018•肥城市模拟)如图,在四棱锥P﹣ABCD中,PB⊥底面ABCD,底面ABCD为梯形,AD∥BC,AD⊥AB,且PB=AB=AD=3,BC=1.(Ⅰ)若点F为PD上一点且,证明:CF∥平面PAB;(Ⅱ)求二面角B﹣PD﹣A的大小;(Ⅲ)在线段PD上是否存在一点M,使得CM⊥PA?若存在,求出PM的长;若不存在,说明理由.12.(2018•盐湖区校级模拟)如图,AB为圆O的直径,点E、F在圆O上,AB ∥EF,矩形ABCD和圆O所在的平面互相垂直,已知AB=2,EF=1.(Ⅰ)求证:平面DAF⊥平面CBF;(Ⅱ)当AD的长为何值时,二面角D﹣FE﹣B的大小为60°.13.(2018•安阳一模)如图,在空间直角坐标系O﹣xyz中,正四面体(各条棱均相等的三棱锥)ABCD的顶点A,B,C分别在x轴,y轴,z轴上.(Ⅰ)求证:CD∥平面OAB;(Ⅱ)求二面角C﹣AB﹣D的余弦值.14.(2018•丰台区一模)如图所示,在四棱锥P﹣ABCD中,平面PAB⊥平面ABCD,AD∥BC,AD=2BC,∠DAB=∠ABP=90°.(Ⅰ)求证:AD⊥平面PAB;(Ⅱ)求证:AB⊥PC;(Ⅲ)若点E在棱PD上,且CE∥平面PAB,求的值.15.(2018•马鞍山三模)如图,三棱柱ABC﹣A1B1C1中,AA1⊥平面ABC,AB=AC=AA1=2,D,E分别为B1C1,AB中点.(1)证明:平面AA1D⊥平面EB1C1;(2)若AB⊥AC,求点B到平面EB1C1的距离.16.(2018•黄州区校级模拟)在如图所示的几何体中,EA⊥平面ABCD,四边形ABCD为等腰梯形,AD BC,AD=AE=1,∠ABC=60°,EF AC.(Ⅱ)求二面角B﹣EF﹣D的余弦值.17.(2018•黄山一模)如图,在三棱锥P﹣ABC中,PA=PB=AB=2,BC=3,∠ABC=90°,平面PAB⊥平面ABC,D,E分别为AB,AC中点.(1)求证:DE∥平面PBC;(2)求证:AB⊥PE;(3)求三棱锥P﹣BEC的体积.18.(2018•九江三模)如图,在三棱柱ABC﹣A1B1C1中,侧面AA1B1B是边长为1的菱形,∠A1B1B=60°,E为A1C1的中点,AC1=B1C1=1,A1C1=BC1,A1B∩AB1=O.(Ⅰ)证明:平面AB1C1⊥平面AA1B1B;(Ⅱ)求二面角A﹣OE﹣C的余弦值.19.(2018•河南一模)四棱锥P﹣ABCD中,底面ABCD为矩形,AB=2,BC=.PA=PB,侧面PAB⊥底面ABCD.(2)设BD与平面PAD所成的角为45°,求二面角B﹣PC﹣D的余弦值.20.(2018•洛阳二模)如图,在三棱锥P﹣ABC中,PA=PB=AB=BC,∠ABC=90°,D为AC的中点.(1)求证:AB⊥PD;(2)若∠PBC=90°,求二面角B﹣PD﹣C的余弦值.21.(2018•衡阳一模)在四棱锥P﹣ABCD中,底面ABCD是边长为2的菱形,∠ABC=60°,PB=PC=PD.(1)证明:PA⊥平面ABCD;(2)若PA=2,求二面角A﹣PD﹣B的余弦值.22.(2018•安庆二模)如图所示,四棱锥B﹣AEDC中,平面AEDC⊥平面ABC,F为BC的中点,P为BD的中点,且AE∥DC,∠ACD=∠BAC=90°,DC=AC=AB=2AE.(Ⅰ)证明:EP⊥平面BCD;(Ⅱ)若DC=2,求三棱锥E﹣BDF的体积.23.(2018•朝阳一模)在如图所示的几何体ABCDEF中,平面ABCD⊥平面ABEF,四边形ABCD和四边形ABEF都是正方形,且边长为2,Q是AD的中点.(1)求证:直线AE∥平面FQC;(2)求二面角A﹣FC﹣B的大小.24.(2018•厦门二模)已知四棱锥P﹣ABCD的底面ABCD是直角梯形,AD,BC=2AD=2,E为CD的中点,PB⊥AE.(1)证明:平面PBD⊥平面ABCD;(2)若PB=PD,且PC与平面ABCD所成角为,求二面角B﹣PD﹣C的余弦值.25.(2018•贵阳二模)已知如图1所示,在边长为12的正方形AA′A1A1,中,BB1∥CC1∥AA1,且AB=3,BC=4,AA′1分别交BB1,CC1于点P,Q,将该正方形沿BB1,CC1,折叠,使得A′A1与AA1重合,构成如图2所示的三棱柱ABC﹣A1B1C1,在该三棱柱底边AC上有一点M,满足AM=kMC(0<k<1);请在图2中解决下列问题:(I)求证:当k=时,BM∥平面APQ;(Ⅱ)若直线BM与平面APQ所成角的正弦值为,求k的值26.(2018•烟台二模)如图,在三棱锥P﹣ABC中,D为AC中点,P在平面ABC 内的射影O在AC上,BC=AB=2AP,AB⊥BC,∠PAC=45°.(1)求证:AP⊥平面PBD;(2)求二面角A﹣PC﹣B的余弦值.27.(2018•徐州一模)如图,在直三棱柱ABC﹣A1B1C1中,∠ABC=90°,AB=AA1,M,N分别是AC,B1C1的中点.求证:(1)MN∥平面ABB1A1;(2)AN⊥A1B.28.(2018•广西三模)如图,三棱柱ABC﹣A1B1C1中,A1A⊥平面ABC,AB=2,AC=CB=2,M,N分别是AB、A1C的中点.(1)求证:MN∥平面BB1C1C;(2)若平面CMN⊥平面B1MN,求直线AB与平面B1MN所成角的正弦值.29.(2018•聊城一模)如图,四棱锥P﹣ABCD中,△PAD为等边三角形,且平面PAD⊥平面ABCD,AD=2BC=2,AB⊥AD,AB⊥BC.(Ⅰ)证明:PC⊥BC;(Ⅱ)若直线PC与平面ABCD所成角为60°,求二面角B﹣PC﹣D的余弦值.30.(2018•三明二模)在四棱锥P﹣ABCD中,AB∥CD,CD=2AB,AC与BD相交于点M,点N在线段AP上,AN=λAP(λ>0),且MN∥平面PCD.(1)求实数λ的值;(2)若,∠BAD=60°,求点N到平面PCD的距离.31.(2018•淄博一模)直角三角形ABC中,∠C=90°,AC=4,BC=2,E是AC的中点,F是线段AB上一个动点,且,如图所示,沿BE将△CEB翻折至△DEB,使得平面DEB⊥平面ABE.(1)当时,证明:BD⊥平面DEF;(2)是否存在λ,使得DF与平面ADE所成的角的正弦值是?若存在,求出λ的值;若不存在,请说明理由.32.(2018•西宁模拟)在四棱锥P﹣ABCD中,四边形ABCD是矩形,平面PAB ⊥平面ABCD,点E、F分别为BC、AP中点.(1)求证:EF∥平面PCD;(2)若AD=AP=PB=AB=1,求三棱锥P﹣DEF的体积.33.(2018•铜山区模拟)如图,在直三棱柱ABC﹣A1B1C中,已知∠ACB=90°,BC=CC1,E,F分别为AB,AA1的中点.(1)求证:直线EF∥平面BC1A1;(2)求证:EF⊥B1C.34.(2018•泉州一模)如图1,在四边形ABCD中,AD∥BC,∠BAD=90°,,BC=4,AD=6,E是AD上的点,.将△ABE沿BE折起到△A1BE的位置,且A1C=4,如图2.(Ⅰ)求证:平面A1BE⊥平面BCDE;(Ⅱ)若P为线段BE上任一点,求直线PA1与平面A1CD所成角的正弦值的最大值.35.(2018•河南一模)如图,在四棱锥P﹣ABCD中,底面ABCD是平行四边形,且平面PAD⊥平面ABCD,PA⊥AB.(1)求证:四边形ABCD是矩形;(2)若PA=PD=AD=DC,求二面角A﹣PB﹣C的余弦值.36.(2018•全国二模)如图,五边形ABSCD中,四边形ABCD为长方形,三角形SBC为边长为2的正三角形,将三角形SBC沿BC折起,使得点S在平面ABCD上的射影恰好在AD上.(Ⅰ)当时,证明:平面SAB⊥平面SCD;(Ⅱ)若AB=1,求平面SCD与平面SBC所成二面角的余弦值的绝对值.37.(2018•静海区校级模拟)如图,等腰直角三角形AEF的斜边EF的中点为D,四边形ABCD为矩形,平面ABCD⊥平面AEF,点G为DF的中点,AD=2AB=2.(1)证明:BF∥平面ACG;(2)求二面角D﹣BC﹣F的正弦值;(3)点H为直线CE上的点,且=﹣5,求直线AH和平面BCF所成角的正弦值.38.(2018•玉溪模拟)如图,平面ACEF⊥平面ABCD,四边形ABCD是菱形,∠ABC=60°,AF∥CE,AF⊥AC,AB=AF=2,CE=1.(1)求四棱锥B﹣ACEF的体积;(2)在BF上有一点P,使得AP∥DE,求的值.39.(2018•潍坊三模)如图所示五面体ABCDEF,四边形ACFE是等腰三角形,AD∥FC,,BC⊥pmACFD,CA=CB=CF=1,AD=2CF,点G为AC的中点.(1)在AD上是否存在一点H,使GH∥平面BCD?若存在,指出点H的位置并给出证明;若不存在,说明理由;(2)求三棱锥G﹣ECD的体积.40.(2018•芜湖模拟)如图,在三棱柱ABC﹣A1B1C1中,∠AA1B1=45°,AC=BC,平面BB1C1C⊥平面AA1B1B,E为CC1中点.(1)求证:BB1⊥AC;(2)若AA1=2,AB=,直线A1C1与平面ABB1A1所成角为45°,求平面A1B1E 与平面ABC所成锐二面角的余弦值.参考答案与试题解析一.解答题(共40小题)1.【分析】(Ⅰ)连接PE,G,F为EC和PC的中点,得到FG∥PE,利用线面平行的判定定理可证;(Ⅱ)利用菱形的性质得到BD⊥AC,再由PA⊥面ABCD,得到BD⊥PA,结合线面垂直的判定定理得到BD⊥平面PAC,进一步由线面垂直的性质得到所证.【解答】证明:(Ⅰ)连接PE,G、F为EC和PC的中点,∴FG∥PE,FG⊄平面PBD,PE⊂平面PBD,∴FG∥平面PBD…(6分)(Ⅱ)∵菱形ABCD,∴BD⊥AC,又PA⊥面ABCD,BD⊂平面ABCD,∴BD⊥PA,∵PA⊂平面PAC,AC⊂平面PAC,且PA∩AC=A,∴BD⊥平面PAC,FG⊂平面PAC,∴BD⊥FG…(14分)【点评】本题考查了线面平行的判定定理的运用和线面垂直的判定定理和性质定理的运用,关键是熟练相关的定理.2.【分析】(I)由A1A⊥AB,AC⊥AB可知AB⊥平面ACC1A1,故E到平面ACC1A1的距离等于AB,于是VV=V,根据体积列出方程解出A1A;(II)连结AB1交A1E于F,连结MF,由矩形知识可知AF=,故MF∥CB1,所以CB1∥平面A1EM.【解答】解:(I)∵A1A⊥平面ABC,AB⊂平面ABC,∴A1A⊥AB,又A1A⊥AC,A1A⊂平面ACC1A1,AC⊂平面ACC1A1,A1A∩AC=A,∴AB⊥平面ACC1A1,∵BB1∥平面ACC1A1,∴V=V====.∴A1A=.(II)连结AB1交A1E于F,连结MF,∵E是B1B的中点,∴AF=,又AM=,∴MF∥CB1,又MF⊂平面A1ME,CB1⊄平面A1ME∴CB1∥平面A1EM.【点评】本题考查了线面平行的判定,棱锥的体积计算,属于基础题.3.【分析】(Ⅰ)过点B作BM⊥AE于M,过点C作CN⊥ED于N,连接MN,证明BC∥MN即可;(Ⅱ)以E为原点,ED为x轴,EA为y轴,建立空间直角坐标系E﹣xyz,求出平面CEB的法向量,平面AEB的法向量,计算cos<,>即可.【解答】解:(Ⅰ)证明:过点B作BM⊥AE,垂足为M,过点C作CN⊥ED于N,连接MN,如图所示;∵平面BAE⊥平面ADE,平面DCE⊥平面ADE,∴BM⊥平面ADE,CN⊥ADE,∴BM∥CN;由题意知Rt△ABE≌Rt△DCE,∴BM=CN,∴四边形BCNM是平行四边形,∴BC∥MN;又BC⊄平面ADE,MN⊂平面ADE,∴BC∥平面ADE;(Ⅱ)由已知,AE、DE互相垂直,以E为原点,ED为x轴,EA为y轴,建立空间直角坐标系E﹣xyz,如图所示;则E(0,0,0),B(0,,),C(,0,),=(0,,),=(,0,),设平面CEB的法向量为=(x,y,z),则,即,令y=﹣1,则z=1,x=1,∴=(﹣1,﹣1,1);设平面AEB的法向量为=(x,y,z),则,易求得=(1,0,0);又cos<,>===﹣,∴当二面角A﹣BE﹣C的平面角为锐角时,余弦值为,当二面角A﹣BE﹣C的平面角为钝角时,余弦值为﹣.【点评】本题考查了空间几何体以及空间向量的应用问题,是中档题.4.【分析】(Ⅰ)推导出DD1∥平面BCC1,AD∥平面BCC1,从而平面ADD1∥平面BCC1,由此能证明AD1∥平面BCC1.(Ⅱ)推导出CC1⊥平面ABCD,从而CC1⊥BC,CC1⊥CD,过点C作CE⊥AD交AD于点E,连接C1E,推导出AB⊥平面CC1B,BC1⊥AB,从而AD⊥平面CC1E,AD⊥C1E,由此能求出四棱锥C1﹣ABCD的侧面积.【解答】解:(Ⅰ)因为CC1∥DD1,CC1⊂平面BCC1,DD1⊄平面BCC1,所以DD1∥平面BCC1,同理可得AD∥平面BCC1,又因为AD∩DD1=D,所以平面ADD1∥平面BCC1,因为AD1⊂平面ADD1,所以AD1∥平面BCC1.(Ⅱ)因为平面ABCD⊥平面CC1D1D,平面ABCD∩平面CC1D1D=CD,CC1⊥CD,所以CC1⊥平面ABCD,∴CC1⊥BC,CC1⊥CD,过点C作CE⊥AD交AD于点E,连接C1E,因为AD=4,AB=1,BC=CC1=1,由题意得:,所以,,因为CC1⊥AB,CB⊥AB,CB∩CC1=C,∴AB⊥平面CC1B,所以BC1⊥AB,,由AD⊥CC1,CE∩CC1=C,得AD⊥平面CC1E,所以AD⊥C1E,因为CE=CC1=1,所以,,所以四棱锥C1﹣ABCD的侧面积为.【点评】本题考查线面平行的证明,考查四棱锥的侧面积的求法,考查空间中线线、线面、面面间的位置关系等基础知识,考查推理论证能力、运算求解能力、空间想象能力,考查化归与转化思想、函数与方程思想、数形结合思想,是中档题.5.【分析】(Ⅰ)在△ABD中,由余弦定理得求得BD,可得AD2+BD2=AB2,则AD ⊥BD,再由已知得到PD⊥BC.由线面垂直的判定可得BC⊥平面PBD;(Ⅱ)由Q为PC的中点,得三棱锥A﹣PBQ的体积与三棱锥A﹣QBC的体积相等,然后利用等积法求解.【解答】(Ⅰ)证明:在△ABD中,由余弦定理得:BD2=BA2+AD2﹣2BA•AD•cos60°=3,∵AD2+BD2=AB2,∴AD⊥BD,∵AD∥BC,∴BC⊥BD.又∵PD⊥底面ABCD,BC⊂平面ABCD,∴PD⊥BC.∵PD∩BD=D,∴BC⊥平面PBD;(Ⅱ)解:∵Q为PC的中点,∴三棱锥A﹣PBQ的体积与三棱锥A﹣QBC的体积相等,而=.∴三棱锥A﹣PBQ的体积.【点评】本题考查直线与平面垂直的判定,考查空间想象能力与思维能力,训练了利用等积法求多面体的体积,是中档题.6.【分析】(Ⅰ)推导出D1D⊥AF,△ADF≌△DCE,AF⊥DE,由此能证明AF⊥平面D1DE.(Ⅱ)以D为原点,DA为x轴,DC为y轴,DD1为z轴,建立空间直角坐标系,利用向量法能求出点E到平面AFD1的距离.【解答】证明:(Ⅰ)∵D1D⊥平面ABCD,AF⊂平面ABCD,∴D1D⊥AF,∵点E,F分别是BC,D1C的中点,∴DF=CE,又∵AD=DC,∠ADF=∠DCE=90°,∴△ADF≌△DCE,∴∠AFD=∠DEC,又∵∠CDE+∠DEC=90°,∴∠CDE+∠AFD=90°,∴∠DOF=180°﹣(∠CDE+∠AFD)=90°,∴AF⊥DE,又∵D1D∩DE=D,∴AF⊥平面D1DE.解:(Ⅱ)以D为原点,DA为x轴,DC为y轴,DD1为z轴,建立空间直角坐标系,E (,a ,0),A (a ,0,0),F (0,,0),D 1(0,0,a ), =(﹣,a ,0),=(﹣a ,,0),=(﹣a ,0,a ),设平面AFD 1的法向量=(x ,y ,z ),则,取x=1,得=(1,2,1),∴点E 到平面AFD 1的距离d===.【点评】本题考查线面垂直的证明,考查点到平面的距离的求法,考查空间中线线、线面、面面间的位置关系等基础知识,考查运算求解能力,考查函数与方程思想,是中档题. 7.【分析】(Ⅰ)推导出PE ⊥BC ,AB ⊥BC ,从而BC ⊥平面PAB ,进而BC ⊥AP ,再由AP ⊥CP ,得AP ⊥平面PBC ,由此能证明AP ⊥PB .(Ⅱ) 三棱锥P ﹣EBC 的表面积为S=S △PEB +S △EBC +S △PEC +S △PBC . 【解答】证明:(Ⅰ)由题知PE ⊥平面ABC , 又BC ⊂平面ABC ,∴PE ⊥BC ,又AB ⊥BC ,且AB ∩PE=E ,∴BC ⊥平面PAB ,又AP⊂平面PAB,∴BC⊥AP,又AP⊥CP,且BC∩CP=C,∴AP⊥平面PBC,又PB⊂平面PBC,∴AP⊥PB.解:(Ⅱ)在△PAB中,由(Ⅰ)得AP⊥PB,AB=4,AP=2,∴,∴BE=3∴在△EBC中,EB=3,BC=2,∴,在△PEC中,∴,∴,∴三棱锥P﹣EBC的表面积为:.【点评】本题考查线线垂直的证明,考查三棱锥的表面积的求法,考查空间中线线、线面、面面间的位置关系等基础知识,考查推理论证能力、运算求解能力、空间想象能力,考查化归与转化思想、函数与方程思想、数形结合思想,是中档题.8.【分析】(Ⅰ)取CF的中点G,连接OG,AG.又点O为DF的中点,可得OG CD,利用已知可得AB OG.可得四边形ABOE为平行四边形,可得OB∥AE.再利用线面平行的判定定理即可证明结论.(Ⅱ)由CD=2,DE=2=CF,DF=4,可得CD2+DF2=DE2.于是CD⊥DF.又DB⊥平面CDEF,以FD,DC,DB所在直线分别为x轴,y轴,z轴建立空间直角坐标系.利用向量法能求出三棱锥B﹣DEF的表面积.【解答】证明:(Ⅰ)取CF的中点G,连接OG,AG又点O为DF的中点,∴OG CD,又AB∥CD,AB=1,CD=2,∴AB OG.∴四边形ABOE为平行四边形,∴OB∥AE.又OB⊄平面ACF,AE⊂平面ACF,∴OB∥平面ACF.(Ⅱ)解:∵CD=2,DE=2=CF,DF=4,∴CD2+DF2=DE2.∴∠CDF=90°,∴CD⊥DF.连结BF,又DB⊥平面CDEF,∴S===4,△BDF==4,==2,==2,∴三棱锥B﹣DEF的表面积:S=S△BDF+S△DEF+S△BDE+S△BDF==8+4.【点评】本题考查线面平行的证明,考查三棱锥的表面积的求法,考查空间中线线、线面、面面间的位置关系等基础知识,考查推理论证能力、运算求解能力、空间想象能力,考查化归与转化思想、函数与方程思想、数形结合思想,是中档题.9.【分析】(1)取A1B1的中点D,连结HD、C1D推导出HD⊥A1B1,A1B1⊥C1H,C1H ⊥AB1,从而C1H⊥平面AA1B1B,由此能证明平面C1AB1⊥平面AA1B1B.(2)建立空间直角坐标系,利用向量法能求出二面角C﹣BC1﹣A1的余弦值.【解答】证明:(1)取A1B1的中点D,连结HD、C1D∵CA=CB,∴C1D⊥A1B1,∵四边形AA1B1D是正方形,∴HD⊥A1B1,又HD∩C1D=D,∴A1B1⊥平面C1HD,∴A1B1⊥C1H,∵C1在线段AB1上的射影为H,∴C1H⊥AB1,∵AB1∩A1B1=B1,∴C1H⊥平面AA1B1B,∴平面C1AB1⊥平面AA1B1B.解:(2)如图建系:由AA1=2,得A1H=B1H=2,∴A1(2,0,0),A(0,﹣2,0),B1(0,2,0),B(﹣2,0,0),C1(0,0,),设C(x,y,z),则=(x,y,z﹣),=(﹣2,﹣2,0),由=,得x=﹣2,y=﹣2,z=,∴C(﹣2,﹣2,),平面BC1A1的法向量=(0,1,0),=(2,0,),=(0,﹣2,),平面BC1C的法向量=(x,y,z),则,取x=,得=(,﹣,﹣2),设二面角C﹣BC1﹣A1的平面角为θ,由图形得θ为钝角,∴cosθ=﹣=﹣,∴二面角C﹣BC1﹣A1的余弦值为﹣.【点评】本题考查面面垂直的证明,考查二面角的余弦值的求法,考查线面垂直的性质与判定,面面垂直的判定定理等基础知识,考查运算求解能力,考查函数与方程思想,是中档题.10.【分析】(Ⅰ)以C为原点,在平面ABC中过C作BC的垂线为x轴,CB为y轴,CC1为z轴,建立空间直角坐标系,利用向量法能证明CE⊥平面ADF.(Ⅱ)求出平面ADF的法向量和平面ADE的法向量,利用向量法能求出二面角F ﹣AD﹣E的余弦值.【解答】证明:(Ⅰ)以C为原点,在平面ABC中过C作BC的垂线为x轴,CB 为y轴,CC1为z轴,建立空间直角坐标系,C(0,0,0),E(0,2,1),A(,0),D(0,1,0),F(0,0,2),=(0,2,1),=(),=(0,1,﹣2),∴=0,=0,∴CE⊥FA,CE⊥FD,又FA∩FD=F,∴CE⊥平面ADF.解:(Ⅱ)=(﹣,0,0),=(﹣,1,1),设平面ADF的法向量=(x,y,z),则,取z=1,得=(0,2,1),设平面ADE的法向量=(x,y,z),则,取y=1,得=(0,1,﹣1),设二面角F﹣AD﹣E的平面角为θ,则cosθ===.∴二面角F﹣AD﹣E的余弦值为.【点评】本题考查线面垂直的证明,考查二面角的余弦值的求法,考查空间中线线、线面、面面间的位置关系等基础知识,考查运算求解能力,考查函数与方程思想,是中档题.11.【分析】(Ⅰ)过点F作FH∥AD,交PA于H,连接BH,证明HF∥BC,CF∥BH,然后证明CF∥平面PAD.(Ⅱ)说明BC⊥AB.PB⊥AB,PB⊥BC,以B为原点,BC,BA,BP所在直线为x,y,z轴建立空间直角坐标系,求出平面BPD的一个法向量,平面APD的一个法向量,通过向量的数量积求解二面角B﹣PD﹣A的大小.(Ⅲ)假设存在点M,设,利用向量的数量积求解即可.【解答】解:(Ⅰ)证明:过点F作FH∥AD,交PA于H,连接BH,因为,所以.….(1分)又FH∥AD,AD∥BC,所以HF∥BC.….(2分)所以BCFH为平行四边形,所以CF∥BH.….(3分)又BH⊂平面PAB,CF⊄平面PAB,….(4分)(一个都没写的,则这(1分)不给)所以CF∥平面PAB.….(5分)(Ⅱ)因为梯形ABCD中,AD∥BC,AD⊥AB,所以BC⊥AB.因为PB⊥平面ABCD,所以PB⊥AB,PB⊥BC,如图,以B为原点,BC,BA,BP所在直线为x,y,z轴建立空间直角坐标系,….(6分)所以C(1,0,0),D(3,3,0),A(0,3,0),P(0,0,3).设平面BPD的一个法向量为,平面APD的一个法向量为,因为,所以,即,….(7分)取x=1得到,….(8分)同理可得,….(9分)所以,….(10分)因为二面角B﹣PD﹣A为锐角,所以二面角B﹣PD﹣A为.….(11分)(Ⅲ)假设存在点M,设,所以,….(12分)所以,解得,….(13分)所以存在点M,且.….(14分)【点评】本题考查直线与平面平行的判定定理的应用,二面角的平面角的求法,向量的数量积的应用,考查空间想象能力以及计算能力.12.【分析】(I)利用面面垂直的性质,可得CB⊥平面ABEF,再利用线面垂直的判定,证明AF⊥平面CBF,从而利用面面垂直的判定可得平面DAF⊥平面CBF;(II)建立空间直角坐标系,求出平面DCF的法向量和平面CBF的一个法向量,利用向量的夹角公式,即可求得AD的长.【解答】(Ⅰ)∵平面ABCD⊥平面ABEF,CB⊥AB,平面ABCD∩平面ABEF=AB,∴CB⊥平面ABEF,∵AF⊂平面ABEF∴AF⊥CB,又∵AB为圆O的直径,∴AF⊥BF,∴AF⊥平面CBF,∵AF⊂平面ADF,∴平面DAF⊥平面CBF.(Ⅱ)设EF中点为G,以O为坐标原点,OA,OG,AD方向分别为x轴、y轴、z轴方向建立空间直角坐标系(如图).设AD=t,则点D的坐标为(1,0,t),则C(﹣1,0,t),又A(1,0,0),B(﹣1,0,0),F(,,0),∴,,设平面DCF的法向量为=(x,y,z),则,即,可取.由(1)可知AF⊥平面CFB,取平面CFB的一个法向量为,|cos|=cos60°,即=,解得t=,因此,当AD的长为时,平面DFC与平面FCB所成的锐二面角的大小为60°.【点评】本题考查面面垂直,考查面面角,考查向量知识的运用,考查学生分析解决问题的能力,求出平面的法向量是关键.13.【分析】(Ⅰ)由AB=BC=CA,可得OA=OB=OC.设OA=a,则,求得A,B,C的坐标,设D点的坐标为(x,y,z),则由,求得x=y=z=a,得到.结合平面OAB的一个法向量为,利用,可得CD∥平面OAB;(Ⅱ)设F为AB的中点,连接CF,DF,可得∠CFD为二面角C﹣AB﹣D的平面角.然后利用余弦定理求解二面角C﹣AB﹣D的余弦值.【解答】(Ⅰ)证明:由AB=BC=CA,可得OA=OB=OC.设OA=a,则,A(a,0,0),B(0,a,0),C(0,0,a),设D点的坐标为(x,y,z),则由,可得(x﹣a)2+y2+z2=x2+(y﹣a)2+z2=x2+y2+(z﹣a)2=2a2,解得x=y=z=a,∴.又平面OAB的一个法向量为,∴,∴CD∥平面OAB;(Ⅱ)解:设F为AB的中点,连接CF,DF,则CF⊥AB,DF⊥AB,∠CFD为二面角C﹣AB﹣D的平面角.由(Ⅰ)知,在△CFD中,,,则由余弦定理知,即二面角C﹣AB﹣D的余弦值为.【点评】本题考查利用空间向量证明直线与平面平行,考查二面角的平面角的求法,是中档题.14.【分析】(Ⅰ)由AD⊥AB.平面PAB⊥平面ABCD,可得AD⊥平面PAB.(Ⅱ)由已知得AD⊥AB,PB⊥AB,即可得AB⊥平面PBC,AB⊥PC.(Ⅲ)过E作EF∥AD交PA于F,连接BF.可得E,F,B,C四点共面,由四边形BCEF为平行四边形,【解答】(Ⅰ)证明:因为∠DAB=90°,所以AD⊥AB.……………………(1分)因为平面PAB⊥平面ABCD,……………………(2分)且平面PAB∩平面ABCD=AB,……………………(3分)所以AD⊥平面PAB.……………………(4分)(Ⅱ)证明:由已知得AD⊥AB因为AD∥BC,所以BC⊥AB.……………………(5分)又因为∠ABP=90°,所以PB⊥AB.……………………(6分)因为PB∩BC=B……………………(7分)所以AB⊥平面PBC……………………(8分)所以AB⊥PC.……………………(9分)(Ⅲ)解:过E作EF∥AD交PA于F,连接BF.……………………(10分)因为AD∥BC,所以EF∥BC.所以E,F,B,C四点共面.……………………(11分)又因为CE∥平面PAB,且CE⊂平面BCEF,且平面BCEF∩平面PAB=BF,所以CE∥BF,……………………(13分)所以四边形BCEF为平行四边形,所以EF=BC.在△PAD中,因为EF∥AD,所以,……………………(14分)即.【点评】本题考查线面垂直、线线垂直,并探索线面平行的存在性.着重考查了面面垂直的性质、线面垂直的判定与性质和利用空间向量研究面面角、线面平行等知识,属于中档题.15.【分析】(1)推导出B1C1⊥AD,B1C1⊥AA1,从而B1C1⊥平面AA1D,由此能证明平面AA1D⊥平面EB1C1.(2)连接EC,设点B到平面EB1C1的距离为h,由,能求出点B到平面EB1C1的距离.【解答】证明:(1)由已知可得,B1C1⊥AD,B1C1⊥AA1,∴B1C1⊥平面AA1D,∵B1C1⊂平面EB1C1,∴平面AA1D⊥平面EB1C1.…………………………5分(2)连接EC,由已知,在Rt△AEC中,,∴在Rt△ECC1中,得EC1=3,由题可得,在Rt△EBB1中,,在Rt△A1B1C1中,,∴在△EB1C1中,根据余弦定理可得:,∴,∴………………………………9分∵C1A1⊥A1B1,C1A1⊥AA1,∴C1A1⊥平面BB1E,∵,∴,设点B到平面EB1C1的距离为h由得,解得:即点B到平面EB1C1的距离为.………………………………12分【点评】本题考查面面垂直的证明,考查点到平面的距离的求法,考查空间中线线、线面、面面间的位置关系,考查运算求解能力,考查函数与方程思想,是中档题.16.【分析】(Ⅰ)证明BA⊥AE.过点A作AH⊥BC于H,AB⊥AC,推出AB⊥平面ACFE.即可证明AB⊥CF.(Ⅱ)解:以A为坐标原点,AB,AC,AE分别为x,y,z轴,建立空间直角坐标系,求出平面BEF的一个法向量,平面DEF的一个法向量,通过向量的数量积求解二面角的余弦函数值即可.【解答】(Ⅰ)证明:由题知EA⊥平面ABCD,BA⊥平面ABCD,∴BA⊥AE.过点A作AH⊥BC于H,在RT△ABH中,,∴AB=1,在△ABC中,AC2=AB2+BC2﹣2AB•BCcos60°=3,∴AB2+AC2=BC2,∴AB⊥AC,且AC∩EA=A,∴AB⊥平面ACFE.又∵CF⊂平面ACFE,∴AB⊥CF.﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(6分)(Ⅱ)解:以A为坐标原点,AB,AC,AE分别为x,y,z轴,建立空间直角坐标系,则,∴设为平面BEF的一个法向量,则令x=1,得,同理可求平面DEF的一个法向量,∴﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(12分)【点评】本题考查直线与平面垂直的判断定理的应用.二面角的平面角的求法,考查空间想象能力以及计算能力.17.【分析】(1)利用中位线定理即可得出DE∥BC,故而DE∥平面PBC;(2)连结PD,又AB⊥PD,AB⊥DE得出AB⊥平面PAB,故而AB⊥PE;(3)利用面面垂直的性质得出PD⊥平面ABC,计算PD,则V P=V P﹣ABC.﹣BCE【解答】证明:(1)∵D,E分别为AB,AC的中点,∴DE∥BC,又DE⊄平面PBC,BC⊂平面PBC,∴DE∥平面PBC.(2)连接PD,∵DE∥BC,又∠ABC=90°,∴DE⊥AB,又PA=PB,D为AB中点,∴PD⊥AB,又PD∩DE=D,PD⊂平面PDE,DE⊂平面PDE,∴AB⊥平面PDE,又PE⊂平面PDE,∴AB⊥PE.(3)∵平面PAB⊥平面ABC,平面PAB∩平面ABC=AB,PD⊥AB,PD⊂平面PAB,∴PD⊥平面ABC,∵△PAB是边长为2的等边三角形,∴PD=,∵E是AC的中点,∴.【点评】本题考查了线面平行,线面垂直的判定,棱锥的体积计算,属于中档题.18.【分析】(Ⅰ)连结OC1,推导出OC1⊥A1B,OC1⊥AB1,从而OC1⊥平面AA1B1B,由此能证明平面AB1C1⊥平面AA1B1B.(Ⅱ)以O为原点,OA为x轴,OA1为y轴,OC1为z轴,建立空间直角坐标系,利用向量法能求出二面角A﹣OE﹣C的余弦值.【解答】证明:(Ⅰ)连结OC1,∵A1C1=BC1,O为A1B的中点,∴OC1⊥A1B,同理得OC1⊥AB1,又A1B∩AB1=O,A1B,AB1⊂平面AA1B1B,∴OC1⊥平面AA1B1B,又OC1⊂平面AB1C1,∴平面AB1C1⊥平面AA1B1B.解:(Ⅱ)∵OC1⊥平面AA1B1B,A1B⊥AB1,∴以O为原点,OA为x轴,OA1为y轴,OC1为z轴,建立空间直角坐标系,在菱形AA1B1B中,∵∠A1B1B=60°,A1B1=1,∴OB1=,又B1C1=1,∴OC1=,则A(,0,0),B(﹣,0),B1(﹣,0,0),C1(0,0,),E(0,),设=(x,y,z)为平面COE的法向量,==(),则,取x=2,得=(2,),设=(x,y,z)为平面AOE的法向量,则,取y=1,得=(0,1,﹣1),∴cos<>==,∴二面角A﹣OE﹣C的余弦值为.【点评】本题考查面面垂直的证明,考查二面角的余弦值的求法,考查空间中线线、线面、面面间的位置关系等基础知识,考查分析问题和解决问题的能力,属于中档题.19.【分析】(1)证法一:设AB中点为O,连接PO,由已知PA=PB,所以PO⊥AB,而平面PAB⊥平面ABCD,交线为AB,以O为原点、OP为z轴,OB为y轴,如图建立空间直角坐标系,并设PO=h,求出相关的坐标,利用向量的数量积求解,推出PC⊥BD.证法二:设AB中点为O,连接PO,由已知PA=PB,所以PO⊥AB,而平面PAB ⊥平面ABCD,交线为AB,证明BD⊥PO,连接CO,设CO与BD交于M,通过计算∠BCM+∠CBM=∠CDB+∠CBM=90°,推出BD⊥CO,然后证明PC⊥BD(2)由AD⊥AB,平面PAB⊥平面ABCD,交线为AB,可得AD⊥平面PAB,平面PAB⊥平面PAD,交线为PA过B作BH⊥PA,垂足为H,则BH⊥平面PAD,BD 与平面PAD所成的角即为∠BDH,通过求解三角形即可得到结果.(也可用向量法求出PO:)设P(0,0,h),求出平面PAD的一个法向量,通过cos<,BD >=sin45°可解得h=,求出平面BPC的一个法向量,平面DPC的一个法向量,利用空间向量的数量积求解即可.【解答】(1)证法一:设AB中点为O,连接PO,由已知PA=PB,所以PO⊥AB,而平面PAB⊥平面ABCD,交线为AB,故PO⊥平面ABCD,以O为原点、OP为z轴,OB为y轴,如图建立空间直角坐标系,并设PO=h,则P(0,0,h),B(0,1,0),C(,1,0),D(,﹣1,0)所以=(,1,﹣h),=(,﹣2,0),所以PC⊥BD…(6分)证法二:设AB中点为O,连接PO,由已知PA=PB,所以PO⊥AB,而平面PAB⊥平面ABCD,交线为AB,故PO⊥平面ABCD,从而BD⊥PO…①在矩形ABCD中,连接CO,设CO与BD交于M,则由CD:BC=BC:MO知△BCD∽△OBC,所以∠BCO=∠CDB,所以∠BCM+∠CBM=∠CDB+∠CBM=90°,故BD⊥CO…②由①②知BD⊥平面PCO,所以PC⊥BD.(2)解:由AD⊥AB,平面PAB⊥平面ABCD,交线为AB,可得AD⊥平面PAB,所以平面PAB⊥平面PAD,交线为PA,过B作BH⊥PA,垂足为H,则BH⊥平面PAD,BD与平面PAD所成的角即为角BDH,所以BH=BD=,从而三角形PAB为等边三角形,PO=.…(8分)(也可用向量法求出PO:)设P(0,0,h),则A(0,﹣1,0),B(0,1,0),D(,﹣1,0),可求得平面PAD的一个法向量为=(0,h,﹣1),而,由cos<,BD>=sin45°可解得h=,设平面BPC的一个法向量为,则,,可取=(0,,1),设平面DPC的一个法向量为,则,,可取=(,0,﹣)于是cos<>=﹣,…(11分)故二面角B﹣PC﹣D的余弦值为﹣…(12分)【点评】本题考查直线与平面垂直的判定定理以及性质定理的应用,二面角的平面角的求法,考查空间想象能力以及计算能力.20.【分析】(1)根据已知条件,取AB的中点O,连结OD,OP,得到AB⊥OP,再利用线面垂直判定定理可得AB⊥平面POD,从而得到AB⊥PD;(2)由已知可得BC⊥平面PBA,又OD⊥平面PBA,得到OD⊥OP,由此建立空间直角坐标系,利用向量法能求出二面角B﹣PD﹣C的余弦值.【解答】(1)证明:取AB的中点为O,连接OD,OP,∵PA=PB,∴AB⊥OP,∵OD∥BC,∠ABC=90°,∴AB⊥OD,又OD∩OP=O,∴AB⊥平面POD,从而AB⊥PD;(2)解:∵∠PBC=90°,即PB⊥BC,∴BC⊥平面PBA,∴OD⊥平面PBA,∴OD⊥OP,以O为坐标原点,OB,OD,OP所在的直线为x,y,z轴建立空间直角坐标系,设OB=1,则,∴,设是平面PDB的一个法向量,则,即,不妨设z=1,则,∴,同理可求得平面PDC的一个法向量为,∴,∵二面角B﹣PD﹣C是锐二面角,∴其余弦值为.【点评】本题考查空间中直线与直线的位置关系,考查了空间想象能力和思维能力,考查了用空间向量法求二面角的余弦值,是中档题.21.【分析】(1)连接AC,取BC中点E,连接AE,PE,推导出BC⊥AE,BC⊥PE,从而BC⊥PA.同理CD⊥PA,由此能证明PA⊥平面ABCD.(2)以A为原点,建立空间直角坐标系A﹣xyz,利用向量法能求出二面角A﹣PD﹣B的余弦值.【解答】证明:(1)连接AC,则△ABC和△ACD都是正三角形.取BC中点E,连接AE,PE,因为E为BC的中点,所以在△ABC中,BC⊥AE,因为PB=PC,所以BC⊥PE,又因为PE∩AE=E,所以BC⊥平面PAE,又PA⊂平面PAE,所以BC⊥PA.同理CD⊥PA,又因为BC∩CD=C,所以PA⊥平面ABCD. (6)解:(2)如图,以A为原点,建立空间直角坐标系A﹣xyz,则B(,﹣1,0),D(0,2,0),P(0,0,2),=(0,2,﹣2),=(﹣,3,0),设平面PBD的法向量为=(x,y,z),则,取x=,得=(),取平面PAD的法向量=(1,0,0),则cos<>==,所以二面角A﹣PD﹣B的余弦值是.…(12分)【点评】本题考查线面垂直的证明,考查二面角的余弦值的求法,是中档题,解题时要认真审题,注意向量法的合理运用.22.(Ⅰ)推导出AF⊥BC,从而DC⊥平面ABC,进而AF⊥DC,AF⊥平面BCD.连【分析】结PF,则PF∥DC,则AE∥DC,得AE∥PF,AE=PF,AFPE是平行四边形,EP∥AF,由此能证明EP⊥平面BCD.(Ⅱ)推导出EP是三棱锥E﹣BDF的高.EP=AF=BC=,由此能求出三棱锥E ﹣BDF的体积.【解答】证明:(Ⅰ)由题意知△ABC为等腰直角三角形,而F为BC的中点,所以AF⊥BC.又因为平面AEDC⊥平面ABC,且∠ACD=90°,所以DC⊥平面ABC.……(2分)而AF⊂平面ABC,所以AF⊥DC.而BC∩DC=C,所以AF⊥平面BCD.连结PF,则PF∥DC,PF=DC,…………(4分)而AE∥DC,AE=DC,所以AE∥PF,AE=PF,AFPE是平行四边形,因此EP∥AF,故EP⊥平面BCD.…………(7分)解:(Ⅱ)因为EP⊥平面BCD,所以EP⊥平面BDF,EP是三棱锥E﹣BDF的高.所以EP=AF=BC==.故三棱锥E﹣BDF的体积为:V===.…………(12分)【点评】本题考查线面垂直的证明,考查三棱锥的体积的求法,考查空间中线线、线面、面面间的位置关系等基础知识,考查运算求解能力,考查函数与方程思想,是中档题.23.【分析】(1)由已知证明几何体ADF﹣BCE是三棱柱.进一步证得为直三棱柱.再根据四边形ABCD和四边形ABEF都是正方形,可得四边形DCEF为矩形.然后结合P是DE中点,Q是AD的中点,可得PQ∥DE,由线面平行的判定可得直线AE∥平面FQC;(2)解:由于平面ABCD⊥平面ABEF,AB⊥BC,可得BC⊥平面ABEF,则BC⊥BE.于是AB,BC,BE两两垂直.以BA,BC,BE所在直线分别为x,y,z轴建立空间直角坐标系,分别求出平面BFC与平面AFC的一个法向量,由两法向量所成角的余弦值可得二面角A﹣FC﹣B的大小.【解答】(1)证明:∵AF∥BE,AD∥BC,。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
M F E C D A B 2018年北京高三模拟题分类汇编之立体几何大题精心校对版题号一二总分得分△注意事项:1.本系列试题包含2018北京市各城区一模二模真题。
2.本系列文档有相关的试题分类汇编,具体见封面。
3.本系列文档为北京双高教育精心校对版本4.本系列试题涵盖北京历年(2011年-2020年)高考所有学科一、填空题(本大题共2小题,共0分)1.(2018北京东城区高三一模数学(文))如图,四边形ABCD 为菱形,60DAB o ,ED 平面ABCD ,22ED AD EF ,EF ∥AB ,M 为BC 中点.(Ⅰ)求证:FM ∥平面BDE ;(Ⅱ)求证:AC BE ;(Ⅲ)若G 为线段BE 上的点,当三棱锥G BCD 的体积为239时,求BG BE 的值.2.(2018北京丰台区高三二模数学(文))如图,在矩形A B C D 中,4AB ,2AD ,E 为AB 的中点.将△ADE 沿DE 翻折,得到四棱锥1A DEBC .设1AC 的中点为M ,在翻折过程中,有下列三个命题:①总有BM ∥平面1A DE ;②线段BM 的长为定值;③存在某个位置,使DE 与1AC 所成的角为90.姓名:__________班级:__________考号:__________●-------------------------密--------------封-
-------------线--------------内--------------请--------------不--------------要--------------答--------------题-------------------------●A 1M E D C
B A。
