[高中数学]立体几何.球专题附练习题不看后悔
高中数学立体几何外接球专题练习(含解析)

外接球专题练习1.已知菱形ABCD满足,|AB|=2,∠ABC=,将菱形ABCD沿对角线AC折成一个直二面角B﹣AC﹣D,则三棱锥B﹣ACD外接球的表面积为()A.πB.8πC.7πD.2.如图,四面体ABCD中,面ABD和面BCD都是等腰Rt△,AB=,∠BAD=∠CBD=,且二面角A﹣BD﹣C的大小为,若四面体ABCD的顶点都在球O上,则球O的表面积为()A.12πB.20πC.24πD.36π3.如图,网格纸上小正方形的边长为2,粗实线及粗虚线画出的是某四棱锥的三视图,则该四棱锥的外接球的表面积为()A.B.C.41πD.31π4.已知一个几何体是由半径为2的球挖去一个三棱锥得到(三棱锥的顶点均在球面上).若该几何体的三视图如图所示(侧视图中的四边形为菱形),则该三棱锥的体积为()A.B.C.D.5.已知一个几何体的三视图如图所示,则该几何体的表面积是()A.2+2+2B.4+4+2C.2+4+4D.4+4+4 6.某三棱锥的三视图如图所示,则它的外接球表面积为()A.25πB.C.D.40π7.如图是某几何体的三视图,则该几何体的表面积是()A.18+2+B.15++C.12++D.18++ 8.在四面体ABCD中,AD⊥底面ABC,,E为棱BC的中点,点G在AE上且满足AG=2GE,若四面体ABCD的外接球的表面积为,则tan∠AGD=()A.B.2C.D.9.在三棱锥S﹣ABC中,,且三棱锥S﹣ABC的体积为,则该三棱锥的外接球的表面积为()A.4πB.16πC.36πD.72π10.如图所示,正方形ABCD的边长为2,切去阴影部分围成一个正四棱锥,则当正四棱锥体积最大时,该正四棱锥外接球的表面积为()A.B.C.D.11.已知三棱锥P﹣ABC所有顶点都在球O的球面上,底面△ABC是以C为直角顶点的直角三角形,AB=2,PA=PB=PC=,则球O的表面积为()A.9πB.C.4πD.π12.四棱锥P﹣ABCD的侧面PAB垂直于底面ABCD,且三角形PAB是等边三角形,底面ABCD是边长为2的正方形,则四棱锥P﹣ABCD外接球的表面积为()A.πB.C.4πD.π13.已知三棱锥D﹣ABC所有顶点都在球O的球面上,△ABC为边长为的正三角形,△ABD是以BD为斜边的直角三角形,且AD=8,二面角C﹣AB﹣D 为120°,则球O的表面积为()A.B.124πC.D.31π14.已知直三棱柱(侧棱垂直于底面的三棱柱)ABC﹣A1B1C1的顶点在球O上,∠ABC=120°,AA1=BC=AB=1,则球O的表面积为()A.7πB.6πC.5πD.4π15.三棱锥P﹣ABC中,平面PAC⊥平面ABC,AB⊥AC,PA=PC=AC=2,AB=4,则三棱锥P﹣ABC的外接球的表面积为()A.23πB.C.D.64π16.已知三棱锥S﹣ABC的底面是以AB为斜边的等腰直角三角形,且AB=SA=SB=SC=2,则该三棱锥的外接球的表面积为()A.B.C.D.17.在正方体ABCD﹣A1B1C1D1中,E为BC的中点,已知平面α经过点A1,且平行于平面B1D1E,平面α与平面ABCD交于直线m,与平面ABB1A1交于直线n,则直线m,n所成角的余弦值为()A.B.C.D.18.如图,在四棱锥P﹣ABCD中,PO⊥平面ABCD,E为线段AP的中点,底面ABCD为菱形,若BD=2,PC=4,则异面直线DE与PC所成角的余弦值为()A.B.C.D.19.已知异面直线a,b所成的角为60°,过空间一点O的直线与a,b所成的角均为60°,这样的直线有()A.1条B.2条C.3条D.4条20.在正方体ABCD﹣A1B1C1D1中,E是侧面ADD1A1内的动点,且B1E∥平面BDC1,则直线B1E与直线AB所成角的正弦值的最小值是()A.B.C.D.21.四个同样大小的球O1,O2,O3,O4两两相切,点M是球O1上的动点,则直线O2M与直线O3O4所成角的正弦值的取值范围为()A.[]B.[]C.[]D.[]第Ⅱ卷(非选择题)二.解答题(共19小题)22.如图,已知四棱锥P﹣ABCD,BC∥AD,CD⊥AD,PC=AD=2CD=2CB=PA=PD,F为AD的中点.(1)证明:PB⊥BC;(2)求直线CF与平面PBC所成角的正弦值.23.如图,四棱锥S﹣ABCD的底面是正方形,CD=SB=,SD=4,P为侧棱SD 上的点,SD⊥面APC.(1)求二面角S﹣AC﹣D的余弦值;(2)侧棱SC上是否存在一点E,使得BE∥平面APC,若存在,求出SE:EC的值;若不存在,试说明理由.24.如图,四棱锥P﹣ABCD中,底面ABCD为平行四边形,∠DAB=60°,PD=AD=,PD⊥底面ABCD.(Ⅰ)证明:PA⊥BD;(Ⅱ)求平面PAD与平面PBC所成的锐二面角的大小.25.如图,三棱柱ABC﹣A1B1C1中,∠BCA=90°,AC=BC=AA1=A1C=2,平面ACC1A1⊥平面ABC.现以边AC的中点D为坐标原点,平面ABC内垂直于AC的直线为x轴,直线AC为y轴,直线DA1为z轴建立空间直角坐标系,解决以下问题:(1)求异面直线AB与A1C所成角的余弦值;(2)求直线AB与平面A1BC所成角的正弦值.26.如图,四棱锥P﹣ABCD中,PA⊥平面ABCD,△ABC是边长为2的等边三角形,直线PB与底面ABCD所成的角为45°,PA=2CD,PD=,E是棱PD的中点.(1)求证:CD⊥AE;(2)在棱PB上是否存在一点T,使得平面ATE与平面APB所成锐二面角的余弦值为?若存在,请指出T的位置;若不存在,请说明理由.27.已知几何体的直观图和三视图如图所示,其正视图为矩形,侧视图为等腰直角三角形,俯视图为直角梯形.(1)连接B1C,若M为AB的中点,在线段CB上是否存在一点P,使得MP∥平面CNB1?若存在,求出BP的长;若不存在,请说明理由.(2)求二面角C﹣NB1﹣C1的余弦值.28.已知四棱锥S﹣ABCD,四边形ABCD是正方形,BA=AS=SD=2,S△ABS=2.(1)证明:平面ABCD⊥平面SAD;(2)若M为SD的中点,求二面角B﹣CM﹣S的余弦值.29.如图1,ABCD为梯形,AB∥CD,∠C=60°,点E在CD上,AB=EC=DE=2,BD⊥BC.现将△ADE沿AE折起如图2,使得平面DBC⊥平面ABCE.(Ⅰ)求证:BD⊥平面ABCE;(Ⅱ)求二面角D﹣AE﹣C的平面角的余弦值.30.如图,在四棱锥P﹣ABCD中,BC⊥PB,AB⊥BC,AD∥BC,AD=3,PA=BC=2AB=2,.(1)求二面角P﹣CD﹣A的余弦值;(2)若点E在棱PA上,且BE∥平面PCD,求线段BE的长.参考答案与试题解析一.选择题(共21小题)1.已知菱形ABCD满足,|AB|=2,∠ABC=,将菱形ABCD沿对角线AC折成一个直二面角B﹣AC﹣D,则三棱锥B﹣ACD外接球的表面积为()A.πB.8πC.7πD.【解答】解:由题意菱形ABCD满足,|AB|=2,∠ABC=,∴AC=2,DB=,将菱形ABCD沿对角线AC折成一个直二面角B﹣AC﹣D,∴三棱锥B﹣ACD高为.底面ACD外接圆半径为,外接球半径为R,球心与圆心的距离为d,d2+r2=R2……①……②由①②解得:R2=外接球的表面积S=.故选:A.2.如图,四面体ABCD中,面ABD和面BCD都是等腰Rt△,AB=,∠BAD=∠CBD=,且二面角A﹣BD﹣C的大小为,若四面体ABCD的顶点都在球O上,则球O的表面积为()A.12πB.20πC.24πD.36π【解答】解:取CD中点E,BD中点F,连结BE、AF、EF,∵四面体ABCD中,面ABD和面BCD都是等腰Rt△,AB=,∠BAD=∠CBD=,且二面角A﹣BD﹣C的大小为,∴AF⊥BD,EF⊥BD,∴∠AFE是二面角A﹣BD﹣C的平面角,,BD=BC==2,CD=,CE=DE=,AF=BF=DF=EF=1,,则点E为△BCD外接圆的圆心,点F为△ABD外接圆的圆心,过点E作平面BCD的垂线EO,过点F作平面ABD的垂线FO,且直线EO与直线FO交于点O,则点O为四面体ABCD外接球的球心,如下图所示,易知,,所以,,所以,,则四面体ABCD的外接球半径为,因此,球O的表面积为,故选:B.3.如图,网格纸上小正方形的边长为2,粗实线及粗虚线画出的是某四棱锥的三视图,则该四棱锥的外接球的表面积为()A.B.C.41πD.31π【解答】解:根据三视图得出:该几何体是镶嵌在正方体中的四棱锥O﹣ABCD,正方体的棱长为4,A,D为棱的中点,根据几何体可以判断:球心应该在过A,D的平行于底面的中截面上,设球心到截面BCO的距离为x,则到AD的距离为:4﹣x,∴R2=x2+(2)2,R2=22+(4﹣x)2,解得出:x=,R=,该多面体外接球的表面积为:4πR2=41π,故选:C.4.已知一个几何体是由半径为2的球挖去一个三棱锥得到(三棱锥的顶点均在球面上).若该几何体的三视图如图所示(侧视图中的四边形为菱形),则该三棱锥的体积为()A.B.C.D.【解答】解:由题意可知几何体的直观图如图:A﹣BCD,E为CD的中点,由题意可知AB=4,OE=,OA=OB=2,OD=2,则DE=,所以三棱锥A﹣BCD的体积为:×=.故选:C.5.已知一个几何体的三视图如图所示,则该几何体的表面积是()A.2+2+2B.4+4+2C.2+4+4D.4+4+4【解答】解:由题意几何体的直观图如图:是正方体的一部分,正方体的棱长为:2,可知几何体的表面积为:=4+4+2.故选:B.6.某三棱锥的三视图如图所示,则它的外接球表面积为()A.25πB.C.D.40π【解答】解:由三视图还原几何体的直观图如图:该几何体为三棱锥,底面三角形ABC为直角三角形,面PAC为等边三角形,且面PAC⊥底面ABC,取BC中点G,则G为三角形ABC的外心,过G作平面ABC的垂线,取等边三角形PAC的外心为H,过H作平面PAC的垂线,则两垂线交于点O,O为三棱锥P﹣ABC外接球的球心,OG=PH=,GC=BC=,∴OC==,∴三棱锥外接球表面积为4π×()2=.故选:C.7.如图是某几何体的三视图,则该几何体的表面积是()A.18+2+B.15++C.12++D.18++【解答】解:几何体的三视图,可知几何体是组合体,下部是四棱柱,上部是四棱锥,底面是直角梯形,下底为2,上底边长为1,高为2,四棱柱的高为2,棱锥的高为1,如图:该几何体的表面积是:++=15++.故选:B.8.在四面体ABCD中,AD⊥底面ABC,,E为棱BC的中点,点G在AE上且满足AG=2GE,若四面体ABCD的外接球的表面积为,则tan∠AGD=()A.B.2C.D.【解答】解:由题意可得,点G是△ABC的重心,∴AG=AE=,设△ABC的外心为O,由题意点O在AE上,令OA=r,则OE2+EC2=OC2,即(3﹣r)2+12=r2,解得r=,∵AD⊥平面ABC,∴四面体ABCD的外接球的半径R2=r2+()2=+,由题意得4πR2=4π(+)=,解得AD=4,∴tan∠AGD=.故选:B.9.在三棱锥S﹣ABC中,,且三棱锥S﹣ABC的体积为,则该三棱锥的外接球的表面积为()A.4πB.16πC.36πD.72π【解答】解:如图,取SC的中点O,连接OB,OA,∵SB⊥BC,SA⊥AC,SB=BC,SA=AC,∴OB⊥SC,OA⊥SC,OB=SC,OA=SC,∴SC⊥平面OAB,O为三棱锥的外接球的球心,SC为球O的直径,设球O得半径为R,则AB=SC=R,∴△AOBRt正三角形,则∠BOA=90°,=V S﹣OAB+V C﹣OAB===,∴V S﹣ABC∴R=2,则该三棱锥的外接球的表面积为4πR2=16π.故选:B.10.如图所示,正方形ABCD的边长为2,切去阴影部分围成一个正四棱锥,则当正四棱锥体积最大时,该正四棱锥外接球的表面积为()A.B.C.D.【解答】解:由题意,正方形ABCD的边长为2,可得对角线的一半为,折成正四棱锥后,设正四棱锥边长为a,高为h,可得:h2=2﹣,(0).正四棱锥体积V=最大时,即.由y=,则y′=8,令y′=0,可得a=,即当a=体积取得最大值;∴h=.正四棱锥底面正方形外接圆r=.正四棱锥外接球的半径R,可得解得:正四棱锥外接球的表面积S=.故选:D.11.已知三棱锥P﹣ABC所有顶点都在球O的球面上,底面△ABC是以C为直角顶点的直角三角形,AB=2,PA=PB=PC=,则球O的表面积为()A.9πB.C.4πD.π【解答】解析:设AB中点为D,则D为△ABC的外心,因为PA=PB=PC=,易证PD⊥面ABC,,所以球心O在直线PD上,又PA=,AB=2,算得PD=1,设球半径为R,则△AOD中,(R﹣1)2+2=R2,可得:R=.则球O的表面积S=4πR2=9π,故选:A.12.四棱锥P﹣ABCD的侧面PAB垂直于底面ABCD,且三角形PAB是等边三角形,底面ABCD是边长为2的正方形,则四棱锥P﹣ABCD外接球的表面积为()A.πB.C.4πD.π【解答】解:由题意,可以将四棱锥P﹣ABCD补成以△PAB为底面的直三棱柱,直三棱柱外接球的半径,△PAB是边长为2的等边三角形,其外接圆的半径为;所以球的半径r=,则球的表面积S=4πr2=.故选:D.13.已知三棱锥D﹣ABC所有顶点都在球O的球面上,△ABC为边长为的正三角形,△ABD是以BD为斜边的直角三角形,且AD=8,二面角C﹣AB﹣D 为120°,则球O的表面积为()A.B.124πC.D.31π【解答】解:作图如下:O1为经过△ABC外接圆圆心,O2为经过△ABD外接圆圆心,则O2为BD中点,取AB中点M,则∠CMO2为二面角C﹣AB﹣D的平面角,易得|O2M|=4,|O1M|=1,,由余弦定理得|O1O2|=,由正弦定理得,所以R2=|OM|2+|AM|2=31⇒S=124π,故选:B.14.已知直三棱柱(侧棱垂直于底面的三棱柱)ABC﹣A1B1C1的顶点在球O上,∠ABC=120°,AA1=BC=AB=1,则球O的表面积为()A.7πB.6πC.5πD.4π【解答】解:如图:外接球的球心为O,底面三角形的外心为:O1,由正弦定理可得:2A1O1=,可得A1O1=1,R2=12+=,外接球的表面积为:4π•R2=5π.故选:C.15.三棱锥P﹣ABC中,平面PAC⊥平面ABC,AB⊥AC,PA=PC=AC=2,AB=4,则三棱锥P﹣ABC的外接球的表面积为()A.23πB.C.D.64π【解答】解:根据题意,得到三棱锥P﹣ABC的外接球的球心在等边三角形PAC 的中线高线和过直角三角形ABC斜边BC的中点的高的交点位置,如图所示:三棱锥P﹣ABC中,平面PAC⊥平面ABC,AB⊥AC,PA=PC=AC=2,AB=4,所以PF=,,在直角三角形ABC中,BC2=AB2+AC2,解得:BC=2,所以CD=,三棱锥的外接球半径r==,则S=4,故选:C.16.已知三棱锥S﹣ABC的底面是以AB为斜边的等腰直角三角形,且AB=SA=SB=SC=2,则该三棱锥的外接球的表面积为()A.B.C.D.【解答】解:如图所示:三棱锥S﹣ABC的底面是以AB为斜边的等腰直角三角形,且AB=SA=SB=SC=2,则:SD=,设外接球的半径为R,则:在△BOD中,利用勾股定理:,解得:R=所以:S=4π•R2=4.故选:D.17.在正方体ABCD﹣A1B1C1D1中,E为BC的中点,已知平面α经过点A1,且平行于平面B1D1E,平面α与平面ABCD交于直线m,与平面ABB1A1交于直线n,则直线m,n所成角的余弦值为()A.B.C.D.【解答】解:设正方体的边长为2,取CD的中点F,AB的中点为M,AD的中点为N,连接EF,DB,MN,可得MN∥BD∥EF∥B1D1,由于平面α经过点A1,且平行于平面B1D1E即有平面A1MN即为平面α,直线MN即为直线m,直线A1M即为直线n,∠A1MN即为直线m,n所成角,由A1M=A1N==,MN=,可得cos∠A1MN==.故选:B.18.如图,在四棱锥P﹣ABCD中,PO⊥平面ABCD,E为线段AP的中点,底面ABCD为菱形,若BD=2,PC=4,则异面直线DE与PC所成角的余弦值为()A.B.C.D.【解答】解:由题意,连接EO,O是底面ABCD为菱形的中点,又E为线段AP的中点,∴EO∥PC,则异面直线DE与PC所成角的平面角为∠DEO,∵PO⊥平面ABCD,底面ABCD为菱形,AC⊥BD,POC是直角三角形,∴PC⊥BD,则EO⊥BD,∴△DEO是直角三角形,∵BD=2,PC=4,∴OD=1,EO=2,则ED=.∴cos∠DEO=.故选:A.19.已知异面直线a,b所成的角为60°,过空间一点O的直线与a,b所成的角均为60°,这样的直线有()A.1条B.2条C.3条D.4条【解答】解:过O作a′∥a,b′∥b,设直线a′、b′确定的平面为α,∵异面直线a、b成60°角,∴直线a′、b′所成锐角为60°①当直线l在平面α内时,若直线l平分直线a′、b′所成的钝角,则直线l与a、b都成60°角;②当直线l与平面α斜交时,若它在平面α内的射影恰好落在直线a′、b′所成的锐角平分线上时,直线l与a、b所成角相等.此时l与a′、b′所成角的范围为[30°,90°],适当调整l的位置,可使直线l与a、b也都成60°角,这样的直线l有两条.综上所述,过点P与a′、b′都成60°角的直线,可以作3条∵a′∥a,b′∥b,∴过点O与a′、b′都成60°角的直线,与a、b也都成60°的角.故选:C.20.在正方体ABCD﹣A1B1C1D1中,E是侧面ADD1A1内的动点,且B1E∥平面BDC1,则直线B1E与直线AB所成角的正弦值的最小值是()A.B.C.D.【解答】解:以D为原点,DA为x轴,DC为y轴,DD1为z轴,建立空间直角坐标系,设正方体ABCD﹣A1B1C1D1中棱长为1,设E(a,0,c),0≤a≤1,0≤c≤1,B1(1,1,1),B(1,1,0),D(0,0,0),C1(0,1,1),=(a﹣1,﹣1,c﹣1),=(1,1,0),=(0,1,1),设平面DBC1的法向量=(x,y,z),则,取x=1,得=(1,﹣1,1),∵B1E∥平面BDC1,∴=a﹣1+1+c﹣1=0,解得a+c=1,∴a2+c2=(a+c)2﹣2ac=1﹣2ac,ac≤()2=,设直线B1E与直线AB所成角为θ,∵=(0,1,0),∴cosθ==,∵ac≤()2=,∴2﹣2ac≥,∴,∴sinθ====≥=.∴直线B1E与直线AB所成角的正弦值的最小值是.故选:B.21.四个同样大小的球O1,O2,O3,O4两两相切,点M是球O1上的动点,则直线O2M与直线O3O4所成角的正弦值的取值范围为()A.[]B.[]C.[]D.[]【解答】解:如图O1O2O O4是正四面体,设边长为2r,过O1作O1O⊥底面O2O3O4,可得O为底面的中心,由O2O⊥O3O4,可得O2O1⊥O3O4,则M在直线O1O2上,可得直线O2M与直线O3O4垂直,即有所成角的正弦值为1,过O2作大圆的切线,设切点为M,可得O2M与O1O2成30°的角,由O2N∥O3O4,可得O3O4与O2M成60°的角,即有所成角的正弦值为,则直线O2M与直线O3O4所成角的正弦值的取值范围为[,1].故选:C.二.解答题(共19小题)22.如图,已知四棱锥P﹣ABCD,BC∥AD,CD⊥AD,PC=AD=2CD=2CB=PA=PD,F为AD的中点.(1)证明:PB⊥BC;(2)求直线CF与平面PBC所成角的正弦值.【解答】解:(1)证明:在△PAD中,PA=PD,F为AD的中点,可得AD⊥PF,在四边形ABCD中,连接BF,由题意可得四边形BCDF为平行四边形,可得BF∥CD,由CD⊥AD,可得AD⊥BF,而BF∩PF=F,可得AD⊥平面PBF,由AD∥BC,可得BC⊥平面PBF,则BC⊥PB;(2)设PC=AD=2CD=2CB=PA=PD=2,可得CD=CB=1,PA=PD=,过F在△PBF中作FH⊥PB于H,连接CH,由BC⊥平面PBF,可得BC⊥FH,即有FH⊥平面PBC,则∠FCH为CF和平面PBC所成角,由BC⊥PB,可得PB==,由PF==1,BF=CD=1,cos∠PFB==﹣,可得∠PFB=120°,可得H为PB的中点,即有FH⊥PB,即有FH=BFcos∠BFH=1×=,则直线CF与平面PBC所成角的正弦值为==.23.如图,四棱锥S﹣ABCD的底面是正方形,CD=SB=,SD=4,P为侧棱SD 上的点,SD⊥面APC.(1)求二面角S﹣AC﹣D的余弦值;(2)侧棱SC上是否存在一点E,使得BE∥平面APC,若存在,求出SE:EC的值;若不存在,试说明理由.【解答】解::(1)连BD,设AC交BD于O,SD⊥面APC,可得SD⊥AP,SD⊥PC,可得△PAD≌△PCD,可得∠SDA=∠SDC,可得SA=SC,SO⊥AC,在正方形ABCD中,AC⊥BD,可得∠SOD为二面角S﹣AC﹣D的平面角,在△SBD中,SB=2,BD=4,SD=4,可得cos∠SBD==,SO==2,可得cos∠SOB==,即有二面角S﹣AC﹣D的余弦值为﹣;(2)若SD⊥平面PAC,则SD⊥OP,正方形ABCD的边长为2,SD=4,OD=BD=2,则PD=ODcos∠SDB=2•=,故可在SP上取一点N,使PN=PD,过N作PC的平行线与SC的交点即为E,连BN.在△BDN中知BN∥PO,又由于NE∥PC,故平面BEN∥面PAC,得BE∥面PAC,由于SN:NP=2:3,故SE:EC=2:3.24.如图,四棱锥P﹣ABCD中,底面ABCD为平行四边形,∠DAB=60°,PD=AD=,PD⊥底面ABCD.(Ⅰ)证明:PA⊥BD;(Ⅱ)求平面PAD与平面PBC所成的锐二面角的大小.【解答】证明:(Ⅰ)因为∠DAB=60°,AB=2AD,由余弦定理得BD=,…………(1分)从而BD2+AD2=AB2,故BD⊥AD,…………(3分)又PD⊥底面ABCD,可得BD⊥PD,…………(4分)所以BD⊥平面PAD.…………(5分)故PA⊥BD…………(6分)解:(Ⅱ)如图,以D为坐标原点,AD的长为单位长,射线DA为x轴的正半轴,建立空间直角坐标系D﹣xyz,…………(7分)则B(0,,0),C(﹣1,,0),P(0,0,1),=(﹣1,,0),=(0,,﹣1),=(﹣1,0,0),平面PAD的一个法向量为=(0,1,0),…………(8分)设平面PBC的法向量为=(x,y,z),则,…………(9分)取y=1,得=(0,1,),…………(10分)|cos<>|==,…………(11分)故平面PAD与平面PBC所成的锐二面角的大小为60°.…………(12分)25.如图,三棱柱ABC﹣A1B1C1中,∠BCA=90°,AC=BC=AA1=A1C=2,平面ACC1A1⊥平面ABC.现以边AC的中点D为坐标原点,平面ABC内垂直于AC的直线为x轴,直线AC为y轴,直线DA1为z轴建立空间直角坐标系,解决以下问题:(1)求异面直线AB与A1C所成角的余弦值;(2)求直线AB与平面A1BC所成角的正弦值.【解答】解:(1)三棱柱ABC﹣A1B1C1中,∠BCA=90°,AC=BC=AA1=A1C=2,平面ACC1A1⊥平面ABC.以边AC的中点D为坐标原点,平面ABC内垂直于AC的直线为x轴,直线AC为y轴,直线DA1为z轴建立空间直角坐标系,根据题中空间直角坐标系可知:A(0,﹣1,0),C(0,1,0),B(2,1,0),A1(0,0,),…(1分)∴=(2,2,0),=(0,1,﹣),∴cos<>===,…(3分)设异面直线AB与A1C的所成角为α,则,∴异面直线AB与A1C所成角的余弦值为.…(4分)(2)由(1)得:=(2,1,﹣),=(﹣2,0,0),设平面A1BC的法向量为=(x,y,z),∴,取z=1,则=(0,),…(7分)∴cos<,>===.…(9分)设直线AB与平面A1BC所成角为β,β∈(0,],则sinβ=|cos<,>|=.故直线AB与平面A1BC所成角的正弦值为.…(10分)26.如图,四棱锥P﹣ABCD中,PA⊥平面ABCD,△ABC是边长为2的等边三角形,直线PB与底面ABCD所成的角为45°,PA=2CD,PD=,E是棱PD的中点.(1)求证:CD⊥AE;(2)在棱PB上是否存在一点T,使得平面ATE与平面APB所成锐二面角的余弦值为?若存在,请指出T的位置;若不存在,请说明理由.【解答】(1)证明:∵PA⊥平面ABCD,AB⊂平面ABCD,CD⊂平面ABCD,AD ⊂平面ABCD,∴PA⊥AB,PA⊥CD,PA⊥AD,∵直线PB与底面ABCD所成的角为45°,∴∠PBA=45°,∵△ABC是边长为2的等边三角形,∴PA=AB=2,又PA=2CD,∴CD=1.在Rt△PAD中,∵PD=,PA=2,∴AD=,在三角形ADC中,AD=,CD=1,AC=2,∴AD2+CD2=AC2,可得CD⊥AD,又AD∩PA=A,∴CD⊥平面PAD,又AE⊂平面PAD,∴CD⊥AE;(2)解:假设在棱PB上存在一点T,满足题意,则(0<λ≤1),由(1)可知,∠DAC=30°,∴∠DAB=90°,以A为原点,分别以AB,AD,AP所在直线为x,y,z轴建立空间直角坐标系.则A(0,0,0),B(2,0,0),P(0,0,2),D(0,,0),E(0,,1).设T(x1,y1,z1),则,又,∴(x1,y1,z1﹣2)=(2λ,0,﹣2λ),得x1=2λ,y1=0,z1=2﹣2λ,∴,.设平面ATE的法向量为.则有,取y2=2,得.而平面PAB的一个法向量为,∴|cos<>|=||==,解得.故在棱PB上存在一点T,使得平面ATE与平面APB所成锐二面角的余弦值为.27.已知几何体的直观图和三视图如图所示,其正视图为矩形,侧视图为等腰直角三角形,俯视图为直角梯形.(1)连接B1C,若M为AB的中点,在线段CB上是否存在一点P,使得MP∥平面CNB1?若存在,求出BP的长;若不存在,请说明理由.(2)求二面角C﹣NB1﹣C1的余弦值.【解答】解:建立空间直角坐标系如图,则由该几何体的三视图可知:C(0,0,4),N(4,4,0),B1(0,8,0),C1(0,8,4).(1)设平面CNB1的法向量为,由,,得,其x=1,得.设P(0,0,a)(0≤a≤4),由于M(2,0,0),则.∵MP∥平面CNB1,∴,得a=1.∴在线段CB上存在一点P,使得MP∥平面CNB1,此时BP=1;(2)设平面C1NB1的法向量为,由,得,取x=1,可得.∴cos<>=.由图可知,所求二面角为锐角,故二面角C﹣NB1﹣C1的余弦值为.28.已知四棱锥S﹣ABCD,四边形ABCD是正方形,BA=AS=SD=2,S△ABS=2.(1)证明:平面ABCD⊥平面SAD;(2)若M为SD的中点,求二面角B﹣CM﹣S的余弦值.【解答】证明:(1)∵,∴sin∠BAS=1,即BA⊥AS,又∵ABCD为正方形,∴BA⊥AD,∵BA∩AS=A,∴BA⊥平面SAD,∵BA⊂平面ABCD,∴平面ABCD⊥平面SAD.解:(2)设AD的中点为O,∵AS=SD,∴SO⊥AD,由(1)可知平面ABCD⊥平面SAD,且平面ABCD∩平面SAD=AD,∴SO⊥平面ABCD,在平面ABCD内,过O作直线Ox⊥AD,则Ox,OD,OS两两垂直.以O为坐标原点,Ox,OD,OS所在直线为x轴,y轴,z轴,建立空间直角坐标系,则,∴,设平面BCM的法向量为,则,,即,取,设平面CMS的法向量为,则,,即,取,,由图可知,二面角B﹣CM﹣S的余弦值为.29.如图1,ABCD为梯形,AB∥CD,∠C=60°,点E在CD上,AB=EC=DE=2,BD⊥BC.现将△ADE沿AE折起如图2,使得平面DBC⊥平面ABCE.(Ⅰ)求证:BD⊥平面ABCE;(Ⅱ)求二面角D﹣AE﹣C的平面角的余弦值.【解答】(本题满分15分)证明:(Ⅰ)∵DF⊥AE,BF⊥AE,∴AE⊥面BDF,又BD⊂面BDF,∴AE⊥BD.﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(3分)∵面BCD⊥面ABCE,BC∥AE,BF⊥AE,∴BF⊥BC,∴BF⊥面BCD,∵BD⊂面BCD,∴BF⊥BD,又∴BF∩BC=B,∴BD⊥面BCEF.﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(8分)解:(Ⅱ)∵DF⊥AE,BF⊥AE,∴∠BFD即为二面角D﹣AE﹣C的平面角.﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(10分)又∵﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(12分)在Rt△BDE中,,∴二面角D﹣AE﹣C的平面角的余弦值为.﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(15分)30.如图,在四棱锥P﹣ABCD中,BC⊥PB,AB⊥BC,AD∥BC,AD=3,PA=BC=2AB=2,.(1)求二面角P﹣CD﹣A的余弦值;(2)若点E在棱PA上,且BE∥平面PCD,求线段BE的长.【解答】解:(1)∵在四棱锥P﹣ABCD中,由PA=2AB=2,,得PB2+AB2=PA2,则PB⊥AB,又BC⊥PB,AB⊥BC,∴以B为原点,BA为x轴,BC为y轴,BP为z轴,建立空间直角坐标系,则B(0,0,0),A(1,0,0),C(0,2,0),D(1,3,0),P(0,0,),=(0,1,0),=(0,2,﹣),由图可知,平面ABCD的一个法向量为=(0,0,1),设平面PCD的法向量为,则,取z=2,得,设二面角P﹣CD﹣A的平面角为α,则cosα=|cos<>|=.∴二面角P﹣CD﹣A的余弦值为;(2)∵点E在PA上,∴,λ∈[0,1],∵,∴,=(1﹣λ,0,),又∵BE∥平面PCD,为平面PCD的法向量,∴,即,解得,∴,则BE=||=.。
高中数学空间几何体的外接球专题(附经典例题与解析)
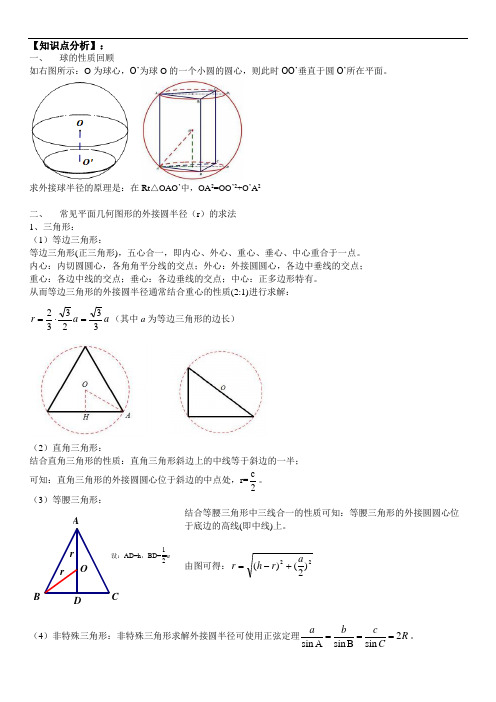
【知识点分析】: 一、 球的性质回顾如右图所示:O 为球心,O’为球O 的一个小圆的圆心,则此时OO’垂直于圆O’所在平面。
求外接球半径的原理是:在Rt △OAO ’中,OA 2=OO ’2+O ’A 2二、 常见平面几何图形的外接圆半径(r )的求法1、三角形:(1)等边三角形:等边三角形(正三角形),五心合一,即内心、外心、重心、垂心、中心重合于一点。
内心:内切圆圆心,各角角平分线的交点;外心:外接圆圆心,各边中垂线的交点;重心:各边中线的交点;垂心:各边垂线的交点;中心:正多边形特有。
从而等边三角形的外接圆半径通常结合重心的性质(2:1)进行求解:a a r 332332=⋅=(其中a 为等边三角形的边长)(2)直角三角形:结合直角三角形的性质:直角三角形斜边上的中线等于斜边的一半;可知:直角三角形的外接圆圆心位于斜边的中点处,r=2c 。
(3)等腰三角形: 结合等腰三角形中三线合一的性质可知:等腰三角形的外接圆圆心位于底边的高线(即中线)上。
由图可得:22)2()(a r h r +-=(4)非特殊三角形:非特殊三角形求解外接圆半径可使用正弦定理2sin sin sin a b c R C===A B 。
rrAD=h ,BD=12a B CO2、四边形常见具有外接圆的四边形有:正方形、矩形、等腰梯形,其中正方形与长方形半径求解方法转化为直角三角形,等腰梯形的外接圆圆心不在中学考察范围内。
外接圆圆心是在圆心到各个顶点距离相同的点;外接球球心则是球心到几何体各个顶点距离相同的点。
结论:几何体的外接球球心与底面外心的连线垂直于底面,(也即球心落在过底面外心的垂线上,)简单称之为:球心落在底面外心的正上方。
【相似题练习】2.半径为2的球的内接三棱锥P﹣ABC,PA=PB=PC=2,AB=AC=BC,则三棱锥的高为()A.3B.C.2D.3【知识点分析】:类型一:直(正)棱柱:上下两底面三角形的外心连线与侧棱平行与底面垂直,从而球心O 必位于上下两底面外心连线的中点处,即121'AA OO =,从而R 可求.【相似题练习】1.三棱柱ABC ﹣A 1B 1C 1中,底面ABC 是边长为2的正三角形,侧棱AA 1垂直于底面ABC ,且AA 1=4,则此三棱柱外接球的表面积为( )A .B .C .D .【知识点分析】:类型二:侧棱垂直底面的三棱锥,法一:补形法:该几何体可由正三棱柱沿平面PBC 切割得来,故可转化为原三棱柱的外接球;法二:先确定底面三角形ABC 的外心O’,从而球心位于O’的正上方,即OO’ ⊥平面ABC ,同时:OP=OA ,故,过O 作OM ⊥PA 于M ,此时M 必为PA 中点,从而四边形OMAO’为矩形,所以PA AM OO 21'==,在直角三角形OO’A 中有:222'OO r R +=.【相似题练习】2.已知在三棱锥P ﹣ABC 中,△ABC 是边长为2的正三角形,若PA ⊥底面ABC 且PA =2,则该三棱锥的外接球的表面积为( )A .32πB .28πC .24πD .20π3.在三棱锥P ﹣ABC 中,PA ⊥平面ABC ,PA =2,AB =4,AC =3,∠BAC =,则三棱锥P ﹣ABC 的外接球的半径R =( )A .B .C .D .【知识点分析】:类型三:正三棱锥:由底面正三角形边长可得r ,在直角三角形OO’A 中,222'OO r R +=,故只需确定OO’的长度即可,结合图形,OO’=PO’-OP=H-R ,代入222)(R H r R -+=即可求解.【相似题练习】3.正三棱锥P ﹣ABC 侧棱长为,侧棱与底面ABC 所成的角为60°,则该正三棱锥外接球半径为 .2.某几何体的三视图如图所示,其中网格纸上小正方形的边长为1,则该几何体的外接球的表面积为( )【知识点分析】:类型四:侧面垂直于底面的三棱锥:设△ABC和△PAB的外心分别为O’,O’’,则PM⊥AB,球心设为O,则OO’ ⊥平面ABC,OO’’⊥平面PAB,从而四边形OO’MO’’是矩形,可得:OO’=O’’M,在Rt△OO’C中用勾股定理求解.【讲透例题】1.在四面体A﹣BCD中,AB=5,BC=CD=3,DB=2,AC=4,∠ACD=60°,则该四面体的外接球的表面积为.解析:如图:取AB的中点O,在△ACD中,由余弦定理得:AD2=AC2+CD2﹣2×AC×CD cos60°=13,在△ABD中,∵AB2=BD2+AD2,∴∠ADB=90°,∴OA=OB=OD,在△ABC中,∵AB2=BC2+AC2,∴∠ACB=90°,∴OA=OB=OC,∴OA=OB=OC=OD,∴O为四面体ABCD的外接球的球心,其半径R=AB=,∴S球=4πR2=4π()2=25π.故答案为:25π.【相似题练习】4.在三棱锥P-ABC中,面PAB⊥面ABC,三角形ABC和三角形PAB均为等边三角形,且AB=3,求该几何体外接球半径.2.在边长为2的菱形ABCD中,,将菱形ABCD沿对角线AC折起,使得平面ABC⊥平面ACD,则所得三棱锥A﹣BCD的外接球表面积为()A.B.C.D.1.已知点A是以BC为直径的圆O上异于B,C的动点,P为平面ABC外一点,且平面PBC⊥平面ABC,BC=3,PB=2,PC=,则三棱锥P﹣ABC外接球的表面积为.5、如图,在四棱锥P﹣ABCD中,底面ABCD为长方形,PA⊥底面ABCD,AD=AP=2,AB=2,E为棱PD中点.(1)求证:PD⊥平面ABE;(2)求四棱锥P﹣ABCD外接球的体积.1.如图,在正四棱锥P﹣AMDE,底面AMDE的边长为2,侧棱PA=,B,C分别为AM,MD的中点.F为棱PE的中点,平面ABF与棱PD,PC,PM分别交于点G,H,K.(1)求证:AB∥FG;(2)求正四棱锥P﹣AMDE的外接球的表面积.1.如图,四凌锥P﹣ABCD而底面ABCD是矩形,侧面PAD是等腰直角三角形∠APD=90°,且平面PAD⊥平面ABCD.(Ⅰ)求证:平面PAD⊥平面PCD;(Ⅱ)在AD=2,AB=4,求三棱锥P﹣ABD的体积;(Ⅲ)在条件(Ⅱ)下,求四棱锥P﹣ABCD外接球的表面积.7、如图,网格纸上小正方形的边长为1,粗实线画出的是某四棱锥的三视图,已知其俯视图是正三角形,则该四棱锥的外接球的表面积是()A.B.C.19πD.22π课后作业:1.如图,一个正三棱柱的主视图是长为,宽为2的矩形,俯视图是边长为的正三角形,则它的外接球的表面积等于()A.16πB.12πC.8πD.4π2.某四面体的三视图如图所示,正视图、侧视图、俯视图都是边长为1的正方形,则此四面体的外接球的表面积为()A.πB.3πC.πD.π3.某四棱锥的三视图如图所示,则该棱锥的外接球的表面积为()A.3πB.C.6πD.12π4.四棱锥P﹣ABCD中,ABCD为矩形,AD=2,AB=2,PA=PD,∠APD=,且平面PAD⊥平面ABCD.(1)证明:PA⊥PC;(2)求四棱锥P﹣ABCD的外接球的体积.参考答案与解析12.(5分)已知A,B,C为球O的球面上的三个点,⊙O1为△ABC的外接圆.若⊙O1的面积为4π,AB=BC=AC=OO1,则球O的表面积为()A.64πB.48πC.36πD.32π【解答】解:由题意可知图形如图:⊙O1的面积为4π,可得O1A=2,则AO1=AB sin60°,,∴AB=BC=AC=OO1=2,外接球的半径为:R==4,球O的表面积:4×π×42=64π.故选:A.1.1.一个几何的三视图如图所示,它们都是腰长为1的等腰直角三角形,则该几何体的外接球的体积等于()A.B.C.πD.2π解析:由三视图可知:该几何体是一个如图所示的三棱锥,其中底面是一个两直角边都为1的直角三角形,PC⊥底面ABC,且PC=1.将此三棱锥恢复为棱长为1的正方体,可知该正方体的外接球的直径即为正方体的对角线,∴V外接球==.故选:B.1.半径为2的球的内接三棱锥P﹣ABC,PA=PB=PC=2,AB=AC=BC,则三棱锥的高为()A.3B.C.2D.3【解答】解:三棱锥P﹣ABC中,PA=PB=PC=2,AB=AC=BC,如图,过点p作PM⊥平面ABC的垂足为M,则球O的内接三棱锥P﹣ABC的球心O在PM所在直线上,∵球O的半径为2,∴OB=OP=2,∴由余弦定理得cos∠BPM==∴∠BPM=30°,∴在Rt△PMB中,∠PBM=60°,∴PM=PB sin∠PBM=3.故选:D.1.三棱柱ABC﹣A1B1C1中,底面ABC是边长为2的正三角形,侧棱AA1垂直于底面ABC,且AA1=4,则此三棱柱外接球的表面积为()A.B.C.D.【解答】解:∵正三棱柱ABC﹣A1B1C1的中,底面边长为2,高为4,由题意可得:三棱柱上下底面中心连线的中点,到三棱柱顶点的距离相等,说明中心就是外接球的球心,∴正三棱柱ABC﹣A1B1C1的外接球的球心为O,外接球的半径为r,表面积为:4πr2.球心到底面的距离为2,底面中心到底面三角形的顶点的距离为:=,所以球的半径为r==.外接球的表面积为:4πr2=π故选:D.2.已知在三棱锥P﹣ABC中,△ABC是边长为2的正三角形,若PA⊥底面ABC且PA=2,则该三棱锥的外接球的表面积为()A.32πB.28πC.24πD.20π【解答】解:由正弦定理可知,正△ABC的外接圆的直径为,∵PA⊥平面ABC,所以,该三棱锥的外接球的直径为,则.因此,该三棱锥的外接球的表面积为4πR2=20π.故选:D.3.在三棱锥P﹣ABC中,PA⊥平面ABC,PA=2,AB=4,AC=3,∠BAC=,则三棱锥P﹣ABC的外接球的半径R=()A.B.C.D.【解答】解:∵AC=3,AB=4,∠BAC=,∴由余弦定理可得BC=,∴△ABC外接圆的半径r=,设球心到平面ABC的距离为d,则d=PA=1.由勾股定理可得R =,故选:D .3.正三棱锥P ﹣ABC 侧棱长为,侧棱与底面ABC 所成的角为60°,则该正三棱锥外接球半径为 1 . 【解答】解:过点P 作PH ⊥平面ABC 于H ,则∵AH 是PA 在平面ABC 内的射影 ∴∠PAH 是直线PA 与底面ABC 所成的角,得∠PAH =60°, ∴Rt △PAH 中,AH =PA cos60°=,PH =PA sin60°=设三棱锥外接球的球心为O ,∵PA =PB =PC ,∴P 在平面ABC 内的射影H 是△ABC 的外心由此可得,外接球心O 必定在PH 上,连接OA 、OB 、OC ∵△POA 中,OP =OA , ∴∠OAP =∠OPA =30°,可得PA =OA =,∴三棱锥外接球的半径R =OA =1故答案为:1.2.某几何体的三视图如图所示,其中网格纸上小正方形的边长为1,则该几何体的外接球的表面积为( )A .16πB .12πC .9πD .8π【解答】解:根据几何体的三视图转换为直观图为:该几何体为底面为等腰直角三角形,高为2的三棱锥体. 如图所示:所以该三棱锥体的外接球的球心为O ,外接球的半径为OA =r ,则:,解得.故S =.故选:C .4.在三棱锥P-ABC 中,面PAB ⊥面ABC ,三角形ABC 和三角形PAB 均为等边三角形,且AB=3,求该几何体外接球半径.由题可得:333,2331'''=====AB r PM M O OO ,所以215'22=+=OO r R2.在边长为2的菱形ABCD中,,将菱形ABCD沿对角线AC折起,使得平面ABC⊥平面ACD,则所得三棱锥A﹣BCD的外接球表面积为()A.B.C.D.【解答】解:∵在边长为2的菱形ABCD中,;如图,由已知可得,△ABC与△ACD均为等边三角形,取AC中点G,连接BG,DG,则BG⊥AC,∴DG=⇒cos∠GDA=⇒∠GDA=⇒∠ADC=;∵二面角B﹣AC﹣D为直二面角,则BG⊥平面ACD,分别取△BCD与△ABD的外心E,F,过E,F分别作两面的垂线,相交于O,则O为三棱锥A﹣BCD的外接球的球心,由△BCA与△ACD均为等边三角形且边长为2,可得OE=OF=DG=.∴DE=DG﹣GE=.∴OD===.∴三棱锥A﹣BCD的外接球的表面积为4π×R2=4π×()2=.故选:C.1.已知点A是以BC为直径的圆O上异于B,C的动点,P为平面ABC外一点,且平面PBC⊥平面ABC,BC=3,PB=2,PC=,则三棱锥P﹣ABC外接球的表面积为10π.【解答】解:因为O为△ABC外接圆的圆心,且平面PBC⊥平面ABC,过O作面ABC的垂线l,则垂线l一定在面PBC内,根据球的性质,球心一定在垂线l,∵球心O1一定在面PBC内,即球心O1也是△PBC外接圆的圆心,在△PBC中,由余弦定理得cos B=,⇒sin B=,由正弦定理得:,解得R=,∴三棱锥P﹣ABC外接球的表面积为s=4πR2=10π,故答案为:10π.1.如图,在四棱锥P﹣ABCD中,底面ABCD为正方形,PA⊥底面ABCD,AD=AP=2,AB=2,E为棱PD 中点.(1)求证:PD⊥平面ABE;(2)求四棱锥P﹣ABCD外接球的体积.【解答】证明:(1)∵PA⊥底面ABCD,AB⊂底面ABCD,∴PA⊥AB,又∵底面ABCD为矩形,∴AB⊥AD,PA∩AD,又PA⊂平面PAD,AD⊂平面PAD,∴AB⊥平面PAD,又PD⊂平面PAD,∴AB⊥PD,AD=AP,E为PD中点,∴AE⊥PD,AE∩AB=A,AE⊂平面ABE,AB⊂平面ABE,∴PD⊥平面ABE.解:(II)四棱锥P﹣ABCD外接球球心是线段BD和线段PA的垂直平分线交点O,由已知BD===4,设C为BD中点,∴AM=2,OM=AP=1,∴OA===3,∴四棱锥P﹣ABCD外接球的体积是=36π.1.如图,在正四棱锥P﹣AMDE,底面AMDE的边长为2,侧棱PA=,B,C分别为AM,MD的中点.F为棱PE的中点,平面ABF与棱PD,PC,PM分别交于点G,H,K.(1)求证:AB∥FG;(2)求正四棱锥P﹣AMDE的外接球的表面积.【解答】(1)证明:在正方形AMDE中,因为B是AM的中点,所以AB∥DE.又因为AB⊄平面PDE,DE⊂平面PDE,所以AB∥平面PDE.因为AB⊂平面ABF,且平面ABF∩平面PDE=FG,所以AB∥FG.(2)解:连接AD,EM,相交于O′,易得AO′=,PO′=.由正四棱锥P﹣AMDE的对称性,得正四棱锥P﹣AMDE得外接球球心在线段PO′上,不妨设为O点.设OA=OP=R,则OO′=﹣R,∵AO2=AO′2+OO′2,∴R2=2+(﹣R)2,∴R=∴S=4πR2=,∴正四棱锥P﹣AMDE的外接球的表面积为.1.如图,四凌锥P﹣ABCD而底面ABCD是矩形,侧面PAD是等腰直角三角形∠APD=90°,且平面PAD⊥平面ABCD.(Ⅰ)求证:平面PAD⊥平面PCD;(Ⅱ)在AD=2,AB=4,求三棱锥P﹣ABD的体积;(Ⅲ)在条件(Ⅱ)下,求四棱锥P﹣ABCD外接球的表面积.【解答】解:(I)∵四边形ABCD是矩形,∴AD⊥CD,又∵平面PAD⊥平面ABCD,平面PAD∩平面ABCD=AD,CD⊂平面ABCD,∴CD⊥平面PAD,∵CD⊂平面PCD,∴平面PAD⊥平面PCD.(II)过P作PE⊥AD,垂足为E,∵△PAD是等腰直角三角形,∠APD=90°,∴PE==1.∵平面PAD⊥平面ABCD,平面PAD∩平面ABCD=AD,PE⊂平面PAD,PE⊥AD,∴PE⊥平面ABCD,∴V棱锥P﹣ABD=S△ABD•PE=••2•4•1=.(III)取BD中点M,过M作MN⊥平面ABCD,则球心O在直线MN上,连接AM,则AM==.∵PE⊥平面ABCD,∴MN∥PE.∵四棱锥P﹣ABCD内接于球,,∴OA==.∴S⊙O=4πOA2=20π.∴E为外心,∴OM=1.如图,网格纸上小正方形的边长为1,粗实线画出的是某四棱锥的三视图,已知其俯视图是正三角形,则该四棱锥的外接球的表面积是()A.B.C.19πD.22π【解答】解:几何体的直观图如图:是长方体的一部分,上底面PCD的外接圆的半径:O1D==,几何体的外接球的半径为:OD==,该四棱锥的外接球的表面积是:4=π.故选:A.课后作业答案:1.如图,一个正三棱柱的主视图是长为,宽为2的矩形,俯视图是边长为的正三角形,则它的外接球的表面积等于()A.16πB.12πC.8πD.4π【解答】解:设正三棱柱的外接球的半径为R,则∵俯视图是边长为的正三角形∴底面三角形外接圆的半径为=1,∵正三棱柱的高为2∴正三棱柱的外接球的半径为=∴正三棱柱的外接球的表面积等于4π×=8π故选:C.2.某四面体的三视图如图所示,正视图、侧视图、俯视图都是边长为1的正方形,则此四面体的外接球的表面积为()A.πB.3πC.πD.π【解答】解:由三视图可知:该四面体是正方体的一个内接正四面体.∴此四面体的外接球的直径为正方体的对角线长=.∴此四面体的外接球的表面积为表面积==3π.故选:B.3.某四棱锥的三视图如图所示,则该棱锥的外接球的表面积为()A.3πB.C.6πD.12π【解答】解:由题意可知,几何体的直观图如图:是四棱锥D1﹣ABCD,是棱长为1的正方体的一部分,外接球奇数正方体的外接球,取得直径是体对角线,r=,外接球的表面积为:4=3π.故选:A.4.四棱锥P﹣ABCD中,ABCD为矩形,AD=2,AB=2,PA=PD,∠APD=,且平面PAD⊥平面ABCD.(1)证明:PA⊥PC;(2)求四棱锥P﹣ABCD的外接球的体积.【解答】证明:(1)设AD的中点为E,则∵PA=PD,∴PE⊥AD,∵平面PAD⊥平面ABCD,平面PAD∩平面ABCD=AD,∴PE⊥平面ABCD,∵PA在平面ABCD内的射影为AE,AE⊥CD,∴PA⊥CD,∵PA⊥PD,CD∩PD=D,∴PA⊥平面PCD∴PA⊥PC;解:(2)连接AC交BD于F,球心O在底面的射影必为点F,取截面PEF,PE=,EF=1.假设OF=x,则由OA2=x2+4=1+得x=0,∴球的半径为2,∴四棱锥P﹣ABCD的外接球的体积为=.。
[高中数学]立体几何.球专题附练习题不看后悔
![[高中数学]立体几何.球专题附练习题不看后悔](https://img.taocdn.com/s3/m/ca271daa6c85ec3a87c2c5bb.png)
练习 1.下列四个命题中错误的个数是 ()①经过球面上任意两点,可以作且只可以作一个球的大圆 球面距离,是这两点所在截面圆上以这两点为端点的劣弧的长A.0B.1C.2预备1. 球心到截面的距离 d 与球半径R 及截面的半径r 有以下关系: ______________________ .2. 球面被经过球心的平面截得的圆叫 ___________ .被不经过球心的平面截得的圆叫 ______________________3. 在球面上两点之间的最短连线的长度,就是经过这两点的大圆在这两点间的一段劣弧长,这个弧长叫 ____________________ .4. 球的表面积表面积 S = _____________ ;球的体积 V = ____________ .5. 球面距离计算公式: _____________ 典例剖析 (1) 球面距离,截面圆问题1例1•球面上有3个点,其中任意两点的球面距离都等于大圆周长的 -,经过这3个点的小圆的周长为 4n,那么6这个球的半径为练习: 球面上有三点 A B 、C , A 和B 及A 和C 之间的球面距离是大圆周长的 周长的丄,且球心到截面 ABC 的距离是—兰,求球的体积.67(2) 若 CBE 90 ,CE 、.3,AD 1,求B 、D 两点间的球面距离.立体几何-球-专题学案2. 一平面截一球得到直径为 6 cm 的圆面,球心到这个平面的距离是 A. cm 3 3 208n B. ------- 33cmC •匹 cm 334 cm ,则该球的体积是416.、3n 3 D. cm33.某地球仪上北纬30°纬线的长度为12 n cm ,该地球仪的半径是cm ,表面积是2cm.②球面积是它大圆面积的四倍③球面上两点的D.3A.4B.2 .. 3C.2D. 3-,B 和C 之间的球面距离是大圆4例2.如图,四棱锥A -BCDE 中, AD 底面 BCDE ,且 AC 丄 BC, AE ± BE.(1) 求证:A 、B 、CD E 五点都在以AB 为直径的同一球面上;(2)注意体会立体空间想象能力,不要把图形想象错误例3.在底面边长为2的正方体容器中,放入大球,再放入一个小球,正好可以盖住盖子(小球与大球都与盖子相切),求小球的半径。
专题9:立体几何中球的相关问题高考真题

专题9:立体几何中球的相关问题高考真题一、单选题1.2020年全国统一高考数学试卷(文科)(新课标Ⅰ)已知,,A B C 为球O 的球面上的三个点,⊙1O 为ABC 的外接圆,若⊙1O 的面积为4π,1AB BC AC OO ===,则球O 的表面积为( )A .64πB .48πC .36πD .32π【答案】A 【分析】由已知可得等边ABC 的外接圆半径,进而求出其边长,得出1OO 的值,根据球的截面性质,求出球的半径,即可得出结论. 【详解】设圆1O 半径为r ,球的半径为R ,依题意, 得24,2r r ππ=∴=,ABC 为等边三角形,由正弦定理可得2sin 6023AB r =︒=,123OO AB ∴==,根据球的截面性质1OO ⊥平面ABC ,222211111,4OO O A R OA OO O A OO r ∴⊥==+=+=, ∴球O 的表面积2464S R ππ==.故选:A【点睛】本题考查球的表面积,应用球的截面性质是解题的关键,考查计算求解能力,属于基础题.2.2020年全国统一高考数学试卷(文科)(新课标Ⅱ)已知△ABC 是面积为93的等边三角形,且其顶点都在球O 的球面上.若球O 的表面积为16π,则O 到平面ABC 的距离为( ) A .3 B .32C .1D .32【答案】C 【分析】根据球O 的表面积和ABC 的面积可求得球O 的半径R 和ABC 外接圆半径r ,由球的性质可知所求距离22d R r =-.【详解】设球O 的半径为R ,则2416R ππ=,解得:2R =. 设ABC 外接圆半径为r ,边长为a ,ABC 93213932a ∴=,解得:3a =,22229933434a r a ∴=-=-=,∴球心O 到平面ABC 的距离22431d R r --=.故选:C. 【点睛】本题考查球的相关问题的求解,涉及到球的表面积公式和三角形面积公式的应用;解题关键是明确球的性质,即球心和三角形外接圆圆心的连线必垂直于三角形所在平面. 3.2018年全国卷Ⅲ理数高考试题设A B C D ,,,是同一个半径为4的球的球面上四点,ABC 为等边三角形且其面积为3D ABC -体积的最大值为 A .123B .183C .243D .543【答案】B 【详解】分析:作图,D 为MO 与球的交点,点M 为三角形ABC 的中心,判断出当DM ⊥平面ABC 时,三棱锥D ABC -体积最大,然后进行计算可得. 详解:如图所示,点M 为三角形ABC 的中心,E 为AC 中点, 当DM ⊥平面ABC 时,三棱锥D ABC -体积最大 此时,OD OB R 4===23934ABCSAB == AB 6∴=,点M 为三角形ABC 的中心2BM 233BE ∴==Rt OMB ∴中,有22OM 2OB BM -=DM OD OM 426∴=+=+=()max 19361833D ABC V -∴=⨯=故选B.点睛:本题主要考查三棱锥的外接球,考查了勾股定理,三角形的面积公式和三棱锥的体积公式,判断出当DM ⊥平面ABC 时,三棱锥D ABC -体积最大很关键,由M 为三角形ABC 的重心,计算得到2BM 233BE ==再由勾股定理得到OM ,进而得到结果,属于较难题型.4.2015年全国普通高等学校招生统一考试理科数学(新课标Ⅱ)如图,已知A ,B 是球O 的球面上两点,∠AOB =90°,C 为该球面上的动点,若三棱锥O -ABC 体积的最大值为36,则球O 的表面积为( )A .36πB .64πC .144πD .256π 【答案】C【解析】如图所示,当点C 位于垂直于面的直径端点时,三棱锥的体积最大,设球的半径为,此时,故,则球的表面积为,故选C .考点:外接球表面积和椎体的体积.5.2019年全国统一高考数学试卷(理科)(新课标Ⅰ)已知三棱锥P -ABC 的四个顶点在球O 的球面上,PA =PB =PC ,△ABC 是边长为2的正三角形,E ,F 分别是PA ,AB 的中点,∠CEF =90°,则球O 的体积为 A .6π B .46πC .26πD 6π【答案】D 【分析】先证得PB ⊥平面PAC ,再求得2PA PB PC ===P ABC -为正方体一部分,进而知正方体的体对角线即为球直径,从而得解. 【详解】 解法一:,PA PB PC ABC ==∆为边长为2的等边三角形,P ABC ∴-为正三棱锥,PB AC ∴⊥,又E ,F 分别为PA 、AB 中点,//EF PB ∴,EF AC ∴⊥,又EF CE ⊥,,CE AC C EF =∴⊥平面PAC ,PB ⊥平面PAC ,2APB PA PB PC ∴∠=90︒,∴===,P ABC ∴-为正方体一部分,22226R =++=,即 364466,62338R V R =∴=π=⨯=ππ,故选D .解法二:设2PA PB PC x ===,,E F 分别为,PA AB 中点,//EF PB ∴,且12EF PB x ==,ABC ∆为边长为2的等边三角形, 3CF ∴=又90CEF ∠=︒213,2CE x AE PA x ∴=-==AEC ∆中余弦定理()2243cos 22x x EAC x+--∠=⨯⨯,作PD AC ⊥于D ,PA PC =,D 为AC 中点,1cos 2AD EAC PA x ∠==,2243142x x x x +-+∴=, 221221222x x x ∴+=∴==,2PA PB PC ∴===,又===2AB BC AC ,,,PA PB PC ∴两两垂直,22226R ∴=++=6R ∴=,344666338V R ∴=π=π⨯=π,故选D . 【点睛】本题考查学生空间想象能力,补体法解决外接球问题.可通过线面垂直定理,得到三棱两两互相垂直关系,快速得到侧棱长,进而补体成正方体解决. 6.2016年全国普通高等学校招生统一考试理科数学(新课标1卷)如图,某几何体的三视图是三个半径相等的圆及每个圆中两条互相垂直的半径.若该几何体的体积是,则它的表面积是A .17πB .18πC .20πD .28π【答案】A 【解析】试题分析:由三视图知,该几何体的直观图如图所示:是一个球被切掉左上角的,即该几何体是个球,设球的半径为,则,解得,所以它的表面积是的球面面积和三个扇形面积之和,即,故选A .【考点】三视图及球的表面积与体积【名师点睛】由于三视图能有效地考查学生的空间想象能力,所以以三视图为载体的立体几何题基本上是高考每年必考内容,高考试题中三视图一般与几何体的表面积与体积相结合.由三视图还原出原几何体是解决此类问题的关键.7.2017年全国普通高等学校招生统一考试文科数学(新课标3卷)已知圆柱的高为1,它的两个底面的圆周在直径为2的同一个球的球面上,则该圆柱的体积为A.πB.3π4C.π2D.π4【答案】B 【解析】绘制圆柱的轴截面如图所示,由题意可得:11,2 AC AB==,结合勾股定理,底面半径221312r⎛⎫=-=⎪⎝⎭,由圆柱的体积公式,可得圆柱的体积是2233ππ1π24V r h⎛⎫==⨯⨯=⎪⎪⎝⎭,故选B.【名师点睛】涉及球与棱柱、棱锥的切、接问题时,一般过球心及多面体中的特殊点(一般为接、切点)或线作截面,把空间问题转化为平面问题,再利用平面几何知识寻找几何体中元素间的关系,或只画内切、外接的几何体的直观图,确定球心的位置,弄清球的半径(直径)与该几何体已知量的关系,列方程(组)求解.8.2016年全国普通高等学校招生统一考试文科数学(全国2卷)体积为8的正方体的顶点都在同一球面上,则该球面的表面积为A.12πB.323πC.8πD.4π【答案】A 【解析】试题分析:因为正方体的体积为8,所以棱长为2,所以正方体的体对角线长为23,所以正方体的外接球的半径为3,所以该球的表面积为24(3)12ππ⋅=,故选A. 【考点】 正方体的性质,球的表面积【名师点睛】与棱长为a 的正方体相关的球有三个: 外接球、内切球和与各条棱都相切的球,其半径分别为32a 、2a和22a .9.2016年全国普通高等学校招生统一考试文科数学(新课标3卷) 在封闭的直三棱柱内有一个体积为V 的球,若,,,,则该球体积V 的最大值是A .B .C .D .【答案】B 【解析】 试题分析:设的内切圆半径为,则,故球的最大半径为,故选B.考点:球及其性质.10.2015年全国普通高等学校招生统一考试文科数学(新课标Ⅱ) 已知是球的球面上两点,,为该球面上的动点.若三棱锥体积的最大值为36,则球的表面积为( )A .36πB .64πC .144πD .256π【答案】C 【详解】如图所示,当点C 位于垂直于面AOB 的直径端点时,三棱锥O ABC -的体积最大,设球O 的半径为R ,此时2311136326O ABC C AOB V V R R R --==⨯⨯==,故6R =,则球O 的表面积为24144S R ππ==,故选C . 考点:外接球表面积和椎体的体积.11.2010年普通高等学校招生全国统一考试(全国卷)新课标文科数学设长方体的长、宽、高分别为2,,a a a ,其顶点都在一个球面上,则该球的表面积为 A .3πa 2 B .6πa 2C .12πa 2D .24πa 2【答案】B 【详解】方体的长、宽、高分别为2,,a a a ,其顶点都在一个球面上,长方体的对角线的 6a ,6,所以球的表面积是22646a ππ⎫=⎪⎪⎝⎭,故选B二、填空题12.2017年全国普通高等学校招生统一考试文科数学(新课标1卷)已知三棱锥S ABC -的所有顶点都在球O 的球面上,SC 是球O 的直径.若平面SCA ⊥平面SCB ,SA AC =,SB BC =,三棱锥S ABC -的体积为9,则球O 的表面积为______. 【答案】36π 【解析】三棱锥S−ABC 的所有顶点都在球O 的球面上,SC 是球O 的直径,若平面SCA ⊥平面SCB ,SA=AC ,SB=BC ,三棱锥S−ABC 的体积为9, 可知三角形SBC 与三角形SAC 都是等腰直角三角形,设球的半径为r ,可得112932r r r ⨯⨯⨯⨯= ,解得r=3.球O 的表面积为:2436r ππ= .点睛:与球有关的组合体问题,一种是内切,一种是外接.解题时要认真分析图形,明确切点和接点的位置,确定有关元素间的数量关系,并作出合适的截面图,如球内切于正方体,切点为正方体各个面的中心,正方体的棱长等于球的直径;球外接于正方体,正方体的顶点均在球面上,正方体的体对角线长等于球的直径.13.2017年全国普通高等学校招生统一考试数学(江苏卷)如图,在圆柱O 1 O 2 内有一个球O ,该球与圆柱的上、下底面及母线均相切.记圆柱O 1O 2 的体积为V 1 ,球O 的体积为V 2 ,则12V V 的值是_____【答案】32【解析】设球半径为r ,则213223423V r r V r π⨯==π.故答案为32. 点睛:空间几何体体积问题的常见类型及解题策略:①若给定的几何体是可直接用公式求解的柱体、锥体或台体,则可直接利用公式进行求解;②若所给定的几何体的体积不能直接利用公式得出,则常用转换法、分割法、补形法等方法进行求解.14.浙江省理科数学试卷(带解析)如图,已知球O 是棱长为1 的正方体1111ABCD A B C D -的内切球,则平面1ACD 截球O 的截面面积为 .试卷第11页,总11页【答案】【解析】 试题分析:由题意可知:截面是MNP ∆的外接圆,而MNP ∆是边长为22的等边三角形, 所以外接圆02222sin 603r ==6r =2266S r πππ==⨯=. 考点:1.平面截圆的性质;2.三角形外接圆半径的求法.。
高三数学立体几何练习题及答案

高三数学立体几何练习题及答案第一题:已知一个长方体的长、宽、高分别为3cm、4cm、5cm,求该长方体的体积和表面积。
解答:长方体的体积可以通过公式V = lwh 计算,其中l、w、h分别为长、宽、高。
根据题目给出的数据,代入公式可得 V = 3cm × 4cm × 5cm = 60cm³。
因此,该长方体的体积为60立方厘米。
长方体的表面积可以通过公式 S = 2lw + 2lh + 2wh 计算。
根据题目给出的数据,代入公式可得 S = 2 × 3cm × 4cm + 2 × 3cm ×5cm + 2 × 4cm × 5cm = 94cm²。
因此,该长方体的表面积为94平方厘米。
答案:体积:60立方厘米表面积:94平方厘米第二题:一个正方体的棱长为a,求该正方体所有顶点到一个固定点之间的最短距离之和。
解答:正方体的每个顶点到固定点的最短距离为正方体的对角线长。
对于正方体而言,其对角线的长度可以通过勾股定理求解。
设每个边长为a,则对角线长d满足 d² = a² + a² + a² = 3a²。
因此,每个顶点到固定点的最短距离之和为 8 × 3a² = 24a²。
答案:每个顶点到固定点的最短距离之和为24a²。
第三题:一个球体的直径为10cm,求该球体的体积和表面积(结果保留π)。
解答:球体的体积可以通过公式V = 4/3πr³ 计算,其中r为球体的半径。
根据题目给出的数据,直径d为10cm,因此半径r = d/2 = 5cm。
代入公式可得V = 4/3 × π × (5cm)³ ≈ 523.6cm³。
因此,该球体的体积约为523.6立方厘米。
球体的表面积可以通过公式S = 4πr² 计算,其中r为球体的半径。
数学题目立体几何的表面积与体积练习题

数学题目立体几何的表面积与体积练习题数学题目:立体几何的表面积与体积练习题1. 题目一:计算一个半径为3厘米的球体的表面积和体积。
解答:首先计算球的表面积。
球的表面积公式为S=4πR²,其中R 为球的半径。
代入半径为3厘米,得到表面积S=4π×3²=36π cm²。
接下来计算球的体积。
球的体积公式为V=4/3πR³,代入半径为3厘米,得到体积V=4/3π×3³=36π cm³。
2. 题目二:一个长方体的长、宽和高分别为5厘米、4厘米和6厘米。
求该长方体的表面积和体积。
解答:长方体的表面积公式为S=2(长×宽+长×高+宽×高),代入长为5厘米、宽为4厘米和高为6厘米,得到表面积S=2(5×4+5×6+4×6)=2(20+30+24)=148 cm²。
长方体的体积公式为V=长×宽×高,代入长为5厘米、宽为4厘米和高为6厘米,得到体积V=5×4×6=120 cm³。
3. 题目三:一个圆锥的底面圆半径为2.5厘米,高为7厘米。
求该圆锥的表面积和体积(保留π)。
解答:首先计算圆锥的母线,母线公式为l=√(r²+h²),其中r为底面圆半径,h为圆锥的高。
代入半径为2.5厘米和高为7厘米,得到母线l=√(2.5²+7²)≈7.416 cm。
圆锥的表面积公式为S=πr(r+l),代入底面圆半径为2.5厘米和母线长为7.416厘米,得到表面积S=π×2.5(2.5+7.416)≈82.512 cm²。
圆锥的体积公式为V=1/3πr²h,代入底面圆半径为2.5厘米和高为7厘米,得到体积V=1/3π×2.5²×7≈36.750 cm³。
与球有关的空间几何体问题(例题+习题)

考点一:球的内接柱体设柱体上底的外心为1O ,下底的外心为2O ,则有柱体的外接球球心O 为21O O 的中点。
若柱体底面外接圆半径为r ,高为h ,则外接球半径R 满足:2222h r R +=; 由已学知识可总结出:(1)边长为a 的正三角形的外接圆半径a r 33=; (2)长为a ,宽为b 的的矩形的外接圆半径222b a r += (3)斜边为c 的直角三角形的外接圆半径2c r = 注:球的内接长方体满足:球的直径于长方体的大对角线相等考点二:球的内接椎体1. 球的内接直三棱锥,直四棱锥(有一条侧棱与底面垂直):与长方体相同,是长方体的部分顶点构成的椎体2. 球的内接正三棱锥,正四棱锥:设顶点为P ,底面外接圆圆心1O ,则有正棱锥外接球球心在1PO 上,若正棱锥底面外接圆半径为r ,高为h ,则外接球半径R 满足:222)(R h r R -+=或h l R 22=(l 为侧棱)考点三:多面体的内切球1 多边形内切圆圆心把多边形分成多个高相等的三角形,由面积法可知多边形的内切圆半径r 满足:PS r 2=(S 为多边形面积,P 为多边形周长) 2 多面体内切球球心把多面体分成多个高相等的椎体,由体积法可知 多面体的内切求半径r 满足:S V r 3=(V 为多面体体积,S 为多面体表面积)考点四:圆锥内切球与外接球1 圆锥的外接球:与正棱锥的外接球相同2 圆锥的内切球:圆锥的内切球半径即为圆锥截面三角形的内切圆半径,设圆锥的底面半径为r ,高为h ,则内切球半径R 满足:22222hr r h r R P S r R ++⋅=⇒==小结: 1 球的内接柱体,直椎体:2222h r R += 2 球的内接正棱锥,内接圆锥:hl R 22=(l 为侧棱) 3 多面体的内切球:S V R 3=4 圆锥的内切球:r h r h r R 2222++⋅=典型例题例1 一个球的外切正方体的全面积为6,则球的体积为( ) A 34π B 86π C 6π D 66π 答案:C解析:多面体的内切球,所以球的半径SV R 3=,正方体的棱长为1,则1=V ,所以2163==R ,所以球的体积为6)21(343ππ=⋅⋅,故选C例2 某长方体的三视图的面积分别为20,15,12,求该长方体的外接球的表面积答案:π50解析:设长方体的三边分别为c b a ,,,则有⎪⎩⎪⎨⎧===⇒⎪⎩⎪⎨⎧===534121520c b a ab bc ac ,所以外接球半径为:2252222=++=c b a R ,所以ππ50)225(42=⋅=S例3 某圆锥的截面为边长为2的正三角形,则该圆锥的内切球的表面积为_______ 答案:33 解析:边长为2的正三角形的内切圆半径为336322=⋅==P S r ,则内球球的半径也为33例4 一三棱锥ABC P -,PC PB PA ,,两两垂直,且3,3,1===PC PB PA ,则该三棱锥外接球的表面积是( )A π16B π64 Cπ332 D π3252 答案:A解析:易知,C B A P ,,,是长方体中相邻四个顶点构成的棱锥,所以外接球半径: 22961=++=R ,所以ππ1644=⋅=S ,选A例 5 一底面半径为r ,母线长为r 3的圆锥有一内接正方体,求该正方体的表面积答案:2316r 解析:由题知,圆锥的高为r 22,设正方体的棱长为a ,可知:ra r a r 2222=-,所以: r a a a r 322222=⇒=-,所以,正方体的表面积为:223166r a =例6 若半球内有一内接正方体,则这个半球的表面积与正方体的表面积之比为( )A 12:5πB 6:5πC 3:2πD 4:3π答案:D解析:设半球的半径为R ,正方体的棱长为a ,则有222223)22(a a a R =+=,半球的表面积:22213421R R R S πππ=+⋅=,正方体的表面积226a S =,所以: 4322363222221πππ=⋅==a a a R S S ,故选D例7 某圆柱的底面半径为2,里面有一定的水,现把圆柱横着放,水面的高度变为1,求圆柱里的水的体积与圆柱的体积比 答案:ππ4334- 解析:已知横着放时,底面是一个弓形,所以3431-⋅=πS ,所以体积比为: ππ4334-例8 正四面体外接球与内切球的半径之比为_______答案:3解析:设正四面体半径为a ,则底面积为243a ,高为a 36,所以内切球半径a a a S V R 126336433231=⋅⋅==,外接球半径a a a h l R 463622222===,所以: 3126:46:12==a a R R练习1 已知一个多面体的内切球的半径为1,多面体的表面积为18,则多面体的体积为( )A 18B 12C 6D π12答案: C解析: 5cos )54cos(54cos ππππ-=--=;52cos )53cos(53cos ππππ-=--=,所以 内切球半径满足631833===⇒=RS V S V R ,选C2 用与球心距离为1的平面去截球面,所得截面积为π,则球的体积为________ 答案:π328 解析:截面半径为1,所以球的半径2=R ,球的体积为ππ3282234=⋅3. 64个直径都是4a 的球,记它的体积为1V ,表面积之和为1S ,1个直径都是a 的球,记它的体积为2V ,表面积之和为2S ,则( )A 2121,S S V V >>B 2121,S S V V <<C 2121,S S V V >=D 2121,S S V V ==答案: C解析: 左221331464)8(4;664)8(34a a S a a V ππππ=⋅⋅==⋅⋅=, 221331)2(4;6)2(34a a S a a V ππππ=⋅==⋅=,所以2121,S S V V >=,选C4 高与底面直径之比为1:2的圆柱内接于球,且圆柱的体积为π500,则球的体积为( ) A 3500π B 32500π C π332500 D 312500π 答案: C解析:设圆柱底面半径为r ,则高为r 4,20,550042==⇒=⋅⋅h r r r ππ,所以有:55125)2(222=⇒=+=R h r R ,所以球的体积ππ352500562534=⋅=V ,选C5 求半径为2的球的内接正四面体的体积答案 27364 解析:设正四面体的棱长为a ,则底面外接圆半径a r 33=,高a r a h 3622=-=,所以外接球半径满足:a a a h l R 46362222===,所以 364=a ,2736427666412212236433132=⋅⋅==⋅⋅=a a a V。
立体几何《球》 专题(提高题)(题目及答案)

《球》【类型1:求长度】1、设正三棱锥A BCD -的所有顶点都在球O 的球面上,1BC =,,E F 分别是,AB BC 的中点,EF DE ⊥,则球O 的半径为2、点S 、A 、B 、C 2的同一球面上,点S 到平面ABC 的距离为12,3AB BC CA ===则点S 与ABC ∆中心的距离为( )A 3B 2C .1D .123、已知球O 的半径为4,圆M 与圆N 为该球的两个小圆,AB 为圆M 与圆N 的公共弦,4AB =.若3OM ON ==,则两圆圆心的距离MN = .4、高为24的四棱锥S-ABCD 的底面是边长为1的正方形,点S 、A 、B 、C 、D 均在半径为1的同一球面上,则底面ABCD 的中心与顶点S 之间的距离为5、(2013年辽宁卷)已知三棱柱111C B A ABC - 的6个顶点都在球O 的球面上,若AB = 3,AC = 4 ,AB AC ⊥ 121=AA ,则球O 的半径为( )A 317B .210C .132D .3106、已知球的表面积为20π,球面上有A、B、C三点.如果AB=AC=2,BC=32,则球心到平面ABC的距离为()A.1 B.2C.3D.27、已知球的半径为2,相互垂直的两个平面分别截球面得两个圆.若两圆的公共弦长为2,则两圆的圆心距等于()A.1 B.2C.3D.28、已知两个圆锥有公共底面,且两圆锥的顶点和底面的圆周都在同一个球面上.若圆锥底面面积是这个球面面积的316,则这两个圆锥中,体积较小者的高与体积较大者的高的比值为______________.9、(2013年天津卷)已知一个正方体的所有顶点在一个球面上. 若球的体积为92, 则正方体的棱长为______.【类型2:求面积】1、在四面体ABCD 中,若AB CD ==2AC BD ==,AD BC ==ABCD 的外接球的表面积为( )A .2πB .4πC .6πD .8π2、四棱锥P -ABCD 的底面是边长为42的正方形,侧棱长都等于45,则经过该棱锥五个顶点的球面面积为_________.3、已知点A 、B 、C 、D 均在球O 上,AB =BC =错误!未找到引用源。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
E B C
D A 立体几何-球-专题学案
练习
1.下列四个命题中错误..
的个数是 ( ) ①经过球面上任意两点,可以作且只可以作一个球的大圆 ②球面积是它大圆面积的四倍 ③球面上两点的
球面距离,是这两点所在截面圆上以这两点为端点的劣弧的长
A.0
B.1
C.2
D.3
2.一平面截一球得到直径为6 cm 的圆面,球心到这个平面的距离是4 cm ,则该球的体积是 A.3π100 cm 3
B.3π208 cm 3
C.3π500 cm 3
D.3
π34161 cm 3
3.某地球仪上北纬30°纬线的长度为12π cm ,该地球仪的半径是_____________cm ,表面积是_____________cm 2.
预备
1. 球心到截面的距离d 与球半径R 及截面的半径r 有以下关系: .
2. 球面被经过球心的平面截得的圆叫 .被不经过球心的平面截得的圆叫 .
3. 在球面上两点之间的最短连线的长度,就是经过这两点的大圆在这两点间的一段劣弧长,这个弧长
叫 .
4. 球的表面积表面积S = ;球的体积V = .
5. 球面距离计算公式:__________
典例剖析
(1)球面距离,截面圆问题
例1.球面上有3个点,其中任意两点的球面距离都等于大圆周长的
61,经过这3个点的小圆的周长为4π,那么这个球的半径为 A.43
B.23
C.2
D. 3
练习: 球面上有三点A 、B 、C ,A 和B 及A 和C 之间的球面距离是大圆周长的41,B 和C 之间的球面距离是大圆周长的61,且球心到截面ABC 的距离是7
21,求球的体积.
例2. 如图,四棱锥A -BCDE 中,BCDE AD 底面⊥,且AC ⊥BC ,AE ⊥BE .
(1) 求证:A 、B 、C 、D 、E 五点都在以AB 为直径的同一球面上;
(2) 若,1,3,90===∠AD CE CBE 求B 、D 两点间的球面距离.
(2)注意体会立体空间想象能力,不要把图形想象错误
例3. 在底面边长为2的正方体容器中,放入大球,再放入一个小球,正好可以盖住盖子(小球与大球都与盖子相切), 求小球的半径。
(3)经度,维度问题
例4. 把地球看作半径为R 的球,A 、B 是北纬30°圈上的两点,它们的经度差为60°
,A 、B 两点间的球面距离为_____________
(4)球的外接与内切问题
例5. 求边长为1的正四面体的外接球的表面积和内切球的体积。
练习:1. 求底面边长为1,侧棱长为2的正三棱锥的外接球的体积和内切球的表面积。
2. 三棱锥O-ABC 的三条侧棱两两垂直,且长度分别为3,4,4 ; 求它的外接球和内切球的半径。
归纳
1.常考形式有以下几种:
(1) 球与截面圆的问题
(2) 球与棱柱,棱锥的结合,通常求体积,表面积;
(3) 维度,经度问题。
(4)外接球与内切球问题
2.注意球面距离容易搞错,它是与大圆相关。
3. 注意空间想象力的培养,避免把图形想象错误。
立体几何-球专题训练
A 组题:
1、,A B 是球面上相异两点,则经过,A B 可作的大圆个数为 ( )
(A)只有一个 (B)无数个 (C)两个 (D)一个或无数个
2、半径为5的球被一个平面所截,截面面积为16π,则球心到截面的距离为 ( )
(A) 4 (B) 3 (C)2.5 (D) 2
3、自半径为1的球面上一点Q ,作球的三条互相垂直弦,,QA QB QC ,则222QA QB QC ++=
( )
(A) 4 (B) 2 (C) 1 (D)不能确定
4、已知地球的半径为R ,在南纬α的纬度圈上有A,B 两点,若沿纬度圈这两点间的
距离为cos R πα,则A,B 两点间的球面距离为 ( )
(A) R π (B) cos R πα (C) R α (D) (2)R πα-
5、球的半径为R ,,A B 是球面上两点,且球面距离为3R π
,则球心到过,A B 的
所有平面的距离中,最大距离为 ( )
(A) R R (C) 12
R (D) 不存在 6、两个平行平面去截半径为5的球,若截面面积分别为9,16ππ,则这两个平行
平面间的距离是 ( )
(A) 1 (B) 7 (C) 3或4 (D) 1或7
B 组题:
1. 半径为R 的球“紧贴”在墙角处,则球心到墙角顶点的距离为 ( ) A. R B. R 2 C. R 3 D 。
R 2
2. 正四面体的外接球和内切球的体积之比是___________ , 表面积之比是___________ .
3. 三棱锥O-ABC 的三条棱OA, OB, OC 两两垂直,OA=1,OB=OC=2,则内切球表面积为______ , 外接球体积为_____________ .
4.已知球O 的半径为1,A 、B 、C 三点都在球面上,且每两点间的球面距离均为
2π,则球心O 到平面ABC 的距离为 ( ) A. 31 B. 33 C. 32 D. 3
6
5. 已知过球面上A 、B 、C 三点的截面和球心的距离等于球半径的一半,且AB =BC =CA =2,则球面面积是( ) A.9π16 B.3π8 C.4π D.9
π64
6. 把地球看作半径为R 的球,A 、B 是北纬30°圈上的两点,它们的经度差为60°,A 、B 两点间的球面距离为_____________
.
7. 已知球面上的三点A 、B 、C ,AB =6,BC =8,AC =10,球的半径为13,求球心到平面ABC 的距离.
8. 将半径为R 的四个球,两两相切的放在桌面上固定,上面再放一个球,求上面一个球的球心到桌面的距离.
9. 在一个轴截面是正三角形的圆锥形容器中注入高为h 的水,然后将一个铁球放入这个圆锥形的容器中,若水面恰好和球面相切,求这个铁球的半径.。
