统计学例题讲解
统计学习题与答案解析
第一章绪论一、填空题1．统计一词从不同角度理解有三种涵义，即统计工作、统计资料和统计学。
2．社会经济统计的研究对象是社会经济现象的数量方面。
3．统计总体具有的特点是大量性、同质性和差异性。
4．标志是说明总体单位特征的，可以分为品质标志和数量标志。
5．统计指标是说明总体特征的，其构成要素有6个，即指标名称、数值、计量单位、计算方法、时间范围、空间范围。
6．职工的文化程度是品质标志，工龄是数量标志。
7．企业的机器台数和职工人数是属于离散变量，而固定资产原值和销售收入是连续变量。
8．要了解我国乳品企业的生产情况，总体是所有乳品企业，总体单位是每一个乳品企业。
9．要了解我国乳品企业的设备状况，总体是所有乳品企业，总体单位是每一个乳品企业。
10．学生的性别、民族属于品质标志，而学生的身高、体重是数量标志。
11．统计指标的概念完整表述为：“说明社会经济现象总体的数量特征的概念和具体数值”。
12．按统计指标的性质不同，统计指标可分为数量指标和质量指标。
二、判断题1．随着研究目的的不同，总体与总体单位之间是可以变换的，指标与标志也是可以变换的。
（T ）2．张明同学期末数学成绩85分，这是统计指标。
（F ）3．总体单位的特征用指标来说明，总体的特征用标志来说明。
（F ）4．标志可以用文字表现，也可以用数字表现。
（T ）5．指标可以用文字表现，也可以用数字表现。
（F ）6．指标值是由标志值汇总计算而得到。
（T ）7．在全国人口普查中，“年龄”是变量。
（T ）8．某班学生学习情况调查中，班级名称和学生姓名都是可变标志。
（F ）9．张明同学期末数学成绩85分，“成绩”是连续变量，“85分”是变量值。
（ F ）10．某企业职工的姓名、民族、年龄、工种等都是品质标志。
（F ）11.统计的研究对象是社会经济现象总体的数量方面。
（ F ）三、单项选择题1．社会经济统计学的研究对象是( A )。
A社会经济现象的数量方面B人类生活现象的数量方面C自然科学研究的数量方面D社会经济现象的质量方面2．在确定统计总体时必须注意( A )。
《统计学》第六章统计指数(补充例题)
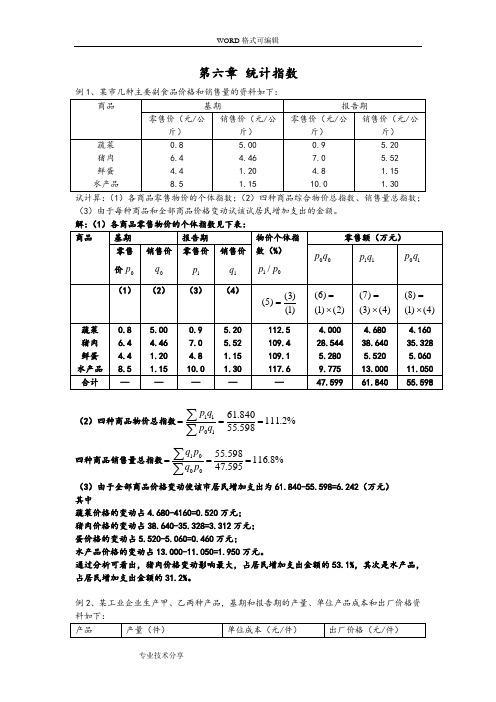
第六章 统计指数（3）由于每种商品和全部商品价格变动试该试居民增加支出的金额。
解：（1）各商品零售物价的个体指数见下表：（2）四种商品物价总指数%2.111598.55840.611011===∑∑qp q p四种商品销售量总指数%8.116595.47598.55001===∑∑pq p q（3）由于全部商品价格变动使该市居民增加支出为61.840-55.598=6.242（万元） 其中蔬菜价格的变动占4.680-4160=0.520万元； 猪肉价格的变动占38.640-35.328=3.312万元； 蛋价格的变动占5.520-5.060=0.460万元；水产品价格的变动占13.000-11.050=1.950万元。
通过分析可看出，猪肉价格变动影响最大，占居民增加支出金额的53.1%，其次是水产品，占居民增加支出金额的31.2%。
例2、某工业企业生产甲、乙两种产品，基期和报告期的产量、单位产品成本和出厂价格资试计算：（1）以单位成本为同度量因素的产量总指数 （2）以出厂价格为同度量因素的产量总指数 （3）单位成本总指数 （4）出厂价格总指数（1）以单位成本为同度量因素的产量总指数%7.1193100037100001===∑∑zq z q（2）以出厂价格为同度量因素的产量总指数%6.115550006360001===∑∑pq p q（3）单位成本总指数%2.14837100550001011===∑∑qz q z（4）出厂价格总指数%8.9963600635001011===∑∑qp q p例3、试根据例2的资料，从相对数和绝对数方面分析： （1）总成本变动受产量和单位成本变动的影响程度 （2）销售额变动受产量和出厂价格变动的影响程度 解：（1）总成本变动：总成本指数%4.1773100055000011===∑∑qz q z增加总成本∑∑=-=-2400031000550000011qz q z （元）其中由于产量变动的影响：产量指数%7.1193100037100001===∑∑zq z q由于产量增长而引起总成本增加：∑∑=-=-610031000371000001zq z q （元）由于单位成本变动的影响： 单位成本指数%2.1483710055000111===∑∑zq z q由于单位成本增长而引起总成本增加：∑∑=-=-1790037100550000111zq z q （元）177.4%=119.7%×148.2% 24000元=6100元+17900元计算表明，该厂两种产品总成本报告期比基期增长77.4%，是由于产品产量增加19.7%和单位成本提高48.2%两因素造成的。
高中数学涉及的统计学知识典型例题分析
高中数学涉及的统计学知识典型例题分析一、基础知识：（一）随机抽样：1、抽签法：把总体中的N 个个体编号，把号码写在号签上，将号签放在一个容器中搅拌均匀后，每次从中抽取一个号签，连续抽取n 次，就得到容量为n 的样本2、系统抽样：也称为等间隔抽样，大致分为以下几个步骤：（1）先将总体的N 个个体编号（2）确定分段间隔k ，设样本容量为n ，若N n 为整数，则N k n= （3）在第一段中用简单随机抽样确定第一个个体编号l ，则后面每段所确定的个体编号与前一段确定的个体编号差距为k ，例如：第2段所确定的个体编号为l k +，第m 段所确定的个体编号为()1l m k +−，直至完成样本注：（1）若N n不是整数，则先用简单随机抽样剔除若干个个体，使得剩下的个体数能被n 整除，再进行系统抽样。
例如501名学生所抽取的样本容量为10，则先随机抽去1个，剩下的500个个体参加系统抽样（2）利用系统抽样所抽出的个体编号排成等差数列，其公差为k3、分层抽样：也称为按比例抽样，是指在抽样时，将总体分成互不交叉的层，然后按照一定的比例，从各层独立地抽取一定数量的个体，将各层取出的个体合在一起作为样本。
分层抽样后样本中各层的比例与总体中各个层次的比例相等，这条结论会经常用到（二）频率分布直方图：1、频数与频率（1）频数：指一组数据中个别数据重复出现的次数或一组数据在某个确定的范围内出现的数据的个数.（2）频率：是频数与数据组中所含数据的个数的比，即频率=频数/总数（3）各试验结果的频率之和等于12、频率分布直方图：若要统计每个小组数据在样本容量所占比例大小，则可通过频率分布表（表格形式）和频率分布直方图（图像形式）直观的列出（1）极差：一组数据中最大值与最小值的差（2）组距：将一组数据平均分成若干组（通常5-12组），则组内数据的极差称为组距，所以有组距=极差/组数（3）统计每组的频数，计算出每组的频率，便可根据频率作出频率分布直方图（4）在频率分布直方图中：横轴按组距分段，纵轴为“频率/组距”（5）频率分布直方图的特点：②因为各试验结果的频率之和等于1，所以可得在频率分布直方图中，各个矩形的面积和为1 （三）茎叶图：通常可用于统计和比较两组数据，其中茎是指中间的一列数，通常体现数据中除了末位数前面的其他数位，叶通常代表每个数据的末位数。
统计学例题讲解-统计学平均增长量例题
第四章计算变异指标；比较平均指标的代表性。
例题：某车间有甲、乙两个生产组，甲组平均每个工人的日产量为36件，标准差为9.6件；乙组工人日产量资料如下：解:5.291002950133438151345343538251515==+++⨯+⨯+⨯+⨯=∑∑fxf x ＝乙()986.810080752==-∑∑ff x x ＝乙σ267.0366.9==x V σ＝甲3046.05.29986.8==x V σ＝乙甲组更有代表性。
乙甲∴<V V第十一章：计算相关系数、建立回归方程并解释回归系数的含义、预测因变量的估计值。
4．计算相关系数；建立直线回归方程并指出回归系数的含义；利用建立的方程预测因变量的估计值。
例题：某企业上半年产品产量与单位成本资料如下：要求： （２）配合回归方程，指出产量每增加1000件时，单位成本 平均变动多少？（３）假定产量为6000件时，单位成本为多少元？n=6∑x =21∑y =426∑x 2=79∑y2=30268∑xy=1481（1） 相关系数:2222)(1)(11∑∑∑∑∑∑∑-⋅-⋅-=y n y x nx y x nxyr =-0.9090说明产量x 和单位成本y 之间存在着高度负相关关系。
（2）设直线回归方程为y c =a+bx n=6∑x =21∑y =426∑x 2=79∑y2=30268∑xy=148122)(11∑∑∑∑∑-⋅-=x n x y x n xy b = (1481-1/6*21*426)/(79-1/6*21*21)=-1.82x b y a -==426/6-(-1.82)*21/6=77.37则y c =77.37-1.82x在这里说明回归系数b 的含义 ，即产量每增加1000件时， 单位成本平均降低1.82元 .（３）假定产量为6000件,即x=6时，单位成本为:则y c =77.37-1.82x =77.37-1.82*6=66.45(元) . 即单位成本为: 66.45元.. -2．根据企业产品销售额(万元)和销售利润率(%)资料计算出如下数据:n=7 ∑x=1890 ∑y=31.1 ∑x2=535500 ∑y2=174.15 ∑xy=9318要求: (1) 确定以利润率为因变量的直线回归方程.(2)解释式中回归系数的经济含义.(3)当销售额为500万元时,利润率为多少?参考答案:(1)确定以利润率为因变量的直线回归方程:Y=-5.5+0.037x(2)解释式中回归系数的经济含义:产品销售额每增加1万元,销售利润率平均增加0.037%.第十四章：数量指标综合指数、质量指标综合指数的计算；从相对数和绝对数角度对总量指标的变动进行因素分析。
统计学课后习题答案(全章节)剖析
第二章、练习题及解答2.为了确定灯泡的使用寿命（小时），在一批灯泡中随机抽取100只进行测试，所得结果如下：700 716 728 719 685 709 691 684 705 718 706 715 712 722 691 708 690 692 707 701 708 729 694 681 695 685 706 661 735 665 668 710 693 697 674 658 698 666 696 698 706 692 691 747 699 682 698 700 710 722 694 690 736 689 696 651 673 749 708 727 688 689 683 685 702 741 698 713 676 702 701 671 718 707 683 717 733 712 683 692 693 697 664 681 721 720 677 679 695 691 713 699 725 726 704 729 703 696 717 688 要求：(2)以组距为10进行等距分组，生成频数分布表，并绘制直方图。
灯泡的使用寿命频数分布表3.某公司下属40个销售点2012年的商品销售收入数据如下：单位：万元152 124 129 116 100 103 92 95 127 104 105 119 114 115 87 103 118 142 135 125 117 108 105 110 107 137 120 136 117 108 97 88 123 115 119 138 112 146 113 126 要求：（1）根据上面的数据进行适当分组，编制频数分布表，绘制直方图。
（2）制作茎叶图，并与直方图进行比较。
解：（1）频数分布表（2）茎叶图第三章、练习题及解答1. 已知下表资料：试根据频数和频率资料，分别计算工人平均日产量。
解：根据频数计算工人平均日产量：687034.35200xf x f===∑∑（件） 根据频率计算工人平均日产量：34.35fx xf==∑∑（件）结论：对同一资料，采用频数和频率资料计算的变量值的平均数是一致的。
统计学计算题例题及计算分析
计算分析题解答参考1.1．某厂三个车间一季度生产情况如下：车间计划完成百分比（％）实际产量（件）f单位产品成本（元/件）x第一车间第二车间第三车间9010511019831522015108合计――733 ――计算一季度三个车间产量平均计划完成百分比和平均单位产品成本。
解：平均计划完成百分比＝实际产量/计划产量＝733/（198/0.9+315/1.05+220/1.1）＝101.81%平均单位产量成本 X=∑xf/∑f=(15*198+10*315+8*220)/733=10.75(元/件)1.2．某企业产品的有关资料如下：产品单位成本（元/件）x98年产量（件）f99年成本总额（元）m甲乙丙25283215001020980245002856048000合计－3500 101060 试分别计算该企业产品98年、99年的平均单位产品成本。
解：该企业98年平均单位产品成本 x=∑xf/∑f=(25*1500+28*1020+32*980)/3500=27.83(元/件)该企业99年平均单位产品成本x=∑xf /∑(m/x)=101060/(24500/25+28560/28+48000/32) =28.87(元/件)1.3．1999年某月甲、乙两市场三种商品价格、销售量和销售额资料如下：商品品种价格（元/件）x甲市场销售量（件）f乙市场销售额（元）m甲乙丙10512013770090011001260009600095900合计――2700 317900 试分别计算三种商品在两个市场上的平均价格。
解：三种商品在甲市场上的平均价格x=∑xf/∑f=(105*700+120*900+137*1100)/2700=123.04(元/件)三种商品在乙市场上的平均价格x=∑m/∑(m/x)=317900/(126000/105+96000/120+95900/137)=117.74(元/件)2.1．某车间有甲、乙两个生产小组，甲组平均每个工人的日产量为22件，标准差为3.5件；乙组工人日产量资料：日产量（件）工人数（人）10－12 13－15 16－18 19－21 10 20 30 40试比较甲、乙两生产小组中的哪个组的日产量更有代表性？解：∵X甲=22件σ甲=3.5件∴V甲=σ甲/ X甲=3.5/22=15.91%列表计算乙组的数据资料如下:日产量组中值(件)x 工人数(人)fxf(x-x)2(x-x)2f1110110363601420280918017305100020408009360合计1001700-900∵x乙=∑xf/∑f=(11*10+14*20+17*30+20*40)/100=17(件)σ乙=√[∑(x-x)2f]/∑f =√900/100 =3(件)∴V乙=σ乙/ x乙=3/17=17.65%由于V甲＜V乙,故甲生产小组的日产量更有代表性。
统计学习题和答案解析[完整]
![统计学习题和答案解析[完整]](https://img.taocdn.com/s3/m/1561afec2dc58bd63186bceb19e8b8f67c1cef63.png)
统计学习题和答案解析[完整]第一部分计量资料的统计描述一、最佳选择题1、描述一组偏态分布资料的变异度，以（）指标较好。
A、全距B、标准差C、变异系数D、四分位数间距E、方差2．用均数和标准差可以全面描述（）资料的特征。
A．正偏态分布 B．负偏态分布 C．正态分布D．对称分布 E．对数正态分布3．各观察值均加（或减）同一数后（）。
A．均数不变，标准差改变 B．均数改变，标准差不变C．两者均不变 D．两者均改变 E．以上都不对4．比较身高和体重两组数据变异度大小宜采用（）。
A．变异系数 B．方差 C．极差 D．标准差 E．四分位数间距5．偏态分布宜用（）描述其分布的集中趋势。
A．算术均数 B．标准差 C．中位数 D．四分位数间距 E．方差6．各观察值同乘以一个不等于0的常数后，（）不变。
A．算术均数 B．标准差 C．几何均数 D．中位数 E．变异系数7．（）分布的资料，均数等于中位数。
A．对数正态 B．正偏态 C．负偏态 D．偏态 E．正态8．对数正态分布是一种（）分布。
（说明：设X变量经Y=lgX变换后服从正态分布，问X变量属何种分布？）A．正态 B．近似正态 C．左偏态 D．右偏态 E．对称9．最小组段无下限或最大组段无上限的频数分布资料，可用（）描述其集中趋势。
A．均数 B．标准差 C．中位数 D．四分位数间距 E．几何均数10．血清学滴度资料最常用来表示其平均水平的指标是（）。
A．算术平均数 B．中位数 C．几何均数 D．变异系数 E．标准差二、简答题1、对于一组近似正态分布的资料，除样本含量n外，还可计算，S和，问各说明什么？2、试述正态分布、标准正态分布及对数正态分布的某单位1999年正常成年女子血清联系和区别。
甘油三酯(mmol/L)测量结果3、说明频数分布表的用途。
4、变异系数的用途是什么？组段频数5、试述正态分布的面积分布规律。
0.6~ 10.7~ 3三、计算分析题0.8~ 91、根据1999年某地某单位的体检资料，116名正常 0.9~ 13成年女子的血清甘油三酯（mmol/L）测量结果如右表， 1.0~ 19 请据此资料： 1.1~ 25（1）描述集中趋势应选择何指标？并计算之。
《统计》知识点总结+典型例题+练习(含答案)
统计考纲要求1.理解总体、个体、样本等概念．2.会指出具体问题中的总体、个体、样本、样本容量．3.了解简单随机抽样、系统抽样、分层抽样等三种抽样方法．4.会根据特征选用合适的抽样方法抽取样本.5.理解用样本的频率分布估计总体．6.理解用样本均值、方差和标准差估计总体的均值、方差和标准差．知识点一：总体与样本1.定义：在统计中，所研究对象的全体叫做总体，组成总体的每个对象叫做个体．2.定义：被抽取出来的个体的集合叫做总体的样本，样本所含个体的数目叫做样本容量. 知识点二：抽样1.简单随机抽样定义：我们采用抽签的方法，将总体按照某种顺序编号，写在小纸片上．将小纸片揉成小团，放到一个不透明的袋子中，充分搅拌后，再从中逐个抽出10个小纸团．最后根据编号找到个体．这种抽样叫做简单随机抽样．注意：简单随机抽样必须保证总体的每个个体被抽到的机会是相同的．也就是说，简单随机抽样是等概率抽样．2.系统抽样定义：当总体所含的个体较多时，可将总体分成均衡的几个部分，然后按照预先定出的规则，从每一部分中抽取一定数目的个体．这种抽样叫做系统抽样（或机械抽样）．主要步骤：从容量为N的总体中，用系统抽样抽取容量为n的样本，按照下面的步骤进行：（1）编号：将总体的N个个体编号；（2）确定间隔：可以考虑用Nn（取整数）作间隔分段，将总体分成n段；（3）抽样：按照一定的规则抽取样本．如抽每段的第k个顺序号的个体(k为小于Nn的整数)，得到容量为n的样本．3.分层抽样当总体是由有明显差异的几个部分组成时，可将总体按差异情况分成互不重叠的几个部分——层，然后按各层个体总数所占的比例来进行抽样，这种抽样叫做分层抽样． 对分层抽样的每一层进行抽样时，可采用简单随机抽样或系统抽样． 知识点三：用样本估计总体 1.用样本的频率分布估计总体频率频率的定义：各组内数据的个数，叫做该组的频数．每组的频数与全体数据的个数之比叫做该组的频率．频率分布直方图：根据频数分布表中各组的频率，得到频率分布表，由频率分布表画出频率分布直方图.用样本的频率分布估计总体的步骤为： （1）选择恰当的抽样方法得到样本数据；（2）计算数据最大值和最小值、确定组距和组数，确定分点并列出频率分布表； （3）绘制频率分布直方图；（4） 观察频率分布表与频率分布直方图，根据样本的频率分布，估计总体中某事件发生的概率．2.用样本均值、标准差估计总体 （1）平均数或均值定义：如果有n 个数1x ，2x ，…，n x ，那么121()n x x x x n=+++叫做这n 个数的平均数或均值，x 读作“x 拔”． 均值反映出这组数据的平均水平． （2）样本方差定义：如果样本由n 个数1x ，2x ，…，n x 组成，那么样本的方差为 2222121()()()1n s x x x x x x n ⎡⎤=-+-++-⎣⎦-． （3）样本标准差由于样本方差的单位是数据的单位的平方，使用起来不方便．因此，人们常使用它的算术平方根来表示个体与样本均值之间偏离程度，叫做样本标准差．即(+-n s x ．题型一 总体、个体、样本、样本容量例1 某地区为了掌握7岁儿童身高状况，随机抽取200名儿童测试身高，请指出其中的总体、个体、样本与样本容量．解答：该地区所有7岁儿童的身高是总体，每一个7岁儿童的身高是个体，被抽取的200名7岁儿童的身高是样本，样本容量是200．题型二抽样例2某中职学校为了解2009级新生的身体发育情况，从1000名新生中，利用系统抽样，抽取一个容量为50的样本．请你来完成这个抽样．解答：将这1000名学生编号（也可以利用新生录取号），由于100020 50，所以取每段间隔为20，将编号分成50段，规定各段抽取第16个顺序号的学生，得到容量为50的样本．其学生号码依次为16，36，56，76， (996)题型三用样本均值、标准差估计总体例3 科研人员在研究地里的麦苗长势时，随机抽取20株，测得各株高为（单位：mm): 61675867656459625866645960635860 62606363求样本均值、样本方差、样本标准差.分析：应用公式解答：样本均值61.95，样本方差约为8.68，样本标准差约为2.95.一、选择题1.要能清楚的表示各部分在总体中所占的百分比，应选择（）.A 扇形统计图B 折线统计图C条形统计图 D 表框统计2.某社区有400个家庭，其中高等收入家庭120户，中等收入家庭180户，低收入家庭100户，为了调查社会购买力的某项指标，要从中抽取一个容量为100的样本记作①；某校高一年级有12名女排球运动员，要从中选出3人调查学习情况记作②.那么，完成上述2项调查应采用的抽样方法是( ).A. ①用随机抽样法，②用系统抽样法B.①用分层抽样法，②用随机抽样法C.①用系统抽样法，②用分层抽样法D.①用分层抽样法，②用系统抽样法3. 以下物征数中能反映一组数据波动大小的是（）.A极差B平均数C方差D以上都不是4.某同学参加跳远比赛前，若教练想对他10次的训练成绩进行了分析以判断他的成绩是否稳定，则教练需要知道该同学这10次成绩的( ).A平均数 B.方差 C.频数 D.频率5.数据5，7，7，8，10，11的平均值是( ).A.2B. 4C.8D. 16.一组数据：5，7，7，a，10，11，它们的平均值是8，则a的值是( ).A2 B.4 C.8 D.17.扇形统计图中，占圆面积40％的扇形的圆心角的度数是（B ）A 162°B 144°C 150°D 120°8.用随机数表法从100名学生(男生25人)中抽选20人进行问卷调查，某男生被抽到的概率是( C ).A.1100B.125C.15D.149. 为了了解1200名学生对课改试验的意见，计划从中抽取一个容量为30的样本，若采用系统抽样的方法，则分段间隔为( ).A.40B.30C.20D.1210. 数据－1，－2，0，1，2的标准差是（）A 1B 2 C、0 D二、判断题1.数据1，2，3，2 的众数是2, ( )2.为了了解某校学生早餐就餐情况，四位同学做了不同的调查：小华向初一年级的三个班级的全体同学做了调查；小明向初二年级的三个班级的全体同学做了调查；小华向初三年级的全体同学做了调查；小珍分别向初一（1）班、初二（1）、初三（1）班的全体同学做了调查，则小华同学的抽样调查较科学.（）3.要了解一批灯泡的使用寿命，从中抽取60只灯泡进行试验，在这个问题中，样本是抽取的60只灯泡.（）4.为了考查某地区初中毕业生的数学毕业会考情况，从中抽查了200名考生的数学成绩，在这个问题中总体是被抽查的200名考生.（）5.某校一个年级有12个班，每个班有50名学生，每班的学号都是1~50，为了了解学生的课外兴趣爱好，要求对每班学号为20的学生进行问卷调查，那么这里采用的抽样方法是抽签法.（）6.某职业学校高一年级有机电、财经、医护这三个专业，其学生人数之比是5∶3∶2，若用分层抽样的方法抽取容量为100的样本，则应从医护专业中抽取20个个体．（）7. 为了知道一锅汤的味道，妈妈从锅里舀了一勺汤尝尝，这种调查方式是抽样调查．（）8.若数据1，2，5，3，4的平均数为3．（）9.青年歌手大奖赛共有10名选手参赛，并请了7名评委，下表是7名评委给参加最后决赛的两位选手甲评定的成绩，去掉一个最高分和一个最低分后，甲、乙选手剩余数据的平均成绩分别为84．（）10. 有四位同学从编号为1-50的总体中抽取8个个体组成一个样本，他们选取的样本中个体编别为：①05，10，15，20，25，30，35，40；②43，44，45，46，47，48，49，50；③1，3，5，7，9，11，13，15，17；④43，25，2，17，35，9，24，19.认为样本④较具有随机性.（）三、填空题1．从某工厂生产的某一批零件中，随机抽取10件，测得长度为（单位：cm）：79、81、80、78、79、81、79、82、79、78，则总体是_______，个体是_______，样本是_______，样本容量是_______.2．0，－1，1，－2，1 的中位数是为________．3.数据2，4，6，8 的平均数是是________．4．小新家今年6月份头6天用米量如下表：请你运用统计知识，估计小新家6月份（30天）用米量为________千克。
统计学课后习题答案(全章节)剖析
第二章、练习题及解答2.为了确定灯泡的使用寿命（小时），在一批灯泡中随机抽取100只进行测试，所得结果如下：700 716 728 719 685 709 691 684 705 718 706 715 712 722 691 708 690 692 707 701 708 729 694 681 695 685 706 661 735 665 668 710 693 697 674 658 698 666 696 698 706 692 691 747 699 682 698 700 710 722 694 690 736 689 696 651 673 749 708 727 688 689 683 685 702 741 698 713 676 702 701 671 718 707 683 717 733 712 683 692 693 697 664 681 721 720 677 679 695 691 713 699 725 726 704 729 703 696 717 688 要求：(2)以组距为10进行等距分组，生成频数分布表，并绘制直方图。
灯泡的使用寿命频数分布表3.某公司下属40个销售点2012年的商品销售收入数据如下：单位：万元152 124 129 116 100 103 92 95 127 104 105 119 114 115 87 103 118 142 135 125 117 108 105 110 107 137 120 136 117 108 97 88 123 115 119 138 112 146 113 126 要求：（1）根据上面的数据进行适当分组，编制频数分布表，绘制直方图。
（2）制作茎叶图，并与直方图进行比较。
解：（1）频数分布表（2）茎叶图第三章、练习题及解答1. 已知下表资料：试根据频数和频率资料，分别计算工人平均日产量。
解：根据频数计算工人平均日产量：687034.35200xf x f===∑∑（件） 根据频率计算工人平均日产量：34.35fx xf==∑∑（件）结论：对同一资料，采用频数和频率资料计算的变量值的平均数是一致的。
统计学原理例题分析(三)
= 30（千元）
注意：在既有期初又有期末登记资料的时点数列中，间隔的计算一定要仔细，以免发生错误。
13．某百货公司月商品销售额及月初库存资料如下：
4月 5月 6月 7月
销售额
150 200 240 276
50
30
5.0
17.5
13.5
合计
--
--
100
36.0
(元)
答题分析: 第一，此题给出销售单价和销售量资料，即给出了计算平均指标的分母资料，所以需采用算术平均数计算平均价格。第二，所给资料是组距数列，因此需计算出组中值。采用加权算术平均数计算平均价格。第三，此题所给的是比重权数，因此需采用以比重形式表示的加权算术平均数公式计算。
10．某企业生产甲、乙、丙三种产品，1984年产品产量分别比1983年增长2%、5%、8%。1983年甲、乙、丙产品产值分别为5000元，1200元，24000元，问1984年三种产品产量比1983年增加多少？由于产量增加而增加的产值是多少？
参考答案：
11.某集团公司销售的三种商品的销售额及价格提高幅度资料如下：
（1）计算结果如下表：
年 份
2002年
2003年
2004年
2005年
2006年
粮食产量（万斤）
434
472
516
584
618
环比发展速度（%）
-
108．76
109．32
113．18
105．82
平均增长量 （万斤）
（或平均增长量 ）
（2）如果从2006年起该地区的粮食生产以10%的增长速度发展，预计到2010年该地区的粮食产量将达到：
专题42 统计【考点精讲】(含答案解析)
专题42统计【考点精讲】-【中考高分导航】备战2022年中考数学考点总复习（全国通用）考点42统计考点1：统计初步知识1.常用的统计调查方式：全面调查、抽样调查．2.所要考察的对象的全体称为总体．组成总体的每一个对象称为个体．3.从总体中抽取的一部分各体叫做总体的一个样本，样本中的个体的数目叫做样本容量．4.在抽取样本的过程中，总体中的每个个体都以相等的机会被抽到，像这样的抽样方法叫做简单随机抽样．【例1】（2021·广东惠州·二模）1．以下调查中，最适合采用全面调查的是（）A．检测长征运载火箭的零部件质量情况B．了解全国中小学生课外阅读情况C．调查某批次汽车的抗撞击能力D．检测某城市的空气质量（1）样本是总体中所抽取的一部分个体，而样本容量则是指样本中个体的数目；（2）对于具有破坏性的调查，无法进行普查，普查的意义或价值不大时，应选择抽样调查，而对于精确度要求高的调查或事关重大的调查往往采用普查．2．某校有4000名学生，随机抽取了400名学生进行体重调查，下列说法错误的是（）A．总体是该校4000名学生的体重B．个体是每一个学生C．样本是抽取的400名学生的体重D．样本容量是400考点2：平均数、中位数、众数1.平均数：x1，x2，…，xn的平均数1xn=（x1＋x2＋…＋xn）．2.加权平均数：如果n个数据中，x1出现f1次，x2出现f2次，…，xR出现fR次（这里f1＋f2＋…＋fR＝n），则1xn=（x1f1＋x2f2＋…＋xRfR）．3.中位数：将一组数据按大小顺序排列，处在最中间位置上的数据叫做这组数据的中位数；如果数据的个数为偶数，中位数就是处在中间位置上的两个数据的平均数．4.众数：在一组数据中，出现次数最多的数据叫做这组数据的众数．【例2】（2021·湖南张家界市·中考真题）3．如图是张家界市某周每天最高气温的折线统计图，则这7天的最高气温的中位数是______℃．【例3】（2020•无锡）4．已知一组数据：21，23，25，25，26，这组数据的平均数和中位数分别是（）A．24，25B．24，24C．25，24D．25，25【例4】（2020•淮安）5．一组数据9、10、10、11、8的众数是（）A．10B．9C．11D．8（2021·广东深圳·模拟预测）6．为了了解学生线上学习情况，老师抽查某组10名学生的单元测试成绩如下：78，86，A．95，99B．94，99C．94，90D．95，108（2021·广东香洲·二模）7．在一次献爱心的捐款活动中，八（2）班50名同学捐款金额如图所示，则在这次捐款活动中，该班同学捐款金额的众数和中位数分别是（）A．20，10B．10，20C．10，10D．10，15（2021·广东深圳·一模）8．某校为了解学生的课外阅读情况，随机抽取了一个班的学生，对他们一周的课外阅读时间进行了统计，统计数据如下表，则该班学生一周课外阅读时间的中位数和众数分别是（）读书时间6小时及以下7小时8小时9小时10小时及以上学生人数611887A．8，7B．8，8C．8.5，8D．8.5，7考点3：方差1.方差：x1，x2，…，xn的方差s2＝1n[（x1－x）2＋（x2－x）2＋…＋（xn－x）2]．2.方差是衡量一组数据波动大小的量，方差越小，数据的波动越小；方差越大，数据的波动越大．【例5】（2020•营口）9．从甲、乙、丙三人中选拔一人参加职业技能大赛，经过几轮初赛选拔，他们的平均成绩都是87.9分，方差分别是s甲2＝3.83，s乙2＝2.71，s丙2＝1.52．若选取成绩稳定的一人参加比赛，你认为适合参加比赛的选手是_____．【例6】（2021·四川乐山市·中考真题）10．如图是根据甲、乙两人5次射击的成绩（环数）制作的折线统计图．你认为谁的成绩较为稳？________（填“甲”或“乙”）方差是衡量一组数据波动大小的量，方差越小，数据的波动越小；方差越大，数据的波动越大（2020•湘西州）11．从甲、乙两种玉米种子中选择一种合适的推荐给某地．考虑到庄稼人对玉米的产量和产量的稳定性十分的关心，选择之前，为了解甲、乙两种玉米种子的情况，某单位各用了10块自然条件相同的试验田进行试验，得到各试验田每公顷产量（单位：t ）的数据，这两组数据的平均数分别是x 甲7.5≈，x 乙7.5≈，方差分别是s 2甲0.010,s ≈2乙0.002≈，你认为应该选择的玉米种子是_________．（2020•绥化）12．甲、乙两位同学在近五次数学测试中，平均成绩均为90分，方差分别为22=0.70=0.73s s 甲乙；，甲、乙两位同学成绩较稳定的是________同学．（2020•郴州）13．某5人学习小组在寒假期间进行线上测试，其成绩（分）分别为：86,88,90,92,94，方差为28.0s =．后来老师发现每人都少加了2分，每人补加2分后，这5人新成绩的方差2s =新__________．考点4：频数、频率、用样本估计总体1.频数：在我们研究的对象中，每个对象出现的次数叫做频数．2.频率：每个对象出现的次数与总次数的比值叫做频率．3.绘制频数分布直方图的步骤：①计算最大值与最小值的差；②决定组距与组数；③列频数分布表；④画频数分布直方图．【例7】（2020•徐州）14．在一个不透明的袋子里装有红球、黄球共20个，这些球除颜色外都相同．小明通过多次实验发现，摸出红球的频率稳定在0.25左右，则袋子中红球的个数最有可能是（）A．5B．10C．12D．15（1）频率反映了各组频数的大小在总数中所占的分量；（2）样本估计总体的公式：总数×相应的频率．（2021·福建中考真题）15．某校共有1000名学生．为了解学生的中长跑成绩分布情况，随机抽取100名学生的中长跑成绩，画出条形统计图，如图．根据所学的统计知识可估计该校中长跑成绩优秀的学生人数是_________．（2020•南京）16．为了了解某地居民的用电量情况，随机抽取了该地200户居民六月份的用电量（单位：kW h ）进行调查，整理样本数据得到下面的频数分布表：组别用电量分组频数x≤<501893x≤<100293178x≤<343178263x≤<114263348x≤<15348433x≤<16433518x≤<27518603x≤<18603688根据抽样调查的结果，回答下列问题：（1）该地这200户居民六月份的用电量的中位数落在第组内．（2）估计该地1万户居民六月份的用电量低于178kW h⋅的大约有多少户．考点5：常见统计图表的综合应用1.常见的统计图有条形统计图、扇形统计图、折线统计图．条线统计图能显示每组中的具体数据；扇形统计图能显示部分在总体中所占百分比；折线统计图能显示数据的变化趋势．2.扇形统计图的制作步骤：①根据有关数据先算出各部分在总体中所占的百分比（即部分数据÷总体数据），再算出各部分圆心角的度数，公式：各部分扇形圆心角的度数＝部分占总体的百分比×360；②按比例，取适当半径画一个圆；③按扇形圆心角的度数用量角器在圆内量出各个扇形的圆心角的度数；④在各扇形内写上相应的名称及百分比；⑤写出统计图的名称、制作日期．【例8】（2021·浙江温州市·中考真题）17．如图是某天参观温州数学名人馆的学生人数统计图．若大学生有60人，则初中生有（）A．45人B．75人C．120人D．300人常见的统计图有条形统计图、扇形统计图、折线统计图．条线统计图能显示每组中的具体数据；扇形统计图能显示部分在总体中所占百分比；折线统计图能显示数据的变化趋势．（2021·江西中考真题）18．如图是2020年中国新能源汽车购买用户地区分布图，由图可知下列说法错误的是（）A．一线城市购买新能源汽车的用户最多B．二线城市购买新能源汽车用户达37%C．三四线城市购买新能源汽车用户达到11万D．四线城市以下购买新能源汽车用户最少（2021·山东聊城市·中考真题）19．为了保护环境加强环保教育，某中学组织学生参加义务收集废旧电池的活动，下面是随机抽取40名学生对收集废旧电池的数量进行的统计：废旧电池数/节45678人数/人9111154请根据学生收集到的废旧电池数，判断下列说法正确的是（）A．样本为40名学生B．众数是11节C．中位数是6节D．平均数是5.6节（2021·湖北随州市·中考真题）20．如图是小明某一天测得的7次体温情况的折线统计图，下列信息不正确的是（）A．测得的最高体温为37.1℃B．前3次测得的体温在下降C．这组数据的众数是36.8D．这组数据的中位数是36.6参考答案：1．A【分析】根据普查得到的调查结果比较准确，但所费人力、物力和时间较多，而抽样调查得到的调查结果比较近似解答即可．【详解】A.检测长征运载火箭的零部件质量情况,必须全面调查才能得到准确数据；B.了解全国中小学生课外阅读情况，量比较大，用抽样调查；C.调查某批次汽车的抗撞击能力，具有破坏性，用抽样调查；D.检测某城市的空气质量，不可能全面调查，用抽样调查.【点睛】本题考查的是抽样调查和全面调查的区别，选择普查还是抽样调查要根据所要考查的对象的特征灵活选用，一般来说，对于具有破坏性的调查、无法进行普查、普查的意义或价值不大，应选择抽样调查，对于精确度要求高的调查，事关重大的调查往往选用普查．2．B【分析】根据总体、个体、样本、样本容量的知识解答．总体是指所要考查对象的全体；个体是指每一个考查对象；样本是指从总体中抽取的部分考查对象称为样本；样本容量是指样本所含个体的个数(不含单位)．【详解】解：A、总体是该校4000名学生的体重，此选项正确，不符合题意；B、个体是每一个学生的体重，此选项错误，符合题意；C、样本是抽取的400名学生的体重，此选项正确，不符合题意；D、样本容量是400，此选项正确，不符合题意；故选：B．【点睛】本题主要考查了总体、个体、样本、样本容量的定义，解题要分清具体问题中的总体、个体与样本，关键是明确考查的对象．总体、个体和样本的考查对象是相同的，所不同的是范围的大小．样本容量是样本中包含的个体的数量，不能带单位．3．26【分析】将7天的最高气温按从小到大排列以后根据中位数的定义求解即可．【详解】解：根据7天的最高气温折线统计图，将这7天的最高气温按从小到大排列为：20，22，24，26，28，28，30，故中位数为26℃．故答案为：26．【点睛】本题主要考查中位数的定义，将一组数据按照从小到大(或从大到小)的顺序排列，如果这组数据的个数是奇数，则处于中间位置的数就是这组数据的中位数；如果这组数据的个数是偶数，则中间两个数据的平均数就是这组数据的中位数．4．A【分析】根据平均数的计算公式和中位数的定义分别进行解答即可．【详解】解：这组数据的平均数是：（21+23+25+25+26）÷5=24；把这组数据从小到大排列为：21，23，25，25，26，最中间的数是25，则中位数是25；故应选：A．【点睛】此题考查了平均数和中位数，掌握平均数的计算公式和中位数的定义是本题的关键．5．A【分析】根据众数的定义进行判断即可．【详解】在这组数据中出现最多的数是10，∴众数为10，故选：A．【点睛】本题考查了众数的定义，掌握知识点是解题关键．6．B【分析】按照平均数和中位数的计算方法进行计算即可．【详解】平均数为：788660108112116+90+120+54+116=9410+++++将数据按照从小到大进行排列为：54，60，78，86，90，108，112，116，116，120中位数为：90+108=99 2故选：B．【点睛】本题考查了平均数，中位数的计算，熟知以上计算方法是解题的关键．7．C【分析】根据众数和中位数的定义可得答案．【详解】解：捐款金额学生数最多的是10元，故众数为10；共50名学生，中位数在第25名、26名学生处，故中位数为10+102=10；故选：C．【点睛】本题考查了众数及中位数的知识，解答本题的关键是熟练掌握众数及中位数的定义．8．A【分析】根据众数与中位数的定义可以直接得到答案．【详解】解：因为全班抽取了61188740++++=人，所以一共有40个数据，且表中数据已是从小到大排列的，最中间两个数据分别为8，8，所以这一组数据的中位数是888 2+=，这一组数据中出现次数最多的是7，所以众数是7．故选A．【点睛】本题考查的是中位数与众数的概念，掌握这两个概念是解题的关键．9．丙【分析】根据方差表示数据的波动大小的量即可解答．【详解】解：∵平均成绩都是87.9分，s甲2＝3.83，s乙2＝2.71，s丙2＝1.52，∴s丙2＜s乙2＜s甲2，∴选手丙的成绩更稳定，即适合参加比赛的选手是丙．故答案为：丙．【点睛】本题考查了方差的意义，理解方差是表示数据波动大小的量是解答本题的关键．10．甲【分析】先分别求出甲乙的平均数，再求出甲乙的方差，由方差越小成绩越稳定做出判断即可．【详解】解：x甲=（7+6+9+6+7）÷5=7（环），x乙=（5+9+6+7+8）÷5=7（环），2s甲=[（7﹣7）2+（6﹣7）2+（9﹣7）2+（6﹣7）2+（7﹣7）2]÷5=1.2，2s乙=[（5﹣7）2+（9﹣7）2+（6﹣7）2+（7﹣7）2+（8﹣7）2]÷5=2，∵1.2＜2，∴甲的成绩较为稳定，故答案为：甲．【点睛】本题考查平均数、方差、折线统计图，会求一组数据的平均数、方差，会根据方差判断一组数据的稳定性是解答的关键．11．乙【分析】通过平均数和方差的性质判断稳定性即可．【详解】∵x 甲7.5≈，x 乙7.5≈，∴x 甲=x 乙，∴甲，乙的每公顷产量相同，∵2s 甲0.010≈，2s 乙0.002≈，∴2s 甲>2s 乙，∴乙的产量比甲的产量稳定，故答案为：乙．【点睛】本题考查了方差和平均数，掌握方差和平均数的意义是解题关键．12．甲【分析】根据方差的定义，方差越小数据越稳定．【详解】解：∵甲的方差是20.70s =甲，乙的方差是20.73s =乙，0.73＞0.70，∴甲比乙的成绩稳定.∴甲、乙两位同学成绩较稳定的是甲同学.故答案是：甲．【点睛】本题考查方差的意义．方差是用来衡量一组数据波动大小的量，方差越大，表明这组数据偏离平均数越大，即波动越大，数据越不稳定；反之，方差越小，表明这组数据分布比较集中，各数据偏离平均数越小，即波动越小，数据越稳定．13．8.0【分析】根据一组数据中的每一个数据都加上同一个非零常数，那么这组数据的波动情况不变，即方差不变，即可得出答案．【详解】∵一组数据中的每一个数据都加上（或都减去）同一个常数后，它的平均数都加上（或都减去）这一个常数，方差不变，∴所得到的一组新数据的方差为S 新2=8.0；故答案为：8.0．【点睛】本题考查方差的意义，它反映了一组数据的波动大小，方差越大，波动性越大，反之也成立，关键是掌握一组数据都加上同一个非零常数，方差不变．14．A【分析】设袋子中红球有x 个，根据摸出红球的频率稳定在0.25左右列出关于x 的方程，求出x 的值即可得答案．【详解】解：设袋子中红球有x 个，根据题意，得：0.25,20x =解得5,x =答：袋子中红球有5个．故选：A ．【点睛】本题主要考查利用频率估计概率，大量重复实验时，事件发生的频率在某个固定位置左右摆动，并且摆动的幅度越来越小，根据这个频率稳定性定理，可以用频率的集中趋势来估计概率，这个固定的近似值就是这个事件的概率．15．270【分析】利用样本中的优秀率来估计整体中的优秀率，从而得出总体中的中长跑成绩优秀的学生人数．【详解】解：由图知：样本中优秀学生的比例为：2727%100=，∴该校中长跑成绩优秀的学生人数是：100027%270⨯=（人）故答案是：270．【点睛】本题考查了利用样本估计总体的统计思想，解题的关键是：根据图中信息求出样本中优秀率作为总体中的优秀率，即可求出总体中优秀的人数．16．（1）2；（2）7500【分析】（1）将200个数据按大小顺序排列最中间两个数的平均数即为中位数，进而可解决问题；（2）求出用电量低于178kW h ⋅的户数的百分比，根据总户数求出答案．.【详解】解：（1）将200个数据按大小顺序排列最中间两个数即第100和101个数，它们的平均数即为中位数，这两个数都落在第2组，故答案为：2；（2）50100100007500200+⨯=（户）因此，估计该地1万户居民六月的用电量低于178kW h ⋅的大约有7500户.【点睛】本题考查频数分布表，利用统计表获取信息的能力，以及利用样本估计总体，利用统计表获取信息时，必须认真观察、分析、研究统计表，才能作出正确的判断和解决问题．17．C【分析】根据大学生的人数与所占的百分比求出总人数为300人，再用初中生所占的百分比乘以总人数即可得到答案．【详解】解：总人数=6020%÷=300（人）；30040%⨯=120（人），故选：C ．【点睛】本题主要考查了根据扇形统计图求总人数和单项的人数，关键在于公式的灵活运用．18．C【分析】根据扇形统计图分别求出各组人数以及圆心角度数，进而得出答案．【详解】A 、一线城市购买新能源汽车的用户达46%，用户最多，符合题意；B 、二线城市购买新能源汽车用户达37%，说法正确，符合题意；C 、三四线城市购买新能源汽车用户达11%，不能说用户达到11万，不符合题意；D 、四线城市以下购买新能源汽车用户只占6%，最少，说法正确，符合题意；故选：C ．【点睛】本题考查了扇形统计图，试题以图表为载体，要求学生能从中提取信息来解题，与实际生活息息相关．19．D【分析】根据样本定义可判定A ，利用众数定义可判定B ，利用中位数定义可判定C ，利用加权平均数计算可判定D 即可．【详解】解：A .随机抽取40名学生对收集废旧电池的数量是样本，故选项A 样本为40名学生不正确；B .根据众数定义重复出现次数最多的数据是5节或6节，故选项B 众数是11节不正确，C .根据中位数定义样本容量为40，中位数位于4020,212=两个位置数据的平均数，第20位、第21位两个数据为5节与6节的平均数65 5.52+=节，故选项C 中位数是6节不正确；D .根据样本平均数()1495116117584 5.640x =⨯+⨯+⨯+⨯+⨯=节故选项D 平均数是5.6节正确．故选择：D ．【点睛】本题考查样本，众数，中位数，平均数，熟练掌握样本，众数，中位数，平均数是解题关键．20．D【分析】根据折线图判断最高体温以及上升下降情况，根据众数、中位数的性质判断即可．【详解】解：A、由折线统计图可知，7次最高体温为37.1℃，A选项正确，不符合题意；B、由折线统计图可知，前3次体温在下降，B选项正确，不符合题意；C、由7组数据可知，众数为36.8，C选项正确，不符合题意；D、根据中位数定义可知，中位数为36.8，D选项错误，符合题意；故选：D．【点睛】本题主要考查折线统计图、众数以及中位数的定义，正确读懂统计图，正确理解众数、中位数定义是解题关键，注意必须从大到小或者从小到大排列后再求中位数．。
统计学典型例题(课堂PPT)
解：样本p=n1/n=80/400=20%
μp
p1 p
n
0.2 0.8 2% 400
32
3、某灯泡厂对10000个产品进行使用 寿命检验，随机抽取2%样本进行测试， 按规定，灯泡使用寿命在1000小时以上 者为合格品。测得样本数据如下：
灯泡平均使用时间 x=1057小时， 灯泡使用时间标准差为s=53.63小时，
质量指标指数
19
【分析】
工资总额E 职工人数 f 平均工资X
E1 X 0 f1 X1 f1 f1 X1 E 0 X 0 f0 X 0 f1 f0 X 0
E1 E0 X 0 f1 X 0 f0 X1 f1 X 0 f1 X 0 f1 f0 f1X1 X 0
644.3
107.38
121.39
79.1 88.5 96.4 95.7 107.3 115.4
582.4
97.07
109.73
64.0 293.7
73.425
68.7 324.0
81
68.5 346.0
86.5
69.9 347.5
86.875
78.4 388.5
97.125
90.3 423.3 105.825
4
②该企业第二季度的月平均劳动生产率：
ca 1000102.614.616.33 b 220002000 22002220041
690.746元人
③该企业第二季度的劳动生产率：
Ca 12.614.616.310000
b 200020020200220041
2
2
207.2184元人 Nc
5
•二、速度分析指标
8 255
统计学课后习题答案全章节剖析
第二章、练习题及解答2。
为了确定灯泡的使用寿命（小时），在一批灯泡中随机抽取100只进行测试,所得结果如下：700 716 728 719 685 709 691 684 705 718 706 715 712 722 691 708 690 692 707 701 708 729 694 681 695 685 706 661 735 665 668 710 693 697 674 658 698 666 696 698 706 692 691 747 699 682 698 700 710 722 694 690 736 689 696 651 673 749 708 727 688 689 683 685 702 741 698 713 676 702 701 671 718 707 683 717 733 712 683 692 693 697 664 681 721 720 677 679 695 691 713 699 725 726 704 729 703 696 717 688 要求：(2）以组距为10进行等距分组，生成频数分布表,并绘制直方图.灯泡的使用寿命频数分布表3。
某公司下属40个销售点2012年的商品销售收入数据如下：单位：万元152 124 129 116 100 103 92 95 127 104 105 119 114 115 87 103 118 142 135 125 117 108 105 110 107 137 120 136 117 108 97 88 123 115 119 138 112 146 113 126 要求：（1）根据上面的数据进行适当分组,编制频数分布表，绘制直方图。
（2）制作茎叶图,并与直方图进行比较。
解：（1）频数分布表(2）茎叶图第三章、练习题及解答1。
已知下表资料:试根据频数和频率资料，分别计算工人平均日产量. 解:计算表根据频数计算工人平均日产量:(件）根据频率计算工人平均日产量：（件）结论:对同一资料,采用频数和频率资料计算的变量值的平均数是一致的。
统计学例题讲解
第四章计算变异指标；比较平均指标的代表性。
例题：某车间有甲、乙两个生产组，甲组平均每个工人的日产量为36件，标准差为9.6件；乙组工人日产量资料如下：解:5.291002950133438151345343538251515==+++⨯+⨯+⨯+⨯=∑∑fxf x ＝乙()986.810080752==-∑∑ff x x ＝乙σ267.0366.9==x V σ＝甲3046.05.29986.8==x V σ＝乙甲组更有代表性。
乙甲∴<V V第十一章：计算相关系数、建立回归方程并解释回归系数的含义、预测因变量的估计值。
4．计算相关系数；建立直线回归方程并指出回归系数的含义；利用建立的方程预测因变量的估计值。
例题：（２）配合回归方程，指出产量每增加1000件时，单位成本 平均变动多少？（３）假定产量为6000件时，单位成本为多少元？n=6 ∑x =21 ∑y =426∑x2=79∑y2=30268 ∑xy=1481（1） 相关系数:2222)(1)(11∑∑∑∑∑∑∑-⋅-⋅-=y n y x nx y x nxy r =-0.9090说明产量x 和单位成本y 之间存在着高度负相关关系。
（2）设直线回归方程为y c =a+bx n=6 ∑x =21 ∑y =426∑x2=79∑y2=30268∑xy=148122)(11∑∑∑∑∑-⋅-=x n x y x n xy b = (1481-1/6*21*426)/(79-1/6*21*21)=-1.82x b y a -==426/6-(-1.82)*21/6=77.37 则y c =77.37-1.82x在这里说明回归系数b 的含义 ，即产量每增加1000件时， 单位成本平均降低1.82元 .（３）假定产量为6000件,即x=6时，单位成本为:则y c=77.37-1.82x =77.37-1.82*6=66.45(元) .即单位成本为: 66.45元.2．根据企业产品销售额(万元)和销售利润率(%)资料计算出如下数据:n=7 ∑x=1890 ∑y=31.1 ∑x2=535500 ∑y2=174.15 ∑xy=9318 要求: (1) 确定以利润率为因变量的直线回归方程.(2)解释式中回归系数的经济含义.(3)当销售额为500万元时,利润率为多少?参考答案:(1)确定以利润率为因变量的直线回归方程:Y=-5.5+0.037x(2)解释式中回归系数的经济含义:产品销售额每增加1万元,销售利润率平均增加0.037%.第十四章：数量指标综合指数、质量指标综合指数的计算；从相对数和绝对数角度对总量指标的变动进行因素分析。
统计知识点及例题讲解(学生版)
必修3 统计【知识点、题型、方法、易错点总结】知识点（一）：抽样方法1、简单随机抽样1、简单随机抽样的概念:注意：简单随机抽样必须具备下列特点：（1）简单随机抽样要求被抽取的样本的总体个数N是有限的。
（2）简单随机样本数n小于等于样本总体的个数N。
（3）简单随机样本是从总体中逐个抽取的。
（4）简单随机抽样是一种不放回的抽样。
（5）简单随机抽样的每个个体入样的可能性均为n/N。
思考：下列抽样的方式是否属于简单随机抽样？为什么？（1）从无限多个个体中抽取50个个体作为样本。
（2）箱子里共有100个零件，从中选出10个零件进行质量检验，在抽样操作中，从中任意取出一个零件进行质量检验后，再把它放回箱子。
2、抽签法和随机数法（1）、抽签法的定义抽签法的一般步骤：a、将总体的个体编号。
b、连续抽签获取样本号码。
思考：你认为抽签法有什么优点和缺点：当总体中的个体数很多时，用抽签法方便吗？（2）随机数表法：利用随机数表、随机数骰子或计算机产生的随机数进行抽样，叫随机数表法.例1：人们打桥牌时，将洗好的扑克牌随机确定一张为起始牌，这时按次序搬牌时，对任何一家来说，都是从52张牌中抽取13张牌，问这种抽样方法是否是简单随机抽样？例2：某车间工人加工一种轴100件，为了了解这种轴的直径，要从中抽取10件轴在同一条件下测量，如何采用简单随机抽样的方法抽取样本？2、系统抽样1、系统抽样的定义：注意：系统抽样的特证：（1）当总体容量N较大时，采用系统抽样。
（2）将总体分成均衡的若干部分指的是将总体分段，分段的间隔要求相等，因此，N系统抽样又称等距抽样，这时间隔一般为k＝[].n（3）预先制定的规则指的是：在第1段内采用简单随机抽样确定一个起始编号，在此编号的基础上加上分段间隔的整倍数即为抽样编号。
2、系统抽样的一般步骤。
（1）采用随机抽样的方法将总体中的N个个编号。
（2）将整体按编号进行分段，确定分段间隔k(k∈N,L≤k).（3）在第一段用简单随机抽样确定起始个体的编号L（L∈N,L≤k）。
标准正态分布例题解析
标准正态分布例题解析标准正态分布是指均值为0，标准差为1的正态分布。
它在统计学中有着广泛的应用。
下面我们来看一些标准正态分布的例题。
例题1：某公司的员工身高服从正态分布，均值为170cm，标准差为5cm。
现在有一位员工，身高为180cm，问他的身高在该公司员工身高分布中的位置排名是多少？解答：首先，要将员工身高转化为标准正态分布，即计算它与均值之间的标准差差异。
公式为：z = (x -μ) / σ其中，x为员工身高，μ为均值，σ为标准差。
将x = 180，μ= 170，σ= 5代入公式中，得到：z = (180 - 170) / 5 = 2然后，我们需要查表或使用计算器等工具，得出z = 2时的累积概率。
查表可知，z = 2时的累积概率为0.9772。
因此，该员工的身高在该公司员工身高分布中的位置排名为97.72%。
例题2：某班级考试成绩服从正态分布，均值为80分，标准差为10分。
如果班级的平均分为85分，问该班级的成绩排名在多少？解答：同样地，需要将班级的平均分转化为标准正态分布。
公式为：z = (x -μ) / (σ/ √n)其中，x为班级平均分，μ为均值，σ为标准差，n为样本量（即班级人数）。
将x = 85，μ= 80，σ= 10，n = 30代入公式中，得到：z = (85 - 80) / (10 / √30) ≈2.04再次查表或使用计算器，得出z = 2.04时的累积概率为0.9808。
因此，该班级的成绩排名在98.08%左右。
总结：标准正态分布在统计学中应用广泛，掌握计算标准正态分布的方法和查表技巧十分重要。
需要注意的是，计算时要注意单位的一致性，并注意查表时使用的是双侧概率表还是单侧概率表。
统计学原理例题分析一
统计学原理例题分析（一）一、判断题（把“√”或“×”填在题后的括号里）１. 社会经济统计的研究对象是社会经济现象总体的各个方面。
（）参考答案：×2. 总体单位是标志的承担者，标志是依附于单位的。
（）参考答案：√3. 标志通常分为品质标志和数量标志两种。
（）参考答案：√4. 当对品质标志的标志表现所对应的单位进行总计时就形成统计指标。
（）参考答案：√5. 调查方案的首要问题是确定调查对象。
（）参考答案：√6. 我国目前基本的统计调查方法是统计报表、抽样调查和普查。
（）参考答案：√7. 调查单位和填报单位在任何情况下都不可能一致。
（）参考答案：×8. 按数量标志分组，各组的变量值能准确的反映社会经济现象性质上的差别。
（）参考答案：×9. 在确定组限时，最大组的上限应低于最大变量值。
（）参考答案：×10. 按数量标志分组的目的，就是要区别各组在数量上的差别。
（）参考答案：×11. 离散型变量可以作单项式分组或组距式分组，而连续型变量只能作组距式分组。
（）参考答案：√12. 对于任何两个性质相同的变量数列，比较其平均数的代表性，都可以采用标准差指标。
（）参考答案：×13. 样本成数是指在样本中具有被研究标志表现的单位数占全部样本单位数的比重。
（）参考答案：√14. 样本容量指从一个总体中可能抽取的样本个数。
（）参考答案：×15. 在抽样推断中，作为推断对象的总体和作为观察对象的样本都是确定、唯一的。
（）参考答案：×16. 产量增加，则单位产品成本降低，这种现象属于函数关系。
（）参考答案：×17. 在直线回归方程Ｙ＝a ＋ｂｘ中，ｂ值可以是正的，也可以是负的。
（）参考答案：√18. 回归系数ｂ和相关系数γ都可用来判断现象之间相关的密切程度。
（）参考答案：×19. 平均指标指数是综合指数的一种变形。
统计学原理例题分析
=77（分〉统计学原理例题分析（三）1.某班40名学生某课程成绩分别为:68 89 88 84 86 87 75 73 72 68 75 82 97 58 81 54 79 76 95 76 71 60 90 65 76 72 76 85 89 9264 57 83 81 78 77 72 61 70 81按学校规定：60分以下为不及格.60-70分为及格,70-80分为中,80-90分为良,90-100分为优。
要求：（1）将学生的考核成绩分组并编制一张考核成绩次数分配表：（2） 指出分组标志及类型及釆用的分组方法： （3） 计算本班学生的考核平均成绩并分析本班学生考核情况。
解（1）-_ZV_3080.X = -------- = ----------Zf 40答题分析：先计算出组距式分组数列的组中值。
本题掌握各组平均成绩和对应的学生数资料（频数人 掌握被平均标志值X 及频数、频率、用加权平均数计算。
（4）本班学生的考核成绩的分布呈两头小，中间大的”正态分布”的形态，平均成绩为77分，说明大多 数宁生对木课程知识的掌握达到了课程*习的要求。
根据资料计算三种规格商品的平均销售价格。
参考答案：比重（%）= O#y = 36（元）答题分析：第一，此题给出销售单价和销售虽资料，即给出了计算平均指标的分母资料，所以需釆用 算术平均数计算平均价格。
第二，所给资料是组距数列，因此需计算出组中值。
采用加权算术平均数计算 平均价格。
第三，此题所给的是比重权数，因此需采用以比重形式表示的加权算术平均数公式计算。
3.试比较哪个企业的工人平均口产虽更具代表性? 参考答案："甲=-2^- = — = 17.6% v z = -2^- = "3= 12.6%x 甲 17 ' x 乙 26.1可见，乙企业的平均日产呈更具有代表性。
答题分析:这显然是两组水平不同的现象总体，不能直接用标准差的大小分析平均水平的代表性，必须 计算标准着系数。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
统计学例题讲解
Document serial number【KKGB-LBS98YT-BS8CB-BSUT-BST108】
第四章计算变异指标；比较平均指标的代表性。
例题：某车间有甲、乙两个生产组，甲组平均每个工人的日产量为36件，标准差为件；乙组工人日产量资料如下：
要求：⑴计算乙组平均每个工人的日产量和标准差；
⑵比较甲、乙两生产小组哪个组的日产量更有代表性
解:
第十一章：计算相关系数、建立回归方程并解释回归系数的含义、预测因变量的估计
值。
4．计算相关系数；建立直线回归方程并指出回归系数的含义；利用建立的方程预测因变量的估计值。
例题：
要求：
（２）配合回归方程，指出产量每增加1000件时，单位成本
平均变动多少
（３）假定产量为6000件时，单位成本为多少元
∑x2=79
n=6 ∑x=21 ∑y=426
∑y2=30268 ∑xy=1481
（1） 相关系数:
2
222
)(1
)(1
1
∑∑
∑∑∑∑∑-⋅-⋅-
=
y n y x n
x y x n
xy
r =
说明产量x 和单位成本y 之间存在着高度负相关关系。
（2）设直线回归方程为y c =a+bx n=6 ∑x =21 ∑y =426 ∑x 2
=79
∑
y 2
=30268 ∑xy =1481
= (1481-1/6*21*426)/(79-1/6*21*21)=
x b y a -==426/6-*21/6= 则y c =
在这里说明回归系数b 的含义 ，即产量每增加1000件时， 单位成本平均降低元 .
（３）假定产量为6000件,即x=6时，单位成本为:
则y c = =元) .
即单位成本为: 元.
2．根据企业产品销售额(万元)和销售利润率(%)资料计算出如下数据:
n=7 ∑x =1890 ∑y = ∑x 2=535500 ∑y 2= ∑xy =9318
要求: (1) 确定以利润率为因变量的直线回归方程. (2)解释式中回归系数的经济含义.
(3)当销售额为500万元时,利润率为多少 参考答案:
(1) 确定以利润率为因变量的直线回归方程:
Y=+
(2)解释式中回归系数的经济含义:
产品销售额每增加1万元,销售利润率平均增加%.
第十四章：数量指标综合指数、质量指标综合指数的计算；
从相对数和绝对数角度对总量指标的变动进行因素分析。
5．计算综合指数及平均指数（加权、调和）并同时指出变动绝对值、计算平均数指数。
例题1
（1）计算两种产品总成本指数及总成本变动的绝对额；
（2）计算两种产品产量总指数及由于产量变动影响总成本的绝对额；
（3）计算两种产品单位成本总指数及由于单位成本影响总成本的绝对额。
总成本变动绝对额：
640220028400
1
1
=-=-∑∑q
p q p (元)
（2）计算两种产品产量总指数及由于产量变动影响总成本的绝对额；
产量总指数:
由于产量变动而增加的总成本：
（3）计算两种产品单位成本总指数及由于单位成本影响总成本的绝对额。
单位成本总指数:
由于单位成本而增加的总成本：
总结：以上计算可见：
通过指数体系分析如下：
总成本指数＝产量总指数 ＊ 单位成本总指数
% ＝%＊%
总成本变动绝对额＝产量变动绝对额＋单位成本变动绝对额
640=200+440
可见，两种产品的总成本增加了%, 增加了640元；其中由于产量增加了%, 而使总成本增加了200元，由于单位成本增加了%,而使总成本增加了440元。
类似例题讲解：
（1）计算三种产品单位成本总指数及由于单位成本影响总成本的绝对额。
（2）计算三种产品产量总指数及由于产量变动影响总成本的绝对额；
（3）计算三种产品总成本指数及总成本变动的绝对额； 解答：（1）三种产品的单位成本总指数：
由于单位成本而增加的总成本： （2）三种产品的产量总指数：
由于产量变动而增加的总成本： （3）指数体系分析如下：
总成本指数＝产量总指数＊单位成本总指数
总成本变动绝对额＝产量变动绝对额＋单位成本变动绝对额
可见，三种产品的总成本增加了%, 增加了4750元；其中由于产量 增加了%, 而使总成本增加了750元，由于单位成本增加了%, 而使总成本增加了4000元。
试计算：
⑴销售额指数及销售额增加绝对值。
⑵销售量指数及由销售量变动而增加的销售额。
(3)计算商品销售价格总指数和由于价格变动对销售额的影响绝对额。
解答：（1）销售额指数＝
%156750
1170
11==
∑∑p
q p q ∑∑=-=-420750117000
1
1
p q
p q （万元）
（2）销售量总指数＝%
93.110750/832750
%
115*400%105*200%108*1500
==++=
∑∑q
p q
Kp 由于销售量增长％，使销售额增加：
∑
∑=-=-82
7508320
00
0q
p q Kp （万元）
第十三章：计算各期环比、定基发展速度、增长速度、年平均增长量、
平均发展速度、平均增长速度；
（2）计算1995年-1999年该地区粮食产量的年平均增长量和粮食产量的年平均发展速度； 解答：
（1）计算各年的逐期增长量、累积增长量、环比发展速度、定基发展速度；
（2）
产量的年平均发展速度；
粮食产量的年平均增长量=（700－300）÷4=100(万斤)
粮食产量的年平均增长速度=
1
24
.1
1
300
700
14-
=
-
=
-
n
n
a
a
=24%。