课课练九年级数学下册用三种方式表示二次函数测试题

合集下载

九年级数学二次函数练习题

九年级数学二次函数练习题二次函数是九年级数学中一个重要的内容，掌握好二次函数的基本概念和解题方法对于学生的数学学习至关重要。

为了帮助九年级的同学更好地理解和掌握二次函数的相关知识，下面将给出一些二次函数的练习题及解答，供同学们进行练习和巩固。

题目1：求下列二次函数的对称轴、顶点和求值范围。

（1）f(x) = x^2 + 4x +5（2）g(x) = -2x^2 - 6x + 3解答1：（1）对称轴：二次函数的对称轴可以通过以下公式计算出来：x = -b/ (2a)代入函数f(x) = x^2 + 4x +5中，得到x = -4 / (2*1) = -2所以，函数f(x)的对称轴为x = -2。

顶点：对于二次函数f(x) = ax^2 + bx + c，其顶点坐标可以通过以下公式计算得出：(x, y) = (-b/(2a), f(-b/(2a)))代入函数f(x) = x^2 + 4x +5中，得到(x, y) = (-(-4)/(2*1), f(-(-4)/(2*1))) = (2, 1)所以，函数f(x)的顶点为(2, 1)。

求值范围：对于二次函数f(x) = ax^2 + bx + c，当a>0时，函数的值域为[f(x0)，+∞)，其中，f(x0)是函数的最小值。

由于a>0，可以得出函数的最小值对应的点为顶点，即此题中的顶点(2, 1)。

所以，函数f(x)的求值范围为[1, +∞)。

（2）对称轴：代入函数g(x) = -2x^2 - 6x + 3中的公式，得到x = -(-6) / (2*(-2)) = -6 / 4 = -1.5所以，函数g(x)的对称轴为x = -1.5。

顶点：代入函数g(x) = -2x^2 - 6x + 3中的公式，得到(x, y) = (-(-6) / (2*(-2)), g(-(-6) / (2*(-2))))= (-6 / 4, g(3/4))= (-1.5, -3)所以，函数g(x)的顶点为(-1.5, -3)。

二次函数测试题及答案

二次函数测试题及答案一、选择题1. 下列哪个选项是二次函数的一般形式？A. y = x + 2B. y = x^2 + 3x + 1C. y = 2x^3D. y = 1/x答案：B2. 二次函数y = ax^2 + bx + c（a ≠ 0）的顶点坐标是：A. (-b, a)B. (-b/a, c)C. (-b/2a, 4ac - b^2/4a)D. (-b/2a, 4ac + b^2/4a)答案：C3. 如果二次函数y = ax^2 + bx + c的图像与x轴有两个交点，那么a、b、c之间的关系是：A. b^2 - 4ac > 0B. b^2 - 4ac < 0C. b^2 - 4ac = 0D. b^2 - 4ac ≠ 0答案：A二、填空题4. 二次函数y = -3x^2 + 6x - 5的顶点坐标是______。

答案：(1, -2)5. 如果二次函数y = ax^2 + bx + c的图像开口向上，那么a的值是______。

答案：> 0三、解答题6. 已知二次函数y = 2x^2 - 4x + 3，求其图像与x轴的交点。

解：令y = 0，得到方程2x^2 - 4x + 3 = 0。

通过求解这个方程，我们可以得到x的值。

首先计算判别式Δ = b^2 - 4ac = (-4)^2 - 4 * 2 * 3 = 16 - 24 = -8。

因为Δ < 0，所以这个二次方程没有实数解，即二次函数的图像与x轴没有交点。

7. 已知二次函数y = 3x^2 + 6x - 5，求其图像的对称轴。

解：二次函数y = ax^2 + bx + c的对称轴是x = -b/(2a)。

将a= 3, b = 6代入公式，得到对称轴为x = -6 / (2 * 3) = -1。

四、应用题8. 某工厂生产一种产品，其成本函数为C(x) = 0.5x^2 - 100x + 1000，其中x表示产品的数量。

(必考题)初中数学九年级数学下册第二单元《二次函数》检测卷(包含答案解析)

一、选择题1．如图，抛物线y ＝ax 2+bx +c 的顶点坐标为（1，﹣4a ），点A （4，y 1）是该抛物线上一点，若点B （x 2，y 2）是该抛物线上任意一点，有下列结论：①4a ﹣2b +c ＞0；②抛物线y ＝ax 2+bx +c 与x 轴交于点（﹣1，0），（3，0）；③若y 2＞y 1，则x 2＞4；④若0≤x 2≤4，则﹣3a ≤y 2≤5a ．其中，正确结论的个数是（）A ．0B ．1C ．2D ．32．二次函数2y ax bx c =++的图象如图所示，则函数值y 0>时，x 的取值范围是（）A ．x 2<-B ．x 5>C ．2x 5-<<D ．x 2<-或x 5>3．已知二次函数()222y mx m x =+-，它的图象可能是（）A ．B ．C ．D ．4．已知二次函数()()12y a x x x x =--与x 轴的交点是（1，0）和（3，0），关于x 的方程()()12a x x x x m --=（其中0m >）的两个解分别是1-和5，关于x 的方程()()12a x x x x n --=（其中0n m <<）也有两个整数解，这两个整数解分别是（）A ．1和4B ．2和5C ．0和4D ．0和55．已知二次函数2(0)y ax bx c a =++≠的图象如图所示，在下列六个结论中：①20a b -<；②0abc <；③0a b c ++<；④0a b c -+>；⑤420a b c ++>；⑥240b ac -<．其中正确的个数有（）A ．1个B ．2个C ．3个D ．4个6．如图，二次函数()20y ax bx c a =++≠图象的顶点为D ，其图像与x 轴的交点A 、B 的横坐标分别为-1，3，与y 轴负半轴交于点C ．在下面四个结论中：①0a b c ++<； ②13a c =-；③只有当12a =时，ABD △是等腰直角三角形； ④使ACB △为等腰三角形的a 值可以有两个．其中正确的结论有A ．1个B ．2个C ．3个D ．4个7．将二次函数y ＝2x +6x+2化成y ＝2-x h （）+k 的形式应为（） A ．y ＝23x +（）﹣7 B ．y ＝23x -（）+11 C ．y ＝23x +（）﹣11 D ．y ＝22x +（）+4 8．二次函数223y x =-+在14x -≤≤内的最小值是（） A ．3B ．2C ．－29D ．－309．如图，抛物线y ＝ax 2+bx +c （a ≠0）的对称轴为直线x ＝1，与x 轴的一个交点坐标为（﹣1，0），其部分图象如图所示，下列结论：①a ＞0；②b ＞0； ③方程ax 2+bx +c ＝0的两个根是x 1＝﹣1，x 2＝3；④当y ＞0时，x 的取值范围是﹣1＜x ＜3；其中结论正确的个数是（）A ．4个B ．3个C ．2个D ．1个10．已知二次函数24y x x m =-+的图象与x 轴有两个交点，若其中一个交点的横坐标为1，则另一个交点的横坐标为（） A ．1- B ．2-C ．2D ．311．如图，抛物线2y ax bx c =++的对称轴是直线1x =-，下列结论：①0abc >；②240b ac -≥；③80a c +<；④5320a b c -+<，正确的有（）A ．1个B ．2个C ．3个D ．4个12．在平面直角坐标系中，下列二次函数的图象开口向上的是（）A ．22y x =B ．221y x x =-++C ．22y x x =-+D ．20.5y x x =-+二、填空题13．如图，直线334y x =-+与x 轴交于点C ，与y 轴交于点B ，抛物线233384y x x =-++经过B ，C 两点，点E 是直线BC 上方抛物线上的一动点，过点E 作y 轴的平行线交直线BC 于点M ，则EM 的最大值为_____．14．函数y ＝ax 2+bx +c （a ≠0）图像如图所示，过点（﹣1，0），对称轴为x ＝2，下列结论正确的是_____． ①4a +b ＝0； ②24a +2b +3c <0；③若A （﹣3，y 1），B （﹣0.5，y 2），C （3.5，y 3）三点都在抛物线上，y 1<y 2<y 3； ④当y 1>﹣1时，y 随x 增大而增大．15．如图，二次函数2y ax bx c =++与反比例函数ky x=的图象相交于点()()()1231,1,3,A y B y C y -、、三个点，则不等式2k ax bx c x++>的解是____．16．已知抛物线22y x x n =-+与x 轴只有一个公共点，则n =__________． 17．如图，抛物线2y ax bx c =++的对称轴是x ＝1，下列结论：①abc ＞0；②240b ac ->；③8a+c ＜0；④5a+b+2c ＞0，正确的有___（填序号）．18．已知抛物线22(0)y ax bx a =+-≠的顶点在第三象限，且过点(1,0)，若-a b 的值为整数，则b 的值为___________．19．已知抛物线2(0)y ax bx c a =++>经过(2,0)A ，(4,0)B 两点．若()15,P y ，()2,Q m y 是抛物线上的两点，且12y y >，则m 的取值范围是______．20．已知二次函数2y ax bx c =++（a 、b 、c 是常数，且0a ≠），函数值y 与自变量x 的部分对应值如下表： x… 1-0 1 2 3 4 … y …101y2125…当1时，自变量的取值范围是______．三、解答题21．已知抛物线2y x bx c =++经过(3,),(2,)A n B n -两点．（1）求b 的值；（2）当11x -<<时，抛物线与x 轴有且只有一个公共点，求c 的取值范围；（3）若方程20x bx c ++=的两实根12,x x 满足2139x x -<，且22123p x x =-，求p 的最大值．22．已知二次函数22y x x m =++的图象与x 轴有且只有一个公共点．（1）求该二次函数的图象的顶点坐标；（2）若()1,P n y ，()22,Q n y +是该二次函数的图象上的两点，且12yy >，求实数n 的取值范围．23．已知二次函数223(0)y mx mx m m =-->的图像与x 轴交于A ，B 两点（点A 在点B 左侧），顶点为C ．（1）求A，B两点的坐标；BC AC，若ABC为等边三角形，求m的值．（2）连接,24．在二次函数y＝ax2＋bx＋c（a≠0）中，函数y与自变量x的部分对应值如表：x…01234…y…30﹣10m…m的值；并利用所给的坐标网格，画出该函数图象；（2）将这个二次函数向左平移2个单位，再向上平移1个单位，求平移后的函数解析式．25．网络销售已经成为一种热门的销售方式．某公司在某网络平台上进行直播销售防疫包，已知防疫包的成本价格为6元/个，每日销售量y（单位：个）与销售单价x（单位：元/个）满足一次函数关系，如表记录的是有关数据，经销售发现，销售单价不低于成本价且不高于30元，设公司销售防疫包的日获利为w（元）．（日获利＝日销售额﹣成本）x（元/个）789y（个）430042004100x之间的函数关系式；（2）当销售单价定为多少时，销售这种防疫包的日获利w最大？最大利润为多少元？0,2．试寻找一些点，使他们满足“到点26．如图，在平面直角坐标系中，点A的坐标是()A与到x轴的距离相等”．小明在探究过程中首先想到了OA 的中点M 满足条件，点M 到点A 和x 轴的距离都是1．接着，小明过x 轴上一点()4,0B 作x 轴的垂线l ．他认为在l 上应该有一个点N 到点A 与到x 轴的距离相等．（1）请你用尺规作图找出点N （不写画法，保留作图痕迹）并求出点N 的坐标；（2）小明用同样的方法又找出了一些符合条件的点，并把这些点用平滑的曲线连接起来他发现这些点在一条对称轴为y 轴的抛物线上．请你根据以上探究和发现，求出这条抛物线的解析式；（3）请直接写出平面内到点A 和直线2y =-距离相等的点所在抛物线的解析式．【参考答案】***试卷处理标记，请不要删除一、选择题 1．C 解析：C 【分析】利用对称轴公式和顶点坐标得出﹣4a ＝a +b +c ，b ＝﹣2a ，c ＝﹣3a ，则可对①进行判断；抛物线解析式为y ＝ax 2﹣2ax ﹣3a ，配成交点式得y ＝a （x ﹣3）（x +1），可对②进行判断；根据二次函数对称性和二次函数的性质可对③进行判断；计算x ＝4时，y ＝5a ，则根据二次函数的性质可对④进行判断．【详解】解：①∵二次函数y ＝ax 2+bx +c （a ≠0）的顶点坐标为（1，﹣4a ），∴x ＝﹣2ba＝1，且﹣4a ＝a +b +c ， ∴b ＝﹣2a ，c ＝﹣3a ，∵抛物线开口向上，则a ＞0，∴4a ﹣2b +c ＝4a +4a ﹣3a ＝5a ＞0，故结论①正确； ②∵b ＝﹣2a ，c ＝﹣3a ，∴y ＝ax 2﹣2ax ﹣3a ＝a （x ﹣3）（x +1），∴抛物线y ＝ax 2+bx +c 与x 轴交于点（﹣1，0），（3，0），故结论②正确； ③∵点A （4，y 1）关于直线x ＝1的对称点为（﹣2，y 1）， ∴当y 2＞y 1，则x 2＞4或x 2＜﹣2，故结论③错误； ④当x ＝4时，y 1＝16a +4b +c ＝16a ﹣8a ﹣3c ＝5a ， ∴当0≤x 2≤4，则﹣4a ≤y 2≤5a ，故结论④错误．故选：C ．【点睛】本题考查了二次函数的图象与性质，掌握二次函数图象与性质的相关知识并能灵活运用所学知识求解是解题的关键．2．C解析：C 【分析】根据函数图象求出与x 轴的交点坐标，再由图象得出答案．【详解】解：有函数图象观察可知，当25x -<<时，函数值0y >．故选：C ．【点睛】本题考查二次函数与不等式．掌握数形结合思想是解题关键．3．B解析：B 【分析】分m ＞0，m ＜0两种情形，判断对称轴与x=14的位置关系即可. 【详解】∵()222y mx m x =+-，∴抛物线一定经过原点， ∴选项A 排除；∵()222y mx m x =+- ，∴对称轴为直线x=22224m m m m---=⨯，∵24m m --14=24m m m --=24m-，当m ＞0时，抛物线开口向上，24m-＜0， ∴对称轴在直线x=14的左边， B 选项的图像符合；C 选项的图像不符合；当m ＜0时，抛物线开口向下，24m-＞0， ∴对称轴在直线x=14的右边， D 选项的图像不符合；故选B. 【点睛】本题考查了二次函数的图像，熟练掌握抛物线经过原点的条件，抛物线对称轴的位置与定直线的关系的判定是解题的关键.4．C解析：C 【分析】先根据二次函数y=a(x-x 1)(x-x 2)与x 轴的交点是(1，0)和(3，0)判断二次函数的对称轴方程，再根据关于x 的方程a(x-x 1)(x-x 2)=m(其中m>0)的两个解分别是-1和5判断开口方向，最后根据二次函数图象的性质即可得到答案；【详解】∵二次函数y=a(x-x 1)(x-x 2)与x 轴的交点是(1，0)和(3，0)， ∴得到二次函数的对称轴方程为：x=2，又∵关于x 的方程a(x-x 1)(x-x 2)=m(其中m>0)的两个解分别是-1和5， ∴二次函数y=a(x-x 1)(x-x 2)开口向上（远离对称轴的点纵坐标变大），又∵x 的方程a(x-x 1)(x-x 2)=n 也有两个整数解，根据0<n<m 得到解在-1和5之间， ∵解为正数且关于x=2对称，故选：C ．【点睛】本题主要考查了二次函数图象的性质，根据图象的性质求解二次函数的整数解，熟练掌握二次函数的图象的性质是解题的关键5．D解析：D 【分析】由抛物线的开口方向判断a 与0的关系，由抛物线与y 轴的交点判断c 与0的关系，利用图象判断1，-1，2所对应的y 的值，进而对所得结论进行判断．【详解】解：①∵由函数图象开口向下可知，a ＜0，由函数的对称轴12b a ->-，故12b a<， ∵a ＜0， ∴b ＞2a ，∴2a -b ＜0，①正确；②∵a ＜0，对称轴在y 轴左侧，a ，b 同号，图象与y 轴交于负半轴，则c ＜0，故abc ＜0；②正确；③当x=1时，y=a+b+c ＜0，③正确； ④当x=-1时，y=a -b+c ＜0，④错误； ⑤当x=2时，y=4a+2b+c ＜0，⑤错误； ⑥∵图象与x 轴无交点， ∴b 2-4ac ＜0，⑥正确；故正确的有①②③⑥，共4个．故选：D ．【点睛】此题主要考查了二次函数图象与系数的关系，熟练利用数形结合得出是解题关键．6．D解析：D 【分析】先根据图象与x 轴的交点A ，B 的横坐标分别为﹣1，3确定出AB 的长及对称轴，再由抛物线的开口方向判断a 与0的关系，由抛物线与y 轴的交点判断c 与0的关系，然后根据对称轴及抛物线与x 轴交点情况进行推理，进而对所得结论进行判断．【详解】解：①由抛物线的开口方向向上可推出a ＞0， ∵图像与x 轴的交点A 、B 的横坐标分别为-1，3， ∴对称轴x ＝1， ∴当x ＝1时，y ＜0， ∴a +b +c ＜0；故①正确；②∵点A 的坐标为（﹣1，0）， ∴a ﹣b +c ＝0，又∵b ＝﹣2a ， ∴a ﹣（﹣2a ）+c ＝0， ∴c ＝﹣3a ， ∴13a c =- ∴结论②正确．③如图1，连接AD ，BD ，作DE ⊥x 轴于点E ，，要使△ABD 是等腰直角三角形，则AD ＝BD ，∠ADB ＝90°，∵DE ⊥x 轴，∴点E 是AB 的中点，∴DE ＝BE ，即|244ac b a -|()312--==2，又∵b ＝﹣2a ，c ＝﹣3a ，∴|()()24324a a a a⨯---|＝2，a ＞0，解得a 12=， ∴只有当a 12=时，△ABD 是等腰直角三角形，结论③正确 ④要使△ACB 为等腰三角形，则AB ＝BC ＝4，AB ＝AC ＝4，或AC ＝BC ，Ⅰ、当AB ＝BC ＝4时，在Rt △OBC 中，∵OB ＝3，BC ＝4，∴OC 2＝BC 2﹣OB 2＝42﹣32＝16﹣9＝7，即c 2＝7，∵抛物线与y 轴负半轴交于点C ，∴c ＜0，c 7=-，∴a 73c =-=． Ⅱ、当AB ＝AC ＝4时，在Rt △OAC 中，∵OA ＝1，AC ＝4，∴OC 2＝AC 2﹣OA 2＝42﹣12＝16﹣1＝15，即c 2＝15，∵抛物线与y 轴负半轴交于点C ，∴c ＜0，c=，∴a 33c =-=． Ⅲ、当AC ＝BC 时，∵OC ⊥AB ，∴点O 是AB 的中点，∴AO ＝BO ，这与AO ＝1，BO ＝3矛盾，∴AC ＝BC 不成立．∴使△ACB 为等腰三角形的a ．结论④正确．故答案选：D【点睛】二次函数y ＝ax 2+bx +c 系数符号的确定：（1）a 由抛物线开口方向确定：开口方向向上，则a ＞0；否则a ＜0；（2）b 由对称轴和a 的符号确定：由对称轴公式x 2b a=-判断符，（3）c 由抛物线与y 轴的交点确定：交点在y 轴正半轴，则c ＞0；否则c ＜0；（4）b 2﹣4ac 由抛物线与x 轴交点的个数确定：①2个交点，b 2﹣4ac ＞0；②1个交点，b 2﹣4ac ＝0；③没有交点，b 2﹣4ac ＜0．7．A解析：A【分析】根据配方法的基本步骤，规范配方，后对照选项作出判断．【详解】∵y ＝2x +6x+2=2x +6x+226()32-+2=()23x +﹣7，故选A ．【点睛】本题考查了将一般形式的二次函数进行配方化成配方式，熟练掌握配方的基本步骤，规范配方是解题的关键． 8．C解析：C【分析】根据图象，直接代入计算即可解答【详解】解：由图可知，当x=4时，函数取得最小值y 最小值=-2×16+3=-29．故选：C ．【点睛】本题考查二次函数最小（大）值的求法．求二次函数的最大（小）值有三种方法，第一种可由图象直接得出，第二种是配方法，第三种是公式法．9．B解析：B【分析】根据抛物线与系数的关系判断即可．【详解】解：抛物线开口向下，a<0，故①错误；对称轴在y 轴右侧，a 、b 异号，b ＞0,故②正确；抛物线与x 轴交点为（﹣1，0），对称轴为直线x ＝1，根据对称性，另一个交点为（3,0），故③正确；根据图象可知，x 的取值范围是﹣1＜x ＜3时；抛物线在x 轴上方，故④正确；故选：B ．【点睛】本题考查二次函数图象与系数的关系，解题的关键是熟练正确理解二次函数图象与系数的关系，本题属于中等题型．10．D解析：D【分析】函数的对称轴为：x=-22b a，一个交点的坐标为（1，0），则另一个交点的坐标为（3，0），即可求解．【详解】解：∵二次函数y=x 2-4x+m 中a=1，b=-4，∴函数的对称轴为：x=-22b a=， ∵一个交点的坐标为（1，0）与另一个交点的坐标关于对称轴对称，∴另一个交点的坐标为（3，0），即另一个交点的横坐标为3．故选：D ．【点睛】本题考查的是抛物线与x 轴的交点，主要考查函数图象上点的坐标特征，要求学生非常熟悉函数与坐标轴的交点、顶点等点坐标的求法，及这些点代表的意义及函数特征． 11．B解析：B【分析】首先根据函数图像分别判断出a 、b 、c 的符号判断结论①；再利用与x 轴交点的个数得出24b ac -的正负判断结论②；利用对称轴以及当2x =时函数值的正负判断结论③；利用当1x =-和2x =-时的函数值的正负来判断结论④.【详解】结论①由抛物线开口方向向上可得0a >；对称轴在y 轴左侧可得a 、b 符号相同，即0b >；函数图像与y 轴交于负半轴，可得0c <；由此可知0abc <，故①错误. 结论②由函数图像与x 轴有两个交点可得240b ac ->，故②正确.结论③由函数图像可知抛物线对称轴为1x =-，所以12b a-=-，整理可得2b a =；当2x =时，420a b c ++>，将2b a =代入420a b c ++>可得，80a c +>，故③错误. 结论④由函数图像可知当2x =-时，420a b c -+<，当1x =-时，0a b c -+<，所以532(42)()0a b c a b c a b c -+=-++-+<，故④正确.综上所述，本题正确结论为②④，共2个.故选B.【点睛】本题主要考查二次函数的系数与图像的关系，关键在利用函数中当1x =-、2x =-和1x =-时的函数值的大小来判断③④结论的对错.12．A解析：A【分析】二次函数y ＝ax 2+bx +c （a ≠0），①当a ＞0时，抛物线y ＝ax 2+bx +c （a ≠0）的开口向上；②当a ＜0时，抛物线y ＝ax 2+bx +c （a ≠0）的开口向下，据此判断即可．【详解】解：A 、∵a ＞0， ∴2y =的图象开口向上，故本选项符合题意；B 、∵a ＝﹣1＜0，∴y ＝﹣x 2+2x +1的图象开口向下，故本选项不符合题意；C 、∵a ＝﹣2＜0，∴y ＝﹣2x 2+x 的图象开口向下，故本选项不符合题意；D 、∵a ＝﹣0.5＜0，∴y ＝﹣0.5x 2+x 的图象开口向下，故本选项不符合题意；故选：A ．【点睛】本题考查二次函数的图象和性质，解答本题的关键是明确题意，利用二次函数的性质解答．二、填空题13．【分析】设出E 的坐标表示出M 坐标进而表示出EM 化成顶点式即可求得EM 的最大值【详解】解：∵点E 是直线BC 上方抛物线上的一动点∴点E 的坐标是（m ）点M 的坐标是（m ）∴EM ＝﹣（）＝＝（m2﹣4m ）＝（解析：32【分析】设出E 的坐标，表示出M 坐标，进而表示出EM ，化成顶点式即可求得EM 的最大值．【详解】解：∵点E 是直线BC 上方抛物线上的一动点，∴点E 的坐标是（m ，233384m m -++），点M 的坐标是（m ，334m -+）， ∴EM ＝233384m m -++﹣（334m -+）＝23382m m -+＝38-（m 2﹣4m ）＝38-（m ﹣2）2+32， ∴当m ＝2时，EM 有最大值为32，故答案为32．【点睛】本题考查了二次函数图象上点的坐标特征，一次函数图象上点的坐标特征，熟练掌握二次函数的性质是解题的关键．14．①②③【分析】由抛物线的对称轴可判断①；由①可得出过点（﹣10）代入可得出c ＝﹣5a 代入化简即可判断②；根据二次函数的增减性知抛物线上点离对称轴水平距离越小函数值越大据此可判断③；由抛物线的图像的增解析：①②③【分析】由抛物线的对称轴可判断①；由①可得出=4b a -，过点（﹣1，0），代入可得出c ＝﹣5a ，代入化简即可判断②；根据二次函数的增减性知抛物线上点离对称轴水平距离越小，函数值越大，据此可判断③；由抛物线的图像的增减性直接判断④．【详解】函数y ＝ax 2+bx +c （a ≠0）的对称轴2b x a =-， ∵ 对称轴2x =， ∴=22b a-， ∴=4b a -，∴ 4+=0a b ，故①正确；有图可知，a ＜0，∴=4b a -，∴ 2=8b a -，过点（﹣1，0），∴ a-b+c ＝0，∴ b=a+c ，即a+c=﹣4a ，∴ c ＝﹣5a ，∴24a +2b +3c ＝24a －8a －15a ＝a ＜0，故②正确；当x ＝0时，y ＝c ，∵A （﹣3，y 1），B （﹣0.5，y 2），C （3.5，y 3）三点都在抛物线上，点A 与2x =的水平距离为5，点B 与2x =的水平距离为2.5，点C 与2x =的水平距离为1.5，∵5＞2.5＞1.5，∴ 123y y y <<，故③正确；有图可知，当11y >-，y 随x 增大先增大后减小，故④不正确；综上，正确的有：①②③．故答案为：①②③．【点睛】本题考查的是二次函数图象与系数的关系，要求学生熟悉函数的基本性质，能熟练求解函数与坐标轴的交点及顶点的坐标等．15．或【分析】不等式的解集对应图象上面为二次函数图象比反比例函数图象高的部分找出x 的范围即可【详解】解：不等式的解对应图象上面为二次函数图象比反比例函数图象高的部分∴不等式的解为或故答案为：或【点睛】本解析：10x -<<或13x <<【分析】不等式的解集对应图象上面为二次函数图象比反比例函数图象高的部分，找出x 的范围即可．【详解】解：不等式2k ax bx c x++>的解对应图象上面为二次函数图象比反比例函数图象高的部分，∴不等式2k ax bx c x++>的解为10x -<<或13x <<，故答案为：10x -<<或13x <<．【点睛】本题考查利用函数图象解不等式，即比较图象的高低．16．【分析】由抛物线与x 轴只有一个公共点可知对应的一元二次方程根的判别式△＝b2−4ac ＝0由此即可得到关于n 的方程解方程即可求得n 的值【详解】解：∵抛物线与x 轴只有一个公共点∴△＝4−4×1×n ＝0解解析：1【分析】由抛物线22y x x n =-+与x 轴只有一个公共点可知，对应的一元二次方程220x x n -+=根的判别式△＝b 2−4ac ＝0，由此即可得到关于n 的方程，解方程即可求得n 的值．【详解】解：∵抛物线22y x x n =-+与x 轴只有一个公共点，∴△＝4−4×1×n ＝0，解得n ＝1．故答案为：1．【点睛】此题主要考查了抛物线与x 轴的交点问题，利用二次函数根的判别式的和抛物线与x 轴的交点个数建立方程是解题的关键．17．②③④【分析】由抛物线的性质和对称轴是分别判断abc 的符号即可判断①；抛物线与x 轴有两个交点可判断②；由得令求函数值即可判断③；令时则令时即可判断④；然后得到答案【详解】解：根据题意则∵∴∴故①错误解析：②③④【分析】由抛物线的性质和对称轴是1x =，分别判断a 、b 、c 的符号，即可判断①；抛物线与x 轴有两个交点，可判断②；由12b x a=-=，得2b a =-，令2x =-，求函数值，即可判断③；令2x =时，则420y a b c =++>，令1x =-时，0y a b c =-+>，即可判断④；然后得到答案．【详解】解：根据题意，则0a <，0c >， ∵12b x a=-=， ∴20b a =->， ∴0abc <，故①错误；由抛物线与x 轴有两个交点，则240b ac ->，故②正确；∵2b a =-，令2x =-时，420y a b c =-+<，∴80a c +<，故③正确；在2y ax bx c =++中，令2x =时，则420y a b c =++>，令1x =-时，0y a b c =-+>，由两式相加，得520a b c ++>，故④正确；综上，正确的结论有：②③④；故答案为：②③④．【点睛】本题考查了二次函数的图象和性质，解题的关键是熟练掌握二次函数的性质，熟练判断各个式子的符号． 18．或1或【分析】首先根据题意确定ab 的符号然后进一步确定b 的取值范围根据a-b 的值为整数确定ab 的值从而确定答案【详解】解：∵抛物线的顶点在第三象限且过点∴a ＞0∴b ＞0a=2-ba-b=2-b-b= 解析：32或1或12 【分析】首先根据题意确定a 、b 的符号，然后进一步确定b 的取值范围，根据a-b 的值为整数确定a 、b 的值，从而确定答案．【详解】解：∵抛物线22(0)y ax bx a =+-≠的顶点在第三象限，且过点(1,0)，∴a ＞0，02b a-<，20a b +-=， ∴b ＞0，a=2-b ，a-b=2-b-b=2-2b ，∴2-b ＞0，∴0＜b ＜2，∴-2＜2-2b ＜2，∵a-b 的值为整数，∴a-b=-1或0或1，∴2-2b=-1或2-2b=0或2-2b=1，解得：b=32或b=1或b=12， ∴b=32或1或12，故答案为：32或1或12．【点睛】此题主要考查了二次函数的性质和应用，二次函数的图象与系数的关系，要熟练掌握，解答此题的关键是分别求出a 、b 的取值范围．19．【分析】根据图像经过的两点确定抛物线的对称轴利用对称轴确定P 的对称点利用数形结合思想确定m 的范围即可【详解】∵抛物线经过两点∴解得b=-6a ∴抛物线的对称轴为直线x==3∴的对称点为∵∴故填【点睛】解析：15m <<.【分析】根据图像经过的两点，确定抛物线的对称轴，利用对称轴，确定P 的对称点，利用数形结合思想，确定m 的范围即可.【详解】∵抛物线2(0)y ax bx c a =++>经过(2,0)A ，(4,0)B 两点，∴4201640a b c a b c ++=⎧⎨++=⎩，解得b=-6a ，∴抛物线的对称轴为直线x=2b a-=3, ∴()15,P y 的对称点为()11,P y '，∵12y y >，∴15m <<，故填15m <<.【点睛】本题考查了二次函数的对称性，熟记二次函数的性质是解题的关键.20．【分析】根据表格中的数据可知抛物线的开口方向对称轴及顶点坐标结合表格及抛物线特征可得当时自变量的取值范围【详解】解：由表格知：抛物线开口向上顶尖坐标为（21）故当x=0时与x=4时函数值相同∴=5当解析：04x <<．【分析】根据表格中的数据可知抛物线的开口方向，对称轴及顶点坐标，结合表格及抛物线特征可得当1y y <时，自变量x 的取值范围．【详解】解：由表格知：抛物线开口向上，顶尖坐标为（2，1），故当x=0时与x=4时函数值相同，∴1y =5，当1y y <时，即当y ＜5时，由表格得04x <<．故答案为：04x <<．【点睛】本题考查了二次函数数的特征，解题关键是根据表格得出抛物线的开口方向，对称轴及顶点坐标．三、解答题21．（1）1b =；（2）14c =或20c -<；（3）当21x =时，p 最大值为1 【分析】（1）利用抛物线的对称轴为直线12x =-求解即可；（2）分两种情况讨论①当公共点是顶点时，②当公共点不是顶点时，解答即可；（3）根据根与系数的关系得出x 的取值范围，再根据二次函数的增减性求出p 的最大值．【详解】解：（1）∵抛物线经过(3,),(2,)A n B n -两点，∴抛物线的对称轴为直线12x =-． 122b ∴-=-． 1b ∴=．（2）由（1）得，抛物线的解析式为2y x x c =++，对称轴为直线12x =-，且当11x -<<时，抛物线与x 轴有且只有一个公共点，①当公共点是顶点时，140c ∴=-=，解得14c =． ②当公共点不是顶点时， ∴当1x =-时，110c -+，且当1x =时，110c ++>．解得20c -<．综上所述，c 的取值范围是14c =或20c -<．（3）解法一：由（1）知1b =，设2y x x c =++．方程20x x c ++=的两实根为12x x ，，∴抛物线2y x x c =++与x 轴交点的横坐标为12,x x ，12122x x +∴=-，即121x x +=-． 211x x ∴=--．2139x x -<， ()11319x x ∴---<．152x ∴-<-．22123p x x ∴=-()221131x x =---2133222x ⎛⎫=-++ ⎪⎝⎭．当152x -<-时，p 随1x 的增大而增大， ∴当12x =-时，p 的最大值为1.解法二：由（1）知1b =．方程20x x c ++=的两实根为12,x x ，2110x x c ∴++=，即211x x c =--，①2220x x c ++=，即222x x c =--②①－②，得()221212x x x x -=--， ()()()121212x x x x x x ∴+-=--．2139x x -<，120x x ∴-≠．121x x ∴+=-．即121x x =--．()22319x x ∴---<214x ∴<22123p x x ∴=-()222213x x =--- 2213222x ⎛⎫=--+ ⎪⎝⎭ 当214x <时，p 随2x 的增大而减少， ∴当21x =时，p 最大值为1.【点睛】本题考查了抛物线与x 轴的交点，二次函数的性质，不等式的性质等知识，解题的关键是能用分类讨论的思想解决问题．22．（1）顶点坐标为()1,0-；（2）2n <-【分析】（1）利用配方法将二次函数解析式变形为顶点式，再利用图象与x 轴有且只有一个公共点，则顶点的纵坐标为0，故函数图象的顶点坐标为（-1，0），（2）将n ，n+2代入二次函数解析式即可得出n 的取值范围．【详解】解：（1）()22211y x x m x m =++=++-，对称轴1x =-∵与x 轴有且只有一个公共点，∴顶点的纵坐标为0．∴函数图象的顶点坐标为()1,0-（2）∵()1,P n y ，()22,Q n y +是该二次函数的图象上的两点，且12y y >，()()22212221n n n n ++>++++，化简整理得，480n +<，∴2n <-，∴实数n 的取值范围是2n <-．【点睛】本题考查了二次函数的性质及解不等式，利用数形结合思想解题是关键．23．（1）(1,0)A -，(3,0)B ；（2）2m =【分析】（1）把y=0代入，解方程即可；（2）求出顶点坐标，过C 作CD AB ⊥于D ，求出CD 即可．【详解】解：（1）2230mx mx m --=，∵0m >，方程两边同时除以m 得， 2230x x --=解得，13x =，21x =-∴A ，B 两点的坐标分别为：(1,0)A -，(3,0)B ．（2）抛物线223(0)y mx mx m m =-->的顶点横坐标为：212m x m-=-=，把x=1代入223y mx mx m =--得，y=-4m ，抛物线的顶点C 的坐标为：(1,4)C m -由（1）得，AB=4，过C 作CD AB ⊥于D ，∵ABC为等边三角形，∴AD=2，AC=4，∴2222=-=-=CD AC AD4223∵点C在第四象限，m=∴43∴3m=．2【点睛】本题考查求二次函数与x轴交点，等边三角形的性质，解题关键是熟练的解一元二次方程，根据已知条件，找到坐标与线段的关系．24．（1）y＝x2﹣4x＋3，m的值为3，见解析；（2）y＝x2【分析】（1）由二次函数图象经过点（1，0），（3，0），设出交点式，利用待定系数法求函数解析式，进一步代入点得出m的值；然后利用表中的点描点，画出函数图象即可；（2）将抛物线解析式化为顶点式，再根据“上加下减、左加右减”的原则进行解答即可．【详解】解：（1）抛物线y＝ax2＋bx＋c（a≠0）过点（1，0），（3，0），可设抛物线解析式为y ＝a（x﹣1）（x﹣3）∵过点（0，3），∴3＝3a，解得a＝1，∴y＝（x﹣1）（x﹣3）＝x2﹣4x＋3，当x＝4时，y＝16﹣16＋3＝3，∴抛物线的解析式为y＝x2﹣4x＋3，m的值为3，函数图象如下：（2）∵y ＝x 2﹣4x ＋3＝（x ﹣2）2﹣1，∴将函数y ＝x 2﹣4x ＋3向左平移2个单位，再向上平移1个单位，得y ＝（x ﹣2＋2）2﹣1＋1，即y ＝x 2，所以平移后的函数解析式为y ＝x 2．【点睛】本题考查了待定系数法、抛物线的平移和画函数图象，解题关键是熟练运用待定系数法，掌握抛物线平移规律．25．（1）y ＝﹣100x +5000（6≤x ≤30）；（2）当销售单价定为28元时，销售这种防疫包的日获利w 最大，最大利润为48400元【分析】（1）观察可得该函数图象是一次函数，设出一次函数解析式为：()0y kx b k =+≠，把其中两点代入即可求得该函数解析式；（2）根据销售利润=每个商品的利润×销售量，把二次函数的关系式配方变为顶点式即可求得相应的最大利润．【详解】解：（1）设y 与x 的函数关系式为：()0y kx b k =+≠，把7x =，4300y =和8x =，4200y =代入得，7430084200k b k b +=⎧⎨+=⎩，解得，1005000k b =-⎧⎨=⎩， ∴1005000y x =-+（6≤x ≤30）；（2）()()61005000w x x =--+2100560030000x x =-+-()21002848400x =--+∵1000a =-<，对称轴为28x =，∴当28x =时，w 有最大值为48400元，∴当销售单价定为28时，销售这种板栗日获利最大，最大利润为48400元；【点睛】本题考查了二次函数的应用，二次函数的性质，利用函数思想解决问题是本题的关键． 26．（1）见解析；N ()4,5；（2）2114y x =+；（3）218y x = 【分析】（1）利用尺规作图，作出线段AB 的垂直平分线即可；（2）设出抛物线的解析式，结合题意分析出点M 为抛物线的顶点，点N 在抛物线上，利用待定系数法直接求解即可；（3）设出抛物线解析式，结合题意分析出抛物线经过原点，且经过点（4、2）点（-4、2）利用待定系数法求解即可．【详解】解：（1）如图，连接AB ，作线段AB 的垂直平分线，与直线l 相交于点N ，点N 即为所求．连接AN ，过点A 作AH BN ⊥于点H ，设点N 的坐标为()4,y由作图可知AN y =，在Rt ANH ∆中，4AH =，2NH y =-，22(2)16y y ∴=-+，解得5y =∴点N 的坐标为()4,5；（2）此抛物线关于y 轴对称，∴点()0,1M 是抛物线的顶点，设抛物线的解析式为21y ax =+，将点()4,5N 代入得，14a =， ∴抛物线的解析式为2114y x =+．（3）设抛物线的解析式为：2y ax bx c =++，结合题意可知抛物线经过原点，和点（4、2）点（-4、2）则有164216420a b b c +=⎧⎪-=⎨⎪=⎩解得1800a b c ⎧=⎪⎪=⎨⎪=⎪⎩∴抛物线的解析式为：218y x =．【点睛】本题考查了线段垂直平分线的尺规作图，待定系数法求函数解析式，解题关键是结合题意确定满足条件的点．。

中考数学《二次函数的三种形式》专项练习题及答案

中考数学《二次函数的三种形式》专项练习题及答案一、单选题1．二次函数y=-2（x-1）2+3的图象的顶点坐标是（）A．（1，3）B．（-1，3）C．（1，-3）D．（-1，-3）2．二次函数y=（x+1）2-1图象的顶点坐标是( )A．（1，1）B．（1，-1）C．（-1，1）D．（-1，-1）3．抛物线y=（x+1）2+2的对称轴为（）A．直线x=1B．直线x=-1C．直线x=2D．直线x=-24．二次函数y=3（x-2）2-1的图象的顶点坐标是（）A．（2，-1）B．（-2，-1）C．（2，1）D．（-2，1）5．若b＞0，则二次函数y=x2+2bx﹣1的图象的顶点在（）A．第一象限B．第二象限C．第三象限D．第四象限6．将抛物线y=2x2向右平移2个单位，再向上平移3个单位，所得抛物线的表达式为（）A．y=2（x+2）2+3B．y=（2x﹣2）2+3C．y=（2x+2）2﹣3D．y=2（x﹣2）2+37．对称轴平行于y轴的抛物线的顶点为点(2，3)且抛物线经过点(3，1)，那么抛物线解析式是() A．y =-2x2 + 8x +3B．y =-2x2 –8x +3C．y = -2x2 + 8x –5D．y =-2x2 –8x +28．二次函数y＝x2－6x＋5的图像的顶点坐标是（）A．(－3，4)B．(3，－4)C．(－1，2)D．(1，－4)9．把二次函数y=x2-4x+3化成y=a（x-h）2+k的形式是（)A．y＝(x－2)2－1B．y＝(x＋2)2－1C．y＝(x－2)2＋7D．y＝(x＋2)2＋710．抛物线y=(x−2)2+1的顶点坐标是()A．(−2， −1)B．(−2， 1)C．(2， −1)D．(2， 1)11．一小球被抛出后，距离地面的高度h（米）和飞行时间t（秒）满足下列函数关系式：h=-5（t-1）2+6，则小球距离地面的最大高度是A．1米B．5米C．6米D．7米12．已知二次函数的解析式为：y=-3（x+5）2﹣7，那么下列说法正确的是（）A．顶点的坐标是（5，-7）B．顶点的坐标是（-7，-5）C．当x=-5时，函数有最大值y=-7D．当x=-5时，函数有最小值y=-7二、填空题13．将抛物线y=﹣﹣12x2﹣3x+1写成y=a（x+h）2+k的形式应为．14．如果二次函数y=x2+bx+c配方后为y=（x﹣2）2+1，那么c的值为15．将二次函数y=x2+4x﹣2配方成y=（x﹣h）2+k的形式，则y=．16．若y=x2﹣2x﹣3化为y=（x﹣m）2+k的形式（其中m，k为常数），则m+k=；当x=时，二次函数y=x2+2x﹣2有最小值．17．把二次函数y=（x﹣2）2+1化为y=x2+bx+c的形式，其中b、c为常数，则b+c=．18．将二次函数y=x2−4x+5化成y=a(x−ℎ)2+k的形式为.三、综合题19．如图，抛物线的顶点M在x轴上，抛物线与y轴交于点N，且OM=ON=4，矩形ABCD的顶点A、B在抛物线上，C、D在x轴上．（1）求抛物线的解析式；（2）设点A的横坐标为t（t＞4），矩形ABCD的周长为l，求l与t之间函数关系式．20．如图，抛物线y=x2+bx+c与x轴交于点A和点B（3，0），与y轴交于点C（0，3）．（1）求抛物线的解析式；（2）若点M是抛物线在x轴下方上的动点，过点M作MN∥y轴交直线BC于点N，求线段MN 的最大值；（3）在（2）的条件下，当MN取得最大值时，在抛物线的对称轴l上是否存在点P，使∥PBN是等腰三角形？若存在，请直接写出所有点P的坐标；若不存在，请说明理由．21．如图，已知二次函数y=ax2+bx+c的图象过点A（﹣1，0）和点C（0，3），对称轴为直线x=1．（1）求该二次函数的关系式和顶点坐标；（2）结合图象，解答下列问题：①当﹣1＜x＜2时，求函数y的取值范围．②当y＜3时，求x的取值范围．22．已知二次函数y=x2−2mx+m2+3（m是常数）．（1）求证：不论m为何值，该函数的图象与x轴没有公共点；（2）把该函数的图象沿y轴向下平移多少个单位长度后，得到的函数的图象与x轴只有一个公共点？23．把下列函数化为y=a（x+m）2+k形式，并求出各函数图象的顶点坐标、对称轴、最大值或最小值：（1）y=x2﹣2x+4；（2）y=100﹣5x2．24．如图，抛物线y=ax2+bx+c（a≠0）与x轴相交于A（﹣1，0），B（3，0），与y轴交于点C（0，3）．（1）求抛物线的解析式；（2）连接BC，点P为抛物线上第一象限内一动点，当∥BCP面积最大时，求点P的坐标；（3）设点D是抛物线的对称轴上的一点，在抛物线上是否存在点Q，使以点B，C，D，Q为顶点的四边形为平行四边形？若存在，求出点Q的坐标；若不存在，说明理由．参考答案1．【答案】A2．【答案】D3．【答案】B4．【答案】A5．【答案】C6．【答案】D7．【答案】C8．【答案】B9．【答案】A10．【答案】D11．【答案】C12．【答案】C13．【答案】y=﹣12（x+3）2+11214．【答案】515．【答案】（x+2）2﹣616．【答案】-4；-117．【答案】118．【答案】y=(x−2)2+119．【答案】（1）解：∵OM=ON=4∴M点坐标为（4，0），N点坐标为（0，4）设抛物线解析式为y=a（x﹣4）2把N（0，4）代入得16a=4，解得a= 1 4所以抛物线的解析式为y= 14（x﹣4）2= 14x2﹣2x+4（2）解：∵点A的横坐标为t ∴DM=t﹣4∴CD=2DM=2（t﹣4）=2t﹣8把x=t代入y= 14x2﹣2x+4得y= 14t2﹣2t+4∴AD= 14t2﹣2t+4∴l=2（AD+CD）=2（14t2﹣2t+4+2t﹣8）= 12t 2﹣8（t ＞4） 20．【答案】（1）解：将点B （3，0）、C （0，3）代入抛物线y=x 2+bx+c 中得： {0=9+3b +c 3=c ，解得： {b =−4c =3 ∴抛物线的解析式为y=x 2﹣4x+3．（2）解：设点M 的坐标为（m ，m 2﹣4m+3），设直线BC 的解析式为y=kx+3 把点点B （3，0）代入y=kx+3中得：0=3k+3，解得：k=﹣1 ∴直线BC 的解析式为y=﹣x+3． ∵MN∥y 轴∴点N 的坐标为（m ，﹣m+3）．∵抛物线的解析式为y=x 2﹣4x+3=（x ﹣2）2﹣1 ∴抛物线的对称轴为x=2 ∴点（1，0）在抛物线的图象上 ∴1＜m ＜3．∵线段MN=﹣m+3﹣（m 2﹣4m+3）=﹣m 2+3m=﹣ 12 + 94∴当m= 32 时，线段MN 取最大值，最大值为 94 ．（3）解：假设存在．设点P 的坐标为（2，n ）．当m= 32 时，点N 的坐标为（ 32 ， 32） ∴PB= √(2−3)2+(n −0)2 = √1+n 2 ，PN= √(2−32)2+(n −32)2 ，BN= √(3−32)2+(0−32)2=3√22．∥PBN 为等腰三角形分三种情况：①当PB=PN 时，即 √1+n 2 = √(2−32)2+(n −32)2解得：n= 12此时点P 的坐标为（2， 12）；②当PB=BN 时，即 √1+n 2 = 3√22解得：n=± √142此时点P 的坐标为（2，﹣ √142 ）或（2， √142）；③当PN=BN 时，即 √(2−32)2+(n −32)2 = 3√22解得：n= 3±√172此时点P 的坐标为（2， 3−√172 ）或（2， 3+√172）．综上可知：在抛物线的对称轴l 上存在点P ，使∥PBN 是等腰三角形，点的坐标为（2， 12）、（2，﹣√142 ）、（2， √142 ）、（2， 3−√172 ）或（2， 3+√172）． 21．【答案】（1）解：根据题意得 {a −b +c =0c =3−b2a =1 ，解得 {a =−1b =2c =3，所以二次函数关系式为y=﹣x 2+2x+3，因为y=﹣（x ﹣1）2+4 所以抛物线的顶点坐标为（1，4）；（2）解：①当x=﹣1时，y=0；x=2时，y=3；而抛物线的顶点坐标为（1，4），且开口向下所以当﹣1＜x ＜2时，0＜y≤4；②当y=3时，﹣x 2+2x+3=3，解得x=0或2 所以当y ＜3时，x ＜0或x ＞2．22．【答案】（1）解：∵∥=（﹣2m ）2﹣4×1×（m 2+3）=4m 2﹣4m 2﹣12=﹣12＜0∴方程x 2﹣2mx+m 2+3=0没有实数解，即不论m 为何值，该函数的图象与x 轴没有公共点；（2）解：y=x 2﹣2mx+m 2+3=（x ﹣m ）2+3∴把函数y=x 2﹣2mx+m 2+3的图象沿y 轴向下平移3个单位长度后，得到的函数的图象与x 轴只有一个公共点．23．【答案】（1）解：y=x 2﹣2x+4=x 2﹣2x+1+3=（x ﹣1）2+3．顶点坐标是（1，﹣1），对称轴为x=1，最小值为﹣1 （2）解：y=100﹣5x 2．顶点坐标是（0，100），对称轴为x=0，最大值为10024．【答案】（1）解：设抛物线解析式为y=a （x+1）（x ﹣3）把C （0，3）代入得a•1•（﹣3）=3，解得a=﹣1所以抛物线解析式为y=﹣（x+1）（x ﹣3），即y=﹣x 2+2x+3 （2）解：设直线BC 的解析式为y=kx+m把B （3，0），C （0，3）代入得 {3k +m =0m =3 ，解得 {k =−1m =3所以直线BC 的解析式为y=﹣x+3 作PM∥y 轴交BC 于M ，如图1设P（x，﹣x2+2x+3），（0＜x＜3），则M（x，﹣x+3）∴PM=﹣x2+2x+3﹣（﹣x+3）=﹣x2+3x∴S∥PCB= 12•3•PM=﹣32x2+ 92=﹣32（x﹣32）2+ 278当x= 32时，∥BCP的面积最大，此时P点坐标为（32，154）（3）解：如图2抛物线的对称轴为直线x=1当四边形BCDQ为平行四边形，设D（1，a），则Q（4，a﹣3）把Q（4，a﹣3）代入y=﹣x2+2x+3得a﹣3=﹣16+8+3，解得a=﹣2∴Q（4，﹣5）；当四边形BCQD为平行四边形时，设D（1，a），则Q（﹣2，3+a）把Q（﹣2，3+a）代入y=﹣x2+2x+3得3+a=﹣4﹣4+3，解得a=﹣8∴Q（﹣2，﹣5）；当四边形BQCD为平行四边形时，设D（1，a），则Q（2，3﹣a）把Q（2，3﹣a）代入y=﹣x2+2x+3得3﹣a=﹣4+4+3，解得a=0∴Q（2，3）综上所述，满足条件的Q点坐标为（4，﹣5）或（﹣2，﹣5）或（2，3）．。

【课课练】九年级数学下册 2.5 用三种方式表示二次函数测试题

３),那么函数的解析式是．
(第３题 )
５．把
y＝
１２x２
－３
的
图
象
向
平
移
个
单
位
得
y＝
１２
(x－２)２－３
的
图
象
,再
向
平
移
个单位ຫໍສະໝຸດ 得y＝１２
(x－２)２＋１
的
图
象
．
６．有一根长为４０cm 的铁丝,把它弯成一个矩形框,当矩形框的长、宽各是多少时,矩形面积最大? 最大面积是多少? 利用图象描述矩形面积的长、宽之间的关系．
∴ 球能越过网．
x＝１８时 ,y＝－６１０(１８－６)２＋２．６＝０．２＞０,
∴ 球会过界．
(３)x＝０,y＝２,代入到y＝a(x－６)２＋h 得a＝２３－６h;
x＝９时 ,y＝２３－６h＝ (９－６)２＋h＝２＋４３h＞２．４３,
①
x＝１８时 ,y＝２３－６h(１８－６)２＋h＝８－３h＞０,
(第１４题 )
５．用三种方式表示二次函数
１．(１)y＝－x２＋１０x (２)略 (３)略 (４)① 对称轴直线 x＝５顶点坐标 (５,２５) ②２５ ③当０＜x≤５时,y 随x 的增大而增大; 当５≤x＜１０时,y 随x 的增大而减小; 当 x＝５时 , y 有最大值２５．
５．用三种方式表示二次函数
１．记住二次函数有三种表达方式 ——— 列表法、图象法、解析法．２．掌握用解析式法表示二次函数的三种表达式:一般式、顶点式、交
点式的特征 ,会灵活运用适当的方法求二次函数的表达式．

中考数学专项复习《二次函数的三种形式》练习题带答案

中考数学专项复习《二次函数的三种形式》练习题带答案一、单选题1．二次函数y=x 2﹣2x+4化为y=a （x ﹣h ）2+k 的形式，下列正确的是（）A ．y=（x ﹣1）2+2B ．y=（x ﹣1）2+3C ．y=（x ﹣2）2+2D ．y=（x ﹣2）2+42．抛物线y=x 2﹣2x ﹣3的对称轴和顶点坐标分别是（）．A ．x=1，（1，﹣4）B ．x=1（1，4）C ．x=﹣1，（﹣1，4）D ．x=﹣1，（﹣1，﹣4）3．把y=4x 2﹣4x+2配方成y=a （x ﹣h ）2+k 的形式是（）A ．y=（2x ﹣1）2+1B ．y=（2x ﹣1）2+2C ．y=（x ﹣ 12）2+1D ．y=4（x ﹣ 12）2+24．若把抛物线y ＝x 2－2x ＋1先向右平移2个单位，再向下平移3个单位，所得到的抛物线的函数关系式为y ＝ax 2＋bx ＋c ，则b 、c 的值为（） A ．b ＝2，c ＝－2 B ．b ＝－8，c ＝14 C ．b ＝－6，c ＝6D ．b ＝－8，c ＝185．直角坐标平面上将二次函数y=x 2-2的图象向左平移1个单位，再向上平移1个单位，则其顶点为（） A ．（0，0）B ．（1，-1）C ．（0，-1）D ．（-1，-1）6．将二次函数y=x 2+4x ﹣8化为y=（x+m ）2+n 的形式正确的是（）A ．y=（x+2）2+8B ．y=（x+2）2﹣8C ．y=（x+2）2+12D ．y=（x+2）2﹣127．若b<0，则二次函数y=x 2-bx-1的图象的顶点在（）A ．第一象限B ．第二象限C ．第三象限D ．第四象限8．通过配方法将二次函数y=ax 2+bx+c （a≠0）化成y=a （x ﹣h ）2+k 的形式，此二次函数可变形为（）A ．y=a （x+ b 2a ）2+ 4ac−b 24aB ．y=a （x ﹣ b 2a ）2+ 4ac−b 24aC ．y=a （x+ b 2a ）2+ b 2−4ac 4aD ．y=a （x ﹣ b 2a ）2+ b 2−4ac 4a9．将二次函数y=x 2﹣2x+3化为y=（x ﹣h ）2+k 的形式，结果为（）A ．y=（x+1）2+4B ．y=（x+1）2+2C ．y=（x ﹣1）2+4D ．y=（x ﹣1）2+210．抛物线y=﹣ 15 x 2+ 25x ﹣1，经过配方化成y=a （x ﹣h ）2+k 的形式是（）A ．y =15(x +1)2−45B ．y =15(x −1)2+45C ．y =15(x −1)2−45D ．y =15(x +1)2+4511．如图，在 ΔABC 中 ∠B =90° ，tan ∠C =34,AB=6cm.动点P 从点A 开始沿边AB 向点B 以1cm/s 的速度移动，动点Q 从点B 开始沿边BC 向点C 以2cm/s 的速度移动.若P,Q 两点分别从A,B 两点同时出发，在运动过程中 ΔPBQ 的最大面积是( )A ．18cm 2B ．12cm 2C ．9cm 2D ．3cm 212．如图，在平面直角坐标系中抛物线所表示的函数解析式为y=﹣2（x ﹣h ）2+k ，则下列结论正确的是( )A ．h ＞0，k ＞0B ．h ＜0，k ＞0C ．h ＜0，k ＜0D ．h ＞0，k ＜0二、填空题13．二次函数 y =−x 2+2x +3 的图象与 x 轴交于 A 、 B 两点， P 为它的顶点，则S △PAB = ．14．把二次函数的表达式y=x 2﹣6x+5化为y=a （x ﹣h ）2+k 的形式，那么h+k= 15．将二次函数y=x 2﹣2x+4化成y=（x ﹣h ）2+k 的形式，则y= ． 16．若二次函数y=x 2+bx+5配方后为y=（x ﹣2）2+k ，则b+k= ．17．若将二次函数y=x 2﹣2x+3配方为y=（x ﹣h ）2+k 的形式，则y= ． 18．已知抛物线的表达式是y =2(x +2)2−1，那么它的顶点坐标是；三、综合题19．如图，抛物线的顶点M 在x 轴上，抛物线与y 轴交于点N ，且OM=ON=4，矩形ABCD 的顶点A 、B 在抛物线上，C 、D 在x 轴上．（1）求抛物线的解析式；（2）设点A的横坐标为t（t＞4），矩形ABCD的周长为l，求l与t之间函数关系式．20．已知二次函数y= 2x2 -4x-6.（1）用配方法将y= 2x2 -4x-6化成y=a (x-h) 2 +k的形式；并写出对称轴和顶点坐标。

初三下二次函数练习题及答案

初三下二次函数练习题及答案一、选择题1.下面哪一个函数是二次函数？A. y = 3x + 1B. y = x² + 2x + 1C. y = 4^xD. y = √x2.二次函数y = ax² + bx + c图象是抛物线，开口向上的条件是：A. a > 0B. a < 0C. b > 0D. b < 03.已知二次函数y = x² - 4x + 3的顶点为（2，-1），则a、b、c的值分别为：A. a = 1，b = -4，c = -1B. a = 1，b = 4，c = -3C. a = 1，b = -4，c = 3D. a = 1，b = -2，c = -3二、计算题1.已知二次函数y = x² - 3x + 2，求该函数的顶点坐标和对称轴的方程式。

解答：顶点的横坐标为x = -b/2a，所以 x = -(-3)/(2*1) = 3/2。

将x = 3/2代入原函数可得y = (3/2)² - 3*(3/2) + 2 = -1/4。

所以，该二次函数的顶点坐标为(3/2, -1/4)。

对称轴的方程式为x = 3/2。

2.已知二次函数y = 2x² - 4x + 1，求该函数的零点。

解答：函数的零点即为使得y = 0的x的值。

将y = 0代入原函数可得2x² - 4x + 1 = 0。

使用求根公式可解得x = (4 ± √(16 - 4*2*1))/(2*2) = (4 ± √8)/4 = (1 ± √2)/2。

所以，该二次函数的零点为x = (1 + √2)/2和x = (1 - √2)/2。

三、应用题1.小明将一长方形花坛围起来，其中一边贴着墙，另外三边用栅栏围起来。

已知墙的一段长为4米，花坛的面积为12平方米。

若栅栏的费用为每米15元，求栅栏的总费用。

解答：设花坛的另外两条边长分别为x和y，则有xy = 12。

中考数学专项复习《二次函数的三种形式》练习题及答案

中考数学专项复习《二次函数的三种形式》练习题及答案一、单选题1．抛物线y=x2﹣2x+3的顶点坐标是（）A．（1，﹣2）B．（1，2）C．（﹣1，2）D．（﹣1，﹣2）2．把二次函数y=x2-4x+3化成y=a（x-h）2+k的形式是（)A．y＝(x－2)2－1B．y＝(x＋2)2－1C．y＝(x－2)2＋7D．y＝(x＋2)2＋73．把二次函数y=x2﹣2x﹣1配方成顶点式为（）A．y=（x﹣1）2B．y=（x+1）2﹣2C．y=（x+1）2+1D．y=（x﹣1）2﹣24．已知二次函数y=(x−1m)(mx−4m)（其中m＞0），下列说法正确的是（）A．当x＞2时，都有y随着x的增大而增大B．当x＜3时，都有y随着x的增大而减小C．若x＜n时，都有y随着x的增大而减小，则n≥2+12mD．若x＜n时，都有y随着x的增大而减小，则n≤2+12m5．将二次函数y=x2﹣2x﹣3化成y=（x﹣h）2+k形式，则h+k结果为（）A．-5B．5C．3D．-36．用配方法将y=x2﹣8x+12化成y=a（x﹣h）2+k的形式为（）A．y=（x﹣4）2+4B．y=（x﹣4）2﹣4C．y=（x﹣8）2+4D．y=（x﹣8）2﹣47．将二次函数y=x2-4x-1化为y=（x-h）2+k的形式，结果为（）A．y=(x+2)2+5B．y=(x+2)2−5C．y=(x−2)2+5D．y=(x−2)2−5 8．将二次函数y=x2﹣2x﹣3化成y=（x﹣h）2+k形式，则h+k结果为（）A．﹣5B．5C．3D．﹣39．抛物线y=(x+2)2−3的对称轴是（）A．直线x=2B．直线x=-2C．直线x=-3D．直线x=310．抛物线y=(x−2)2的顶点坐标是（）A．（2，0）B．（－2，0）C．（0，2）D．（0，－2）11．下列二次函数中，顶点坐标是（2，－3）的函数解析式为（）A．y=(x-2)2+3B．y=(x+2)2+3C．y=(x-2)2-3D．y=(x+2)2-312．通过配方法将二次函数y=ax2+bx+c（a≠0）化成y=a（x﹣h）2+k的形式，此二次函数可变形为（）A ．y=a （x+ b 2a ）2+ 4ac−b 24aB ．y=a （x ﹣ b 2a ）2+ 4ac−b 24aC ．y=a （x+ b 2a ）2+ b 2−4ac 4aD ．y=a （x ﹣ b 2a ）2+ b 2−4ac 4a二、填空题13．关于x 的一元二次方程x 2+bx+c=0的两根为x 1=1，x 2=2，那么抛物线y=x 2+bx+c 的顶点坐标为 .14．如图，正方形ABCD 的顶点A ，B 与正方形EFGH 的顶点G ，H 同在一段抛物线上，且抛物线的顶点同时落在CD 和y 轴上，正方形边AB 与EF 同时落在x 轴上，若正方形ABCD 的边长为4，则正方形EFGH 的边长为15．抛物线y=x 2-2x+5化成y=a(x-h)2+k 的形式是．16．将二次函数y=x 2﹣2x+3写成y=a （x ﹣h ）2+k 的形式为 17．将二次函数y=x 2﹣2x+4化成y=（x ﹣h ）2+k 的形式，则k=18．把二次函数的表达式y=x 2﹣6x+5化为y=a （x ﹣h ）2+k 的形式，那么h+k=三、综合题19．把下列函数化为y=a （x+m ）2+k 形式，并求出各函数图象的顶点坐标、对称轴、最大值或最小值：（1）y=x 2﹣2x+4；（2）y=100﹣5x 2．20．已知二次函数y=x 2﹣6x+8．（1）将解析式化成顶点式；（2）写出它的开口方向、对称轴和顶点坐标；（3）x 取什么值时，y 随x 的增大而增大；x 取什么值时，y 随x 增大而减小．21．如图，抛物线的顶点M 在x 轴上，抛物线与y 轴交于点N ，且OM=ON=4，矩形ABCD 的顶点A 、B 在抛物线上，C 、D 在x 轴上．（1）求抛物线的解析式；（2）设点A的横坐标为t（t＞4），矩形ABCD的周长为l，求l与t之间函数关系式．22．已知二次函数y=x2−2mx+m2+3（m是常数）．（1）求证：不论m为何值，该函数的图象与x轴没有公共点；（2）把该函数的图象沿y轴向下平移多少个单位长度后，得到的函数的图象与x轴只有一个公共点？23．如图，在平面直角坐标系xOy中，抛物线y＝ax2+（2a﹣ma）x﹣2am（a＜0）与x轴分别交于点A、C，顶点坐标为D.（1）当a＝﹣1，m＝1时.①求点D的坐标；②若F为线段AD上一动点，过点F作FH⊥x轴，垂足为H，交抛物线于点P，当PH+OH的值最大时，求点F的坐标.（2）当m＝23时，若另一个抛物线y＝ax2﹣（6a+ma）x+6am的顶点为E.试判断直线AD是否经过点E？请说明理由.24．对于二次函数y= 12x2﹣3x+4（1）配方成y=a（x﹣h）2+k的形式．（2）求出它的图象的顶点坐标和对称轴．（3）求出函数的最大或最小值．参考答案1．【答案】B2．【答案】A3．【答案】D4．【答案】D5．【答案】D6．【答案】B7．【答案】D8．【答案】D9．【答案】B10．【答案】A11．【答案】C12．【答案】A13．【答案】( 32,- 14)14．【答案】2 √5﹣215．【答案】y=(x-1)2+416．【答案】y=（x﹣1）2+217．【答案】318．【答案】﹣119．【答案】（1）解：y=x2﹣2x+4=x2﹣2x+1+3=（x﹣1）2+3．顶点坐标是（1，﹣1），对称轴为x=1，最小值为﹣1（2）解：y=100﹣5x2．顶点坐标是（0，100），对称轴为x=0，最大值为10020．【答案】（1）解：y=x2﹣6x+8=x2﹣6x+9﹣1=（x﹣3）2﹣1（2）解：开口向上，对称轴是x=3，顶点坐标是（3，﹣1）（3）解：x＞3时，y随x的增大而增大；x＜3时，y随x增大而减小21．【答案】（1）解：∵OM=ON=4∴M点坐标为（4，0），N点坐标为（0，4）设抛物线解析式为y=a（x﹣4）2把N（0，4）代入得16a=4，解得a= 1 4所以抛物线的解析式为y= 14（x﹣4）2= 14x2﹣2x+4（2）解：∵点A的横坐标为t∴DM=t﹣4∴CD=2DM=2（t﹣4）=2t﹣8把x=t代入y= 14x2﹣2x+4得y= 14t2﹣2t+4∴AD= 14t2﹣2t+4∴l=2（AD+CD）=2（14t2﹣2t+4+2t﹣8）= 12t2﹣8（t＞4）22．【答案】（1）解：∵⊥=（﹣2m）2﹣4×1×（m2+3）=4m2﹣4m2﹣12=﹣12＜0∴方程x2﹣2mx+m2+3=0没有实数解，即不论m为何值，该函数的图象与x轴没有公共点；（2）解：y=x2﹣2mx+m2+3=（x﹣m）2+3∴把函数y=x2﹣2mx+m2+3的图象沿y轴向下平移3个单位长度后，得到的函数的图象与x轴只有一个公共点．23．【答案】（1）解：①解：当a=-1，m=1时y=−x2−x+2= −(x+12)2+94∴点D的坐标为(−12，94)②∵y=−x2−x+2当y=0时解得：x1=−2∴点A的坐标为(−2，0)设直线AD的表达式为：y=kx+b（k≠0）{0=−2k+b94=−12k+b解得{k=32b=3∴直线AD的表达式为：y=32x+3∵F为线段AD上一动点设点F的横坐标为t∵FH⊥x轴，垂足为H，交抛物线于点P∴点P的横坐标也为t，点P的纵坐标为−t2−t+2∴P (t,−t2−t+2)，H（t，0)∴PH+OH= −t2−t+2+0−t= −t2−2t+2= −(t+1)2+3∴当t=−1时，PH+OH有最大值当t=−1时，y=32×(−1)+3= 32∴F（−1，3 2）（2）解：∵m= 2 3∴y＝ax2+(2a−ma)x−2am= ax2+(2a−23a)x−43a= a(x+23)2−169a∴D (−23，−169a)∵y＝ax2−(6a+ma)x+6am= ax2−(6a+23a)x+4a= a(x−103)2−649a∴E (103，−649a)∵y＝ax2+(2a−23a)x−43a当y=0时，ax2+(2a−23a)x−43a=0解得x1=−2∴A（-2，0）设直线AD的表达式为：y=mx+n{−2m+n=0−23m+n=−169a解得{m=−43an=−83a∴直线AD的表达式为y=−43ax−83a当x=103，y=−43a⋅103−83a= −649a∴点E在直线AD上∴直线AD经过点E.24．【答案】（1）解：y= 12x2﹣3x+4 = 12（x2﹣6x）+4= 12[（x﹣3）2﹣9]+4= 12（x﹣3）2﹣12（2）解：由（1）得：图象的顶点坐标为：（3，﹣1 2）对称轴为：直线x=3（3）解：∵a= 12＞0∴函数的最小值为：﹣1 2。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

２．A ３．D ４．y＝－２x２＋４x＋３５．右２上４６．长１０cm,宽１０cm 时面积最大,最大面积是１００cm２．图略
{a－b＋c＝－１,
７．(１)根据题意,得 c＝２, a＋b＋c＝３,
{a＝－１,
解得 b＝２,
c＝２．所以解析式为 y＝－x２＋２x＋２． (２)如图．
②
由
①
②
得h≥
８３
．
(第７题 )
８．D ９．B
１０．y＝－x２＋２x＋３１１．设 BD 交 y 轴于点 P．因为 BD ＝２,所以 PD ＝１,又
AE∥x轴,CH＝１,所以点 D(１,１),由对称性可知 DE＝
AB＝４,所以 PE＝５,即 E(５,１),易知 F(３,０)．设 y＝ ax２＋bx＋c,把 D、E、F 的坐标分别代入, 得
１４．(１)把 x＝０,y＝２,及 h＝２．６代入到 y＝a(x－６)２＋h, 即２＝a(０－６)２＋２．６,
∴ a＝－６１０．
∴ y＝－６１０(x－６)２＋２．６．
(２)当 h＝２．６时 ,y＝－６１０(x－６)２＋２．６．
x＝９时 ,y＝－６１０(９－６)２＋２．６＝２．４５＞２．４３,
３),那么函数的解析式是．
(第３题 )
５．把
y＝
１２x２
－３
的图象向平移个
单
位
得
y＝
１２
(x－２)２－３
的
图
象
,再
向
平
移
个
单
位
得
y＝
１２
(x－２)２＋１
的
图
象
．
６．有一根长为４０cm 的铁丝,把它弯成一个矩形框,当矩形框的长、宽各是多少时,矩形面积最大? 最大面积是多少? 利用图象描述矩形面积的长、宽之间的关系．
x
－１
０
１
ax２
１
ax２＋bx＋c ８
３
A．y＝x２－４x＋３
B．y＝x２－３x＋４
C．y＝x２－３x＋３
D．y＝x２－４x＋８
３．如图 ,抛物线的函数关系式是 ( )．
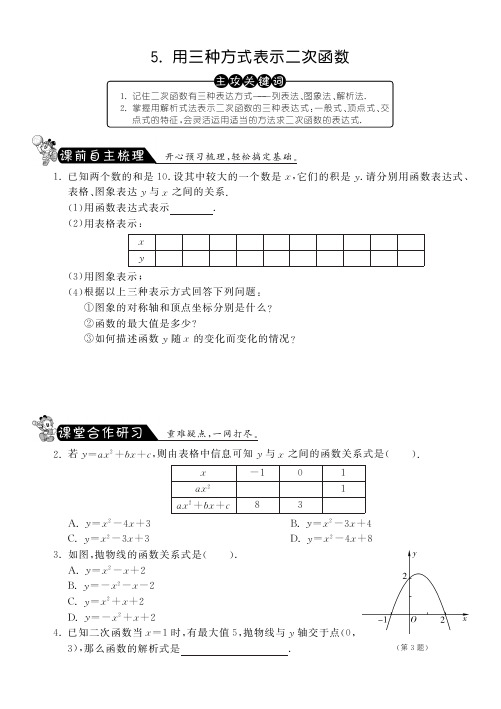
A．y＝x２－x＋２
B．y＝－x２－x－２
C．y＝x２＋x＋２
D．y＝－x２＋x＋２
４．已知二次函数当x＝１时,有最大值５,抛物线与y 轴交于点(０,
∴ m＝１．
故所成二次函数的表达式为 y＝x２－６x＋５．猜想:与一般形式抛物线 y＝ax２＋bx＋c 关于y 轴对称的二次函数为y＝ax２－bx＋c．１３．y＝－x２＋４x－３
７．如图 ,已知二次函数 y＝ax２＋bx＋c 的图象经过 A (－１,－１), B(０,２),C(１,３)． (１)求二次函数的解析式 ; (２)画出二次函数的图象．
(第７题 )
源于教材 ,宽于教材 ,举一反三显身手 .
D．y１≤y２
１０．抛物线 y＝－x２＋bx＋c 的图象如图所示 ,则此抛物线的解析式为．
１１．为了美观,在加工太阳镜时将下半部分轮廓制作成抛物线的形状(如图所示)．对应的两条抛物线关于y 轴对称,AE∥x 轴,AB＝４cm,最低点 C 在x 轴上,高 CH ＝１cm, BD＝２cm．求右轮廓线 DFE 所在抛物线的函数解析式．
x �� ０１２３４ ��
y �� ４１０１４ ��
点 A(x１,y１),B(x２,y２)在函数的图象上,则当１＜x１＜２,３＜x２＜４时,y１与y２的大小关系正确的是 ( )．
A．y１＞y２
B．y１＜y２
C．y１≥y２
(第１４题 )
５．用三种方式表示二次函数
１．(１)y＝－x２＋１０x (２)略 (３)略 (４)① 对称轴直线 x＝５顶点坐标 (５,２５) ②２５ ③当０＜x≤５时,y 随x 的增大而增大; 当５≤x＜１０时,y 随x 的增大而减小; 当 x＝５时 , y 有最大值２５．
x y (３)用图象表示 ; (４)根据以上三种表示方式回答下列问题 : ①图象的对称轴和顶点坐标分别是什么? ②函数的最大值是多少? ③如何描述函数y 随x 的变化而变化的情况?
重难疑点 ,一网打尽 .
２．若y＝ax２＋bx＋c,则由表格中信息可知y 与x 之间的函数关系式是( )．
(第１１题 )
１２．如图,已知抛物线y＝mx２＋nx＋p 与y＝x２＋６x＋５关于y 轴对称．求y＝mx２＋nx＋p的表达式．试猜想出一般形式的抛物线 y＝ax２＋bx＋c 关于y 轴对称的二次函数表达式．(不要求证明 )
(第１２题 )
瞧 ,中考曾经这么考 ! １３．(２０１２��江苏无锡)若抛物线y＝ax２＋bx＋c 的顶点是 A (２,１),且经过点 B(１,０),则抛物
开心预习梳理 ,轻松搞定基础 . １．已知两个数的和是１０．设其中较大的一个数是 x,它们的积是 y．请分别用函数表达式、
表格、图象表达y 与x 之间的关系． (１)用函数表达式表示． (２)用表格表示 :
∴ 球能越过网．
x＝１８时 ,y＝－６１０(１８－６)２＋２．６＝０．２＞０,
∴ 球会过界．
(３)x＝０,y＝２,代入到y＝a(x－６)２＋h 得a＝２３－６h;
x＝９时 ,y＝２３－６h＝ (９－６)２＋h＝２＋４３h＞２．４３,
①
x＝１８时 ,y＝２３－６h(１８－６)２＋h＝８－３h＞０,
{a＋b＋c＝１, ２５a＋５b＋c＝１, ９a＋３b＋c＝０．
ïìa＝
１４
,
解
得
ï íb＝ ï
－
３２
,
ïîc＝
９４
．
所
以
解
析
式
为
y＝
１４x２－
３２x＋
９４
＝
１４
(x－３)２．
１２．y＝x２＋６x＋５的顶点为 (－３,－４),即 y＝mx２＋nx＋p 的顶点为 (３,－４),设 y＝mx２＋nx＋p＝m(x－３)２－４．又y＝x２＋６x＋５与 y 轴交于点 (０,５),故点 (０,５)也在 y＝mx２＋nx＋p 上, ∴ ５＝m(０－３)２－４．
５．用三种方式表示二次函数
１．记住二次函数有三种表达方式 ——— 列表法、图象法、解析法．２．掌握用解析式法表示二次函数的三种表达式:一般式、顶点式、交
点式的特征 ,会灵活运用适当的方法求二次函数的表达式．
８．二次函数 y＝ax２＋bx＋c 的图象如图所示 ,那么下列四个结论 :
①a＜０;②c＞０;③b２－４ac≥０;④ab ＜０．
其中 ,正确的结论有 ( )．
A．１个
B．２个
C．３个
D．４个
(第８题 )
(第１０题 )
９．已知二次函数y＝ax２＋bx＋c中,其函数y 与自变量x 之间的部分对应值如下表所示:
线的函数关系式为．１４．(２０１２��安徽)如图,排球运动员站在点 O 处练习发球,将球从点 O 正上方２m 的 A 处发
出,把球看成点,其运行的高度 y(m)与运行的水平距离 x(m)满足关系式 y＝ a(x－６)２＋h．已知球网与 O 点的水平距离为９m,高度为２．４３m,球场的边界距 O 点的水平距离为１８m． (１)当h＝２．６时,求y 与x 的关系式(不要求写出自变量x 的取值范围); (２)当h＝２．６时,球能否越过球网? 球会不会出界? 请说明理由; (３)若球一定能越过球网,又不出边界,求h 的取值范围．