习题2.1(3)
(完整word版)人工智能课后习题答案(清华大学出版社)
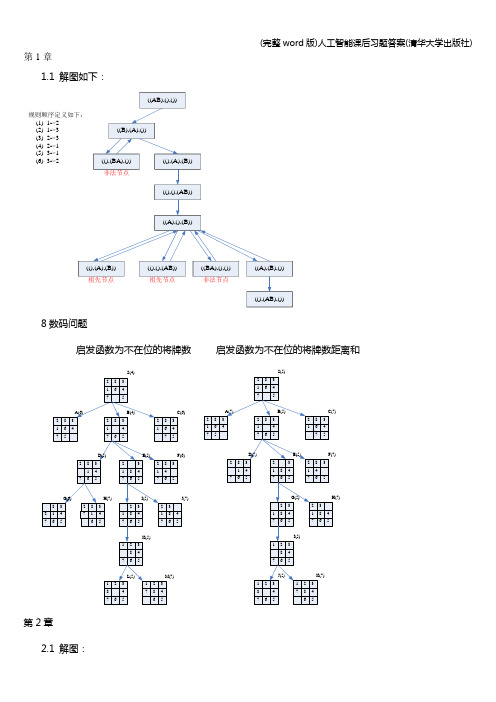
第1章1.1 解图如下:(1) 1->2(2) 1->3(3) 2->3(6) 3->2(5) 3->1(4) 2->1 8数码问题启发函数为不在位的将牌数启发函数为不在位的将牌数距离和S(4)S(5)第2章2.1 解图:第3章3。
18(1)证明:待归结的命题公式为()P Q P ∧→,合取范式为:P Q P ∧∧,求取子句集为{,,}S P Q P =,对子句集中的子句进行归结可得:① P ② Q ③ P④①③归结由上可得原公式成立。
(2)证明:待归结的命题公式为())(()())P Q R P Q P R →→∧→→→(,合取范式为:()()P Q R P Q P R ∨∨∧∨∧∧,求取子句集为{,,,}S P Q R P Q P R =∨∨∨,对子句集中的子句进行归结可得:①P Q R ∨∨ ②P Q ∨③ P④ R ⑤ Q ②③归结 ⑥P R ∨①④归结 ⑦ R ③⑥归结 ⑧④⑦归结由上可得原公式成立。
(3)证明:待归结的命题公式为()(())Q P Q P Q →∧→→,合取范式为:()()Q P Q P Q ∨∧∨∧,求取子句集为{,,}S Q P Q P Q =∨∨,对子句集中的子句进行归结可得: ①Q P ∨②Q③Q P∨④P①②归结⑤P②③归结⑥④⑤归结由上可得原公式成立。
3.19 答案(1){/,/,/}=mgu a x b y b z(2){(())/,()/}=mgu g f v x f v u(3)不可合一(4) {/,/,/}=mgu b x b y b z3.23 证明R1:所有不贫穷且聪明的人都快乐:(()()())∀∧→x Poor x Smart x Happy x R2:那些看书的人是聪明的:(()())∀→x read x Smart xR3:李明能看书且不贫穷:()()∧read Li Poor LiR4:快乐的人过着激动人心的生活:(()())∀→x Happy x Exciting x 结论李明过着激动人心的生活的否定:()Exciting Li将上述谓词公式转化为子句集并进行归结如下:由R1可得子句:①()()()∨∨Poor x Smart x Happy x由R2可得子句:②()()read y Smart y∨由R3可得子句:③()read Li④()Poor Li由R4可得子句:⑤()()∨Happy z Exciting z有结论的否定可得子句:⑥()Exciting Li根据以上6条子句,归结如下:⑦()Happy Li⑤⑥Li/z⑧()()Poor Li Smart Li∨⑦①Li/x⑨()Smart Li⑧④⑩()read Li⑨②Li/y⑪⑩③由上可得原命题成立。
人教版二年级下册数学《2.1 第3课时 平均分(3) 》教案

人教版二年级下册数学《2.1 第3课时平均分(3)》教案一、教学目标1.了解什么是平均数。
2.能够用简单的计算方法求平均数。
3.能够在实际生活中应用平均数的概念。
二、教学重点1.平均数的概念理解。
2.利用具体例子计算平均数。
三、教学难点1.解决实际生活中的问题,应用平均数的概念。
四、教学准备1.教案、黑板、彩色粉笔、学生练习册。
五、教学过程1. 导入(5分钟)老师用一个简单的例子引导学生思考什么是平均数,引起学生的兴趣。
2. 讲解(15分钟)1.通过投影仪展示幻灯片,讲解平均数的概念。
2.举例说明平均数的计算方法。
3. 练习(20分钟)1.让学生在黑板上做几道简单的练习题,巩固平均数的计算方法。
2.分组让学生相互讨论,解决实际生活中的平均数问题。
4. 提高(10分钟)讨论一些稍微复杂一点的问题,引导学生思考更多的平均数应用场景。
5. 小结(5分钟)对本节课的内容进行小结,梳理重点难点。
六、课堂作业1.完成课后练习册上的练习题。
2.思考在生活中还有哪些应用平均数的情况,写下来。
七、板书设计1.平均数:一组数的平均值,计算方法是将一组数相加,然后除以这组数的个数。
2.计算公式:平均数 = (数1 + 数2 + … + 数n)/ n八、教学反思本节课采用了多种教学手段,激发了学生对平均数的兴趣,但在实际生活应用的部分可以再丰富一些,引导学生更加深入地理解平均数的概念。
以上是本节课的教学内容,希望每位同学都能够掌握平均数的计算方法,能够灵活运用在实际生活中。
2020-2021学年部编版道德与法治八年级下册2.1 坚持依宪治国 同步习题

2020-2021学年部编版道德与法治八年级下册2.1-坚持依宪治国同步习题一、单项选择题1.《宪法》规定公民基本权利,《民法典》对公民的隐私权、肖像权、紧急自卫权、继承权、人身权利等公民的基本权利做了详细和深度的规定。
可见()民法典规定的内容是全局性根本性的问题宪法是根本法,规定和制约了民法典内容民法典是其他法律的立法基础和立法依据民法典是基本法,细化并延伸宪法的内容A. B. C. D.2.法治是治国理政的基本方式。
我国的根本法是()A. 宪法B. 刑法C. 立法法D. 义务教育法3.近年来,从设立国家宪法日到开展“宪法宣传周”活动, 再到实施宪法宣誓制度, 中国始终在大力弘扬宪法精神、维护宪法权威、推动宪法实施、加强宪法监督。
关于宪法权威,下列认识正确的是()宪法具有至高无上的权威宪法的权威关系国家的命运、社会的安定和人民的根本利益如果宪法没有权威,法治的权威也能树立起来一切组织和个人都必须在宪法和法律范围内活动,都必须维护宪法权威A. B. C. D.4.宪法规定了国家生活中最根本、最重要的问题。
下列选项中属于宪法规定内容的有()国家性质和根本任务商业贿赂问题国家经济制度中小学生辍学问题A. B. C. D.5.我国现行宪法出台前,多次广泛征询社会各界意见,并进行全民讨论,广大人民群众提出了许多具有建设性的建议。
这表明我国宪法()A. 是所有公民意志的体现B. 是人民意志和利益的集中体现C. 规定了公民生活中的所有问题D. 规定了国家生活中的根本任务6.“如果把我国所有的法律比作一支由众多兵种组成的军队,那么宪法就是这支军队的最高统帅。
如果把我国所有的法律比作一个配有多种乐器的交响乐团,那么宪法就是这个乐团的指挥。
”这是因为宪法()A. 是国家的根本法和治国安邦的总章程B. 对全体社会成员具有普遍约束力C. 体现了广大人民的意志和利益D. 保障国家长治久安和社会健康发展7.如今,随着外卖平台的迅猛发展,食品卫生问题让消费者忧心忡忡。
机械制图(含习题集)(第二版)(章 (3)

第2章 投影的基本知识
图2-16 点的三面投影与坐标的关系
第2章 投影的基本知识 (2) 过a′作OZ轴的垂线交OZ轴于aZ,在垂线上自aZ向右
量取10 mm得a″(a″也可由a通过作圆弧或45°斜线求得)。 a、a′、a″为A点的三面投影。 例2.2 已知B点的正面投影b′和水平投影b,求该点的侧
第2章 投影的基本知识 三视图的配置关系为:俯视图在主视图的正下方,左视图
在主视图的正右方,如图2-8(a)所示。 画图时,投影面的边框线和投影轴均不必画出,同时按上
述方法展开,即按投影关系配置视图时,也不需要说明视图名 称,最后得到的三视图如图2-8(b)所示。
第2章 投影的基本知识
图2-8 物体的三视图
第2章 投影的基本知识
图2-14 三棱锥的三视图和立体图
第2章 投影的基本知识
如图2-15(a)所示,设有一空间点A,由点A分别向H、V和W 面投影,可得到A点的水平投影a、正面投影a′和侧面投影a″。 图中每两条投影线确定一个平面,它们与三投影轴分别相交于 aX、aY和aZ,以空间点A、三个投影a、a′和a″以及aX、aY、aZ 和原点O为顶点可构成一个长方体。
第2章 投影的基本知识
图2-4 不同形体可以得到相同的投影
第2章 投影的基本知识 1.三投影面体系 通常选用三个互相垂直相交的投影面,建立一个三投影面
体系,如图2-5所示。三个投影面分别称为:正立投影面,简 称正面,以V表示;水平投影面,简称水平面,以H表示;侧立 投影面,简称侧面,以W表示。三个投影面之间的交线OX、OY、 OZ称为投影轴,三根互相垂直的投影轴的交点O称为原点。
第2章 投影的基本知识
图2-1 中心投影法
第2章 投影的基本知识 2.投影法的种类 1) 中心投影法 投影线交汇于一点的投影法称为中心投影法,如图2-1所
寿险精算学(第3版)习题答案2

【解2.1】(1)可以被写成=(90−p(r200)18000,又由于达到极限寿命时=0,故=90。
(2)证明:因为,0=1;其次,达到极限寿命=90时,有90=0;且,的导数−110−218000<0,>0。
由此,生存函数的三个条件都被满足。
(3)93333.0)0()10(00010==S S p (4)(030−050)020(5)=−0'(p/0==110+218000−110−2因此,40=0.015833。
【解2.2】作为生存函数的基本属性有:(0)1,S =函数是单调递减的,同时lim ()0x S x →∞=。
(1)由于()exp[0.7(21)](10.72ln 2)xxS x x '=---⨯⨯,(0)0.51480S '=>,说明该函数不满足单调递减的性质。
所以,它不能作为生存函数。
(2)由于(0)1S =,3()2(1)0S x x -'=-+<,21lim ()lim0(1)x x S x x →∞→∞==+。
该函数可以作为生存函数。
(3)由于(0)1S =,()2()(2)0x S x ex -'=-<,lim ()0x S x →∞=。
该函数可以作为生存函数。
【解2.3】(1)4320751001)75(1)75(=--=-=S F (2)20017510040175)()75(=-==-=x x S dx d f (3)501412001)75()75()75(===S f μ【解2.4】(40)40(40)(40)40(40)(40)60(),060(40)60(40)1(),060(40)601()(),06060T t T T t T S t tS t p t S S t t t S t tf x p t t μμ+-===<≤'+=-=<≤+-==<≤【解2.5】()18)100(9)100(6)100(3100)100()100(2)]([2)]([3100)100()100()]([)100()100(222210002221000100022100022x x x x dt x t x t x T E dt p t x T Var xdt x t x dt p x T E x t x l l p xxx t xxx tx t x x t -=---=⎪⎭⎫⎝⎛------=-=-=---==---==⎰⎰⎰⎰----+【解2.6】所有表达式均为非负,因此需要验证是否满足0∞B =∞,使得0)(=∞S (1)∞==∞∞⎰0ln C BC dx BC xx,可以(2)∞=+=+∞∞-⎰001)ln()(x b a dx x b a ,可以(3)21)1(21)1(023=+-=+∞∞-⎰x dx x ,不可以【解2.7】把30.250x q +=代入120.170x q +=式中,得11232120.1700.680x x x x x x q p p q p p ++++++=⋅⋅=⇒=上式与已知条件11210.090x x x q p q+++=⋅=联立求解,解出10.770x p +=,20.117x q +=最后得1212(1)0.230.1170.347x x x x q q p q +++++=-+=+=【解2.8】由()1xS x ω=-,可知~(0,)X U ω,且有(20)~(0,20)T U ω-则[()]2x E T x ω-=,2()[()]12x Var T x ω-=已知020e 40=,即20401002ωω-=⇒=所以2(20)Var[T(20)]533.312ω-==【解2.9】首先计算K 的生存函数k012197k p +1015415则210414()09715151502210422()(21)13509715151513422()()[()]225E K p k k E K k p k k Var K E K E K ==++=∑==+⋅=⋅+⋅+⋅=∑==-=【解2.10】证明:(1)x t x x x t q t T t T p -=<-=≥=1)Pr(1)Pr((2)xu t x t x x x x ut p p u t T t T u t T t q +-=+≥-≥=+≤≤=)Pr()Pr()Pr((3)()()()tx u x t t x x x ut p p u T t T p ++⋅=≥⋂≥=Pr 【解2.11】(1)证明:110111111111+∞+∞+-∞∞+=+≤⋅+=+==⎰⎰⎰⎰⎰⎰x x x t x x t x t x t x t x e dt p dtp p dt p dt p dt p dt p e (2)证明:由于是关于的递减函数,因此有K1B≥所以xk x k k k kx tx t x e p dtp dt p e =≥==∑∑⎰⎰∞=+∞=+∞101【解2.12】证明:()()()()()()()t x t x x t S x t f x t S x t x t p p t t S x S x S x μμ+∂∂++-++====∂∂【解2.13】318.02005exp 20025exp 20015exp )5()25()15(200exp 100exp )(2225101020=⎪⎪⎭⎫⎝⎛-⎪⎪⎭⎫⎝⎛--⎪⎪⎭⎫ ⎝⎛-=-=⎪⎪⎭⎫⎝⎛-=⎭⎬⎫⎩⎨⎧-=⎰S S S q x dt t x S x 【解2.14】[][]8684284p =其中86l 已知,而[][][][][]2848484184841(1)(1)p p p q q ++==--由已知条件推导出[][][]85841848483144508030360.3225550803343640050800.20644556400q q q q q ++-=⋅=⋅=-==⋅⋅=⋅=【解2.15】(1)7[76]=83[76]=1192816608=0.718208(2)6|275+1=82−8475+1=0.084631【解2.16】40+1=40(1−40),40+2=402p [40],43=40+2−40∗2|40,46=43−40+1∗2|340+1.因此343=46/43=1−(1−40)2|340+1/(2p [40]−2|40)=1−(1−0.01608)×0.08964/(0.95977-0.02383)=0.905765【解2.17】151025:2525152540015100.040.04150.06015.40667t t tte p dt p p dtedt eedt--⨯-=+=+=⎰⎰⎰⎰【解2.18】(1)0.752.5=1−53.252.5=1−0.853+0.2540.552+0.553=0.0068381.7|1.252.5=54.2−55.452.5=0.854+0.255−0.655−0.4560.552+0.553=0.022690(2)0.752.5=1−0.5p 52.50.2p 53=1−520.5530.2=0.0068351.7|1.252.5=1.7p 52.51−1.2p 54.2=0.5p 52.5530.2p 541−0.8p 54.20.4p 55=520.553540.21−540.8550.4=0.022668【解2.19】因为{}10102102221exp ()=1exp 2()1exp ()1()1(1)2x x x x x q x t dt x t dt x t dt p q q q μμμ⎡⎤''=--+⎢⎥⎣⎦⎡⎤--+⎢⎥⎣⎦⎡⎤=--+⎢⎥⎣⎦=-=--=-⎰⎰⎰由此推出2x xq q '<。
第2章习题答案

UO = U Z = 6V
IO
= UO RL
=
6 2 ×103
A = 3mA
IR
= UR R
= UI
−UO R
= 18 − 6 1.2 ×103
A = 10mA
I Z = I R − IO = (10 − 3)mA = 7mA
(2)S1 和 S2 均合上时的 IO、IR 和 IZ;R=0 和 Dz 接反两种情况下电路能否起稳压作用。 此时电路是由单相桥式整流电路、电容滤波电路和稳压二极管稳压电路构成。
UO
式中 R2′ 为电位器 RP 滑动端以下的部分电阻。
U o′
=U+
R1
R2′ + + RP
R2 +
R2
U
O
(3)输出电压 Uo 的可调范围有如下关系式
当 R2′ =0 时
U o′ = U XX = U O
R1
R2′ + + RP
R2 +
R2
U
O
+ U XX
=Uo
Uo
−
R2′ + R2 R1 + RP + R2
IR
=
12 3.9
mA
=
3.08mA
IA =0
I B = I R = 3.08mA
(3)DA,DB 均导通,VY 被钳位在 3V。各元器件电流如下:
IR
=
12 − 3 mA = 3.9
2.30mA
IA
=
IB
=
1 2
IR
= 1.15mA
题解图 2
电子技术习题集-答案

第2章 习题2.1.1 如右下图所示电路中,E 12V =, D 为硅二极管,R 10K =Ω,则二极管D 和和电阻R 上的电压各为多少?流过二极管的电流多大?解: 二极管正偏导通:D U 0.7V ≈; R U 120.711.3V =-=D R 11.3I I 1.13mA 10===2.1.2 在下图中的各电路图中,i u 12sin t ω=V ,二极管D 的正向压降忽略不计。
试分别画出输出电压o u 的波形。
(a ) (b ) (c )解:2.1.3二极管电路如图所示,试分别判断图(a )和(b )中的二极管是导通还是截止,并求出AB 两端电压AB U 。
设二极管是理想的。
(a) (b)解:(a) D 导通,AB U 6V =-; (b )D1导通,D2截止;AB U 0V =;2.2.1在下图中,所有稳压二极管均为硅管且稳压电压Z U 6V =,输入电压i u 12sin t ω=V ,画出输出电压o u 波形图。
解:2.2.2在下图所示的(a)和(b )分别为稳压管的并联和串联连接,哪种稳压管的用法不合理?试说明理由。
解:(a )由于稳压管的击穿电压各不相同,击穿电压低的管子工作,而另一个不工作。
(b)可以串联连接,输出电压为两个稳压管稳压电压之和。
2.2.2在如图所示的稳压管稳压电路中, I U 14V =,波动范围10%±;稳压管的稳定电压Z U 6V =,稳定电流Z I 5mA =,最大耗散功率ZM P 180mW =;限流电阻R 200Ω=;输出电流o I 20mA =。
(1)求I U 变化时稳压管的电流变化范围;(2)如果负载电阻开路,会发生什么现象?解:输入电压波动范围:Imin I U 0.9U (0.914)V 12.6V ==⨯=Imax I U 1.1U (1.114)V 15.4V ==⨯=I U 波动时流过限流电阻R 的电流变化范围为:Imin Z R min U U 12.66I 0.033(A)33mA R 200--====Imax Z R max U U 15.46I 0.047(A)47mA R 200--====稳压管最大稳定电流ZM ZM Z P 180I 30mA U 6=== (1)Z D min R min o I I I 332013mA =-=-=Z D max R max o I I I 472027mA =-=-=(2)如果负载电阻开路,即o I 0mA =,则稳压管中电流为限流电阻上的电流。
大气污染控制工程:大气习题(2,3,5,6)

相关知识点:
T ( P ) RCp ( P )0.288 -泊松方程
T0 P0
P0
第五章 习 题
5.5 根据对某旋风除尘器的现场测试得到:除尘器进口的气流 量为10000 mN3/h,含尘浓度为4.2g/mN3 ,除尘器出口的气体流 量为12000 mN3/h ,含尘浓度为340mg/mN3,试计算该除尘器 的处理气体流量、漏风率和除尘效率 (分别按考虑漏风和不考虑漏风两种情况计算)。 解:处理气体流量:
4~5
5~6
6~8 8~10 10~12 20~30
99.63% 99.20% 99.20% 99.33% 99.38% 99.30%
100.00% 99.00% 98.00% 97.00% 96.00% 95.00% 94.00% 93.00%
<0.60.6-0.70.7-0.8 0.8-1 1~2 2~3 3~4 4~5 5~6 6~8 8~1010~12 20~30
产生的烟气量为:
注意单位: 1、浓度单位(体积分数):ppm,% 2、烟气量一般用体积表示
2.2 普通煤的元素分析如下:C65.7%,灰分18.1%,S1.7% H3.2%,水分9.0%,O22.3%(含N量不计) (1)计算燃煤1kg所需要的理论空气量和SO2在烟气中的浓度 (以体积分数计)
(2)假定烟尘的排放因子80%,计算烟气中灰分的浓度(以 mg/m3表示) (3)假定用流化床燃烧技术加石灰石脱硫。石灰石中含Ca35%。 当Ca/S为1.7时,计算燃煤1t需加石灰石的量。
转化为标态下的体积:
(2) 根据(1)中的计算,燃烧1kg重油产生的干烟气量为:
燃料中的S完全转化为SO2时,烟气中SO2的浓度最大。因此烟气中SO2 的最大浓度(体积分数)为
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
感受理解
1、分别根据下列条件,求A、B两点之间的距离
(1)3202,,,BA
(2)3330,,,BA
(3)3353,,,BA
2、已知点P21,,分别求点P关于原点、x轴和y轴的对称点的坐标
3、设点A在x轴,点B在y轴上,线段AB的中点M的坐标是12,,求线段AB的长
4、已知A,B两点都在直线1xy上,且AB的中点M的坐标是12,,求线段AB的
长
5、已知两点4132,,,BA,若点Pyx,到点A,B的距离相等,求实数yx,满足的条件
6、已知点yxP,在直线04yx上,O是坐标原点,求OP的最小值
7、分别根据下列条件,求点P到直线l的距离
(1)12,P,032xl:
(2)0304343yxlP:,,
8、已知直线l到两条平行直线022yx和042yx的距离相等,求直线l的方程
9、已知直线l在y轴上的截距为10,且原点到直线l的距离是8,求直线l的方程
10、已知点P在直线053yx上,且点P到直线01yx的距离等译2,求点P
的坐标
11、已知点4241087,,,,,CBA,求ABC的面积
12、已知直线l过点32,,且原点到直线l的距离是2,求直线l的方程
13、在ABC中,点E、F分别为AB,AC的中点,建立适当的直角坐标系,证明:EF//BC,
且EF=BC21
思考运用
14、过点03,P作直线l,使它被两条相交直线022yx和03yx所截得的线
段恰好被点P平分,求直线l的方程
15、已知光线通过点32,A,经x轴反射,其反射光线通过点75,B,求入射光线和反射
光线所在直线的方程
16、已知光线通过点32,A,经直线01yx反射,其反射光线通过点11,B,分别求入
射光线和反射光线所在直线的方程
17、在直线02yx上求一点P,使它到原点的距离与直线032yx的距离相等
18、已知直线33xyl:,求:
(1)直线l关于点M23,对称的直线的方程
(2)直线02yx关于l对称的直线的方程
19、建立适当的坐标系证明平行四边形的平方和等于两条对角线的平方和
20、求证:点abBbaA,,,关于直线xy对称
拓展研究
21、已知2631,,,NM,点P在x轴上,求使PNPM最小时点P的坐标
22、某人上午8时从山下大本营出发登上,下午4时到达山顶,次日上午8时从山顶沿原路
返回,下午4时回到山下大本营,如果该人以同样的速度匀速上山、下山,那么两天中他可
能在同一时刻经过途中同一地点吗?如果他在上山、下山过程中不是匀速行进,他还可能在
同一时刻经过途中同一地点吗?
