大学物理_静电场2_电场强度
合集下载
第2章静电场
“立个球面”的立体角＝？ 2. “任意曲面”dS对“某点”所张的立体角 (1) 以R0为半径的“球面”
3. “立体角”的重要结论
散度方程微分形式的引出：
请注意：此处的ρ 是指自由电荷的体密度ρvf ！
（强调）散度方程
• 物理意义： 它们描述了静电场的发散性，给出了通过封闭面的 电通量与面内所围电荷量之间的关系； • 积分形式说明： 任意封闭面的电通量＝面内所围电荷总量； 电通量为0，则封闭面内不包含电荷，即面内无源; 进而说明：静电场具有通量源，即自由电荷。 • 微分形式说明： 静电场(电位移)散度＝该点处电荷体密度; 进而，静电场具有散度源，即自由电荷的体密度。
例2. 求电荷分布
已知真空中电场分布,求各处电荷分布的体密度. 分析: 由电场分布可知, 球对称, 电场只有径向分量； 可以直接运用散度方程求解； 仍要分球内和球外两种情况；
作业
• 试计算电荷面密度为σ 的无限大平面周围 的电场。
静电场的旋度方程
• 首先应注意，这是静电场，不是任意电场； • 积分形式: 电场沿任意闭合曲线的积分为0； C指任意闭合曲线； C自身方向与C所围曲面方向满足右手规则； 积分式即电场的环流量； • 微分形式: 静电场的旋度为0 无论在有源区还是无源区； 电荷是静电场的什么源？体密度是什么源？
真空中距离为R的两点电荷q1，q2 q1对q2的作用力，电荷量正比，距离平方反比 矢量方向：q1指向q2 真空中介电常数(Dielectric Constant)
1 12 0 8.85 10 ( F / m) 9 4 9 10
真空中静止点电荷的电场强度
q 2受到的电场力：F R, q1 , q2
总结1：
库仑定律(真空中静止电荷电场)
大学物理：2第二讲 电场强度计算续、高斯定理
2
R
r
x
p dE// x
E
qx
4 0 r 3
iˆ
dE dE
cos x / r
1
讨论：1. x 0 : Eo 0
E
qx
40 (R2
x2 )3/2
iˆ
o
y
r
圆环中心电场为零
2.
x R :
Ep
q
40 x2
iˆ
R
o
z
E
x px
p
R
x
●无论带电体形状如何，在离其足够远处均可视为
点电荷。 2
例4：半径为R的簿圆盘均匀带电，面电荷密度为。
求中心轴线上一点 p处的电场强度。
解：将圆盘分割成许多带 电细圆环，其电量
dq ds 2 rdr
细圆环电场
dr
l
r
Ep
o xpx
dE
dqx
40 (r2
x2 )3/2
2 rxdr rxdr 40 (r2 x2 )3/2 20 (r2 x2 )3/2
3
dE
rxdr 20 (r2 x2
二、电通量
●通过某一曲面的电力线数，叫做 通过该曲面的电通量。记为“e”.
电通量的计算
s
de E dS
e
E dS
S
通过闭合曲面的电通量
e S E dS
规定：曲面正法线由曲面指向外
E de dSn
ds E
ds
E
q
s
11
例：点电荷q位于球面内球心处，求通过该球面的
电通量。
解：球面上的电场强度
各点产生的电场。
解：由对称性可知，该球壳产生的
大学物理电场强度-PPT
E Ei
i 1
三、电场强度得计算
1、 点电荷得电场
E
F q0
q q0
4π 0r2
r0
1 q0
q
4π 0r2
r0
E
E
q
r0
r
PF
q0
r
r
特点:(1)就是球对称得;
当 r 0 时，
(2)就是与 r 平方成反比 得非均匀场。
E ∞? 此时,点电荷模型已失效, 所以这个公式已不能用！
2、 点电荷系得电场
场强的计算
求均匀带电半圆环圆心处的 E，已知 R、
dq
电荷元dq产生得场 dE 4 0 R2 dq
Y
根据对称性 dE y 0
E
dEx
dE
sin
0
Rd 4 0 R2
sin
4 0R2
( cos )
0
2 0 R
d o
R
dE
X
例4、均匀带电圆盘轴线上一点得场强。
设圆盘带电量为q,半径为R。
d E cos
cos x r
dq
r a
y
p d E//
r (a2 x2 )1 2
x
x
z d E dE
E
1
4 0
q
2a
dl r2
cos
1
4 0
q r2
cos
2 a
1
4 0
(a 2
qx x2)3
2
E
4 0 (
xq x2
a2
3
)2
i
xq
E
4 0 (
x2
a2
3
)2
大学物理——静电场汇总
第七章静电场§7.1点电荷库仑定律一、点电荷和狄拉克d 函数❶点电荷:是一个理想模型,忽略带电体本身的大小和形状,而将其抽象成带电荷的质点。
❷电荷连续分布线分布:dl dq =λ面分布:ds dq =σ体分布:vd dq =ρ❸d 函数(),00⎩⎨⎧=∞≠=x x X d ()1=⎰∞∞-dx X d 二、库仑定律❶真空12f 1q 2q 12r 21ff1q 2q12f 21f ,12312211212r r q Kq f f =-=229cNm 100.9-⨯=K设,410πε=K 212120mN C 1085.8---⨯=ε则3120122121124r r q q f f επ =-=电介质312312441221012212112r r q q r r q q f f r πεεεπ ==-=εr 电介质的相对介电常数ε 电介质的介电常数§7.2电场电场强度一、电场电荷周围存在的一种特殊形态的物质,具有能量、动量等。
电场对外表现:其一：电场对引入其中的电荷有力的作用;其二：当电荷在电场中移动时,电场对它要做功。
电荷之间的作用是通过电场实现的。
电荷⇔⇔电荷电场二、电场强度为了描述电场对电荷的施力性质，引入一个基本物理量－－电场强度，简称场强，用表示,其定义为EqF E=三、场强迭加原理处于由产生的电场中q 0n q q q ,,,21 ∑∑=====n i in i iE F FE q q 11四、场强的计算点电荷电场,430rrq q F πε =34r r q E πε =点电荷系电场∑∑==i i i ii i r r q E E 34πε任意带电体电场用积分求解.解体步骤:1.将带电体分成无数个电荷元(电荷元不一定是点电荷)电荷元dq 在空间某点的场强:r rdq E d341πε=2.选取适当的坐标系,写出的各个分量的表达式。
Edzy x dE dE E d ,,3.求zy x dE dE E d ,,,⎰=E d E x x ,⎰=E d E y y ⎰=E d E z z 此步最好利用电荷分布的对称性判断方向,减少计算.E4. 带电体的场强kE j E i E E z y x++=§7.3 电感强度高斯定理一、电感强度D在各向同性的均匀电介质中，任一点处的电感强度等于该点的电场强度和介电常数的乘积，即：D εE EDε=二、电力线和电感线电力线电力线在电场中任一点处,通过垂直于的单位面积的电力线条数等于该点处的量值。
大学物理第10章 电荷和静电场-2
例如 孤立的导体球的电容
Q
Q C V
地球
Q Q 4π 0 R
4π 0 R
6
R
4
RE 6.4 10 m, CE 7 10 F
二 电容器
导体组合，使之不受周 围导体的影响 ——电容器
电容器的电容：
当电容器的两极板分
别带有等值异号电荷Q时 ，电量Q与两极板间相应 的电势差VA-VB的比值。
详细说明如下
二、导体表面的电荷和电场 导体表面电荷的分布与导体本身的形状以及附近 带电体的状况等多种因素有关。
孤立导体的电荷面密度与其表面的曲率有关，曲率越大 电荷面密度越大。 表面突出尖锐部分曲率大, 电荷面密度大;
表面比较平坦部分曲率小, 电荷面密度小; 表面凹进部分曲率为负, 电荷面密度最小。
S
–q'
说明空腔内表面所带总电量与空腔内带电体的电量 相等、符号相反。导体空腔是等势体，腔内场强不 为零，不是等电势区间。
四、导体静电平衡性质的应用
1. 静电屏蔽 (electrostatic shielding)
＋q ＋q ＋q
-q
-q
利用导体静电平衡的性质，使导体空腔内部空 间不受腔外电荷和电场的影响，或者将导体空腔 接地，使腔外空间免受腔内电荷和电场影响，这 类操作都称为静电屏蔽。无线电技术中有广泛应 用，例如，常把测量仪器或整个实验室用金属壳 或金属网罩起来，使测量免受外部电场的影响。
Cn
VB
等效
VA
C
VB
令 U VA VB
q1 C1U
q2 C2U
•导导体表面外附近的场强 E 0
★ 注意：
E 仅由 S 处电荷产生而与其它电荷无关吗？为什么？
大学物理电介质内的电场强度
大学物理电介质内的电场强度
目
CONTENCT
录
• 引言 • 电介质基础知识 • 电介质内的电场强度概念 • 电介质内的电场强度分布 • 电介质内的电场强度与物理现象 • 总结与展望
01
引言
主题简介
电场强度是描述电场中电场力作用强弱的物理量，其大小表示电 场中单位点电荷所受的静电力，方向与正电荷在该点所受的静电 力方向相同。
总结词
电场强度是电磁能量转换的重要参数， 影响电磁波的传播和吸收。
VS
详细描述
在电磁波传播过程中，电场强度是描述电 磁波能量的重要参数。不同频率和方向的 电磁波在介质中传播时，会与介质内的分 子相互作用，将电磁能转换为热能或其他 形式的能量。电场强度越大，电磁波的能 量越强，对介质的加热和吸收效果也越明 显。
03
电介质内的电场强度概念
电场强度的定义与计算
定义
电场强度是描述电场中电场力作用强 弱的物理量，用E表示。
计算
电场强度的大小等于单位电荷在该点所 受的电场力，计算公式为E=F/q，其中 F为点电荷所受的电场力，q为点电荷的 电量。
电场强度与电介质的关系
电介质对电场的影响
在电场中，电介质中的电场强度与真 空中的电场强度不同，因为电介质中 的电荷会受到束缚，使得电介质中的 电场分布和强度发生变化。
详细描述
在电力系统中，电介质起着绝缘作用，保证电气设备的 安全运行。在储能技术中，电介质用于储存电能，如电 解电容器的使用。此外，在电磁波传播方面，电介质如 玻璃、聚乙烯等是重要的传输媒介。在静电场和恒定磁 场中，电介质对场的影响可忽略不计，但在交变电磁场 中，特别是在高频电磁场中，电介质对场的影响不可忽 略，此时需要在原有电磁场方程中增加描述电场和磁场 能量与电介质有关的项，从而得到更精确的电磁场理论 。
目
CONTENCT
录
• 引言 • 电介质基础知识 • 电介质内的电场强度概念 • 电介质内的电场强度分布 • 电介质内的电场强度与物理现象 • 总结与展望
01
引言
主题简介
电场强度是描述电场中电场力作用强弱的物理量，其大小表示电 场中单位点电荷所受的静电力，方向与正电荷在该点所受的静电 力方向相同。
总结词
电场强度是电磁能量转换的重要参数， 影响电磁波的传播和吸收。
VS
详细描述
在电磁波传播过程中，电场强度是描述电 磁波能量的重要参数。不同频率和方向的 电磁波在介质中传播时，会与介质内的分 子相互作用，将电磁能转换为热能或其他 形式的能量。电场强度越大，电磁波的能 量越强，对介质的加热和吸收效果也越明 显。
03
电介质内的电场强度概念
电场强度的定义与计算
定义
电场强度是描述电场中电场力作用强 弱的物理量，用E表示。
计算
电场强度的大小等于单位电荷在该点所 受的电场力，计算公式为E=F/q，其中 F为点电荷所受的电场力，q为点电荷的 电量。
电场强度与电介质的关系
电介质对电场的影响
在电场中，电介质中的电场强度与真 空中的电场强度不同，因为电介质中 的电荷会受到束缚，使得电介质中的 电场分布和强度发生变化。
详细描述
在电力系统中，电介质起着绝缘作用，保证电气设备的 安全运行。在储能技术中，电介质用于储存电能，如电 解电容器的使用。此外，在电磁波传播方面，电介质如 玻璃、聚乙烯等是重要的传输媒介。在静电场和恒定磁 场中，电介质对场的影响可忽略不计，但在交变电磁场 中，特别是在高频电磁场中，电介质对场的影响不可忽 略，此时需要在原有电磁场方程中增加描述电场和磁场 能量与电介质有关的项，从而得到更精确的电磁场理论 。
大学物理 电场强度
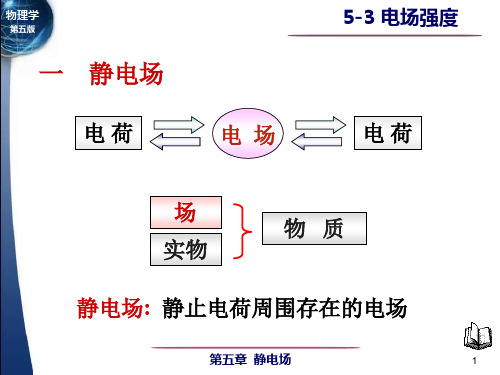
E
1 4πε0
(x
q r0
2)2 i
E
E
E
4
q πε0
(
x
2
2 xr0 r02
4)
2
i
q
q
- O. +
r0 2 r0 2
x
. A
E E
x
第五章 静电场
10
物理学
第五版
5-3 电场强度
E
q 4πε0
(
x
2
2xr0 r02
4)2
i
x r0
E
1
4πε0
2r0q x3
i
1 4πε0
第五章 静电场
12
物理学
第五版
5-3 电场强度
例1:均匀带正电细棒:(已知L,a,电荷线密度λ)，求延长线
上P点的场强。
L, dr
a
p
解：
dr dE 4 0r 2
r
E 由于各dE同向：
a L dr 1 1
E dE
( )
4 0 a r 2 4 0 a a L
若L a : E [1 (1 L)1] L
例2 有一半径为R，电荷均匀分布的薄圆
盘，其电荷面密度为 . 求通过盘心且垂直
盘面的轴线上任意一点处的电场强度.
R
o xPx
第五章 静电场
19
物理学
第五版
5-3 电场强度
解 σ q / πR2 dq 2 π rdr
dEx
4
xdq πε0 (x2
r 2 )3
2
2ε0
xrdr (x2 r2)3
4 0a
a
大学物理电场电场强度
Q1
d
r
Байду номын сангаас观察点
.P
库仑定律： • 1785年，法国库仑（C.A.Coulomb) 库仑
库仑定律
真空中两个静止的点电荷之间的作用力（静电力）， 与它们所带电量的乘积成正比，与它们之间的距离的平方 成反比，作用力沿着这两个点电荷的连线。
F21 ——电荷q1作用于电荷q2的力。
q1q2 F21 F12 k 2 r0 r 1 k 4 0
F31 1 40 q1q3 r2
F3
q3 0.3m j q2
F31
0.6m
9.0 109 140 N
6.5 10 8.6 10 N
5 5
0.62
i
0.52m
q1
x
力 F31 沿x轴和y轴的分量分别为
Fx F31 cos 30 120N
引力
q1q2 1 q1q2 注意：只适用两 r0 r 2 3 个点电荷之间 4 0 r 4 0 r
静电力的叠加原理 作用于某电荷上的总静电力等于其他点电荷单独 存在时作用于该电荷的静电力的矢量和。 数学表达式
离散状态
N F Fi i 1
r10
ri 0
dF
A q0 B
q0
A
FB
（1）点电荷的电场
3.电场强度的计算
（2）场强叠加原理和点电荷系的电场 （3）连续分布电荷的电场
（1)点电荷的电场
1 q0 q F r 3 4 0 r
E
F 1 q E r 3 q0 40 r
E
q 源点
q0
E
场点
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
q
O
q
r0 2 r0 2
E
x
E
A
E
x
1 q 1 q i E i 2 2 4 π 0 ( x r0 2) 4 π 0 ( x r0 2) 2 xr0 q E E E 2 2 2 i 4 π 0 2π RdR
(x R )
2 2 1/ 2
xRdR 2 0 ( x 2 R 2 )3 2
z
R0
R o
dR
x P dE x
q π R
2 0
11-2 电场强度electric field intensity Chapter 11第八章静电场 electric field 8 – 3 电场强度
单位
电场中某点处的电场强度 E
F E q0
Q
q0
F
Q ：场源电荷 q0：试验电荷
NC
1
Vm
1
电荷 q 在电场中受力
F qE
11-2 电场强度electric field intensity Chapter 11第八章静电场 electric field 8 – 3 电场强度
E
e
y
B
r
y
r0
q
e
x
y r0
1 qr0 i 1 p E 3 3 4π 0 y 4π 0 y
11-2 电场强度electric field intensity Chapter 11第八章静电场 electric field 8 – 3 电场强度
物 质
11-2 电场强度electric field intensity Chapter 11第八章静电场 electric field 8 – 3 电场强度
二
电场强度electric field intensity
等于位于该点处的单位试验电荷 （试验电荷为点电 所受的力，其方向为正电荷受力 荷、且足够小,故对 方向. 原电场几乎无影响）
例2 均匀带电薄圆盘轴线上的电场强度. 有一半径为 R0 ,电荷均匀分布的薄圆盘,其电荷面 密度为 . 求通过盘心且垂直盘面的轴线上任意一点 处的电场强度. 解 由例１
qx E 2 2 32 4π 0 (x R ) dq x dE x 4 π 0 ( x 2 R 2 )3 2
四
电场强度的叠加原理
点电荷 qi 对 q 0 的作用力
q1
Fi
由力的叠加原理得 q 0 所受合力 F Fi i F Fi 故 q0 处总电场强度 E q0 i q0
电场强度的叠加原理
1 qi q0 ri 3 4 π 0 ri
q2 q3
r2 q0 r3
11-2 电场强度electric field intensity Chapter 11第八章静电场 electric field 8 – 3 电场强度
一
静电场electric field 实验证实了两静止电荷间存在相互作用的静电力，
但其相互作用是怎样实现的？
电 场 电荷
电荷
场是一种特殊形态的物质
场 实物
x r0
1 2p 1 2r0 q E i 3 3 4π 0 x 4π 0 x
11-2 电场强度electric field intensity Chapter 11第八章静电场 electric field 8 – 3 电场强度
（2）电偶极子轴线的中垂线上一点的电场强度
1 er dq 2 4π 0 r
dq r dE q P
1 er dV 2 4π 0 r
电荷体密度 charge density
点 P处电场强度
dq dV E
V
11-2 电场强度electric field intensity Chapter 11第八章静电场 electric field 8 – 3 电场强度
r1
F3 F2
F1
E Ei
i
11-2 电场强度electric field intensity Chapter 11第八章静电场 electric field 8 – 3 电场强度
电荷连续分布情况
dE
1 dq er 2 4π 0 r
E dE
五
电偶极子electric dipole的电场强度 电偶极子的轴 0 电偶极矩 p qr0 q electric dipole moment
r
讨论
r0
E
p q
（1）电偶极子轴线延长线上一点的电场强度
q
O
q
r0 2 r0 2
x
E
A
x
11-2 电场强度electric field intensity Chapter 11第八章静电场 electric field 8 – 3 电场强度
z
E 2 R 2
P x E
（点电荷电场强度） （2）
x 0 , E0 0
（3） dE 0 , x 2 R dx 2
o
2 R 2
x
11-2 电场强度electric field intensity Chapter 11第八章静电场 electric field 8 – 3 电场强度
xRdR dEx 2 2 32 2 0 ( x R )
y
x 2 0
E dE x
R0
0
RdR 2 2 3/ 2 (x R )
z
R0
R o
dR
P x
dE
x 1 1 E ( ) 2 2 2 0 x 2 x R0
11-2 电场强度electric field intensity Chapter 11第八章静电场 electric field 8 – 3 电场强度
1 q e 2 4 π 0 r 1 q E e 2 4 π 0 r
r r r
E
E
e
E E
y
B
e e
( r0 2 i yj ) r (r0 2 i yj ) r
r0 2 y ( ) 2
例 把一个点电荷（ q 62 10 C ）放在电 6 场中某点处，该电荷受到的电场力为F 3.2 10 i 6 1.3 10 j N ，求该电荷所在处的电场强度. 解
9
2 2 1 大小 E E ( 51 .6) ( 21 .0) N C 55 .71N C
x 1 1 E ( ) 2 2 2 0 x 2 x R0
讨论
x R0
E 2 0
q 4π 0 x
2
无限大均匀带电 平面的电场强度 （点电荷电场强度）
2 0 2
x R0 E
R (1 ) x
2 0 2 1 2
1 R 1 2 x
例1 正电荷 q 均匀分布在半径为 R 的圆环上. 计算在环的轴线上任一点 P 的电场强度.
解
E dE
由对称性有 E E i x
q ( ) 2π R
y dq dl
q R
o
r
x
P
dE
x
1 dl er 2 4π 0 r
z
11-2 电场强度electric field intensity Chapter 11第八章静电场 electric field 8 – 3 电场强度
y
q ) dq dl ( 2π R
q R
o
r
1 dl er z 2 4π 0 r dl x E dE x dE cos 2 l l 4π 0 r r 2π R qx xdl 2 2 32 3 0 4π 0 (x R ) 4π 0r dE
x
P
x
11-2 电场强度electric field intensity Chapter 11第八章静电场 electric field 8 – 3 电场强度
qx E 2 2 32 4π 0 (x R )
讨论
y dq dl
q R
o
q
2
r
（1） x R
x
E
4π 0 x
dq 电荷面密度 ds 1 σ er E ds 2 4π 0 r S
ds
q
dl
r
P
dE
dq 电荷线密度 dl 1 er E dl 2 4π 0 r l
q
r
P
dE
11-2 电场强度electric field intensity Chapter 11第八章静电场 electric field 8 – 3 电场强度
方向
1
F 1 E (51.6i 21.0 j ) N C q
y
o E
arctan
22.1
Ey Ex
q F
x
11-2 电场强度electric field intensity Chapter 11第八章静电场 electric field 8 – 3 电场强度
三
点电荷的电场强度
F 1 Q E e 2 r q0 4 π 0 r
Q Q
r r
q0
E
E
q0
E
Q
E
Q