《数据结构与算法》课后习题答案
Mark Allen Weiss 数据结构与算法分析 课后习题答案9

This flow is not unique. For instance, two units of the flow that goes from G to D to A to E could go by G to H to E.
-47-
9.12 Let T be the tree with root r , and children r 1, r 2, ..., rk , which are the roots of T 1, T 2, ..., Tk , which have maximum incoming flow of c 1, c 2, ..., ck , respectively. By the problem statement, we may take the maximum incoming flow of r to be infinity. The recursive function FindMaxFlow( T, IncomingCap ) finds the value of the maximum flow in T (finding the actual flow is a matter of bookkeeping); the flow is guaranteed not to exceed IncomingCap . If T is a leaf, then FindMaxFlow returns IncomingCap since we have assumed a sink of infinite capacity. Otherwise, a standard postorder traversal can be used to compute the maximum flow in linear time. _ ______________________________________________________________________________ FlowType FindMaxFlow( Tree T, FlowType IncomingCap ) { FlowType ChildFlow, TotalFlow; if( IsLeaf( T ) ) return IncomingCap; else { TotalFlow = 0; for( each subtree Ti of T ) { ChildFlow = FindMaxFlow( Ti , min( IncomingCap, ci ) ); TotalFlow += ChildFlow; IncomingCap -= ChildFlow; } return TotalFlow; } } _ ______________________________________________________________________________ 9.13 (a) Assume that the graph is connected and undirected. If it is not connected, then apply the algorithm to the connected components. Initially, mark all vertices as unknown. Pick any vertex v , color it red, and perform a depth-first search. When a node is first encountered, color it blue if the DFS has just come from a red node, and red otherwise. If at any point, the depth-first search encounters an edge between two identical colors, then the graph is not bipartite; otherwise, it is. A breadth-first search (that is, using a queue) also works. This problem, which is essentially two-coloring a graph, is clearly solvable in linear time. This contrasts with three-coloring, which is NP-complete. (b) Construct an undirected graph with a vertex for each instructor, a vertex for each course, and an edge between (v ,w ) if instructor v is qualified to teach course w . Such a graph is bipartite; a matching of M edges means that M courses can be covered simultaneously. (c) Give each edge in the bipartite graph a weight of 1, and direct the edge from the instructor to the course. Add a vertex s with edges of weight 1 from s to all instructor vertices. Add a vertex t with edges of weight 1 from all course vertices to t . The maximum flow is equal to the maximum matching.
数据结构与算法习题与答案

第1章绪论习题1.简述下列概念:数据、数据元素、数据项、数据对象、数据结构、逻辑结构、存储结构、抽象数据类型。
2.试举一个数据结构的例子,叙述其逻辑结构和存储结构两方面的含义和相互关系。
3.简述逻辑结构的四种基本关系并画出它们的关系图。
4.存储结构由哪两种基本的存储方法实现?5.选择题(1)在数据结构中,从逻辑上可以把数据结构分成()。
A.动态结构和静态结构 B.紧凑结构和非紧凑结构C.线性结构和非线性结构 D.内部结构和外部结构(2)与数据元素本身的形式、内容、相对位置、个数无关的是数据的()。
A.存储结构 B.存储实现C.逻辑结构 D.运算实现(3)通常要求同一逻辑结构中的所有数据元素具有相同的特性,这意味着()。
A.数据具有同一特点B.不仅数据元素所包含的数据项的个数要相同,而且对应数据项的类型要一致C.每个数据元素都一样D.数据元素所包含的数据项的个数要相等(4)以下说法正确的是()。
A.数据元素是数据的最小单位B.数据项是数据的基本单位C.数据结构是带有结构的各数据项的集合D.一些表面上很不相同的数据可以有相同的逻辑结构(5)以下与数据的存储结构无关的术语是()。
A.顺序队列 B. 链表 C.有序表 D. 链栈(6)以下数据结构中,()是非线性数据结构A.树 B.字符串 C.队 D.栈6.试分析下面各程序段的时间复杂度。
(1)x=90; y=100;while(y>0)if(x>100){x=x-10;y--;}else x++;(2)for (i=0; i<n; i++)for (j=0; j<m; j++)a[i][j]=0;(3)s=0;for i=0; i<n; i++)for(j=0; j<n; j++)s+=B[i][j];sum=s;(4)i=1;while(i<=n)i=i*3;(5)x=0;for(i=1; i<n; i++)for (j=1; j<=n-i; j++)x++;(6)x=n; //n>1y=0;while(x≥(y+1)* (y+1))y++;(1)O(1)(2)O(m*n)(3)O(n2)(4)O(log3n)(5)因为x++共执行了n-1+n-2+……+1= n(n-1)/2,所以执行时间为O(n2)(6)O()第2章线性表1.选择题(1)一个向量第一个元素的存储地址是100,每个元素的长度为2,则第5个元素的地址是()。
数据结构与算法分析习题与参考答案
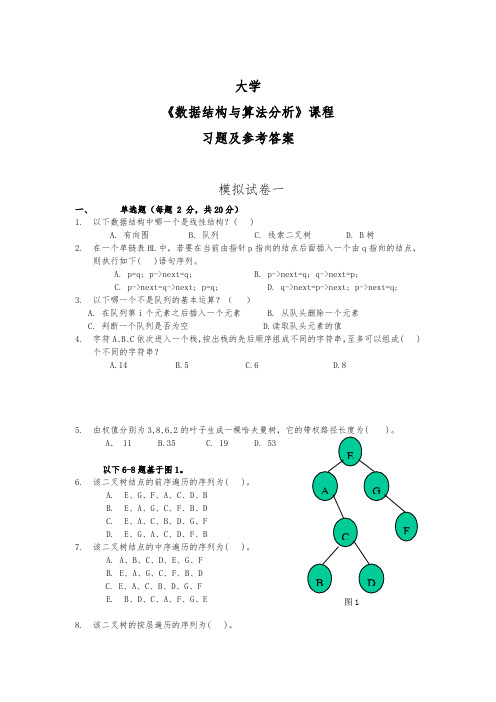
大学《数据结构与算法分析》课程习题及参考答案模拟试卷一一、单选题(每题 2 分,共20分)1.以下数据结构中哪一个是线性结构?( )A. 有向图B. 队列C. 线索二叉树D. B树2.在一个单链表HL中,若要在当前由指针p指向的结点后面插入一个由q指向的结点,则执行如下( )语句序列。
A. p=q; p->next=q;B. p->next=q; q->next=p;C. p->next=q->next; p=q;D. q->next=p->next; p->next=q;3.以下哪一个不是队列的基本运算?()A. 在队列第i个元素之后插入一个元素B. 从队头删除一个元素C. 判断一个队列是否为空D.读取队头元素的值4.字符A、B、C依次进入一个栈,按出栈的先后顺序组成不同的字符串,至多可以组成( )个不同的字符串?A.14B.5C.6D.85.由权值分别为3,8,6,2的叶子生成一棵哈夫曼树,它的带权路径长度为( )。
以下6-8题基于图1。
6.该二叉树结点的前序遍历的序列为( )。
A.E、G、F、A、C、D、BB.E、A、G、C、F、B、DC.E、A、C、B、D、G、FD.E、G、A、C、D、F、B7.该二叉树结点的中序遍历的序列为( )。
A. A、B、C、D、E、G、FB. E、A、G、C、F、B、DC. E、A、C、B、D、G、FE.B、D、C、A、F、G、E8.该二叉树的按层遍历的序列为( )。
A.E、G、F、A、C、D、B B. E、A、C、B、D、G、FC. E、A、G、C、F、B、DD. E、G、A、C、D、F、B9.下面关于图的存储的叙述中正确的是( )。
A.用邻接表法存储图,占用的存储空间大小只与图中边数有关,而与结点个数无关B.用邻接表法存储图,占用的存储空间大小与图中边数和结点个数都有关C. 用邻接矩阵法存储图,占用的存储空间大小与图中结点个数和边数都有关D.用邻接矩阵法存储图,占用的存储空间大小只与图中边数有关,而与结点个数无关10.设有关键码序列(q,g,m,z,a,n,p,x,h),下面哪一个序列是从上述序列出发建堆的结果?( )A. a,g,h,m,n,p,q,x,zB. a,g,m,h,q,n,p,x,zC. g,m,q,a,n,p,x,h,zD. h,g,m,p,a,n,q,x,z二、填空题(每空1分,共26分)1.数据的物理结构被分为_________、________、__________和___________四种。
Mark Allen Weiss 数据结构与算法分析 课后习题答案11

Chapter11:Amortized Analysis11.1When the number of trees after the insertions is more than the number before.11.2Although each insertion takes roughly log N ,and each DeleteMin takes2log N actualtime,our accounting system is charging these particular operations as2for the insertion and3log N −2for the DeleteMin. The total time is still the same;this is an accounting gimmick.If the number of insertions and DeleteMins are roughly equivalent,then it really is just a gimmick and not very meaningful;the bound has more significance if,for instance,there are N insertions and O (N / log N )DeleteMins (in which case,the total time is linear).11.3Insert the sequence N ,N +1,N −1,N +2,N −2,N +3,...,1,2N into an initiallyempty skew heap.The right path has N nodes,so any operation could takeΩ(N )time. 11.5We implement DecreaseKey(X,H)as follows:If lowering the value of X creates a heaporder violation,then cut X from its parent,which creates a new skew heap H 1with the new value of X as a root,and also makes the old skew heap H smaller.This operation might also increase the potential of H ,but only by at most log N .We now merge H andH 1.The total amortized time of the Merge is O (log N ),so the total time of theDecreaseKey operation is O (log N ).11.8For the zig −zig case,the actual cost is2,and the potential change isR f ( X )+ R f ( P )+ R f ( G )− R i ( X )− R i ( P )− R i ( G ).This gives an amortized time bound ofAT zig −zig =2+ R f ( X )+ R f ( P )+ R f ( G )− R i ( X )− R i ( P )− R i ( G )Since R f ( X )= R i ( G ),this reduces to=2+ R f ( P )+ R f ( G )− R i ( X )− R i ( P )Also,R f ( X )> R f ( P )and R i ( X )< R i ( P ),soAT zig −zig <2+ R f ( X )+ R f ( G )−2R i ( X )Since S i ( X )+ S f ( G )< S f ( X ),it follows that R i ( X )+ R f ( G )<2R f ( X )−2.ThusAT zig −zig <3R f ( X )−3R i ( X )11.9(a)Choose W (i )=1/ N for each item.Then for any access of node X ,R f ( X )=0,andR i ( X )≥−log N ,so the amortized access for each item is at most3log N +1,and the net potential drop over the sequence is at most N log N ,giving a bound of O (M log N + M + N log N ),as claimed.(b)Assign a weight of q i /M to items i .Then R f ( X )=0,R i ( X )≥log(q i /M ),so theamortized cost of accessing item i is at most3log(M /q i )+1,and the theorem follows immediately.11.10(a)To merge two splay trees T 1and T 2,we access each node in the smaller tree andinsert it into the larger tree.Each time a node is accessed,it joins a tree that is at leasttwice as large;thus a node can be inserted log N times.This tells us that in any sequence of N −1merges,there are at most N log N inserts,giving a time bound of O (N log2N ).This presumes that we keep track of the tree sizes.Philosophically,this is ugly since it defeats the purpose of self-adjustment.(b)Port and Moffet[6]suggest the following algorithm:If T 2is the smaller tree,insert itsroot into T 1.Then recursively merge the left subtrees of T 1and T 2,and recursively merge their right subtrees.This algorithm is not analyzed;a variant in which the median of T 2is splayed to the rootfirst is with a claim of O (N log N )for the sequence of merges.11.11The potential function is c times the number of insertions since the last rehashing step,where c is a constant.For an insertion that doesn’t require rehashing,the actual time is 1,and the potential increases by c ,for a cost of1+ c .If an insertion causes a table to be rehashed from size S to2S ,then the actual cost is 1+ dS ,where dS represents the cost of initializing the new table and copying the old table back.A table that is rehashed when it reaches size S was last rehashed at size S / 2, so S / 2insertions had taken place prior to the rehash,and the initial potential was cS / 2.The new potential is0,so the potential change is−cS / 2,giving an amortized bound of(d − c / 2)S +1.We choose c =2d ,and obtain an O (1)amortized bound in both cases.11.12We show that the amortized number of node splits is1per insertion.The potential func-tion is the number of three-child nodes in T .If the actual number of nodes splits for an insertion is s ,then the change in the potential function is at most1− s ,because each split converts a three-child node to two two-child nodes,but the parent of the last node split gains a third child(unless it is the root).Thus an insertion costs1node split,amor-tized.An N node tree has N units of potential that might be converted to actual time,so the total cost is O (M + N ).(If we start from an initially empty tree,then the bound is O (M ).)11.13(a)This problem is similar to Exercise3.22.Thefirst four operations are easy to imple-ment by placing two stacks,S L and S R ,next to each other(with bottoms touching).We can implement thefifth operation by using two more stacks,M L and M R (which hold minimums).If both S L and S R never empty,then the operations can be implemented as follows:Push(X,D):push X onto S L ;if X is smaller than or equal to the top of M L ,push X onto M L as well.Inject(X,D):same operation as Push ,except use S R and M R .Pop(D):pop S L ;if the popped item is equal to the top of M L ,then pop M L as well.Eject(D):same operation as Pop ,except use S R and M R .FindMin(D):return the minimum of the top of M L and M R .These operations don’t work if either S L or S R is empty.If a Pop or E j ect is attempted on an empty stack,then we clear M L and M R .We then redistribute the elements so that half are in S L and the rest in S R ,and adjust M L and M R to reflect what the state would be.We can then perform the Pop or E j ect in the normal fashion.Fig. 11.1shows a transfor-mation.Define the potential function to be the absolute value of the number of elements in S L minus the number of elements in S R .Any operation that doesn’t empty S L or S R can3,1,4,6,5,9,2,61,2,63,1,4,65,9,2,6 1,4,65,2S L S R M L RL S RM L M R Fig.11.1.increase the potential by only1;since the actual time for these operations is constant,so is the amortized time.To complete the proof,we show that the cost of a reorganization is O (1)amortized time. Without loss of generality,if S R is empty,then the actual cost of the reorganization is | S L | units.The potential before the reorganization is | S L | ;afterward,it is at most1. Thus the potential change is1− | S L | ,and the amortized bound follows.。
数据结构与算法设计课后习题及答案详解

数据结构与算法设计课后习题及答案详解1. 习题一:数组求和题目描述:给定一个整数数组,编写一个函数来计算它的所有元素之和。
解题思路:遍历数组,将每个元素累加到一个变量中,最后返回累加和。
代码实现:```pythondef sum_array(arr):result = 0for num in arr:result += numreturn result```2. 习题二:链表反转题目描述:给定一个单链表,反转它的节点顺序。
解题思路:采用三指针法,依次将当前节点的下一个节点指向上一个节点,然后更新三个指针的位置,直到链表反转完毕。
代码实现:```pythonclass ListNode:def __init__(self, val=0, next=None):self.val = valself.next = nextdef reverse_list(head):prev = Nonecurr = headwhile curr:next_node = curr.nextcurr.next = prevprev = currcurr = next_nodereturn prev```3. 习题三:二叉树的层序遍历题目描述:给定一个二叉树,返回其节点值的层序遍历结果。
解题思路:采用队列来实现层序遍历,先将根节点入队,然后循环出队并访问出队节点的值,同时将出队节点的左右子节点入队。
代码实现:```pythonclass TreeNode:def __init__(self, val=0, left=None, right=None): self.val = valself.left = leftself.right = rightdef level_order(root):if not root:return []result = []queue = [root]while queue:level = []for _ in range(len(queue)):node = queue.pop(0)level.append(node.val)if node.left:queue.append(node.left)queue.append(node.right)result.append(level)return result```4. 习题四:堆排序题目描述:给定一个无序数组,使用堆排序算法对其进行排序。
Mark Allen Weiss 数据结构与算法分析 课后习题答案1

Σ Fi =
sum on the right is Fk +2 − 2 + Fk +1 = Fk +3 − 2, where the latter equality follows from the definition of the Fibonacci numbers. This proves the claim for N = k + 1, and hence for all N. (b) As in the text, the proof is by induction. Observe that φ + 1 = φ2. This implies that φ−1 + φ−2 = 1. For N = 1 and N = 2, the statement is true. Assume the claim is true for N = 1, 2, ..., k . Fk +1 = Fk + Fk −1 by the definition and we can use the inductive hypothesis on the right-hand side, obtaining Fk +1 < φk + φk −1 < φ−1φk +1 + φ−2φk +1 Fk +1 < (φ−1 + φ−2)φk +1 < φk +1 and proving the theorem. (c) See any of the advanced math references at the end of the chapter. The derivation involves the use of generating functions. 1.10 (a) (2i −1) = 2 Σ i − Σ 1 = N (N +1) − N = N 2. Σ i =1 i =1 i =1
(完整版)数据结构与算法第8章答案

第8 章排序技术课后习题讲解1. 填空题⑴排序的主要目的是为了以后对已排序的数据元素进行()。
【解答】查找【分析】对已排序的记录序列进行查找通常能提高查找效率。
⑵对n个元素进行起泡排序,在()情况下比较的次数最少,其比较次数为()。
在()情况下比较次数最多,其比较次数为()。
【解答】正序,n-1,反序,n(n-1)/2⑶对一组记录(54, 38, 96, 23, 15, 72, 60, 45, 83)进行直接插入排序,当把第7个记录60插入到有序表时,为寻找插入位置需比较()次。
【解答】3【分析】当把第7个记录60插入到有序表时,该有序表中有2个记录大于60。
⑷对一组记录(54, 38, 96, 23, 15, 72, 60, 45, 83)进行快速排序,在递归调用中使用的栈所能达到的最大深度为()。
【解答】3⑸对n个待排序记录序列进行快速排序,所需要的最好时间是(),最坏时间是()。
【解答】O(nlog2n),O(n2)⑹利用简单选择排序对n个记录进行排序,最坏情况下,记录交换的次数为()。
【解答】n-1⑺如果要将序列(50,16,23,68,94,70,73)建成堆,只需把16与()交换。
【解答】50⑻对于键值序列(12,13,11,18,60,15,7,18,25,100),用筛选法建堆,必须从键值为()的结点开始。
【解答】60【分析】60是该键值序列对应的完全二叉树中最后一个分支结点。
2. 选择题⑴下述排序方法中,比较次数与待排序记录的初始状态无关的是()。
A插入排序和快速排序B归并排序和快速排序C选择排序和归并排序D插入排序和归并排序【解答】C【分析】选择排序在最好、最坏、平均情况下的时间性能均为O(n2),归并排序在最好、最坏、平均情况下的时间性能均为O(nlog2n)。
⑵下列序列中,()是执行第一趟快速排序的结果。
A [da,ax,eb,de,bb] ff [ha,gc]B [cd,eb,ax,da] ff [ha,gc,bb]C [gc,ax,eb,cd,bb] ff [da,ha]D [ax,bb,cd,da] ff [eb,gc,ha]【解答】A【分析】此题需要按字典序比较,前半区间中的所有元素都应小于ff,后半区间中的所有元素都应大于ff。
数据结构与算法习题及答案

精心整理第1章绪论习题1.简述下列概念:数据、数据元素、数据项、数据对象、数据结构、逻辑结构、存储结构、抽象数据类型。
2.试举一个数据结构的例子,叙述其逻辑结构和存储结构两方面的含义和相互关系。
3.简述逻辑结构的四种基本关系并画出它们的关系图。
4.存储结构由哪两种基本的存储方法实现5A6{x=x-10;y--;}elsex++;(2)for(i=0;i<n;i++)for(j=0;j<m;j++)a[i][j]=0;(3)s=0;fori=0;i<n;i++)for(j=0;j<n;j++)s+=B[i][j];sum=s;(4)i=1;while(i<=n)i=i*3;(5)x=0;for(i=1;i<n;i++)for(j=1;j<=n-i;j++)x++;(6)x=n;n108 C63.5 C1 C-1 C1 Cext=s;(*s).next=(*p).next;C.s->next=p->next;p->next=s->next;D.s->next=p->next;p->next=s;2,=(rear+1)%=(rear+1)%(m+1)(13)最大容量为n的循环队列,队尾指针是rear,队头是front,则队空的条件是()。
A.(rear+1)%n====frontC.rear+1==frontD.(rear-l)%n==front(14)栈和队列的共同点是()。
A.都是先进先出B.都是先进后出C.只允许在端点处插入和删除元素D.没有共同点(15)一个递归算法必须包括()。
A.递归部分B.终止条件和递归部分C.迭代部分D.终止条件和迭代部分(2)回文是指正读反读均相同的字符序列,如“abba”和“abdba”均是回文,但“good”不是回文。
试写一个算法判定给定的字符向量是否为回文。
(提示:将一半字符入栈)根据提示,算法可设计为:0’9’0’9’0’0’9’0’0’9’0’0’0’M-1]实现循环队列,其中M是队列长度。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2.3 课后习题解答 2.3.2 判断题 1.线性表的逻辑顺序与存储顺序总是一致的。(×) 2.顺序存储的线性表可以按序号随机存取。(√) 3.顺序表的插入和删除操作不需要付出很大的时间代价,因为每次操作平均只有近一半的元素需要移动。(×) 4.线性表中的元素可以是各种各样的,但同一线性表中的数据元素具有相同的特性,因此属于同一数据对象。(√) 5.在线性表的顺序存储结构中,逻辑上相邻的两个元素在物理位置上并不一定相邻。(×) 6.在线性表的链式存储结构中,逻辑上相邻的元素在物理位置上不一定相邻。(√) 7.线性表的链式存储结构优于顺序存储结构。(×) 8.在线性表的顺序存储结构中,插入和删除时移动元素的个数与该元素的位置有关。(√) 9.线性表的链式存储结构是用一组任意的存储单元来存储线性表中数据元素的。(√) 10.在单链表中,要取得某个元素,只要知道该元素的指针即可,因此,单链表是随机存取的存储结构。(×) 11.静态链表既有顺序存储的优点,又有动态链表的优点。所以它存取表中第i个元素的时间与i无关。(×) 12.线性表的特点是每个元素都有一个前驱和一个后继。(×)
2.3.3 算法设计题 1.设线性表存放在向量A[arrsize]的前elenum个分量中,且递增有序。试写一算法,将x 插入到线性表的适当位置上,以保持线性表的有序性,并且分析算法的时间复杂度。 【提示】直接用题目中所给定的数据结构(顺序存储的思想是用物理上的相邻表示逻辑上的相邻,不一定将向量和表示线性表长度的变量封装成一个结构体),因为是顺序存储,分配的存储空间是固定大小的,所以首先确定是否还有存储空间,若有,则根据原线性表中元素的有序性,来确定插入元素的插入位置,后面的元素为它让出位置,(也可以从高下标端开始一边比较,一边移位)然后插入x ,最后修改表示表长的变量。 int insert (datatype A[],int *elenum,datatype x) /*设elenum为表的最大下标*/ {if (*elenum==arrsize-1) return 0; /*表已满,无法插入*/
else {i=*elenum; while (i>=0 && A[i]>x) /*边找位置边移动*/ {A[i+1]=A[i]; i--; } A[i+1]=x; /*找到的位置是插入位的下一位*/ (*elenum)++; return 1; /*插入成功*/ } } 时间复杂度为O(n)。 2.已知一顺序表A,其元素值非递减有序排列,编写一个算法删除顺序表中多余的值相同的元素。 【提示】对顺序表A,从第一个元素开始,查找其后与之值相同的所有元素,将它们删除;再对第二个元素做同样处理,依此类推。 void delete(Seqlist *A) {i=0; while(ilast) /*将第i个元素以后与其值相同的元素删除
*/ {k=i+1; while(k<=A->last&&A->data[i]==A->data[k]) k++; /*使k指向第一个与A[i]不同的元素*/
n=k-i-1; /*n表示要删除元素的个数*/ for(j=k;j<=A->last;j++) A->data[j-n]=A->data[j]; /*删除多余元素*/ A->last= A->last -n; i++; } } 3.写一个算法,从一个给定的顺序表A中删除值在x~y(x<=y)之间的所有元素,要求以较高的效率来实现。 【提示】对顺序表A,从前向后依次判断当前元素A->data[i]是否介于x和y之间,若是,并不立即删除,而是用n记录删除时应前移元素的位移量;若不是,则将A->data[i]向前移动n位。n用来记录当前已删除元素的个数。 void delete(Seqlist *A,int x,int y) {i=0; n=0; while (ilast) {if (A->data[i]>=x && A->data[i]<=y) n++; /*若A->data[i] 介于x和y之间,n自增*/ else A->data[i-n]=A->data[i]; /*否则向前移动A->data[i]*/
i++; } A->last-=n; } 4.线性表中有n个元素,每个元素是一个字符,现存于向量R[n]中,试写一算法,使R中的字符按字母字符、数字字符和其它字符的顺序排列。要求利用原来的存储空间,元素移动次数最小。 【提示】对线性表进行两次扫描,第一次将所有的字母放在前面,第二次将所有的数字放在字母之后,其它字符之前。 int fch(char c) /*判断c是否字母*/ {if(c>='a'&&c<='z'||c>='A'&&c<='Z') return (1); else return (0); } int fnum(char c) /*判断c是否数字*/ {if(c>='0'&&c<='9') return (1); else return (0); } void process(char R[n]) {low=0; high=n-1; while(low/*将字母放在前面*/
{while(lowwhile(lowif(low{k=R[low]; R[low]=R[high]; R[high]=k; } } low=low+1; high=n-1; while(low {while(lowwhile(lowif(low{k=R[low]; R[low]=R[high]; R[high]=k; } } } 5.线性表用顺序存储,设计一个算法,用尽可能少的辅助存储空间将顺序表中前m个元素和后n个元素进行整体互换。即将线性表: (a1, a2, … , am, b1, b2, … , bn)改变为: (b1, b2, … , bn , a1, a2, … , am)。 【提示】比较m和n的大小,若m后移n次。 void process(Seqlist *L,int m,int n) {if(m<=n) for(i=1;i<=m;i++) {x=L->data[0]; for(k=1;k<=L->last;k++) L->data[k-1]=L->data[k]; L->data[L->last]=x; } else for(i=1;i<=n;i++) {x=L->data[L->last]; for(k=L->last-1;k>=0;k- -) L->data[k+1]=L->data[k]; L->data[0]=x; } } 6.已知带头结点的单链表L中的结点是按整数值递增排列的,试写一算法,将值为x 的结点插入到表L中,使得L仍然递增有序,并且分析算法的时间复杂度。 LinkList insert(LinkList L, int x) {p=L; while(p->next && x>p->next->data) p=p->next; /*寻找插入位置*/
s=(LNode *)malloc(sizeof(LNode)); /*申请结点空间*/ s->data=x; /*填装结点*/ s->next=p->next; p->next=s; /*将结点插入到链表中*/ return(L); } 7.假设有两个已排序(递增)的单链表A和B,编写算法将它们合并成一个链表C而不改变其排序性。 LinkList Combine(LinkList A, LinkList B) {C=A; rc=C; pa=A->next; /*pa指向表A的第一个结点*/ pb=B->next; /*pb指向表B的第一个结点*/
free(B); /*释放B的头结点*/ while (pa && pb) /*将pa、pb所指向结点中,值较小的一个插入到链表C的表尾*/ if(pa->datadata) {rc->next=pa; rc=pa; pa=pa->next; } else {rc->next=pb; rc=pb; pb=pb->next; } if(pa) rc->next=pa; else rc->next=pb; /*将链表A或B中剩余的部分链接到链表C的表尾*/ return(C); } 8.假设长度大于1的循环单链表中,既无头结点也无头指针,p为指向该链表中某一结点的指针,编写算法删除该结点的前驱结点。 【提示】利用循环单链表的特点,通过s指针可循环找到其前驱结点p及p的前驱结点q,然后可删除结点*p。 viod delepre(LNode *s) {LNode *p, *q;
