拉普拉斯变换和反变换
拉普拉斯变换及反变换1

——不常用解
方法二: 方法二:查拉氏变换表求解 ——对简单的象函数适用 方法三: 方法三:部分分式法——象函数为有理分式函数时适用
第21页 页
黄河科技学院
控制工程基础
应用部分分式展开式计算拉氏逆变换的 一般步骤 : 的极点; (1)计算有理分式函数F(s)的极点; (2)根据极点把F(s)的分母多项式进行因 式分解、 展开成部分分式; 式分解、并进一步把F(s)展开成部分分式; (3)对F(s)的部分分式展开式两边同时进 行拉氏逆变换。 行拉氏逆变换。
(11)卷积定理 11)
f (t ) * g (t ) = ∫
+∞
−∞
f (τ ) g (t − τ )dτ
= ∫ f (τ ) g (t − τ )dτ
0
t
L[ f (t ) * g (t )] = F ( s ) ⋅ G ( s ) = G ( s ) F ( s )
第19页 页
黄河科技学院
控制工程基础
s +1 c2 = ( s + 3) ( s + 2)( s + 3)
s = −3
(2)对F(s)的分母多项式进行因式分解、并把 (s)展开 ) ( )的分母多项式进行因式分解、并把F( ) 成部分分式
=2
第24页 页
黄河科技学院
控制工程基础
s +1 1 2 F ( s) = 2 =− + s + 5s + 6 s+2 s+3
− st
单位阶跃函数,记作 单位阶跃函数,记作1( t )
t<0 t≥0
1 L[1(t )] = s
(完整版)拉普拉斯变换及其逆变换表
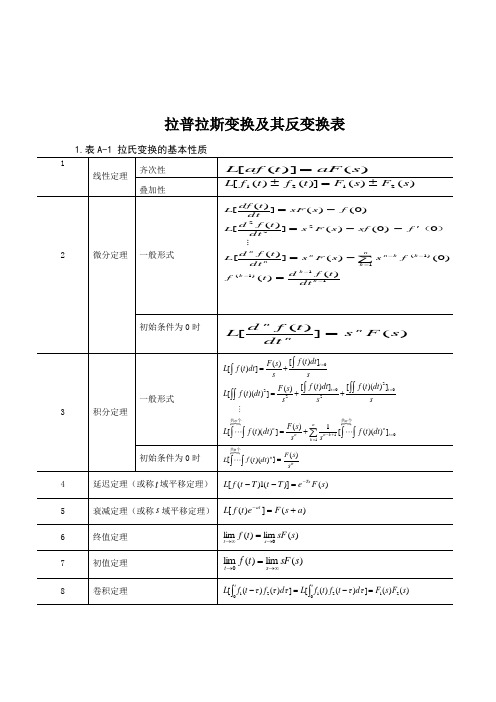
拉普拉斯变换及其反变换表3. 用查表法进行拉氏反变换用查表法进行拉氏反变换的关键在于将变换式进行部分分式展开,然后逐项查表进行反变换。
设)(s F 是s 的有理真分式11n 1n nn11m 1m mmas a s a s a b s b s b s b )s (A )s (B )s (F ++++++++==---- (m n >)式中系数n1n 1a ,a ,...,a ,a-,m1m 1b ,b ,b ,b - 都是实常数;n m ,是正整数。
按代数定理可将)(s F 展开为部分分式。
分以下两种情况讨论。
① 0)(=s A 无重根这时,F(s)可展开为n 个简单的部分分式之和的形式。
∑=-=-++-++-+-=n1i iinnii2211ss cs s c s s c s s c s s c )s (F 式中,Sn 2S 1S ,,, 是特征方程A(s)=0的根。
i c 为待定常数,称为F(s)在i s 处的留数,可按下式计算: )s (F )s s (lim c is s i-=→或is s i)s (A )s (B c='=式中,)(s A '为)(s A 对s 的一阶导数。
根据拉氏变换的性质,从式(F-1)可求得原函数[]t s n 1i i n 1i i i 11i e c s s cL )s (F L )t (f -==--∑∑=⎥⎦⎤⎢⎣⎡-==② 0)(=s A 有重根设0)(=s A 有r 重根1s ,F(s)可写为())s s ()s s ()s s ()s (B s F n1r r 1---=+=nnii1r 1r 111r 11r r 1rss cs s c s s c )s s (c )s s (c )s s (c -++-++-+-++-+-++-- 式中,1s 为F(s)的r 重根,1+r s ,…, n s 为F(s)的n-r 个单根;其中,1+r c ,…, n c 仍按式(F-2)或(F-3)计算,r c ,1-r c ,…, 1c 则按下式计算:)s (F )s s (lim c r1s s r-=→)]s (F )s s ([dsdlim c -=)s (F )s s (dsd lim !j 1c -=)s (F )s s (dsdlim )!1r (1c --=原函数)(t f 为 [])()(1s F L t f -=⎥⎦⎤⎢⎣⎡-++-++-+-++-+-=s s cs s c s s c )s s (c )s s (c )s s (c L e c e c t c t )!2r (c t )!1r (c ∑+⎥⎦⎤⎢⎣⎡+++-+-= (F-6)。
拉普拉斯变换的基本性质、变换及反变换

拉普拉斯变换的基本性质、变换及反变换t t8 卷积定理L[ [f i(t—l)f2&)dE] =L[ [f i(t)f2(t—l)dl] = F i(s)F2(s)用查表法进行拉氏反变换的关键在于将变换式进行部分分式展开,然后逐项查表进行反变换。
设F(s)是s 的有理真分式A(s)二0有重根设A(s) = 0有r 重根s ,F(s)可写为F s-(s-s ,)r(s-s ri ) (s-s n )B(s)b m 「4 g b0A(s)n ,n 」a n S - a n 」s 山…“y s - a 。
式中系数a 0, a i ,..., a n J ,a n , b °,b i , b m 」,b m 都是实常数; 将F(s)展开为部分分式。
分以下两种情况讨论。
m,n 是正整数。
按代数定理可①A(s) = 0无重根这时,F(s)可展开为n 个简单的部分分式之和的形式。
i C 2C jC nF(s) 121— s — s i s — S 2s — ss_s nC i(F-1)式中,q,s 2,…,s n 是特征方程 A(s) = 0的根。
C i 为待定常数,称为 可按下式计算:F(s)在S i 处的留数,式中,C =lim (s _sJF (s)S Tic _ B(s) iA(s)s zs iA (s)为A(s)对s 的一阶导数。
根据拉氏变换的性质,从式(4 I l j n C i =L !F (S )】=L 巨一—S — Sj 一 f(t)C in -s it=' Ci e ii =1(F-2)(F-3)F-1 )可求得原函数(F-4)B(s)式中, 其中,& r -(S —S i) (s—s)C if ,s〜) CriS —■S r iG •…©S - s S—S nS i为F(s)的r重根,S r审,…,s n为F(s)的n-r个单根;C r +,…,C n 仍按式(F-2)或(F-3)计算,C r,C rj,…, C i则按下式计算:f(t)为厂c r =lim (s — sj r F(s)T id rC ri =lim [(s -sj F(s)] dss :siC i原函数f (t)二L°〔F(s) I冷冗加(DEi d(7C i _____ . C r i ....(F-5)(s -S i)r 1(s—s i) S —S r*G *…+C nS — S j S —S nt r^ +…+c2t +G e Sit(r-2)! 2 5S i t°e iF-6)欢迎您的下载,资料仅供参考!致力为企业和个人提供合同协议,策划案计划书,学习资料等等打造全网一站式需求。
拉氏变换及反变换
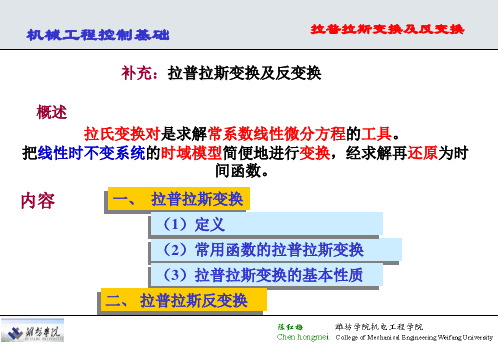
2. f (t) eatu(t) (指数函数)
f
(t)
0
(t 0)
et (t 0)
F(s)= ℒ [eat ] eatestdt 0 ℒ [ejt ] 1 s j
1
e(sa)t
sa
0
1 sa
机械工程控制基础
拉普拉斯变换及反变换
3. f (t) (t) (单位脉冲函数)
(t)
t
s0
机械工程控制基础
拉普拉斯变换及反变换
例1
u(t) t0
lim s 1 s s
1
例2 I(s) 5 2 s1 s2
i(0 ) lim s( 5 2 ) lim( 5 2 ) 3 s s 1 s 2 s 1 1/ s 1 2 / s
例3
I (s) ℒ [1 e-t ] 1 1 s s1
Ui(s) H(s) I(s)
I(s)=Ui(s)H(s)= ℒ[ui(t)] H(s)
=ℒ eat (t)
(5)作Laplace反变换得
1 R Ls
s
1
a
1 L
s
1 R
L
零状态响应电流
i(t)= ℒ-1[I(s)]
1
(e a t
Rt
e L )
(t)
L ( R a)
L
机械工程控制基础
拉普拉斯变换及反变换
的
拉
t
1/s2
普 拉
n!
tn
sn+1
1
斯
e-at
s+a
变 换
1
te-at
(s+a)2
表
tne-at
n!
(s+a)n+1
拉普拉斯Laplace变换

f (t) = 2e − t − e −2t
例2
2s + 12 k1 k2 F(s) = 2 = + s + 2s + 5 s + 1 + 2 j s + 1 − 2 j
2s + 12 k1 = 2 (s + 1 + 2 j) s + 2s + 5
5 k2 = 1− j 2
s =−1− 2 j
5 = 1+ j 2
[a1s + a2 ]s =− p1 B( s) =[ ( s + p1 )( s + p2 )]s =− p1 A( s)
c. F(s)含有多重极点时,可展开为
an br br −1 b1 ar +1 F ( s) = + + ⋅⋅⋅ + + + ⋅⋅⋅ + r r −1 ( s + p1 ) ( s + p1 ) ( s + p1 ) ( s + pr +1 ) ( s + pn )
s =−1
=2
d s 2 + 2s + 3 a12 = [ (s + 1)3 ] s=−1 = 0 ds (s + 1)3 1 d 2 s 2 + 2s + 3 a13 = [ (s + 1)3 ] s =−1 = 1 2! ds 2 (s + 1)3
所以:
2 1 f (t) = L [ + ] = t 2e − t + e − t = (t 2 + 1)e − t (s + 1)3 s + 1
线性定理 位移定理 延迟定理 终值定理
拉普拉斯变换及其逆变换表
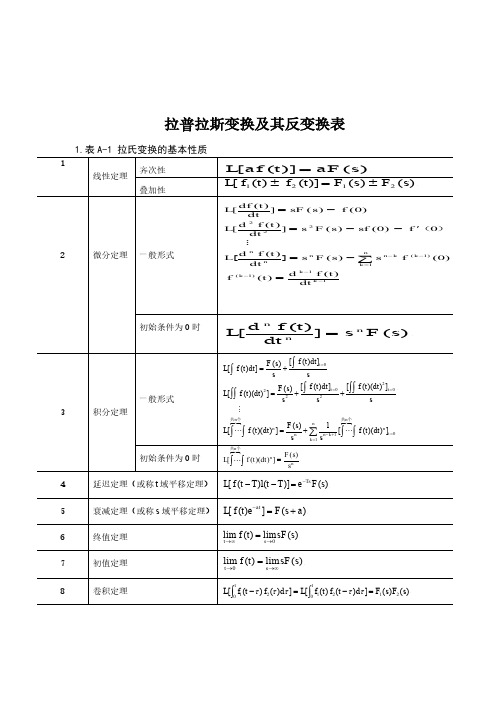
n
F ( s)
L[ f (t )dt ]
一般形式 3 积分定理
L[ f (t )(dt ) 2 ]
共n个
2 F ( s ) [ f (t )dt ]t 0 [ f (t )(dt ) ]t 0 s2 s2 s
共n个 F ( s) n 1 n L[ f (t )(dt ) ] n n k 1 [ f (t )(dt ) n ]t 0 s k 1 s
B( s ) b s b s b s b F (s ) A(s ) a s a s a s a
m m 1 m m 1 1 n n 1 n n 1 1 0
0
(n m)
式中系数 a
0
, a ,..., a , a , b , b ,b , b 都是实常数; m, n 是正整数。按
1(t )
z z 1
1 s2
1 s3
t
t2 2
Tz ( z 1) 2
T 2 z ( z 1) 2( z 1) 3
1 s n 1
1 sa
tn n!
lim
( 1) n n z ( ) n a 0 n! a z e aT
z z e aT
e at te
at
拉普拉斯变换及其反变换表表a1拉氏变换的基本性质1线性定理齐次性叠加性2微分定理一般形式初始条件为0时3积分定理一般形式初始条件为0时4延迟定理或称域平移定理5衰减定理或称域平移定理6终值定理7初值定理8卷积定理2
拉普拉斯变换及其反变换表
1.表 A-1 拉氏变换的基本性质
1 线性定理 齐次性 叠加性
c c t t c t c e c e (r 2)! (r 1)!
拉普拉斯变换及其逆变换表

拉普拉斯变换及其逆变换表Document serial number【KKGB-LBS98YT-BS8CB-BSUT-BST108】拉普拉斯变换及其反变换表3. 用查表法进行拉氏反变换用查表法进行拉氏反变换的关键在于将变换式进行部分分式展开,然后逐项查表进行反变换。
设)(s F 是s 的有理真分式11n 1n n n 011m 1m m m a s a s a s a b s b s b s b )s (A )s (B )s (F ++++++++==---- (m n >) 式中系数n 1n 10a ,a ,...,a ,a -,m1m 10b ,b ,b ,b - 都是实常数;n m ,是正整数。
按代数定理可将)(s F 展开为部分分式。
分以下两种情况讨论。
① 0)(=s A 无重根这时,F(s)可展开为n 个简单的部分分式之和的形式。
∑=-=-++-++-+-=n 1i iin n i i 2211s s c s s c s s c s s c s s c )s (F 式中,Sn 2S 1S ,,, 是特征方程A(s)=0的根。
i c 为待定常数,称为F(s)在i s 处的留数,可按下式计算:或式中,)(s A '为)(s A 对s 的一阶导数。
根据拉氏变换的性质,从式(F-1)可求得原函数② 0)(=s A 有重根设0)(=s A 有r 重根1s ,F(s)可写为 =nni i 1r 1r 111r 11r r 1r s s c s s c s s c )s s (c )s s (c )s s (c -++-++-+-++-+-++-- 式中,1s 为F(s)的r 重根,1+r s ,…, n s 为F(s)的n-r 个单根;其中,1+r c ,…, n c 仍按式(F-2)或(F-3)计算,r c ,1-r c ,…, 1c 则按下式计算: 原函数)(t f 为ts n 1r i it s 122r 1r 1r r 1e c e c t c t )!2r (c t )!1r (c ∑+=---+⎥⎦⎤⎢⎣⎡+++-+-= (F-6)。
拉氏变换及反变换
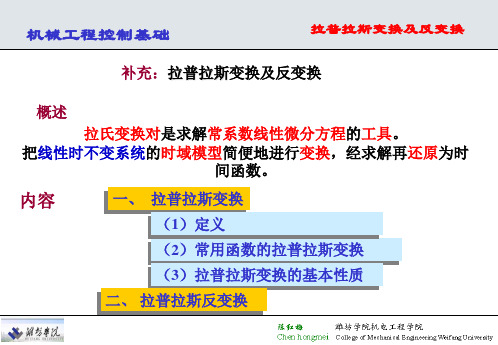
0
t
F(s)=L[f(t)]=
te
0
st
dt
t st 1 st e e dt 0 s 0 s
1 2 s
机械工程控制基础
拉普拉斯变换及反变换
5. f (t ) t
ℒ [t ]
n
n
n
(幂函数)
0
t e dt 0
n st
t n st de s
例1 例2
1 1 ) ℒ [ A(1 e )] A( s s 1 j t [sin t ] ℒ ℒ [ (e e j t )] 2j 1 1 1 [ ] 2 2j s j s j s 2
t
机械工程控制基础
二、微分定理
拉普拉斯变换及反变换
1 d (sin t )] ℒ [cos t ] ℒ [ dt s 1 [s 2 si nt 0 ] 2 2 s 2 s
机械工程控制基础
•例3 某动态电路的输入—输出方程为
拉普拉斯变换及反变换
d2 d d r ( t ) a r ( t ) a r ( t ) b e (t ) b0 e (t ) 1 0 1 2 dt dt dt
拉普拉斯变换及反变换
(t )dt 1
0
t
ℒ [ ( t )]
0
( t )e st dt 0 (t )dt
0
=1
机械工程控制基础
4. f (t ) t (单位斜坡函数)
f(t)
拉普拉斯变换及反变换
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
F (s)s(s2s 2 1 s 5 )1 5 [1 ss2 s 2 s3 5 ]
L 1 [(s 1 s ) 2 3 4 ] L 1 [(s ( 1 s ) 2 1 )4 ] L 1 [(s 1 4 )2 4 ]
0
s
t
L[ 0
t 0
f(t)dnt]s1nF(s)
第16页
黄河科技学院
控制工程基础
(7)初值定理
lim f(t)lim sF (s)
t 0
s
f(0)lim sF(s) s
(8)终值定理
lim f(t)lim sF (s)
t
s 0
f()lim sF(s)
Fssp1
Ns sp2 .......spn
k1 k2 .........kn
sp1 sp2
spn
其中 k i [F s(s p i)s ]p i
第23页
黄河科技学院
控制工程基础
例
F(s)s2
s1 5s6
解:(1)F(s)的极点
s25s60 s1 2 s2 3
Fs 的原函数;L是表示进行拉氏变换的
符号。
第2页
黄河科技学院
控制工程基础
F(s)L[f(t)]
f(t)L1[F(s)]
拉氏变换是这样一种变换,即在一定的 条件下,它能把一实数域中的实变函数
f t 变换为一个在复数域内与之等价的
复变函数 Fs。
第3页
黄河科技学院
控制工程基础
1)、 典型函数的拉氏变换
式中 L1 表示拉普拉斯反变换的符号
第20页
黄河科技学院
控制工程基础
2、拉氏反变换的计算方法 由象函数求原函数的方法:
方法一:利用拉氏反变换定义求 ——不常用解
方法二:查拉氏变换表求解 ——对简单的象函数适用 方法三:部分分式法——象函数为有理分式函数时适用
第21页
黄河科技学院
控制工程基础
应用部分分式展开式计算拉氏逆变换的一 般步骤 :
控制工程基础
(3)抛物函数(又称加速度函数)
f(t)1 2k2t1(t) 1 20k2t
(k =const)
t0 t0
f (t)
f (t)
k
t 0
t 0
(a) 阶跃函数 (b) 斜坡函数
f (t)
t 0 (c) 抛物函数
r(t)
Ra t0
t
0 t0
(d) 脉冲函数
(t)
第28页
黄河科技学院
控制工程基础
例
F(s)s(s2s21s5)
解: F (s)s(s2s 2 1 s5 )c s1s2 c2 s2 sc 35
两边同乘以
s22s5 ss21j2
得
乘共轭
1 1 j2j2 1c2(1j2)c3
(-1-j2)
0tf()g(t)d
L [ f( t ) * g ( t ) F ] ( s ) G ( s ) G ( s ) F ( s )
第19页
黄河科技学院
控制工程基础
二、 拉氏反变换及其计算方法
1、拉氏反变换
f(t)L1(F(s))1 cj F(s)esd t s 2j cj
单位斜坡函数
f(t)t1(t) 0t
t0 t0
f (t)
f (t)
k
t 0
t 0
(a) 阶跃函数 (b) 斜坡函数
f (t)
t 0 (c) 抛物函数
r(t)
Ra t0
t
0 t0
(d) 脉冲函数
(t)
t
0
(e) 单位脉冲函数
r(t)
1
t
0
(f) 正弦函数
F(s)
1 s2
第5页
黄河科技学院
t
0
(e) 单位脉冲函数
r(t)
1
t
0
(f) 正弦函数
F (s)L [f(t) ]0 1 2k2e t sd t ts k 3
单位抛物函数
f(t)12t21(t)120t2
t0 t0
1 F(s) s3
第6页
黄河科技学院
(4)单位脉冲函数
控制工程基础
(t)
F ( s ) ( s b r p 1 ) r ( s b r p 1 1 ) r 1 ( s b 1 p 1 ) ( s a r p r 1 1 ) ( s a n p n )
其中 b r [F s(s p 1 )r]s p 1
f(t)L 1[s 22]L 1[(s 22)2]L 1[(s 1 2)3]L 1[s 23](22t1 2t2)e2t2e3t
第30页
黄河科技学院
控制工程基础
F (s)s(s2s 2 1 s5 )c s1s2 c2 s2 sc 35
(2)对F(s)的分母多项式进行因式分解、并把F(s)展开
成部分分式
F (s ) s2 s5 s 1 6 (s s 2 ) s 1 ( 3 ) sc 1 2 sc 2 3
c1(s2)(ss 2)s 1 (3)
1
s2
s1
c2(s3)(s2)s(3)
黄河科技学院
控制工程基础
拉普拉斯变 换和反变换
第1页
黄河科技学院
控制工程基础
式中,s是复变数,sj( 、
均为实数), e st 称为拉普拉斯积分;Fs 0
是函数 f t 的拉氏变化,它是一个复变函数,
通常称 Fs 为 f t 的象函数,而称 f t 为
解: F ( s ) ( s 2 s ) 3 ( 1 s 3 ) s c 1 2 ( s c 2 2 ) 2 ( s c 3 2 ) 3 s c 4 3
c4(s3)(s2 s) 3(1 s3)
2
s3
c3
s1 (s3)
s2
1
c2
d s1 ds(s3)
2
s3
第24页
黄河科技学院
控制工程基础
F (s)s2 s5 s1 6s 12s 23
(3)进行拉氏反变换
f (t) L1[F(s)]
L1[ 1 ] L1[ 2 ]
s2
s3
e2t 2e3t
第25页
黄河科技学院
控制工程基础
2)当解出s有重根时,对F(s)作因式分解:
特别在零初始条件下
f(0 )f(0 ) f(n 1 )(0 ) 0
L[f(n)(t)]snF(s)
第15页
黄河科技学院
控制工程基础
(6)积分定理
L[tf(t)d] t 1F(s)1tf(t)d t
0
s
s0
t 0
当初始条件为零时,则
L[ tf(t)d]t1F(s)
(1)计算有理分式函数F(s)的极点;
(2)根据极点把F(s)的分母多项式进行因 式分解、并进一步把F(s)展开成部分分式;
(3)对F(s)的部分分式展开式两边同时进
行拉氏逆变换。
第22页
黄河科技学院
控制工程基础
1)当解出 s pi (i1,2,.....n.), 为单
根时,对 F(s) 作因式分解:
s 0
第17页
黄河科技学院
控制工程基础
(9)象函数的微分性质tf (t ) 的拉氏变换
Ltftd Fs
ds
(10)象函数的积分性质 f ( t ) 的拉氏变换
t
Lft11)卷积定理
f(t)*g(t) f()g(t)d
L [cto ] 1 2 s0 (ej t e j t)e sd t s t2 s2 第9页
黄河科技学院
控制工程基础
第10页
黄河科技学院
控制工程基础
第11页
黄河科技学院
控制工程基础
2、拉氏变换的运算法则 (1)线性定理
L [a(t) f b(t) g ]a(s F ) b(s G )
F ( s ) ( s 2 s ) 3 ( 1 s 3 ) s 2 2 ( s 2 2 ) 2 ( s 1 2 ) 3 s 2 3
f( t ) L 1 [ s 2 2 ] L 1 [ ( s 2 2 ) 2 ] L 1 [ ( s 1 2 ) 3 ] L 1 [ s 2 3 ] ( 2 2 t 1 2 t2 ) e 2 t 2 e 3 t
0
s
指数衰减函数
第8页
黄河科技学院
控制工程基础
(6)正弦函数
f(t)si nt1(t)
(t)
et
f (t)
f (t)
1
1
e t
t
0
0
t
t
0
L [sti] n 2 1 j0 (ej t e j t)e sd t ts22
(7)余弦函数
f(t)cots1(t)
(1)阶跃函数(位置函数)
0 f(t)k
t 0 t 0
(k =const)
f (t)
f (t)
k
t 0
t 0
(a) 阶跃函数 (b) 斜坡函数
r(t)
Ra t0
t
0 t0
(d) 脉冲函数
(t)
t
0
(e) 单位脉冲函数
f (t)
t 0 (c) 抛物函数
r(t)
1
t
0
(f) 正弦函数
