2021届高考数学一轮复习第二章函数概念及基本初等函数Ⅰ第4节幂函数与二次函数教学案含解析新人教A版
数学复习:第二章函数的概念、基本初等函数(Ⅰ)及函数的应用.函数模型及其应用
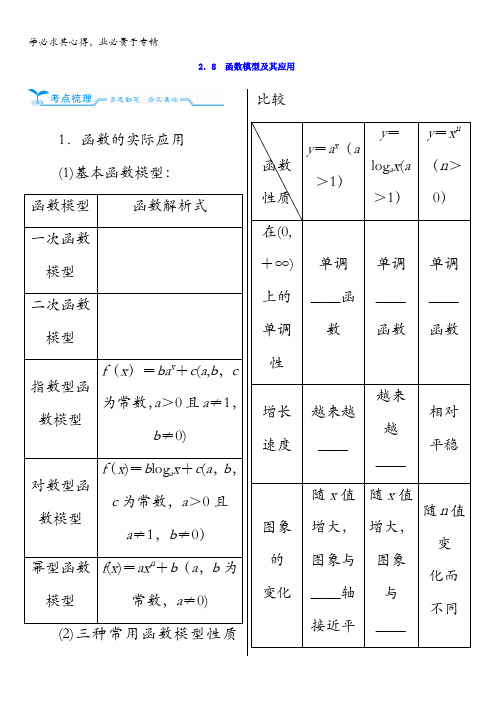
2.8 函数模型及其应用1.函数的实际应用(1)基本函数模型:函数模型函数解析式一次函数模型二次函数模型指数型函数模型f(x)=ba x+c(a,b,c 为常数,a>0且a≠1,b≠0)对数型函数模型f(x)=b log a x+c(a,b,c为常数,a>0且a≠1,b≠0)幂型函数模型f(x)=ax n+b(a,b为常数,a≠0)比较函数性质y=a x(a>1)y=log a x(a>1)y=x n(n>0)在(0,+∞)上的单调性单调____函数单调____函数单调____函数增长速度越来越____越来越____相对平稳图象的变化随x值增大,图象与____轴接近平随x值增大,图象与____随n值变化而不同行轴接近平行2。
函数建模(1)函数模型应用的两个方面:①利用已知函数模型解决问题;②建立恰当的函数模型,并利用所得函数模型解释有关现象,对某些发展趋势进行预测.(2)应用函数模型解决问题的基本过程:、、、.自查自纠1.(1)f(x)=ax+b(a,b为常数,a≠0)f(x)=ax2+bx+c(a,b,c为常数,a≠0)(2)增增增快慢y x2.审题建模解模还原手机的价格不断降低,若每隔半年其价格降低错误!,则现在价格为2 560元的手机,两年后价格可降为()A.900元B.810元C.1 440元D.160元解:半年降价一次,则两年后降价四次,其价格降为2 560×错误!错误!=810元.故选B.(错误!)某公司为激励创新,计划逐年加大研发资金投入.若该公司2015年全年投入研发资金130万元,在此基础上,每年投入的研发资金比上一年增长12%,则该公司全年投入的研发资金开始超过200万元的年份是(参考数据:lg1.12≈0.05,lg1。
3≈0。
11,lg2≈0.30)()A.2018年B.2019年C.2020年D.2021年解:设x年后该公司全年投入的研发资金为200万元,由题可知,130(1+12%)x=200,解得x=log1。
高考第一轮复习——一次函数、二次函数、基本初等函数(理科-)

一、学习目标:1. 了解基本初等函数(一次函数、二次函数、指数函数、对数函数、幂函数)的实际背景。
了解实数指数幂的意义及对数的作用、了解指数函数与对数函数互为反函数的性质。
2. 理解指数、对数的概念及其运算性质,理解指数函数、对数函数,一次函数、二次函数、幂函数的图象与性质。
3. 掌握幂的运算、对数运算及指数函数、对数函数、一次函数、二次函数性质的应用二、重点、难点:重点:(1)指数幂、对数的运算(2)对一次函数、二次函数、指数函数、对数函数的图象与性质的理解。
难点:一次函数、二次函数、指数函数、对数函数的图象与性质的应用三、考点分析:函数这部分内容是高考中的重点与难点,基本的初等函数是高考函数基础知识考查的重点,因此第一轮的复习重点是把握基本函数的基础知识及其简单的应用,这部分知识点是高考命题的“黄金”知识点,命题的题型有选择题、填空题、中等类型的大题等。
注:(1)二次函数的解析式的确定方法有三种形式①一般式:若已知二次函数经过A ,B ,C 三点,可设解析式为c bx ax x f ++=2)(,把三点坐标代入求出a ,b ,c 的值。
②零点式:若已知二次函数图象与x 轴有两个交点)0,(),0,(21x B x A ,可设解析式为:))(()(21x x x x a x f --=,再根据其余的条件确定a 的值。
③顶点式:若已知二次函数的顶点坐标(h ,k ),则可设函数解析式为:k h x a x f +-=2)()(的形式,再根据另外的条件确定a 的值。
(2)二次函数的最值的确定(i )若R x ∈,a >0,当abx 2-=时,函数取得最小值a b ac x f 44)(2min -=;若R x ∈,a<0,当abx 2-=时,函数取得最大值a b ac x f 44)(2max -=。
(ii )当)(],,[n m n m x <∈(或其他区间),讨论对称轴与区间[m ,n ]的三种位置关系。
4 第4讲 二次函数与幂函数

上一页
返回导航
下一页
第二章 函数概念与基本初等函数
18
2.当 0<x<1 时,f(x)=x1.1,g(x)=x0.9,h(x)=x-2 的大小关系是________. 解析:如图所示为函数 f(x),g(x),h(x)在(0,1)上的图象,由此可知 h(x)>g(x)>f(x).
答案:h(x)>g(x)>f(x)
上一页
返回导航
下一页
第二章 函数概念与基本初等函数
15
(2)易知函数 y=x12的定义域为[0,+∞),在定义域内为增函数,所以a3+ -12≥ a≥0, 0, 解得 a+1<3-2a,
-1≤a<23. 【答案】 (1)C (2)-1,23
上一页
返回导航
下一页
第二章 函数概念与基本初等函数
16
幂函数的性质与图象特征的关系 (1)幂函数的形式是 y=xα(α∈R),其中只有一个参数 α,因此只需一个条件即可确定其解 析式. (2)判断幂函数 y=xα(α∈R)的奇偶性时,当 α 是分数时,一般将其先化为根式,再判断. (3)若幂函数 y=xα 在(0,+∞)上单调递增,则 α>0,若在(0,+∞)上单调递减,则 α<0.
上一页
返回导航
下一页
第二章 函数概念与基本初等函数
17
1.已知幂函数 f(x)=xm2-2m-3(m∈Z)的图象关于 y 轴对称,并且 f(x)在第一象限是单调递 减函数,则 m=________. 解析:因为幂函数 f(x)=x m2-2m-3 (m∈Z)的图象关于 y 轴对称, 所以函数 f(x)是偶函数,所以 m2-2m-3 为偶数,所以 m2-2m 为奇数,又 m2-2m<0, 故 m=1. 答案:1
高考数学一轮复习第2章函数的概念及基本初等函数Ⅰ第4节二次函数与幂函数课件理新人教A版

第四节 二次函数与幂函数
栏
课 前 ·基 础 巩 固 1
目
导
课 堂 ·考 点 突 破 2
航
3 课 时 ·跟 踪 检 测
[最新考纲]
[考情分析]
[核心素养]
1.了解幂函数的概念.
2.结合函数 y=x,y=x2,y
幂函数一般不单独命题,常与指数、对数
=x3,y=1x,y=x12的图象,函数交汇命题;二次函数的图象与应用仍是 1.逻辑推理
(2)二次函数的图象和性质
解析式
f(x)=ax2+bx+c(a>0)
图象
定义域 值域
(-∞,+∞) 4ac4-a b2,+∞
f(x)=ax2+bx+c(a<0)
(-∞,+∞) -∞,4ac4-a b2
解析式
f(x)=ax2+bx+c(a>0)
f(x)=ax2+bx+c(a<0)
单调性
在-∞,-2ba上单调递减; 在 6 ___-__∞__,__-__2b_a__上单调递增; 在 5 ___-__2b_a_,__+__∞___上单调递 在-2ba,+∞上单调递减 增
考点二 二次函数的图象与性质 |题组突破|
4.如图是二次函数 y=ax2+bx+c 图象的一部分,图象过点 A(-3,0),对称轴为 x =-1.给出下面四个结论:①b2>4ac;②2a-b=1;③a-b+c=0;④5a<b.其中正确的 是( )
A.②④ B.①④ C.②③ D.①③
解析:选 B 因为图象与 x 轴交于两点,所以 b2-4ac>0,即 b2>4ac,①正确;对称 轴为 x=-1,即-2ba=-1,2a-b=0,②错误;结合图象知,当 x=-1 时,y>0,即 a -b+c>0,③错误;由对称轴为 x=-1 知,b=2a.又函数图象开口向下,所以 a<0,所 以 5a<2a,即 5a<b,④正确.故选 B.
:第二章 函数的概念及基本初等函数(Ⅰ) (6)

第二章函数的概念及基本初等函数(Ⅰ)第四节二次函数与幂函数A级·基础过关|固根基|1.幂函数y=f(x)经过点(3,3),则f(x)是()A.偶函数,且在(0,+∞)上是增函数B.偶函数,且在(0,+∞)上是减函数C.奇函数,且在(0,+∞)上是减函数D.非奇非偶函数,且在(0,+∞)上是增函数解析:选D设幂函数的解析式为y=xα,将(3,3)代入解析式得3α=3,解得α=12,∴y=x12,其是非奇非偶函数,且在(0,+∞)上是增函数.故选D.2.(2019届成都模拟)已知幂函数f(x)=xα,当x>1时,恒有f(x)<x,则α的取值范围是()A.(0,1) B.(-∞,1)C.(0,+∞) D.(-∞,0)解析:选B当x>1时,恒有f(x)<x,即当x>1时,函数f(x)=xα的图象在y =x的图象的下方,作出幂函数f(x)=xα在第一象限的图象,由图象可知(图略)α<1时满足题意.故选B.3.(2019届陕西西安联考)已知函数f(x)=-x2+4x,x∈[m,5]的值域是[-5,4],则实数m的取值范围是()A.(-∞,-1) B.(-1,2]C.[-1,2] D.[2,5]解析:选C∵f(x)=-x2+4x=-(x-2)2+4,∴当x=2时,f(2)=4,由f(x)=-x2+4x=-5,解得x=5或x=-1,∴要使函数在[m,5]的值域是[-5,4],则-1≤m ≤2,故选C .4.函数f (x )=(x -2)(ax +b )为偶函数,且在(0,+∞)单调递增,则f (2-x )>0的解集为( )A .{x |-2<x <2}B .{x |x >2或x <-2}C .{x |0<x <4}D .{x |x >4或x <0}解析:选D 因为函数f (x )=ax 2+(b -2a )x -2b 为偶函数,所以b -2a =0,故f (x )=ax 2-4a =a (x -2)(x +2).因为f (x )在(0,+∞)上单调递增,所以a >0.根据二次函数的性质可知,不等式f (2-x )>0的解集为{x |2-x >2或2-x <-2}={x |x <0或x >4},故选D .5.(2019届河南南阳模拟)设函数f (x )=mx 2-mx -1,若对于x ∈[1,3],f (x )<-m +4恒成立,则实数m 的取值范围为( )A .(-∞,0]B .⎣⎢⎡⎭⎪⎫0,57C .(-∞,0)∪⎝ ⎛⎭⎪⎫0,57D .⎝ ⎛⎭⎪⎫-∞,57解析:选D 由题意知,f (x )<-m +4对于x ∈[1,3]恒成立,即m (x 2-x +1)<5对于x ∈[1,3]恒成立.∵当x ∈[1,3]时,x 2-x +1∈[1,7],∴不等式m (x 2-x +1)<5等价于m <5x 2-x +1.∵当x =3时,5x 2-x +1取最小值57,∴若要不等式m <5x 2-x +1对于x ∈[1,3]恒成立,则必须满足m <57,因此,实数m 的取值范围为⎝ ⎛⎭⎪⎫-∞,57,故选D . 6.函数f (x )=2x 2-mx +3,当x ∈[-2,+∞)时,f (x )是增函数,当x ∈(-∞,-2]时,f (x )是减函数,则f (1)的值为( )A .-3B .13C .7D .5解析:选B 由题意得,函数f (x )=2x 2-mx +3图象的对称轴为x =m 4=-2,所以m =-8,即f (x )=2x 2+8x +3,所以f (1)=2+8+3=13.故选B .7.(2019届宁夏银川一中模拟)已知点(m ,8)在幂函数f (x )=(m -1)x n 的图象上,设a =f ⎝ ⎛⎭⎪⎫33,b =f (ln π),c =f ⎝ ⎛⎭⎪⎫22,则a ,b ,c 的大小关系为( )A .a <c <bB .a <b <cC .b <c <aD .b <a <c解析:选A ∵点(m ,8)在幂函数f (x )=(m -1)x n 的图象上,∴⎩⎪⎨⎪⎧m -1=1,(m -1)m n =8,解得⎩⎪⎨⎪⎧m =2,n =3,∴f (x )=x 3,且f (x )在(-∞,+∞)上单调递增.又33<22<1<ln π,∴a <c <b ,故选A .8.已知函数f (x )=x 2-m 是定义在区间[-3-m ,m 2-m ]上的奇函数,则f (m )=________.解析:由题意得,m 2-m =3+m ,即m 2-2m -3=0, ∴m =3或m =-1.当m =3时,f (x )=x -1,区间[-3-m ,m 2-m ]为[-6,6],f (x )在x =0处无意义,故舍去;当m =-1时,f (x )=x 3,[-3-m ,m 2-m ]为[-2,2],满足题意,∴f (m )=f (-1)=(-1)3=-1.答案:-19.已知二次函数y =x 2+2kx +3-2k ,则顶点位置最高时函数的解析式为____________.解析:由题意,可知y =x 2+2kx +3-2k =(x +k )2-k 2-2k +3,所以该函数的顶点坐标为(-k ,-k 2-2k +3).设顶点的纵坐标为y =-k 2-2k +3=-(k +1)2+4,所以当k =-1时,顶点位置最高,此时函数的解析式为y =x 2-2x +5.答案:y =x 2-2x +510.(2019届福建养正中学模拟)已知函数f (x )=2x ,g (x )=x 2+2ax (-3≤x ≤3). (1)若g (x )在[-3,3]上是单调函数,求a 的取值范围; (2)当a =-1时,求函数y =f [g (x )]的值域. 解:(1)g (x )=(x +a )2-a 2的图象的对称轴为x =-a , ∵g (x )在[-3,3]上是单调函数,∴-a ≥3或-a ≤-3,即a ≤-3或a ≥3, 故a 的取值范围为(-∞,-3]∪[3,+∞).(2)当a =-1时,f [g (x )]=2x 2-2x (-3≤x ≤3),令u =x 2-2x ,y =2u ,∵x ∈[-3,3],∴u =x 2-2x =(x -1)2-1∈[-1,15], 而y =2u 是增函数,∴12≤y ≤215, ∴函数y =f [g (x )]的值域是⎣⎢⎡⎦⎥⎤12,215.11.已知函数f (x )=bx 2-2ax +a (a ,b ∈R )的图象过点⎝ ⎛⎭⎪⎫12,14.(1)当a =2时,求函数f (x )在[0,3]上的最大值和最小值;(2)若a <0,求使函数f (x )的定义域为[-1,1],值域为[-2,2]的a 的值. 解:(1)∵函数f (x )=bx 2-2ax +a (a ,b ∈R )的图象过点⎝ ⎛⎭⎪⎫12,14,∴14=b ×⎝ ⎛⎭⎪⎫122-2a ×12+a ,解得b =1.∴当a =2时,f (x )=x 2-4x +2,其图象关于x =2对称, ∴f (x )在[0,2]上单调递减,在[2,3]上单调递增, ∴f (x )在[0,3]上的最小值为f (2)=-2. 又f (0)=2,f (3)=-1,∴f (x )在[0,3]上的最大值为f (0)=2.(2)由(1)知,f (x )=x 2-2ax +a =(x -a )2-a 2+a ,当-1≤a <0时,有⎩⎨⎧f (1)=2,f (a )=-2,即⎩⎨⎧f (1)=1-a =2,f (a )=a -a 2=-2,解得a =-1; 当a <-1时,有⎩⎨⎧f (-1)=-2,f (1)=2,即⎩⎨⎧1+2a +a =-2,1-2a +a =2,解得a =-1(舍去). 综上所述a =-1.B 级·素养提升 |练能力|12.(2019届湖南五市十校联考)已知函数f (x )=⎩⎨⎧3,x <0,x 2-2ax +2a ,x ≥0的图象上恰好有两对关于原点对称的点,则实数a 的取值范围是( )A .(1,3)B .⎝ ⎛⎭⎪⎫32,+∞C .(-1,3)D .(3,+∞)解析:选D 依题意,当x >0时,f (x )的图象与直线y =-3有两个交点,所以⎩⎪⎨⎪⎧--2a 2>0,f (a )<-3,解得a >3.故选D .13.(2019届合肥质检)函数f (x )=-x 2+3x +a ,g (x )=2x -x 2,若f [g (x )]≥0对x ∈[0,1]恒成立,则实数a 的取值范围是( )A .[-e ,+∞)B .[-ln 2,+∞)C .[-2,+∞)D .⎝ ⎛⎦⎥⎤-12,0解析:选C 如图所示,在同一坐标系中画出y =x 2+1,y =2x,y =x 2+32的图象,由图象可知,在[0,1]上,x 2+1≤2x <x 2+32恒成立,即1≤2x -x 2<32,当且仅当x =0或x =1时等号成立,∴1≤g (x )<32,∴f [g (x )]≥0⇒f (1)≥0⇒-1+3+a ≥0⇒a ≥-2,即实数a 的取值范围是[-2,+∞),故选C .14.(2019届菏泽联考)已知函数f (x )=mx 2+(2-m )x +n (m >0),当-1≤x ≤1时,|f (x )|≤1恒成立,则f ⎝ ⎛⎭⎪⎫23=________.解析:∵当x ∈[-1,1]时,|f (x )|≤1恒成立. ∴⎩⎪⎨⎪⎧|f (0)|≤1⇒|n |≤1⇒-1≤n ≤1;|f (1)|≤1⇒|2+n |≤1⇒-3≤n ≤-1, 因此n =-1,∴f (0)=-1,f (1)=1.由f (x )的图象可知,要满足题意,则图象的对称轴为x =0,∴2-m =0,m =2,∴f (x )=2x 2-1,∴f ⎝ ⎛⎭⎪⎫23=-19.答案:-1915.在平面直角坐标系xOy 中,设定点A (a ,a ),P 是函数y =1x (x >0)图象上一动点,若点P ,A 之间的最短距离为22,则满足条件的实数a 的所有值为________.解析:设P ⎝ ⎛⎭⎪⎫x ,1x ,x >0,则|P A |2=(x -a )2+⎝ ⎛⎭⎪⎫1x -a 2=x 2+1x 2-2a ⎝ ⎛⎭⎪⎫x +1x +2a 2=⎝ ⎛⎭⎪⎫x +1x 2-2a ⎝ ⎛⎭⎪⎫x +1x +2a 2-2.令t =x +1x ,则由x >0,得t ≥2.所以|P A |2=t 2-2at +2a 2-2=(t -a )2+a 2-2, 由|P A |取得最小值,得⎩⎪⎨⎪⎧a ≤2,22-4a +2a 2-2=(22)2或⎩⎪⎨⎪⎧a >2,a 2-2=(22)2,解得a =-1或a =10. 答案:-1,10。
第2章 函数概念与基本初等函数Ⅰ 第4节 幂函数与二次函数

知识诊断 基础夯实
ZHISHIZHENDUANJICHUHANGSHI
知识梳理 1.幂函数
(1)幂函数的定义 一般地,形如___y_=__x_α___的函数称为幂函数,其中x是自变量,α为常数. (2)常见的五种幂函数的图象
索引
(3)幂函数的性质 ①幂函数在(0,+∞)上都有定义; ②当α>0时,幂函数的图象都过点(1,1)和(0,0),且在(0,+∞)上单调递增; ③当α<0时,幂函数的图象都过点(1,1),且在(0,+∞)上单调递减.
索引
感悟提升
求二次函数的解析式,一般用待定系数法,其关键是根据已知条件恰当选择二 次函数解析式的形式,一般选择规律如下:
索引
训练1 (1)已知二次函数f(x)=ax2+bx+1(a,b∈R),x∈R,若函数f(x)的最小值 为f(-1)=0,则f(x)=______x_2+___2_x_+__1. 解析 设函数f(x)的解析式为f(x)=a(x+1)2=ax2+2ax+a, 由已知f(x)=ax2+bx+1, 所以a=1,b=2a=2,故f(x)=x2+2x+1.
D.f(m+1)<0
索引
角度2 二次函数的单调性与最值
例3 (1)函数f(x)=ax2+(a-3)x+1在区间[-1,+∞)上单调递减,则实数a的取
值范围是( D )
A.[-3,0)
B.(-∞,-3]
C.[-2,0]
D.[-3,0]
解析 当a=0时,f(x)=-3x+1在[-1,+∞)上单调递减,满足题意. 当 a≠0 时,f(x)的对称轴为直线 x=3- 2aa,
第二章 函数概念与基本初等函数Ⅰ
索引
考试要求
1.了解幂函数的概念;结合函数 y=x,y=x2,y=x3,y=x12,y=1x的图象, 了解它们的变化情况;2.理解二次函数的图象和性质,能用二次函数、方程、 不等式之间的关系解决简单问题.
高考数学1第二章基本初等函数考点汇总

高考数学1第二章基本初等函数考点汇总一、指数函数(一)指数与指数幂的运算1.根式的概念:一样地,假如,那么叫做的次方根(n th root),其中>1,且∈*.当是奇数时,正数的次方根是一个正数,负数的次方根是一个负数.现在,的次方根用符号表示.式子叫做根式(radical),那个地点叫做根指数(radical exponent),叫做被开方数(radicand).当是偶数时,正数的次方根有两个,这两个数互为相反数.现在,正数的正的次方根用符号表示,负的次方根用符号- 表示.正的次方根与负的次方根能够合并成±( >0).由此可得:负数没有偶次方根;0的任何次方根差不多上0,记作。
注意:当是奇数时,,当是偶数时,2.分数指数幂正数的分数指数幂的意义,规定:0的正分数指数幂等于0,0的负分数指数幂没有意义指出:规定了分数指数幂的意义后,指数的概念就从整数指数推广到了有理数指数,那么整数指数幂的运算性质也同样能够推广到有理数指数幂.3.实数指数幂的运算性质(二)指数函数及其性质1、指数函数的概念:一样地,函数叫做指数函数(exponential functio n),其中x是自变量,函数的定义域为R.注意:指数函数的底数的取值范畴,底数不能是负数、零和1.2、指数函数的图象和性质a>1 0图象特点函数性质向x、y轴正负方向无限延伸函数的定义域为R图象关于原点和y轴不对称非奇非偶函数二、对数函数(一)对数1.对数的概念:一样地,假如,那么数叫做以为底的对数,记作:( —底数,—真数,—对数式)说明:○1 注意底数的限制,且;○2 ;○3 注意对数的书写格式.两个重要对数:○1 常用对数:以10为底的对数;○2 自然对数:以无理数为底的对数的对数.对数式与指数式的互化(二)对数的运算性质假如,且,,,那么:○1 ? + ;○2 - ;○3 .注意:换底公式( ,且; ,且; ).利用换底公式推导下面的结论(1) ;(2) .(二)对数函数1、对数函数的概念:函数,且叫做对数函数,其中是自变量,函数的定义域是(0,+∞).注意:○1 对数函数的定义与指数函数类似,差不多上形式定义,注意辨别。
全国近年高考数学一轮复习第2章函数、导数及其应用第4讲幂函数与二次函数学案(2021年整理)

(全国版)2019版高考数学一轮复习第2章函数、导数及其应用第4讲幂函数与二次函数学案编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望((全国版)2019版高考数学一轮复习第2章函数、导数及其应用第4讲幂函数与二次函数学案)的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为(全国版)2019版高考数学一轮复习第2章函数、导数及其应用第4讲幂函数与二次函数学案的全部内容。
第4讲幂函数与二次函数板块一知识梳理·自主学习[必备知识]考点幂函数的图象和性质1.五种幂函数图象的比较2.幂函数的性质比较[必会结论]1.一元二次不等式恒成立的条件(1)ax2+bx+c>0(a≠0)恒成立的充要条件是错误!(2)ax2+bx+c<0(a≠0)恒成立的充要条件是错误!2.二次函数表达式的三种形式(1)一般式:y=ax2+bx+c(a≠0).(2)顶点式:y=a(x+h)2+k(其中a≠0,顶点坐标为(-h,k)).(3)两根式:y=a(x-x1)(x-x2)(其中a≠0,x1,x2是二次函数的图象与x轴的两个交点的横坐标).[考点自测]1.判断下列结论的正误.(正确的打“√",错误的打“×”)(1)幂函数的图象都经过点(1,1)和(0,0).( )(2)二次函数y=ax2+bx+c(x∈R),不可能是偶函数.()(3)二次函数y=ax2+bx+c,x∈[a,b]的最值一定是错误!.( )(4)当α<0时,幂函数y=xα是定义域上的减函数.( )答案(1)×(2)×(3)×(4)×2.[2018·济南诊断]已知幂函数f(x)=kxα的图象过点错误!,则k+α=( )A.错误!B.1C。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第4节幂函数与二次函数考试要求 1.了解幂函数的概念;结合函数y=x,y=x2,y=x3,y=x 12,y=1x的图象,了解它们的变化情况;2.理解二次函数的图象和性质,能用二次函数、方程、不等式之间的关系解决简单问题.知识梳理1.幂函数(1)幂函数的定义一般地,形如y=xα的函数称为幂函数,其中x是自变量,α为常数.(2)常见的五种幂函数的图象(3)幂函数的性质①幂函数在(0,+∞)上都有定义;②当α>0时,幂函数的图象都过点(1,1)和(0,0),且在(0,+∞)上单调递增;③当α<0时,幂函数的图象都过点(1,1),且在(0,+∞)上单调递减.2.二次函数(1)二次函数解析式的三种形式一般式:f(x)=ax2+bx+c(a≠0).顶点式:f(x)=a(x-m)2+n(a≠0),顶点坐标为(m,n).零点式:f(x)=a(x-x1)(x-x2)(a≠0),x1,x2为f(x)的零点.(2)二次函数的图象和性质函数y=ax2+bx+c(a>0)y=ax2+bx+c(a<0)图象(抛物线)定义域R值域⎣⎢⎡⎭⎪⎫4ac-b24a,+∞⎝⎛⎦⎥⎤-∞,4ac-b24a 对称轴x=-b2a顶点坐标⎝⎛⎭⎪⎫-b2a,4ac-b24a奇偶性当b=0时是偶函数,当b≠0时是非奇非偶函数单调性在⎝⎛⎦⎥⎤-∞,-b2a上是减函数;在⎣⎢⎡⎭⎪⎫-b2a,+∞上是增函数在⎝⎛⎦⎥⎤-∞,-b2a上是增函数;在⎣⎢⎡⎭⎪⎫-b2a,+∞上是减函数[常用结论与微点提醒]1.二次函数的单调性、最值与抛物线的开口方向和对称轴及给定区间的范围有关.2.若f(x)=ax2+bx+c(a≠0),则当⎩⎪⎨⎪⎧a>0,Δ<0时恒有f(x)>0;当⎩⎪⎨⎪⎧a<0,Δ<0时,恒有f(x)<0.3.(1)幂函数的图象一定会出现在第一象限内,一定不会出现在第四象限;(2)幂函数的图象过定点(1,1),如果幂函数的图象与坐标轴相交,则交点一定是原点.诊断自测1.判断下列结论正误(在括号内打“√”或“×”)(1)函数y=2x13是幂函数.( )(2)当α>0时,幂函数y=xα在(0,+∞)上是增函数.( )(3)二次函数y=ax2+bx+c(a≠0)的两个零点可以确定函数的解析式.( )(4)二次函数y=ax2+bx+c(x∈[a,b])的最值一定是4ac-b24a.( )解析(1)由于幂函数的解析式为f(x)=xα,故y=2x13不是幂函数,(1)错.(3)确定二次函数的解析式需要三个独立的条件,两个零点不能确定函数的解析式.(4)对称轴x=-b2a,当-b2a小于a或大于b时,最值不是4ac-b24a,故(4)错.答案 (1)× (2)√ (3)× (4)×2.(老教材必修1P79T1改编)已知幂函数f (x )=k ·x α的图象过点⎝ ⎛⎭⎪⎫12,22,则k +α=( )A.12B.1C.32D.2解析 因为f (x )=k ·x α是幂函数,所以k =1. 又f (x )的图象过点⎝ ⎛⎭⎪⎫12,22,所以⎝ ⎛⎭⎪⎫12α=22, 所以α=12,所以k +α=1+12=32.答案 C3.(新教材必修第一册P86T7改编)如果函数f (x )=ax 2+2x -3在区间(-∞,4)上单调递增,则实数a 的取值范围是________.解析 当a =0时,f (x )=2x -3在(-∞,4)单调递增. 当a ≠0时,f (x )在(-∞,4)上单调递增.则a 需满足⎩⎪⎨⎪⎧a <0,-1a ≥4,解得-14≤a <0.综上可知,-14≤a ≤0.答案 ⎣⎢⎡⎦⎥⎤-14,04.(2016·全国Ⅲ卷)已知a =243,b =323,c =2513,则( ) A.b <a <c B.a <b <c C.b <c <aD.c <a <b解析 因为a =243=423,b =323,c =523又y =x 23在(0,+∞)上是增函数,所以c >a >b . 答案 A5.(2020·河南省实验中学质检)已知函数f (x )=3x 2-2(m +3)x +m +3的值域为[0,+∞),则实数m 的取值范围为( ) A.{0,-3} B.[-3,0]C.{0,3}D.(-∞,-3]∪[0,+∞)解析 依题意,得Δ=4(m +3)2-4×3(m +3)=0,则m =0或m =-3.∴实数m 的取值范围是{0,-3}. 答案 A6.(2018·上海卷)已知α∈⎩⎨⎧-2,-1,-12,⎭⎬⎫12,1,2,3.若幂函数f (x )=x α为奇函数,且在(0,+∞)上递减,则α=______. 解析 由y =x α为奇函数,知α取-1,1,3. 又y =x α在(0,+∞)上递减,∴α<0,取α=-1. 答案 -1考点一 幂函数的图象和性质【例1】 (1)幂函数y =f (x )的图象过点(4,2),则幂函数y =f (x )的大致图象是( )(2)(2020·衡水中学调研)已知点(m ,8)在幂函数f (x )=(m -1)x n的图象上,设a =f ⎝ ⎛⎭⎪⎫13,b=f (ln π),c =f (2-12),则a ,b ,c 的大小关系是( ) A.a <c <b B.a <b <c C.b <c <aD.b <a <c解析 (1)设幂函数的解析式为y =x α, 因为幂函数y =f (x )的图象过点(4,2), 所以2=4α,解得α=12.所以y =x ,其定义域为[0,+∞),且是增函数,当0<x <1时,其图象在直线y =x 的上方,对照选项,C 正确.(2)由于f (x )=(m -1)x n为幂函数, 所以m -1=1,则m =2,f (x )=x n. 又点(2,8)在函数f (x )=x n的图象上,所以8=2n,知n =3,故f (x )=x 3,且在R 上是增函数,又ln π>1>2-12=22>13, 所以f (ln π)>f (2-12)>f ⎝ ⎛⎭⎪⎫13,则b >c >a . 答案 (1)C (2)A规律方法 1.对于幂函数图象的掌握,需记住在第一象限内三条线分第一象限为六个区域,即x =1,y =1,y =x 所分区域.根据α<0,0<α<1,α=1,α>1的取值确定位置后,其余象限部分由奇偶性决定.2.在比较幂值的大小时,必须结合幂值的特点,选择适当的函数,借助其单调性进行比较.【训练1】 (1)(2019·荆门模拟)已知点⎝ ⎛⎭⎪⎫2,12在幂函数f (x )的图象上,则f (x )是( ) A.奇函数B.偶函数C.定义域内的减函数D.定义域内的增函数(2)若幂函数y =x -1,y =x m 与y =x n在第一象限内的图象如图所示,则m 与n 的取值情况为( )A.-1<m <0<n <1B.-1<n <0<mC.-1<m <0<nD.-1<n <0<m <1解析 (1)设幂函数y =f (x )=x α,且图象过点⎝ ⎛⎭⎪⎫2,12,∴2α=12,得α=-1,则f (x )=x -1在x ∈R 且x ≠0时为奇函数,但在定义域内不单调.(2)幂函数y =x α,当α>0时,y =x α在(0,+∞)上为增函数,且0<α<1时,图象上凸,∴0<m <1. 当α<0时,y =x α在(0,+∞)上为减函数. 不妨令x =2,由图象得2-1<2n,则-1<n <0. 综上可知,-1<n <0<m <1. 答案 (1)A (2)D 考点二 二次函数的解析式【例2】 (一题多解)已知二次函数f (x )满足f (2)=-1,f (-1)=-1,且f (x )的最大值是8,试确定该二次函数的解析式. 解 法一 (利用“一般式”解题) 设f (x )=ax 2+bx +c (a ≠0).由题意得⎩⎪⎨⎪⎧4a +2b +c =-1,a -b +c =-1,4ac -b 24a=8,解得⎩⎪⎨⎪⎧a =-4,b =4,c =7.∴所求二次函数的解析式为f (x )=-4x 2+4x +7. 法二 (利用“顶点式”解题) 设f (x )=a (x -m )2+n (a ≠0). 因为f (2)=f (-1), 所以抛物线的对称轴为x =2+(-1)2=12,所以m =12. 又根据题意,函数有最大值8,所以n =8,所以y =f (x )=a ⎝ ⎛⎭⎪⎫x -122+8.因为f (2)=-1,所以a ⎝ ⎛⎭⎪⎫2-122+8=-1,解得a =-4, 所以f (x )=-4⎝ ⎛⎭⎪⎫x -122+8=-4x 2+4x +7.法三 (利用“零点式”解题)由已知f (x )+1=0的两根为x 1=2,x 2=-1, 故可设f (x )+1=a (x -2)(x +1)(a ≠0), 即f (x )=ax 2-ax -2a -1.又函数有最大值8,即4a (-2a -1)-(-a )24a =8.解得a =-4或a =0(舍).故所求函数的解析式为f (x )=-4x 2+4x +7.规律方法 求二次函数的解析式,一般用待定系数法,其关键是根据已知条件恰当选择二次函数解析式的形式,一般选择规律如下:【训练2】已知二次函数f(x)的图象经过点(4,3),它在x轴上截得的线段长为2,并且对任意x∈R,都有f(2-x)=f(2+x),则f(x)=________.解析因为f(2-x)=f(2+x)对x∈R恒成立,所以y=f(x)的图象关于x=2对称.又y=f(x)的图象在x轴上截得的线段长为2,所以f(x)=0的两根为2-22=1或2+22=3.所以二次函数f(x)与x轴的两交点坐标为(1,0)和(3,0).因此设f(x)=a(x-1)(x-3).又点(4,3)在y=f(x)的图象上,所以3a=3,则a=1.故f(x)=(x-1)(x-3)=x2-4x+3.答案x2-4x+3考点三二次函数的图象及应用【例3】 (1)对数函数y=log a x(a>0且a≠1)与二次函数y=(a-1)x2-x在同一坐标系内的图象可能是( )(2)设函数f(x)=x2+x+a(a>0),已知f(m)<0,则( )A.f(m+1)≥0B.f(m+1)≤0C.f(m+1)>0D.f(m+1)<0解析(1)若0<a<1,则y=log a x在(0,+∞)上单调递减,y=(a-1)x2-x开口向下,其图象的对称轴在y轴左侧,排除C,D.若a>1,则y=log a x在(0,+∞)上是增函数,y =(a -1)x 2-x 图象开口向上,且对称轴在y 轴右侧,因此B 项不正确,只有选项A 满足.(2)因为f (x )的对称轴为x =-12,f (0)=a >0,所以f (x )的大致图象如图所示.由f (m )<0,得-1<m <0,所以m +1>0,所以f (m +1)>f (0)>0. 答案 (1)A (2)C规律方法 1.研究二次函数图象应从“三点一线一开口”进行分析,“三点”中有一个点是顶点,另两个点是图象上关于对称轴对称的两个点,常取与x 轴的交点;“一线”是指对称轴这条直线;“一开口”是指抛物线的开口方向.2.求解与二次函数有关的不等式问题,可借助二次函数的图象特征,分析不等关系成立的条件.【训练3】 一次函数y =ax +b 与二次函数y =ax 2+bx +c 在同一坐标系中的图象大致是( )解析 A 中,由一次函数y =ax +b 的图象可得a >0,此时二次函数y =ax 2+bx +c 的图象应该开口向上,A 错误;B 中,由一次函数y =ax +b 的图象可得a >0,b >0,此时二次函数y =ax 2+bx +c 的图象应该开口向上,对称轴x =-b2a <0,B 错误;C 中,由一次函数y =ax +b 的图象可得a <0,b <0,此时二次函数y =ax 2+bx +c 的图象应该开口向下,对称轴x =-b2a<0,C 正确;D 中,由一次函数y =ax +b 的图象可得a <0,b <0,此时二次函数y =ax 2+bx +c 的图象应该开口向下,D 错误. 答案 C考点四 二次函数的性质多维探究角度1 二次函数的单调性与最值【例4-1】 已知二次函数f (x )=ax 2+bx +1(a ,b ∈R 且a ≠0),x ∈R . (1)若函数f (x )的最小值为f (-1)=0,求f (x )的解析式,并写出单调区间; (2)在(1)的条件下,f (x )>x +k 在区间[-3,-1]上恒成立,试求k 的取值范围.解 (1)由题意知⎩⎪⎨⎪⎧a >0,-b 2a =-1,f (-1)=a -b +1=0,解得⎩⎪⎨⎪⎧a =1,b =2.所以f (x )=x 2+2x +1,由f (x )=(x +1)2知,函数f (x )的单调递增区间为[-1,+∞),单调递减区间为(-∞,-1]. (2)由题意知,x 2+2x +1>x +k 在区间[-3,-1]上恒成立,即k <x 2+x +1在区间[-3,-1]上恒成立,令g (x )=x 2+x +1,x ∈[-3,-1],由g (x )=⎝ ⎛⎭⎪⎫x +122+34知g (x )在区间[-3,-1]上是减函数,则g (x )min =g (-1)=1,所以k <1,故k 的取值范围是(-∞,1). 角度2 二次函数中的恒成立问题【例4-2】 (2020·沈阳模拟)已知函数f (x )=-x 2+ax -6,g (x )=x +4.若对任意x 1∈(0,+∞),存在x 2∈(-∞,-1],使f (x 1)≤g (x 2),则实数a 的最大值为( ) A.6B.4C.3D.2解析 由题意f (x )max ≤g (x )max ,(*)由g (x )在(-∞,-1]上单调递增,则g (x )max =g (-1)=3,f (x )=-x 2+ax -6=-⎝ ⎛⎭⎪⎫x -a 22+a24-6.当a ≤0时,f (x )在[0,+∞)上单调递减, 所以f (x )<f (0)=-6,显然f (x )<g (x )max =3. 所以当a ≤0时,(*)恒成立.当a >0时,x =a2∈(0,+∞),∴f (x )max =f ⎝ ⎛⎭⎪⎫a 2=a24-6.此时应有a 24-6≤3,且a >0,解得0<a ≤6. 综上可知a ≤6,则a 的最大值为6. 答案 A规律方法 1.二次函数最值问题的解法:抓住“三点一轴”数形结合,三点是指区间两个端点和中点,一轴指的是对称轴,结合图象,根据函数的单调性及分类讨论的思想求解. 2.由不等式恒成立求参数取值范围的思路及关键(1)一般有两个解题思路:一是分离参数;二是不分离参数.(2)两种思路都是将问题归结为求函数的最值,至于用哪种方法,关键是看参数是否易分离.这两个思路的依据是:a ≥f (x )恒成立⇔a ≥f (x )max ,a ≤f (x )恒成立⇔a ≤f (x )min .【训练4】 (1)(角度1)若函数f (x )=x 2+ax +b 的图象与x 轴的交点为(1,0)和(3,0),则函数f (x )( )A.在(-∞,2]上递减,在[2,+∞)上递增B.在(-∞,3)上递增C.在[1,3]上递增D.单调性不能确定(2)(角度2)若函数f (x )=ax 2-(2a +1)x +a +1对于x ∈[-1,1]时恒有f (x )≥0,则实数a 的取值范围是________.解析 (1)由已知可得该函数图象的对称轴为x =2,又二次项系数为1>0,所以f (x )在(-∞,2]上是递减的,在[2,+∞)上是递增的.(2)∀x ∈[-1,1]时,f (x )≥0⇔a (x -1)2≥x -1.(*) 当x =1时,a ∈R ,(*)式恒成立. 当x ∈[-1,1)时,(*)式等价于a ≥1x -1恒成立. 又t =1x -1在[-1,1)上是减函数,a ≥⎝ ⎛⎭⎪⎫1x -1max=-12. 综上知a ≥-12.答案 (1)A (2)⎣⎢⎡⎭⎪⎫-12,+∞A 级 基础巩固一、选择题1.(2020·濮阳模拟)已知函数f (x )=(m 2-m -1)xm 2+2m -3是幂函数,且其图象与两坐标轴都没有交点,则实数m =( ) A.-1B.2C.3D.2或-1解析 由题意,得m 2-m -1=1,解得m =2或m =-1. 当m =2时,f (x )=x 5的图象与坐标轴有交点,不合题意. 当m =-1时,f (x )=x -4的图象与坐标轴无交点,符合题意. 综上可知,m =-1. 答案 A2.已知p :|m +1|<1,q :幂函数y =(m 2-m -1)x m在(0,+∞)上单调递减,则p 是q 的( ) A.充分不必要条件 B.必要不充分条件 C.充要条件D.既不充分也不必要条件解析 p :由|m +1|<1得-2<m <0,又幂函数y =(m 2-m -1)x m在(0,+∞)上单调递减, 所以m 2-m -1=1,且m <0,解得m =-1. 故p 是q 的必要不充分条件. 答案 B3.若函数f (x )=x 2+ax +b 在区间[0,1]上的最大值是M ,最小值是m ,则M -m ( ) A.与a 有关,且与b 有关 B.与a 有关,但与b 无关 C.与a 无关,且与b 无关 D.与a 无关,但与b 有关解析 设x 1,x 2分别是函数f (x )在[0,1]上的最小值点与最大值点,则m =x 21+ax 1+b ,M =x 22+ax 2+b .所以M -m =x 22-x 21+a (x 2-x 1),显然此值与a 有关,与b 无关. 答案 B4.(2020·长沙一中调研)定义在R 上的函数f (x )=-x 3+m 与函数g (x )=f (x )+x 3+x 2-kx 在[-1,1]上具有相同的单调性,则k 的取值范围是( ) A.(-∞,-2] B.[2,+∞)C.[-2,2]D.(-∞,-2]∪[2,+∞)解析 易知f (x )=-x 3+m 在R 上是减函数.依题设,函数g (x )=x 2-kx +m 在[-1,1]上单调递减. ∴抛物线的对称轴x =k2≥1,则k ≥2.答案 B5.若函数y =x 2-3x -4的定义域为[0,m ],值域为⎣⎢⎡⎦⎥⎤-254,-4,则m 的取值范围是( )A.[0,4]B.⎣⎢⎡⎦⎥⎤32,4C.⎣⎢⎡⎭⎪⎫32,+∞D.⎣⎢⎡⎦⎥⎤32,3 解析 二次函数图象的对称轴为x =32,且f ⎝ ⎛⎭⎪⎫32=-254,f (3)=f (0)=-4,结合函数图象(如图所示),可得m ∈⎣⎢⎡⎦⎥⎤32,3.答案 D 二、填空题6.已知函数f (x )为幂函数,且f (4)=12,则当f (a )=4f (a +3)时,实数a 等于________.解析 设f (x )=x α,则4α=12,所以α=-12.因此f (x )=x -12,从而a -12=4(a +3)-12,解得a =15.答案 157.已知函数f (x )=-x 2+4x +a ,x ∈[0,1],若f (x )有最小值-2,则f (x )的最大值为________. 解析 f (x )=-x 2+4x +a =-(x -2)2+a +4, ∴函数f (x )=-x 2+4x +a 在[0,1]上单调递增,∴当x =0时,f (x )取得最小值,当x =1时,f (x )取得最大值, ∴f (0)=a =-2,f (1)=3+a =3-2=1. 答案 18.已知二次函数f (x )满足f (2+x )=f (2-x ),且f (x )在[0,2]上是增函数,若f (a )≥f (0),则实数a 的取值范围是________.解析由题意可知函数f(x)的图象开口向下,对称轴为x=2(如图),若f(a)≥f(0),从图象观察可知0≤a≤4.答案[0,4]三、解答题9.已知函数f(x)=x2+2ax+3,x∈[-4,6].(1)当a=-2时,求f(x)的最值;(2)求实数a的取值范围,使y=f(x)在区间[-4,6]上是单调函数.解(1)当a=-2时,f(x)=x2-4x+3=(x-2)2-1,由于x∈[-4,6],∴f(x)在[-4,2]上单调递减,在[2,6]上单调递增,∴f(x)的最小值是f(2)=-1,又f(-4)=35,f(6)=15,故f(x)的最大值是35.(2)由于函数f(x)的图象开口向上,对称轴是x=-a,所以要使f(x)在[-4,6]上是单调函数,应有-a≤-4或-a≥6,即a≤-6或a≥4,故a的取值范围是(-∞,-6]∪[4,+∞).10.已知幂函数f(x)=(m-1)2x m 2-4m+2在(0,+∞)上单调递增,函数g(x)=2x-k.(1)求m的值;(2)当x∈[1,2)时,记f(x),g(x)的值域分别为集合A,B,设p:x∈A,q:x∈B,若p是q 成立的必要条件,求实数k的取值范围.解(1)依题意得:(m-1)2=1⇒m=0或m=2,当m=2时,f(x)=x-2在(0,+∞)上单调递减,与题设矛盾,舍去,∴m=0.(2)由(1)得,f(x)=x2,当x∈[1,2)时,f(x)∈[1,4),即A=[1,4),当x∈[1,2)时,g(x)∈[2-k,4-k),即B=[2-k,4-k),因p是q成立的必要条件,则B⊆A,则⎩⎪⎨⎪⎧2-k ≥1,4-k ≤4,即⎩⎪⎨⎪⎧k ≤1,k ≥0,得0≤k ≤1. 故实数k 的取值范围是[0,1].B 级 能力提升11.幂函数y =x α,当α取不同的正数时,在区间[0,1]上它们的图象是一组美丽的曲线(如图),设点A (1,0),B (0,1),连接AB ,线段AB 恰好被其中的两个幂函数y =x a,y =x b的图象三等分,即有BM =MN =NA ,那么a-1b=( )A.0B.1C.12D.2解析 BM =MN =NA ,点A (1,0),B (0,1),所以M ⎝ ⎛⎭⎪⎫13,23,N ⎝ ⎛⎭⎪⎫23,13, 将两点坐标分别代入y =x a ,y =x b,得a =log 1323,b =log 2313,∴a -1b =log 1323-1log 2313=0.答案 A12.已知在(-∞,1]上递减的函数f (x )=x 2-2tx +1,且对任意的x 1,x 2∈[0,t +1],总有|f (x 1)-f (x 2)|≤2,则实数t 的取值范围是( ) A.[-2,2] B.[1,2] C.[2,3]D.[1,2]解析 由于f (x )=x 2-2tx +1的图象的对称轴为x =t , 又y =f (x )在(-∞,1]上是减函数,所以t ≥1. 则在区间[0,t +1]上,f (x )max =f (0)=1,f (x )min =f (t )=t 2-2t 2+1=-t 2+1,要使对任意的x 1,x 2∈[0,t +1],都有|f (x 1)-f (x 2)|≤2, 只需1-(-t 2+1)≤2,解得-2≤t ≤ 2.又t ≥1,∴1≤t ≤ 2. 答案 B13.已知函数f (x )=mx 2+(2-m )x +n (m >0),当-1≤x ≤1时,|f (x )|≤1恒成立,则f ⎝ ⎛⎭⎪⎫23=________.解析 当x ∈[-1,1]时,|f (x )|≤1恒成立.∴⎩⎪⎨⎪⎧|f (0)|≤1⇒|n |≤1⇒-1≤n ≤1;|f (1)|≤1⇒|2+n |≤1⇒-3≤n ≤-1, 因此n =-1,∴f (0)=-1,f (1)=1.由f (x )的图象可知:要满足题意,则图象的对称轴为直线x =0,∴2-m =0,m =2, ∴f (x )=2x 2-1,∴f ⎝ ⎛⎭⎪⎫23=-19.答案 -1914.已知二次函数f (x )满足f (x +1)-f (x )=2x ,且f (0)=1. (1)求f (x )的解析式;(2)当x ∈[-1,1]时,函数y =f (x )的图象恒在函数y =2x +m 的图象的上方,求实数m 的取值范围.解 (1)设f (x )=ax 2+bx +c (a ≠0), 由f (x +1)-f (x )=2x ,得2ax +a +b =2x . 所以,2a =2且a +b =0,解得a =1,b =-1, 又f (0)=1,所以c =1.因此f (x )的解析式为f (x )=x 2-x +1.(2)因为当x ∈[-1,1]时,y =f (x )的图象恒在y =2x +m 的图象上方, 所以在[-1,1]上,x 2-x +1>2x +m 恒成立; 即x 2-3x +1>m 在区间[-1,1]上恒成立.所以令g (x )=x 2-3x +1=⎝ ⎛⎭⎪⎫x -322-54,因为g (x )在[-1,1]上的最小值为g (1)=-1, 所以m <-1.故实数m 的取值范围为(-∞,-1).C 级 创新猜想15.(组合选择题)如图是二次函数y =ax 2+bx +c (a ≠0)图象的一部分,图象过点A (-3,0),对称轴为x=-1.给出下面四个结论:①b2>4ac;②2a-b=1;③a-b+c=0;④5a<b.其中正确的是( )A.②④B.①④C.②③D.①③解析因为图象与x轴交于两点,所以b2-4ac>0,即b2>4ac,①正确.对称轴为x=-1,即-b2a=-1,2a-b=0,②错误. 结合图象,当x=-1时,y>0,即a-b+c>0,③错误. 由对称轴为x=-1知,b=2a.根据抛物线开口向下,知a<0,所以5a<2a,即5a<b,④正确.答案 B。
