基于幅值恢复算法的谐波分析实验
基于FFT的高精度谐波检测算法_薛蕙

基于FFT的高精度谐波检测算法_薛蕙谐波检测是一种在电力系统中广泛应用的技术,用于检测电力系统中的谐波成分。
目前,基于快速傅里叶变换(FFT)的谐波检测算法已经成为主流。
本文将介绍一种基于FFT的高精度谐波检测算法。
首先,我们需要对信号进行采样。
在电力系统中,交流电信号通常以周期函数的形式存在,所以我们可以通过对信号进行周期采样来获得原始数据。
然后,我们可以将采样得到的数据通过FFT变换到频域,通过FFT变换将信号从时域转换到频域后,我们可以使用谱分析的方法来检测谐波成分。
在进行FFT变换之前,我们需要对采样数据进行预处理。
通常情况下,我们需要对信号进行加窗处理,以减小泄漏误差。
加窗处理可以通过乘以一个窗函数来实现,常用的窗函数有矩形窗、汉明窗、哈宁窗等。
加窗处理后,我们可以使用FFT算法将信号从时域转换到频域。
在频域中,我们可以通过计算每个频率分量的幅值和相位来确定谐波的存在。
根据电力系统的特点,我们通常只关心低次谐波(如2次和3次谐波)。
对于每个频率分量,我们可以根据其幅值和相位来判断是否存在谐波成分。
如果幅值超过一个预先定义的阈值,并且相位满足一定的条件,那么我们可以认为存在谐波成分。
为了提高谐波检测的精确性,我们可以对检测到的谐波成分进行进一步的处理。
一种常用的方法是通过对谐波成分进行插值来获得更精细的频率分辨率。
插值可以通过对频谱曲线进行多项式拟合实现。
通过插值可以进一步提高谐波检测的精度和稳定性。
此外,为了避免对非谐波成分的误判,我们还可以对检测到的谐波成分进行验算。
通过检测谐波成分的幅值和相位的稳定性,我们可以判断是否存在谐波成分。
如果幅值和相位均稳定,则可以判断为谐波成分;否则,则可能是噪声或其他非谐波成分。
综上所述,基于FFT的高精度谐波检测算法是一种在电力系统中广泛应用的谐波检测方法。
通过对信号进行采样和预处理,然后使用FFT变换将信号从时域转换到频域,我们可以通过分析频谱曲线来检测谐波成分。
基于FFT算法的电力谐波检测技术研究

基于FFT算法的电力谐波检测技术研究随着电力负荷的增加和各种新能源设备的接入,电力系统中出现的谐波问题越来越严重。
谐波是一种频率与基波频率成整数倍关系的电信号,它们在电力系统中会引起各种问题,例如使电力设备产生热损失、影响电力设备的寿命、降低电力质量、损坏电力设备、以及干扰其他电子设备等。
因此,电力谐波检测技术的研究变得越来越重要。
电力谐波检测技术的目的是检测电力系统中的谐波,并对其进行分析和处理,以避免对电力系统以及其他电子设备造成损坏。
其中,谐波分析是电力谐波检测技术中的一个重要环节。
传统的谐波分析方法主要依赖于滤波技术,这种方法无法满足大数据量、高速实时性、转速变化、载重变化等作业要求。
因此,基于FFT(快速傅里叶变换)算法的电力谐波检测技术应运而生。
FFT算法是现代信号处理中最基本、最常用的算法,它可以将信号从时域变换到频域,使得信号的谱密度直观地呈现在频谱中。
在电力谐波分析中,FFT算法可以将复杂单相或三相的谐波信号进行频域分解,使得谐波频率成分和各种畸变因素在频域上清晰明了地表现出来。
此外,FFT算法在处理谐波时具有处理速度快、精度高、适应性强等优点。
电力谐波检测技术中,FFT算法的关键在于选取合适的采样频率。
采样频率是指采样时间内所进行的采样次数,采样频率越高,则谐波检测的精度越高。
然而,采样频率太高会导致计算复杂度增加,从而降低谐波分析的速度。
因此,如何选取合适的采样频率就变得至关重要。
此外,在电力谐波检测技术中,还需要考虑到其他因素。
例如,应选择合适的DSP芯片进行信号处理,以保证计算速度和准确度;在设计硬件电路时,还需要考虑到电磁噪声、接口兼容等问题。
总之,基于FFT算法的电力谐波检测技术在电力质量监控、电流振动分析、噪声分析等方面具有广泛的应用前景。
随着大数据、云计算等技术的应用,电力谐波检测技术将会得到越来越广泛的应用。
因此,未来的电力谐波检测技术需要不断创新,才能更好地适应市场需求。
电路分析基础谐波分析法五篇范文

电路分析基础谐波分析法五篇范文第一篇:电路分析基础谐波分析法电路分析基础谐波分析法本章实训谐波分析法的验证实训任务引入和介绍在电路分析的应用过程中~遇到非正弦周期电流电路的情况并不少见。
有时候~电流波形非常简单,如矩形波、三角波等,~可以通过简单的计算得出其有效值、平均值及平均功率,但有时候非正弦周期电流的波形非常复杂~那么通过谐波分析法来进行电路分析就显得尤为重要。
本次实训我们就以一个简单的电路为基础~通过简单的理论计算和实际测量的结合来验证谐波分析法。
实训目的1.掌握非正弦周期电流电路的测量方法,2.理解谐波分析法的基本原理,3.学会用谐波分析法进行简单的电路分析。
实训条件100V直流电源、150V/50Hz交流电源、100V/100Hz交流电源、功率计、R=10Ω、L=1H、3C=1.11*10uF、电压表、电流表。
操作步骤(1)连接电路。
如图5-12所示,将在直流、交流电源串联,根据叠加定理,可以知道电路中的电流为非正弦周期电流,且该信号可以分解为100V直流、150V/50Hz交流、100V/100Hz电源给出的信号。
图5-12 实训电路(2)理论计算。
已知: U,100,150sin,t,100sin(2,t,90:)V s R,10, 1X,90,,c,C X,L,10, L ? 直流分量作用于电路时,电感相当于短路,电容相当于开路。
故有: I,0,U,0,P,0000 ? 一次谐波作用于电路时,有: 150 U,,0:Vs12 150,0:U2s1 I,,1.32,82.9:A1R,j(X,X)10,j(10,90)L1C1 U,1.31,82.9:(10,j10),18.5,127.9:V1 ? 二次谐波作用于电路时,有: 100,,90:U2s2 I,,2.63,,21.8:A2R,j(X,X)10,j(20,45)L2C2 U,2.63,,21.8:(10,j20),58.8,41.6:V2 综合以上,根据谐波分析公式(5-11)、(5-12)及功率的计算公式,可计算得出电流、电压的有效值及有功功率: 222I,0,1.32,2.63,2.94A 222 U,0,18.5,58.8,61.7V 22P,1.32,10,2.63,10,86.6W(3)测量比较。
谐波分析实验报告
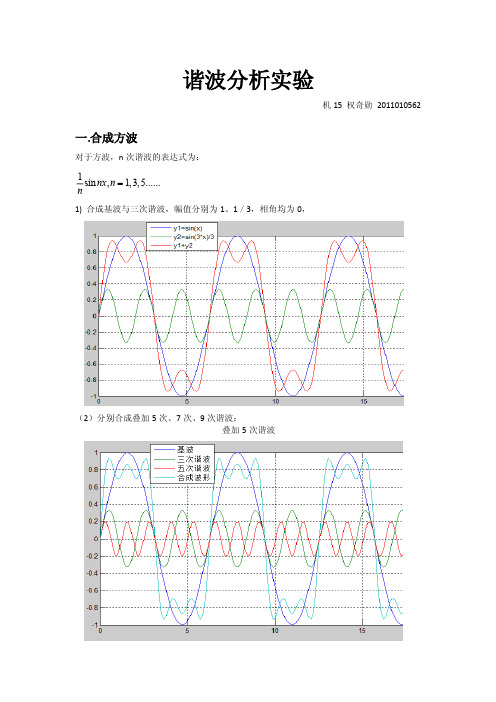
谐波分析实验机15 权奇勋2011010562一.合成方波对于方波,n次谐波的表达式为:1sin nx,n=1,3,5......n1) 合成基波与三次谐波,幅值分别为1、1/3,相角均为0,(2)分别合成叠加5次、7次、9次谐波:叠加5次谐波叠加7次谐波叠加9次谐波通过观察波形,发现:叠加谐波次数越高,合成波形越趋近于方波。
(3)分别改变3、5次谐波与基波间的相角,研究谐波间相角改变对合成波形的影响将3次谐波的初相角改为-π/2将5次谐波的初相角改为-π/2分析结论:改变谐波与基波间的相角,会使合成波形与方波相比有较大的失真。
且改变相角的谐波次数越低,失真越大。
(4)分别改变3、5次谐波与基波间的幅值比例关系,研究谐波间幅值比例改变对合成波形的影响3次谐波幅值改为(1/3)×2=2/35次谐波幅值改为(1/5)×2=2/5分析结论:改变谐波的幅值,会使合成波形与方波相比产生失真;且幅值改变的倍率相同的情况下,改变谐波的次数越低,失真越大。
二.合成锯齿波(最高谐波次数选为9)对于锯齿波,n次谐波的表达式为:π1nx+p),n=1,2,3......1)合成波的形状与谐波次数的关系叠加2次谐波叠加4次谐波叠加9次谐波通过观察波形,发现:叠加谐波次数越高,合成波形越趋近于锯齿波。
(2)分别改变2、4次谐波与基波间的幅值比例关系2次谐波的幅值改为(1/2)×2=14次谐波的幅值改为(1/4×2)=1/2分析结论:改变谐波的幅值,会使合成波形与锯齿波相比产生失真;且幅值改变的倍率相同的情况下,改变谐波的次数越低,失真越大。
(3)分别改变2、4次谐波与基波间的相角2次谐波的初相角改为pi+pi/2=3pi/24次谐波的初相角改为pi+pi/2=3pi/2分析结论:改变谐波与基波间的相角,会使合成波形与锯齿波相比有较大的失真。
且改变相角的谐波次数越低,失真越大。
三.合成三角波(最高谐波次数选为9)对于三角波,n次谐波的表达式为:π×π1nx,n=1,3,5......1)合成波的形状与谐波次数的关系叠加3次谐波叠加5次谐波叠加9次谐波通过观察波形,发现:叠加谐波次数越高,合成波形越趋近于三角波。
基于Morlet复小波变换幅值和相位信息的间谐波检测方法

I e har o c de e to l or t s d on a plt nt r m ni t c i n a g ihm ba e m iude a nd pha e s i o m a i n o o ltc m pl xw a e e r ns o m nf r to fM r e o e v l tt a f r
a l i.Buto y a l ng a pl ud fw a l tta f m e c e t a otr a ie a c r t r oni e e ton be a eof nayss nl pp yi m i e o ve e r nsor co f i n s c n n e lz c u ae ha m t i c d t c i c us s c r m la i pe t u a i sng phe m e no non e e i he M ore om plx w a lt m plt de pha e i or a i oretco pl x w a l t v n n t ltc e vee .A iu — s nf m ton ofM l m e ve e ta s o m sp o r n f r i r pos d t tc r on c a n e ha m on c i hi pe .S al a e o dee tha m i nd i t r r i n t spa r c e r nge i l di g t t td sgn li or a i nc u n he deece i a nf m ton
i h s c l , n t e e d h r c e it c l n mp i d a e g t n Co a i g wi F n c l — mp i d l o i m, n t e e s a e i h n c a a t rsi s a e a d a l u e c n b o t . mp rn t F T a d s a e a l u e a g r h c t e h t t t e meh d c n a o d t e s e t m e k g n it g ih sg a fc o ey fe u n y mp o i g t ep e iin o a o i n h t o a v i h p c r u la a e a d d si u s in lo l s l r q e c ,i r v n h r c so fh r n c a d n m
基于FFT的电力系统谐波检测方法综述

早在19世纪末期的时候人们就发现了电压、电流的畸变问题,但电力系统的谐波问题真正引起人们的广泛关注是在20世纪初。
20世纪70年代以来谐波污染日益严重,国际社会和学术组织开始商讨制定有关限制谐波的标准和规定。
我国的谐波研究起步较晚,但是我国近些年的电网发展速度很快,各种大功率电力电子设备的大量应用、高压直流输电的发展、风电并网以及电气化铁路的快速建设等都引起电网谐波含量的增加,使得电网波形的畸变更严重,给电网的安全稳定运行带了极大影响。
如何能够把谐波污染最大限度地减少,是电力行业和电力电子领域关心的问题,而这一问题的解决首先在于精确地分析谐波的频率、幅值和相位。
可见谐波检测和分析的重要性。
1 电力系统谐波分析的常用方法1.1 采用模拟滤波器硬件电路检测谐波的方法这是最早的谐波测量手段,其装置构成如图1所示,输入信号放大之后送入并行连接的若干组带通滤波器,每个滤波器的中心频率都是固定的以通过特定频率的谐波,再经过检波器送到多路显示器[1]。
这样就得到了输入信号中的谐波成分及其幅值。
这种用模拟滤波器硬件电路检测谐波的方法,原理直观明了,成本也很低,但是其测量精度依赖于滤波器的元件参数,受外界环境影响①基金项目:国家自然科学基金资助项目(51477147)。
作者简介:高云辉(1971,11—),男,汉,河北秦皇岛人,本科,高级工程师,主要研究方向为电能质量在线监测与分析。
牛益国(1975,2—),男,汉,河北秦皇岛人,本科,高级工程师,主要研究方向为电能质量在线监测与分析。
谢小英(1967,7—),女,汉,北京人,硕士,高级工程师,主要研究方向为电能质量在线监测与分析。
肖鑫(1984,11—),男,汉,河北张家口人,硕士研究生,讲师,主要研究方向为电能质量在线监测与分析。
珺王(1979,12—),男,汉,河北秦皇岛人,硕士,讲师,主要研究方向为新能源并网电能质量分析。
DOI:10.16661/ki.1672-3791.2017.05.049基于FFT 的电力系统谐波检测方法综述①高云辉1 谢小英1 牛益国1 肖鑫2 王珺2(1.国网冀北电力有限公司秦皇岛供电公司 河北秦皇岛 066000;2.燕山大学电气工程学院 河北秦皇岛 066004)摘 要:随着我国电网规模的日益扩大,各种非线性用电设备的迅速增加,电网的谐波污染也逐渐严重,如何快速有效地检测和分析网络中的谐波成分是一个大家非常关心的问题。
基于FFT的电力谐波分析方法研究

基于FFT的电力谐波分析方法研究电力谐波是指在电力系统中,频率为整数倍于基频的电压或电流分量。
谐波的存在对电力系统的稳定性和正常运行产生不良影响,如高谐波电流会导致电力设备过热、变压器铁芯饱和等问题。
因此,电力谐波分析方法的研究具有重要的理论和实际意义。
目前,基于FFT(快速傅里叶变换)的电力谐波分析方法是应用最广泛、效果较好的方法之一、FFT将时域信号转换为频域信号,通过对频谱的分析,可以准确地检测和分析电力谐波。
下面将对基于FFT的电力谐波分析方法进行详细探讨。
首先,基于FFT的电力谐波分析方法的核心是信号的频谱分析。
该方法可以将采集到的电压或电流信号转换为其频谱特性,进而对谐波进行检测和分析。
通过FFT算法,可以将任意时域信号分解为各个频率分量的振幅和相位。
其次,基于FFT的电力谐波分析方法需要经过一系列数据预处理步骤。
首先,对采集到的电压或电流信号进行采样,并对采样值进行量化,得到离散时域信号。
然后,对时域信号进行窗函数处理,以减少频谱泄漏。
接着,对处理后的时域信号进行FFT变换,得到频域的振幅谱和相位谱。
在进行FFT变换之后,可以得到频域信号的频谱特性。
基于FFT的电力谐波分析方法常用的分析指标包括谐波幅值、谐波含量、谐波相位等。
谐波幅值表示谐波分量的振幅大小,谐波含量表示谐波分量在总电压或电流中所占的比例,谐波相位表示谐波分量的相位差异。
最后,基于FFT的电力谐波分析方法可以应用于电力系统中的谐波问题诊断和谐波源定位。
通过对电力系统中不同节点的电压或电流信号进行谐波分析,并计算谐波幅值和谐波含量等指标,可以判断系统中是否存在谐波问题及其严重程度。
同时,通过比较不同节点中谐波分量的相位差异,还可以准确定位引起谐波问题的具体设备或线路。
综上所述,基于FFT的电力谐波分析方法是一种有效的谐波分析方法,具有可靠的谐波检测和分析能力。
该方法在电力系统的运行维护和故障诊断中,具有重要的应用价值,可以帮助实现对电力谐波问题的快速定位和解决。
基于FFT算法的电力谐波检测技术研究

基于FFT算法的电力谐波检测技术研究电力系统中的谐波是指频率为电源基波频率的整数倍的信号成分,其存在会对电网和电力设备造成不良影响。
因此,谐波检测和分析技术对于保证电力系统的稳定和安全运行至关重要。
其中,基于快速傅里叶变换(FFT)算法的谐波检测技术被广泛应用,具有高效、准确和实时的特点。
本文将对基于FFT算法的电力谐波检测技术进行研究,从算法的原理、实现方法和应用案例等方面进行探讨。
首先,介绍FFT算法的原理。
FFT算法是一种快速计算离散傅里叶变换的方法,通过将N点的离散信号转换为N/2点的两个离散信号,并重复迭代,最终实现对离散信号的频域表示。
利用FFT算法可以将时域信号转换为频域信号,并计算出各个频率成分的振幅和相位信息。
基于FFT算法的电力谐波检测技术主要分为两个步骤:数据采集和信号分析。
数据采集可以通过电力监测仪或传感器获取电流、电压等信号,并进行模拟到数字的转换。
信号分析则是基于FFT算法对采集到的数据进行处理,得到频率和振幅信息,并判断是否存在谐波。
在信号分析方面,首先需要对采集到的数据进行预处理,包括去直流分量、滤波等操作。
然后,利用FFT算法对预处理后的数据进行频域转换和谱分析,得到各个频率成分的振幅。
通过设置阈值和判据,可以判定是否存在谐波,并对谐波进行定位和分析。
基于FFT算法的电力谐波检测技术已经在电力系统中得到广泛应用。
例如,在电力质量监测中,可以利用FFT算法实时检测电网中的谐波情况,并对谐波进行分类和分析,有助于及时发现和解决电力系统中的谐波问题。
在电力设备的故障诊断中,也可以利用FFT算法检测设备运行时产生的谐波信号,分析其对设备性能的影响,并判断设备是否工作正常。
综上所述,基于FFT算法的电力谐波检测技术是一种高效、准确和实时的检测方法,在电力系统中具有重要的应用价值。
未来的研究可以进一步探索基于FFT算法的谐波检测技术在电力系统的应用,提高其检测和分析的准确性和可靠性。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
0, 当m n, cos mx cos nxdx , 当m n 0, 2 , 当m n 0.
(2.20)
的情况下, 至少可以分析到电流的 25 次谐波。 将三相电流先进行 A.R.M.滤除基波,再对谐波电流做频谱分析,所得结果如图 3-2 所示。
性质。 则在 , 区间内, (2.5.6.1)式即可以写成如下形式:
A As Av
v
(2.21)
其中, As 为 ia 基波的幅值, Av 为 ia 中第 v 次谐波的幅值。 从而就可以用各次谐波来表示 A 的值。通过推导,基波 As 和谐波 Av 分别为:
As 3 Is 2 Nhomakorabea1 2A [ia
ib
其中, ia 、 ib 、 ic 为三相异步电机定子电流的瞬时值, a 为 ia 的转角。A 为谐波的幅值, 由三相电流与其转角的正弦值求得。 通过该算法,可以明显的突出电机谐波分量,方便对电机异 常状态的检测和进一步的分析。 定义在 R2 ([ , ]) 区间的正交向量 {1, cos nx, sin nx, n N } ,有 如下 0 当m n, (2.18) sin mx sin nxdx 当m n;
图 3-3 谐波频谱图(III) Fig.3-3 Spectrum image of Harmonica(III) 由于采样幅值恢复算法对基波进行处理, 使得整个谐波频谱图 的谐波成分十分清晰,尤其是 2 次谐波的频率成分,另外因为总的 采样点数的增加,可以看到 4、6、8、10 次谐波也被凸显出来。 四、结论 本文采用幅值恢复算法对实验中两种型号的电机进行频谱分 析,根据实验结果可以得出在采样频率足够大的情况下,使用该 算法过滤基波后,对微弱的谐波成分有着较好的分析效果。 参考文献: [1]侯新国.基于定子电流信号分析与融合技术的电机故障诊 断方法研究[D].武汉:海军工程大学,2005 [2]牛发亮.感应电机转子断条故障诊断方法研究[D].杭州:浙 江大学,2006 [3]王益全,张炳义.电机测试技术[M].北京:科学出版社,2004 [4]何秀伟.电机测试技术[M].北京:机械工业出版社,1985 [5]黄湘宁.三相异步电机自动测试与控制系统的研究[D].长沙: 湖南大学,2003 [6]Yukun Liu,Yinghui Li,Liwei Guo and Xiaoyun Sun.“An Electrical Machine Testing System on Embedded System”Proceedings of the Eighth International Conference on Electrical Machines and Systems,Nanjing,China,September,2005:57-59 [7]Liu Yukun,Guo Liwei,Wang Qixiang and Fu Dong. “A System of Detection,Analysis and Diagnosis on Electromechanic Systems” Proceedings of the Eighth International Conference on Electronic Measurement and Instruments,Xi’an,China,August,2007,1:772-775
sin a ic ]sin( a 2 / 3) sin( a 2 / 3)
式(2.17)
cos mx sin nxdx 0;
(2.19)
— 61 —
计算机光盘软件与应用
工程技术 Computer CD Software and Applications 2012 年第 2 期
(2.22)
1 1 f v 2 3 f v 2 Av I v cos f 3 2 sin f 3 2 2 s s 1 1 f v f v 2 3 f v 2 I v cos f 3 2 sin f 3 cos f 1 a 2 2 s s s
fv 1) f s 和 fs
s
图 3-1 谐波频谱图(I) Fig.3-1 Spectrum image of Harmonica (I) 对型号为 YS100L-4 电机采集其 3 路三相电流和 A 相电压, 每 路电流一组一次采集 3000 点,每个周期采集 51 个点,采样频谱 为 2550Hz, 共 58 个完整周期。 由香农定理, 在采样频率为 2550Hz
Harmonic Analysis Experiment Based on Amplitude Recovery Methods
Guo Ming ,Liu Xiaoyi (1.Hebei Electric Power Corporation,Information Center,Shijiazhuang 050021,China; 2.TCM Hospital of Shijiazhuang City,Shijiazhuang 050000,China) Abstract:The purpose of this research is aimed induction motor running state monitoring of motor incipient faults can be found in time,reduce the fault severity after the huge loss caused by.This system adopts the analysis of stator current of the motor in running on-site monitoring,in order to solve the fault frequency and power grid frequency is close to the motor,and minor faults in stator current,fault feature component is too small issue,using a new method of harmonic analysis-amplitude recovery methods,the methods combined with Fourier spectrum analysis of motor fault,mild and weak harmonic components make effective analysis. Keywords:Characteristic analysis;Three-phase induction motor;Stator current;Harmonic analysis 本文的研究目的就是针对大型贵重电机的运行状态的监测以 期对电机早期故障能够及时发现,减小故障严重后造成的巨大损 失。由于定子电流信号易于采集,分析电机故障之前只需做降噪 处理,因此简单实用,且基于定子电流的信号分析特别适合与监 测电机运行和对早期异常状态的诊断。因此本文即是采用分析定 子电流的方式对运行中的电机进行现场监测,为解决故障频率与 电网频率接近,且电机轻微故障时,定子电流中故障特征分量幅 值过小的问题,课题组刘玉坤老师提出了一种新的谐波分析方法 [7] ——幅值恢复算法 ,将该算法结合 Fourier 频谱分析,可对电 机轻微故障和微弱的谐波成分做出有效的分析。 一、电机信号分析技术的研究 由电机工作原理可知,其内部存在着几个互相关联的系统: 电路系统、磁路系统、绝缘系统、机械系统和通风散热系统等。 所以,电机故障的起因和故障征兆往往表现出多元性。有时一个 故障,常常表现出多种征兆,比如,电机振动增加,除了可能是 转子断条故障之外,还有可能是由定子绕组匝间短路、定子端部 绕组松动、机座安装不当、铁心松动、转子偏心、定转子相擦、 轴承损坏等故障引起。因此,对这种运行状态复杂、影响因素众 多的电气设备,必须对其结构、原理、运行特征、工作方式、负 载特征进行深入研究。由故障机理分析可知,电机处于异常运行 或故障状态时,必然会引起一些电气量(电压、电流、转矩、功 率等)或非电气量(声、光、热、气、振动、辐射等)的变化, 这些物理量的变化是检测和判断故障类型、程度和原因的重要信 息。现有的电机故障诊断方法,正是基于对这些反映电机运行状 态的物理量故障前后变换规律的认识和总计上逐步发展起来的。 大型电机在工业系统中的重要地位及其昂贵的造价,要求在对其 进行诊断时不能频繁拆卸安装, 而只能通过对其终端参数的测试, 再结合信号处理技术来提取故障特性,这样既避免频繁拆卸造成 [1] 很多人为故障,又可以节约维修费用 。 目前普遍采用的电机运行参数大致可以分为:电压、电流、 功率、磁通、转矩、转速、温度、振动、噪声以及局部放电等。 本文仅以电机的定子电流、 电压参数和转速作为研究的内容。 由于定子电流信号相对于其它参数受环境等外界影响最小, 也因为电流传感器安装方便且最容易获取,因此,长期以来是电 机各类故障诊断的主要参数。当感应电机转子发生断条故障时, 定子电流中将引入频率大小为 f br (1 2 s) f s( s 为转差率, f s 为 电网频率)故障特性分量。对电机定子电流进行 Fourier 变换, 分析定子电流频谱中有无该特征分量及故障严重及其幅值大小来 判断电机是否存在转子故障程度,就是传统定子电流频谱分析的 转子断条故障诊断思想。但是,转子故障特征量在故障初期相对 于基频分量的幅值很小,且电机稳态运行时转差率 s 一般很小, 导致故障特征分量和基频的频率十分接近,由于 Fourier 分析时 的频谱泄漏问题的影响,故障特征往往被基频和环境噪声淹没而 [2] 难以识别,这也成为电机转子故障诊断长期以来的一大瓶颈 。 二、幅值恢复算法 [7] 本文采用幅值恢复算法 对信号进行处理,将基波滤除,突 出谐波成分,以方便对谐波的独立分析。 该方法可以解决局限软硬件发展的两个关键条件:一是有限 的数据存储空间,二是有限的数据处理时间。 基本原理公式如下:
