高三总复习同步练习(三角函数二)

合集下载

三角函数专题复习-三角恒等变换导学案-2023届高三数学二轮专题复习

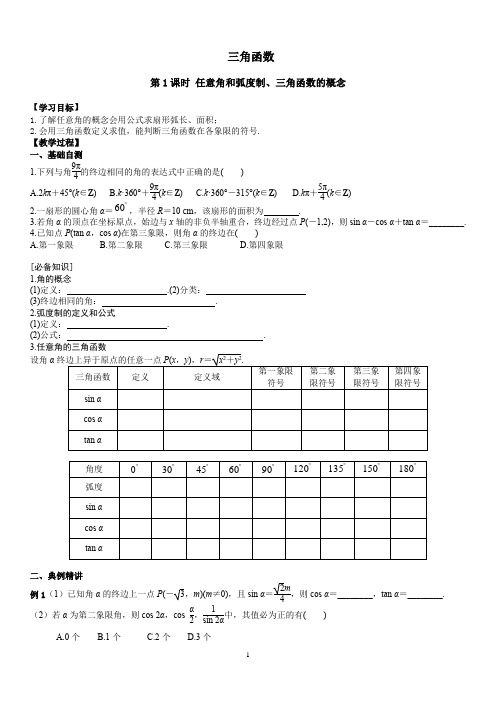
三角函数第1课时任意角和弧度制、三角函数的概念【学习目标】1.了解任意角的概念会用公式求扇形弧长、面积；2.会用三角函数定义求值，能判断三角函数在各象限的符号. 【教学过程】一、基础自测1.下列与角9π4的终边相同的角的表达式中正确的是( )A.2k π＋45°(k ∈Z )B.k ·360°＋9π4(k ∈Z )C.k ·360°－315°(k ∈Z )D.k π＋5π4(k ∈Z )2.一扇形的圆心角α＝︒60，半径R ＝10 cm ，该扇形的面积为 .3.若角α的顶点在坐标原点，始边与x 轴的非负半轴重合，终边经过点P (－1,2)，则sin α－cos α＋tan α＝________.4.已知点P (tan α，cos α)在第三象限，则角α的终边在( )A.第一象限B.第二象限C.第三象限D.第四象限[必备知识] 1.角的概念(1)定义： .(2)分类： (3)终边相同的角： . 2.弧度制的定义和公式(1)定义： .(2)公式： . 3.设角α终边上异于原点的任意一点P (x ，y )，r ＝x 2＋y 2.三角函数定义定义域第一象限符号第二象限符号第三象限符号第四象限符号sin αcos αtan α角度 ︒0 ︒30 ︒45 ︒60 ︒90 ︒120 ︒135 ︒150 ︒180弧度 sin αcos α tan α二、典例精讲例1（1）已知角α的终边上一点P (－3，m )(m ≠0)，且sin α＝2m4，则cos α＝________，tan α＝________. （2）若α为第二象限角，则cos 2α，cos α2，1sin 2α中，其值必为正的有( )A.0个B.1个C.2个D.3个归纳：巩固练习1:（1）已知角α的终边过点P (－8m ，－6sin 30°)，且cos α＝－45，则m 的值为( )A.－12B.－32C.12D.32（2）设θ是第三象限角，且⎪⎪⎪⎪cos θ2＝－cos θ2，则θ2是( ) A.第一象限角 B.第二象限角 C.第三象限角 D.第四象限角例2.扇形周长为20 cm ，这个扇形的面积最大时，扇形的圆心角α为弧度归纳：巩固练习2（多选）已知扇形的周长是6 cm ，面积是2 cm 2，下列选项可能正确的有( ) A.圆的半径为2 B.圆的半径为1 C.圆心角的弧度数是1 D.圆心角的弧度数是2三、达标检测1.若扇形的面积为3π8、半径为1，则扇形的圆心角为( )A.3π2B.3π4C.3π8D.3π162.已知角α的终边经过点(3，－4)，则sin α＋1cos α等于( )A.－15B.3715C.3720D.13153.(多选)角α的终边在第一象限，则sinα2⎪⎪⎪⎪sin α2＋cos α2⎪⎪⎪⎪cos α2＋tan α2⎪⎪⎪⎪tan α2的值为( )A.－1B.1C.－3D.34.若圆弧长度等于该圆内接正方形的边长，则其圆心角的弧度数是________.5.已知1|sin α|＝－1sin α，且lg(cos α)有意义. (1)试判断角α所在的象限； (2)若角α的终边上一点M ),53(m ，且|OM |＝1(O 为坐标原点)，求m 的值及sin α的值.思维导图三角函数任意角与弧度制任意角的三角函数角定义弧度制符号角度与弧度互化特殊角弧度数扇形弧长、面积三角函数第2课时同角三角函数基本关系与诱导公式【学习目标】1.会用同角基本关系式解决给值求值问题；2.熟记诱导公式并会用诱导公式化简求值. 【教学过程】二、基础自测1.若sin α＝55，π2<α<π，则αcos = tan α=2.若sin(π＋α)＝12，α∈02π⎛⎫- ⎪⎝⎭，，则tan(π－α)等于( ) A ．－12B 3C 3D 33．已知()cos 2cos 2παπα⎛⎫+=- ⎪⎝⎭，则()tan α-=（）A ．–2B ．2C ．13- D ．134．sin 1 050°等于( ) A.12 B ．－12 C.32 D ．－32 [必备知识]1.同角三角函数的基本关系平方关系：商数关系： 2.公式角正弦余弦正切口诀① 2k π＋α(k ∈Z )奇变偶不变，符号看象限② －α ③ π－α ④ π＋α⑤ π2－α⑥ π2＋α⑦ 32π＋α⑧ 32π－α三、典例精讲例1（1）已知tan α＝2，则3sin α－cos αsin α＋2cos α等于( )A.54 B ．－54 C.53 D ．－53（2）已知sin θ＋cos θ＝43，θ∈)4,0(π，则sin θ－cos θ的值为．归纳：巩固练习1:（1）已知α是三角形的内角，且tan α＝－13，则sin α＋cos α的值为．（2）已知sin θ＋cos θ＝713，θ∈(0，π)，则sin θ－cos θ= ，tan θ＝ . 例2.（1）在平面直角坐标系xOy 中，角α的终边经过点P (3,4)，则sin )22021(πα-等于( ) A ．－45 B ．－35 C.35 D.45（2）已知sin )3(απ+＝1213，则cos )6(απ-等于( )A.513B.1213 C ．－513 D ．－1213 归纳：巩固练习2：（1）已知α∈(0，π)，且cos α＝－1517，则sin )2(απ+·tan(π＋α)等于( )A ．－1517 B.1517 C ．－817 D.817（2）sin )12(πα-＝13，则cos )1271(πα+＝ .四、达标检测1.已知α是第四象限角，tan α＝－815，则sin α等于( )A.1517 B ．－1517 C.817 D ．－8172.已知(0,)απ∈，若2cos 6πα⎛⎫-= ⎪⎝⎭5sin 6πα⎛⎫+ ⎪⎝⎭的值为（）A ．14B 2C ．2D 143.(多选)在△ABC 中，下列结论正确的是( )A ．sin(A ＋B )＝sinC B ．sin B ＋C 2＝cos A2 C ．tan(A ＋B )＝－tan C )2(π≠C D ．cos(A ＋B )＝cos C4.sin 4π3·cos 5π6·tan )34(π-的值是．5.已知－π2<α<0，且函数f (α)＝cos )23(απ+－sin α·1＋cos α1－cos α－1.(1)化简f (α)； (2)若f (α)＝15，求sin αcos α和sin α－cos α的值．思维导图三角函数第3课时两角和与差的正弦、余弦、正切公式【学习目标】1.会用两角和与差的正弦、余弦、正切公式化简求值；2.会用辅助角公式化简求值. 【教学过程】三、基础自测1.(多选)下面各式中，正确的是( )A.cos π12＝cos π3－cos π4B.cos 5π12＝22sin π3－cos π4cos π3C.cos )12(π-＝cos π4cos π3＋64 D.3sin α＋cos α＝2sin )3(πα+2.已知tan θ＝2，则tan )4(πθ-＝ .3.cos 17°cos 77°＋cos 73°cos 13°＝4.tan 10°＋tan 50°＋3tan 10°tan 50°＝ . [必备知识]两角和与差的余弦、正弦、正切公式(1)公式C α－β：cos(α－β)＝；(2)公式C α＋β：cos(α＋β)＝； (3)公式S α＋β：sin(α＋β)＝；(4)公式S α－β：sin(α－β)＝； (5)公式T α＋β：tan(α＋β)＝；(6)公式T α－β：tan(α－β)＝ . (7)(辅助角公式)a sin α＋b cos α＝ .五、典例精讲例1（1）若cos α＝－45，α是第三象限角，则sin )4(πα+等于( )A.－210B.210C.－7210D.7210（2）已知534cos 23sin 23=+αα，则4sin 3απ⎛⎫+ ⎪⎝⎭的值为（） A ．23B 23C ．45-D ．45归纳：巩固练习1:（1）已知sin α＝35，α∈),2(ππ，tan(π－β)＝12，则tan(α－β)的值为( )A.－211B.211C.112D.－112（2）若3sin s 2a a +=，则tan()πα+=（）A 3B 2C 2D 3例2.已知sin α＝255，sin(β－α)＝－1010，α，β均为锐角，则β等于( )A.5π12B.π3C.π4D.π6归纳：巩固练习2：已知sin α＝55，sin(α－β)＝－1010，α，β均为锐角，则β＝ ..六、达标检测1.－sin 133°cos 197°－cos 47°cos 73°等于( ) A.12 B.33 C.22 D.322.已知α，β∈⎝⎛⎭⎫－π2，π2，tan α，tan β是方程x 2＋12x ＋10＝0的两根，则tan(α＋β)等于( ) A.43 B.－2或12 C.12D.－2 3.（多选）已知3cos α－3sin α＝23cos(α＋φ)，则φ的值可能为（）A.π6 B.613π C. 6π- D.611π 4.已知cos ⎝⎛⎭⎫α＋π6＝3cos α，tan β＝33，则tan(α＋β)＝ . 5.已知α，β均为锐角，且sin α＝35，tan(α－β)＝－13.(1)求sin(α－β)的值； (2)求cos β的值.思维导图辅助角公式 a sin α＋b cos α＝a 2＋b 2sin(α＋φ)，其中sin φ＝b a 2＋b 2，cos φ＝aa 2＋b 2三角函数第4课时三角恒等变换【学习目标】1.熟记正弦、余弦、正切倍角公式；2.会用正弦、余弦、正切倍角公式、半角公式化简求值. 【教学过程】四、基础自测1.sin 15°cos 15°等于( )A.－14B.14C.－12D.122.已知α，β为锐角，tan α＝43，则cos 2α等于( )A.725B.－725C.2425D.－24253.计算：4tanπ123tan 2π12－3等于( )A.233B.－233C.239D.－239[必备知识]二倍角的正弦、余弦、正切公式(1)公式S 2α：sin 2α＝ .(2)公式C 2α：cos 2α＝＝＝ . (3)公式T 2α：tan 2α＝ .(4)(降幂公式)sin 2α＝，cos 2α＝ . (5)(半角公式)=2sinα，=2cosα.七、典例精讲例1（1）(2020·全国Ⅰ)已知α∈(0，π)，且3cos 2α－8cos α＝5，则sin α等于( )A.53B.23C.13D.59正用、逆用公式变形正弦：正余余正符号同余弦：余余正正符号异（2）已知sin 2α＝23，则cos 2⎝⎛⎭⎫α＋π4＝ .归纳：巩固练习1:（1）(2019·全国Ⅱ)已知α∈⎝⎛⎭⎫0，π2，2sin 2α＝cos 2α＋1，则sin α等于( ) A.15 B.55 C.33 D.255（2）已知()5sin 26cos 0απα+-=，0,2πα⎛⎫∈ ⎪⎝⎭，则2cos 24απ⎛⎫ +⎪⎝⎭=（）A ．15-B ．15C ．35D ．45例2.若sin ⎝⎛⎭⎫π3－α＝14，则cos ⎝⎛⎭⎫π3＋2α 等于 . 归纳：巩固练习2：若1010)6cos(=+πθ，则)322cos(πθ- 等于 . 八、达标检测1.已知sin α－cos α＝43，则sin 2α等于( )A.－79B.－29C.29D.792.计算：1－cos 210°cos 80°1－cos 20°等于( )A.22B.12C.32D.－223.(多选)已知函数f (x )＝sin x ·sin ⎝⎛⎭⎫x ＋π3－14，则f (x )的值不可能是( ) A.－12 B.12C.－2D.24.若α∈⎝⎛⎭⎫π2，π，sin α＝31010，则tan 2α＝ . 5.已知sin ⎝⎛⎭⎫α＋π4＝210，α∈⎝⎛⎭⎫π2，π.求： (1)cos α的值；(2)sin ⎝⎛⎭⎫2α－π4的值思维导图。

高三数学回归课本复习材料：三角函数基本概念(二)

三角函数基本概念回归课本复习材料21象限角的概念：已知α为第三象限角，则2α所在的象限是 D （A ）第一或第二象限（B ）第二或第三象限（C ）第一或第三象限（D ）第二或第四象限 2.弧长公式已知球O 的半径为1，A 、B 、C 三点都在球面上，且每两点间的球面距离均为2π，则球心O 到平面ABC 的距离为（B ） A31 B 33 C 32 D 36 4、任意角的三角函数的定义：已知角α的终边经过点P(5，－12)，则ααcos sin +的值为＿＿。

（答：713-）； 5.三角函数线（1）已知sin α＞sin β，那么下列命题成立的是（ D ） A.若α、β是第一象限角，则cos α＞cos β B.若α、β是第二象限角，则tan α＞tan β C.若α、β是第三象限角，则cos α＞cos β D.若α、β是第四象限角，则tan α＞tan β（2）若α为锐角，则,sin ,tan ααα的大小关系为_______ （答：sin tan ααα<<）； 6.特殊角的三角函数值：7. 同角三角函数的基本关系式：8.三角函数诱导公式97costan()sin 2146πππ+-+的值为（答：2323-）； 9、两角和与差的正弦、余弦、正切公式及倍角公式：(2) 函数4()cos f x x =2sin cos x x -4sin x -的最小正周期为____（答：π）；10. 三角函数的恒等变形（1）巧变角已知,αβ为锐角，sin ,cos x y αβ==，3cos()5αβ+=-，则y 与x 的函数关系为___（答：23431(1)555y x x x =--+<<） (2)三角函数名互化(切割化弦)，求值sin50(13tan10)+ （答：1）； (3)公式变形使用tan 20tan 403tan 20tan 40++⋅ 的值为3为sin cos y x x =-得到的图象，只要把函数sin cos y x x =+的图象按向量a 平移，则a等于A ．π(,0)2B ．π(-,0)2C ．4π(,0) D ．π(-,0)4(4)三角函数次数的降升，(5)式子结构的转化(对角、函数名、式子结构化同)。

专题2 三角函数压轴小题(原卷版)

专题2 三角函数压轴小题一、单选题 1．（2022·湖北·宜城市第二高级中学高三开学考试）已知正实数C 满足：对于任意θ，均存在,,0255i j i j ∈≤≤≤Z ，使得2cos iC jθ-≤，记C 的最小值为λ，则（） A ．1120001000λ<< B ．111000500λ<< C ．11500200λ<< D ．11200100λ<< 2．（2022·河南·灵宝市第一高级中学模拟预测（理））已知锐角ABC 的内角A ，B ，C 的对边分别为a ，b ，c ，且cos 2b aC a-=，则sin sin B A +的取值范围是（）A ．32⎫⎪⎪⎝⎭B ．(C ．32⎫⎪⎭D ．⎦3．（2022·湖北·宜城市第二高级中学高三开学考试）已知△ABC 中，AB AC ==，()min 2AB BC R λλ+=∈，2AM MB =，22sin cos AP AB AC αα=⋅+⋅，,63ππα⎡⎤∈⎢⎥⎣⎦，则MP 的最小值为（）A B ．23C D 4．（2023·全国·高三专题练习）在锐角ABC 中，角A ，B ，C 的对边分别为a ，b ，c ，ABC 的面积为S ，若222sin()SA C b a +=-，则1tan 3tan()A B A +-的取值范围为（）A ．⎫+∞⎪⎣⎭B ．43⎤⎥⎣⎦ C ．43⎫⎪⎪⎝⎭D ．43⎫⎪⎪⎣⎭5．（2022·全国·高三专题练习）在ABC 中，角,,A B C 所对应的边分别为,,a b c ，设ABC 的面积为S ，则24Sa bc+的最大值为（）A B C D 6．（2023·全国·高三专题练习）已知函数()sin 4f x x ωπ⎛⎫=+ ⎪⎝⎭(0)>ω在区间[0,]π上有且仅有4条对称轴，给出下列四个结论：△()f x 在区间(0,)π上有且仅有3个不同的零点； △()f x 的最小正周期可能是2π； △ω的取值范围是131744⎡⎫⎪⎢⎣⎭，； △()f x 在区间0,15π⎛⎫⎪⎝⎭上单调递增．其中所有正确结论的序号是（） A ．△△B ．△△C ．△△D ．△△△7．（2022·江苏省滨海中学模拟预测）设函数()211f x x =-，()122x fex --=，()31sin 23f x x π=，99i ia =，0i =、1、2、、99.记()()()()()()10219998k k k k k k k I f a f a f a f a f a f a =-+-++-，1k =、2、3，则（）A ．123I I I <<B ．321I I I <<C ．132I I I <<D ．213I I I <<8．（2022·上海市实验学校高三阶段练习）设a △R ，函数f (x )()()2222215cos x a x a x a x a x a ππ⎧-⎪=⎨-+++≥⎪⎩＜，若函数f (x )在区间（0，+∞）内恰有6个零点，则a 的取值范围是（） A ．（2，94]△（52，114]B ．（74，2]△（52，114]C ．（2，94]△[114，3）D ．（74，2）△[114，3）9．（2022·江苏·高邮市第一中学高三阶段练习）在锐角ABC 中，角A ，B ，C 的对边分别为a ，b ，c ，S 为ABC 的面积，且()222S a b c =--，则222b c bc+的取值范围为（）A ．4359,1515⎛⎫ ⎪⎝⎭B ．4315⎡⎫⎪⎢⎣⎭C ．5915⎡⎫⎪⎢⎣⎭D ．)⎡+∞⎣10．（2022·上海市向明中学高三开学考试）直线1y =与函数π()2sin 26f x x ⎛⎫=- ⎪⎝⎭的图像在y 轴右侧交点的横坐标从左到右依次为12n a a a 、、、，下列结论：△π2cos 23f x x ⎛⎫-=- ⎪⎝⎭；△()f x 在π5π,612⎡⎤⎢⎥⎣⎦上是减函数；△12n a a a 、、、为等差数列；△121234πa a a +++=．其中正确的个数是（）A ．3B ．2C ．1D ．011．（2022·上海交大附中高三开学考试）已知()sin |||sin |cos |||cos |=+++f x x x x x ，给出下述四个结论: △()y f x =是偶函数; △()y f x =在3,22ππ⎛⎫⎪⎝⎭上为减函数;△()y f x =在(,2)ππ上为增函数; △()y f x =的最大值为其中所有正确结论的编号是（） A ．△△△B ．△△△C ．△△△D ．△△12．（2022·广东汕头·高三阶段练习）已知函数()()()()()222sin 2π2πR 216,x a x a f x a x a x a x a⎧-<⎪=∈⎨-++-+≥⎪⎩，若()f x 在区间()0,∞+内恰好有7个零点，则a 的取值范围是（） A ．5817,,3236⎛⎤⎛⎤⋃ ⎥⎥⎝⎦⎝⎦B ．581711,,2363⎛⎤⎛⎤⋃ ⎥⎥⎝⎦⎝⎦C ．51711,3,263⎛⎤⎛⎤⋃ ⎥⎥⎝⎦⎝⎦D ．81711,3,363⎛⎤⎛⎤⋃ ⎥⎥⎝⎦⎝⎦13．（2022·广西·模拟预测（理））已知函数()()()sin cos cos sin f x x x =+，则下列结论正确的是（） A ．()f x 是奇函数 B ．()f x 的最大值为2 C ．()(),x f x f x π∀∈-=RD ．[]()0,,0x f x ππ∀∈+>14．（2022·湖南湘潭·高三开学考试）已知 11sin 65a =, 11sin 56b =, 15cos 156c =, 则（）A ．a b c <<B ．b a c <<C ．a c b <<D ． c a b <<15．（2022·全国·高三专题练习）在ABC 中，角A B C ､､所对的边分别是,120,a b c A D =､､是边BC 上一点，AB AD ⊥且AD =2b c +的最小值是（）A ．4B ．6C ．8D ．916．（2022·江苏南通·高三开学考试）已知锐角ABC 满足AB =60C ∠=°且O 为ABC 的外接圆圆心，若OC OA OB λμ=+，则2λμ-的取值范围为（） A ．(2,1)-B ．(1,2)-C ．[2,2)-D ．(2,2)-17．（2023·全国·高三专题练习）已知,x y ∈R ，则表达式22cos cos cos x y xy （）A ．既有最大值，也有最小值B ．有最大值，无最小值C ．无最大值，有最小值D ．既无最大值，也无最小值18．（2023·全国·高三专题练习）设数列{}n a 的通项公式为()()()*121cos 1N 2nn n a n n π=--⋅+∈，其前n 项和为n S ，则120S =（） A ．60-B ．120-C ．180D ．24019．（2023·全国·高三专题练习）在ABC 中，7cos 25A =，ABC 的内切圆的面积为16π，则边BC 长度的最小值为（） A ．16B ．24C ．25D ．3620．（2023·全国·高三专题练习）在锐角ABC cos cos ()sin sin A CA B C a c+=，且cos 2C C +=，则a b +的取值范围是（）A ．(4⎤⎦B ．(2,C ．(]0,4D ．(]2,421．（2022·山西·忻州一中模拟预测（文））定义：设不等式()0f x >的解集为A ，若A 中只有唯一整数，则称A 为“和谐解集”．若关于x 的不等式sin cos 2sin cos x x mx x x +>+-在(0,)π上存在“和谐解集”，则实数m 的取值范围为（） A ．cos2[,cos1)2B ．cos2(,cos1]2C ．[]cos2,cos1D ．[]cos2,sin 222．（2023·全国·高三专题练习）设ω∈R ，函数()()22,0,6314,0,22sin x x f x g x x x x x πωωω⎧⎛⎫+≥ ⎪⎪⎪⎝⎭==⎨⎪++<⎪⎩．若()f x 在1,32π⎛⎫- ⎪⎝⎭上单调递增，且函数()f x 与()g x 的图象有三个交点，则ω的取值范围是（） A ．12,43⎛⎤⎥⎝⎦ B．23⎤⎥⎝⎦ C．14⎡⎢⎣⎭D ．4412,0,33⎡⎫⎡⎤-⎪⎢⎢⎥⎣⎭⎣⎦23．（2022·全国·高三专题练习（文））在三角函数部分，我们研究过二倍角公式2cos 22cos 1x x =-，实际上类似的还有三倍角公式，则下列说法中不正确的有（） A ．3cos34cos 3cos x x x =- B ．存在||1x ≤时，使得3|43|1x x -> C ．给定正整数n ，若||1i x ≤，(1,2,,)i n =，且310n i i x ==∑，则1||3ni i n x =≤∑ D ．设方程38610x x --=的三个实数根为1x ，2x ，3x ，并且123x x x <<，则2232312()x xx x -=-二、多选题24．（2022·湖北·襄阳四中模拟预测）若()sin cos x x x x f x =-，则下列说法正确的是（） A ．()f x 的最小正周期是2πB ．()f x 的对称轴方程为212k x ππ=-，()k ∈Z C ．存在实数a ，使得对任意的x ∈R ，都存在125,01,2x x π⎡⎤∈-⎢⎥⎣⎦且12x x ≠，满足()()()210k f x af x f x -+=⎡⎤⎣⎦，()1,2k =D ．若函数()()2g x f x b =+，250,12x π⎡⎤∈⎢⎥⎣⎦，（b 是实常数），有奇数个零点()12221,,,,N n n x x x x n +⋅⋅⋅∈，则()1232215023n n x x x x x π++++⋅⋅⋅++=25．（2022·重庆十八中两江实验中学高三阶段练习）已知在平行四边形ABCD 中，3AB =，2AD =，60A ∠=︒，把△ABD 沿BD 折起使得A 点变为'A ，则（） A．BD =B ．三棱锥'A BCD -C ．当'A C BD =时，三棱锥'A BCD -D ．当'A C BD =时，'60A BC ∠=︒26．（2022·辽宁·东北育才学校高三阶段练习）已知函数()()()sin 0,f x x ωϕωϕ=+>∈R 在区间75,126ππ⎛⎫⎪⎝⎭上单调，且满足73124f f ππ⎛⎫⎛⎫=- ⎪ ⎪⎝⎭⎝⎭有下列结论正确的有( )A ．203f π⎛⎫=⎪⎝⎭B ．若()56f x f x π⎛⎫-= ⎪⎝⎭，则函数()f x 的最小正周期为π； C ．关于x 的方程()1f x =在区间[0,2)π上最多有4个不相等的实数解 D ．若函数()f x 在区间213,36ππ⎡⎫⎪⎢⎣⎭上恰有5个零点，则ω的取值范围为8,33⎛⎤⎥⎝⎦ 27．（2022·全国·高三专题练习（文））由倍角公式2cos 22cos 1x x =-，可知cos2x 可以表示为cos x 的二次多项式．一般地，存在一个n （n *∈N ）次多项式()12012n n n n n P t a t a ta t a --=+++⋅⋅⋅+（012,,,n a a a a ⋅⋅⋅∈R ），使得()cos cos n nx P x =，这些多项式()n P t 称为切比雪夫（P ．L ．Tschebyscheff )多项式．运用探究切比雪夫多项式的方法可得（）A ．()3343P t t t =-+B ．()424881P t t t =-+C ．sin18︒=D ．cos18︒=28．（2022·全国·高三专题练习）设正整数k 使得关于x 的方程sin kx x =在区间()33ππ-，内恰有5个实根12345x x x x x <<<<，则（）A ．123450x x x x x +++=+B ．5295122x ππ<< C ．55tan x x =D ．2x ，4x ，5x 成等差数列三、填空题29．（2022·安徽淮南·二模（理））ABC 中，120,BAC AO ∠︒=为BC 边上的中线，AO =2AB AC -的取值范围是________．30．（2023·全国·高三专题练习）△ABC 中，角A ，B ，C 所对的三边分别为a ，b ，c ，c ＝2b ，若△ABC 的面积为1，则BC 的最小值是________ ．31．（2022·全国·高三专题练习（文））1643年法国数学家费马曾提出了一个著名的几何问题：已知一个三角形，求作一点，使其到这个三角形的三个顶点的距离之和为最小.它的答案是：当三角形的三个角均小于120°时，所求的点为三角形的正等角中心（即该点与三角形的三个顶点的连线段两两成角120°），该点称为费马点.已知ABC 中，其中60A ∠=︒，1BC =，P 为费马点，则PB PC PA +-的取值范围是__________. 32．（2022·全国·高三专题练习）如图，在边长为2的正方形ABCD 中，M ，N 分别为边BC ，CD 上的动点，以MN 为边作等边PMN ，使得点A ，P 位于直线MN 的两侧，则PN PB ⋅的最小值为______．33．（2021·安徽·六安市裕安区新安中学高三阶段练习（文））设△A n B n C n 的三边长分别为a n ，b n ，c n ，n =1，2，3…，若11b c >，1112b c a +=，11,2n n n n n a c a a b +++==，12n n n a bc ++=，则n A ∠的最大值是________________. 34．（2022·天津西青·高三期末）在等腰直角三角形ABC 中，π2C ∠=，点P 在三角形内，满足2(222)0PA PB PC +++=，则APB ∠=______.35．（2022·全国·高三专题练习（理））函数ππ5sin (1510)55y x x ⎛⎫=+-≤≤ ⎪⎝⎭的图象与函数25(1)22x y x x +=++图象的所有交点的横坐标之和为___________.36．（2022·全国·高三专题练习）△ABC 内接于半径为2的圆，三个内角A ，B ，C 的平分线延长后分别交此圆于1A ，1B ，1C .则111coscos cos 222sin sin sin A B CAA BB CC A B C++++的值为_____________.37．（2022·福建师大附中高三阶段练习）已知非零实数,x y 满足222x yxy x y y x++=-，则22x y +的最小值为_____．38．（2022·全国·成都七中高三开学考试（文））ABC 的外心为O ，三个内角A B C ，，所对的边分别为1825a b c AO BC a a c ⎛⎫⋅=- ⎪⎝⎭，，，，4b =.则ABC 面积的最大值为____________. 39．（2022·上海·华师大二附中高三开学考试）对开区间(),I a b =，定义Ib a =-，当实数集合M 为n 段（n为正整数）互不相交的开区间12n I I I ､､､的并集时，定义1||nk k M I ==∑，若对任意上述形式的()0,2π的子集A ，总存在Z k ∈，使得k A A λ≥，其中|,|tan 14k k A x x A x π⎧⎫⎛⎫=∈+⎨⎬ ⎪⎝⎭⎩⎭∣，则λ的最大值为___________. 40．（2021·江苏·南京市第一中学高三阶段练习）在ABC 中，角A ，B ，C 的对边分别为a ，b ，c .已知4C π，222a b -=，则A ＝____________.41．（2022·安徽·高三开学考试）有下列命题: △函数tan y x =在定义域内是增函数;△函数1π()cos 34f x x ⎛⎫=+ ⎪⎝⎭的最小正周期为3π;△直线πx =为函数()sin(cos )cos f x x x =+图像的一条对称轴;△函数()|sin |cos f x x x =+的值域为[-. 其中所有正确命题的序号为_____.42．（2021·江西南昌·高三阶段练习）已知ABC 的内角,,A B C 所对应的边分别为,,a b c ，且满足2224,4c c a b ==+，则ABC 的面积取得最大值时，cos C =______．43．（2022·江苏·泗洪县洪翔中学高三阶段练习）在ABC 中，角A ，B ，C 所对的边为a ，b ，c ，若sin sin cos cos3sin B C A C A a c =+，且ABC 的面积222)ABC S a b c +-△，则c a b +的取值范围是___________.44．（2022·全国·高三专题练习）已知,0,2παβ⎛⎫∈ ⎪⎝⎭，()sin 22sin αββ+=，则tan β的最大值为________.45．（2022·北京·测试学校四高三）若ABC 三边长为等差数列，则cos cos cos A B C ++的取值范围是___________.46．（2023·全国·高三专题练习）在ABC 中，()2ABCcSa b =-，其外接圆半径2R =，且())224sin sin sin A B b B -=-，则sinsin 22A B C-+=___________. 47．（2022·北京·测试学校四高三）已知凸四边形ABCD 满足50,40ABD BDC CAD ACB ∠∠∠∠====，则符合题意且不相似的凸四边形ABCD 的个数为___________.48．（2023·全国·高三专题练习）已知函数()sin()f x x ωϕ=+，其中0>ω，0πϕ<< ，π()()4f x f ≤恒成立，且()y f x =在区间3π0,8⎛⎫⎪⎝⎭上恰有3个零点，则ω的取值范围是______________．49．（2022·上海金山·二模）设()sin f x a x =+，若存在125,,,,36n x x x ππ⎡⎤∈⎢⎥⎣⎦，使()()()()121n n f x f x f x f x -+++=成立的最大正整数n 为9，则实数a 的取值范围是__________.50．（2023·全国·高三专题练习）已知锐角三角形ABC 的内角A ，B ，C 所对的边分别是a ，b ，c ，且A B >，若7sin 2cos sin 25C A B =+，则tan B 的取值范围为_______．四、双空题51．（2022·辽宁·东北育才双语学校一模）记ABC 的内角A ，B ，C 的对边分别为a ，b ，c ，已知222222a b a b c c ab -+-=，若4C π，则A =___________；若ABC 为锐角三角形，则2cos ab B的取值范围是___________.52．（2022·广东佛山·高三期末）菱形ABCD 中，ππ1,,32AB A ⎡⎤=∈⎢⎥⎣⎦，点E ，F 分别是线段,AD CD 上的动点（包括端点），AE CF =，则()AE CF AC +⋅=___________，ED EB ⋅的最小值为___________. 53．（2022·全国·高三专题练习）在ABC 中，D 是BC 边上一点，且6B π=，12AD BD =，若D 是BC 的中点，则ACAB=______；若AC =ADC 的面积的最大值为_________．。

高三数学总复习专题二三角函数教学案

芯衣州星海市涌泉学校赣榆县智贤中学高三数学总复习专题二第1讲三角函数〔1〕教学案教学内容：三角函数的图象与性质〔1〕教学目的：1三角函数的图象与解析式2.利用三角函数的图象与解析式教学重点：1.求三角函数的解析式；教学难点：三角函数的图象与解析式教学过程：一、知识点复习：1．必记的概念与定理(1)同角关系：sin2α＋cos2α＝1，＝tanα.(2)诱导公式：在＋α，k∈Z的诱导公式中“奇变偶不变，符号看象限〞．(3)三角函数的图象及常用性质函数y＝sinx y＝cosx y＝tanx图象单调性在[－＋2kπ，＋2kπ](k∈Z)上单调递增；在[＋2kπ，＋2kπ](k∈Z)上单调递减在[－π＋2kπ，2kπ](k∈Z)上单调递增；在[2kπ，π＋2kπ](k∈Z)上单调递减在(－＋kπ，＋kπ)(k∈Z)上单调递增对称性对称中心：(kπ，0)(k∈Z)；对称轴：x＝＋kπ(k∈Z)对称中心：(＋kπ，0)(k∈Z)；对称轴：x＝kπ(k∈Z)对称中心：(，0)(k∈Z)2.记住几个常用的公式与结论对于函数y＝Asin(ωx＋φ)(A>0，ω>0)要记住下面几个常用结论：(1)定义域：R.(2)值域：[－A，A]．当x＝(k∈Z)时，y取最大值A；当x＝(k∈Z)时，y取最小值－A.(3)周期性：周期函数，周期为.(4)单调性：单调递增区间是(k∈Z)；单调递减区间是(k∈Z).(5)对称性：函数图象与x轴的交点是对称中心，即对称中心是(，0)，对称轴与函数图象的交点纵坐标是函数的最值，即对称轴是直线x＝，其中k∈Z.(6)函数y＝Asin(ωx＋φ)(A>0，ω>0)中，A影响函数图象的最高点和最低点，即函数的最值；ω影响函数图象每隔多少重复出现，即函数的周期；φ影响函数的初相．(7)对于函数y＝Asin(ωx＋φ)(A>0，ω>0)的图象，相邻的两个对称中心或者者两条对称轴相距半个周期；相邻的一个对称中心和一条对称轴相距周期的四分之一．复备栏3．需要关注的易错易混点三角函数图象平移问题(1)看平移要求：拿到这类问题，首先要看题目要求由哪个函数平移到哪个函数，这是判断挪动方向的关键点．(2)看挪动方向：在学习中，挪动的方向一般我们会记为“正向左，负向右〞，其实，这样不理解的记忆是很危险的．上述规那么不是简单地看y＝Asin(ωx＋φ)中φ的正负，而是和它的平移要求有关．正确地理解应该是：平移变换中，将x变换为x＋φ，这时才是“正向左，负向右〞．(3)看挪动单位：在函数y＝Asin(ωx＋φ)中，周期变换和相位变换都是沿x轴方向的，所以ω和φ之间有一定的关系，φ是初相位，再经过ω的压缩，最后挪动的单位是||.二、根底训练：1．函数y＝tan的定义域是________．解析：∵x－≠kπ＋，∴x≠kπ＋，k∈Z.答案：2．(2021·模拟)函数f(x)＝sinxcosx的最小正周期是________．解析：由题知f(x)＝sin2x，所以T＝＝π.答案：π3．将函数y＝2sinx的图象上每一点向右平移1个单位长度，再将所得图象上每一点的横坐标扩大为原来的倍(纵坐标保持不变)，得函数y＝f(x)的图象，那么f(x)的解析式为________．解析：函数y＝2sinx向右平移1个单位得y＝2sin(x－1)＝2sin，将所得图象上每一点的横坐标扩大为原来的倍(纵坐标保持不变)，那么y＝2sin，即y＝2sin.答案：y＝2sin4．(2021·模拟)函数f(x)＝2sin，x∈[－π，0]的单调增区间为________．解析：当x－∈，k∈Z时，f(x)单调递增，又因为x∈[－π，0],故取k＝0得x∈.答案：1三、例题教学：例1、(2021·模拟)假设函数f(x)＝Asin(ωx＋φ)(A>0，ω>0，|φ|<)的图象如下列图，这个函数的解析式为________．[解析]由题意知：周期T＝2(－)＝π，ω＝＝2，设f(x)＝Asin(2x＋φ)，点(，0)为五点作图中的第三点，所以2×＋φ＝π，即φ＝.设f(x)＝Asin(2x＋)，因为点(0，)在原函数的图象上，故Asin＝，所以A＝，综上知：f(x)＝sin(2x＋)．[答案]f(x)＝sin(2x＋)变式训练：1．(2021·高考卷)函数y＝cosx与y＝sin(2x＋φ)(0≤φ<π)，它们的图象有一个横坐标为的交点，那么φ的值是________．解析：由题意，得sin＝cos，因为0≤φ<π，所以φ＝.答案：例2、2021·模拟)函数f(x)＝2sin(ωx＋φ)(ω>0，－<φ<)的图象如下列图，直线x＝，x ＝是其两条对称轴．(1)求函数f(x)的解析式并写出函数的单调增区间；(2)假设f(α)＝，且<α<，求f(＋α)的值．[解](1)由题意，＝－＝，∴T＝π，又ω>0，故ω＝2，∴f(x)＝2sin(2x＋φ)，由f()＝2sin(＋φ)＝2，解得φ＝2kπ－(k∈Z)，又－<φ<，∴φ＝－，∴f(x)＝2sin(2x－)，由2kπ－≤2x－≤2kπ＋(k∈Z)知，kπ－≤x≤kπ＋，(k∈Z)，∴函数f(x)的单调增区间为[kπ－，kπ＋](k∈Z)．(2)依题意得：2sin(2α－)＝，即sin(2α－)＝，∵<α<，∴0<2α－<，∴cos(2α－)＝＝＝，f(＋α)＝2sin[(2α－)＋]，∵sin[(2α－)＋]＝sin(2α－)cos＋cos(2α－)sin＝(＋)＝，∴f(＋α)＝.稳固练习：完成专题强化训练。

高三数学第二轮专题复习三角函数(有答案)

高三数学第二轮专题复习三角函数班级姓名1.cos300︒=( )A.312 C .1232.cos13计算sin43cos 43-sin13的值等于（）A ．12B 3C ．22D 33.设0ω>,函数sin()23y x πω=++的图像向右平移43π个单位后与原图像重合，则ω的最小值是A ．23 B. 43 C . 32D. 3 4.已知2sin 3α=，则cos(2)x α-=A.5- B .19- C.1955.为了得到函数的图像，只需把函数的图像 A.向左平移个长度单位 B .向右平移个长度单位C.向左平移个长度单位 D.向右平移个长度单位6.下列函数中，周期为π，且在[,]42ππ上为减函数的是 A.sin(2)2y x π=+B.cos(2)2y x π=+C.sin()2y x π=+D.cos()2y x π=+ 7.已知函数()sin (0,)2y x πωϕωϕ=+><的部分图象如题（6）图所示，则A. ω=1 ϕ= 6πB. ω=1 ϕ=- 6πC. ω=2 ϕ= 6π D . ω=2 ϕ= -6π8.观察2'()2x x =，4'3()4x x =，'(cos )sin x x =-，由归纳推理可得：若定义在R 上的函数()f x 满足()()f x f x -=，记()g x 为()f x 的导函数，则()g x -=( )A.()f xB.()f x -C. ()g x D .()g x -9.在△ABC 中，内角A,B,C 的对边分别是a,b,c ，若223a b bc -=，sin 23C B =，则A=A .030 B.060 C.0120 D.0150sin(2)3y x π=-sin(2)6y x π=+4π4π2π2π10.函数2()sin(2)4f x x x π=--的最小正周期是__________________ .11.在ABC 中，角A ，B ，C 所对的边分别为a ，b ，c ，若a =2b =,sin cos B B +=则角A 的大小为 .12.已知α为第二象限的角，3sin 5a =,则tan 2α= .13.在ABC ∆中，4π=A ，1010cos =B .（Ⅰ）求C cos ；（Ⅱ）设5=BC ，求CB CA ⋅的值.14.在ABC ∆中，AB =1BC =，3cos 4C =.（1）求sin A 的值；（2）求CA BC ⋅的值.15.在△ABC 中，角,,A B C 所对的边分别为,,a b c ，已知2a =，3c =，1cos 4B =．（1）求b 的值；（2）求sinC 的值．16,已知向量(cos sin ,sin )a x x x =+，(cos sin ,2cos )b x x x =-，设()f x a b =⋅.（1）求函数()f x 的最小正周期. （2）当,44x ππ⎡⎤∈-⎢⎥⎣⎦时，求函数()f x 的最大值及最小17.已知函数22()sin 2sin cos 3cos f x x x x x =++，x R ∈.求: (I) 函数()f x 的最大值及取得最大值的自变量x 的集合；(II) 函数()f x 的单调增区间.18.已知函数2()sin 22sin f x x x =- （I ）求函数()f x 的最小正周期. (II) 求函数()f x 的最大值及()f x 取最大值时x 的集合。

高三理科数学最值微专题(2)三角函数篇

高三理科数学二轮复习最值专题（2）三角函数篇类型一：形如y ＝a sin x ＋b cos x ＋c 的三角函数化为y ＝A sin(ωx ＋φ)＋c 的形式，再求值域(最值)。

例1．函数f (x )＝sin ⎝⎛⎭⎫2x －π4在区间⎣⎡⎦⎤0，π2上的最小值为( ) A ．－1 B ．－22C ．0 D.22解析：因为0≤x ≤π2，所以－π4≤2x －π4≤3π4，由正弦函数的图象知，1≥sin ⎝⎛⎭⎫2x －π4≥－22，所以函数f (x )＝sin ⎝⎛⎭⎫2x －π4在区间⎣⎡⎦⎤0，π2上的最小值为－22，故选B. 例2．已知函数f (x )＝(sin x ＋cos x )2＋cos 2x .(1)求f (x )的最小正周期；(2)求f (x )在区间⎣⎡⎦⎤0，π2上的最大值和最小值．解：(1)因为f (x )＝sin 2x ＋cos 2x ＋2sin x cos x ＋cos 2x ＝1＋sin 2x ＋cos 2x ＝2sin ⎝⎛⎭⎫2x ＋π4＋1，所以函数f (x )的最小正周期T ＝2π2＝π. (2)由(1)知，f (x )＝2sin ⎝⎛⎭⎫2x ＋π4＋1. 当x ∈⎣⎡⎦⎤0，π2时，2x ＋π4∈⎣⎡⎦⎤π4，5π4，由正弦函数y ＝sin x 在⎣⎡⎦⎤π4，5π4上的图象知，当2x ＋π4＝π2，即x ＝π8时，f (x )取最大值2＋1；当2x ＋π4＝5π4，即x ＝π2时，f (x )取最小值0.综上，f (x )在⎣⎡⎦⎤0，π2上的最大值为2＋1，最小值为0.类型二：形如y ＝a sin 2x ＋b sin x ＋c 的三角函数，可先设sin x ＝t ，化为关于t 的二次函数求值域(最值)。

例3、求函数y ＝cos 2x ＋sin x ⎝⎛⎭⎫|x |≤π4的最大值与最小值． [思路点拨] 利用换元法求解，令t ＝sin x ．转化为二次函数最值问题．[解]：令t ＝sin x ，∵|x |≤π4，∴t ∈⎣⎡⎦⎤－22，22.∴y ＝－t 2＋t ＋1＝－⎝⎛⎭⎫t －122＋54，∴当t ＝12时，y max ＝54，t ＝－22时，y min ＝1－22.∴函数y ＝cos 2x ＋sin x ⎝⎛⎭⎫|x |≤π4的最大值为54，最小值为1－22. 类型三：形如y ＝a sin x cos x ＋b (sin x ±cos x )＋c 的三角函数，可设t ＝sin x ±cos x ，再化为关于t 的二次函数求值域(最值)．例4、求函数y ＝sin x ＋cos x ＋3cos x sin x 的最值．[解] 令t ＝sin x ＋cos x ，∴t ∈[－2， 2 ]．又(sin x ＋cos x )2－2sin x cos x ＝1，∴sin x cos x ＝t 2－12， ∴y ＝32t 2＋t －32，t ∈[－2，2]，∵t 对＝－13∈[－2，2]，∴y 小＝f ⎝⎛⎭⎫－13＝32×19－13－32＝－53，y 大＝f (2)＝32＋ 2. 类型四：“逆向题”，即已知函数的最值去求某参数的值。

大题专项训练6：三角函数与解三角形(综合练习二)-2021届高三数学二轮复习

二轮大题专练6—三角函数与解三角形（综合练习二）1．在△ABC中，角A，B，C的对边分别为a，b，c，已知．（1）若a，b，c成等差数列，求cos B的值；（2）是否存在△ABC满足B为直角？若存在，求sin A的值；若不存在，请说明理由．2．已知△ABC的内角A，B，C的对边分别为a，b，c，且a cos C﹣c sin A＝b．（1）求A；（2）若c＝2，且BC边上的中线长为，求b．3．设函数f（x）＝sin（ωx+φ）（ω＞0，﹣＜φ＜）最小正周期为2π，且f（x）的图象过坐标原点．（1）求ω、φ的值；（2）在△ABC中，若2f2（B）+3f2（C）＝2f（A）•f（B）•f（C）+f2（4），且三边a、b、c所对的角依次为A、B、C，试求的值．4．已知在△ABC中，sin（A+B）＝1+2sin2．（1）求角C的大小；（2）若∠BAC与∠ABC的内角平分线交于点Ⅰ，△ABC的外接圆半径为2，求△ABI周长的最大值．5．已知f（x）＝cos2x﹣1+sin x cos x，x∈R．（1）求f（x）的单调递增区间；（2）在△ABC中，角A，B，C所对的边分别为a，b，c，若c cos B+b cos C＝1且f（A）＝0，求△ABC的面积的最大值．6.已知函数的最小值为﹣2，其图象经过点（0，﹣1），且图象上相邻的最高点与最低点的横坐标之差的绝对值为．（Ⅰ）求函数f（x）的解析式；（Ⅱ）若关于x的方程f（x）﹣k＝0在上有且仅有两个实数根x1，x2，求实数k的取值范围，并求出x1+x2的值．7．已知函数21()sin sin()cos ()6122f x x x x ππ=++--．（1）求函数()f x 的最小正周期及单调递减区间；（2）已知锐角ABC ∆的内角A ，B ，C 的对边分别为a ，b ，c ，且3(),32B f b ==，求cos cos a B b C -的取值范围．8．已知函数f （x ）＝4cos ωx sin （ωx +φ）﹣1（0＜φ＜π，ω＞0）的图象关于直线对称，且两相邻对称中心之间的距离为．（Ⅰ）求函数y ＝f （x ）的单调递增区间；（Ⅱ）若x ∈[0，π]时，函数g （x ）＝f （x ）﹣b 有两个不同的零点x 1，x 2，求b 的取值范围及x 1+x 2的值．二轮大题专练6—三角函数与解三角形（综合练习二）答案1.解：（1）若a ，b ，c 成等差数列，所以a +c ＝2b ，由于．所以cos B ＝＝，由于，所以．（2）假设B为直角，则sin B＝1，sin C＝cos A，由于，根据正弦定理（sin A+sin C）sin B＝，即sin A+cos A＝，上式两边平方得：，所以（9sin2A+5）（4sin2A﹣5）＝0，由于0＜sin2A≤1，所以9sin2A+5＞0，4sin2A﹣5＜0，与（9sin2A+5）（4sin2A﹣5）＝0矛盾，故不存在△ABC满足B为直角．2.解：（1）因为a cos C﹣c sin A＝b，由正弦定理可得sin A cos C﹣sin C sin A＝sin B，因为B＝π﹣A﹣C，所以sin A cos C﹣sin C sin A＝sin A cos C+cos A sin C，可得﹣sin C sin A＝cos A sin C，因为sin C≠0，所以sin A＝﹣cos A，可得tan A＝﹣，又因为A∈（0，π），可得A＝．（2）由余弦定理可得a2＝b2+c2﹣2bc cos A＝b2+4+2b，①又在△ABC中，cos B＝＝，设BC的中点为D，在△ABD中，cos B＝＝，可得＝，可得a2+4﹣2b2＝0，②由①②可得b2﹣2b﹣8＝0，解得b＝4．3.解：（1）依题意，得，ω＝1．故f（x）＝sin（x+φ）．因为f（x）的图象过坐标原点，所以f（0）＝0，即sinφ＝0，∵﹣＜φ＜，∴φ＝0．（2）由（1）知f（x）＝sin x，因为2f2（B）+3f2（C）＝2f（A）•f（B）•f（C）+f2（4），所以2sin2B+3sin2C＝2sin A sin B sin C+sin2A，由正弦定理可得：2b2+3c2＝2sin A•bc+a2，又a2＝b2+c2﹣2bc cos A，∴＝，又，∴sin A﹣cos A＝，且b＝，∴A＝．∴＝＝．4.解：（1）∵sin（A+B）＝1+2sin2，且A+B+C＝π，∴sin C＝1+1﹣cos C＝2﹣cos C，即sin C+cos C＝2，∴2sin（C+）＝2．∵C∈（0，π），∴C+∈（，），∴C+＝，即C＝．（2）∵△ABC的外接圆半径为2，∴由正弦定理知，＝＝2×2＝4，∴AB＝，∵∠ACB＝，∴∠ABC+∠BAC＝，∵∠BAC与∠ABC的内角平分线交于点Ⅰ，∴∠ABI+∠BAI＝，∴∠AIB＝，设∠ABI＝θ，则∠BAI＝﹣θ，且0＜θ＜，在△ABI中，由正弦定理得，＝＝＝＝4，∴BI＝4sin（﹣θ），AI＝4sinθ，∴△ABI的周长为2+4sin（﹣θ）+4sinθ＝2+4（cosθ﹣sinθ）+4sinθ＝2+2cosθ+2sinθ＝4sin（θ+）+2，∵0＜θ＜，∴＜θ+＜，∴当θ+＝，即时，△ABI的周长取得最大值，为4+2，故△ABI的周长的最大值为4+2．5.解：（1）f（x）＝cos2x﹣1+sin x cos x＝cos2x﹣+sin2x＝sin（2x+）﹣，令2x+∈[+2kπ，+2kπ]，k∈Z，则x∈[+kπ，+kπ]，k∈Z，∴f（x）的单调递增区间为[+kπ，+kπ]，k∈Z．（2）∵f（A）＝sin（2A+）﹣＝0，∴sin（2A+）＝，∵A∈（0，π），∴A＝，∵c cos B+b cos C＝1，∴c•+b•＝1，即a2＝a，∵a≠0，∴a＝1，由正弦定理知，＝＝＝＝，∴b＝sin B，c＝sin C，∴bc＝sin B sin C＝sin B sin（+B）＝sin B（cos B+sin B）＝sin2B﹣cos2B+＝sin（2B﹣）+，∵B∈（0，），∴2B﹣∈（﹣，），sin（2B﹣）∈（，1]，∴bc≤1，∴△ABC的面积S＝bc sin A≤×1×sin＝，故△ABC的面积的最大值为．6.解：（Ⅰ）由题意，得A＝2，．∴T＝π，．∴f（x）＝2sin（2x+φ）．又函数f（x）的图象经过点（0，﹣1），则2sinφ＝﹣1．由，得．∴．（Ⅱ）由题意，关于x的方程f（x）﹣k＝0在上有且仅有两个实数根x1，x2，即函数y＝f（x）与y＝k的图象在上有且仅有两个交点．由（Ⅰ）知．令，则y＝2sin t．∵，∴．则y∈[﹣2，2]．其函数图象如图所示．由图可知，实数k的取值范围为．①当k ∈[1，2）时，t 1，t 2，关于对称，则．解得．②当时，t 1，t 2关于对称，则．解得．综上，实数k 的取值范围为，x 1+x 2的值为或．7.解：（1）由题意可得21()sin sin()cos ()6122f x x x x ππ=++-- 311sin (cos )cos(2)226x x x x π++- 3(1cos2)131sin 2sin 244x x x x -=++ 13sin 22x =+，所以函数()f x 的最小正周期22T ππ==，令322222k x k ππππ++，k Z ∈，解得344k x k ππππ++，k Z ∈，故函数()f x 的单调递减区间为[4k ππ+，3]4k ππ+，k Z ∈．（2）由（1）知133()sin 22B f B =+=，解得3sin B =，因为(0,)2B π∈，所以3B π=，由正弦定理可知32sin sin sin 3a b c A B C ====，则2sin a A =，2sin c C =，所以3331cos cos 3cos sin 3cos()sin 3cos()sin cos sin cos sin cos()233226a a B b C C A A A A A A A A A A ππππ-=-=---=++=+-=-=+，在锐角ABC ∆中，可得230,202A C A C πππ+=⎧⎪<<⎪⎨⎪<<⎪⎩可得62A ππ<<，因此2363A πππ<+<，则1cos()(62A π+∈-，1)2，故cos cos a B b C -的取值范围为1(2-，1)2． 8.解：（Ⅰ）f （x ）＝4cos ωx sin （ωx +φ）﹣1＝4cos ωx （sin ωx cos φ+cos ωx sin φ）﹣1＝4sin ωx cos ωx cos φ+4cos 2ωx sin φ﹣1＝2sin2ωx cos φ+2（1+cos2ωx ）sin φ﹣1＝2sin2ωx cos φ+2cos2ωx sin φ+2sin φ﹣1＝2sin （2ωx +φ）+2sin φ﹣1，因为两相邻对称中心之间的距离为，所以函数f （x ）的周期为π，则，所以ω＝1，则f（x）＝2sin（2x+φ）+2sinφ﹣1，又f（x）的图象关于直线对称，所以有φ＝，解得φ＝，因为0＜φ＜π，所以φ＝，故，令，解得，所以函数y＝f（x）的单调递增区间为；（Ⅱ）当x∈[0，π]时，函数g（x）＝f（x）﹣b有两个不同的零点x1，x2，即当x∈[0，π]时，方程＝有两个不同的根x1，x2，令t＝，则t∈，所以方程sin t＝在上有两个不同的根t1，t2，作出函数的图象如图所示，①当，即1＜b＜2时，y＝与y＝sin t有两个交点，则t1+t2＝，即，解得；②当，即﹣2＜b＜0时，y＝与y＝sin t有两个交点，则t1+t2＝，即，解得；综上可得，当﹣2＜b＜0时，；当1＜b＜2时，．。

专题：三角函数(高三用)

三角函数复习专题（一）一、核心知识点归纳： 1．弧长、扇形面积的公式：设扇形的弧长为l ，圆心角大小为α(rad)，半径为r ，则弧长公式l ＝，扇形的面积公式S ＝＝ . 2.（1）三角函数定义（角α终边上任一点(),Px y ）：其中r =sin α= ;cos α= ; tan α= （2）符号规律：sin α cos α tan α（3）同角三角函数的基本关系：①倒数关系： ②商数关系：，③平方关系：注意三兄弟（三剑客）的应用：对于sin α＋cos α，sin αcos α，sin α－cos α这三个式子，利用(sin α±cos α)2＝1±2sin αcos α，可以知一求二．（4）特殊角的三角函数值表：（5）诱导公式：（奇变偶不变，符号看象限）k ·π/2+a 所谓奇偶指的是整数k 的奇偶性：①sin(2)cos(2)tan(2)k k k παπαπα±=⎧⎪±=⎨⎪±=⎩ ；②sin()cos()tan()παπαπα+=⎧⎪+=⎨⎪+=⎩ ；③sin()cos()tan()ααα-=⎧⎪-=⎨⎪-=⎩④sin()cos()tan()παπαπα-=⎧⎪-=⎨⎪-=⎩ ； ⑤sin(2)cos(2)tan(2)παπαπα-=⎧⎪-=⎨⎪-=⎩ ；⑥sin()2cos()2παπα⎧-=⎪⎪⎨⎪-=⎪⎩ ⑦sin()2cos()2παπα⎧+=⎪⎪⎨⎪+=⎪⎩ ；⑧3sin()23cos()2παπα⎧-=⎪⎪⎨⎪-=⎪⎩ ：⑨3sin()23cos()2παπα⎧+=⎪⎪⎨⎪+=⎪⎩5.两角和与差的三角函数：（1）和（差）角公式：①sin()αβ+= ；sin()αβ-= ②cos()αβ+= ；cos()αβ-= ③tan()αβ+= ；tan()αβ-= 注：公式的逆用或者变形．．．．．．．．．（2）二倍角公式：=a 2sin =a 2cos=a 2tan从二倍角的余弦公式里面可得出降幂公式：=a 2cos ， =a 2sin6．辅助角公式：sin cos a b αα+=三、基础练习 1、（1）弧长为3π，圆心角为135°的扇形半径为________，面积为________ (2)已知扇形周长为40，当它的半径和圆心角取何值时，才使扇形面积最大？2、（1）求值：sin(－1 200°)·cos 1 290°＋cos(－1020°)·sin(－1 050°)＋tan 945°.点评：利用诱导公式化简求值时的原则—3、已知f (x )＝a sin(πx ＋α)＋b cos(πx ＋β)＋4 (其中a ，b ，α，β为非零实数)， f (2 011)＝5，则f (2 012)＝ ( )A ．3B ．5C ．1D ．不能确定四、典型例题考点一：三角函数的概念例1若P (4，y )是角θ终边上一点，且sin θ＝－255，则y ＝____.练习1.(2012·潍坊质检)已知角α的终边经过点P (m ，－3)，且cos α＝－45，则m 等于 ( )A ．－114 B.114C ．－4D ．4练习2. 若角α的终边经过点P (1,-2),则tan 2α的值为 .变：若角α的终边与单位圆交于点255,55p ⎛⎫-- ⎪⎪⎝⎭，则sin 2a 的值为 . 考点二、同角三角函数的关系（注意22sin cos 1αα+=，这是一个隐含条件）例2、(2011·全国卷)已知α∈⎝ ⎛⎭⎪⎫π，3π2，tan α＝2，则cos α＝________.变式：若例题中条件变为“若sin θ＝－45，tan θ>0”，则cos θ＝________.练：若cos 2sin 5,αα+=-则tan α=( )（A ）21 （B ）2 （C ）21- （D ）2- 例3、已知sin α＋3cos α3cos α－sin α＝5，则sin 2α－sin αcos α的值是 ( )A.25 B ．－25C ．－2D ．2练习1．若tan α＝2，则2sin α－cos αsin α＋2cos α的值为 ( )A ．0 B.34 C ．1 D.54练习2．(2011·杭州师大附中月考)如果f (tan x )＝sin 2x －5sin x cos x ，那么f (5)＝________. 巩固练习：1、已知扇形的周长是6 cm ，面积是2 cm 2，则扇形的圆心角的弧度数是( )A ．1或4B ．1C ．4D ．82、已知1＋tan π＋α1＋tan 2π－α＝3＋22，求cos 2(π－α)＋sin ⎝ ⎛⎭⎪⎫3π2＋α·cos ⎝ ⎛⎭⎪⎫π2＋α＋2sin 2(α－π)的值．3、已知函数2()322sin f x x x =-.（Ⅰ）若点(1,3)P -在角α的终边上，求()f α的值；（Ⅱ）若[,]63x ππ∈-，求()f x 的值域.三角函数复习专题（二）sin y x =cos y x = tan y x =图象定义域值域最值周期性奇偶性单调性对称性函数性质题型一：三角函数的定义域、值域例1．(2012·珠海模拟)函数y ＝lg(2sin x －1)＋1－2cos x 的定义域为_ 练习1.函数y ＝tan ⎝ ⎛⎭⎪⎫π4－x 的定义域是 ( )A.⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x |x ≠π4，x ∈RB.⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x |x ≠－π4，x ∈R C.⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x |x ≠k π＋π4，k ∈Z ，x ∈R D.⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x |x ≠k π＋3π4，k ∈Z ，x ∈R 例2 (2010·江西高考)函数y ＝sin 2x ＋sin x －1的值域为( ) A ．[－1,1] B ．[－54，－1] C ．[－54，1] D ．[－1，54]变式：若例2中函数变为“y ＝2cos 2x ＋5sin x －4”试求值域．练习2． y ＝2－3cos ⎝ ⎛⎭⎪⎫x ＋π4的最大值为________．此时x ＝________.练习3．(2012·湛江)函数y ＝2sin ⎝⎛⎭⎪⎫2x ＋π3⎝ ⎛⎭⎪⎫－π6<x <π6的值域为____ ____．题型二：三角函数的单调性:注意区分下列两种形式的单调增区间不同(1)y ＝sin ⎝ ⎛⎭⎪⎫2x －π4； (2)y ＝sin ⎝ ⎛⎭⎪⎫π4－2x .例3 (2011·全国卷)设函数f (x )＝sin ⎝ ⎛⎭⎪⎫2x ＋π4＋cos ⎝ ⎛⎭⎪⎫2x ＋π4，则 ( )A ．y ＝f (x )在⎝⎛⎭⎪⎫0，π2单调递增，其图象关于直线x ＝π4对称B ．y ＝f (x )在⎝⎛⎭⎪⎫0，π2单调递增，其图象关于直线x ＝π2对称C ．y ＝f (x )在⎝⎛⎭⎪⎫0，π2单调递减，其图象关于直线x ＝π4对称D ．y ＝f (x )在⎝⎛⎭⎪⎫0，π2单调递减，其图象关于直线x ＝π2对称练习4．函数y ＝|sin x |的一个单调增区间是 ( )A.⎝ ⎛⎭⎪⎫－π4，π4B.⎝ ⎛⎭⎪⎫π4，3π4C.⎝ ⎛⎭⎪⎫π，3π2D.⎝⎛⎭⎪⎫3π2，2π 练习5．(2012·华南师大附中模拟)已知函数y ＝sin ⎝ ⎛⎭⎪⎫π3－2x ，求：(1)函数的周期； (2)求函数在[－π，0]上的单调递减区间．题型三：三角函数的周期性和奇偶性例4.(2010湖北高考)函数f (x )＝3sin ⎝ ⎛⎭⎪⎫x 2－π4，x ∈R 的最小正周期为 ( )A.π2B ．πC ．2πD ．4π练习6．下列函数中，周期为π，且在⎣⎢⎡⎦⎥⎤π4，π2上为减函数的是 ( )A ．y ＝sin ⎝ ⎛⎭⎪⎫2x ＋π2B ．y ＝cos ⎝ ⎛⎭⎪⎫2x ＋π2C ．y ＝sin ⎝ ⎛⎭⎪⎫x ＋π2D ．y ＝cos ⎝⎛⎭⎪⎫x ＋π2练习7. (2011·北京高考)已知函数f (x )＝4cos x sin ⎝⎛⎭⎪⎫x ＋π6－1.(1)求f (x )的最小正周期； (2)求f (x )在区间⎣⎡⎦⎤－π6，π4上的最大值和最小值．题型四：利用图像解题例5.（1）设2sin7a π=，2cos 7b π=，2tan 7c π=，则（） A ．a b c << B ．a c b << C ．b c a << D ．b a c << （2）．函数y =－x ·cos x 的部分图象是（）练习8.在（0，2π）内，使sin x ＞c os x 成立的x 取值范围为（）A ．（4π，2π）∪（π，45π） B ．（4π，π） C ．（4π，45π） D ．（4π，π）∪（45π，23π）练习9.函数ππln cos 22y x x ⎛⎫=-<< ⎪⎝⎭的图象是（）yx π2- π2Oyx π2-π2Oyx π2-π2Oyxπ2-π2OA ．B ．C ．D ．三角函数复习专题（三）1、函数B x A y ++=)sin(ϕω），（其中00>>ωA（1）.最大值是，最小值是，周期是，频率是，相位是，初相是； y ＝A sin(ωx ＋φ)+B 的图象有无穷多条对称轴，可由方程 (k ∈Z)解出x 的值就是对称轴；它还有无穷多个对称中心，它们是图象与x 轴的交点，可由 (k ∈Z)，解得x ＝k π－φω(k ∈Z)的值作为对称中心横坐标，即其对称中心为(k π－φω，0)(k ∈Z)．（2）．相邻两对称轴间的距离为T2，相邻两对称中心间的距离也为T2.（3）．由y ＝sin x 的图象变换出y ＝sin(ωx ＋ϕ)的图象一般有两个途径，只有区别开这两个途径，才能灵活进行图象变换。

2023届新高考数学二轮复习：专题(三角函数的范围与最值)提分练习(附答案)

2023届新高考数学二轮复习：专题（三角函数的范围与最值）提分练习【总结】一、三角函数()sin()f x A x ωϕ=+中ω的大小及取值范围 1、任意两条对称轴之间的距离为半周期的整数倍，即()2Tkk ∈Z ； 2、任意两个对称中心之间的距离为半周期的整数倍，即()2Tk k ∈Z ； 3、任意对称轴与对称中心之间的距离为14周期加半周期的整数倍，即()42T Tk k +∈Z ； 4、()sin()f x A x ωϕ=+在区间(,)a b 内单调2Tb a ⇒-…且()22k a b k k πππωϕωϕπ-+++∈Z 剟?5、()sin()f x A x ωϕ=+在区间(,)a b 内不单调(,)a b ⇒内至少有一条对称轴，2a kb πωϕπωϕ+++剟()k ∈Z6、()sin()f x A x ωϕ=+在区间(,)a b 内没有零点2Tb a ⇒-…且(1)()k a b k k πωϕωϕπ+++∈Z 剟?7、()sin()f x A x ωϕ=+在区间(,)a b 内有n 个零点(1)()(1)()k a k k k n b k n πωϕππωϕπ-+<⎧⇒∈⎨+-<++⎩Z ……．二、三角形范围与最值问题1、坐标法：把动点转为为轨迹方程2、几何法3、引入角度，将边转化为角的关系4、最值问题的求解，常用的方法有：（1）函数法；（2）导数法；（3）数形结合法；（4）基本不等式法．要根据已知条件灵活选择方法求解．【典型例题】例1．（2023ꞏ全国ꞏ高三专题练习）在ABC 中，7cos 25A =，ABC 的内切圆的面积为16π，则边BC 长度的最小值为（）A ．16B ．24C ．25D ．36例2．（2023ꞏ全国ꞏ高三专题练习）已知函数()sin()f x x ωϕ=+，其中0ω>，||,24ππϕ≤-为()f x的零点：且()4f x f π⎛⎫≤ ⎪⎝⎭恒成立，()f x 在,1224ππ⎛⎫- ⎪⎝⎭区间上有最小值无最大值，则ω的最大值是（） A ．11 B ．13C ．15D ．17例3．（2023ꞏ高一课时练习）如图，直角ABC ∆的斜边BC 长为2，30C ∠=︒，且点,B C 分别在x 轴，y 轴正半轴上滑动，点A 在线段BC 的右上方．设OA xOB yOC =+，（,x y ∈R ），记M OA OC =⋅，N x y =+，分别考查,M N 的所有运算结果，则A ．M 有最小值，N 有最大值B ．M 有最大值，N 有最小值C ．M 有最大值，N 有最大值D ．M 有最小值，N 有最小值例4．（2023ꞏ全国ꞏ高三专题练习）已知函数()sin cos f x a x b x cx =++图象上存在两条互相垂直的切线，且221a b +=，则a b c ++的最大值为（） A．B．CD例5．（2023ꞏ全国ꞏ高三专题练习）已知0m >，函数(2)ln(1),1,()πcos 3,π,4x x x m f x x m x -+-<≤⎧⎪=⎨⎛⎫+<≤ ⎪⎪⎝⎭⎩恰有3个零点，则m 的取值范围是（）A ．π5π3π,2,12124⎡⎫⎡⎫⎪⎪⎢⎢⎣⎭⎣⎭B ．π5π3π,2,12124⎡⎫⎡⎤⎪⎢⎢⎥⎣⎭⎣⎦C ．5π3π0,2,124⎛⎫⎡⎫⎪⎪⎢⎝⎭⎣⎭ D ．5π3π0,2,124⎛⎫⎡⎤ ⎪⎢⎥⎝⎭⎣⎦例6．（2023ꞏ全国ꞏ高三专题练习）已知函数()πcos (0)3f x x ωω⎛⎫=-> ⎪⎝⎭在ππ,64⎡⎤⎢⎥⎣⎦上单调递增，且当ππ,43x ⎡⎤∈⎢⎥⎣⎦时，()0f x ≥恒成立，则ω的取值范围为（）A ．522170,,232⎛⎤⎡⎤ ⎥⎢⎥⎝⎦⎣⎦B ．4170,8,32⎛⎤⎡⎤ ⎥⎢⎥⎝⎦⎣⎦C ．4280,8,33⎛⎤⎡⎤⎥⎢⎥⎝⎦⎣⎦D ．5220,,823⎛⎤⎡⎤ ⎥⎢⎥⎝⎦⎣⎦例7．（2023ꞏ全国ꞏ高三专题练习）在锐角ABC 中，角A ，B ，C 的对边分别为a ，b ，c ，ABC 的面积为S ，若222sin()SA C b a +=-，则1tan 3tan()A B A +-的取值范围为（）A ．3⎡⎫+∞⎪⎢⎣⎭B ．43⎤⎥⎣⎦ C ．43⎫⎪⎪⎝⎭D ．43⎫⎪⎪⎣⎭例8．（2023ꞏ上海ꞏ高三专题练习）在钝角ABC 中，,,a b c 分别是ABC 的内角,,A B C 所对的边，点G 是ABC 的重心，若AG BG ⊥，则cos C 的取值范围是（）A ．0,3⎛⎫⎪ ⎪⎝⎭B ．453⎡⎫⎪⎢⎪⎣⎭ C ．3⎛⎫⎪ ⎪⎝⎭D ．4,15⎡⎫⎪⎢⎣⎭例9．（2023ꞏ全国ꞏ高三专题练习）设锐角ABC 的内角,,A B C 所对的边分别为,,a b c ，若,3A a π==，则2b 2c bc ++的取值范围为（）A ．(1，9]B ．(3，9]C ．(5，9]D ．(7，9]例10．（2023ꞏ上海ꞏ高三专题练习）某公园有一个湖，如图所示，湖的边界是圆心为O 的圆，已知圆O 的半径为100米．为更好地服务游客，进一步提升公园亲水景观，公园拟搭建亲水木平台与亲水玻璃桥，设计弓形,,,MN NP PQ QM 为亲水木平台区域（四边形MNPQ 是矩形，A ，D 分别为,MN PQ 的中点，50OA OD ==米），亲水玻璃桥以点A 为一出入口，另两出入口B ，C 分别在平台区域,MQ NP 边界上（不含端点），且设计成2BAC π∠=，另一段玻璃桥F D E --满足//,,//,FD AC FD AC ED AB ED AB ==．(1)若计划在B ，F 间修建一休闲长廊该长廊的长度可否设计为70米？请说明理由；（附：1.732≈≈）(2)设玻璃桥造价为0.3万元/米，求亲水玻璃桥的造价的最小值．（玻璃桥总长为AB AC DE DF +++，宽度、连接处忽略不计）．例11．（2023ꞏ全国ꞏ高三专题练习）在ABC 中，角A ，B ，C 的对边分别是a ，b ，c ，满足πsin sin 3b A a B ⎛⎫=+ ⎪⎝⎭(1)设3a =，2c =，过B 作BD 垂直AC 于点D ，点E 为线段BD 的中点，求BE EA ⋅的值；(2)若ABC 为锐角三角形，2c =，求ABC 面积的取值范围．【过关测试】一、单选题1．（2023ꞏ全国ꞏ高三专题练习）已知,a b R ∈，设函数1()cos 2f x x =，2()cos f x a b x =-，若当12()()f x f x ≤对[,]()∈<x m n m n 恒成立时，n m -的最大值为3π2，则（） A．1a ≥ B．1a ≤ C．2≥b D．2≤b 2．（2023ꞏ全国ꞏ高三专题练习）ABC中，4AB ACB π=∠=，O 是ABC 外接圆圆心，是OC AB CA CB ⋅+⋅的最大值为（）A ．0B ．1C ．3D ．53．（2023ꞏ全国ꞏ高三专题练习）在锐角ABCcos cos ()sin sin A CA B C a c+=，且cos 2C C +=，则a b +的取值范围是（） A．(4⎤⎦B．(2,C ．(]0,4D ．(]2,44．（2023ꞏ全国ꞏ高三专题练习）设ω∈R ，函数()()22,0,6314,0,22sin x x f x g x x x x x πωωω⎧⎛⎫+≥ ⎪⎪⎪⎝⎭==⎨⎪++<⎪⎩．若()f x 在1,32π⎛⎫- ⎪⎝⎭上单调递增，且函数()f x 与()g x 的图象有三个交点，则ω的取值范围是（）A ．12,43⎛⎤ ⎝⎦B．233⎛⎤ ⎥ ⎝⎦C．14⎡⎢⎣⎭D ．4412,0,33⎡⎫⎡⎤-⎪⎢⎢⎥⎣⎭⎣⎦5．（2023秋ꞏ湖南长沙ꞏ高三长郡中学校考阶段练习）已知函数π()sin (0)3f x x ωω⎛⎫=+> ⎪⎝⎭在π,π3⎡⎤⎢⎥⎣⎦上恰有3个零点，则ω的取值范围是（） A ．81114,4,333⎡⎫⎛⎫⋃⎪ ⎪⎢⎣⎭⎝⎭B ．111417,4,333⎡⎫⎡⎫⋃⎪⎪⎢⎢⎣⎭⎣⎭C ．111417,5,333⎡⎫⎛⎫⋃⎪ ⎪⎢⎣⎭⎝⎭D ．141720,5,333⎡⎫⎡⎫⋃⎪⎪⎢⎢⎣⎭⎣⎭6．（2023ꞏ全国ꞏ高三专题练习）已知函数()sin 4f x x ωπ⎛⎫=+ ⎪⎝⎭(0)>ω在区间[0,]π上有且仅有4条对称轴，给出下列四个结论：①()f x 在区间(0,)π上有且仅有3个不同的零点； ②()f x 的最小正周期可能是2π；③ω的取值范围是131744⎡⎫⎪⎢⎣⎭，； ④()f x 在区间0,15π⎛⎫⎪⎝⎭上单调递增．其中所有正确结论的序号是（）A ．①④B ．②③C ．②④D ．②③④7．（2023ꞏ全国ꞏ高三专题练习）函数()sin 06y x πωω⎛⎫=-> ⎪⎝⎭在[]0,π有且仅有3个零点，则下列说法正确的是（）A ．在()0,π不存在1x ，2x 使得()()122f x f x -=B ．函数()f x 在()0,π仅有1个最大值点C ．函数()f x 在0,2π⎛⎫⎪⎝⎭上单调进增D ．实数ω的取值范围是1319,66⎡⎫⎪⎢⎣⎭8．（2023ꞏ上海ꞏ高三专题练习）在ABC 中，角A ，B ，C 的对边分别为a ，b ，c ，若cos cos sin sin()sin B C AA C bc C ⎛⎫++=⎪⎝⎭，3B π=，则a c +的取值范围是（）A ．⎝B ．32⎛ ⎝C ．2⎢⎣D ．32⎡⎢⎣二、多选题9．（2023秋ꞏ山东济南ꞏ高三统考期中）在ABC 中，内角,,A B C 所对的边分别为,,a b c ，且()()tan 1tan tan A B A B +-= ） A ．π6A =B ．若b c -=，则ABC 为直角三角形C ．若ABC 面积为1，则三条高乘积平方的最大值为D ．若D 为边BC 上一点，且1,:2:AD BD DC c b ==，则2b c +的最小值为710．（2023秋ꞏ江苏苏州ꞏ高三苏州中学校考阶段练习）已知函数()2sin 212cos xf x x=+，则下列说法中正确的是（）A ．()()f x f x π+=B ．()f xC ．()f x 在,22ππ⎛⎫- ⎪⎝⎭上单调递增D ．若函数()f x 在区间[)0,a 上恰有2022个极大值点，则a 的取值范围为60646067,33ππ⎛⎤⎥⎝⎦ 11．（2023ꞏ全国ꞏ高三专题练习）在ABC 中，角A 、B 、C 的对边分别为a 、b 、c ，面积为S ，有以下四个命题中正确的是（）A ．22S a bc +的最大值为12B ．当2a =，sin 2sin BC =时，ABC 不可能是直角三角形C ．当2a =，sin 2sin B C =，2A C =时，ABC 的周长为2+D ．当2a =，sin 2sin B C =，2A C =时，若O 为ABC 的内心，则AOB 12．（2023ꞏ全国ꞏ高三专题练习）在锐角ABC 中，角,,A B C 所对的边分别为,,a b c ，且2cos c b b A -=，则下列结论正确的有（）A ．2AB = B ．B 的取值范围为0,4π⎛⎫⎪⎝⎭C ．ab的取值范围为)2D ．112sin tan tan A B A -+的取值范围为⎫⎪⎪⎝⎭三、填空题13．（2023ꞏ全国ꞏ高三专题练习）已知函数()sin ,06f x x πωω⎛⎫=+> ⎪⎝⎭，若5412f f ππ⎛⎫⎛⎫= ⎪ ⎪⎝⎭⎝⎭且()f x 在区间5,412ππ⎛⎫⎪⎝⎭上有最小值无最大值，则ω=_______． 14．（2023ꞏ全国ꞏ高三专题练习）函数()()π3sin 0,2f x x ωϕωϕ⎛⎫=+>< ⎪⎝⎭，已知π33f ⎛⎫= ⎪⎝⎭且对于任意的x R ∈都有ππ066f x f x ⎛⎫⎛⎫-++--= ⎪ ⎪⎝⎭⎝⎭，若()f x 在5π2π,369⎛⎫ ⎪⎝⎭上单调，则ω的最大值为______.15．（2023ꞏ全国ꞏ高三专题练习）已知函数()sin()f x x ωϕ=+，其中0ω>，||2πϕ…，4π-为()f x 的零点，且()4f x f π⎛⎫⎪⎝⎭…恒成立，()f x 在区间,1224ππ⎡⎫-⎪⎢⎣⎭上有最小值无最大值，则ω的最大值是_______16．（2023ꞏ全国ꞏ高三对口高考）在ABC 中，)(),cos ,cos ,sin AB x x AC x x ==，则ABC 面积的最大值是____________17．（2023ꞏ高一课时练习）用I M 表示函数sin y x =在闭区间I 上的最大值．若正数a 满足[0,][,2]2a a a M M ≥，则a 的最大值为________．18．（2023ꞏ上海ꞏ高三专题练习）在ABC 中，角,,A B C 的对边分别为,,a b c ，已知2a =，cos cos 4b C c B -=，43C ππ≤≤，则tan A 的最大值为_______.19．（2023ꞏ全国ꞏ高三专题练习）在ABC 中，若120BAC ∠=︒，点D 为边BC 的中点，1AD =，则AB AC ⋅uu u r uuu r的最小值为______.20．（2023ꞏ全国ꞏ高三专题练习）△ABC 中，角A ，B ，C 所对的三边分别为a ，b ，c ，c ＝2b ，若△ABC 的面积为1，则BC 的最小值是________ ．21．（2023ꞏ全国ꞏ高三专题练习）已知0θ>，对任意*n ∈N ，总存在实数ϕ，使得cos()n θϕ+<θ的最小值是___ 22．（2023ꞏ上海ꞏ高三专题练习）已知函数()sin()f x x ωϕ=+，其中0ω>，0πϕ<< ，π()()4f x f ≤恒成立，且()y f x =在区间3π0,8⎛⎫ ⎪⎝⎭上恰有3个零点，则ω的取值范围是______________．23．（2023ꞏ全国ꞏ高三专题练习）已知锐角三角形ABC 的内角A ，B ，C 所对的边分别是a ，b ，c ，且A B >，若7sin 2cos sin 25C A B =+，则tan B 的取值范围为_______． 24．（2023ꞏ全国ꞏ高三专题练习）若函数()41sin 2cos 33f x x x a x =-+在(),-∞+∞内单调递增，则实数a 的取值范围是___________.25．（2023秋ꞏ湖南衡阳ꞏ高一衡阳市八中校考期末）设函数()()2sin 1(0)f x x ωϕω=+->，若对于任意实数ϕ，()f x 在区间π3π,44⎡⎤⎢⎥⎣⎦上至少有2个零点，至多有3个零点，则ω的取值范围是________．26．（2023ꞏ全国ꞏ高三专题练习）已知函数()()211(sin )sin 20,22f x x x R ωωωω=+->∈，若()f x 在区间(),2ππ内没有极值点，则ω的取值范围是___________.27．（2023秋ꞏ江苏苏州ꞏ高三苏州中学校考阶段练习）某小区有一个半径为r 米，圆心角是直角的扇形区域，现计划照图将其改造出一块矩形休闲运动场地，然后在区域I （区域ACD ），区域II （区域CBE ）内分别种上甲和乙两种花卉（如图），已知甲种花卉每平方米造价是a 元，乙种花卉每平方米造价是3a 元，设∠BOC =θ，中植花卉总造价记为()f θ，现某同学已正确求得：()()2f arg θθ=，则()g θ=___________；种植花卉总造价最小值为___________.28．（2023ꞏ全国ꞏ高三专题练习）已知函数()()2sin cos 0,06f x x a x a πωωω⎛⎫=++>> ⎪⎝⎭对任意12,x x R ∈都有()()12f x f x +≤若()f x 在[]0,π上的取值范围是3,⎡⎣，则实数ω的取值范围是__________．29．（2023ꞏ全国ꞏ高三专题练习）已知a ，b ，c 分别为锐角ABC 的三个内角A ，B ，C 的对边，若2a =，且2sin sin (sin sin )B A A C =+，则ABC 的周长的取值范围为__________． 30．（2023ꞏ全国ꞏ高三专题练习）在锐角ABC ∆中，2BC =，sin sin 2sin B C A +=，则中线AD长的取值范围是_______; 四、解答题31．（2023ꞏ全国ꞏ高三专题练习）已知函数()2sin 216f x x πω⎛⎫=++ ⎪⎝⎭.(1)若()()()12f x f x f x ≤≤，12min2x x π-=，求()f x 的对称中心；(2)已知05ω<<，函数()f x 图象向右平移6π个单位得到函数()g x 的图象，3x π=是()g x 的一个零点，若函数()g x 在[],m n （m ，n R ∈且m n <）上恰好有10个零点，求n m -的最小值；32．（2023ꞏ全国ꞏ模拟预测）在ABC 中，内角,,A B C 的对边分别为,,,sin cos 6a b c b A a B π⎛⎫=- ⎪⎝⎭．（1）求角B 的大小；（2）设点D 是AC 的中点，若BD =，求a c +的取值范围．参考答案【总结】一、三角函数()sin()f x A x ωϕ=+中ω的大小及取值范围 1、任意两条对称轴之间的距离为半周期的整数倍，即()2Tkk ∈Z ； 2、任意两个对称中心之间的距离为半周期的整数倍，即()2Tk k ∈Z ； 3、任意对称轴与对称中心之间的距离为14周期加半周期的整数倍，即()42T Tk k +∈Z ； 4、()sin()f x A x ωϕ=+在区间(,)a b 内单调2Tb a ⇒-…且()22k a b k k πππωϕωϕπ-+++∈Z 剟?5、()sin()f x A x ωϕ=+在区间(,)a b 内不单调(,)a b ⇒内至少有一条对称轴，2a kb πωϕπωϕ+++剟()k ∈Z6、()sin()f x A x ωϕ=+在区间(,)a b 内没有零点2Tb a ⇒-…且(1)()k a b k k πωϕωϕπ+++∈Z 剟?7、()sin()f x A x ωϕ=+在区间(,)a b 内有n 个零点(1)()(1)()k a k k k n b k n πωϕππωϕπ-+<⎧⇒∈⎨+-<++⎩Z ……．二、三角形范围与最值问题1、坐标法：把动点转为为轨迹方程2、几何法3、引入角度，将边转化为角的关系4、最值问题的求解，常用的方法有：（1）函数法；（2）导数法；（3）数形结合法；（4）基本不等式法．要根据已知条件灵活选择方法求解．【典型例题】例1．（2023ꞏ全国ꞏ高三专题练习）在ABC 中，7cos 25A =，ABC 的内切圆的面积为16π，则边BC 长度的最小值为（）A ．16B ．24C ．25D ．36【答案】A【答案解析】因为ABC 的内切圆的面积为16π，所以ABC 的内切圆半径为4．设ABC 内角A ，B ，C 所对的边分别为a ，b ，c ．因为7cos 25A =，所以24sin 25A =，所以24tan 7A =．因为1sin 2ABC S bc A ==△1()42a b c ++⨯，所以25()6bc a b c =++．设内切圆与边AC 切于点D ，由24tan 7A =可求得3tan 24A ==4AD ，则163AD =．又因为2b c a AD +-=，所以323b c a +=+．所以2532251626333bc a a ⎛⎫⎛⎫=+=+ ⎪ ⎪⎝⎭⎝⎭．又因为b c +≥323a +≥即23210016333a a ⎛⎫⎛⎫+≥+ ⎪ ⎪⎝⎭⎝⎭，整理得21264a a --0≥．因为0a >，所以16a ≥，当且仅当403b c ==时，a 取得最小值．故选：A ．例2．（2023ꞏ全国ꞏ高三专题练习）已知函数()sin()f x x ωϕ=+，其中0ω>，||,24ππϕ≤-为()f x 的零点：且()4f x f π⎛⎫≤ ⎪⎝⎭恒成立，()f x 在,1224ππ⎛⎫- ⎪⎝⎭区间上有最小值无最大值，则ω的最大值是（）A ．11B ．13C ．15D ．17【答案】C【答案解析】由题意，4x π=是()f x 的一条对称轴，所以14f π⎛⎫=± ⎪⎝⎭，即11,42k k Z ππωϕπ+=+∈①又04f π⎛⎫-= ⎪⎝⎭，所以22,4k k Z πωϕπ-+=∈②由①②，得()1221k k ω=-+，12,k k Z ∈又()f x 在,1224ππ⎛⎫- ⎪⎝⎭区间上有最小值无最大值，所以24128T πππ⎛⎫≥--= ⎪⎝⎭ 即28ππω≥，解得16ω≤，要求ω最大，结合选项，先检验15ω=当15ω=时，由①得1115,42k k Z ππϕπ⨯+=+∈，即1113,4k k Z πϕπ=-∈，又||2πϕ≤ 所以4πϕ=-，此时()sin 154f x x π⎛⎫=- ⎪⎝⎭，当,1224x ππ⎛⎫∈- ⎪⎝⎭时，3315,428x πππ⎛⎫-∈- ⎪⎝⎭，当1542x ππ-=-即60x π=-时，()f x 取最小值，无最大值，满足题意.故选：C例3．（2023ꞏ高一课时练习）如图，直角ABC ∆的斜边BC 长为2，30C ∠=︒，且点,B C 分别在x 轴，y 轴正半轴上滑动，点A 在线段BC 的右上方．设OA xOB yOC =+，（,x y ∈R ），记M OA OC =⋅，N x y =+，分别考查,M N 的所有运算结果，则A ．M 有最小值，N 有最大值B ．M 有最大值，N 有最小值C ．M 有最大值，N 有最大值D ．M 有最小值，N 有最小值【答案】B【答案解析】依题意30,2,90BCA BC A ∠==∠= ，所以1AC AB ==.设OCB α∠=，则30,090ABx αα∠=+<< ，所以()())30,sin 30Aαα++ ，()()2sin ,0,0,2cos B C αα，所以()()12cos sin 30sin 2302M OA OC ααα==+=++⋅ ，当23090,30αα+== 时，M 取得最大值为13122+=.OA xOB yOC =+ ，所以()()30sin 30,2sin 2cos x y αααα++==，所以()()30sin 302sin 2cos N x y αααα++=+=+12sin 2α=+，当290,45αα== 时，N 有最小值为1故选B. 例4．（2023ꞏ全国ꞏ高三专题练习）已知函数()sin cos f x a x b x cx =++图象上存在两条互相垂直的切线，且221a b +=，则a b c ++的最大值为（）A ．B ．C D 【答案】D【答案解析】由221a b +=，令sin ,cos a b θθ==，由()sin cos f x a x b x cx =++，得()cos sin sin cos cos sin f x a x b x c x x c θθ'=-+=-+()sin x c θ=-+，所以()11c f x c '-≤≤+由题意可知，存在12,x x ，使得12()()1f x f x ''=-，只需要21111c c c -+=-≥，即211c -≤-，所以20c ≤，0c =，πsin cos 4a b c a b θθθ⎛⎫++=+=+=+≤ ⎪⎝⎭所以a b c ++故选: D.例5．（2023ꞏ全国ꞏ高三专题练习）已知0m >，函数(2)ln(1),1,()πcos 3,π,4x x x m f x x m x -+-<≤⎧⎪=⎨⎛⎫+<≤ ⎪⎪⎝⎭⎩恰有3个零点，则m 的取值范围是（）A ．π5π3π,2,12124⎡⎫⎡⎫⎪⎪⎢⎢⎣⎭⎣⎭B ．π5π3π,2,12124⎡⎫⎡⎤⎪⎢⎢⎥⎣⎭⎣⎦C ．5π3π0,2,124⎛⎫⎡⎫ ⎪⎪⎢⎝⎭⎣⎭D ．5π3π0,2,124⎛⎫⎡⎤⎪⎢⎥⎝⎭⎣⎦【答案】A【答案解析】设()(2)ln(1)g x x x =-+，()cos 34h x x π⎛⎫+ ⎝=⎪⎭，求导()23ln(1)ln(1)111x g x x x x x -'=++=++-++ 由反比例函数及对数函数性质知()g x '在(]1,,0m m ->上单调递增，且102g ⎛⎫'< ⎪⎝⎭，()10g '>，故()g x '在1,12⎛⎫⎪⎝⎭内必有唯一零点0x ，当()01,x x ∈-时，()0g x '<，()g x 单调递减；当(]0,x x m ∈时，()0g x '>，()g x 单调递增；令()0g x =，解得0x =或2，可作出函数()g x 的图像，令()0h x =，即3,42x k k Z πππ+=+∈，在(]0,π之间解得12x π=或512π或34π，作出图像如下图数形结合可得：π5π3π,2,12124⎡⎫⎡⎫⎪⎪⎢⎢⎣⎭⎣⎭ ，故选：A例6．（2023ꞏ全国ꞏ高三专题练习）已知函数()πcos (0)3f x x ωω⎛⎫=-> ⎪⎝⎭在ππ,64⎡⎤⎢⎣⎦上单调递增，且当ππ,43x ⎡⎤∈⎢⎥⎣⎦时，()0f x ≥恒成立，则ω的取值范围为（）A ．522170,,232⎛⎤⎡⎤ ⎥⎢⎥⎝⎦⎣⎦B ．4170,8,32⎛⎤⎡⎤ ⎥⎢⎥⎝⎦⎣⎦C ．4280,8,33⎛⎤⎡⎤⎥⎢⎥⎝⎦⎣⎦D ．5220,,823⎛⎤⎡⎤ ⎥⎢⎥⎝⎦⎣⎦【答案】B【答案解析】由已知，函数()πcos (0)3f x x ωω⎛⎫=-> ⎪⎝⎭在ππ,64⎡⎤⎢⎥⎣⎦上单调递增，所以()111π2ππ2πZ 3k x k k ω-≤-≤∈，解得：()1112π2π2ππZ 33k k x k ωωωω-≤≤+∈，由于()111Z π,π,642π2π2ππ33k k k ωωωω⎡⎤⎡⎤⊆⎢⎢⎥⎣⎦⎣⎦-+∈，所以112ππ2π632πππ43k k ωωωω⎧≥-⎪⎪⎨⎪≤+⎪⎩，解得：()11141248Z 3k k k ω-≤≤+∈① 又因为函数()πcos (0)3f x x ωω⎛⎫=-> ⎪⎝⎭在ππ,43x ⎡⎤∈⎢⎥⎣⎦上()0f x ≥恒成立，所以()222πππ2π2π+Z 232k x k k ω-≤-≤∈，解得：()2222π2ππ5πZ 66k k x k ωωωω-≤≤+∈，由于()2222π2ππ5π,Z 6π,46π3k k k ωωωω-+⎡⎤⎡⎤⊆⎢⎥⎢⎥⎣⎦⎣∈⎦，所以222πππ462ππ5π36k k ωωωω⎧≥-⎪⎪⎨⎪≤+⎪⎩，解得：()2222586Z 32k k k ω-≤≤+∈② 又因为0ω>，当120k k ==时，由①②可知：04432532ωωω⎧⎪>⎪⎪-≤≤⎨⎪⎪-≤≤⎪⎩，解得403ω⎛⎤∈ ⎥⎝⎦，；当121k k ==时，由①②可知：02883221732ωωω⎧⎪>⎪⎪≤≤⎨⎪⎪≤≤⎪⎩，解得1782ω⎡⎤∈⎢⎥⎣⎦，.所以ω的取值范围为4170,8,32⎛⎤⎡⎤⎥⎢⎥⎝⎦⎣⎦.故选：B.例7．（2023ꞏ全国ꞏ高三专题练习）在锐角ABC 中，角A ，B ，C 的对边分别为a ，b ，c ，ABC 的面积为S ，若222sin()SA C b a +=-，则1tan 3tan()A B A +-的取值范围为（）A．3⎡⎫+∞⎪⎢⎣⎭B．433⎡⎤⎢⎥⎣⎦ C．4,33⎛⎫⎪ ⎪⎝⎭D．4,33⎡⎫⎪⎢⎪⎣⎭【答案】C【答案解析】在ABC 中，1sin()sin ,sin 2A CB S ac B +==，故题干条件可化为22b a ac -=，由余弦定理得2222cos b a c ac B =+-，故2cos c a B a =+，又由正弦定理化简得：sin 2sin cos sin sin cos cos sin C A B A A B A B =+=+，整理得sin()sin B A A -=，故B A A -=或B A A -=π-（舍去），得2B A =ABC 为锐角三角形，故02022032A A A ππππ⎧<<⎪⎪⎪<<⎨⎪⎪<-<⎪⎩，解得64A ππ<<tan 1A <<114tan tan (,3tan()3tan 33A AB A A +=+∈- 故选：C例8．（2023ꞏ上海ꞏ高三专题练习）在钝角ABC 中，,,a b c 分别是ABC 的内角,,A B C 所对的边，点G 是ABC 的重心，若AG BG ⊥，则cos C 的取值范围是（）A．⎛ ⎝⎭ B．45⎡⎢⎣⎭ C．⎫⎪⎪⎝⎭D ．4,15⎡⎫⎪⎢⎣⎭【答案】C【答案解析】延长CG 交AB 于D ，如下图所示：G 为ABC 的重心，D ∴为AB 中点且3CD DG =，AG BG ⊥ ，12DG AB ∴=，3322CD AB c ∴==；在ADC △中，2222222225522cos 3232c bAD CD AC c b ADC AD CD c c -+--∠===⋅；在BDC 中，2222222225522cos 3232c a BD CD BC c a BDC BD CD c c -+--∠===⋅； BDC ADC π∠+∠= ，cos cos BDC ADC ∴∠=-∠，即222222525233c a c b c c--=-，整理可得：22225a b c c +=>，C ∴为锐角；设A 为钝角，则222b c a +<，222a c b +>，a b >，2222222255a ba b a b b a ⎧+>+⎪⎪∴⎨+⎪<+⎪⎩，22221115511155b b a a b b a a ⎧⎛⎫⎛⎫++<⎪ ⎪ ⎪⎪⎝⎭⎝⎭∴⎨⎛⎫⎛⎫⎪<++ ⎪ ⎪⎪⎝⎭⎝⎭⎩，解得：223b a ⎛⎫< ⎪⎝⎭， 0a b >>，03b a ∴<<，由余弦定理得：22222222cos 255533a b c a b a b C ab ab b a ⎛⎫+-+⎛⎫==⋅=+>⨯+= ⎪ ⎝⎭⎝，又C为锐角，cos 1C <<，即cos C的取值范围为3⎛⎫ ⎪ ⎪⎝⎭. 故选：C.例9．（2023ꞏ全国ꞏ高三专题练习）设锐角ABC 的内角,,A B C 所对的边分别为,,a b c，若,3A a π==，则2b 2c bc ++的取值范围为（）A ．(1，9]B ．(3，9]C ．(5，9]D ．(7，9]【答案】D【答案解析】因为,3A a π==，由正弦定理可得22sin sin sin 3ab cAB B π====⎛⎫-⎪⎝⎭，则有22sin ,2sin 3b B c B π⎛⎫==- ⎪⎝⎭，由ABC 的内角,,A B C 为锐角，可得0,220,32B B πππ⎧<<⎪⎪⎨⎪<-<⎪⎩，512sin 2124sin 2462666266B B B B πππππππ⎛⎫⎛⎫∴<<⇒<-<⇒<-≤⇒<-≤ ⎪ ⎪⎝⎭⎝⎭，由余弦定理可得222222cos 3,a b c bc A b c bc =+-⇒=+- 因此有2223b c bc bc ++=+28sin sin 33B B π⎛⎫=-+ ⎪⎝⎭2cos 4sin 3B B B =++22cos 25B B =-+(]54sin 27,96B π⎛⎫=+-∈ ⎪⎝⎭故选：D.例10．（2023ꞏ上海ꞏ高三专题练习）某公园有一个湖，如图所示，湖的边界是圆心为O 的圆，已知圆O 的半径为100米．为更好地服务游客，进一步提升公园亲水景观，公园拟搭建亲水木平台与亲水玻璃桥，设计弓形,,,MN NP PQ QM 为亲水木平台区域（四边形MNPQ 是矩形，A ，D 分别为,MN PQ 的中点，50OA OD ==米），亲水玻璃桥以点A 为一出入口，另两出入口B ，C 分别在平台区域,MQ NP 边界上（不含端点），且设计成2BAC π∠=，另一段玻璃桥F D E --满足//,,//,FD AC FD AC ED AB ED AB ==．(1)若计划在B ，F 间修建一休闲长廊该长廊的长度可否设计为70米？请说明理由；（附：1.732≈≈）(2)设玻璃桥造价为0.3万元/米，求亲水玻璃桥的造价的最小值．（玻璃桥总长为AB AC DE DF +++，宽度、连接处忽略不计）．【答案解析】（1）由题意，50,100OA OM ==，则100,2MQ AM BAC π==∠=，设,2MAB NAC πθαθ∠=∠==-．若C ，P重合，1tan tan tan 2αθα=====75MB =，∴75tan tan MB MB AM θθθ<<<<=⋅=，tan NC AN α=⋅=而100100MF CP NC ==-=∴1tan 1001)tan BF MB MF θθ⎫=-=+-≥⎪⎭，当tan 1θ=（符合题意）时取等号，又1)70->， ∴可以修建70米长廊．（2）cos cos AM AN AB AC θα====cos )cos sin sin cos AB AC θθθθθθ++=+=．设sin cos 4t πθθθ⎛⎫=+=+ ⎪⎝⎭，则212sin cos t θθ=+，即21sin cos 2t θθ-=．AB AC t t+==-1）知tan 2θ<<，而132<<<<θ∃使42ππθ+=且3444πππθ<+<，即112t t t <≤<-≤，∴AB AC t t+=≥-4t πθ==时取等号．由题意，AB AC DE DF +=+，则玻璃桥总长的最小值为米，∴铺设好亲水玻璃桥，最少需0.3=例11．（2023ꞏ全国ꞏ高三专题练习）在ABC 中，角A ，B ，C 的对边分别是a ，b ，c ，满足πsin sin 3b A a B ⎛⎫=+ ⎪⎝⎭(1)设3a =，2c =，过B 作BD 垂直AC 于点D ，点E 为线段BD 的中点，求BE EA ⋅的值；(2)若ABC 为锐角三角形，2c =，求ABC 面积的取值范围．【答案解析】(1)πsin sin 3b A a B ⎛⎫=+ ⎪⎝⎭，由正弦定理得：π1sin sin sin sin sin sin sin cos 322B A A B A B A B ⎛⎫=+=+ ⎪⎝⎭，所以1sin sin cos 02A B A B =，因为()0,πA ∈，所以sin 0A ≠，所以1sin 02B B =，即tan B =因为()0,πB ∈，所以π3B =，因为3a =，2c =，由余弦定理得：2222cos 9467b a c ac B =+-=+-=，因为0b >，所以b =，其中11sin 3222ABC S ac B ==⨯⨯=△，所以2ABC S BD AC === 因为点E 为线段BD的中点，所以BE = 由题意得：EA ED DA BE DA =+=+，所以()227028BE EA BE BE DA BE ⋅=⋅+=+= . (2)由（1）知：π3B =，又2c =，由正弦定理得：2πsin sin sin 3a cA CA ==⎛⎫+ ⎪⎝⎭，所以2sin πsin 3A a A ===⎛⎫+ ⎪⎝⎭，因为ABC 为锐角三角形，所以π0,22ππ0,32A C A ⎧⎛⎫∈ ⎪⎪⎪⎝⎭⎨⎛⎫⎪=-∈ ⎪⎪⎝⎭⎩，解得：ππ,62A ⎛⎫∈ ⎪⎝⎭，则tan A ⎫∈+∞⎪⎪⎝⎭()0,3，()11,4tan A +∈，故()1,4a =，ABC面积为1sin ,222S ac B a ⎛==∈ ⎝ 故ABC面积的取值范围是2⎛ ⎝.【过关测试】一、单选题1．（2023ꞏ全国ꞏ高三专题练习）已知,a b R ∈，设函数1()cos 2f x x =，2()cos f x a b x =-，若当12()()f x f x ≤对[,]()∈<x m n m n 恒成立时，n m -的最大值为3π2，则（） A．1a ≥ B ．1a C ．2≥b D ．2≤b 【答案】A【答案解析】设[]cos ,x t x m n ∈=，，因为n m -的最大值为3ππ22T>=，所以[,]x m n ∈时，cos t x =必取到最值，当3π2n m -=时，根据余弦函数对称性得cos 12π22m n m Z nk k ++=⇒=∈,，此时3π3πcos cos(cos(2π)cos 22442m n n mm k +-=-=-==-3π3πcos cos(cos(2π)cos 22442m n n m n k +-=+=+==-或者cos1π+2π22m n m n Z k k ++=-⇒=∈,，此时3π3πcos cos(cos(2π+π)cos 22442m n n m m k +-=-=-=-=3π3πcos cos(cos(2π+π)cos 22442m n n m n k +-=+=+=-=由()2212()()2cos 1cos 2cos cos 10f x f x x a b x x b x a ≤⇒-≤-⇒+-+≤，设[]cos ,x t x m n ∈=，时 ()2210t bt a +-+≤对应解为12t t t ≤≤，由上分析可知当1t =，21t ≥或11t ≤-，2t =n m -的最大值为3π2，所以122t t ≤-，即122a +-≤，所以1a ≥.12122b t t -=+≥-或12122b t t -=+≤-+，即2b ≤或2≥-b 故选：A.2．（2023ꞏ全国ꞏ高三专题练习）ABC 中，4AB ACB π=∠=，O 是ABC 外接圆圆心，是OC AB CA CB ⋅+⋅的最大值为（）A ．0B ．1C ．3D ．5【答案】C【答案解析】过点O 作,OD AC OE BC ⊥⊥，垂足分别为D ，E ，如图，因O 是ABC 外接圆圆心，则D ，E 分别为AC ，BC 的中点，在ABC 中，AB CB CA =-，则222||||||2AB CA CB CA CB =+-⋅ ，即22||||22CA CB CA CB +-⋅=，21|cos |2CO CA CO CA OCA CD CA CA ⋅=∠=⋅=，同理21||2CO CB CB ⋅= ，因此，()OC AB CA CB OC CB CA CA CB CO CA CO CB CA CB ⋅+⋅=⋅-+⋅=⋅-⋅+⋅ 2222211||||2||||||1222CA CB CA CB CA +-=-+=-，由正弦定理得：||sin ||2sin 2sin sin 4AB B BCA B ACB π===≤∠ ，当且仅当2B π=时取“=”，所以OC AB CA CB ⋅+⋅的最大值为3. 故选：C3．（2023ꞏ全国ꞏ高三专题练习）在锐角ABCcos cos ()sin sin A CA B C a c+=，且cos 2C C +=，则a b +的取值范围是（） A．(4⎤⎦B．(2,C ．(]0,4D ．(]2,4【答案】Acos 2sin()26C C C π+=+=，得262C k πππ+=+，Z k ∈，(0,)2C π∈ ，3C π∴=．由题cos cos A C a c +=cos cos 2b A Cb a ca +==，故cos cos sin sin 2sin A C bA C A+=，即sin cos sin sin cos 2b C A C A C ⋅+⋅==故()sin sin A C B +==即sin b B =由正弦定理有sin sin sin a b c A B C ===，故a A =，b B =，又锐角ABC ，且3C π=，(0,)2A π∴∈，2(0,)32B A ππ=-∈，解得(6A π∈，2π，2sin )sin()]3a b A B A A π∴+=++-1sin )4sin(26A A A A π+=+， (6A π∈ ，2π，(63A ππ∴+∈，2)3π，sin()6A π+∈1]， a b ∴+的取值范围为(4⎤⎦．故选：A ．4．（2023ꞏ全国ꞏ高三专题练习）设ω∈R ，函数()()22,0,6314,0,22sin x x f x g x x x x x πωωω⎧⎛⎫+≥ ⎪⎪⎪⎝⎭==⎨⎪++<⎪⎩．若()f x 在1,32π⎛⎫- ⎪⎝⎭上单调递增，且函数()f x 与()g x 的图象有三个交点，则ω的取值范围是（）A ．12,43⎛⎤ ⎝⎦B．23⎤⎥⎝⎦C．143⎡⎫⎪⎢⎣⎭D ．4412,0,33⎡⎫⎡⎤-⎪⎢⎢⎥⎣⎭⎣⎦【答案】B【答案解析】当0,2x π⎡⎫∈⎪⎢⎣⎭时，,6626x πππωπω⎡⎫+∈+⎪⎢⎣⎭，因为()f x 在1,32π⎛⎫- ⎪⎝⎭上单调递增，所以262413312sin 62πωππωπ⎧+≤⎪⎪⎪-≤-⎨⎪⎪≥⎪⎩，解得1243ω≤≤，又因函数()f x 与()g x 的图象有三个交点，所以在(),0x ∈-∞上函数()f x 与()g x 的图象有两个交点，即方程231422x x x ωω++=在(),0x ∈-∞上有两个不同的实数根，即方程23610x x ω++=在(),0x ∈-∞上有两个不同的实数根，所以22Δ3612003060102ωωω⎧⎪=->⎪-<⎨⎪⎪⨯+⨯+>⎩，解得3ω>，当233ω⎛⎤∈ ⎥ ⎝⎦时，当0x ≥时，令()()2sin 6f x g x x x πωω⎛⎫-=+- ⎪⎝⎭，由()()10f x g x -=>，当562x ππω+=时，73x πω=，此时，()()7203f xg x π-=-<，结合图象，所以0x ≥时，函数()f x 与()g x 的图象只有一个交点，综上所述，233ω⎛⎤∈ ⎥ ⎝⎦. 故选：B.5．（2023秋ꞏ湖南长沙ꞏ高三长郡中学校考阶段练习）已知函数π()sin (0)3f x x ωω⎛⎫=+> ⎪⎝⎭在π,π3⎡⎤⎢⎥⎣⎦上恰有3个零点，则ω的取值范围是（） A ．81114,4,333⎡⎫⎛⎫⋃⎪ ⎪⎢⎣⎭⎝⎭B ．111417,4,333⎡⎫⎡⎫⋃⎪⎪⎢⎢⎣⎭⎣⎭C ．111417,5,333⎡⎫⎛⎫⋃⎪ ⎪⎢⎣⎭⎝⎭D ．141720,5,333⎡⎫⎡⎫⋃⎪⎪⎢⎢⎣⎭⎣⎭【答案】C【答案解析】π,π3x ⎡⎤∈⎢⎥⎣⎦，ππππ,π3333x ωωω⎡⎤+∈++⎢⎥⎣⎦，其中2ππ4ππ3ωω≤-<，解得：36ω≤<，则ππ4π333ω+≥，要想保证函数在π,π3⎡⎤⎢⎥⎣⎦恰有三个零点，满足①1111πππ+2π2π+2π33π4π+2π<π5π+2π3k k k k ωω⎧≤+<⎪⎪⎨⎪+≤⎪⎩，1k Z ∈，令10k =，解得：1114,33ω⎡⎫∈⎪⎢⎣⎭；或要满足②2222ππ2ππ+2π33π2π+3π<π2π+4π3k k k k ωω⎧≤+<⎪⎪⎨⎪+≤⎪⎩，2k Z ∈，令21k =，解得：175,3ω⎛⎫∈ ⎪⎝⎭；经检验，满足题意，其他情况均不满足36ω≤<条件，综上：ω的取值范围是111417,5,333⎡⎫⎛⎫⋃⎪ ⎪⎢⎣⎭⎝⎭.故选：C6．（2023ꞏ全国ꞏ高三专题练习）已知函数()sin 4f x x ωπ⎛⎫=+ ⎪⎝⎭(0)>ω在区间[0,]π上有且仅有4条对称轴，给出下列四个结论：①()f x 在区间(0,)π上有且仅有3个不同的零点； ②()f x 的最小正周期可能是2π；③ω的取值范围是131744⎡⎫⎪⎢⎣⎭，； ④()f x 在区间0,15π⎛⎫⎪⎝⎭上单调递增．其中所有正确结论的序号是（） A ．①④B ．②③C ．②④D ．②③④【答案】B【答案解析】由函数()sin 4f x x ωπ⎛⎫=+ ⎪⎝⎭(0)>ω，令,42x k k Z ππωπ+=+∈，则()14,4k x k Zπω+=∈函数()f x 在区间[0,]π上有且仅有4条对称轴，即()1404k ππω+≤≤有4个整数k 符合，由()1404k ππω+≤≤，得140101444k k ωω+≤≤⇒≤+≤，则0,1,2,3k =，即1434144ω+⨯≤<+⨯，131744ω∴≤<，故③正确；对于①，(0,)x π∈ ，,444x ωωππππ⎡⎫∴+∈+⎪⎢⎣⎭，79,422ππωππ⎛⎫∴+∈ ⎪⎝⎭当,442x ωππ7π⎡⎫+∈⎪⎢⎣⎭时，()f x 在区间(0,)π上有且仅有3个不同的零点；当,442x ωππ9π⎡⎫+∈⎪⎢⎣⎭时，()f x 在区间(0,)π上有且仅有4个不同的零点；故①错误；对于②，周期2T πω=，由131744ω≤<，则4141713ω<≤，881713T ππ∴<≤，又88,21713πππ⎛⎤∈ ⎥⎝⎦，所以()f x 的最小正周期可能是2π，故②正确；对于④，015x π⎛⎫∈ ⎪⎝⎭Q ,，44154x ωωππππ⎛⎫∴+∈+ ⎪⎝⎭,，又131744ω⎡⎫∈⎪⎢⎣⎭，，78,1541515ωππππ⎛⎫∴+∈ ⎪⎝⎭ 又8152ππ>，所以()f x 在区间0,15π⎛⎫⎪⎝⎭上不一定单调递增，故④错误．故正确结论的序号是：②③ 故选：B7．（2023ꞏ全国ꞏ高三专题练习）函数()sin 06y x πωω⎛⎫=-> ⎪⎝⎭在[]0,π有且仅有3个零点，则下列说法正确的是（）A ．在()0,π不存在1x ，2x 使得()()122f x f x -=B ．函数()f x 在()0,π仅有1个最大值点C ．函数()f x 在0,2π⎛⎫⎪⎝⎭上单调进增D ．实数ω的取值范围是1319,66⎡⎫⎪⎢⎣⎭【答案】D【答案解析】对于A,()f x 在[]0,π上有且仅有3个零点，则函数的最小正周期T π< ，所以在[]0,π上存在12,x x ，且12()1,()1f x f x ==- ，使得()()122f x f x -=，故A 错误；由图象可知，函数在()0,π可能有两个最大值，故B 错误; 对于选项D,令,6x k k Z πωπ-=∈ ，则函数的零点为1(6x k k Z ππω=+∈ ,所以函数在y 轴右侧的四个零点分别是：71319,,,6666ππππωωωω，函数()sin 06y x πωω⎛⎫=-> ⎪⎝⎭在[]0,π有且仅有3个零点，所以136196ππωππω⎧≤⎪⎪⎨⎪>⎪⎩ ，解得1319[,66ω∈ ，故D 正确；由对选项D 的分析可知，ω的最小值为136，当02x π<< 时，11(,)6612x πππω-∈-，但11(,)612ππ-不是0,2π⎛⎫⎪⎝⎭的子集，所以函数()f x 在0,2π⎛⎫⎪⎝⎭上不是单调进增的，故C 错，故选：D.8．（2023ꞏ上海ꞏ高三专题练习）在ABC 中，角A ，B ，C 的对边分别为a ，b ，c ，若cos cos sin sin()sin B C A A C bc C ⎛⎫++=⎪⎝⎭，3B π=，则a c +的取值范围是（） A．2⎝ B．32⎛ ⎝C．2⎢⎣D．32⎡⎢⎣【答案】A【答案解析】由题知cos cos sin sin()sin B C AA C bc C ⎛⎫++=⎪⎝⎭，3B π= ∴cos cos sin sin sin B C AB b cC ⎛⎫+= ⎪⎝⎭即cos cos 3sin B C Ab c C+=由正弦定理化简得∴cos cos c B b C ⋅+⋅==∴sin sin cos cos sin 3A C B C B +=∴sin()sin B C A +==∴2b =3B π=∴1sin sin sin a b cA B C===∴23sin sin sin sin()sin 326a c A C A A A A A ππ+=+=+-==+203A π<<∴5666A πππ<+<∴)26A π<+≤a c <+≤故选：A . 二、多选题9．（2023秋ꞏ山东济南ꞏ高三统考期中）在ABC 中，内角,,A B C 所对的边分别为,,a b c ，且()()tan 1tan tan A B A B +-= ） A ．π6A =B ．若b c -=，则ABC 为直角三角形C ．若ABC 面积为1，则三条高乘积平方的最大值为D ．若D 为边BC 上一点，且1,:2:AD BD DC c b ==，则2b c +的最小值为7【答案】BCD【答案解析】对于A ，因为()()tan 1tan tan A B A B +-=tan tan A B +=，()sin cos tan tan C A B A B =+()sin sin cos cos sin sin sin cos sin sin cos cos cos cos A B A B A B CA B A A A B A A++=⋅=⋅=⋅，cos sin sin C A A C =，因为0πC <<，所以sin 0C >，故tan A = 又0πA <<，所以π3A =，故A 错误；对于B ，由余弦定理得222222cos a b c bc A b c bc =+-=+-，因为3b c a -=，即3b a c =+，代入上式得222a c c c c ⎫=+⎫⎪⎪⎝+-+⎪⎭⎭⎪⎝，整理得22320c a +-=，解得a =或2a c =-（舍去），则2b c =，所以222b a c =+，故B 正确；对于C ，设,,AB AC BC 边上的高分别是,,CE BF AD ，则由三角形面积公式易得222,,AD BF CE a b c ===，则()228AD BF CE abc ⎛⎫⨯⨯= ⎪⎝⎭，因为111a b c ++≥111a b c ==，即a b c ==时，等号成立，此时21sin 12S bc A ===，得2b =所以()228AD BF CE abc ⎛⎫⨯⨯=≤ ⎪⎝⎭C 正确；对于D ，因为:2:BD DC c b =，所以22c AD AB AB BC b c BD =+=++()22222c b c AB AC AB AB AC b c b c b c=+-=++++ ，可得22222224212cos 60(2)(2)(2)b c bc c b cb b c b c b c ︒=+++++，整理得()22227b c b c +=，故12c b +=所以()1222225b c b c b c c b c b ⎫⎫+=++=++⎪⎪⎭⎭57⎛⎫≥=⎪⎪⎭，当且仅当22b c c b =且12c b +=，即7b c ==时，等号成立，所以2b c +≥2b c +D 正确. 故选：BCD.10．（2023秋ꞏ江苏苏州ꞏ高三苏州中学校考阶段练习）已知函数()2sin 212cos xf x x=+，则下列说法中正确的是（） A ．()()f x f x π+=B ．()f xC ．()f x 在,22ππ⎛⎫- ⎪⎝⎭上单调递增D ．若函数()f x 在区间[)0,a 上恰有2022个极大值点，则a 的取值范围为60646067,33ππ⎛⎤⎥⎝⎦ 【答案】ABD【答案解析】()2sin 2sin 2sin 21cos 212cos 2cos 2122xx xf x x xx ===+++⎛⎫+ ⎪⎝⎭， A 选项：()()()()sin 22sin 22cos 222cos 2x xf x f x x xπππ++===+++，A 选项正确；B 选项：设()sin 22cos 2xf x t x==+，则()sin 2cos 222x t x t x ϕ-==+≤解得213t ≤，t ≤≤，即max t =，即()f xB 选项正确；C 选项：因为022f f ππ⎛⎫⎛⎫-== ⎪ ⎪⎝⎭⎝⎭，所以()f x 在,22ππ⎛⎫- ⎪⎝⎭上不单调，C 选项错误；D 选项：()()()()()222cos 22cos 2sin 22sin 24cos 222cos 22cos 2x x x x x f x x x +--+'==++，令()0f x '=，解得1cos 22x =-，即3x k ππ=+或23x k ππ=+，Z k ∈，当2,33x k k ππππ⎛⎫∈++ ⎪⎝⎭，Z k ∈时，()0f x '<，函数单调递减，当当24,33x k k ππππ⎛⎫∈++⎪⎝⎭，Z k ∈时，()0f x ¢>，函数单调递增，所以函数()f x 的极大值点为3π，43π，L ，()13n ππ+-，又函数()f x 在区间[)0,a 上恰有2022个极大值点，则2021,202233a ππππ⎛⎤∈++ ⎥⎝⎦，即60646067,33a ππ⎛⎤∈ ⎥⎝⎦，D 选项正确；故选：ABD.11．（2023ꞏ全国ꞏ高三专题练习）在ABC 中，角A 、B 、C 的对边分别为a 、b 、c ，面积为S ，有以下四个命题中正确的是（） A ．22S a bc +B ．当2a =，sin 2sin BC =时，ABC 不可能是直角三角形 C ．当2a =，sin 2sin B C =，2A C =时，ABC的周长为2+D ．当2a =，sin 2sin B C =，2A C =时，若O 为ABC 的内心，则AOB的面积为13【答案】ACD【答案解析】对于选项A ：。

高三总复习同步练习(三角函数二)

高三复习数学同步练习 ——三角函数（二）班级：姓名：总分：命题人：邓少奎一、选择题1．设函数f (x )＝sin ⎝⎛⎭⎫2x －π2，x ∈R ，则f (x )是( ) A ．最小正周期为π的奇函数 B ．最小正周期为π的偶函数 C ．最小正周期为π2的奇函数 D ．最小正周期为π2的偶函数2．(2011·天津高考)已知函数f (x )＝2sin(ωx ＋φ)，x ∈R ，其中ω＞0，－π＜φ≤π.若f (x )的最小正周期为6π，且当x ＝π2时，f (x )取得最大值，则( )A ．f (x )在区间[－2π，0]上是增函数B ．f (x )在区间[－3π，－π]上是增函数C ．f (x )在区间[3π，5π]上是减函数D ．f (x )在区间[4π，6π]上是减函数3．将函数y ＝sin 2x 的图象向左平移π12个单位，得到函数y ＝sin(2x ＋φ)⎝⎛⎭⎫0<φ<π2的图象，则φ＝( )A.π3B.π4C.π6D.π124．已知函数f (x )＝sin ⎝⎛⎭⎫ωx ＋π3(ω>0)的最小正周期为π，则该函数的图象( )A ．关于直线x ＝π3对称B ．关于点⎝⎛⎭⎫π3，0对称C ．关于直线x ＝－π6对称D ．关于点⎝⎛⎭⎫π6，0对称5．电流强度I (安)随时间t (秒)变化的函数I ＝A sin(ωt ＋φ)(A >0，ω>0,0<φ<π2)的图象如图所示，则当t ＝1100秒时，电流强度是( )A ．－5安B ．5安C ．53安D ．10安 6．函数y ＝2sin x －1的定义域为( )A.⎣⎡⎦⎤π6，5π6B.⎣⎡⎦⎤2k π＋π6，2k π＋5π6(k ∈Z)C.⎝⎛⎭⎫2k π＋π6，2k π＋5π6(k ∈Z)D.⎣⎡⎦⎤k π＋π6，k π＋5π6(k ∈Z) 7．下列区间是函数y ＝2|cos x |的单调递减区间的是( )A ．(0，π) B.⎝⎛⎭⎫－π2，0 C.⎝⎛⎭⎫3π22π D.⎝⎛⎭⎫－π，－π2 8．如图所示，点P 是函数y ＝2sin(ωx ＋φ)(x ∈R ，ω>0)的图象的最高点，M 、N 是图象与x 轴的交点，若PM ·PN＝0，则ω＝( )A ．8 B.π8 C.π4 D ．4二、填空题9．定义在R 上的函数f (x )既是偶函数又是周期函数，若f (x )的最小正周期是π，且当x ∈[0，π2]时，f (x )＝sin x ，则f ⎝⎛⎭⎫5π3的值为________．10．给出下列六种图象变换方法：(1)图象上所有点的纵坐标不变，横坐标缩短到原来的12；(2)图象上所有点的纵坐标不变，横坐标伸长到原来的2倍；(3)图象向右平移π3个单位；(4)图象向左平移π3个单位；(5)图象向右平移2π3个单位；(6)图象向左平移2π3个单位．请用上述变换中的两种变换，将函数y ＝sin x 的图象变换到函数y ＝sin ⎝⎛⎭⎫x 2＋π3的图象，那么这两种变换正确的标号是________(要求按变换先后顺序填上一种你认为正确的标号即可)．三、解答题11．设函数f (x )＝sin(2x ＋φ)(－π<φ<0)，y ＝f (x )的图象的一条对称轴是直线x ＝π8.(1)求φ；(2)求函数y ＝f (x )的单调递增区间．12．已知函数y ＝3sin ⎝⎛⎭⎫12x －π4，(1)用五点法作出函数的图象； (2)说明此图象是由y ＝sin x 的图象经过怎么样的变化得到的；(3)求此函数的振幅、周期和初相；(4)求此函数图象的对称轴方程、对称中心．答案1.解析：∵f (x )＝sin ⎝⎛⎭⎫2x －π2＝－cos 2x ，∴T ＝2π2，且f (x )为偶函数．答案：B2.解析：∵f (x )的最小正周期为6π，∴ω＝13，∵当x ＝π2时，f (x )有最大值，∴13×π2＋φ＝π2＋2k π(k ∈Z)，φ＝π3＋2k π，∵－π＜φ≤π，∴φ＝π3. ∴f (x )＝2sin ⎝⎛⎭⎫x 3＋π3，由此函数图象易得，在区间[－2π，0]上是增函数，而在区间[－3π，－π]或[3π，5π]上均没单调性，在区间[4π，6π]上是单调增函数．答案：A3.解析：将函数y ＝sin 2x 的图象向左平移π12个单位，得到函数y ＝sin 2⎝⎛⎭⎫x ＋π12＝sin⎝⎛⎭⎫2x ＋π6的图象，故φ＝2k π＋π6k ∈Z)，又0<φ<π2，所以φ＝π6.答案：C4.解析：由题意知T ＝2πω＝π，则ω＝2，所以f (x )＝sin ⎝⎛⎭⎫2x ＋π3，又f ⎝⎛⎭⎫π3＝sin ⎝⎛⎭⎫23π＋π3＝sin π＝0.答案：B5.解析：由函数图象知A ＝10，T 2＝4300－1300＝1100.∴T ＝150＝2πω，∴ω＝100π.∴I ＝10sin(100πt ＋φ)．又∵点⎝⎛⎭⎫1300，10在图象上，∴10＝10sin ⎝⎛⎭⎫100π×1300＋φ ∴π3＋φ＝π2，∴φ＝π6，∴I ＝10sin ⎝⎛⎭⎫100πt ＋π6.当t ＝1100时，I ＝10sin ⎝⎛⎭⎫100π×1100＋π6＝－5.答案：A6.解析：由2sin x －1≥0得sin x ≥12，所以2k π＋π6≤x ≤2k π＋5π6，k ∈Z.即函数的定义域为⎣⎡2k π＋π6，2k π＋5π6(k ∈Z)．答案：B7.解析：作出函数y ＝2|cos x |的图象，结合图象判断．答案：D8.解析：由PM ·PN＝0得PM ⊥PN ，又PM ＝PN ，所以△PMN 为等腰直角三角形，因此MN ＝2y P ＝4，T ＝8＝2πω，得ω＝π4.答案：C9.解析：f ⎝⎛⎭⎫5π3＝f ⎝⎛－π3＝f ⎝⎛⎭⎫π3＝sin π3＝32.答案：3210.解析：y ＝sin x ――→(4) y ＝sin ⎝⎛⎭⎫x ＋π3――→(2)y ＝sin ⎝⎛⎭⎫x 2＋π3，或y ＝sin x ――→(2) y ＝sin 12x ――→(6) y ＝sin 12⎝⎛⎭⎫x ＋2π3＝sin⎝⎛⎭⎫x 2＋π3.答案：(4)(2)或(2)(6) 11.解：(1)∵x ＝π8是函数y ＝f (x )的图象的对称轴，∴sin ⎝⎛⎭⎫2×π8φ＝±1. ∴π4＋φ＝k π＋π2，k ∈Z.∴φ＝k π＋π4，k ∈Z.又∵－π<φ<0，∴φ＝－3π4(2)由(1)知y ＝sin ⎝⎛⎭⎫2x －3π4，由题意得2k π－π2≤2x －3π4≤2k π＋π2k ∈Z ， ∴k π＋π8≤x ≤k π＋5π8，k ∈Z.∴函数y ＝sin(2x －3π4)的单调递增区间为⎣⎡⎦⎤k π＋π8，k π＋5π8，k ∈Z.12.解：(1)列表：(2)“先平移，后伸缩”．先把y ＝sin x 的图象上所有点向右平移π4个单位，得到y ＝sin ⎝⎛⎭⎫x －π4的图象；再把y ＝sin⎝⎛⎭⎫x －π4的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变)，得到y ＝sin ⎝⎛⎭⎫12－π4的图象，最后将y ＝sin ⎝⎛⎭⎫12x －π4的图象上所有点的纵坐标伸长到原来的3倍(横坐标不变)，就得到y ＝3sin ⎝⎛⎭⎫12x －π4的图象．(3)周期T ＝2πω＝2π12＝4π，振幅A ＝3，初相是－π4.(4)令12－π4＝π2＋k π(k ∈Z)，得x ＝2k π＋32k ∈Z)，此为对称轴方程．令12x －π4＝k π(k ∈Z)，得x ＝π2＋2k π(k ∈Z)．对称中心为⎝⎛⎭⎫2k π＋π2，0(k ∈Z)．一、选择题4．若函数y ＝2cos ωx 在区间[0，2π3]上递减，且有最小值1，则ω的值可以是( )A ．2 B.12C ．3 D.13解析：由y ＝2cos ωx 在[0，23π]上是递减的，且有最小值为1，则有f ⎝⎛⎭⎫23π＝1，即2×cos(ω×23π)＝1⇒cos 2π3ω＝12.检验各数据，得出B 项符合．答案：B3．为把函数y ＝sin x 的图象上所有点的横坐标都缩小到原来的一半，纵坐标保持不变，再把图象向左平移π4个单位，这时对应于这个图象的解析式( )A ．y ＝cos 2xB ．y ＝－sin 2xC ．y ＝sin(2x －π4)D ．y ＝sin(2x ＋π4)解析：函数y ＝sin x 的图象上所有点的横坐标缩为原来的一半得到函数y ＝sin 2x 的图象，再把图象向左平移π4个单位，得到函数y ＝sin 2⎝⎛⎭⎫x ＋π4＝sin ⎝⎛⎭⎫2x ＋π2＝cos 2x 的图象．答案：A3．已知圆的半径为4，a 、b 、c 为该圆的内接三角形的三边，若abc ＝162，则三角形的面积为( )A ．2 2B ．8 2 C. 2 D.22解析：∵a sin A ＝b sin B ＝c sin C ＝2R ＝8，∴sin C ＝c 8. ∴S △ABC ＝12ab sin C ＝116abc ＝116×162＝ 2.答案：C10．已知函数f (x )＝sin(ωx ＋φ)⎝⎛⎭⎫ω>0，－π2≤φ≤π2的图象上的两个相邻的最高点和最低点的距离为22，则ω＝________.解析：由已知两相邻最高点和最低点的距离为22，而f (x )max －f (x )min ＝2，由勾股定理可得T2＝(22)2－22＝2，∴T ＝4，∴ω＝2πT ＝π2. 答案：π211．已知函数f (x )＝2sin(π－x )cos x . (1)求f (x )的最小正周期；(2)求f (x )在区间⎣⎡⎦⎤－π6，π2上的最大值和最小值．解：(1)∵f (x )＝2sin(π－x )cos x ＝2sin x cos x ＝sin 2x ∴函数f (x )的最小正周期为π. (2)∵－π6≤x ≤π2∴－π3≤2x ≤π，则－32≤sin 2x ≤1.所以f (x )在区间⎣⎡⎦⎤－π6，π2上的最大值为1，最小值为－32.。

2024届高三数学一轮复习-三角函数与解三角形第2练同角三角函数的基本关系及诱导公式(解析版)

第2练同角三角函数的基本关系及诱导公式一、单选题
二、多选题
A．()f x 的值域为2,2⎡⎤-⎣⎦
B．()f x 的最小正周期为πC．π
6
ϕ=
D．将函数f （x ）的图象向左平移14．（2023·全国·高三专题练习）2022的形成需要两股涌潮，一股是波状涌潮，鱼鳞一样的涌潮．若波状涌潮的图象近似函数而破碎的涌潮的图象近似()f x '（两潮有一个交叉点，且破碎的涌潮的波谷为A．2
ω=C．π4f x ⎛
⎫'+ ⎪⎝
⎭的图象关于原点对称
三、填空题
15．（2023·全国·高三专题练习）已知16．（2023·湖南衡阳·衡阳市八中校考模拟预测）已知π
四、解答题
(1)若AM BM =，求
AC
AM
的值；(2)若AM 为BAC ∠的平分线，且20．（2023·全国·高三专题练习）a c <，且ππsin cos 36A ⎛⎫⎛- ⎪ ⎝⎭⎝(1)求A 的大小；
(2)若sin sin 43sin a A c C +=
参考答案：。

高三数学三角函数(二)

三角函数五年高考荟萃（二） 13.（湖北卷文）“sin =”是“”的（） A.充分而不必要条件 B.必要而不充分条件 C.充要条件 D.既不充分也不必要条件答案 A 解析由可得，故成立的充分不必要条件，故选A.14.（重庆卷文）下列关系式中正确的是（）A ．B ．C ．D ．答案 C解析因为，由于正弦函数在区间上为递增函数，因此，即二、填空题15.（北京文）若，则 .答案解析本题主要考查简单的三角函数的运算.属于基础知识、基本运算的考查.由已知，在第三象限，∴，∴应填.16.(湖北卷理)已知函数则的值为 .答案 1解析因为所以α21212cos =α1cos 22a =21sin 2a =±211sin sin24a a ==是000sin11cos10sin168<<000sin168sin11cos10<<000sin11sin168cos10<<000sin168cos10sin11<<sin160sin(18012)sin12,cos10cos(9080)sin80︒︒︒︒︒︒︒︒=-==-=sin y x =[0,90]︒︒sin11sin12sin80︒︒︒<<sin11sin160cos10︒︒︒<<4sin ,tan 05θθ=->cos θ=35-θ3cos 5θ===-35-()'()cos sin ,4f x f x x π=+()4f π'()'()sin cos 4f x f x x π=-⋅+'()'()sincos4444f f ππππ=-⋅+故三、解答题17.（江苏，15）设向量（1）若与垂直，求的值；（2）求的最大值;（3）若，求证：∥.分析本小题主要考查向量的基本概念，同时考查同角三角函数的基本关系式、二倍角的正弦、两角和的正弦与余弦公式，考查运算和证明得基本能力。

三角函数练习题2答案

<<三角函数>>练习题2参考答案1、(江苏省启东中学高三综合测试四)已知函数．（Ⅰ）求的最大值，并求出此时x的值；（Ⅱ）写出的单调递增区间．解：（Ⅰ）当，即时，取得最大值.（Ⅱ）当，即时，所以函数的单调递增区间是．2、(四川省巴蜀联盟2008届高三年级第二次联考)已知函数，（1）求函数的最小正周期；（2）求函数的单调减区间；解：（1），（2）由得，所以，减区间为3、(四川省成都市新都一中高2008级12月月考)已知函数(1)求函数的最小正周期；(2)若存在，使不等式成立，求实数m的取值范围.解析：(1)∴函数f(x)的最小正周期(2)当时∴当，即时，f(x)取最小值－1所以使题设成立的充要条件是，故m的取值范围是(－1,＋∞)4、(安徽省淮南市2008届高三第一次模拟考试)设函数f (x)=2cosx (cosx+sinx)－1,x∈R (1)求f (x)的最小正周期T；(2)求f (x)的单调递增区间.解：（1）.（2）由2k( –( 2x + ( 2k( + , 得：k( –( x ( k( + （k (Z）,f ( x ) 单调递增区间是[k( –，k( +]（k (Z）5、(山东省博兴二中高三第三次月考)已知函数的定义域为，值域为[(5,4].求a和b. 解：f(x)=a(1－cos2x)－sin2x＋b=－a(cos2x＋sin2x)＋a＋b=－2a sin(2x＋)＋a＋b . ∵x∈，∴2x＋，sin(2x＋)(.显然a=0不合题意.(1) 当a＞0时,值域为,即(2) 当a＜0时,值域为,即6,(吉林省吉林市2008届上期末)已知函数（1）求的最小正周期的最小值；（2）求上的单调递减区间；解：（1）由…2分令时（2）设则又上的单调减区间为7、(甘肃省河西五市2008年高三第一次联考)已知函数.（I）求的最小正周期及最大值（II）求使≥2的的取值范围解：（I）……2分（II）由得的x的取值范围是8、(广东省韶关市2008届高三第一次调研考试)已知，（Ⅰ）求函数的最小正周期;(Ⅱ) 当,求函数的零点.解：（Ⅰ）= 故（Ⅱ）令，=0，又故函数的零点是9、(贵州省贵阳六中、遵义四中2008年高三联考)已知函数f(x)＝2sinxcosx＋cos2x.(Ⅰ)求f ()的值；(Ⅱ)设∈(0，)，f ()＝，求cos2的值.解：（Ⅰ）∵f(x)=sin2x+cos2x,∴f()=sin+cos=1（Ⅱ）∵f()=sinα+cosα=,∴1+sin2α=, sin2α=,∴cos2α=∵α∈（0，π）∴2α∈（π，π）∴cos2α<0.故cos2α=10、(湖北省黄冈市2007年秋季高三年级期末考试)已知函数，且满足，求的最大值和最小值。

新教材老高考适用2023高考数学一轮总复习高考解答题专项二三角函数中的综合问题北师大版

高考解答题专项二三角函数中的综合问题1.已知函数f (x )=2sin ωx cos ωx-π6-12(0<ω<2),函数f (x )在[a ,b ]上单调递增,且b-a 的最大值为π2,求f (x )在-π2,π2上的单调递减区间.2.(2021湖南怀化高三二模)在△ABC 中,内角A ,B ,C 所对的边长分别为a ,b ,c ,且满足2tanBtanA+tanB =bc . (1)求角A ;(2)若a=√13,b=3,求△ABC 的面积.3.(2021天津静海一中高三月考)已知锐角三角形ABC的三个角A,B,C所对的边为a,b,c,且b cos C+√3b sin C=a+c.(1)求B;(2)若b=2,△ABC的面积为√3,求a,c.4.平面凸四边形ABCD中,∠BAD=∠BCD=90°,AD=3,AB=4.(1)若∠ABC=45°,求CD;(2)若BC=2√5,求AC.5.(2021江苏徐州高三二模)若f(x)=sin(ωx+φ)ω>0,0<φ<π2的部分图象如图所示,f(0)=12,f5π12=0.(1)求f(x)的解析式;(2)在锐角三角形ABC中,若A>B,f A-B2−π12=35,求cos A-B2,并证明sin A>2√55.6.(2021河南郑州高三三模)在△ABC中,AB=2AC,点D在BC边上,AD平分∠BAC.(1)若sin∠ABC=√5,求cos∠BAC;5(2)若AD=AC,且△ABC的面积为√7,求BC.高考解答题专项二三角函数中的综合问题1.解f (x )=2sin ωx cos ωx-π6-12=2sin ωx cos ωx cos π6+sin ωx sin π6-12=√3cos ωx sin ωx+sin 2ωx-12=√32sin2ωx-12cos2ωx=sin 2ωx-π6.若f (x )在[a ,b ]上单调递增,且b-a 的最大值为π2, 则T=π=2π2ω,故ω=1,所以f (x )=sin 2x-π6.由π2+2k π≤2x-π6≤3π2+2k π(k ∈Z ),得π3+k π≤x ≤5π6+k π(k ∈Z ),令k=0,得π3≤x ≤5π6;令k=-1,得-2π3≤k ≤-π6.又-π2≤x ≤π2, 所以f (x )在-π2,π2上单调递减区间为-π2,-π6,π3,π2.2.解(1)由2tanBtanA+tanB =bc 及正弦定理可知,2sinBcosB sinA cosA +sinBcosB=sinBsinC ,所以2sinB cosB·cosA ·cosB sin(A+B)=sinB sinC,因此2cos A=1.又A ∈(0,π),所以A=π3.(2)由余弦定理a 2=b 2+c 2-2bc cos A ,得13=9+c 2-3c , 所以c 2-3c-4=0,即(c-4)(c+1)=0,解得c=4. 从而S △ABC =12bc sin A=12×3×4×√32=3√3.3.解(1)由正弦定理得sin B cos C+√3sin B sin C=sin A+sin C=sin(B+C )+sin C=sin B cos C+cos B sin C+sin C. 因为C 为三角形内角,sin C ≠0,所以√3sin B-cos B=1,sin B-π6=12.因为-π6<B-π6<π3,则B-π6=π6,即B=π3. (2)由已知S=12ac sin B=√34ac=√3,得ac=4.又a 2+c 2-b 2=2ac cos B ,即a 2+c 2-4=ac ,解得a=c=2.4.解(1)连接BD ,在Rt △BAD 中,由AB=4,AD=3,∠BAD=90°, 得BD=5,∴sin ∠ABD=35,cos ∠ABD=45.∵∠ABC=45°,∴∠DBC=45°-∠ABD ,∴sin ∠DBC=sin45°·cos ∠ABD-cos45°·sin ∠ABD=√22×45−√22×35=√210. 在Rt △BCD 中,由∠BCD=90°,知CD=BD ·sin ∠DBC=5×√210=√22.(2)连接AC ,由(1)知BD=5,在Rt △ABD 中易知sin ∠ABD=35,cos ∠ABD=45. 在Rt △BCD 中,由BC=2√5,BD=5,得CD=√5. 易知sin ∠CBD=√55,cos ∠CBD=2√55. ∴cos ∠ABC=cos(∠ABD+∠CBD )=cos ∠ABD ·cos ∠CBD-sin ∠ABD ·sin ∠CBD=45×2√55−35×√55=√55. 在△ABC 中,由余弦定理得AC 2=AB 2+BC 2-2AB ·BC cos ∠ABC=42+(2√5)2-2×4×2√5×√55=20, ∴AC=2√5.5.解(1)由f (0)=12,得sin φ=12.又0<φ<π2,故φ=π6. 由f5π12=0,得sin ω·5π12+π6=0,所以ω·5π12+π6=2k π+π(k ∈Z ),即ω=2+24k5(k ∈Z ).由ω>0,结合函数图象可知12·2πω>5π12,所以0<ω<125.又k ∈Z ,所以k=0,从而ω=2,因此f (x )=sin 2x+π6.(2)由fA -B 2−π12=sin(A-B )=35,因为0<B<A<π2,所以0<A-B<π2,故cos(A-B )=45. 因为cos(A-B )=2cos 2A -B2-1,于是cosA -B 2=√1+cos(A -B)2=3√1010. 所以sinA -B 2=√1-cos 2A -B 2=√1010. 又A+B>π2,故A=A+B 2+A -B 2>π4+A -B 2.又y=sin x 在0,π2上单调递增,且A ∈0,π2,π4+A -B 2∈0,π2, 所以sin A>sinπ4+A -B 2=sin π4cosA -B 2+cos π4sinA -B 2=√22×3√1010+√1010=2√55.6.解(1)令△ABC 的边AC ,AB ,BC 为b ,c ,a ,由题意可得c=2b , ∵AB>AC ,∴∠ABC<∠ACB ,∴∠ABC 为锐角,即cos ∠ABC=√1-15=2√55.∵AC sin ∠ABC=AB sin ∠ACB,∴sin ∠ACB=2√55.∵∠ACB ∈(0,π),∴cos ∠ACB=±√55. ∴cos ∠BAC=-cos(∠ABC+∠ACB )=sin ∠ABC sin ∠ACB-cos ∠ABC cos ∠ACB.当cos ∠ACB=√55时,cos ∠BAC=√55×2√55−2√55×√55=0. 当cos ∠ACB=-√55时,cos ∠BAC=√55×2√55+2√55×√55=45.所以cos ∠BAC=0或45.(2)设∠CAD=∠DAB=θ,由于S △ABC =S △ACD +S △ADB , 所以12AC ·AD sin θ+12AB ·AD sin θ=12AB ·AC sin2θ, 由AD=AC ,AB=2AC 可得3sin θ=4sin θcos θ.因为sin θ≠0,则cos θ=34,sin θ=√1-cos 2θ=√74, S △ABC =12AC ·AB sin2θ=b 2sin2θ=2b 2sin θcos θ=√7,解得b 2=83.又cos2θ=2cos 2θ-1=18,∴a=√b 2+4b 2-2b ·2bcos2θ=2√3,即BC=2√3.。

高三数学-专题复习-三角函数(2)解斜三角形(正弦定理余弦定理应用)

三角函数（2）解斜三角形（正余弦定理应用）1.正弦定理：A a sin =B b sin =Ccsin =2R.（关键点“比”,用法：边角转化）利用正弦定理，可以解决以下两类有关三角形的问题. （1）已知两角和任一边，求其他两边和一角；（2）已知两边和其中一边的对角，求另一边的对角.（从而进一步求出其他的边和角） 2.余弦定理：a 2=b 2+c 2－2bccosA ； cos B =cab ac 2222-+；在余弦定理中，令C =90°，这时cos C =0，所以c 2=a 2+b 2. 利用余弦定理，可以解决以下两类有关三角形的问题：（1）已知三边，求三个角；（2）已知两边和它们的夹角，求第三边和其他两个角. 可能出现一解、两解或无解的情况，这时应结合“三角形中大边对大角定理及几何作图来理解”.题型一、判断三角形的形状：1.在△ABC 中，若2cos B sin A =sin C ，则△ABC 的形状一定是（）答案：CA.等腰直角三角形B.直角三角形C.等腰三角形D.等边三角形2.下列条件中，△ABC 是锐角三角形的是（） A.sin A +cos A =51B.AB ·BC ＞0C.tan A +tan B +tan C ＞0D.b =3，c =33，B =30° 答案：C解析：由sin A +cos A =51 得2sin A cos A =－2524＜0，∴A 为钝角. 由AB ·BC ＞0，得BA ·BC ＜0，∴cos 〈BA ，BC 〉＜0.∴B 为钝角.由tan A +tan B +tan C ＞0，得tan （A +B ）·（1－tan A tan B ）+tan C ＞0. ∴tan A tan B tan C ＞0，A 、B 、C 都为锐角.由B b sin =C c sin ，得sin C =23，∴C =3π或3π2.3.在△ABC 中，sin A =CB CB cos cos sin sin ++，判断这个三角形的形状.解：△ABC 是直角三角形. 题型二、解斜三角形（求角度和长度）4.已知（a +b +c ）（b +c －a ）=3bc ，则∠A =_______. 解析：由已知得（b +c ）2－a 2=3bc ，∴b 2+c 2－a2=bc .∴bc a c b 2222-+=21.∴∠A =3π. 答案：3π5.在△ABC 中，“A ＞30°”是“sin A ＞21”的 A.充分而不必要条件 B.必要而不充分条件 C.充分必要条件 D.既不充分也不必要条件解析：在△ABC 中，A ＞30°⇒0＜sin A ＜1 sin A ＞21；sin A ＞21⇒30°＜A ＜150°⇒A ＞30°答案：B6.在△ABC 中，角A 、B 、C 所对的边分别是a 、b 、c ，若三角形的面积S =41（a 2+b 2－c 2），则∠C 的度数是_______.解析：由S =41（a 2+b 2－c 2）得21ab sin C =41·2ab cos C .∴tan C =1.∴C =4π. 答案：45° 7.△ABC 的三个内角A 、B 、C 的对边分别是a 、b 、c ，如果a 2=b （b +c ），求证：A =2B . 证明：用正弦定理，a =2R sin A ，b =2R sin B ，c =2R sin C ，代入a 2=b （b +c ）中，得sin 2A =sin B （sin B +sin C ）⇒sin 2A －sin 2B =sin B sin C ⇒22cos 1A -－22cos 1B- =sin B sin （A +B ）⇒21（cos2B －cos2A ）=sin B sin （A +B ） ⇒sin （A +B ）sin （A －B ）=sin B sin （A +B ），因为A 、B 、C 为三角形的三内角，所以sin （A +B ）≠0.所以sin （A －B ）=sin B .所以只能有A －B =B ，即A =2B .该题若用余弦定理如何解决?解：利用余弦定理，由a 2=b （b +c ），得cos A =bc a c b 2222-+=bc c b b c b 222）（）（+-+=b bc 2-，cos2B =2cos 2B －1=2（ac b c a 2222-+）2－1=2222cc b b c c b ）（）（++－1=b b c 2-. 所以cos A =cos2B .因为A 、B 是△ABC 的内角，所以A =2B .评述：高考题中，涉及到三角形的题目，重点考查正弦、余弦定理，考查的侧重点还在于三角转换.这是命题者的初衷.8.△ABC 中，a 、b 、c 分别为∠A 、∠B 、∠C 的对边，如果a 、b 、c 成等差数列，∠B =30°，△ABC 的面积为23，那么b 等于（）A.231+ B.1+3 C.232+ D.2+3答案：B9.已知锐角△ABC 中，sin （A +B ）=53，sin （A －B ）=51. （1）求证：tan A =2tan B ；（2）设AB =3，求AB 边上的高. （1）证明：∵sin （A +B ）=53，sin （A －B ）=51，∴⎪⎪⎩⎪⎪⎨⎧=-=+51sin cos cos sin 53sin cos cos sin B A B A B A B A B A B A B A tan tan 51sin cos 52cos sin ⇒⎪⎪⎩⎪⎪⎨⎧==⇒=2. ∴tan A =2tan B . （2）解：2π＜A +B ＜π，∴sin （A +B ）=53. ∴tan （A +B ）=－43，即BA BA tan tan 1tan tan -+=－43.将tan A =2tanB 代入上式整理得2tan 2B －4tan B －1=0，解得tan B =262±（负值舍去）.得tan B =262+，∴tan A =2tan B =2+6. 设AB边上的高为CD ，则AB =AD +DB =A CD tan +B CDtan =623+CD .由AB =3得CD =2+6，所以AB 边上的高为2+6.10.在△ABC 中，a 、b 、c 分别是∠A 、∠B 、∠C 的对边长，已知a 、b 、c 成等比数列，且a 2－c 2=ac －bc ，求∠A 的大小及cBb sin 的值. 解cBb sin =sin A =23.11.在△ABC 中，若∠C =60°，则ca bc b a +++=_______. 解析：c a bc b a +++=））（（c a c b bc b ac a +++++22 =222c bc ac ab bc ac b a ++++++. （*）∵∠C =60°，∴a 2+b 2－c 2=2ab cos C =ab . ∴a 2+b 2=ab +c 2. 代入（*）式得222cbc ac ab bc ac b a ++++++=1. 答案：1题型三、取值范围题目12.在△ABC 中，角A 、B 、C 所对的边分别为a 、b 、c ，依次成等比数列，求y =BB Bcos sin 2sin 1++的取值范围.解：∵b2=ac ，∴cos B =ac b c a 2222-+=ac ac c a 222-+=21（c a +a c ）－21≥21. ∴0＜B ≤3π，y =BB B cos sin 2sin 1++=B B B B cos sin cos sin 2++）（=sin B +cos B =2sin （B +4π）.∵4π＜B +4π≤12π7， ∴22＜sin （B +4π）≤1. 故1＜y ≤2.13.已知△ABC 中，22（sin 2A －sin 2C ）=（a －b ）sin B ，外接圆半径为2. （1）求∠C ；（2）求△ABC 面积的最大值.解：（1）由22（sin 2A －sin 2C ）=（a －b ）·sin B 得22（224R a －224R c ）=（a －b ）Rb2. 又∵R =2，∴a 2－c 2=ab －b 2.∴a 2+b 2－c2=ab . ∴cos C =ab c b a 2222-+=21.又∵0°＜C＜180°，∴C =60°. （2）S =21ab sin C =21×23ab =23sin A sin B =23sin A sin （120°－A ）=23sin A（sin120°cos A －cos120°sin A ）=3sin A cos A +3sin 2A =23sin2A －23sin2A cos2A +23=3sin （2A －30°）+23. ∴当2A =120°，即A =60°时，S max =233. 14.在锐角△ABC 中，边长a =1，b =2，则边长c 的取值范围是_______.解析：若c 是最大边，则cos C ＞0.∴abc b a 2222-+＞0，∴c ＜5.又c ＞b －a =1， ∴1＜c ＜5.●思悟小结1.在△ABC 中，∵A +B +C =π，∴sin2B A +=cos 2C ，cos 2B A +=sin 2C2.∠A 、∠B 、∠C 成等差数列的充分必要条件是∠B =60°.3.在非直角三角形中，tan A +tan B +tan C =tan A ·tan B ·tan C .。

高三复习高中数学三角函数基础过关习题(有答案)

2015年高三复习高中数学三角函数基础过关习题一．选择题（共15 小题）5．（2014?宝鸡二模）函数 y=2sin（2x+ ）的最小正周期为（）A ．4πB．πC．2π D ．6．（ 2014?宁波二模）将函数 y=sin （4x﹣）图象上各点的横坐标伸长到原来的 2 倍，再向左平移个单位，纵坐标不变，所得函数图象的一条对称轴的方程是（）A ．B．x= C． D ．x= x= ﹣7．（ 2014?邯郸二模）已知函数 f （x）=2sin （x+φ），且 f （0）=1，f' （0）＜ 0，则函数图象的一条对称轴的方程为（）A ．x=0 B．x= C．x= D ．x=8．（ 2014?上海模拟）将函数的图象向左平移个单位，再将图象上各点的横坐标伸长到原来的 2 倍（纵坐标不变），所得函数图象的一条对称轴是（）A ．B．C．x=π D ．x= 1．（2014?陕西）函数 f（x）=cos（2x﹣）的最小正周期是（）A ．B．πC．2π D ． 4π2．（2014?陕西）函数 f（x）=cos（2x+ ）的最小正周期是（）A ．B．πC．2π D ． 4π3．（ 2014?香洲区模拟）函数是（）A ．周期为π的奇函数B．周期为π的偶函数C．周期为 2π的奇函数 D ．周期为 2π的偶函数4．（ 2014?浙江模拟）函数f（x）=sin （2x+）（x∈R）的最小正周期为（）A ．B． 4πC．2πD ．π-来源网络，仅供个人学习参考9．（2014?云南模拟）为了得到函数y=sin x 的图象，只需把函数y=sinx 图象上所有的点的（）A ．横坐标伸长到原来的 3 倍，纵坐标不变B．横坐标缩小到原来的倍，纵坐标不变C．纵坐标伸长到原来的 3 倍，横坐标不变D ．纵坐标伸长到原来的倍，横坐标不变10．（ 2013?陕西）设△ ABC的内角 A，B，C所对的边分别为a，b，c，若 bcosC+ccosB=asinA，则△ ABC的形状为（）A ．锐角三角形B．直角三角形C．钝角三角形D ．不确定11．（2013?湖南）在锐角△ ABC中，角 A，B 所对的边长分别为a，b．若 2asinB= b，则角 A 等于（）A．B．C．D．12．（2013?天津模拟）将函数 y=cos（ x﹣）的图象上所有点的横坐标伸长到原来的2 倍（纵坐标不变），再将所得图象向左平移个单位，则所得函数图象对应的解析式是（）A．y=cos（﹣）B．）C．y=sin2x D ．）y=cos（2x﹣y=cos（﹣13．（2013?安庆三模）将函数 f （x）=sin （ 2x ）的图象向左平移个单位，得到 g（x）的图象，则 g（x）的解析式为（）A ．g（ x） =cos2x B． g（ x） = ﹣ cos2x C．g（ x） =sin2x D．g（ x） =sin （ 2x+ ）14．（ 2013?泰安一模）在△ ABC中，∠ A=60°， AB=2，且△ ABC 的面积为，则 BC的长为（）A ．B． 3 C． D ． 7 15．（2012?杭州一模）已知函数，下面四个结论中正确的是（）A ．函数 f（ x）的最小正周期为 2πB．函数 f（ x）的图象关于直线对称C．函数 f（ x）的图象是由 y=2cos2x 的图象向左平移个单位得到-来源网络，仅供个人学习参考D ．函数是奇函数二．解答题（共15 小题）18．（2014?长安区三模）已知函数f （x）=sin （2x﹣）+2cos2x﹣1．（Ⅰ）求函数 f （x）的单调增区间；（Ⅱ）在△ ABC中， a、b、c 分别是角 A、B、C 的对边，且 a=1，b+c=2，f （A）= ，求△ ABC的面积．19．（2014?诸暨市模拟） A、B 是直线图象的两个相邻交点，且．（Ⅰ）求ω 的值；（Ⅱ）在锐角△ ABC中， a，b，c 分别是角 A，B，C 的对边，若的面积为，求 a 的值．16．（2015?重庆一模）已知函数f （x）=cosx?sin （x+）﹣cos2x+．（1）求 f （x）的最小正周期；（2）若 f （x）＜m在上恒成立，求实数m的取值范围．17．（2014?东莞二模）已知函数．（Ⅰ）求的值；（Ⅱ）求 f （x）的最大值和最小正周期；（Ⅲ）若，α 是第二象限的角，求sin2 α．20．（2014?广安一模）已知函数 f （x）= sin2x+2cos2x+1．（Ⅰ）求函数 f （x）的单调递增区间；-来源网络，仅供个人学习参考（Ⅱ）设△ABC内角A，B，C的对边分别为a，b，c，且c= ，f （C）=3，若向量 =（sinA ，﹣ 1）与向量 =（ 2，sinB ）垂直，求a，b 的值．21．（2014?张掖三模）已知 f （ x）= sin ωx﹣ 2sin 2（ω＞0）的最小正周期为3π．（Ⅰ）当 x∈[，]时，求函数 f （ x）的最小值；（Ⅱ）在△ ABC，若 f （ C）=1，且 2sin 2B=cosB+cos（ A﹣C），求sinA 的值．22．（2014?漳州三模）在△ ABC中， a，b，c 分别是内角 A，B，C 所对的边，，若向量 =（ 1，sinA ）， =（2，sinB ），且∥ ．（Ⅰ）求 b，c 的值；（Ⅱ）求角 A 的大小及△ ABC的面积．23．（2013?青岛一模）已知a， b，c 为△ ABC的内角 A，B，C的对边，满足，函数 f （x）=sin ωx（ω＞ 0）在区间上单调递增，在区间上单调递减．（Ⅰ）证明： b+c=2a；（Ⅱ）若，证明：△ ABC为等边三角形．24．（2012?南昌模拟）已知函数．（1）若 f （α） =5，求 tan α的值；（2）设△ ABC三内角 A，B，C所对边分别为a，b，c，且，求 f （x）在（ 0，B]上的值域．25．（2012?河北区一模）已知函数．（Ⅰ）求 f （x）的单调递增区间；-来源网络，仅供个人学习参考（Ⅱ）在△ ABC中，三内角 A，B，C的对边分别为 a，b，c，已知成等差数列，且=9，求 a 的值．26．（2012?韶关一模）已知函数 f（x）=2cos2ωx+2 si nωxcosωx ﹣1（ω＞ 0）的最小正周期为π．（1）求 f （）的值；（2）求函数 f （x）的单调递增区间及其图象的对称轴方程．27．（2012?杭州一模）已知函数f （x）=．（Ⅰ）求 f （x）的最小正周期、对称轴方程及单调区间；（Ⅱ）现保持纵坐标不变，把f （x）图象上所有点的横坐标伸长到原来的 4 倍，得到新的函数h（x）；（ⅰ）求 h（x）的解析式；（ⅱ）△ABC中，角 A、B、C的对边分别为 a、b、c，且满足，h（A）=，c=2，试求△ ABC的面积．28．（2011?辽宁）△ ABC的三个内角 A、B、C所对的边分别为a、b、c，asinAsinB+bcos 2A= a．（Ⅰ）求；（Ⅱ）若 c2 =b2+a2，求 B．29．（2011?合肥二模）将函数 y=f （x）的图象上各点的横坐标缩短为原来的（纵坐标不变），再向左平移个单位后，得到的图象与函数 g（x）=sin2x 的图象重合．（1）写出函数 y=f （x）的图象的一条对称轴方程；（2）若 A 为三角形的内角，且 f （A）= ?，求 g（）的值．-来源网络，仅供个人学习参考30．（2011?河池模拟）已知△ ABC的内角 A、B、C的对边分别为a、b、c，向量 m=（ sinB ，1﹣cosB）与向量 n=（2，0）的夹角为，求的最大值．2015 年高三复习高中数学三角函数基础过关习题（有答案）参考答案与试题解析一．选择题（共 15 小题）1．（2014?陕西）函数 f（x）=cos（2x﹣）的最小正周期是（）A ．B．πC． 2π D ． 4π考三角函数的周期性及其求法．点：专三角函数的图像与性质．题：分由题意得ω =2 ，再代入复合三角函数的周期公式求解．析：解解：根据复合三角函数的周期公式得，答：函数 f（ x） =cos（2x﹣）的最小正周期是π，故选 B．点本题考查了三角函数的周期性，以及复合三角函数的周期公式应用，属于基础题．评：2．（2014?陕西）函数 f（x）=cos（2x+ ）的最小正周期是（）A ．B．πC． 2π D ． 4π考三角函数的周期性及其求法．点：专三角函数的图像与性质．题：分由题意得ω =2 ，再代入复合三角函数的周期公式求解．析：解解：根据复合三角函数的周期公式得，答：函数 f（ x） =cos（2x+ ）的最小正周期是π，故选： B．点本题考查了三角函数的周期性，以及复合三角函数的周期公式应用，属于基础题．评：3．（ 2014?香洲区模拟）函数是（）-来源网络，仅供个人学习参考A．周期为π的奇函数B．周期为π的偶函数C．周期为 2π的奇函数 D ．周期为 2π的偶函数考点：三角函数的周期性及其求法；正弦函数的奇偶性．专题：计算题．分析：利用诱导公式化简函数，然后直接求出周期，和奇偶性，确定选项．解答：=2cos2x，解：因为：所以函数是偶函数，周期为：π故选 B．点评：本题考查三角函数的周期性及其求法，正弦函数的奇偶性，考查计算能力，是基础题．4．（ 2014?浙江模拟）函数 f （x）=sin （2x+ ）（x∈R）的最小正周期为（）A ．B．4πC． 2π D ．π考三角函数的周期性及其求法．点：专三角函数的图像与性质．题：分由条件利用利用函数 y=Asin （ω x+ φ）的周期为，求得结果．析：解解：函数 f（ x）=sin （ 2x+ ）（ x∈R）的最小正周期为 T==π，答：故选： D．点本题主要考查函数y=Asin （ω x+ φ）的周期性，利用了函数 y=Asin （ω x+ φ）的周期为，属于基础题．评：5．（2014?宝鸡二模）函数 y=2sin（2x+ ）的最小正周期为（）A ． 4πB．πC． 2π D ．考三角函数的周期性及其求法．点：专三角函数的图像与性质．题：分根据 y=Asin （ω x+ φ）的周期等于T= ，得出结论．析：解解：函数 y=2sin（ 2x+ ）的最小正周期为 T= =π，答：故选： B．点本题主要考查三角函数的周期性及其求法，利用了y=Asin （ω x+ φ）的周期等于T= ，属于基础题．评：6．（ 2014?宁波二模）将函数 y=sin （4x﹣）图象上各点的横坐标伸长到原来的 2 倍，再向左平移个单位，纵坐标不变，所得函数图象的一条对称轴的方程是（）-来源网络，仅供个人学习参考A ．B．x= C． D ．x= x= ﹣考函数 y=Asin （ω x+ φ）的图象变换．点：专三角函数的图像与性质．题：分利用函数 y=Asin （ω x+ φ）的图象变换，可求得变换后的函数的解析式为y=sin（8x﹣），利用正弦函数的析：对称性即可求得答案．解解：将函数 y=sin（ 4x﹣）图象上各点的横坐标伸长到原来的 2 倍，得到的函数解析式为： g（x）=sin（ 2x 答：﹣），再将 g（ x）=sin（ 2x﹣）的图象向左平移个单位（纵坐标不变）得到y=g（ x+ ） =sin[2（ x+ ）﹣]=sin （ 2x+ ﹣） =sin （ 2x+ ），由 2x+ =k π+（ k∈Z ），得： x= + ， k∈Z ．∴当 k=0 时， x= ，即 x= 是变化后的函数图象的一条对称轴的方程，故选： A．点本题考查函数y=Asin （ω x+ φ）的图象变换，求得变换后的函数的解析式是关键，考查正弦函数的对称性的评：应用，属于中档题．7．（ 2014?邯郸二模）已知函数f （x）=2sin （x+φ），且 f （0）=1，f' （0）＜ 0，则函数图象的一条对称轴的方程为（）A ． x=0 B．x= C．x= D ．x=考函数 y=Asin （ω x+ φ）的图象变换．点：专三角函数的图像与性质．题：分由题意可得2sin φ =1且，2cos φ＜0，可取φ=，可得函数f（ x）的解析式，从而得到函数析：的解析式，再根据z 余弦函数的图象的对称性得出结论．解解：∵函数f（ x） =2sin （ x+ φ，）且 f（ 0） =1 ， f'（ 0）＜ 0，∴ 2sin φ =1 ，2cos且φ＜0，答：∴可取φ=，函数f（x）=2sin（x+）．∴函数=2sin（x+）=2cosx，故函数图象的对称轴的方程为x=k π，k∈z．结合所给的选项，故选： A．点本题主要考查三角函数的导数，余弦函数的图象的对称性，属于基础题．评：-来源网络，仅供个人学习参考8．（ 2014?上海模拟）将函数的图象向左平移个单位，再将图象上各点的横坐标伸长到原来的 2 倍（纵坐标不变），所得函数图象的一条对称轴是（）A ．B．C． x=π D ．x=考函数 y=Asin （ω x+ φ）的图象变换．点：专三角函数的图像与性质．题：分由条件根据函数 y=Asin（ω x+ φ）的图象变换规律可得得函数图象对应的函数解析式为y=cosx，再利用余弦析：函数的图象的对称性求得所得函数图象的一条对称轴方程．解解：将函数的图象向左平移个单位，可得函数 y=cos[2（ x+ ）﹣]=cos2x 的图答：象；再将图象上各点的横坐标伸长到原来的2 倍（纵坐标不变），所得函数图象对应的函数解析式为y=cosx，故所得函数的对称轴方程为x=k π，k∈z，故选： C．点本题主要考查函数 y=Asin （ω x+ φ）的图象变换规律，余弦函数的图象的对称性，属于基础题．评：9．（2014?云南模拟）为了得到函数y=sin x 的图象，只需把函数y=sinx 图象上所有的点的（）A．横坐标伸长到原来的 3 倍，纵坐标不变B．横坐标缩小到原来的倍，纵坐标不变C．纵坐标伸长到原来的 3 倍，横坐标不变D ．纵坐标伸长到原来的倍，横坐标不变考点：函数 y=Asin （ω x+ φ）的图象变换．专题：三角函数的图像与性质．分析：由条件根据函数 y=Asin （ω x+ φ）的图象变换规律，可得结论．解答：解：把函数 y=sinx图象上所有的点的横坐标伸长到原来的 3 倍，纵坐标不变，可得函数y=sin x 的图象，故选： A．点评：本题主要考查函数y=Asin （ω x+ φ）的图象变换规律，属于基础题．10．（ 2013?陕西）设△ ABC的内角 A，B，C所对的边分别为a，b，c，若 bcosC+ccosB=asinA，则△ ABC的形状为（）A ．锐角三角形B．直角三角形C．钝角三角形D ．不确定考正弦定理．点：专解三角形．题：-来源网络，仅供个人学习参考分由条件利用正弦定理可得sinBcosC+sinCcosB=sinAsinA ，再由两角和的正弦公式、诱导公式求得sinA=1 ，析：可得 A= ，由此可得△ABC的形状．解解：△ ABC的内角 A， B， C 所对的边分别为 a， b，c，答：∵ bcosC+ccosB=asinA ，则由正弦定理可得sinBcosC+sinCcosB=sinAsinA ，即 sin（B+C ）=sinAsinA ，可得 sinA=1 ，故 A= ，故三角形为直角三角形，故选 B．点本题主要考查正弦定理以及两角和的正弦公式、诱导公式的应用，根据三角函数的值求角，属于中档题．评：11．（2013?湖南）在锐角△A BC中，角 A，B 所对的边长分别为a，b．若 2asinB= b，则角 A 等于（）A ．B．C． D ．考正弦定理．点：专计算题；解三角形．题：分利用正弦定理可求得sinA，结合题意可求得角 A ．析：解解：∵在△ ABC中， 2asinB= b，答：∴由正弦定理==2R 得： 2sinAsinB= sinB，∴sinA= ，又△ ABC为锐角三角形，∴A= ．故选 D．点本题考查正弦定理，将“边”化所对“角”的正弦是关键，属于基础题．评：12．（2013?天津模拟）将函数 y=cos（ x﹣）的图象上所有点的横坐标伸长到原来的2 倍（纵坐标不变），再将所得图象向左平移个单位，则所得函数图象对应的解析式是（）A．B．y=cos（2x﹣）C． y=sin2x D ．y=cos（﹣）y=cos（﹣）考函数 y=Asin （ω x+ φ）的图象变换．点：专三角函数的图像与性质．题：分由条件利用y=Asin （ω x+ φ）的图象变换规律，可得结论．析：解解：将函数y=cos（ x﹣）的图象上所有点的横坐标伸长到原来的2 倍（纵坐标不变），答：-来源网络，仅供个人学习参考可得函数y=cos（x﹣）的图象再将所得图象向左平移个单位，则所得函数图象对应的解析式是y=cos[（x+）﹣] =cos（x﹣），故选： D．点本题主要考查y=Asin （ω x+ φ）的图象变换规律，属于基础题．评：13．（2013?安庆三模）将函数 f （x）=sin （ 2x ）的图象向左平移个单位，得到 g（x）的图象，则 g（x）的解析式为（）A ． g（ x） =cos2x B．g（x）= ﹣ cos2x C． g（ x） =sin2x D．g（ x） =sin （ 2x+ ）考函数 y=Asin （ω x+ φ）的图象变换．点：专计算题；三角函数的图像与性质．题：分直接利用平移原则，左加右减上加下减，化简求解即可．析：解解：将函数 f（ x） =sin （ 2x ）的图象向左平移个单位，答：得到 g（ x） =sin[2 （ x+ ） + ]=sin （ 2x+ ） =cos2x，g（ x）的解析式： g（ x） =cos2x ，故选 A．点本题考查三角函数的平移．三角函数的平移原则为左加右减上加下减．以及诱导公式的应用．评：14．（ 2013?泰安一模）在△ ABC中，∠ A=60°， AB=2，且△ ABC 的面积为，则 BC的长为（）A ．B．3 C． D ． 7考余弦定理．点：专解三角形．题：分由△ ABC 的面积 S△ABC=，求出AC=1，由余弦定理可得BC，计算可得答案．析：解解：∵S△ABC= = × AB× ACsin60 °=× 2× AC×，答：∴AC=1，△ ABC 中，由余弦定理可得BC==，故选 A．点本题考查三角形的面积公式，余弦定理的应用，求出AC，是解题的关键．评：-来源网络，仅供个人学习参考15．（2012?杭州一模）已知函数，下面四个结论中正确的是（）A．函数 f（ x）的最小正周期为2πB．函数 f（ x）的图象关于直线对称C．函数 f（ x）的图象是由y=2cos2x 的图象向左平移个单位得到D．函数是奇函数考点：函数 y=Asin（ω x+ φ的）图象变换；三角函数的周期性及其求法；余弦函数的奇偶性；余弦函数的对称性．专题：计算题．分析：由 f （ x） =2cos（ 2x+ ）可求得周期 T=π，从而可判断 A 的正误；将代入 f（ x） =2cos（2x+ ）可得 f（）的值，看是否为最大值或最小值，即可判断 B 的正误；y=2cos2x 的图象向左平移个单位得到 y=2cos2（ x+ ） =2cos（ 2x+ ），显然 C 不对；f（ x+ ） =2cos（ 2x+ ） = ﹣2sinx，可判断 D 的正误．解答：解：∵ f （x） =2cos（ 2x+ ），故周期 T=π，可排除 A；将代入 f（ x） =2cos（ 2x+ ）可得： f（） =2cos =0 ≠± 2，故可排除 B；y=2cos2x 的图象向左平移个单位得到 y=2cos2（ x+ ） =2cos（ 2x+ ），故可排除 C；f（ x+ ） =2cos（ 2x+ ） = ﹣2sinx，显然为奇函数，故 D 正确．故选 D．点评：本题考查余弦函数的奇偶性与对称性及其周期的求法，关键是熟练掌握三角函数的性质，易错点在于函数图象的平移变换的判断，属于中档题．二．解答题（共15 小题）16．（2015?重庆一模）已知函数f （x）=cosx?sin （x+）﹣cos2x+．（1）求 f （x）的最小正周期；（2）若 f （x）＜m在上恒成立，求实数m的取值范围．考点：三角函数的最值；两角和与差的正弦函数．专题：三角函数的图像与性质．分析：（1）由条件利用三角函数的恒等变换求得f（ x）的解析式，再根据正弦函数的周期性求得f（ x）的最小正周期．（ 2）由条件利用正弦函数的定义域和值域求得f（ x）的最大值，可得实数m 的取值范围．-来源网络，仅供个人学习参考解答：解：（1）∵函数 f （ x） =cosx?sin（ x+）﹣cos2x+=cosx（ sinx+ cosx）﹣? + =sin2x﹣ cos2x= sin（ 2x﹣），∴函数的最小正周期为．（2）∵，∴，∴．∵ f （x）＜ m 在上恒成立，∴．点评：本题主要考查三角函数的恒等变换及化简求值，三角函数的周期性和求法，正弦函数的定义域和值域，函数的恒成立问题，属于基础题．17．（2014?东莞二模）已知函数．（Ⅰ）求的值；（Ⅱ）求 f （x）的最大值和最小正周期；（Ⅲ）若，α 是第二象限的角，求sin2 α．考点：正弦函数的定义域和值域；同角三角函数间的基本关系；两角和与差的正弦函数；三角函数的周期性及其求法．专题：常规题型；计算题．分析：（Ⅰ）将代入已知函数关系式计算即可；（Ⅱ）利用辅助角公式将f（ x）化为 f（ x） =2sin（ 2x+ ）即可求 f（ x）的最大值和最小正周期；（Ⅲ）由 f（） =2sin α=，可求得 sin α，是α第二象限的角，可求得cos α =，利用正弦函数的二倍角公式即可求得sin2 α．解答：解：（Ⅰ） f （） = sin（ 2×）+ cos（ 2×） = × ﹣×=0 ；（Ⅱ）∵ f （x） =2 （sin2x+ cos2x） =2 （ cos sin2x+sin cos2x） =2sin （ 2x+ ）．∴ f （x）的最大值为2，最小正周期 T= =π；（Ⅲ）由（Ⅱ）知f （ x） =2sin（ 2x+），∴ f （）=2sinα= ，即sinα= ，又α是第二象限的角，∴ cos α =﹣=﹣，∴ sin2 α =2sinα cosα ×=2（×﹣）=﹣．点评：本题考查两角和与差的正弦函数，考查同角三角函数间的基本关系，考查正弦函数的性质及应用，利用辅助角公式求得f （ x） =2sin（ 2x+）是关键，属于中档题．，-来源网络，仅供个人学习参考18．（2014?长安区三模）已知函数f （x）=sin （2x﹣）+2cos2x﹣1．（Ⅰ）求函数 f （x）的单调增区间；（Ⅱ）在△ ABC中， a、b、c 分别是角 A、B、C 的对边，且 a=1，b+c=2，f （A）= ，求△ ABC的面积．考点：正弦函数的单调性；余弦定理．分析：（Ⅰ）函数f（ x）展开后，利用两角和的咨询公司化简为一个角的一个三角函数的形式，结合正弦函数的单调增区间求函数f（ x）的单调增区间．（Ⅱ）利用 f（ A） = ，求出 A 的大小，利用余弦定理求出bc 的值，然后求出△ABC的面积．解答：=解：（Ⅰ）因为==所以函数f（ x）的单调递增区间是〔〕（k∈Z）（Ⅱ）因为f（ A） =，所以又 0＜ A ＜π所以从而故 A=在△ ABC 中，∵a=1 ，b+c=2 ， A=∴1=b2+c 2﹣2bccosA，即 1=4﹣3bc．故 bc=1从而 S△ABC=点评：本题是基础题，考查三角函数的化简求值，单调增区间的求法，余弦定理的应用，考查计算能力，注意A的求法，容易出错．常考题型．19．（2014?诸暨市模拟） A、B 是直线图象的两个相邻交点，且．（Ⅰ）求ω 的值；-来源网络，仅供个人学习参考（Ⅱ）在锐角△ ABC中， a，b，c 分别是角 A，B，C 的对边，若的面积为，求 a 的值．考点：余弦定理的应用；由y=Asin （ω x+ φ）的部分图象确定其解析式．专题：计算题．分析：（ I ）利用二倍角公式，两角差的正弦公式，化简函数f（ x）的解析式为﹣sin（ω x﹣），根据周期，解得ω的值．（ II ）由 f（ A） = ﹣，求得sin（2A﹣）=，结合A的范围求得A 的值，再根据三角形的面积求出边 b 的值，利用余弦定理求出 a 的值．解答：．解：（I）由函数的图象及，得到函数的周期，解得ω =2 ．（II ）∵，∴．又∵△ ABC是锐角三角形，，∴，即．由，由余弦定理，得，即．点评：本题考查正弦定理、余弦定理的应用，二倍角公式，两角差的正弦公式，正弦函数的周期性，根据三角函数的值求角，求出A 的大小，是解题的关键．20．（2014?广安一模）已知函数 f （x）= sin2x+2cos2x+1．（Ⅰ）求函数 f （x）的单调递增区间；（Ⅱ）设△ABC内角A，B，C的对边分别为a，b，c，且c= ，f （C）=3，若向量 =（sinA ，﹣ 1）与向量 =（ 2，sinB ）垂直，求a，b 的值．考点：余弦定理；两角和与差的正弦函数；二倍角的正弦；二倍角的余弦；三角函数的周期性及其求法．专题：计算题．分析：化简 f（ x）；利用三角函数的周期（ I ）利用二倍角公式即公式公式求出周期；令整体角在正弦的递增区间上求出x 的范围即为递增区间．（ II ）先求出角 C，利用向量垂直的充要条件列出方程得到边a， b 的关系；利用余弦定理得到a， b， c 的关系，求出 a， b．解答：（2 分）解：（Ⅰ）∵-来源网络，仅供个人学习参考令，∴函数f （ x）的单调递增区间为，（4 分）（Ⅱ）由题意可知，，∴，∵ 0＜C＜π，∴（舍）或（6分）∵垂直，∴2sinA sinB=0﹣，即 2a=b（ 8 分）∵②（10分）由①②解得，a=1， b=2 ．（ 12 分）点评：本题考查三角函数的二倍角公式、考查三角函数的公式、考查求三角函数的性质常用的方法是整体角处理的方法、考查三角形中的余弦定理．21．（2014?张掖三模）已知 f （ x）= sin ωx﹣ 2sin 2（ω＞0）的最小正周期为3π．（Ⅰ）当 x∈[，]时，求函数 f （ x）的最小值；（Ⅱ）在△ ABC，若 f （ C）=1，且 2sin 2B=cosB+cos（ A﹣C），求 sinA 的值．考三角函数的最值；三角函数的恒等变换及化简求值；由y=Asin （ω x+ φ）的部分图象确定其解析式．点：专综合题．题：分先利用二倍角公式的变形形式及辅助角公式把函数化简为y=2sin（ω x+ ）﹣ 1，根据周期公式可求ω，进析：而求 f（ x）（ I）由 x 的范围求出的范围，结合正弦函数的图象及性质可求（II ）由及 f（C）=1 可得，，结合已知 C 的范围可求 C 2及 A+B ，代入 2sin B=cosB+cos （ A﹣ C），整理可得关于sinA 的方程，解方程可得解解：答：==依题意函数f（ x）的最小正周期为3π，即，解得，所以（Ⅰ）由得，-来源网络，仅供个人学习参考所以，当时，（Ⅱ）由及 f （ C） =1 ，得而，所以，解得在 Rt △ ABC中，，2sin2B=cosB+cos（A﹣C）2cos2A﹣sinA﹣sinA=0，∴ sin2A+sinA ﹣ 1=0 ，解得∵ 0＜sinA＜1，点以三角形为载体，综合考查了二倍角公式的变形形式，辅助角公式在三角函数化简中的应用，考查了三角评：函数的性质（周期、单调区间、最值取得的条件）时常把ω x+φ作为一个整体．22．（2014?漳州三模）在△ ABC中， a，b，c 分别是内角 A，B，C 所对的边，，若向量 =（ 1，sinA ）， =（2，sinB ），且∥ ．（Ⅰ）求 b，c 的值；（Ⅱ）求角 A 的大小及△ ABC的面积．考点：解三角形；平面向量共线（平行）的坐标表示．分析：（Ⅰ）通过向量平行，求出A ， B 的关系式，利用正弦定理求出b 的值，通过余弦定理求出c 的值；（Ⅱ）直接利用正弦定理求出A 的正弦函数值，然后求角A 的大小，结合 C 的值确定 A 的值，利用三角形的面积公式直接求解△ABC的面积．解答：解：（Ⅰ）∵= （1， sinA），= （ 2， sinB），，∴sinB ﹣2sinA=0 ，由正弦定理可知b=2a=2，222又∵c=a +b ﹣ 2abcosC，，所以 c2= （）2+（2）2﹣2cos=9 ，∴c=3 ；（Ⅱ）由，得，∴ sinA=，A=或，又C=，∴A=，所以△ABC的面积 S===．点评：本题是中档题，考查正弦定理与余弦定理的应用，注意向量的平行条件的应用，考查计算能力．-来源网络，仅供个人学习参考23．（2013?青岛一模）已知a， b，c 为△ ABC的内角 A，B，C的对边，满足，函数 f （x）=sin ωx（ω＞ 0）在区间上单调递增，在区间上单调递减．（Ⅰ）证明： b+c=2a；（Ⅱ）若，证明：△ ABC为等边三角形．考点：余弦定理的应用；三角函数恒等式的证明；正弦定理．专题：解三角形．分析：（Ⅰ）通过已知表达式，去分母化简，利用两角和与差的三角函数，化简表达式通过正弦定理直接推出b+c=2a ；（Ⅱ）利用函数的周期求出ω，通过，求出的值，利用余弦定理说明三角形是正三角形，即可．解答：（本小题满分12 分）解：（Ⅰ）∵∴sinBcosA+sinCcosA=2sinA cosBsinA﹣﹣ cosCsinA∴sinBcosA+cosBsinA+sinCcosA+cosCsinA=2sinAsin （ A+B ） +sin （ A+C ）=2sinA （3 分）sinC+sinB=2sinA5（分）所以 b+c=2a （6 分）（Ⅱ）由题意知：由题意知：，解得：，（8分）因为， A ∈（ 0，π），所以（9分）由余弦定理知：（ 10 分）所以 b2+c 2﹣ a2=bc 因为 b+c=2a ，所以，即： b2+c 2﹣ 2bc=0 所以 b=c （ 11 分）又，所以△ABC为等边三角形．（12 分）点评：本题考查三角函数的化简求值，两角和与差的三角函数，正弦定理与余弦定理的应用，考查计算能力．24．（2012?南昌模拟）已知函数．（1）若 f （α） =5，求 tan α的值；-来源网络，仅供个人学习参考（2）设△ ABC三内角 A，B，C所对边分别为a，b，c，且，求 f （x）在（ 0，B]上的值域．考点：正弦函数的定义域和值域；三角函数的恒等变换及化简求值；解三角形．专题：计算题．分析：（ 1）把 f （α）=5 代入整理可得，，利用二倍角公式化简可求tan α（ 2）由，利用余弦定理可得，，即，再由正弦定理化简可求B，对函数化简可得 f （ x） =2sin （2x+ ）+4，由可求．解答：解：（1）由 f（α）=5 ，得．∴．∴，即，∴．（5 分）（ 2）由，即，得，则，又∵B 为三角形内角，∴，（8 分）又= = （10分）由，则，故 5≤ f （x）≤ 6，即值域是 [5， 6] ．（ 12 分）点评：本题主要考查了利用正弦及余弦定理解三角形，辅助角公式的应用，及正弦函数性质等知识的简单综合的运用，属于中档试题．25．（2012?河北区一模）已知函数．（Ⅰ）求 f （x）的单调递增区间；（Ⅱ）在△ ABC中，三内角 A，B，C的对边分别为 a，b，c，已知成等差数列，且=9，求 a 的值．考点：正弦函数的单调性；数列与三角函数的综合；三角函数中的恒等变换应用．-来源网络，仅供个人学习参考专题：计算题．分析：（ I ）利用两角和差的三角公式化简f（x）的解析式，得到 sin（ 2x+ ），由 2k π﹣≤（2x+ ）≤ 2k π+，解出 x 的范围，即得f（ x）的单调递增区间．（ II ）在△ABC中，由，可得sin（2A+）值，可求得A ，用余弦定理求得a 值．解答：解：（I ） f （ x） = = sin2x+ cos2x=sin（2x+ ）．令 2k π﹣≤（ 2x+ ）≤ 2k π+，可得 kπ﹣≤ x≤ kπ+， k∈z．即 f （ x）的单调递增区间为[k π﹣， kπ+ ] ， k∈z．（ II ）在△ ABC中，由，可得 sin（ 2A+ ）= ，∵＜ 2A+ ＜ 2π+，∴＜2A+ = 或，∴ A= （或 A=0 舍去）．∵ b，a， c 成等差数列可得2b=a+c ，∵=9 ，∴ bccosA=9 ．由余弦定理可得a2=b 2+c 2﹣ 2bc?cosA=（ b+c ）2﹣ 3bc=18，∴ a=3．点评：本题考查等差数列的性质，正弦函数的单调性，两角和差的三角公式、余弦定理的应用，化简函数的解析式是解题的突破口．26．（2012?韶关一模）已知函数 f（x）=2cos2ωx+2 sin ωxcosωx ﹣1（ω＞ 0）的最小正周期为π．（1）求 f （）的值；（2）求函数 f （x）的单调递增区间及其图象的对称轴方程．考点：由 y=Asin （ω x+ φ）的部分图象确定其解析式；三角函数的化简求值；三角函数中的恒等变换应用；复合三角函数的单调性．分析：（ 1）利用三角函数的恒等变换化简函数f （x）的解析式为 2sin（ 2ω x+ ），由此求得 f（）的值．（ 2）由 2k π﹣≤ 2x+ ≤ 2k π+， k∈z，求出函数 f（ x）的单调递增区间．由 2x+ =k π+求得 x 的值，从而得到 f （ x）图象的对称轴方程．解答：解：（1）函数 f （ x） =2cos2ω x+2sin ω xcos ω x﹣ 1=cos2 ωsin2x+ ω x=2sin （ 2ω）x+，因为 f（x）最小正周期为π，所以=π，解得ω =1 ，所以 f（x）=2sin （ 2x+ ）， f（） =2sin=1 ．（ 2）由 2k π﹣≤ 2x+ ≤ 2k π+， k∈z，可得 kπ﹣≤ x≤ kπ+，k∈z，所以，函数 f（ x）的单调递增区间为[k π﹣， kπ+ ]， k∈z．-来源网络，仅供个人学习参考由 2x+ =k π+可得 x= kπ+， k∈z．所以， f （ x）图象的对称轴方程为x= kπ+， k∈z．（ 12 分）点评：本题主要考查三角函数的恒等变换及化简求值，复合三角函数的单调性，属于中档题．27．（2012?杭州一模）已知函数f （x）=．（Ⅰ）求 f （x）的最小正周期、对称轴方程及单调区间；（Ⅱ）现保持纵坐标不变，把f （x）图象上所有点的横坐标伸长到原来的 4 倍，得到新的函数 h（x）；（ⅰ）求 h（x）的解析式；（ⅱ）△ABC中，角 A、B、C的对边分别为 a、b、c，且满足，h（A）= ，c=2，试求△ ABC的面积．考点：正弦定理的应用；两角和与差的正弦函数；二倍角的正弦；二倍角的余弦；函数y=Asin （ω x+ φ）的图象变换．分析：f（x）=sin （ 2x+ ）﹣，再结合函数（ I ）利用二倍角的三角函数公式降次，再用辅助角公式合并得y=Asin （ω x+ φ）的图象与性质的有关公式，可得 f （ x）的最小正周期、对称轴方程及单调区间；（ II ）（ i）根据函数 y=Asin（ω x+ φ的）图象变换的公式，不难得到 h（ x）的解析式为 h（ x）=sin（ x+ ）﹣；（ ii）根据 h（ A ）的值结合三角形内角的范围和特殊三角函数的值，求得A= ，再由结合正弦定理，讨论得三角形是等腰三角形或是直角三角形，最后在两种情况下分别解此三角形，再结合面积公式可求出△ABC的面积．解答：= sin2x﹣=sin2xcos +cos2xsin ﹣，解：（I ）∵ f （x）=∴ f （x） =sin （ 2x+ ）﹣，f （x）的最小正周期为 T= =π．令 2x+ = +k π，得x= + kπ，k∈Z ，所以函数图象的对称轴方程为：x= + kπ（，k∈Z）令﹣+2k π≤ 2x+ ≤+2k π，解之得﹣+k π≤ x≤ +k π，所以函数的单调增区间为 [﹣， +k π]，（ k∈Z ）同理可得，函数的单调减区间为[ +k π，+k π]，（ k∈Z ）（ II ）∵保持纵坐标不变，把f（ x）图象上所有点的横坐标伸长到原来的 4 倍，得到新的函数h（ x）∴ h（x） =f （ x） =sin （ x+ ）﹣，（ i） h（ x）的解析式为 h（ x） =sin （ x+ ）﹣；-来源网络，仅供个人学习参考（ ii）∵ h（A） =sin （ A+ ）﹣= ，∴ sin （ A+ ） = ，结合 A ∈（ 0，π）得 A= ∵=∴ sinAcosA=sinBcosB ，可sin2A=sin2B得，即 A=B 或 A+B=①当 A=B 时，因为 c=2 ， A= ，所以△ ABC是边长为 2 的等边三角形，因此，△ABC的面积S=2．×2=②当 A+B= 时，因为 c=2 ，A= ，所以△ ABC是斜边为 2 的直角三角形∴ a=csinA=2 × = ， b=ccosA=2 × =1因此，△ABC的面积S= ×× 1= ．综上所述，得△ABC的面积是或．点评：本题综合了三角恒变换、函数y=Asin （ω x+ φ）的图象变换、利用正余弦定理解三角形等知识，对三角函数的知识进行了综合考查，是一道中档题．28．（2011?辽宁）△ ABC的三个内角 A、B、C所对的边分别为a、b、c，asinAsinB+bcos 2A= a．（Ⅰ）求；（Ⅱ）若 c2 =b2+ a2，求 B．考点：解三角形．专题：计算题．分析：（Ⅰ）先由正弦定理把题设等式中边转化成角的正弦，化简整理求得sinB 和 sinA 的关系式，进而求得 a 和 b 的关系．（Ⅱ）把题设等式代入余弦定理中求得cosB 的表达式，把（Ⅰ）中 a 和 b 的关系代入求得 cosB 的值，进而求得 B．解答：sinA，解：（Ⅰ）由正弦定理得， sin2AsinB+sinBcos 2A=即 sinB（ sin2A+cos 2A） =sinA∴sinB= sinA， =（Ⅱ）由余弦定理和C2=b 2+a2，得 cosB=由（Ⅰ）知b2=2a2，故 c2=（ 2+）a2，可得 cos2B=，又cosB＞0，故cosB=-来源网络，仅供个人学习参考。

专题2 三角函数压轴小题(解析版)

专题2三角函数压轴小题一、单选题 1．（2021·上海市吴淞中学高三期中）如图，半径为1的半圆O 与等边三角形ABC 夹在两平行线12,l l 之间，12l l //，l 与半圆相交于F 、G 两点，与三角形ABC 两边相交于点E 、D ，设弧FG 的长为x (0)x π<<，y EB BC CD =++，若l 从1l 平行移动到2l ，则函数()y f x =的图像大致是（）A ．B ．C ．D ．【答案】D 【分析】根据给定条件求出函数()y f x =的解析式，再借助函数性质即可判断作答. 【详解】依题意，正ABC 的高为1，则其边长BC =如图，连接OF ，OG ，过O 作ON ⊥l 1于N ，交l 于点M ，过E 作EH ⊥l 1于H ，因OF =1，弧FG 的长为x (0)x π<<，则FOG x ∠=，又12////l l l ，即有1122FON FOG x ∠=∠=，于是得cos cos 2x OM OF FON =⋅∠=，1cos 2x EH MN ON OM ==-=-，2cos )sin 6032EH xEB ==-，因此，2cos )22x xy EB BC CD EB BC =++=+=-=，即()2xf x =，0πx <<，显然()f x 在(0,)π上单调递增，且图象是曲线，排除选项A ，B ，而2312432fππ+⎛⎫==<=⎪⎝⎭⎭，C选项不满足，D选项符合要求，所以函数()y f x=的图像大致是选项D.故选：D【点睛】方法点睛：函数图象的识辨可从以下方面入手：(1)从函数的定义域，判断图象的左右位置；从函数的值域，判断图象的上下位置．(2)从函数的单调性，判断图象的变化趋势．(3)从函数的奇偶性，判断图象的对称性．(4)从函数的特征点，排除不合要求的图象．利用上述方法排除、筛选选项．2．（2021·上海市晋元高级中学高三期中）已知(){}|sin,A y y n n Zωϕ==+∈，若存在ϕ使得集合A中恰有3个元素，则ω的取值不可能是（）A．27πB．25πC．2πD．23π【答案】A【分析】利用赋值法逐项写出一个周期中的元素，再结合三角函数诱导公式判断是否存在ϕ符合题意即可.【详解】解：对A，当2=7πω，27siny nϕπ⎛⎫=+⎪⎝⎭，函数的周期为22727Tπππω===在一个周期内，对n赋值当0n=时，sinyϕ=；当1n=时，27sinyπϕ⎛⎫=+⎪⎝⎭；当2n=时，47sinyπϕ⎛⎫=+⎪⎝⎭；当3n=时，67sinyπϕ⎛⎫=+⎪⎝⎭；当4n=时，867s n si7i nyϕππϕ⎛⎫⎛⎫=+=+⎪ ⎪⎝⎭⎝⎭-；当5n=时，10s4n7i n7siyππϕϕ⎛⎫⎛⎫=+=+⎪-⎪⎝⎭⎝⎭；当6n=时，12s2n7i n7siyππϕϕ⎛⎫⎛⎫=+=+⎪-⎪⎝⎭⎝⎭；令2ϕπ=时，sin sin12πϕ==sin sin cos27722227πππππ-⎛⎫⎛⎫+=+=⎪ ⎪⎝⎭⎝⎭sin sin cos47724247πππππ-⎛⎫⎛⎫+=+=⎪ ⎪⎝⎭⎝⎭sin sin cos 67726267πππππ-⎛⎫⎛⎫+=+= ⎪ ⎪⎝⎭⎝⎭所以存在ϕ使得1n =时的y 值等于6n =时的y 值，2n =时的y 值等于5n =时的y 值，3n =时的y 值等于4n =时的y 值.但是当n 等于0、1、2、3时，不存在ϕ使得这个y 值中的任何两个相等所以当2=7πω时，集合A 中至少有四个元素，不符合题意，故A 错误；对B ，当2=5πω，25sin y n ϕπ⎛⎫=+ ⎪⎝⎭，函数的周期为22525T πππω=== 在一个周期内，对n 赋值当0n =时，sin y ϕ=；当1n =时，25sin y πϕ⎛⎫=+ ⎪⎝⎭；当2n =时，45sin y πϕ⎛⎫=+ ⎪⎝⎭；当3n =时，645s n si 5i n y ϕππϕ⎛⎫⎛⎫=+=+ ⎪ ⎪⎝⎭⎝⎭-；当4n =时，825s n si 5i n y ϕππϕ⎛⎫⎛⎫=+=+ ⎪ ⎪⎝⎭⎝⎭-；令2ϕπ=，sin 12π= sin sin cos 25522225πππππ-⎛⎫⎛⎫+=+= ⎪ ⎪⎝⎭⎝⎭sin sin cos 45524245πππππ-⎛⎫⎛⎫+=+= ⎪ ⎪⎝⎭⎝⎭所以当2=5πω时，符合题意，故B 正确；对C ，当=2πω，2sin y n πϕ⎛⎫=+ ⎪⎝⎭，函数的周期为2242T πππω=== 在一个周期内，对n 赋值当0n =时，sin y ϕ=；当1n =时，sin cos 2y πϕϕ⎛⎫=+= ⎪⎝⎭；当2n =时，()sin sin y ϕπϕ=+=-；当3n =时，sin os 3c 2y πϕϕ⎛⎫=+=- ⎪⎝⎭；令0ϕ=，则sin0sin00=-=，cos01=，cos01-=- 所以当=2πω时，符合题意，故C 正确；对D ，当32=πω，23sin y n ϕπ⎛⎫=+ ⎪⎝⎭，函数的周期为22323T πππω=== 在一个周期内，对n 赋值当0n =时，sin y ϕ=；当1n =时，23sin y πϕ⎛⎫=+ ⎪⎝⎭；当2n =时，43sin y πϕ⎛⎫=+ ⎪⎝⎭；令0ϕ=，sin00=，2sin 3π=4sin 3π= 所以当32=πω时，符合题意，故D 正确. 故选：A. 【点睛】方法点睛：本题一共有三个变量：ω，n ，ϕ.属于多变量题目，对于该题，要先确定一个变量，再对第二个变量赋值，然后再对第三个变量赋值，以此分类讨论即可.3．（2021·广西南宁·高三月考（文））已知函数f (xx +4cos x )+2sin x ，则f (x )的最大值为（） A ．B ．172C ．6D ．【答案】B 【分析】先将sin 2x 展开，提公因式并结合拼凑法可得())()21sin 24f x x x =++-，结合22a b ab +⎛⎫≤ ⎪⎝⎭放缩，联立辅助角公式化简，即可求解. 【详解】()))sin 24cos 2sin 2sin cos 4cos 2sin f x x x x x x x x ++++()())()sin 22sin 2421sin 24x x x x x =+++-=++-，由sin 20x +>可知，要求()f x最大值，只需10x +>即可，结合基本不等式22a b ab +⎛⎫≤ ⎪⎝⎭可得())()222sin 3321sin 242442x f x x x π⎛⎫⎛⎫++ ⎪ ⎪⎝⎭⎝⎭=++-≤⋅-=-⎝⎭172≤，当且仅当1sin 2sin 13x x x π+=+⎨⎛⎫+=⎪ ⎪⎝⎭⎩，即62,x k k Z ππ=+∈时等号成立，因此当62,x k k Z ππ=+∈时()f x的最大值为172. 故选：B4．（2021·江苏扬州·高三月考）已知△ABC 的内角,,A B C 所对的边分别为,,a b c 若sin sin 2B Cb a B +=，且△ABC 内切圆面积为9π，则△ABC 面积的最小值为（）AB ．C ．D ．【答案】D 【分析】根据已知条件及正弦定理可得3A π=，由内切圆的面积可得内切圆半径3r =，最后根据()1sin 22ABCr a b c Sbc A ++==及余弦定理，并结合基本不等式求bc 的范围，进而求△ABC 面积的最小值. 【详解】由题设，sin sin sin sin 2B C B A B +=，而sin 0B ≠且222B C Aπ+=-， ∴cos sin 2sin cos 222A A A A ==，022A π<<，则1sin 22A =，∴3A π=，由题设△ABC 内切圆半径3r =，又()1sin 22ABCr a b c Sbc A ++==，∴)a b c bc ++=，而222222cos a b c bc A b c bc bc =+-=+-≥，即a ≥∴bc ≥108bc ≥，当且仅当a b c ===.∴1sin 2ABCSbc A =≥ 故选：D5．（2021·四川绵阳·高三月考（理））函数()()3sin x x f ωϕ=+（0>ω，2πϕ<），已知||33f π⎛⎫= ⎪⎝⎭，且对于任意的R x ∈都有066f x f x ππ⎛⎫⎛⎫-++--= ⎪ ⎪⎝⎭⎝⎭，若()f x 在52,369ππ⎛⎫⎪⎝⎭上单调，则ω的最大值为（）A ．11B ．9C ．7D ．5【答案】D 【分析】结合正弦函数的最值，对称性求ϕ的值，再结合单调性确定ω的最大值. 【详解】∵ ||33f π⎛⎫= ⎪⎝⎭，()()3sin x x f ωϕ=+，∴32k ππωϕπ+=+，k Z ∈，又对于任意的R x ∈都有066f x f x ππ⎛⎫⎛⎫-++--= ⎪ ⎪⎝⎭⎝⎭， ∴ 6m πωϕπ-+=，m Z ∈，∴ 3(2)2k m πϕπ=++，又2πϕ<，∴ 6π=ϕ或6πϕ=-，当6π=ϕ时， 31w k =+，k Z ∈且61w m =-+，当7w =时，()3sin 76f x x π⎛⎫ ⎪⎝=⎭+，若52,369x，则4131736618x πππ≤+≤， ∴()f x 在52,369ππ⎛⎫⎪⎝⎭上不单调，C 错误，当6πϕ=-时， 32w k =+，k Z ∈且61w m =--，当11w =时，()3sin 116f x x π⎛⎫ ⎪⎝-⎭=，若52,369x，则49411136618x πππ≤-≤， ∴()f x 在52,369ππ⎛⎫ ⎪⎝⎭上不单调，A 错误，当5w =时，()3sin 56f x x π⎛⎫ ⎪⎝=⎭-，若52,369x，则1917536618x πππ≤-≤， ∴()f x 在52,369ππ⎛⎫⎪⎝⎭上单调，D 正确，故选：D. 【点睛】已知f (x )＝Asin (ωx ＋φ)(A ＞0，ω＞0)的性质求函数解析式的关键在于转化为正弦函数的问题.6．（2021·河北·邯郸市肥乡区第一中学高三开学考试）在ABC 中，角A ，B ，C 的对边分别为a ，b ，c ，若cos cos sin sin()sin B C AA C bc C ⎛⎫++=⎪⎝⎭，3B π=，则a c +的取值范围是（）A ．⎝B ．32⎛ ⎝C ．⎣D ．32⎡⎢⎣【答案】A 【分析】利用三角恒等变换及正弦定理将cos cos sin sin()sin B C AA C b c C⎛⎫++= ⎪⎝⎭进行化简，可求出b 的值，再利用边化角将a c +化成角，然后利用辅助角公式及角的范围即可得到答案. 【详解】由题知cos cos sin sin()sin B C AA C bc C ⎛⎫++=⎪⎝⎭，3B π= ∴cos cos sin sin sin B C AB bc C ⎛⎫+=⎪⎝⎭即cos cos B C b c +=由正弦定理化简得∴cos cos c B b C ⋅+⋅==∴sin cos cos sin C B C B +∴sin()sin B C A +==∴b =3B π=∴1sin sin sin a b cA B C===∴23sin sin sin sin()sin )326a c A C A A A A A ππ+=+=+-=+=+203A π<<∴5666A πππ<+<∴)6A π<+≤a c <+≤故选：A .【点睛】方法点睛：边角互化的方法（1）边化角：利用正弦定理2sin sin sin a b cr A B C===（r 为ABC 外接圆半径）得2sin a r A =，2sin b r B =，2sin c r C =；（2）角化边： ①利用正弦定理：sin 2aA r=，sin 2b B r =，sin 2c C r= ②利用余弦定理：222cos 2b c a A bc+-=7．（2021·四川·绵阳中学实验学校模拟预测）某城市要在广场中央的圆形地面设计一块浮雕，彰显城市积极向上的活力.某公司设计方案如图，等腰PMN 的顶点P 在半径为20m 的大⊙O 上，点M ，N 在半径为10m 的小⊙O 上，点O ，点P 在弦MN 的同侧.设2(0)2MON παα=<<∠，当PMN 的面积最大时，对于其它区域中的某材料成本最省，则此时cos α=（）A ．12B C D 【答案】C 【分析】用α表示出PMN 的面积为()S α，求导()S α'，令()0S α'=求得极值点，从而求得PMN 面积最大时对应的cos α值. 【详解】如图所示，等腰PMN 中，2(0)2MON παα=<<∠设PMN 的面积为()S α，则()2OPN OMNS SSα=⨯+1122010sin()1010sin 222παα⎡⎤=⨯⨯⨯⨯-+⨯⨯⨯⎢⎥⎣⎦200sin 50sin 2,(0)2πααα=+<<求导()200cos 250cos 2200cos 100cos 2S ααααα'=+⨯=+22200cos 100(2cos 1)100(2cos 2cos 1)αααα=+-=+-令()0S α'=，即22cos 2cos 10αα+-=，解得：1cos 2α=-记01cos 2α=-， 00,2πα⎛⎫∈ ⎪⎝⎭当()00,αα∈，()0S α'>，函数单调递增；当 0,2παα⎛⎫∈ ⎪⎝⎭，()0S α'<，函数单调递减；故当0αα=时，即1cos 2α=-， ()S α取得极大值，即最大值.故选：C8．（2021·北京八中高三月考）已知()()3sin 2f x x ϕ=+（ϕ∈R ）既不是奇函数也不是偶函数，若()y f x m =+的图像关于原点对称，()y f x n =+的图像关于y 轴对称，则m n +的最小值为（） A ．π B ．2π C ．4π D ．8π 【答案】C 【分析】结合五点作图法及函数图象进行计算求解即可. 【详解】可设0ϕ满足00,22ππϕπ⎛⎫⎛⎫∈⋃ ⎪ ⎪⎝⎭⎝⎭，, 且02t ϕπϕ=+（t Z ∈）,则()()03sin 2f x x ϕ=+,注意到五点作图法的最左边端点为0,02ϕ⎛⎫- ⎪⎝⎭,而22T π=,44T π=,故有0000min ,min ,2222m ϕπϕϕπϕ--⎛⎫⎛⎫=- ⎪ ⎪⎝=⎭⎝⎭,002244n ϕππϕ-=-+=, 当002πϕ⎛⎫∈ ⎪⎝⎭，时，02m ϕ=，024n πϕ-=，此时4m n π+=；当0,2πϕπ⎛⎫∈ ⎪⎝⎭时，02m πϕ-=，024n ϕπ-=，此时002244m n πϕϕππ--+=+=, 故选：C ．9．（2021·吉林·梅河口市第五中学高三月考（理））已知点,024A π⎛⎫⎪⎝⎭在函数()()cos f x x ωϕ=+（0>ω且，*ω∈N ，0ϕπ<<）的图像上，直线6x π=是函数()f x 图像的一条对称轴.若()f x 在区间,63ππ⎛⎫⎪⎝⎭上单调，则ϕ=（） A ．6πB ．4πC ．3π D ．23π【答案】C 【分析】由()f x 在区间,63ππ⎛⎫⎪⎝⎭内单调求出ω的范围，先由函数零点与对称轴之间的关系求出周期，进而求得ω，利用对称轴即可求出ϕ. 【详解】∵()f x 在区间,63ππ⎛⎫⎪⎝⎭内单调，3662T πππ∴-=≤，得1226ππω⨯≥，所以06ω<≤ ∵24x π=是函数()()cos f x x ωϕ=+的零点，直线6x π=是函数()f x 的图象的一条对称轴，∴6248πππ-=，若84T π=，则2T π=，此时22ππω=，得4ω=，满足条件，若384T π=，则6T π=，此时26ππω=，得12ω=，不满足条件，综上可知，函数()()cos 4f x x ϕ=+， ∵6x π=是函数()f x 的图象的一条对称轴，∴4,6k k Z πϕπ⨯+=∈，即2,3k k Z πϕπ=-∈， ∵0ϕπ<<，∴3πϕ=，故选：C 【点睛】关键点点睛：本题主要考查三角函数性质的应用，结合的单调区间以及对称轴对称中心之间的关系求出周期和ω是解决本题的关键，属于一般题.10．（2021·浙江·高三专题练习）如图，某人在垂直于水平地面ABC 的墙面前的点A 处进行射击训练，已知点A 到墙面的距离为AB ，某目标点P 沿墙面上的射线CM 移动，此人为了准确瞄准目标点P ，需计算由点A 观察点P 的仰角θ的大小，若15,25,30AB cm AC cm BCM ==∠=︒，则tan θ的最大值是（）.（仰角θ为直线AP 与平面ABC 所成的角）A B C D 【答案】D 【分析】由题可得，20BC =，过P 作PP BC '⊥，交BC 于P '，连接'AP ，则tan PP AP θ'='，设(0)BP x x '=>，分类讨论，若P '在线段BC 上，则20CP x '=-，可求出PP '和'AP ，从而可得出220tan 225x x θ-=+利用函数的单调性，可得出0x =时，取得最大值；若P '在CB 的延长线上，同理求出PP '和'AP ，可得出220tan 225x x θ++，可得当454x =时，函数取得最大值；结合两种情况的结果，即可得出结论．【详解】解：15,25AB cm AC cm ==，AB BC ⊥，由勾股定理知，20BC =，过点P 作PP BC '⊥交BC 于P '，连结'AP ，则tan PP AP θ'='，设(0)BP x x '=>，若P '在线段BC 上，则20CP x '=-，由30BCM ∠=︒，得tan30)PP CP x ''=︒-，在直角ABP '△中，AP '2320tan 225x x θ-∴=+令y ，则函数在[0x ∈，20]单调递减，0x ∴=若P '在CB 的延长线上，tan30)PP CP x ''=︒+，在直角ABP '△中，AP '2320tan 225x x θ+∴=+令22(20)225x y x +=+，则0y '=可得454x =.．11．（2021·全国·高三专题练习）设△ABC 的三边长为BC a =，=CA b ，AB c =，若tan 2A a b c =+，tan 2B ba c=+，则△ABC 是（）． A ．等腰三角形B ．直角三角形C ．等腰三角形或直角三角形D ．等腰直角三角形【答案】B 【分析】若三角形各边长为a 、b 、c 且内切圆半径为r ，法一：由内切圆的性质有tan2A a b c =+、tan 2B ba c=+，根据边角关系可得a b =或222+=a b c ，注意讨论所得关系验证所得关系的内在联系；法二：由半角正切公式、正弦定理可得A B =或π2A B +=，结合三角形内角的性质讨论所得关系判断三角形的形状. 【详解】设()12P a b c =++，△ABC 的内切圆半径为r ，如图所示，法一： ∴tan2A r a p a b c ==-+①；tan 2B r b p b a c==-+②. ①÷②，得：p b a a cp a b c b -+=⋅-+，即()()()()22p b a a c p a b b c -+=-+．于是()()()()b b c c a b a a c b c a ++-=++-，232232ab b bc a b a ac -+=-+，()()2220a b a b c -+-=，从而得a b =或222+=a b c ，∴A B ∠=∠或90C ∠=︒．故△ABC 为等腰三角形或直角三角形，（1）当a b =时，内心I 在等腰三角形CAB 的底边上的高CD 上，12ABCS AB CD c =⋅△，从而得2S r a b c ==++．又()1122p a b c a c -=+-=()22a abc a ca c c ==+++⋅a a c=+，上式两边同时平方，得：()2222a c a a c a c -=++，化简2220c a -=，即c ．即△ABC 直角三角形， ∴△ABC 为等腰直角三角形．（2）当222+=a b c 时，易得()12r a b c =+-．代入②式，得()()1212a b c b a c a c b +-=++-，此式恒成立，综上，△ABC 为直角三角形．法二：利用sin tan21cos A A A =+，sin tan 21cos B B B =+及正弦定理和题设条件，得sin sin 1cos sin sin A A A B C=++①，sin sin 1cos sin sin B B B A C=++②.∴1cos sin sin A B C +=+③；1cos sin sin B A C +=+④.由③和④得：1cos sin 1cos sin A B B A +-=+-，即sin cos sin cos A A B B +=+，ππsin sin 44A B ⎛⎫⎛⎫+=+ ⎪ ⎪⎝⎭⎝⎭，因为,A B 为三角形内角， ∴ππ44A B +=+或πππ44A B +=--，即A B =或π2A B+=．（1）若A B =，代入③得：1cos sin sin A B C +=+⑤又ππ2C A B A =--=-，将其代入⑤，得：1cos sin sin 2A A A +=+．变形得()()2sin cos sin cos 0A A A A ---=，即()()sin cos sin cos 10A A A A ---=⑥，由A B =知A 为锐角，从而知sin cos 10A A --≠． ∴由⑥，得：sin cos 0A A -=，即π4A =，从而π4B =，π2C =．因此，△ABC 为等腰直角三角形．（2）若π2A B +=，即π2C =，此时③④恒成立，综上，△ABC 为直角三角形．故选：B12．（2021·河北·石家庄一中高三月考）在锐角ABC 中，角、、A B C 所对的边分别为,,a b c ，若22a c bc -=，则113sin tan tan A C A-+的取值范围为（）A ．)+∞B ．C ．(6D ．)6【答案】C 【分析】根据余弦定理以及正弦定理化简条件得A 、C 关系，再根据二倍角正切公式以及函数单调性求范围．【详解】∵22a c bc -=，∴所以22cos 2cos sin 2sin cos sin ,b bc A bc b c A c B C A C -=∴-=∴-=sin()2sin cos sin ,sin()sin ,2A C C A C A C C A C C A C +-=∴-=∴-==因此22111111tan 1tan 3sin =3sin 3sin 3sin tan tan tan tan 2tan 2tan 2tan C CA A A A C A C C C C C-+-+-+=-+=+ 113sin 3sin 2sin cos sin A A C C A=+=+设sin A t =，∵ABC 是锐角三角形，∴(0,),(0,),(0,)22222A A A C B A ππππ∈=∈=--∈，∴(,)32A ππ∈∴sin A t =∈，1+3t t 在t ∈上单调递增，∴1113sin +34)tan tan A t C A t -+=∈，故选：C13．（2021·贵州遵义·高三月考（文））已知函数()()cos 33f x a x x a ππ⎛⎫⎛⎫=--∈ ⎪ ⎪⎝⎭⎝⎭R 是偶函数.若将曲线()2y f x =向左平移12π个单位长度后，再向上平移1个单位长度得到曲线()y g x =，若关于x 的方程()g x m =在70,12π⎡⎤⎢⎥⎣⎦有两个不相等实根，则实数m 的取值范围是（）A ．[]0,3B ．[)0,3C ．[)2,3D ．)1,3【答案】C 【分析】本题首先可根据函数()f x 是偶函数得出33f f ππ⎛⎫⎛⎫=- ⎪ ⎪⎝⎭⎝⎭，通过计算得出1a =-，然后通过转化得出()2sin 2f x x π⎛⎫=- ⎪⎝⎭，通过图像变换得出()2sin 213g x x π⎛⎫=-+ ⎪⎝⎭，最后根据正弦函数对称性得出52,636x πππ⎡⎤-∈⎢⎥⎣⎦且232x ππ-≠，通过求出此时()g x 的值域即可得出结果. 【详解】因为函数()()cos 33f x a x x a ππ⎛⎫⎛⎫=--∈ ⎪ ⎪⎝⎭⎝⎭R 是偶函数，所以33f f ππ⎛⎫⎛⎫=- ⎪ ⎪⎝⎭⎝⎭，即22cos 00cos 33a a ππ⎛⎫⎛⎫=-- ⎪ ⎪⎝⎭⎝⎭， 1322a a =--，解得1a =-，()cos 33f x x x ππ⎛⎫⎛⎫=--- ⎪ ⎪⎝⎭⎝⎭，则()1cos 2cos 33323f x x x x x ππππ⎤⎛⎫⎛⎫⎛⎫⎛⎫---=---⎥ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦2sin 32sin 62x x πππ⎛⎫⎛⎫--=- ⎪ ⎪⎝⎭⎝⎭=，则()22sin 22y f x x π⎛⎫==- ⎪⎝⎭，向左平移12π个单位长度后，得到2sin 23y x π⎛⎫=- ⎪⎝⎭，向上平移1个单位长度，得到()2sin 213y g x x π⎛⎫- ⎝=+⎪⎭=，当70,12x π⎡⎤∈⎢⎥⎣⎦时，52,336x πππ⎡⎤-∈-⎢⎥⎣⎦，结合正弦函数对称性易知，()g x m =在70,12π⎡⎤⎢⎥⎣⎦有两个不相等实根，则52,636x πππ⎡⎤-∈⎢⎥⎣⎦且232x ππ-≠，此时()[)2,3g x ∈，实数m 的取值范围是[)2,3，故选：C. 【点睛】关键点点睛：本题考查三角函数图像变换、正弦函数性质、偶函数的性质的应用以及两角差的正弦公式，能够根据偶函数的性质求出1a =-是解决本题的关键，考查计算能力，考查化归与转化思想，体现了综合性，是难题.14．（2021·全国·高三专题练习（文））在ABC 中，()sin sin sin A B B C -+=，点D 在边BC 上，且22CD BD ==，设sin sin ABDk BAD∠=∠，则当k 取最大值时，sin ACD ∠=（）A ．14BCD【答案】B 【分析】根据()sin sin sin A B B C -+=，利用两角和与差的正弦公式化简得到sin 2cos sin B A B =，进而求得A ，根据点D 在边BC 上，且2CD BD =，得到sin 3sin ABD AD AD k BAD BD BC∠===∠，再由余弦定理结合2133AD AB AC =+两边平方，得到2222242421c b c b bc b c k c b c b bc b c ++++==+-+-，令c t b =，得到()222142421111t t t t k f t t t t t ++++===-++-，用基本不等式法或者导数法求得最大值时a ，b ，c 的关系，再利用正弦定理求解. 【详解】因为()sin sin sin A B B C -+=，所以()()sin sin sin A B B A B -+=+，即sin 2cos sin B A B =，因为()0,B π∈，所以sin 0B ≠，1cos 2A =，因为()0,A π∈，所以3A π=，因为点D 在边BC 上，且2CD BD =，所以sin 3sin ABD AD ADk BAD BD BC∠===∠，设,,AB c AC b BC a ===，则13AD ak =，在ABC 中，由余弦定理得222222cos a c b bc A c b bc =+-=+-，()121333AD AB BD AB BA AC AB AC =+=++=+，所以222133AD AB AC ⎛⎫=+ ⎪⎝⎭，即22221414cos 9999a k c b bc BAC =++∠，即222242a k c b bc =++，所以222222224242421c bc b bc c b bc b c k c b a c b bc b c++++++===+-+-，令c t b =，得()222142421111t t t t k f t t t t t ++++===-++-，下面采用基本不等式和导数两种方法求解：方法一：利用基本不等式求解：222211426()4212411311()24t t t t t k t t t t t ++-++===+-++--+，要使k 最大，需2k 最大，当2k 取最大值时，必有102t ->，2216()6244441313()()12424()2t k t t t -=+=+≤+=+-+-+-当且仅当13124()2t t -==-t所以t 2224211t t k t t ++=-+有最大值4+k的最大值为1c b =所以)1b c =，解得a ==，在ABC 中，由正弦定理得sin sin a cA C=，解得sin sin c A C a ==，即sin ACD ∠=下面采用导数的方法求解：求导得()()2226631t t f t tt -++'=-+，令()0f t '=，解得t =，当0t <<()0f t '>，当t >()0f t '<，所以当t =时，()f t 取得最大值，此时c b =，所以)1b c =，解得a ==，在ABC 中，由正弦定理得sin sin a cA C=，解得sin sin c A C a ==，即sin ACD ∠= 故选：B. 【点睛】关键点点睛：本题关键是利用正弦定理得到sin 3sin ABD AD ADk BAD BD BC∠===∠，然后利用余弦定理表示BC ，利用平面向量表示AD 而得解.15．（2021·新疆·莎车县第一中学高三期中）已知函数()()sin 02f x x πωω⎛⎫=+> ⎪⎝⎭，将()f x 的图象向右平移3ωπ个单位得到函数()g x 的图象，点A ，B ，C 是()f x 与()g x 图象的连续相邻的三个交点，若ABC 是钝角三角形，则ω的取值范围是（）A ．,⎫+∞⎪⎪⎝⎭B ．,⎫+∞⎪⎪⎝⎭C ．⎛⎫⎪ ⎪⎝⎭ D ．⎛⎫⎪ ⎪⎝⎭【答案】D 【分析】由函数图象的平移可得()πcos 3g x x ω⎛⎫=- ⎪⎝⎭，作出函数的图象，结合三角函数的图象与性质、平面几何的知1<，即可得解. 【详解】由条件可得，()πcos 3g x x ω⎛⎫=- ⎪⎝⎭，作出两个函数图象，如图：A ，B ，C 为连续三交点，(不妨设B 在x 轴下方)，D 为AC 的中点，.由对称性可得ABC 是以B 为顶角的等腰三角形，2π2AC T CD ω===，由πcos cos 3x x ωω⎛⎫=- ⎪⎝⎭，整理得cos x x ωω=，得cos x ω=，则C B y y =-=2B BD y = 要使ABC 为钝角三角形，只需π4ACB ∠<即可，由tan 1BD ACB DC ∠==<，所以0ω<<.故选：D. 【点睛】关键点点睛：解决本题的关键是准确把握三角函数的图象与性质，合理转化条件，得到关于ω的不等式，运算即可.16．（2021·全国·高三专题练习（理））已知2()2sin 1(0)3f x x πωω⎛⎫=+-> ⎪⎝⎭，给出下列结论：①若f (x 1)=1，f (x 2)=﹣1，且|x 1﹣x 2|min =π，则ω=1；②存在ω∈(0，2)，使得f (x )的图象向左平移6π个单位长度后得到的图象关于y 轴对称； ③若f (x )在[0，2π]上恰有7个零点，则ω的取值范围为4147,2424⎡⎤⎢⎥⎣⎦；④若f (x )在,64ππ⎡⎤-⎢⎥⎣⎦上单调递增，则ω的取值范围为20,3⎛⎤⎥⎝⎦.其中，所有正确结论的编号是（）A ．①②B ．②③C ．①③D ．②④【答案】D 【分析】对函数()f x 化简可得()sin 26f x x πω⎛⎫=+ ⎪⎝⎭，进而结合三角函数的最值、周期性、单调性、零点、对称性及平移变换，对四个命题逐个分析，可选出答案. 【详解】∵22()2sin 1cos 2sin 2336f x x x x πππωωω⎛⎫⎛⎫⎛⎫=+-=-+=+ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭，∴()f x 的最小正周期为22ππωω=. 对于① ：因为f (x 1)=1，f (x 2)=﹣1，且|x 1﹣x 2|min =π，所以()f x 的最小正周期为T =2π，122ππωω∴=⇒=. 故① 错误；对于② ：图象变换后所得函数为sin 236y x ωππω⎛⎫=++ ⎪⎝⎭，若其图象关于y 轴对称，则362k ωππππ+=+，k ∈Z ，解得ω=1+3k ，k ∈Z ，当k =0时，1(0,2)ω=∈.故② 正确；对于③ ：设26t x πω=+，当[]0,2x π∈时，2,4666t x πππωωπ⎡⎤=+∈+⎢⎥⎣⎦. ()f x 在[0,2]π上有7个零点，即sin y t =在,466t ππωπ⎡⎤∈+⎢⎥⎣⎦上有7个零点.则7486ππωππ≤+<，解得41472424ω≤<. 故③错误；对于④ ：由222,262k x k k Z ππππωπ-+++∈，得,,36k k xk Z ππππωωωω-++∈，取k =0，可得36x ππωω-，若f (x )在,64ππ⎡⎤-⎢⎥⎣⎦上单调递增，则3664ππωππω⎧--⎪⎪⎨⎪⎪⎩，解得203ω<.故④ 正确. 故选：D. 【点睛】关键点睛：本题考查三角函数的恒等变形和正弦函数的单调性、周期性、奇偶性、零点等知识，解答③的关键是先化简函数不等式得()sin 26f x x πω⎛⎫=+ ⎪⎝⎭，设26t x πω=+，当[]0,2x π∈时，2,4666t x πππωωπ⎡⎤=+∈+⎢⎥⎣⎦，将问题转化为sin y t =在,466t ππωπ⎡⎤∈+⎢⎥⎣⎦上有7个零点.17．（2021·浙江·高三专题练习）已知,,αβγ是互不相同的锐角，则在sin cos ,sin cos ,sin cos αββγγα三个值中，大于12的个数的最大值是（） A ．0 B ．1 C ．2 D ．3【答案】C 【分析】利用基本不等式或排序不等式得3sin cos sin cos sin cos 2αββγγα++≤，从而可判断三个代数式不可能均大于12，再结合特例可得三式中大于12的个数的最大值. 【详解】法1：由基本不等式有22sin cos sin cos 2αβαβ+≤，同理22sin cos sin cos 2βγβγ+≤，22sin cos sin cos 2γαγα+≤，故3sin cos sin cos sin cos 2αββγγα++≤，故sin cos ,sin cos ,sin cos αββγγα不可能均大于12. 取6πα=，3πβ=，4πγ=，则1111sin cos ,sin cos ,sin cos 4222αββγγα=<=>=>，故三式中大于12的个数的最大值为2，故选：C.法2：不妨设αβγ<<，则cos cos cos ,sin sin sin αβγαβγ>><<，由排列不等式可得：sin cos sin cos sin cos sin cos sin cos sin cos αββγγααγββγα++≤++，而()13sin cos sin cos sin cos sin sin 222αγββγαγαβ++=++≤，故sin cos ,sin cos ,sin cos αββγγα不可能均大于12. 取6πα=，3πβ=，4πγ=，则1111sin cos ,sin cos ,sin cos 4222αββγγα=<=>=>，故三式中大于12的个数的最大值为2，故选：C. 【点睛】思路分析：代数式的大小问题，可根据代数式的积的特征选择用基本不等式或拍雪进行放缩，注意根据三角变换的公式特征选择放缩的方向.视频18．（2021·天津市天津中学高三月考）函数()()2sin (0,0)f x x ωϕωϕπ=+><<的图象如图，把函数()f x 的图象上所有的点向右平移6π个单位长度，可得到函数()y g x =的图象，下列结论中： ①3πϕ=；②函数()g x 的最小正周期为π；③函数()g x 在区间,312ππ⎡⎤-⎢⎥⎣⎦上单调递增；④函数()g x 关于点,03π⎛-⎫⎪⎝⎭中心对称其中正确结论的个数是（）．A ．4B ．3C ．2D ．1【答案】C 【分析】对①，先根据图象分析出ω的取值范围，然后根据()0f ϕ的可取值，然后分类讨论ϕ的可取值是否成立，由此确定出,ωϕ的取值；对②，根据图象平移确定出()g x 的解析式，利用最小正周期的计算公式即可判断；对③，先求解出()g x 的单调递增区间，然后根据k 的取值确定出,312ππ⎡⎤-⎢⎥⎣⎦是否为单调递增区间；对④，根据3g π⎛⎫- ⎪⎝⎭的值是否为0,即可判断.【详解】解：由图可知： 1112113124T T ππ⎧<⎪⎪⎨⎪>⎪⎩，11211129πππω∴<<，即18241111ω<<，又()02sin f ϕ==0ϕπ<<，由图可知：23ϕπ=，又11112sin 21212f ππωϕ⎛⎫⎛⎫=+= ⎪ ⎪⎝⎭⎝⎭， 112,122k k Z ππωϕπ∴+=+∈，且113,2122ππωπ⎛⎫∈ ⎪⎝⎭， 113,3122ππωϕπ⎛⎫⎛⎫∴+∈ ⎪ ⎪⎝⎭⎝⎭，故1k =，当23ϕπ=时，1111126πωπ=，解得：2ω=，满足条件， ()22sin 23f x x π⎛⎫∴=+⎪⎝⎭，故()22sin 22sin 2633g x x x πππ⎛⎫⎛⎫⎛⎫=-+=+ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭，对①，由上述可知①错误；对②，()2sin 23g x x π⎛⎫=+ ⎪⎝⎭，()g x ∴的最小正周期为2=2ππ，故②正确；对③，令222,232k x k k Z πππππ-≤+≤+∈，即5,1212k x k k Z ππππ-≤≤+∈，令0k =，此时单调递增区间为5,1212ππ⎡⎤-⎢⎥⎣⎦，且5,,3121212ππππ⎡⎤⎡⎤-⊆-⎢⎥⎢⎥⎣⎦⎣⎦，故③正确；对④，2sin 20333g πππ⎛⎫⎛⎫⎛⎫-=⨯-+=≠ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭，,03π⎛⎫∴- ⎪⎝⎭不是对称中心，故④错误；故选：C. 【点睛】方法点睛：已知函数()()sin g x A x ωϕ=+()0ω>，若求函数()g x 的单调递增区间，则令ππ2π2π22k x k ωϕ-<+<+，Z k ∈；若求函数()g x 的单调递减区间，则令π3π2π2π22k x k ωϕ+<+<+，Z k ∈；若求函数()g x 图象的对称轴，则令ππ2x k ωϕ+=+，Z k ∈；若求函数()g x 图象的对称中心或零点，则令πx k ωϕ+=，Z k ∈．19．（2021·山西太原·三模（理））在ABC 中，()sin sin sin A B B C -+=，点D 在边BC 上，且2CD BD =，设sin sin ABDk BAD∠=∠，则当k 取最大值时，sin ACD ∠=（）A ．14BCD．(36【答案】B 【分析】根据()sin sin sin A B B C -+=，利用两角和与差的正弦公式化简得到sin 2cos sin B A B =，进而求得A ，根据点D 在边BC 上，且2CD BD =，得到sin 3sin ABD AD AD k BAD BD BC∠===∠，再由余弦定理结合2133AD AB AC =+两边平方，得到2222242421c b c b bc b c k c b c b bc b c ++++==+-+-，令c t b =，得到()222142421111t t t t k f t t t t t ++++===-++-，用导数法求得最大值时a ，b ，c 的关系，再利用正弦定理求解. 【详解】因为()sin sin sin A B B C -+=，所以()()sin sin sin A B B A B -+=+，即sin 2cos sin B A B =，因为()0,B π∈，所以sin 0B ≠，1cos 2A =，因为()0,A π∈，所以3A π=，因为点D 在边BC 上，且2CD BD =，所以sin 3sin ABD AD ADk BAD BD BC∠===∠，设,,AB c AC b BC a ===，则13AD ak =，在ABC 中，由余弦定理得222222cos a c b bc A c b bc =+-=+-，()121333AD AB BD AB BA AC AB AC =+=++=+，所以222133AD AB AC ⎛⎫=+ ⎪⎝⎭，即22221414cos 9999a k c b bc BAC =++∠，即222242a k c b bc =++，所以222222224242421c bc b bc c b bc b c k c b a c b bc b c++++++===+-+-，令c t b =，得()222142421111t t t t k f t t t t t ++++===-++-，则()()2226631t t f t tt -++'=-+，令()0f t '=，解得t当0t <<()0f t '>，当t >()0f t '<，所以当t =时，()f t取得最大值，此时c b =，所以)1b c =，解得a ==，在ABC 中，由正弦定理得sin sin a c A C =，解得sin sin c A C a ==即sin ACD ∠= 故选：B 【点睛】关键点点睛：本题关键是利用正弦定理得到sin 3sin ABD AD ADk BAD BD BC∠===∠，然后利用余弦定理表示BC ，利用平面向量表示AD 而得解.20．（2021·山西太原·一模（理））已知函数()sin()0,||2f x x πωϕωϕ⎛⎫=+>< ⎪⎝⎭的图象关于3x π=-对称，且06f π⎛⎫= ⎪⎝⎭，()f x 在11,324ππ⎡⎤⎢⎥⎣⎦上单调递增，则ω的所有取值的个数是（） A ．3 B ．4 C ．1 D ．2【答案】D 【分析】直接利用正弦型函数的性质对称性和单调性的应用求出结果. 【详解】由于函数()sin()0,||2f x x πωϕωϕ⎛⎫=+>< ⎪⎝⎭的图象关于3x π=-对称，则：132k ππωϕπ-+=+，()1k ∈Z ①，由于06f π⎛⎫= ⎪⎝⎭，所以2()6k k πωϕπ+=∈Z ②，-②①得：()2122k k ππωπ=--，所以()()211221k k k k ω=---∈Z ，故ω为奇数，且()f x 在11,324ππ⎡⎤⎢⎥⎣⎦上单调递增，所以112243T πππω=≥-，解得08ω<≤．当211,2,3,4k k -=，故ω的取值为：1，3，5，7，当1ω=时，可以求得()sin()6f x x π=-，11,324x ππ⎡⎤∈⎢⎥⎣⎦时，7[,][,]662422x πππππ-∈⊆-，满足条件；当3ω=时，因为2πϕ<，所以不满足条件；当5ω=时，()sin(5)6f x x π=+，11,324x ππ⎡⎤∈⎢⎥⎣⎦时，1159355[,][,]662422x πππππ+∈⊆，满足条件；当7ω=时，()sin(7)6f x x π=-，13737[,]6624x πππ-∈，既有增区间，又有减区间，所以不满足条件；所以满足条件的ω的所有取值的个数是2，故选：D ．【点睛】关键点点睛：该题考查的是有关正弦型函数的性质，正确解题的关键是要明确正弦型函数的对称性与单调性.21．（2021·江西鹰潭·一模（理））函数()sin()0,||2f x x πωϕωϕ⎛⎫=+>≤ ⎪⎝⎭，已知,06π⎛⎫- ⎪⎝⎭为()f x 图象的一个对称中心，直线1312x π=为() f x 图象的一条对称轴，且() f x 在1319,1212ππ⎡⎤⎢⎥⎣⎦上单调递减．记满足条件的所有ω的值的和为S ，则S 的值为（） A ．125 B ．85C ．165D ．185【答案】A 【分析】由一条对称轴和一个对称中心可以得到131264T kT ππ+=+或133,1264T kT k ππ+=+∈Z ，由() f x 在1319,1212ππ⎡⎤⎢⎥⎣⎦上单调递减可以得到191312122Tππ-≤，算出ω的大致范围，验证即可. 【详解】由题意知：131264T kT ππ+=+或133,1264TkT k ππ+=+∈Z ∴51244k ππω⎛⎫=+⋅ ⎪⎝⎭或53244k ππω⎛⎫=+⋅ ⎪⎝⎭ ∴2(14)5k ω=+或2(34),5k k Z ω=+∈∵()f x 在1319,1212ππ⎡⎤⎢⎥⎣⎦上单调递减，∴191312122T ππ-≤ ∴12222ππωω≤⋅⇒≤①当2(14)5k ω=+时，取0k =知25ω=此时2()sin 515f x x π⎛⎫=+ ⎪⎝⎭，当1319,1212x ππ⎡⎤∈⎢⎥⎣⎦时，27,515210x πππ⎡⎤+∈⎢⎥⎣⎦满足()f x 在1319,1212ππ⎡⎤⎢⎥⎣⎦上单调递减，∴25ω=符合取1k =时，2ω=，此时()sin 23f x x π⎛⎫=+ ⎪⎝⎭，当1319,1212x ππ⎡⎤∈⎢⎥⎣⎦时，572,322x πππ⎛⎫+∈ ⎪⎝⎭满足()f x 在1319,1212ππ⎡⎤⎢⎥⎣⎦上单调递减，∴2ω=符合当1k ≤-时，0ω<，舍去，当2k ≥时，2ω>也舍去②当2(34)5k ω=+时，取0k =知65ω=此时6()sin 55f x x π⎛⎫=+ ⎪⎝⎭，当1319,1212x ππ⎡⎤∈⎢⎥⎣⎦时，6321,55210x πππ⎡⎤+∈⎢⎥⎣⎦，此时()f x 在1319,1212ππ⎡⎤⎢⎥⎣⎦上单调递增，舍去当1k ≤-时，0ω<，舍去，当1k 时，2ω>也舍去综上：25ω=或2，212255S =+=.故选：A. 【点睛】本题考查三角函数的图象与性质，难度较大，易错点在于已知一条对称轴和一个对称中心要分两种情况分析.22．（2021·山东·模拟预测）函数()sin 24cos f x x x =-的最大值为（）A B ．C D 【答案】A 【分析】根据周期性只需考虑[]0,2x π∈函数最值，结合()()sin 24cos 2cos sin 2f x x x x x =-=-得3,2x ππ⎛⎫∈ ⎪⎝⎭时函数取得最大值，利用导函数分析单调性，结合隐零点求解最值. 【详解】由题()()sin 24cos 2f x x x f x π=-=+，只需考虑[]0,2x π∈函数最值即可，()()sin 24cos 2cos sin 2f x x x x x =-=-，所以当sin 0,cos 0x x <<即3,2x ππ⎛⎫∈ ⎪⎝⎭时函数取得最大值， ()()222cos 24sin 212sin 4sin 4sin 4sin 2f x x x x x x x '=+=-+=-++，考虑函数()()2442,1,0h t t t t =-++∈-，()()10,00h h -<>，所以必存在唯一零点0t ，()2000210,2t h t t +==，且()01,t t ∈-()2442h t t t =-++递减，()0,0t t ∈()2442h t t t =-++递增，记00sin t x =，由正弦函数单调性可得：()0,x x π∈函数()f x 递增，03,2x x π⎛⎫∈ ⎪⎝⎭函数()f x 递减，所以函数()()()000max 2cos sin 2f x f x x x ==-2002sin 1sin 2x x +=，解得00sin x x ==所以()()()000max 2cos sin 222f x f x x x ⎛⎫ ==-=⨯=⎪⎪ ⎝⎭⎝ 故选：A 【点睛】此题考查求函数的最值，关键在于准确分析函数的周期性和单调性，结合导函数解决隐零点问题求解最值，属于难题.二、多选题23．（2021·全国·模拟预测）已知函数()44sin cos 66f x x x ππ⎛⎫⎛⎫ ⎪ ⎪⎝⎭⎝=+-⎭+在区间(),88t t t R ππ⎡⎤-+∈⎢⎥⎣⎦上的最大值为()M t ，最小值为()m t ，令()()()h t M t m t =-，则下列结论中正确的是（）A ．2h π⎛⎫= ⎪⎝⎭B ．()h tC ．()h t 的最小值为1D ．当()1h t =时，()5Z 6t k k ππ=+∈ 【答案】AB【分析】应用同角平方关系、二倍角余弦公式得()sin(2)6f x x π=-，A 将2t π=代入求区间，根据正弦型函数的性质即可求2h π⎛⎫ ⎪⎝⎭，B 、C 讨论(),88t t t R ππ⎡⎤-+∈⎢⎥⎣⎦与()f x 的递增区间的关系，结合已知区间的长度为4T ，分析不同情况下的()h t 的取值范围，进而确定最大、小值，D 由题设知()1M t =，()0m t =或()0M t =，()1m t =-，结合区间长度即可求t . 【详解】()4422sin cos sin cos cos 266663f x x x x x x πππππ⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫=+-+=+-+=-+ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭sin 2sin 266x x ππ⎛⎫⎛⎫=--=- ⎪ ⎪⎝⎭⎝⎭．A ：当2t π=时，由,88x t t ππ⎡⎤∈-+⎢⎥⎣⎦，得35,88x ππ⎡⎤∈⎢⎥⎣⎦，此时7132,61212x πππ⎡⎤-∈⎢⎥⎣⎦，∴()7sin 12M t π=，()13sin 12m t π=，于是()()()713sin sin cos sin 12121212124h t M t m t ππππππ⎛⎫=-=-=++ ⎪⎝⎭3π==由()222262k x k k Z πππππ-≤-≤+∈可得()63k x k k Z ππππ-≤≤+∈，所以函数()f x 的单调递增区间为(),63k k k Z ππππ⎡⎤-+∈⎢⎥⎣⎦．当()6883k t t k k Z ππππππ-≤-<+≤+∈，即()52424k t k k Z ππππ-≤≤+∈时，则有()()()88h t M t m t f t f t ππ⎛⎫⎛⎫=-=+--= ⎪ ⎪⎝⎭⎝⎭sin 2sin 28686t t ππππ⎡⎤⎡⎤⎛⎫⎛⎫+---- ⎪ ⎪⎢⎥⎢⎥⎝⎭⎝⎭⎣⎦⎣⎦5sin 2sin 2sin 2121212t t t πππ⎛⎫⎛⎫⎛⎫=+--=+ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭cos 22123t t ππ⎛⎫⎛⎫++=+ ⎪ ⎪⎝⎭⎝⎭，而()3222434k t k k Z πππππ+≤+≤+∈，23t π⎛⎫⎡+∈ ⎪⎣⎝⎭，即()h t ⎡∈⎣．当()8823t t k k Z ππππ⎛⎫⎛⎫-++ ⎪ ⎪⎝⎭⎝⎭=+∈，即()3t k k Z ππ=+∈时，()()()5324h t M t m t f k f k ππππ⎛⎫⎛⎫=-=+-+= ⎪ ⎪⎝⎭⎝⎭5sin 2sin 21362462k k ππππππ⎡⎤⎡⎤⎛⎫⎛⎫+--+-=- ⎪ ⎪⎢⎥⎢⎥⎝⎭⎝⎭⎣⎦⎣⎦． ∵函数()f x 的最小正周期T π=，而区间,88t t ππ⎡⎤-+⎢⎥⎣⎦的长度为4π，即4T ，。

高三总复习数学章节测试题(三角函数)

高三总复习数学章节测试题——三角函数班级：姓名：总分：命题人：邓少奎一、选择题（本大题共12小题，每小题5分，共60分．）1.在△ABC 中，若60A ∠=，45B ∠=，BC =AC =（）A. B. C. D.2.函数f(x)=sin(x-4π)的图像的一条对称轴是（）A.x=4πB.x=2πC.x=-4πD.x=-2π3.在ABC ∆中，若C B A 222sin sin sin <+，则ABC ∆的形状是（）A ．锐角三角形B ．直角三角形C ．钝角三角形D ．不能确定.3。

4. 函数f （x ）=sinx-cos(x+6π)的值域为 ( )A ．] 5.已知0ω>，函数()s i n()4f x x πω=+在(,)2ππ上单调递减.则ω的取值范围是（）A .15[,]24 .B 13[,]24C. 1(0,]2 D.(0,2]6.设则“0=ϕ”是“))(cos()(R x x x f ∈+=ϕ为偶函数”的( ) A.充分而不必要条件 B.必要而不充分条件C.充分必要条件D.既不充分与不必要条件7.已知sin cos αα-=，α∈(0，π)，则tan α= ( )A. -1B. 2-C. 2D. 1 8.若tan θ+1tan θ =4,则sin2θ= ( ) A ．15 B. 14 C. 13 D. 129. 在△ABC 中，，BC=2，B =60°，则BC 边上的高等于( )A 10.已知2()sin ()4f x x π=+若a =f （lg5），1(lg )5b f =则 ( ) A.a+b=0 B.a-b=0 C.a+b=1 D.a-b=111.在ABC ∆中，内角A ，B ，C 所对的边分别是c b a ,,，已知8b=5c ，C=2B ，则cosC= ( ) A.257 B.257- C.257± D.252412. 把函数y=cos2x+1的图象上所有点的横坐标伸长到原来的2倍（纵坐标不变），然后向左平移1个单位长度，再向下平移 1个单位长度，得到的图像是 ( )二、填空题（本大题共4小题，每小题4分，共16分）13.函数f （x ）=sin(x ωϕ+)的导函数'()y f x =的部分图像如图4所示，其中，P 为图像与y 轴的交点，A,C 为图像与x 轴的两个交点，B 为图像的最低点.若6πϕ=，点P 的坐标为（0，则ω= ; 14.设△ABC 的内角A ，B ，C 所对的边分别为a ，b ，c . 若()()a b c a b c ab +-++=，则角C = ．15.当函数sin (02)y x x x π=≤<取得最大值时，x=___________.16.设α为锐角，若4cos 65απ⎛⎫+= ⎪⎝⎭，则)122sin(π+a 的值为．三、解答题（本大题共6小题，共74分）17.（本小题满分12分）已知,,a b c 分别为ABC ∆三个内角,,A B C 的对边，c o s s i n 0a C a Cbc --= （1）求A （2）若2a =，ABC ∆的面积为3；求,b c .18.（本小题满分12分）已知函数)6cos(2)(πω+=x x f ，（其中ω＞0，x ∈R ）的最小正周期为10π．（1）求ω的值；（2）设]2,0[,πβα∈，56)355(-=+παf ，1716)655(=-πβf ，求cos （α＋β）的值．19.（本小题满分12分）已知向量(sin ,1),(3cos ,cos 2)(0)2Am x n A x x A ==>，函数()f x m n =⋅的最大值为6.（Ⅰ）求A ；（Ⅱ）将函数()y f x =的图象向左平移12π个单位，再将所得图象上各点的横坐标缩短为原来的12倍，纵坐标不变，得到函数()y g x =的图象.求()g x 在5[0,]24π上的值域.20.（本小题共13分）已知函数xxx x x f sin 2sin )cos (sin )(-=。

高三一轮复习：三角函数恒等变换(二)

高三一轮复习：三角函数恒等变换(二)1、已知函数)cos(3)(ϕω+=x x f （02<<-ϕπ，0>ω）的最小正周期为π，且其图象经过点)0,125(π （1）求函数)(x f 的解析式；（2）若函数)62()(π+=x f x g ，)2,0(,πβα∈，且,423)(,1)(==βαg g 求)(βα-g 的值.2、已知函数)(2cos cos sin 2)(R x x x x x f ∈+=（1）求)(x f 的最小正周期和最大值；（2）若θ为锐角，且32)8(=+πθf ，求θ2tan 的值.3、设函数()sin cos f x m x x =+()x R ∈的图象经过点,12π⎛⎫⎪⎝⎭．（1）求()f x 的解析式，并求函数的最小正周期；（2）若32()45f πα+=且(0,)2πα∈，求(2)4f πα-的值.4、已知函数()2sin 22cos2,f x x x x R =+∈.（1）求38f π⎛⎫⎪⎝⎭的值；（2）求()f x 的最大值和最小正周期；（3）若3282f απ⎛⎫-=⎪⎝⎭，α是第二象限的角，求sin 2α.【参考答案】1、解：（1）π=T ，πωπ=∴2，2=∴ω 0)1252cos(3)125(=+⋅=ϕππf ，即0)65cos(3=+ϕπ 又 02<<-ϕπ，65653πϕππ<+<∴，265πϕπ=+∴，解得3πϕ-= )32cos(3)(π-=∴x x f （2）x x x f x g cos 3)33cos(3)62()(=-+=+=πππ 1c o s 3)(==ααg ，31cos =∴α 423c o s 3)(==ββg ，42cos =∴β 又 )2,0(,πβα∈322c o s 1s i n 2=-=∴αα，414cos 1sin 2=-=ββ )s i n s i n c o s (c o s 3)c o s(3)(βαβαβαβα+=-=-∴g 4742)4143224231(3+=⋅+⋅⋅= 2、解：（1） )4sin 2cos 4cos 2(sin 2)222cos 222(sin 22cos 2sin )(ππx x x x x x x f +=⋅+⋅=+=)42sin(2π+=x ∴最小正周期ππ==22T ，最大值为2 （2） 322cos 2)22sin(2)442sin(2)8(==+=++=+θπθππθπθf 312cos =∴θ 20πθ<< ，πθ<<∴20 ∴3222cos 12sin 2=-=θθ，222cos 2sin 2tan ==∴θθθ3、解：（1）函数()sin cos f x m x x =+()x R ∈的图象经过点π2⎛⎫ ⎪⎝⎭，1 sin cos 122m ππ∴+= ，1m ∴= …………………….2分()sin cos 2sin()4f x x x x π∴=+=+ …………………….3分 ∴函数的最小正周期2T π= ……………………4分（2）32()2sin()2sin()2cos 44425f ππππαααα+=++=+==………6分 3cos 5α∴= 又因为(0,)2πα∈ 24sin 1cos 5αα∴=-=…………………………………………………………9分 242(2)2sin(2)2sin 222sin cos 44425f πππααααα∴-=-+===………12分 4、解：(1))42sin(2)2cos 4sin 2sin 4(cos 2)2cos 222sin 22(2)(πππ+=+=+=x x x x x x f 0sin 2)4832sin(2)83(==+⨯=∴ππππf ……… 3分 (2))42sin(2)2cos 4sin 2sin 4(cos 2)2cos 222sin 22(2)(πππ+=+=+=x x x x x x f )(x f ∴的最大值为2，最小正周期为ππ==22T ．……… 7分 (3) 由(2)知: )42sin(2)(π+=x x f,23sin 2)82(==-∴απαf 即,43sin =α……… 9分又因为α是第二象限的角, 413)43(1sin 1cos 22-=--=--=∴αα…11分.839)413(432cos sin 22sin -=-⨯⨯==∴ααα……… 13分。

高三总复习同步练习(三角函数二)

三角函数专题复习-三角恒等变换导学案-2023届高三数学二轮专题复习

高三数学回归课本复习材料：三角函数基本概念(二)

专题2 三角函数压轴小题(原卷版)

高三数学总复习 专题二三角函数教学案

高三数学第二轮专题复习 三角函数(有答案)

高三理科数学最值微专题(2)三角函数篇

大题专项训练6：三角函数与解三角形(综合练习二)-2021届高三数学二轮复习

专题：三角函数(高三用)

2023届新高考数学二轮复习：专题(三角函数的范围与最值)提分练习(附答案)

高三总复习同步练习(三角函数二)

2024届高三数学一轮复习-三角函数与解三角形 第2练 同角三角函数的基本关系及诱导公式(解析版)

高三数学三角函数(二)

三角函数练习题2答案

新教材老高考适用2023高考数学一轮总复习高考解答题专项二三角函数中的综合问题北师大版

高三数学-专题复习-三角函数(2)解斜三角形(正弦定理余弦定理应用)

高三复习高中数学三角函数基础过关习题(有答案)

专题2 三角函数压轴小题(解析版)

高三总复习数学章节测试题(三角函数)

高三一轮复习：三角函数恒等变换(二)

高三数学总复习专题二三角函数教学案

高三数学第二轮专题复习三角函数(有答案)

2024届高三数学一轮复习-三角函数与解三角形第2练同角三角函数的基本关系及诱导公式(解析版)