电磁学第四章(1、2)
电动力学-几何光学的电磁学基础-第四章 电磁波的传播

4、平面波及其参数
光波场的空间频率
E
E0eitkr0
i t kx xk y ykz z0
E e0
i 2 t 2 f x x f y y f z z 0 E e0
仿照时间频率,定义空间频率 f 1
空间频率是观察方向的函数,定义为沿某观察 方向单位长度的光波场周期数
fx
cos
r
r
r
f f f
r k
r E0
exp
k
rr
4. 平面电磁波的性质
(1) E E0 eikxt ik E0eikxt ik E
由于E=0,所以 k E 0 , 表示电场波动是横波
E可在垂直于k的任意方向上振荡。E的取向称为电 磁波的偏振方向, E有两个独立的偏振方向,对于每 一个k,存在两个独立的偏振波。
为Fx T sin1 x,θ1是x的函数,在x+dx处张力的垂直分量为
Fxdx T sin2 xdx
该元段上的垂直方向上的合力
dFx
T
sin2
xdx
T
sin1
x
θ1和θ2很小
sin 1
tan 1
x
x
sin 2
tan 2
x
x dx
dFx
T
x
x dx
x
x
dFx
电场分量和磁场分量均以波动形式传播---电磁波。
其波速为 c 1/ 00 3.0108 m/s
c与频率无关,真空中一切电磁波(无线电波、光波
X射线和射线等)都以速度c传播,最基本的物理常
量之一;波动方程的解包括各种形式的电磁波;电磁
波的传输不需要介质,相互激发.
2. 介质中的电磁波:
大学物理简明教程(吕金钟)第四章习题答案
第四章电磁学基础静电学部分4.2解:平衡状态下受力分析+q受到的力为:处于平衡状态:(1)同理,4q 受到的力为:(2)通过(1)和(2)联立,可得:,4.3解:根据点电荷的电场公式:点电荷到场点的距离为:两个正电荷在P点产生的电场强度关于中垂线对称:所以:当与点电荷电场分布相似,在很远处,两个正电荷q组成的电荷系的电场分布,与带电量为2q的点电荷的电场分布一样。
4.4解:取一线元,在圆心处产生场强:分解,垂直x方向的分量抵消,沿x方向的分量叠加:方向:沿x正方向4.5解:(1(2)两电荷异号,电场强度为零的点在外侧。
4.7解:线密度为λ,分析半圆部分:点电荷电场公式:++在本题中:电场分布关于x 轴对称:,进行积分处理,上限为,下限为:方向沿x轴向右,正方向分析两个半无限长:,,,两个半无限长,关于x轴对称,在y方向的分量为0,在x方向的分量:在本题中,r为场点O到半无限长线的垂直距离。
电场强度的方向沿x轴负方向,向左。
那么大O点的电场强度为:4.8解:E的方向与半球面的轴平行,那么通过以R为半径圆周边线的任意曲面的电通量相等。
所以通过S1和S2的电通量等效于通过以R为半径圆面的电通量,即:4.9解:均匀带电球面的场强分布:球面R 1、R2的场强分布为:根据叠加原理,整个空间分为三部分:根据高斯定理,取高斯面求场强:图4-94 习题4.8用图S1S2RO场强分布:方向:沿径向向外4.10解:(1)、这是个球对称的问题当时,高斯面对包围电荷为Q当,高斯面内包围电荷为q方向沿径向(2)、证明:设电荷体密度为这是一个电荷非足够对称分布的带电体,不能直接用高斯定理求解。
但可以把这一带电体看成半径为R、电荷体密度为ρ的均匀带电球体和半径为R`、电荷体密度为-ρ的均匀带电体球相叠加,相当于在原空腔同时补上电荷体密度为ρ和-ρ的球体。
由电场叠加原理,空腔内任一点P的电场强度为:在电荷体密度为ρ球体内部某点电场为:在电荷体密度为-ρ球体内部某点电场为:所以4.11解:利用高斯定理,把空间分成三部分场强分布:方向:沿径向向外4.12 解:取闭合圆柱面为高斯面,高斯定理场强分布:方向沿径矢方向4.14 解:无限大带电平面的电场分布为:,场强叠加(1)电荷面密度均为σ在一区:在二区:在三区:(2)电荷面密度分别为σ和-σ在一区:在二区:在三区:方向为垂直于平面方向4.16解:把总的电场力做功看做是正电荷+q电场力做功和负电荷-q电场力做功的叠加,得用公式(4—14):(1)把单位正电荷从O点沿OCD移到D点,电场力做功。
电磁场与微波技术第4章1-2传输线理论
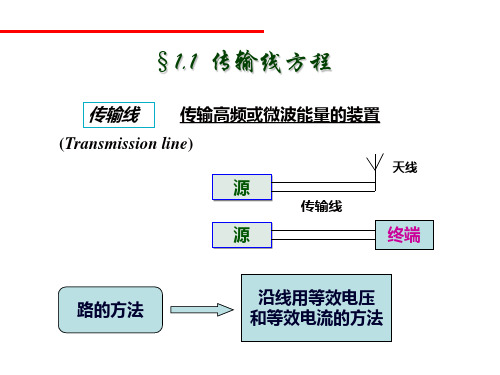
Dz传输线上的等效电路
§1.1 传输线方程
应用基尔霍夫定律:
v( z, t ) Dz z i( z, t ) i( z Dz, t ) i( z, t ) Dz z v( z Dz, t ) v( z, t )
上式两端除以Dz,并令Dz→0,可得一般传输线方程 (电报方程):
如传输线上无损耗,则为无耗传输线。即R=0, G=0。
有耗线
无耗线
§1.1 传输线方程
对于铜材料的同轴线(0.8cm—2cm),其所填充介质为
r 2.5,
则其各分布参数为:
108 S / m
当f =2GHz时
可忽略R和G的影响。——低耗线
§1.1 传输线方程
P17表2.1-1给出了双导线、同轴线和平行板传输线的 分布参数与材料及尺寸的关系。
l
而传输线的长度一般都在几米甚至是几十米之长。 因此在传输线上的等效电压和等效电流是沿线变化的。
——→与低频状态完全不同。
§1.1 传输线方程
传输线理论 长线理论
传输线是以TEM导模方式传 输电磁波能量。 其截面尺寸远小于线的长度, 而其轴向尺寸远比工作波长大 时,此时线上电压只沿传输线 方向变化。
§1.1 传输线方程
均匀传输线
沿线的分布参数 Rl, Gl , Ll , Cl与距 离无关的传输线
不均匀传输线
沿线的分布参数 Rl, Gl , Ll , Cl与距 离有关的传输线
§1.1 传输线方程
3) 均匀传输线的电路模型
均匀传输线
单位长度上的分布电阻为Rl、分布电导为Gl、分布电容 为Cl、分布电感为Ll, 其值与传输线的形状、尺寸、导 线的材料、及所填充的介质的参数有关。
电磁学第四章恒定电流和电路

电磁学第四章恒定电流和电路前三章讨论了静电场,场源电荷相对于观察者是静止不动的。
从本章起讨论电荷运动时引起的有关现象。
若电荷作有规则的定向运动就会形成电流,要维持电流的存在,必须要有相应的电场,所以本章主要讨论恒定电流和电场,并引入许多重要的物理概念。
§ 4.1恒定电流一、电流、电流强度、电流密度导体放在静电场中时,导体中的自由电子在外电场作用下发生定向运动,当导体内部场强为零时,定向运动停止。
若能使内部场强不为零,定向运动就会持续下去,这时,在导体中就有电流产生。
1、电流(1)定义:带电粒子(在外电场作用下)作宏观的定向运动便形成电流(叫做电流)本章只讨论:导体内部的电流。
(2)载流子:导体中的能在电场力作用下发生定向运动的带电粒子叫做该导体的载流子,它们是形成电流的内在因素。
不同性质的导体有不同的载流子:金属导体的载流子是自由电子,酸、碱、盐的水溶液中的载流子:是正负离子等。
(3)电流的方向正电荷运动的方向为电流的方向。
结论:A :导体中电流的方向总是沿着电场方向,从高电势处指向低电势处;B :导体中的载流子为负电荷(自由电子),此时可以把电流等效为等量的正电荷沿负电荷的反方向运动形成。
2、电流强度描述,电流的大小(1)定义:单位时间内通过导体任一横截面的电荷量,叫做该截面的电流强度。
(这里的截面可以推广到任意曲面)Aq表示为:I 二lim t >0-△t(2)电流强度I是反映导体中某一截面整体特征的标量。
A qI就某S面:1=三:平均地反映了S面的电流特征。
3、电流密度J(1)定义:导体中每一点的J的方向是该点正电荷运动方向(电场方向),J的大小等于过该点并与电流方向(正电荷运动方向)垂直的单位面积上的电流强度,写为:(2) J与I有不同:I是一个标量,描写导体中的一个面;J是矢量点函数,描写导体中的一个点。
(3) J与I的普遍关系只反映了J与I的特殊关系(要求面元与J垂直),下面推dS_导J与I的一般关系nJ在导体中某点处取一任意面元dS (dS与J并非垂直),面元dS的法线方向n?与该点的J夹角为二,则dS在与J垂直的平面上的投影为:dS〕二dScos^而dl 二JdS = JdScos^ (标量)二J r?d^ = J dS(二矢量点乘仍为标量)所以通过导体中任意曲面S的电流强度I与J的关系为:I 二J dSS此式说明:一曲面上的I是J对该曲面的通量(J通量)。
大物电磁学课后答案4

/
4 8r 2;5
6 B5 0 ;
Idl 7
321 8来自 B7 B8
0Id
l
r7
0Id l r8
/ /
4r7 3 4r83
0
Id
l
k
/ 4R
2;
20Id lk / 8R2
.
4-3 在电子仪器中,常把载有大小相等方向相反电流的导线扭 在一起,这是为什么?
找出 idt 与 Fdt 的关系)
解:(1) F BI L, Fdt BLIdt mV m 2gh 即 BL Idt BLq m 2gh ,
B
×××××× ××××××
L
m 2gh
q
BL
K
(2)m 10克,L 20厘米,h 0.30米,b 0.10特,求得q 1(库仑)
解:
B
0I 2a
(sin
1
sin
2
)
0
I
A
L
0I 2L sin
600
(cos2
cos1
)
1.73
104
(特斯拉)。
4-14 如图所示,一根宽为a的“无限长”平面载流铜板,其厚 度可以忽略,铜板中的电流为I,求铜板中心上方h处的磁感应 强度B,并讨论h>>a,h<<a两种情况,其结果说明了什么?
4-13一半径为R=0.10米的半圆形闭合线圈,载有电流I=10安 培,放在均匀外磁场中,磁场方向与线圈平面平行,磁感应强 度 B=5.0x103高斯。(1)求线圈的磁矩P;(2)求线圈所受磁 力矩的大小和方向;(3)在此力矩作用下线圈转90o(即转到线 圈平面与B垂直),求力矩作功。
程稼夫电磁学第二版第四章习题解析

前言:特别感谢质心教育的题库与解析,以及“程稼夫力学、电磁学习题答案详解”的作者前辈和血色の寂宁前辈的资料.4-1动生电动势,电路中的电流要使功率最大,应取最小值1,即.4-2原题图片和答案结果不符,现分两种情况:(1)按答案来:整体绕过o点且于磁感应强度平行的轴转动将运动分解为绕c的平动和转动,转动对电势差无贡献4-3(1)OP电势相等时,OP速度沿磁场方向,显然当OP位于YOZ平面时,OP电势相等(2)当OP在YOZ平面右侧即X>0时,电势差(3)当OP在XOZ平面第一象限时,电势差最大4-4在任意时刻t,线圈中的电流为,则由电磁感应定律和欧姆定律得,该式也可以由能量得到4-5其中后一项式中与直杆平行,当与直杆方向垂直时,电动势绝对值最大故有.4-6对于回路有,故有力矩平衡故有.4-7(1)当转轮在磁场中旋转时,每一根轮辐上的感应电动势为四根辐条作为电源是并联的,轮子产生的感应电动势不变(2)根据戴维宁定理,将轮子作为电源,此时将外电路断路计算等效电动势. 4-8式中当转轮1和转轮2分别以ω1和ω2旋转并达到稳定时,闭合回路中感应电流为注意,因转轮1的四根轮辐并联,总电阻为;转轮2类似,其余连接导线、电刷、轮边缘的电阻均忽略不计.又,因转轮1和转轮2同方向旋转,ε1和ε2同方向,但在电路中的作用是彼此减弱的稳定转动时,转轮2所受磁力矩应与阻力矩抵消.磁力矩是四轮辐所受安培力产生的力矩,为式中是转轮2每根轮辐中的电流.阻力矩是阻力闸提供的力矩,因阻力恒为F,故有稳定将要向下滑动时安培力加滑动摩擦力等于重力分力解得可变电阻最大值匀速向上滑动时,电路中同时杆受力平衡,有联立解得.4-11注意题文描述中磁场竖直向上而所给图垂直于轨道平面,此处以文字为正.(1)下滑时,动生电动势与电源同向,故当加速下滑时,电流增大,V2读数增大,V1减小.(2)由牛顿第二定律及欧姆定律得:4-4-4-内电阻阻值负载电阻与内阻相等时,负载上功率最大.4-15平板的宽度d切割磁感线产生感应电动势,积累电荷产生电场,使自由电荷磁场力和4-16由受力平衡,;由力矩平衡,解得.4-17由于圆盘有厚度D,故当圆盘在磁场区域内竖直下落的速度为v时,在圆盘的厚度方向分离变量:两边积分:又初态,代入得:最大焦耳热:4-23(1)如图所示,当小球在管中任意位置x时,设该处的涡旋电场为E,则故式中r是小球在x位置时与O′的距离,式中的负号表示E的方向如图所示,即E与B的变化构成左手螺旋.因此,E的x分量为其中用到几何关系表示沿y轴正方向.小球所受洛仑兹力沿y方向,无x分量,为可见,即洛仑兹力沿y轴负方向小球在y方向还受管的支持力,因三力平衡,故管对小球的支持力为,于是,小球对管的作用力为.4-24法一:cd法二:记圆心为O,连接,.封闭回路中,与段无感生电动势,则.4-25由图中磁场方向及均匀减小,可知圆周上感应电动势方向为顺时针,大小为已知,联立解出故A、B两点电势差.4-26磁场变化产生感应电动势(负号代表逆时针方向)圆环电阻阻值,感应电流电功率.4-27回路以逆时针指向纸外为正,则磁通ab上解得做功.4-29K反向时,励磁电流反向,磁场反向,磁通量变化量大小为原来的两倍,方向相反.4-32根据自感定义,单匝线圈磁通为.4-36设原线圈电路电流为,副线圈电路电流为,由理想变压器性质由题整理得要求灯正常发光,所以算出额定电流,然后能得到每个回路上的电流.4-38(1)如图,由输入等效电路原理(2)原线圈上的电压;副线圈上的电压(3)变压比为.4-39(1)由题,安培力等于阻力(2)代入,(3)单位时间克服阻力做功单位时间电路中消耗代入得(2)当C2断路时,没有感应电流,C1中无互感电动势此时C2中只有互感电动势,a′、b′两端的电压为.。
第四章 电磁学基础
由电力叠
in
q
加原理 由场强定义
e 整理后得
f
fi
i 1 f
in fi
E
E
q
Ei
i1 q
in 或 E
i
i1
qi
ei
in
fi
i1 q
qi
40ri2
i
.
*若带电体可看作是电荷连续分布的,如d图q示Q
把带电体看作是由许多个电荷元组成,
然后利用场强叠加原理。
E dE
Q
Q
dq
q
q
-+ r0
.
(1)轴线延长线上一点的电场强度
E
1 4πε0
q (xr0
2)2
i
E4π1ε0
q (xr0
2)2i
E Ex E 4rπ01 ε0E 2xr 03q4iπ qε04(π1xε20 22xxr0 p320r4)2i
q
q
- O. + r0 2 r0 2
.A
x E
E
x
.
(2)轴线中垂线上一点的电场强度
《电磁学》 就此诞生!
.
法拉第提出:变化的电流、 变化的磁场、稳恒电流的运 动以及导体在磁场中的运动 都会产生感应电流。
1864年麦克斯韦总结了前人 以及自己对电磁理论的研究 成果,归纳出著名的麦克斯 韦方程组。
.
D dS q
S
Edl dm
L
dt
BdS 0
S
Hdl Ic Id
L
第四章 电磁学基础
◆静电场的基础知识 ◆静磁场的基础知识 ◆电磁感应与电磁波 .
I.静电场的基础知识
电磁学第四章习题答案
第四章 习题一(磁场)1、一根载有电流I 的无限长直导线,在A 处弯成半径为R 的圆形,由于导线外有绝缘层,在A 处两导线并不短路,则在圆心处磁感应强度B的大小为( C )(A) I (μ0+1)/(2πR) (B) μ0πI /(2πR) (C) μ0I(1+π)/(2πR) (D) μ0I(1+π)/(4πR)2、载有电流为I 的无限长导线,弯成如图形状,其中一段是半径为a 的半圆,则圆心处的磁感应强度B的大小为( D )(A) μ0I /(4a ) + μ0I /(4πa )(B))8/(2)4/()4/(a I a I a I o o o πμπμμ++(C) ∞(D))4/(2)4/()4/(a I a I a I o o o πμπμμ+-3、如图,电流I 均匀地自下而上通过宽度为a 的 无限长导体薄平板,求薄平板所在平面上距板的一 边为d 的P 点的磁感应强度。
解:该薄板可以看成是由许多无限长的细直载流 导线组成的,每一条载流线的电流为dI =Idx /a , 根据无限长直载流线磁场公式,它们在P 点产 生的磁感应强度的大小为xdxa πI μx πdI μdB 2200==,B d 的方向⊗ ∴ dad a πI μx dx a πI μdB B a d d ad d+===⎰⎰++ln 2200,B 的方向⊗PB4、电流均匀地自下而上通过宽为2a 的无限长导体薄平板,电流为I ,通过板的中线并与板面垂直的平面上有一点P ,P 到板的垂直距离为x ,设板厚可略去不计,求P 点磁感应强度B 。
解:面电流线密度a I j 2/=在离轴线y 处取一宽为dy 的窄条,其电流为dy a Ijdy dI 2==, 22y x r +=P 点B d的方向如图所示。
r πdI μdB 20=220044yx dy a πI μr dy a πI μ+== 22cos sin yx x rx φθ+===,22sin cos yx y ry φθ+===2204cos y x ydya πI μθdB dB x +==,2204sin y x xdy a πI μθdB dB y+== 04220=+==⎰⎰--a a aa x x yx ydya πI μdB Bxaa πI μx y a πI μy x dy aπIx μdB B aa aa aa y y arctan 2arctan 4400220==+==---⎰⎰ y y y x x e x a aπIμe B e B B ⎪⎭⎫ ⎝⎛=+=arctan 205、求上题当a →∞,但维持aIj 2=(单位宽度上的电流,叫做电流线密度)为一常量时P 点的磁感应强度。
电磁学第四章恒定电流和电路
dq en dS u dt
J enu
铜导线一般 n~1028m-3 ,u~0.15mm/sec 所以,电流密度大小为J~104 库/秒米2。
6
4. I 与 J 的关系:
通过导体中任意截面 S的电流 强度为:
I
导体中各点的 J 可以有不同的量值和方向,它是空
电流密度矢量的通量等于该面内 电荷量的减少率. 物理实质:电荷守恒定律. 3.恒定电流和恒定电场
S
要在导体中维持恒定电流,必须在导体内建立 dq 一个不随时间变化的恒定电场.这就要求激发 dt 0 电场的电荷分布不随时间变化,即
9
电流稳恒条件
J dS 0
S
上式表明,形成恒定电流时,在导体内从任一闭合 曲面流入的电荷量等于流出的电荷量. 恒定电场 激发电场的电荷分布不随时间变化,所建立 起的电场也不随时间变化,称为恒定电场. 讨论: ①稳恒的含义是指物理量不随时间改变. 稳恒条件可说成电荷分布不随时间变化,而并不意 味着电荷不能运动. 形成恒定电流的电荷处于宏观的定向运动状态之中.
电流线上每一点的切线方向就是 的方向,电流线的疏密表示它 J 的大小。 J 即| | 电流线的疏密度。
根据电荷守恒,在有电流分布的空间作一闭合 曲面,单位时间内穿入、穿出该曲面的电量等于 曲面内电量变化速率的负值。
8
2.电流连续性方程
dq J dS dt S
§4.4 电动势和全电路欧姆定律
4.4.1 非静电力
稳恒电流线必然是闭合的。然而仅有静电场不可能实现稳恒 电流。因为静电场的一个重要性质是
E dl 0
L
即电场力沿闭合回路移动电荷所做的功为0。若电场力将电 荷从一点移到另一点做正功,电势能减小,则从后一位置 回到原来位置电场力做负功,电势能增加。由于导体存在 电阻,电场移动电荷所做的功转化为电阻上消耗的焦耳热, 这就不可能使电荷再返回电势能较高的原来位置,即电流 线不可能是闭合的。结果引起电荷堆积,破坏稳恒条件。
《中学物理》第3册 电磁学 第4章 电磁感应—知识重点(修订版)
《中学物理》第3册电磁学第4章电磁感应知识重点在“第4章电磁感应”主要是研究感生电流、感生电动势的大小、方向、自感现象、自感电动势等物理基础知识。
电场、磁场只是局限于静态场。
而楞次定律则是涉及到了变化的磁场、变化的感应电流磁场之间的相互关系,属于是动态场。
由“静”到“动”,这是1个飞跃过程。
所以说,楞次定律是学习物理学的又1个难点问题。
一、感生电流⒈产生闭合导体放在变化磁通量(Ф原)的磁场(B新)中,产生感应电动势(ε)。
而感应电动势(ε)则驱使导体中的自由电子移动,而形成了感生电流(I )(感应电流)。
⒉作用在闭合回路的原有磁场(B原)中,产生了新的磁场(B新),来阻碍原有磁场(B 的磁通量(Ф原)发生变化。
原)分析:①当闭合回路中的1部分导体,在磁场中做切割磁感线运动时,闭合回路中的磁通量一定会发生变化。
②在这1部分导体两端,就会产生了感应电动势。
于是,在闭合回路中,就会产生了感应电流。
⒊描述描述产生感生电流(I )的2种方法。
①线圈内的磁通量:通过线圈的磁通量(Ф)发生变化时,线圈里就产生感生电动势(ε)。
如果电路是闭合的,电路中就会产生感生电流(I )。
②导体切割磁力线:导体在磁场里,切割磁力线时,导体内部就产生感生电动势(ε)。
如果导体是闭合电路的一部分,就会产生感生电流(I )。
⒋因素影响感生电流(I )大小的因素:①导体(L)切割的速度(v)大小。
②导体(L)切割的运动(α)方向。
③永磁体的磁力强度(B)。
④切割导体(L)的条数(n)。
⑤切割导体的有效长度(L)。
二、感生电动势的大小⒈切割磁力线导体做切割磁力线运动时,感生电动势(ε):ε= B L v sinα其中:ε:感生电动势。
单位:伏特(v)。
B:磁感应强度。
单位:特斯拉(T)。
L:导线的长度。
单位:米(m)。
v:运动速度。
单位:米/秒(m / s)。
α:磁场方向(B)与运动速度(v)方向之间的夹角。
单位:度(°)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
环面的轴以 沿逆时针方向旋转。环上带电+Q ,求环心
O 处的磁感应强度。
解:环的面电荷密度: Q
Q
(b2 a2 )
a
在r处取宽为dr的环,带电为 dq 2rdr dr r O b
以旋转时,相当于(等效于)电流
di dq / T dq 2rdr rdr
3) 磁感应强度叠加原理。
根据 实验基础,可以把任何载流导体分成无限多个电流元 Id先l 求出每个电流元在周围空间某场点产生的 ,再根据
d B B
场叠加原理,求 得整个载流导体在该点产生的 选电流元 Idl ,在P 点产生的 磁感应 强度dB
。
Idl
Idl dB
B dB
dB ? rP
L
2、毕奥─萨伐尔定律:
dBsinθ
μ0 4π
Idl r2
R r
μ0 4π
IRdl r3
B Bx
L dBX
sin dB
L
L
μ 0 R IdL 4π r r 2
IRμ 0
4π L
dL r3
μ
0 IR 2r 3
2
2
μ 0 IR2 R2 x2
3 2
方向沿X轴正向
讨论:
B
0 IR 2
2 R2 x2
dB
k
Idl sin
r2
dB的方向与Idl
r同向,标在图上。
3、若所有dB 同向, 则 B dB
若方向不同, 则先取分量。dBx dBcos dBy dBcos
Bx dBx By dBy
4、选取适当积分变量,方便计算 。
5、由 Bx , By 求出 dB dBxi dBy j
§4-2 毕奥─萨伐尔定律
讨论电流和运动电荷在真空中产生的磁场。 一、毕奥─萨伐尔定律
1、毕奥─萨伐尔定律的实验基础
1)实验验证长直载流导线在周围空间某点P产生的磁感应强度
B与I 成正比,与P 到导线的距离r成反比,即 B I
2)折线电流实验:P点处的磁感强度
B折
k折
I r
tg
2
I
r
rP
由上述两个实验,应用数学方法得到电流元产I 生磁场的规律。
直的方向上出现横向电势差──霍耳效应。
实验证明:
U AA
K IB d
2、经典解释:
K 1 nq
K 为霍耳系数
若电量为q 的粒子以速率v 运动,则受磁场力为:
A
大小: fm qvB
f
v
B
方向: 竖直向上。
I
A
在磁场力的作用下,带电粒子在导体板内发生偏转,在A、
A′面上分别聚集了等量异号的电荷,从而形成霍尔电场。
d 0I arctg a
a
2y
dx
dx
a dI
x
讨论:
B 0I arctg a
a
2y
(1)a y, arctg a a B 0I a 0I
2y 2y
a 2 y 2y
无限长直导线
(2)a y, arctg a
2y 2
B
0 I
2a
1 2
0
j
无限大载流平面
y
dB
P r
dB r
dx
r2
(1)
统一积分变量
r a a
sin sin
x actg actg a d
dx sin2
将以上各式代入(1)式,得:
y
dB P
ar
1 O
I
x
dx
2
x
B 0I 2
4 1
Isin d
a
B
0I 4a
cos1
cos2
讨论: (1)方向:垂直纸面向外(由右手螺旋法则来定)
(2)L>>a
1
0, 2
时,
B
0I 2a
时, (3)半无限长
1
2
, 2
时B
0I 4a
(4)注
意
a,1
,
的
2
意
义
。
无限长
[例3]无限长载流平铜片,厚度忽略,宽度为a ,电流为I 。
求:铜片中心线正上方P点的B。 解:坐标系如图。将铜片分为无限多个宽度为dx 的窄条,
每个窄条可看成载有电流dI的无限长直导线
dI Idx / a
dB
0 4
Idl r
r3
0 4
Idl
rˆ
r2
整个载流导线产生的磁感应强度:
B dB
0
L
L 4
Idl
rˆ
r2
说明:1)毕—萨定律的正确性是不能用实验验证的。因为 电流元不可能单独存在。
2)毕—萨定律的正确性是通过计算载流导体产生的 B
与实验测定的结果相符合而验证的。
3、关于毕奥─萨伐尔定律的说明:
(2)安培实验
动电生磁。
(3)磁铁对运动电荷有力的作用。
本章讨论恒定电流在真空中产生的磁场, 稳恒磁场: 恒定电流激发的磁场。也称为静磁场。
即在空间的分布不随时间变化的磁场。
二、主要内容: (1)电流及运动电荷产生磁场的规律。 (2)磁场对电流或对运动电荷的作用力。 (安培力,洛仑兹力)
磁场在研究方法上与静电场有许多类似之处,在学习中 要注意和静电场的类比。
第四章 稳恒磁场 Static( Steady ) Magnetic Field
一、磁研究的演变
1、基本磁现象:天然磁石对铁的吸引。 磁体的应用与指南针的发明 磁极:N极与S极,同性相斥异性相吸。
2、电现象和磁现象的联系
1820年丹麦科学家奥斯特发现了电流的磁效应。
(1)通电导体 磁针受到力的作用。
B1 0
I
R
3
BO B1 B2 B3
B 30I 0I 8R 4R
方向:⊙
B2
3 4
0I
2R
B3
0I 4R
O
三、运动电荷的磁场
由经典电子理论,金属导体中的电流是由大量电子作定向
运动形成的,所以电流产生的磁场本质上是运动电荷在其周围
激发的磁场。
设导体中载流子的数密度 为n ,载流 S
r2
一个以速度 v 运动的电荷 q 产生的磁场为
B
dB N
0 4
qv r
r2
r 为运动电荷到场点的距离。
rˆ 为运动电荷到场点的单位矢量。
与电流元的磁场公式比较:
dB
0 4
Idl r
r3
0 4
Idl
rˆ
r2
B
dB N
0 4
qv
r
r2
[例5]内外半径分别为a,b的均匀带电圆盘,绕过圆心O且垂直于
1、规定:
磁感应线上任意一点沿其正向的切向为该点 B 的方向;
切线表示方向
垂直于 B 的单位面积上通过的磁感应线的条数等于该处
B 的大小。 密疏表示强弱
根据毕奥─萨伐尔定律可以判定磁感应线必定是闭合曲线。
2、根据毕奥─萨伐尔定律可以判定磁感应线应具有下列性质: 任何磁场中,磁感应线都不会相交; 每一条磁感应线都是闭合曲线。 ③每一闭合曲线都与电流相套连,二者相互嵌套时服从有 右手定则。磁场是有旋场。
F
在SI中,B 的单位为特斯拉(T)。
1T 1N / C m / s
三、洛伦兹力 F
大小: F qvBsin
q
v
B v
方向: 即垂直 v又垂直 B,垂直于 v和 B所确定的平面.
F
qv
B
当 q>0 时,三者满足右手螺旋
——洛仑兹力 关系。
四、带电粒子在均匀磁场中的运动(自学,是考试内容)
1)大小: dB 0 4
Idl sin
r2
dB Idl dB sin
dB
k
Idl sin
r2
dB
1 r2
在SI中 k 107Tm / A 107 N / A7
k 0 4
0 真空中的磁导率
0 12 . 57 10 7 H m1 ( 亨利 /
2)方向: 由毕奥─萨伐尔定律
可知 dB 既垂直 Idl 又垂直
方向:规定该点处小磁针 N 极所指的方向。
当试探电荷 q 以速度 v 通过 P点时,实验发现磁场对运
动电荷有如下的作用规律:
q 所受的磁场力与v 的大小和方向都有关。 当q 以相同的速率沿不同的方向通过P 点时,q 所受的磁场
力大小不同。
当v 与磁场方向在同一直线上时,q 所受的磁场力为零。
当v 垂直磁场方向时,q 所受的磁场力最大。
[例1]求长为L ,电流为 I 的载流直导线外P 点的B 。
y
解:取坐标系如图
取电流元Idx,该电流元 在P点产生的 dB的大小为:
dB P
dB μ 0 4π
Idxsin
r2
方向:垂直纸面向外
a
1 O
r
I
x
dx
2
x
由于导线上各电流元在P点激发的磁场方向相同,所以:
B dB 0
L
4
L
Isin dx
3、应用: 1)K 与载流子的浓度 n 有关。 霍尔效应为研究半导体载流子浓度的变化提供重要的方法。
2)K 的正负取决于载流子电荷的正负。 根据 K 的正负,可以判断半导体的载流子的类型。
P型,k>0,载流子为带正电的空穴。 n型,k<0,载流子为带负电的电子。AfvB
I
A
A
f
v
B
I
A
