均相反应动力学方程的建立
化学反应工程第二章均相反应动力学基础

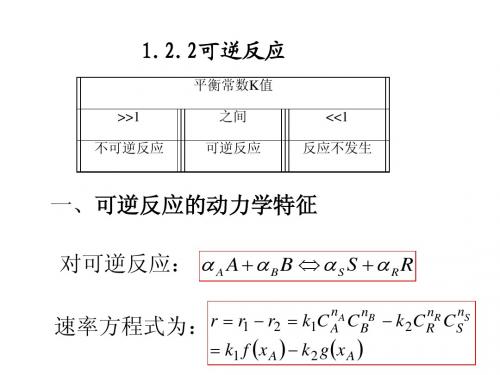
A
A+P
P
P+P
(2-8)
(2-9)
2.1.3 反应的转化率、选择性和收率
⑴转化率 转化率一般用关键组分来表示。所谓关键组分必须是反 应物,生产上选择的关键组分一般是反应物料中的主要
组分,即价值较高且不应是过量的,因此转化率的高低,
会一定程度上反映过程的经济效果,对反应过程的评价 提供直观的信息。
2.1.3 反应的转化率、选择性和收率
对于选择率一般有平均选择率和瞬时选择率之分,以平 行反应(2-5)、(2-6)为例,
两种选择率的定义为: 平均选择率 瞬时选择率 (2-2)
2.1.3 反应的转化率、选择性和收率
⑶收率Y 收率的定义为:
Y 生成目的产物所消耗的 A摩尔数 A的起始摩尔数
(2-3)
COCl2
3 2 2 CO CO Cl 2
(2-12)
该反应的速率方程为:
(rCO ) k c c
(2-18)
则对于氯气的反应级数是分数。
2.1.5 反应动力学方程
⑵反应速率常数kA 由式(2-13)知,当A、B组分的浓度等于1
(rA )k A ,说明kA就是浓度为1时的速率。 时,
温度是影响反应速率的主要因素,随着温度的升高速
三级反应常见。例如下面的气相反应(2-11):
2NO+O2 动力学速率方程为:
2 (rNO ) k NO cNO cO2
2NO2
(2-11)
(2-17)
2.1.5 反应动力学方程
级数在一定温度范围内保持不变,它的绝对值不会超过3, 但可以是分数,也可以是负数。例如下面的光气合成反 应:
CO+Cl2
生产上还经常遇到循环反应器,如合成氨或合成甲醇的 合成塔等,由于化学平衡或其他原因的限制,原料一次 通过反应器后,转化率一般很低,需要把出口的反应混
均相反应动力学基础

齐齐哈尔大学化学反应工程教案第二章均相反应的动力学基础2.1 基本概念与术语均相反应:是指在均一的液相或气相中进行的反应。
均相反应动力学是研究各种因素如温度、催化剂、反应物组成和压力等对反应速率反应产物分布的影响,并确定表达这些因素与反应速率间定量关系的速率方程。
2.1- 1化学计量方程它是表示各反应物、生成物在反应过程的变化关系的方程。
如N2+3H2===2NH3一般形式为:2NH3- N2-3H2== 0有S个组分参与反应,计量方程::人g2A2亠亠:s A s =0SZ ctjAi =0或i生式中:A i表示i组分a i为i组分的计量系数反应物a i为负数,产物为正值。
注意:1.化学计量方程仅是表示由于反应而引起的各个参与反应的物质之间量的变化关系,计量方程本身与反应的实际历程无关。
2. 乘以一非零的系数入i后,可得一个计量系数不同的新的计量方程S ■- .p r- i A i =0i 13. 只用一个计量方程即可唯一的给出各反应组分之间的变化关系的反应体系——单一反应;必须用两个(或多个)计量方程方能确定各反应组分在反应时量的变化关系的反应,成为复合反应。
CO+2H2=CH3OH CO+ 3H2=CH4+ H2O2.1- 2化学反应速率的定义化学反应速率是以单位时间,单位反应容积内着眼(或称关键)组分K的物质量摩尔数变化来定义K组分的反应速率。
:A A :B B=、s S :R R_ dnA (由于反应而消耗的A的摩尔数)Vdt (单位体积)(单位时间)1 dn A 1 dn B 1 dn s 1 dn Rr B r s r R二V dt V dt V dt V dt齐齐哈尔大学化学反应工程教案4.n 0 yK 0KnK0 - n KnK0 K当V 恒定时,组分K 反应掉的摩尔数 n K0 - n K反应程度是用个组分在反应前后的摩尔数变化与计量系数的比值来定义的,用Z 表示。
n i - ng n K 卞。
化学反应工程chap 1 均相单一反应动力学和理想反应器

活化能隐含的反应速率对温度敏感程度的度量
例子: 例子:现有两个反应的活化能分别为100kJ/mol和
150kJ/mol ,试计算两者分别(a)温度由300K上 升10K,(b)温度由400K上升10K时速率常数k的 增大倍数。
E(KJ/mol) 100 100 150 150 温度(K) 300-310 400-410 300-310 400-410 速率常数增大倍数 3.64 2.08 6.96 3.00
22
对于体系中只进行一个不可逆反应的过程。 对于体系中只进行一个不可逆反应的过程。
aA+bB→rR + sS
m n −rA = kccAcB
m ⋅ m−3 ⋅s−1 ol
度上,符合阿累尼乌斯关系。 度上,符合阿累尼乌斯关系。
kc为以浓度表示的反应速率常数,随反应级数的不同 为以浓度表示的反应速率常数, 有不同的因次。一般, 是温度的函数, 有不同的因次。一般,kc是温度的函数,在一般工业精
∆nI nI −nI 0 ξ= = aI aI
相应地, 相应地,反应进行到某一时刻
nI = nI 0 + aIξ
10
反应程度的性质
※ ※ ※ ※ 时间的函数, 时间的函数,随反应的进行而不同 积累量,恒大于0 积累量,恒大于0 广度量 与反应式的写法有关
和性,如:功 和性,
广度量:描述体系的广度性质, 广度量:描述体系的广度性质,具有加 强度量:描述体系的强度性质, 强度量:描述体系的强度性质,不具加
7
对于化学反应计量方程 对于化学反应计量方程
aA+bB+L = rR+ sS +L L L
表示化学反应过程中各个组份间量的变化关系。亦 表示化学反应过程中各个组份间量的变化关系。 可以写成其它若干形式: 可以写成其它若干形式:
化学反应工程第二章解析

第二章 均相反应动力学基础均相反应 均相反应是指参予反应的各物质均处同一个相内进行化学反应。
在一个相中的反应物料是以分子尺度混合的,要求:①必须是均相体系 (微观条件) ②强烈的混合手段 (宏观条件) ③反应速率远小于分子扩散速度一、计量方程反应物计量系数为负,生成物计量系数为正。
计量方程表示物质量之间关系,与实际反应历程无关; 计量系数只有一个公因子;用一个计量方程表示物质量之间关系的体系称为单一反应,反之称为复合反应。
二、化学反应速率单位时间、单位反应容积内组分的物质的量(摩尔数)的变化称之为该组分的反应速率。
反应物:生成物:对于反应三、化学反应速率方程r 是反应物系的组成、温度和压力的函数。
32223NH H N =+032223=--N H NH A A Adn r Vd d t C dt=-=-R R Rdn r Vdt dC dt==A B S R A B S Rαααα+=+SABRABSRr r r r αααα===AA AB r [k (T)][f(C ,C ,)]=有两类;双曲函数型和幂函数型。
k -化学反应速率常数; a(b)-反应级数。
(1)反应级数(i) 反应级数与反应机理无直接的关系,也不等于各组份的计量系数; (ii) 反应级数表明反应速率对各组分浓度的敏感程度;(iii) 反应级数是由实验获得的经验值,只能在获得其值的实验条件范围内加以应用。
(2)反应速率常数k[k]: s -1·(mol/m 3)1-nE :是活化能,把反应分子“激发”到可进行反应的“活化状态”时所需的能量。
E 愈大,通常所需的反应温度亦愈高,反应速率对温度就愈敏感。
k 0 —指前因子,其单位与 反应速率常数相同;E— 化学反应的活化能,J/mol ; R — 气体常数,8.314J/(mol .K)。
a b A A B r kC C=2220.512H Br HBrHBrBr k c c r c k c =+0exp[]E k k RT=-01ln ln E k k R T=-⨯ln klnk 0 slop=-E/R1/T⏹ 反应速率的温度函数关系● 活化能越高,斜率越大,该反应对温度越敏感; ● 对于一定反应,低温时反应速率对温度变化更敏感。
第二章均相反应动力学基础1要点

同的则为强度性质。
反应进度被应用于反应热的计算、化学平衡和反应 速率的定义等方面。
例:如下反应 N2 + 3H2 → 2NH3
开始浓度/(mol· L-1)
2s末浓度/ /(mol· L-1)
1.0
0.8
3.0
2.4
0
0.4
ni ni 0 vi
0.8 1.0 2.4 3.0 0.4 0 0.2 1 3 2
2N2 6H2 4NH3 0
化学计量方程(化学计量式)
aA bB =rR sS
是用元素符号和分子式来表示一个化学反应的等
式,表示参加反应的各组分的数量关系,即在反 (用等号=)
亦可以写成其它若干形式:化学计量式的通式
应过程中量的变化关系。与反应的实际历程无关。
反应进度 对于反应物, ni< ni0, ⅴi <0;对于反应产物 ni> ni0, ⅴi > 0,并且由化学反应的计量关系决定,各组分生成 或消耗的量与其计量系数的比值相同,
n A n A 0 n B n B0 n R n R 0 nS nS 0 A B R S
对一般情况,设在一反应体系中,存在n个 反应组分 A1、 A2、 …An,它们之间进行一个化 学反应,根据质量衡算原理,反应物消失的质 量必定等于反应产物生成的质量,其化学计量 方程可用如下通式表示。
• 化学计量式的通式如何表示? 一个由n个组份参予的反应体系,其计量方程可写成: v1A1+v2A2+…… +vnAn= 0 或
nS 。以终态减去初态即为变化量, 根据化学反应计
量学可知,各组分的变化量符合下列关系
(nA - nA0): (nB - nB0): (nR - nR0): (nS - nS0) = αA :αB :αR :αS
均相反应的动力学基础

均相反应的动力学基础化学反应工程第二章均相反应动力学基础1§2.1基本概念和术语若参于反应的各物质均处同一个相内进行化学反应则称为均相反应。
均相反应动力学:研究各种因素如温度、催化剂、反应物组成和压力等对反应速率、反应产物分布的影响,并确定表达这些影响因素与反应速率之间定量关系的速率方程。
§2.1.1化学计量方程化学计量方程:表示各反应物、生成物在反应过程中量的变化关系的方程。
一个由S个组分参予的反应体系,其计量方程可写成:Si1iAi0式中:Ai表示i组分,i为i组分的计量系数。
通常反应物的计量系数为负数,反应产物的计量系数为正值。
注意:1.计量方程本身与反应的实际历程无关,仅表示由于反应引起的各个参予反应的物质之间量的变化关系。
2.规定在计量方程的计量系数之间不应含有除1以外的任何公因子。
这是为了消除计量系数在数值上的不确定性。
单一反应:只用一个计量方程即可唯一给出各反应组分之间量的变化关系的反应体系。
复杂反应:必须用两个或多个计量方程方能确定各反应组分之间量的变化关系的反应体系例如,合成氨反应的计量方程通常写成:N23H写成一般化的形式为:N23H而错误的形式有:2N26H2222NH32NH304NH30§2.1.2反应程度和转化率反应程度是各组分在反应前后的摩尔数变化与其计量系数的比值,用符化学反应工程第二章均相反应动力学基础2号ξ来表示,即:n1n10nini0nknk01ik或写成:nini0ii1.不论哪一个组分,其反应程度均是一致的,且恒为正值。
2.如果在一个反应体系中同时进行数个反应,各个反应各自有自己的反应程度,则任一反应组分i的反应量应等于各个反应所作贡献的代数和,即:Mnini0j1ijj其中:M为化学反应数,ij为第j个反应中组分I的化学计量系数。
转化率是指某一反应物转化的百分率或分率,其定义为:某某一反应物的转化量该反应物的起始量nk0nknk01.如果反应物不只一种,根据不同反应物计算所得的转化率数值可能是不一样的,但它们反映的都是同一个客观事实。
化学反应工程-3-第一章-均相反应动力学
n n0 2 2 n A0 n A 1
2xA PB P 1 2xA dP 2P dxA B dt (1 2 x A ) 2 dt
求
dx A dt
n nA0 (1 2 xA )
PA P
nA 1 xA P n 1 2xA
dPA 1 dxA 3P dt 1 2 xA 2 dt
1.2.3均相催化反应
k AC R C
是C为催化剂,Cc为常数。
dC A rA kC A C C k C A 反应速率: dt
1.2.4自催化反应
k AC 2C R ……(1) • 自催化反应:
速率方程:
dn A rA kC A C C Vdt
• k0、E、a1、b1、c1、d1为模型参数,通常应用线性或非线性最小二乘法进行参数估 值。 •
A 2.5 P, 例1:在0℃时纯气体组分A在一恒容间歇反应器中依以下计量方程进行反应: 实验测得如下数据:
组分A分压随时间变化关系
时间/min
0
2
4
6
8
10
12
14
∞
PA/105Pa
1
n
CR R CS S C A A CB B
技 巧:
• 为使速率方程能够同时满足动力学和热力学平衡,可将反应速率方程表示成以下形式:
S R C C R S r kC C C C 1 K C A C B C A B
a1 A b1 B c1 R d1 S
CM 0 2
∴在中间某时刻,-rA必将达到最大,有最大值存在。
结论: 当 CA
均相反应速率及反应动力学

P=CRT
所以有rA,P=rA,CRT,即用分压表示的反应速 率是用浓度表示的反应速率的RT倍。
注意:这里的R=8.314J/(mol.K),T的单位为K。
返回
课程纲要 反应速率 动力学方程 阿氏方程 课程作业
基元反应
若反应物分子在碰撞中一步直接转化为产物分子, 则称该反应为基元反应。 此时,根据化学反应式的计量系数可以直接写出反 应速率式中各浓度项的指数。
课程纲要 反应速率 动力学方程 阿氏方程 课程作业
本课总结
(1)化学反应速率方程 (严格定义和变形公式) (2)化学反应动力学方程式 (3)阿伦尼乌斯方程
课程纲要
反应速率
动力学方程
阿氏方程
课程作业
课程作业
作业:依据反应速率方程,请你说明通 过哪些方式可以提高不可逆的单一反应 的反应速率? 预习:第4课 反应器设计和优化
返回
课程纲要 反应速率 动力学方程 阿氏方程 课程作业
非基元反应
若反应物分子在碰撞中要经过若干步,即经过几个 基元反应才能转化为产物分子,则称该反应为非基 元反应。 此时,应该先写出各基元反应,然后根据基元反应, 逐个产物写反应速率方程(包括中间产物),在最 终产物的速率方程中,消去中间产物浓度未知量, 才能得到反应的速率方程表达式。
课程纲要 反应速率 动力学方程 阿氏方程 课程作业
间歇系统的反应速率
间歇系统 反应物料一次加入,经过一定时间,一次取出的系 统。 特点 (1)反应过程中没有物料的输出和输入; (2)浓度、温度、压力等系统参数在每一瞬时是 一致的——集中参数; (3)各个参数随时间变化——自变量是时间。
课程纲要
反应速率
返回
课程纲要 反应速率 动力学方程 阿氏方程 课程作业
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
平行反应的浓度-时间变化示意图
练习:
二级不可逆反应: A + B→ P
试推导动力学方程积分式。 (1) CA0=CB0 , CP0 =0 (2) CA0≠CB0 , CP0 =0, 设CB0/CA0=β
(1) CA0=CB0 , CP0 =0
[例] 反应物A在液相恒容系统中生成产物 R和T。在25℃,CA0 = 0.0238mol/L的条件 下进行动力学实验,不同反应时间 t 测得 的各组分浓度见下表。试分析所给数据, 并建立该反应的动力学关系。
•
⑴ CA-t 曲线仍具有一级不可逆反应
的特点,ln(CA/CA0)对t 作图,所得直线斜
率为-(k1+k2)。
•
⑵ T 恒定时,CP/ CS = k1/k2 = 常数,
即两产物生成量的比值仅是T 的函数;
CP对CS作图可得一直线,斜率为k1/k2, 由此可求得 k1、 k2各自的值。
⑶ CA、CP、CS对t 作图,可得浓度随 t 变化的曲线(图2-8)。
rA
dC A dt
kC
A
C
B
kf (C)
⑵ 将实验所得数据在 CA- t 两维相平面 上标绘出光滑曲线;
在各浓度值位置求曲线斜率dCA/dt ,
即为相应浓度下的反应速率值 (-rA);
⑶ 假设α和β的数值;
将所得-rA值对
f
(C
)
C
A
C
B
作图,若
得到一通过原点的直线,则表明所设α和β
值是正确的;
• 动力学方程式反映出参与反应的各组分浓 度随时间的变化情况或组分浓度随时间分 布情况,可为反应过程或反应器的优化设 计提供理论依据。
Q5:动力学方程建立的过程?
1、动力学方程式的建立以实验数据为基础。 2、测定动力学数据的实验室反应器?
间歇操作或连续操作反应器。均匀液相反应, 大多采用间歇操作反应器。 3、维持等温条件下进行化学反应,利用化学中的 分析方法,得到不同反应时间的各物料浓度数据
kC
2 A
11 kt
C A C A0
1 ( xA ) kt C A0 1 xA
(2-16)
• 以(1/CA-1/CA0)对t 作图,得一通过原 点的斜率为k 的直线。
⑶ 若为n级反应,则
dC A dt
kC
n A
积分得
dC A
C
n A
kdt
C
1 n A
C 1n A0
(n 1)kt
以
C 1n A
rP dCP dt k1CA
⑴
rS dCS dt k2CA
⑵
反应物 A总消耗速率为:
rA dCA
dt
k1C A
k2C A
(k1
k2
)C
⑶
A
初始条件:t =0时,CA= CA0 ,CP0 = CS0=0 式⑶积分得:
ln(C A / C A0 ) (k1 k2 )t (2-32)
或 C A C A0 exp[ (k1 k2 )t]
• 恒温恒容条件下,复合反应动力学方程的 建立
• 变容体系中,动力学方程的建立
简单(单一)反应动力学方程式的
• 单一反应 ?
建立
只用一个计量方程即可唯一地给出各反 应组份之间量的变化关系的反应体系。
• 复合反应 ?
必须用两个或更多计量方程方能确定各 反应组份在反应时量的变化关系的反应。
单一 不可逆反应:反应只沿一个方向进行 反应 可逆反应:反应同时朝两个方向进行
(C-t) ;
4、对数据进行适当的数学处理→动力学方程式。
Q6:动力学方程建立的方法(数据处理 方法)?
• 实验数据的处理方法? 积分法、微分法等。 利用积分法求取动力学方程式的过程,
实际上是一个试差的过程,一般在反应级 数是简单整数时使用;
当级数是分数时,试差困难,最好用 微分法。
积分法
• 积分法?(求某一函数原函数的过程)
⑷
ln(CA0/CA)对t 作图2-7,所得直线斜率 为k1+k2 。
⑴/⑵得: 积分:
rP dCP k1 rS dCS k2 C P C P0 C P k1 (2-33) CS CS0 CS k2
将CP对CS作图2-7,得一直线,斜率为 k1/k2 ;再根据k1+k2 ,可分别求得k1、k2 。
斜率为 k1+ k2 ,再结合⑵式或K,即可分别
求得k1 和 k2 。
k1=?
k1+ k2已知
k2=?
2.3.2 微分法 • 微分法?
利用微分形式的速率表达式,根据实 验数据确定动力学方程的形式。
• 优点?
处理非整数级数反应比积分法更有效。
• 程序?
⑴ 对任一不可逆单一反应(等温恒容), 假定一反应机理,列出动力学方程式:
• 不可逆反应 一级反应 二级反应 n 级反应
• 可逆反应
返回
2.3.1.1 不可逆反应
不可逆反应 A → P 设其动力学方程为:
rA
dC A dt
kC
n A
(n为反应级数)
反应初始条件:t =0时,CA= CA0 , CP0 =0。
⑴ 若n=1,则
rA
dC A dt
kC A
积分:
dCA kdt CA
k2
C Ae
将⑵代入⑴,得
(2) (2-22)
rA
dC A dt
(k1
k2 )(C A
C Ae )
积分或直接将2-22代入2-20,得
ln C A0 C Ae C A C Ae
(k1 k2 )t
k1(1
1 )t K
(2-23)
以ln C A0 C Ae 对t作图2-5,得一直线, C A C Ae
xA 0
1
(1
xA )
(
1
x
A
)
dx
A
kC A0t
ln
( (1
xA ) xA )
CA0 (
1)k t
(CB0
CA0)kt
ln
CBCA0 CACB0
(CB0
CA0)k t
2.3.1.2 可逆反应
如 N2+3H2
2NH3
为简明起见,以正逆方向均为一级反 应的例子来讨论可逆反应的一般规律。
C 1n A0
对t作图,得一通过原点的
n1
斜率为 k 的直线。
1
2
3
小结:
• 当 n 取某一个值以致能在图上绘成某 一种直线时,所取 n 就可表示反应级数, 如不然,就要重新假设 n ,再尝试。
• 实际上,不论 n为何值,实验点不可能 严格与方程轨迹一致,因此,求得的 k 都 带有一定的偏差,但只要偏差小至一定程 度,就认为可以接受。
Q2:动力学方程建立的定义?
• 反应速率的定义式是微分式,将其与速率方程 式关联并积分,可得到反应物浓度随时间变化 的关系。该过程称为动力学方程式的建立或反 应速率式的解析。
Q3:动力学方程与反应速率方程之间 的区别?
• 定义上的区别? • 形式上的区别? • 物理意义区别?
Q4:动力学方程建立的目的?
A k1 P
k2
初始条件:t =0时,CA= CA0 , CP0 =0。
任一时刻 t: r正 = k1CA
r逆 = k2CP
A的净消耗速率:
rA
dC A dt
k1C A
k2CP
k1C A k2 (C A0 C A )
Hale Waihona Puke (k1 k2 )C A k2C A0
(1)
令K= k1/ k2,积分得
• 等温恒容不可逆反应的速率方程及积 分式见表2-4
(2) CA0≠CB0 , CP0 =0, 设CB0/CA0=β
CB0 / C A0
rA
dC A dt
C A0
dx A dt
kC
2 A0
(1
xA )(
xA )
xA 0
(1
dx A
x A )(
xA )
kC A0
t
dt
0
1
( 1)
•
⑷ 或以CP或CS对{1-exp[-(k1+k2) t ]}
作图,得一直线,斜率为k1CA0 /(k1+k2)或
k2CA0 /(k1+k2) 。
•
⑸ 若改变CA0,生成P和S的初速率应
与CA0成正比关系。
• ⑹ 其它平行进行的各反应具有相同的
反应级数的平行不可逆反应与一级不可逆
平行反应有相同的动力学特征。
如
A+B P S+R
•
此外,还有由平行和串联反应组合在
一起的复合反应,如
A+B P P+B R
R
A
S
P
2.4.3 复合反应动力学方程的建立
• 复合反应是由若干个单一反应组合而
成的,如
A
+A +B
P R
+A +P
S M
• 该反应由4个单一反应组成:
A + A k1 P
A+B P+A
k2 R
k-2
k3 S
否则需重新设定。
该直线的斜率即为在此 T 下的速率常 数值 k。
• 缺点?
受操作者技巧水平所限,图解微分法求取-rA偏 差较大。
复合反应动力学方程式的建立
复合反应? 几个反应同时进行,需要用两个或更
多独立的计量方程或动力学方程来描述。 • 复合反应的分类 • 复合反应动力学方程的建立
