第三章化学反应动力学基础

合集下载

第三章化学反应速率、方向和限度

①逆过程G与正过程的G数值相等，符号相反。
②如果一个反应是多个反应的和，总反应的rG等于各反应G之总和。
二、判断一个反应进行的方向时，如果：
rG<0反应自发进行
rG>0反应不自发进行
rG=0平衡状态
当rG<0时(产物的G<反应物的G)该反应就自动向生成产物的方向进行，在反应中反应物不断减小而产物不
由上面的rG(T)=rH(298K)-TrS(298K) 公式可得下列结果：
类型 H
S
G
反应的自发性
1 2 3 4
+ +
+ +
永远是永远是+ 受温度影响受温度影响
永远自发永远非自发温度低时自发温度高时自发
例：求标准状态下CaCO3(s)===CaO(s)+CO2(g)
的分解温度?
Kc=[CrO42-]2[H+]2/[Cr2O72-]
对于气体反应，写平衡常数关系式，除可以用平衡时的浓度表示外，也可以用平衡时各气体的分压表示。如： N2+3H2=2NH3 可写出两个平衡常数关系式
Kc=[NH3]2/([N2][H2]3)
Kp=p2(NH3)/[p(N2)p3(H2)]
3.1
的因素以及反应的机理。
化学平衡
化学动力学是研究化学反应的速度、影响反应速度热力学研究物理或化学变化中能量的相互转化和热的影响因素（如温度）对转化的影响。特别是研究在
指定条件下一个变化自动进行的可能性（自发性），
从而确定变化的方向和范围。但热力学不能解决变化的速度问题。化学热力学研究化学变化中能量的相互转化和热的影响因素（如温度）对转化的影响。

第三章化学反应动力学的计算

.2 常微分方程组的R-K方法在化学化工动力学的实际问题中，经常遇到的是一阶微分方程组，就如我们在本章开始时所提到的几个例子。一阶微分方程组的一般形式为：
(3.15) 式中函数，是变元的函数。若函数族在区间上是确定且可微的，当时，满足关系式：
则称是微分方程组(3.15)的解。在真实的化学反应体系中，总能满足上述要求，因此一定存在数值解，具体的解是用计算机寻找满足初始条件的数值解。给定的初值是已知常数。为了书写方便，一阶微分方程组(3.15)式使用微向量表示，即初值。现以（3.16）为例说明微分方程组的R-K算法。初始条件： R-K公式为：
9.93522×10-3 1.40291×10-5 5.07574×10-5
9.87084×10-3 1.46652×10-5 1.14494×10-4
9.80689×10-5 1.46078×10-5
0.1×10-7 0.333×10-6 0.356×10-6
0 0.47×10-7 0.44×10-7
开式子： Eular法只取了前二项而忽略了高次项，所以产生了误差。
3． Runge-Kutta方法 .1 常微分方程的Runge-Kutta方法 Runge-Kutta方法是建立在泰勒公式基础上的一种方法。通常采用的是四
阶R－K公式，即考虑了泰勒公式中四次项，而Eular公式只取了一次项。故R-K公式比Eular公式有了很大的改进。R-K方法在求解范围大、精度要求主的情况下是一种比较好的方法，并且计算工作量不算太大，所以在化学化工中应用颇多。四阶的R-K公式为：
有已斜率的小线段，即可得方向场的略图(图3-2)
从方向场各点的略图可以推出微分方程的原函数图形。例如画出微
分方程的方向场略图，其解为：在平面上（除原点外）的若干个点，画

普通化学——化学动力学基础PPT课件

(产物取正，生成物取负)
显然，两种方法定义的数值不一样，它们之间的关系为： r ri 1 dci vi vi dt
式中，vi为反应系数，符号一律取正)
||
||
5
3.1.2 反应动力学方程
1 积分形式的动力学方程
描述反应体系中某组分浓度与时间的关系的函数称为积分形式的动力学方程：
ci = g(t)
||
||
10
3.2 简单级数的反应的动力学方程
常见的简单级数的反应有零级反应、一级反应和二级反应，三级反应的例子不多。零级反应(准)——气、固相催化反应，酶催化反应一级反应——同位素衰变反应，部分取代反应二级反应——水解反应，部分取代反应
||
||
11
3.2.1 一级反应
一级反应：A → P dc kc dt
t
图3.2 一级反应
||
||
13
一级反应计算示例
例3.1 从考古发现的某古书卷中取出的小块纸片，测得其中 14C/12C 的比值为现在活的植物体内 14C/12C 的比值的0.795 倍。试估算该古书卷的年代。
解：已知 1 4 7 1 4 7 - 0 1 e - ， t 12 5730a
可用式(2.34)求得此一级反应速率常数k
第三章化学动力学基础
第三章化学动力学基础
化学热力学为我们提供了判断反应能否自发进行的依据。但是一个热力学自发的反应不一定能够进行，例如:
H2(g)+O2(g) = H2O(g) 298.15K时标准摩尔反应吉布斯函数变为–457kJ·mol-1,但在此温度下，不点燃或无撞击的情况下几天甚至几月都观察不到水分子的产生。
2 微分形式的动力学方程

北理无机化学第3章-化学动力学基础

例：
基元反应
§3.2 浓度对反应速率的影响
NO2(g)+CO(g) NO(g)+CO2(g)
v=kc(NO2)c(CO)
反应级数 n = 2
基元反应 2NO(g)+O2(g)2NO2(g)
v=kc(NO)2c(O2)
反应级数 n = 3
第三章化学动力学基础
3．注意
§3.2 浓度对反应速率的影响
或
lg{k}
Ea 2.303RT
lg{k0}
k：反应速率常数，由反应的性质和温度决定；
Ea：实验活化能，单位为kJ·mol-1，是表示反应特性的常数；
k0：指数前因子，频率因子，对指定反应为一常数。
第三章化学动力学基础
§3.3 温度对反应速率的影响
3.3.2 Arrhenius 方程式的应用
vB ΔcB Δt
vC
ΔcC
t
vD ΔcD Δt
浓度的单位：mol·L-1 时间的单位：s（h、min）
第三章化学动力学基础
例：
起始浓度/（mol·L-1）
§3.1 反应速率的意义
N2 + 3H2 → 2NH3
13
0
2秒后浓度/（mol·L-1）
0.8 2.4 0.4
同一反应，可用不同物质的浓度的变化表示反应速率，其值可能不同。
vN2
-
(0.8-1) 2
0.1mol
L-1
S-1
vH2
-
(2.4- 3) 2
0.3 mol
L-1
S-1
vNH3
(0.42
0)
0.2 mol
L-1
S-1
第三章化学动力学基础

第三章化学反应动力学的计算

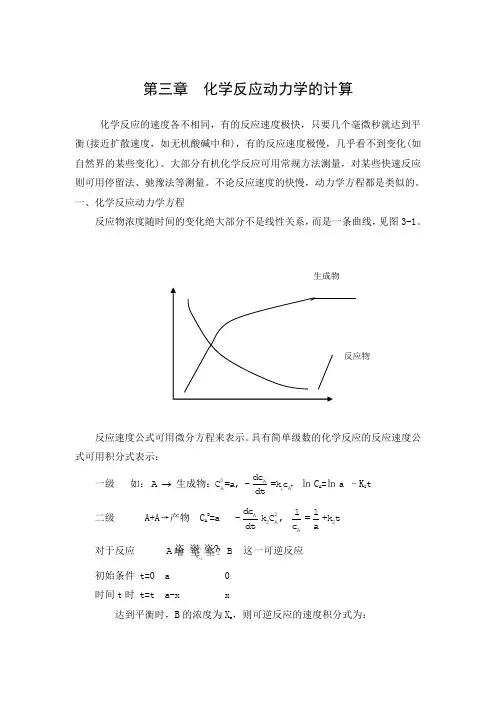
第三章化学反应动力学的计算化学反应的速度各不相同，有的反应速度极快，只要几个毫微秒就达到平衡(接近扩散速度，如无机酸碱中和)，有的反应速度极慢，几乎看不到变化(如自然界的某些变化)。

大部分有机化学反应可用常规方法测量，对某些快速反应则可用停留法、驰豫法等测量。

不论反应速度的快慢，动力学方程都是类似的。

一、化学反应动力学方程反应物浓度随时间的变化绝大部分不是线性关系，而是一条曲线，见图3-1。

反应速度公式可用微分方程来表示。

具有简单级数的化学反应的反应速度公式可用积分式表示：一级如：0AA1Adc A C =a, -=k c dt 生成物：，㏑C A =㏑a –K 1t 二级 A+A →产物 C A 0=a 2A 2A 2A d c 11-k C , =+k t d t c a对于反应 1-1k k A B 这一可逆反应初始条件 t=0 a 0 时间t 时 t=t a-x x达到平衡时，B 的浓度为X e ，则可逆反应的速度积分式为：级数：1-1 1-10k A A e e 1A -1B k 0e 0C =a dc x xA B=-k C +k C : =kt dt a x -xC =0ln 1-21-10Ak0A e e e B 1A -1B C k e e 0CC =a dc x ax +x(a-x )A B+C C =0=-k C +k C C : =kt dt 2a-x a(x -x)C =0ln 二、常微分方程的解化学反应动力学方程是用微分方程表示的，对于简单的反应，可直接求得微分方程的解。

微分方程：()(1)(,,,......)......(1)n n y f x y y y -'=在区间a<x<b 的解，是指()y x ϕ=,这样一个函数，在所述区间内存在导数()(),(),......()n x x x ϕϕϕ'''。

且对于区间a<x<b 内的每一个x ，等式(1)都成立。

江苏师范大学《无机化学》习题库及答案第三章化学动力学基础

第三章化学动力学基础一、判断题（每题1分，共10分）1. 溶液中，反应物A在t1时的浓度为c1，t2时的浓度为c2，则可以由(c1－c2)/(t1-t2)计算反应速率，当△t→0时，则为平均速率。

（）2. 反应2A+2B→C，其速率方程式r = kc(A)[c(B)]2，则反应级数为3。

（）3. 化学反应3A(aq)+B(aq)→2C(aq)，当其速率方程式中各物质浓度均为1.0 mol∙L--1时，其反应速率系数在数值上等于其反应速率。

（）4. 对零级反应来说，反应速率与反应物浓度无关。

（）5. 反应aA(aq)+bB(aq)→gG(aq)的反应速率方程式为r = k[c(A)]a[c(B)]b，则此反应一定是一步完成的简单反应。

（）6. 可根据反应速率系数的单位来确定反应级数。

若k的单位是mol1-n∙L n-1∙s-1，则反应级数为n。

（）7. 对不同化学反应来说，活化能越大者，活化分子分数越多。

（）8. 通常升高同样温度，E a较大的反应速率增大倍数较多。

（）9. 一般温度升高，化学反应速率加快。

如果活化能越大，则反应速率受温度的影响也越大。

（）10. 催化剂只能改变反应的活化能，不能改变反应的热效应。

（）二、填空题（每空2分，共40分）1. 元反应A+B→C的反应速率方程式r =________________，其反应级数为_______。

2. 质量作用定律仅适用于________反应；反应速率系数k的单位与元反应方程式中的_____________有关。

3. 某反应的反应速率系数单位为：mol∙L-1·s-1，则该反应的反应级数为________.4. 某反应A→B+C，当A的浓度为0.20 mol·L-1时，反应速率是0.0050 mol∙L-1∙s-1，若是零级反应，反应速率系数为____________，若是一级反应，反应速率系数为_______________。

大学无机化学第五版第三章化学动力学基础

aA(aq) + bB(aq)
yY(aq) + zZ(aq)
r dcA dcB dcY dcZ adt bdt ydt zdt
对于定容的气相反应：
r 1 dpB
B dt
§3.2 浓度对反应速率的影响 —速率方程
3.2.1 化学反应速率方程
3.2.2 由实验确定反应速率方程的简单方法——初始速率法
反应速率—— mol·L-1·s-1等分类：平均速率（ r ）、瞬时速率（ r ）
若以C1、C2代表时间t1、t2时，某反应物或生成物的浓度则：
平均速率：化学反应在某一有限时段内浓度的变化量。
_
r= ±
C2 - C1 t2 - t1
△C =±
△t
为使反应速率为正值：若用反应物浓度表示 C2﹤C1，△C为负，则前面加负号；若用生成物浓度表示 C2﹥C1，△C为正，则前面取正号。
答：各物质的系数不同；各数值除以系数后相等。
对于一般的化学反应： 0 BB
B
定容条件下，定义：r d
Vdt
r——定容条件下的反应速率(mol·L-1·s-1)
d dnB dt Bdt r d dnB 1 dcB Vdt V Bdt Bdt
溶液中的化学反应：
反应级数
2
1+1
2NOg O2 g 2NO2 g r k[c(NO)]2c(O2) 2+1
2+1 2NOg 2H2 g N2 g H2Og r k[c(NO)]2 c(H2 )
S2O82 aq 3I aq 2SO24 aq I3 aq
t/ s
VSTP O2 /mL cN2O5 / mol L1

化学反应动力学-第三章-基元反应动力学

Arrhenius理论假定Ea与温度无关,但与碰撞理
论相比较, Ea却是和温度有关的,即 Ea = f (T)
一般来说,当Ec较大且在低温下反应时,Ea=Ec; 当Ec较小且在高温下反应时,只有采用 ln( k 2 ) 1 1 作图才能得较为理想的直线。
上一内容下一内容
T
T
返回
五、概率因子碰撞理论假定分子为刚性硬球,主要考虑了硬
假设A、B双分子的反应是：
A + B A B 产物
只有处于活化状态的（A……B）才能进一步反
应，利用Maxwell的速率分布定律、玻尔兹曼
分布律及统计力学，可得出反应的活化能：
E N0 a
上一内容下一内容

返回
四、碰撞理论的反应速率公式与讨论依据分子碰撞理论的两个基本假定，反应速率公式有二：
以上这些问题在分子碰撞理论中将予解释。
上一内容
下一内容
返回
二、分子碰撞理论和碰撞频率（一）分子碰撞模型 ⑴分子碰撞的弹性刚球模型：假定分子是刚性的实心球体,分子占有一定体积,不考虑分子作用力,分子不能压缩。刚球为光滑表面,碰撞无摩擦阻力,碰撞时切面方向和对相对速度不产生任何影响,分子的碰撞是弹性碰撞。
e
E0 / RT
用此式可求出具有能量ε（≥ 0 ）的分子分数。式 0 E0 / N(N0为中kB为玻尔兹曼常数，显然 0 Avogadro常数)。这表明反应速率常数与能量大 0 于（即 E0 / N 0 ）的分子数成正比。可见，只有具有能量大于 0 的反应物分子才能进行反应。可见，温度的影响表现在活化能因子 - E0 / RT 上，即活化分子的百分数上，由于T是在 e 指数项上，故其影响显著。

化学反应动力学(全套课件582P)

r 1 d[A] 1 d[B] 1 d[C] 1 d[D] a dt b dt c dt d dt
或 r 1 d[Ri ]
i dt
对于气相反应，也可用压力表示反应速率：
rP
1 a
dPA dt
1 b
dPB dt
1 c
dPC dt
1 d
dPD dt
或：
rP
1
i
dPRi dt
对于理想气体： Pi ci RT
化学反应动力学
课程属性：学科基础课学时/学分：60/3
教材:
《 Chemical Kinetics and Dynamics 》 J. I. Steinfeld, et al, 1999 ( Prentice Hall )
参考书：
1《化学反应动力学原理》（上、下册）赵学庄编（高等教育出版社）
k = 2×104
k = 1×10-2
§1-2 反应速率的定义
( Definition of the Rate of a Chemical Reaction ) 若一个反应的化学计量式如下：
(1) a A + b B c C + d D 或写为： (2) 0 = iRi
式(2) 中,
Ri：反应物和产物。 i：化学计量系数, 它对于反应物为负,
1 给定乙醛的初始浓度, 测定不同反应时间的反应速率及乙醛浓度，从而确定反应的反应级数。
则反应速率与[CH3CHO]的平方成正比，即称其时间级数为二级的。
2 以乙醛的不同初始浓度进行实验, 测定不同初始浓度下的反应速率，从而确定反应级数。
则反应速率与乙醛的初始浓度的一次方成正比，即称其浓度级数为一级的。

化学反应动力学基础N

c-t图
r-c图
40℃,CCl4中N2O5分解反应的r:c( N2O5 )
t /s
0 300 600 900 1200
r : c N 2 O5 / s1

t /s
1800 2400 3000 4200 5400
r : c N 2 O5 / s

1
3.6510
4
4
3.64104 3.6210 3.6910
反应反应速级数率方程积分速率方程式对 t 的图直线是直线斜率
t
1/2
0
r k At kt A0
1 1 kt At A0
At
ln At
1 At
-k -k
A0 2k
1 r kA ln At kt ln A0 2
0.693 k
r kA
取一般通式:
r (1 /n B )dcB / dt
例：2N2O5(CCl4) 2N2O4(CCl4)+ O2(g)
例如2700s时的瞬时速率：
0.144 0 2.58105 A点的斜率= 2 (55.8 0) 10
r 2.5810 mol L s
ln 2 0.693 Qt1/ 2 k k 0.693 \k t1/ 2 t1/ 2 1 A0 1.297 9 1.7 10 (年) t ln ln k A 0.693 1.000
美国科学家利比因发明利用测定放射性14C 确定地质年代的方法获1960年诺贝尔奖。
第三节
反应级数不同，k的单位不同。 k的单位：零级反应 mol· -1 ·-1；一级反应 s-1； L s 二级反应 (mol· -1)-1 ·-1。 L s

化学反应的反应动力学

化学反应的反应动力学化学反应是物质转化的过程，其中反应速率是一个重要的性质。

反应动力学研究的就是反应速率随时间的变化规律，旨在揭示反应速率与反应条件和反应物浓度之间的关系。

本文将介绍反应动力学的基本概念、影响因素以及实验方法。

一、反应动力学的基本概念反应速率指的是在单位时间内，反应物浓度的变化量。

反应动力学则是研究反应速率与反应条件和反应物浓度之间的关系。

反应速率可以用反应物消失速率或产物生成速率来表示。

1. 反应物消失速率（消失相速率）：当反应物A以浓度a参与反应，反应速率可以用A消失的速率来表示，可以用下式表示：v = -（Δ[A] / Δt）其中，v表示反应速率，Δ[A]表示反应物A浓度的变化量，Δt表示时间的变化量。

2. 产物生成速率（生成相速率）：当产物B以浓度b生成，反应速率可以用B生成的速率来表示，可以用下式表示：v = （Δ[B] / Δt）二、影响反应速率的因素反应速率受多个因素的影响，包括温度、浓度、催化剂等。

1. 温度：温度对反应速率有显著影响。

一般来说，温度升高会使反应速率增加，因为高温下分子动能增加，反应物分子的能量更容易达到活化能，促使反应发生。

2. 浓度：反应物浓度的增加会导致反应速率的增加。

这是因为反应物浓度越高，其中的分子碰撞的次数越多，发生反应的几率也就越大。

3. 催化剂：催化剂可以降低反应的活化能，从而提高反应速率。

它通过提供一个新的反应途径，降低了反应物分子之间的碰撞能量要求，使得反应更容易进行。

三、实验方法反应动力学的研究通常采用实验方法来获得反应速率与反应物浓度之间的关系。

1. 初始速率法：通过在反应初期测量多个不同浓度下的反应速率，可以得到反应速率与反应物浓度之间的关系。

这种方法需要在反应初期进行测量，比较适用于反应物快速消耗的反应。

2. 变温法：通过在不同温度下测量反应速率，可以研究温度对反应速率的影响。

变温法需要控制其他条件不变，只改变温度来观察反应速率的变化。

化学反应动力学

化学反应动力学化学反应动力学是研究化学反应速率及其与反应条件、反应物浓度和反应机理之间关系的学科。

本文将围绕化学反应动力学的基本定义、重要指标以及影响因素等方面展开讨论。

1. 动力学基础化学反应动力学是研究化学反应速率及其与反应条件、反应物浓度和反应机理之间关系的学科。

它关注反应速率的测定、速率方程式的建立和解释以及影响速率的因素等问题。

2. 反应速率与反应物浓度的关系反应速率是描述单位时间内反应物消失或生成的量的变化率。

反应速率与反应物浓度之间存在一定的关系。

根据反应速率与反应物浓度之间的关系，我们可以推导出速率方程式。

3. 反应速率常数反应速率常数是衡量反应速率快慢的重要指标。

它是速率方程式中的常数项，表示单位时间内单位浓度反应物消失或生成的量。

反应速率常数与反应条件、反应物浓度以及反应机理等因素有关。

通过实验测定可以确定反应速率常数的值。

4. 反应级数与速率方程式反应级数是衡量反应速率与反应物浓度之间关系的指标，主要体现在速率方程式中的指数项上。

反应级数可以帮助我们了解反应机制，从而进一步推导出速率方程式。

5. 影响反应速率的因素反应速率受多种因素影响，包括反应物浓度、温度、催化剂和反应体系等。

反应物浓度越大，反应速率越快；温度升高也可以加快反应速率；催化剂可以提高反应速率而不参与反应本身；反应体系的状态对反应速率有重要影响。

6. 动力学实验方法化学反应动力学的研究需要进行一系列的实验来测定反应速率。

常见的实验方法包括初始速率法、半衰期法和瞬态法等。

这些方法可以通过实验数据来确定速率方程式以及反应速率常数的值。

7. 应用领域化学反应动力学研究的成果在很多领域都有广泛的应用，如工业生产中的反应优化、环境污染治理、药物研发以及生物化学等领域。

通过深入研究反应速率与反应条件之间的关系，可以为这些领域的实际问题提供有效的解决方案。

结语：化学反应动力学是一门重要的学科，它研究了化学反应速率及其与反应条件、反应物浓度和反应机理之间的关系。

催化化学第三、四章

令酶的原始浓度为[E]0，反应达稳态后，一部分变为中间化合物[ES]，余下的浓度为[E]
[E] [E]0 [ES]
[E][S] ([E]0 [ES])[S] [ES] KM KM
[E]0 [S] [ES] K M [S]
k2 [E]0 [S] d[P] r k2 [ES] dt K M [S]
（二）速率方程与动力学参数
微分形式的速率方程又有幂式和双曲线式两种，幂式速率方程形式如
r kPA PB
其中k为速率常数，α，β…为反应级数。双曲线式速率方程有以下或类似的形式
ki Pi r 1 1P 2 P2 ... 1
其中， i 1 2 ... 为常数，k为反应速率常数
2.高效率倍。
它比人造催化剂的效率高出108至1012
一般在常温、常压下进行。
3.反应条件温和
4.兼有均相催化和多相催化的特点 5.反应历程复杂受pH、温度、离子强度影响较大。酶本身结构复杂，活性可以进行调节
气固多相催化反应动力学基础
一、基本概念
（一）反应速率
（二）速率方程或动力学参数（三）速率控制步骤（四）表面质量作用定律
（二）速率方程与动力学参数
基元过程一般服从Arrhenius定律
k A exp- E / RT
其中，A为指前因子，E为活化能。在总包反应情况下，总反应速率常数有时在形式上遵从Arrhenius 定律，此时所对应的E称为表观活化能，表观活化能是否有具体的物理意义视情况而定。动力学参数包括速率常数，反应级数，指前因子和活化能等。
k1 S E k1
ES E P

《反应动力学基础》课件

实验结果。
B
C
D
结果应用与展望
探讨实验结果在实际生产和科研中的应用前景和价值，同时提出进一步的研究方向和展望。
结果比较与验证
将实验结果与已有的研究结果进行比较和分析，验证实验结果的可靠性和准确性。
06
反应动力学的应用
在化学工业中的应用
化学反应过程优化
反应动力学基础能够帮助我们理解化学反应过程，从而优化反应条件，提高产物的收率和选择性。
动力学的微分方程。
质量作用定律
02 根据质量作用定律，推导出反应速率与反应物质浓度
的关系式，进而得到微分方程。
平衡常数的影响
03
考虑平衡常数对反应速率的影响，将平衡常数纳入微
分方程的推导过程中。
微分方程的解法
分离变量法
通过分离变量法，将微分方程转化为多个常微分方程，简化求解过程。
积分因子法
利用积分因子法，消除微分方程中的积分项，从而得到方程的解。
反应速率常数
总结词
反应速率常数是反应速率方程中的比例系数，表示反应速率的大小。
详细描述
反应速率常数是化学动力学中的一个重要参数，它是反应速率方程中的比例系数。它表示了在一定条件下，反应速率的大小。反应速率常数越大，反应速率越快；反之，则越慢。
反应机理
总结词
反应机理是描述化学反应过程中各步骤的详细过程的模型。
详细描述
反应速率描述了化学反应的快慢程度，通常用单位时间内反应物或生成物的浓度变化来表示。在单位时间内，反应物浓度的减少或生成物浓度的增加量即为该反应的反应速率。
反应速率方程
总结词
反应速率方程是用来描述反应速率与反应物浓度的关系的数学表达式。
详细描述

3气固多相反应动力学基础

7.动力学参数有那些
速率常数，反应级数，指前因子和活化能
第三章催化反应动力学
本次课内容和要求
1.速率控制步骤 2.推导表面过程动力学方程时的两种方法 (平衡浓度法和稳定浓度法 3.化学反应、吸附和脱附为控制步骤的动力学方程 4.不存在控制步骤的动力学方程
5.两步机理模型
掌握速率控制步骤的内涵
要掌握由表面反应,吸附或脱附分别为速控步骤时的速率方程
K为速率常数，α1、α2等为级数
第三章催化反应动力学
3.3理想吸附层的速率方程
双曲线式方程有以下或类似的形式
此式描述的是SO2的氧化，其中A，B为常数，K为反应的平衡常数基元过程一般服从Arrehnius定律
其中A为指前因子，E为活化能 •在总包反应情况下，总反应速率常数有时在形式上遵从 Arrehnius定律，此时所对应的E称为表观活化能，表观活化能是否有具体的物理意义视情况而定
ห้องสมุดไป่ตู้
第三章催化反应动力学
第三章气固多相催化反应动力学基础
[教学难点]
1. 两步机理模型的两个假定，三个定理 2. 反应区间的识别
[主要内容]
1. 多相催化反应过程和表面质量作用定律 2. 化学反应，吸附和脱附为控制步骤的动力学方程 3. 两步机理模型的两个假定，三个定理 4. 外扩散和内扩散对反应动力学的影响 5. 外扩散和内扩散阻滞效应的识别
第三章催化反应动力学
3.1多相催化反应过程
• 研究气固多相反应动力学，从实用的角度说，为工业催化过程确定最佳生产条件，为反应器的设计打基础
• 从理论上说，是为认识催化剂的特性提供依据，因为催化剂的动力学参量是催化剂化学特性的重要依据。这些参量是现有催化剂改进以及新型催化剂设计的依据

无机及分析化学(第三章化学动力学基础)

反应机理
讨论的问题：一个反应是如何进行的？ 1）基元反应与复杂反应（非基元反应） ▲ 反应物分子直接碰撞而发生的化学反应称为基元反应，它是一步完成的反应。 • 由一个基元反应构成的化学反应称为简单反应。 • ▲ 由两个或两个以上的基元反应构成的化学反应称为非基元反应或复合反应。 • ▲ 由一个基元反应构成的化学反应并不多，因此，一个化学反应方程式，除非特别注明，都属于化学计量方程式，而不代表基元反应。 • 例如：
基元反应的化学反应速率方程：
式中：k为反应速度常数 CA、CB为物质A、B的浓度 a为A物质的反应级数 b为B物质的反应级数 a + b则为整个反应的级数。当： a = 1时，对A物质是1级反应 b = 1时，对为B物质是1级反应 a+b = n时，则整个反应为n级反应。
1）速率常数k
▲上式中的比例系数k称为速率常数。 ▲ k的物理意义：单位浓度时的反应速率。 ▲速率常数 k 取决于反应的本性，其它条件相同时快反应通常有较大的速率常数； ▲速率常数k与浓度无关； ▲ k 是温度的函数，温度升高， k 值增大。
• 解：求Ea，已知k1 、k2 T1和T2，利用下式：
即可求得Ea；同理，利用给定的条件和求得的 Ea，则可求得速度常数k。
4 反应速率理论和反应机理简介
定量地描述温度、浓度对反应速率影响的速率方程式和 Arrehenius方程都是实验事实的总结，反应为什么能进行，活化能的本质和物理意义是什么，等等问题靠实验事实不能解决，需要我们讨论反应速率理论。
可见，总反应（或一般的化学计量反应是由若干个基元反应组成的。
2）反应的控速步骤（Rate - contralling step)
任何一个复杂反应都是由多个基元反应组成的，

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

产生中间活化络合物的历程。
3）1950年代后，新的实验手段的利用，微
观反应动力学（分子反应动态学）得到
发展。
• 利用激光、交叉分子束等新实验手段，研究某一量子态的反应物变化到某一确定量子态的产物的速率及反应历程（态-态反应的层次）； • 从分子水平上研究微观反应动力学，使得化学
动力学取得了新的进展。
1986李远哲获诺贝尔化学奖
李远哲，1936年出生于台湾新竹县，1962年去美国深造，于1965年获化学博士学位。 1974年加入美国籍。主要是因为他对交叉分子束方法的研究，他们将激光、光电子能谱与分子束结合，设计了“分子束碰撞器”和 “离子束交叉仪器” ，实现了在单次碰撞下研究单个分子间发生的反应机理的设想，使化学家有可能在电子、原子、分子和量子层次上研究化学反应所出现的各种动态，以探究化学反应和化学相互作用的微观机理和作用机制，对了解化学物相互反应的基本原理，做出了重要突破。
二、瞬时速率——某瞬间的反应速率
化学动力学(chemical kinetics)
是研究化学反应速率（rate of reaction）和反应机理（mechanism of reaction）的化学分支学科。
化学动力学的主要内容
确定化学反应的速率以及温度、压力、催化剂、溶剂和光照等外界因素对反应速率的影响；研究化学反应机理，揭示化学反应速率本质；探求物质结构与反应能力之间的关系和规律。
动力学与热力学联系
热力学上不能发生的过程，在现实中一定不能发生，研究其动力学没有意义。热力学研究无限缓慢的可逆过程，故不考虑时间因素，所以热力学上可以发生的过程只是现实可能发生的过程，不是必然发生的。变化的可能性-化学热力学：解决变化的方向、限度及变化过程的能量转化变化的现实性-化学动力学：解决变化的速率及分析变化的具体过程。
t2时的浓度则
c(A)2 c(B)2 ∆ t = t2 - t1
c(C)2 c(D)2 ∆c = c2 - c1
∆c(D) (D) = ∆t
∆c(A) (A) = - ∆t
单位: mol· L-1· s-1; mol· L-1· min-1; mol· L-1· h-1
如：
反应
2N2O5 = 4NO2 + O2 2.10 1.95 0 0 0.30 0.075
指导设计安全、稳定及有效的制剂处方
提出有关制剂正确的工艺技术及合适的贮存条件

制订合理的用药方案
引入动力学的研究方法之后，药物研究才真正摆脱经验阶段而进入科学阶段
第一节
化学反应速率
反应速率 ∆t时间内反应物浓度和生成物浓度的变化值如：
t1时的浓度
aA + bB → cC + dD
c(A)1 c(B)1 c(C)1 c(D)1
υ (N O ): υ (NO ): υ (O ) = 2:4:1 2 5 2 2 不同物质表示的反应速率数值是不同的即等于方程式相应物质分子式前的系数比
一、平均速率 ∆t时间内反应物浓度和生成物浓度的变化值 IUPAC建议
1 cB B t
B——化学方程式中的计量系数规定—反应物取“-” 生成物取“+”
Very fast reaction
反应速率
Slow reaction
化学反应，有的进行得很快，例如爆炸反应、强酸和强碱的中和反应等，几乎在顷刻之间完成，有的则进行得很慢，例如岩石的风化、钟乳石的生长、镭的衰变等，历时千百万年才有显著的变化。有的反应，用热力学预见是可以发生的，但却因为反应速度太慢而事实上并不发生，如金刚石在常温常压下转化为石墨，在常温下氢气和氧气反应生成水等，这是由于，化学热力学只讨论反应的可能性、趋势与程度，却不讨论反应的速度。
李远哲
药物代谢动力学研究内容
• 药物体内过程：机体对药物的处置吸收(absorption) 分布 (distribution) 代谢(metabolism) 排泄 (excretion) • 体内药物浓度（血药浓度）动力学规律
非血管途径给药的药-时曲线

预测制剂中化学活性物质的稳定性
ห้องสมุดไป่ตู้ 化学动力学发展
特点：相对于热力学发展较晚，不系统。 1）19世纪中叶起，宏观动力学研究： a. 浓度对反应的影响质量作用定律； b. 温度对反应的影响 Arrhenius 经验式； c. 活化能概念的提出：反应物必须得到一定的
能量才能起反应。
2）20世纪前叶：反应速率理论的创立 a. 碰撞理论：把反应看作两个反应球体碰撞的结果； b. 过渡态理论：
化学动力学意义
通过化学动力学的研究，可以知道如何控制反应条件，提高主反应的速率，增加产品产量，抑制副反应的速率，减少原料消耗，减少副产物，提高纯度，提高产品质量。化学动力学也研究如何避免危险品的爆炸、材料的腐蚀、产品的变质与老化等问题。所以化学动力学的研究有理论与实践上的重大意义。
C0/(mol· L-1) C100S/(mol· L-1)
∆c(N2O5) 1.95-2.10 =1.5×10-3mol· L-1· s-1 υ(N2O5)= = ∆t 100 ∆c(NO2) 0.30-0 υ(NO2)= = =3.0×10-3mol· L-1· s-1 ∆t 100 ∆c(O2) 0.0750-0 υ(O2) = = =7.5×10-4mol· L-1· s-1 ∆t 100
飞秒化学(Femtochemistry)
20世纪70年代，基于快速激光脉冲的飞秒光谱技术发展，使时间标度达到了飞秒数量级，用飞秒激光技术来研究超快过程和过渡态使飞秒化学随之发展起来。从20世纪 80年代开始，艾哈迈德-泽维尔(Ahmed H. Zewail埃及出生美籍) 因用飞秒化学研究化学反应的过渡态而获得了 1999年度的诺贝尔化学奖。 “Zewail教授在飞秒化学领域所做出的贡献使我们可以断言，化学家研究反应历程的努力已接近终点，任何化学反应的速率都不可能比飞秒量级更快。化学将有可能对各类化学反应的历程做出合乎实际的推断” －诺贝尔化学奖公报

第三章 化学反应动力学基础

第三章 化学反应速率、方向和限度

第三章 化学反应动力学的计算

普通化学——化学动力学基础PPT课件

北理无机化学第3章-化学动力学基础

第三章 化学反应动力学的计算

江苏师范大学《无机化学》习题库及答案第三章 化学动力学基础

大学无机化学第五版第三章化学动力学基础

化学反应动力学-第三章-基元反应动力学

化学反应动力学(全套课件582P)

化学反应动力学基础N

最新《无机化学》第三章化学动力学基础

化学反应的反应动力学

化学反应动力学

催化化学第三、四章

《反应动力学基础》课件

3气固多相反应动力学基础

无机及分析化学(第三章化学动力学基础)

第三章化学反应动力学基础

第三章化学反应速率、方向和限度

第三章化学反应动力学的计算

第三章化学反应动力学的计算

江苏师范大学《无机化学》习题库及答案第三章化学动力学基础