高二数学(理科)答题卡
四川省成都市蓉城名校联盟2020-2021学年高二下学期期中联考数学(理)Word版含答案

蓉城名校联盟2020~2021学年度下期高中2019级期中联考理科数学考试时间120分钟,满分150分注意事项:1.答题前,考生务必在答题卡上将自己的学校、姓名、班级、准考证号用0.5毫米黑色签字笔填写清楚,考生考试条形码由监考老师粘贴在答题卡上的“条形码粘贴处”。
2.选择题使用2B 铅笔填涂在答题卡上对应题目标号的位置上,如需改动,用橡皮擦擦干净后再填涂其它答案;非选择题用0.5毫米黑色签字笔在答题卡的对应区域内作答,超出答题区域答题的答案无效;在草稿纸上、试卷上答题无效。
3.考试结束后由监考老师将答题卡收回。
一、选择题:本题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知函数f(x)=x 3+1,当自变量x 由1变为2时,函数f(x)的平均变化率为 A.3 B.5 C.7 D.92.已知空间两点A(2,1,1),B(3,2,1),下列选项中的a 与AB 共线的是 A.a =(1,0,1) B.a =(2,1,1) C.a =(2,-2,0) D.a =(2,2,0)3.已知向量a =(1,2,0),b =(0,2,1),a ,b 的夹角为θ,则sinθ= A.35 B.45 C.-35 D.-454.已知函数f(x)的导数是f'(x),且f'(3)=1,则()()h 0f 3f 3h lim h→-+=A.1B.-1C.3D.-3 5.下列关于空间向量的四个命题中正确的是 A.若空间向量a ,b 满足|a|=|b|,则a =bB.若{a ,b ,c}为空间中一组基底,则{a +b ,a -b ,c}可构成空间另一组基底C.若11OC OA OB 24=+,则A 、B 、C 三点一定共线 D.已知A ,B ,C 三点不共线,若111OD OA OB OC 234=++,则A ,B ,C ,D 四点一定共面6.已知函数f(x)的导数是f'(x),且满足f(x)=f'(2π)cosx +2x ,则f(0)=A.0B.1C.2D.4 7.定积分()1x1e1dx -+⎰的值为A.e -1e +1 B.e +1e +1 C.e -1e +2 D.e -1e8.已知R 上可导函数f(x)的图象如图所示,则不等式(x -3)f'(x)>0的解集为A.(-2,2)∪(3,+∞)B.(-∞,-3)∪(3,+∞)C.(-∞,-2)∪(3,+∞)D.(-∞,-2)∪(2,+∞)9.如图,在三棱锥S -ABC 中,点E ,F 分别是SA ,BC 的中点,点G 在棱EF 上,且满足EG 1GF 2=,若SA a SB b SC c ===,,,则SG =A.13a -12b +16c B.13a +16b +16c C.16a -13b +12c D.13a -16b +12c 10.如图,在四棱锥S -ABCD 中,侧面SCD 是等边三角形,底面ABCD 是直角梯形,∠BCD =2π,AD =CD =4,BC =8,侧面SCD ⊥底面ABCD ,点M 是SD 的中点,则直线SC 与AM 所成角的余弦值是A.-5B.5C.-9510D.951011.已知函数f(x)是定义域R上的可导函数,其导函数为f'(x),且满足f(x)>f'(x)恒成立,则下列不等式一定正确的是A.5f(ln2)>2f(ln5)B.6f(ln3)<3f(ln6)C.5f(ln5)<2f(ln2)D.3f(ln3)>6f(n6)12.已知函数f(x)=e x-1+ax2+1的图象在x=1处的切线与直线x+3y-1=0垂直,若对任意的x∈R,不等式f(x)-kx≥0恒成立,则实数k的最大值为A.1B.2C.3D.4二、填空题:本题共4小题,每小题5分,共20分。
河北省张家口市2022高二数学下学期期末考试试题 理(含解析)

.
(Ⅱ) ,
,
, .
【点睛】本题主要考查复数的求法和复数的运算,考查复数模的计算,意在考查学生对这些知识的理解掌握水平,属于基础题.
18.某地为了调查市民对“一带一路”倡议的了解程度,随机选取了 名年龄在 岁至 岁的市民进行问卷调查,并通过问卷的分数把市民划分为了解“一带一路”倡议与不了解“一带一路”倡议两类.得到下表:
【详解】解:(Ⅰ)根据已知数据得到如下列联表
年龄低于 岁 人数
年龄不低于 岁的人数
合计
了解
不了解
合计
故有 的把握认为以 岁为分界点“一带一路”倡议的了解有差异.
(Ⅱ)由题意,得市民了解“一带一路”倡议的概率为 , .
, , ,
, ,
则 的分布列为
, .
【点睛】本题要注意选取4人是在总体中选,而不是在100人的样本中选,如果看成是在样本中100人选4人,很容易误用超几何分布模型求解.
(2)对方程根的个数转化为函数零点个数,通过对参数 进行分类讨论,利用函数的单调性、最值、零点存在定理等,判断函数图象与 轴的交点个数.
【详解】(Ⅰ) 的导数为 .
在区间 , , 是增函数;在区间 上, , 是减函数.
为奇函数, ,
令 ,其图象如图所示,则 ,
设曲边梯形ABCD的面积为 ,则 ,
,
原式的值为 .
【点睛】在求积分时,如果原函数不易求时,可考虑用积分的几何意义,把求积分值转化为求面积问题.
12.函数 ,若 有8个不相等的实数根,则 的取值范围是
A. B. C. D.
【答案】A
【解析】
【分析】
方程有8个不相等的实数根指存在8个不同 的值;根据函数 的图象,可知方程 必存在2个大于1的不等实根.
2022-2023学年四川省泸县第五中学高二上学期期末考数学(理)试卷带讲解

12.数学美的表现形式不同于自然美或艺术美那样直观,它蕴藏于特有的抽象概念,公式符号,推理论证,思维方法等之中,揭示了规律性,是一种科学的真实美.平面直角坐标系中,曲线 : 就是一条形状优美的曲线,对于此曲线,给出如下结论:
【详解】∵直线方程 可整理为
∴定点为
∵点A在直线 上
∴
∴ ,当且仅当 时取等号
故答案为:
16.过点 作抛物线 的两条切线,切点分别为 和 ,又直线 经过拋物线 的焦点 ,那么 的最小值为_________.
16
【分析】设 ,写出以 为切点的切线方程,由判别式求出切线斜率,得到以 为切点的切线方程,同理求出以 为切点的切线方程,结合 在两条切线上得直线 的方程,联立直线 与抛物线方程,根据根与系数的关系,结合抛物线定义得出结果.
【考点】圆的方程,点到直线的距离公式
【名师点睛】直线与圆的位置关系有三种情况:相交、相切和相离.已知直线与圆的位置关系时,常用几何法将位置关系转化为圆心到直线的距离d与半径r的大小关系,以此来确定参数的值或取值范围.
9.已知 , ,若不等式 恒成立,则正数 的最小值是()
A. 2B. 4
C. 6D. 8
第八组[190,195].如图是按上述分组方法得到的频率分布直方图的一部分,已知第一组与第八组人数
相同,第六组的人数为4人.
(Ⅰ)求第七组的频率;
(Ⅱ)估计该校的800名男生的身高的中位数以及身高在180cm以上(含180cm)的人数;
福建省清流一中2014-2015学年高二上学期第三次阶段测试数学理试题 Word版含答案
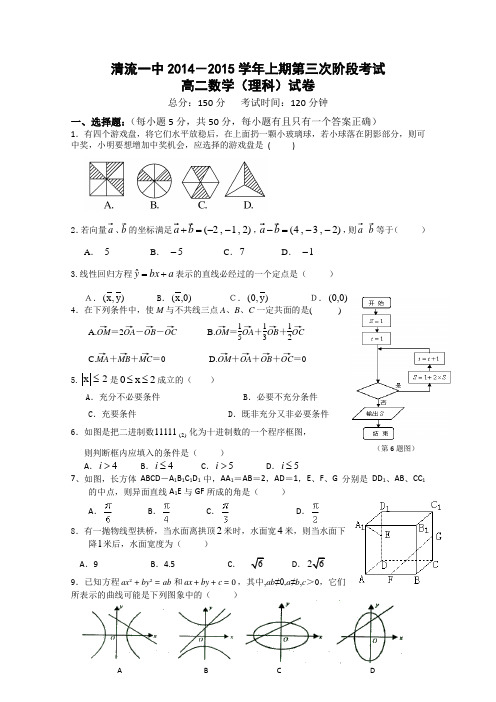
清流一中2014-2015学年上期第三次阶段考试高二数学(理科)试卷总分:150分 考试时间:120分钟一、选择题:(每小题5分,共50分,每小题有且只有一个答案正确)1.有四个游戏盘,将它们水平放稳后,在上面扔一颗小玻璃球,若小球落在阴影部分,则可中奖,小明要想增加中奖机会,应选择的游戏盘是 ()2.若向量、的坐标满足)2,1,2(--=+b a ,)2,3,4(--=-b a ,则·等于( ) A . 5 B . 5- C .7 D . 1-3.线性回归方程a bx y+=ˆ表示的直线必经过的一个定点是( ) A.)y ,x ( B .)0,x ( C.)y ,0( D.)0,0( 4.在下列条件中,使M 与不共线三点A 、B 、C 一定共面的是( )A.OM →=2OA →-OB →-OC →B.OM →=15OA →+13OB →+12OC →C.MA →+MB →+MC →=0D.OM →+OA →+OB →+OC →=0 5.2x ≤是2x 0≤≤成立的( )A .充分不必要条件B .必要不充分条件C .充要条件D .既非充分又非必要条件6.如图是把二进制数)2(11111化为十进制数的一个程序框图,则判断框内应填入的条件是( )A .4i >B .4i ≤C .5i >D .5i ≤7、如图,长方体ABCD -A 1B 1C 1D 1中,AA 1=AB =2,AD =1,E 、F 、G 分别是DD 1、AB 、CC 1的中点,则异面直线A 1E 与GF 所成的角是( )A .B .C .D .8.有一抛物线型拱桥,当水面离拱顶2米时,水面宽4米,则当水面下降1米后,水面宽度为( ) A .9 B .4.5 C .D. 9.已知方程22ax by ab +=和0ax by c ++=,其中,ab ≠0,a ≠b ,c >0,它们所表示的曲线可能是下列图象中的( )(第6题图)A B C D10.已知双曲线()+∈=-N b by x 14222的两个焦点为21,F F ,O 为坐标原点,点P 在双曲线上,且5<OP ,若1PF 、21F F 、2PF 成等比数列,则2b 等于( ) A .1 B .2 C .3 D .4 二、填空题:(每小题4分,共20分,把正确的答案填在相应的横线上.)11.写出命题“0(0,)x π∃∈,使得00sin x x <”的否定形式是 .12. 当3a =时,右边的程序段输出的结果是13.若双曲线)0(13222>=-a y a x 的离心率为2,则双曲 线的渐近线方程为14. 已知点P 是抛物线x y 22=上的动点,点P 在y 轴上的射影是M ,)4,27(A ,则PM PA +的最小值是 . 15.给出以下四个命题:① “正三角形都相似”的逆命题;② 已知样本9,10,11,,x y 的平均数是10100=xy ;③ “53<<-m ”是“方程13522=++-m y m x 表示椭圆”的必要不充分条件; ④ABC ∆中,顶点B A ,的坐标为)0,2(),0,2(B A -,则直角顶点C 的轨迹方程是422=+y x 其中正确命题的序号是 (写出所有正确命题的序号).清流一中2014-2015学年上期第三次阶段考试高二数学(理科)答题卡总分:150分 考试时间:120分钟座………………(第12题图)二、填空题:(每小题4分,共20分,把正确的答案填在相应的横线上.)11、_____________________________; 12、_____________________________;13、_____________________________; 14、_____________________________;15、_____________________________.三、解答题:(共80分,解答题应写出文字说明、证明过程或演算步骤)16.(本小题满分13分)(Ⅰ)已知曲线y =x 24-3ln x 的一条切线的斜率为12,求切点的横坐标.(Ⅱ)求下列函数的导函数(1)y = (2x +1) 2 (2)y =x 2cos x (3) y =sin xx解:17.(本小题满分13分)已知p :“直线0=-+m y x 与圆1)1(22=+-y x 相交”;q :“方程042=-+-m x x 的两根异号”.若q p ∨为真,p ⌝为真,求实数m 的取值范围.18.(本小题满分13分)如图,长方体1111ABCD A B C D -中,2==AD AB ,41=AA ,点E 在1CC 上,且EC E C 31=. (Ⅰ)证明:⊥C A 1平面BDE ; (Ⅱ)求二面角B DE A --1的余弦值.解:AB CD EA 1B 1C 1D 1O 19. (本题满分13分)已知直线l 经过抛物线y 2=4x 的焦点F ,且与抛物线相交于A 、B 两点. (1) 若|AF |=4,求点A 的坐标;(2) 设直线l 的斜率为k ,当线段AB 的长等于5时,求k 的值. 解:20.(本小题满分14分)某高校在2013年的自主招生考试成绩中随机抽取40名学生的笔试成绩,按成绩共分成五组:第1组)8075[,,第2组)8580[,,第3组)9085[,,第4组)9590[,,第5组]10095[,,得到的频率分布直方图如图所示,同时规定成绩在85分以上(含85分)的学生为“优秀”,成绩小于85分的学生为“良好”,且只有成绩为“优秀”的学生才能获得面试资格.(Ⅰ)求出第4组的频率,并补全频率分布直方图;(Ⅱ)根据样本频率分布直方图估计样本的中位数; (Ⅲ)如果用分层抽样的方法从“优秀”和“良好” 的 学生中共选出5人,再从这5人中选2人,那么至少 有一人是“优秀”的概率是多少?解:21.(本小题满分14分)设x 、y ∈R ,i 、j 为直角坐标平面内x 、y 轴正方向上的单位向量,向量a =x i +(y +2)j ,b =xi +(y -2)j ,且|a |+|b |=8.(1)求点M (x ,y )的轨迹C 的方程;(2)过点(0,3)作直线l 与曲线C 交于A 、B 两点,设OB OA OP +=,是否存在这样的直 线l ,使得四边形OAPB 是矩形?若存在,求出直线l 的方程;若不存在,试说明理由清流一中2014-2015学年上期第三次阶段考试(理科)答案1——10 ABACB BDDBA11.,使得; 12. ;13.; 14. ; 15.③16解:(Ⅰ)∵y ′=2x -x 3(x >0),又k =21,∴2x -x 3=21,∴x =3.................4 (Ⅱ)(1)y ′= 8x +4.................7 (2)y ′= (x 2cos x )′=(x 2)′.cos x +x 2.(cos x )′=2x cos x -x 2sin x (10)(3)y ′=x sin x ′=x2x ′=x2xcos x -sin x. (13)17解:∵为真,为真, ∴假真.若为假:由圆心到直线的距离不小于半径,即,∴或. …………9分若为真:由韦达定理知:即.所以当假真时,或.故的取值范围是:. (13)18.(本小题满分13分)解:(Ⅰ)以为坐标原点,分别以、、所在的直线为轴、……… 2分……… 6分10分13分19解:由y 2=4x ,得p =2,其准线方程为x =-1,焦点F (1,0).设A (x 1,y 1),B (x 2,y 2).(1) |AF |=x 1+2p,从而x 1=4-1=3.代入y 2=4x , 得y =±2 .∴点A 为(3,2)或(3,-2)-6分(2)直线l 的方程为y =k (x -1).与抛物线方程联立,得y2=4x x -1, 消去y ,整理得k 2x 2-(2k 2+4)x +k 2=0(*),--9分 因为直线与抛物线相交于A 、B 两点,则k ≠0,并设其两根为x 1,x 2,则x 1+x 2=2+k24. ----11分由抛物线的定义可知,|AB |=x 1+x 2+p =4+k24=5,解得k =±2 ------13分20.解:(Ⅰ)其它组的频率为(0.01+0.07+0.06+0.02)×5=0.8, 所以第四组的频率为0.2,-----2分 频率/组距是0.04频率分布图如图: ……4分5分……………7分1/8,所以采用分层抽样的方法抽取的5人中有优秀3人,良好2人 ……9分 法1:记从这5人中选2人至少有1人是优秀为事件M将考试成绩优秀的三名学生记为A,B ,C , 考试成绩良好的两名学生记为a,b 从这5人中任选2人的所有基本事件包括:AB,AC,BC ,Aa,Ab,Ba,Bb ,Ca,Cb,ab 共10个基本事件 …………………11分 事件M 含的情况是:AB,AC,BC ,Aa,Ab,Ba,Bb ,Ca,Cb ,共9个 ……12分………………14分法2:解:(1)∵a =x i +(y +2)j ,b =xi +(y -2)j ,且| a |+| b |=8∴点M(x,y)到两个定点F1(0,-2),F2(0,2)的距离之和为8∴轨迹C为以F1,F2 (5)(2(0,3)A、B两点是椭圆的顶点,∴P与O重合,与四边形OAPB是矩形矛盾. (6)y=kx+3,A(x1,y1),B (x2,y2) (8) (10)OAPB是平行四边OAPB是矩形,则OA⊥OB,即 (12)∴存在直线l OAPB是矩形. (14).年段平均分85。
县级中学2009-2010学年度高二数学竞赛(理科)

2009-2010学年度高二数学竞赛(理科)一、选择题(本题共6小题,每小题6分,共计36分) 1.已知集合{}{}221,,20R A y y x x B x x x =+=+-∈=>,则下列结论正确的是( ) A .{}1,A B y y => B.{}2A B y y => C. {}21A B y y =-<< D. {}21A B y y y =<>- 或2.已知函数20()20x x f x x x +⎧=⎨-+>⎩,≤,,,则不等式2()f x x ≥的解集为( )A .[]11-,B .[]22-,C .[]21-,D .[]12-, 3. 已知函数x b x a x f cos sin )(-=(a 、b 为常数,0≠a ,R x ∈)在4π=x 处取得最小值,则函数)43(x f y -=π是( ) A .偶函数且它的图象关于点)0,(π对称 B .偶函数且它的图象关于点)0,23(π对称 C .奇函数且它的图象关于点)0,23(π对称D .奇函数且它的图象关于点)0,(π对称4. 已知︱OA ︱=1,︱OB ︱=3,OB OA ∙=0,点C 在∠AOB 内,且∠AOC =30°,设=m +n (m 、n ∈R ),则nm等于( ) A.31 B.3 C.33 D.3 5.已知函数()()1||xf x x R x =∈+ 时,则下列结论不.正确的是( ) A .x R ∀∈,等式()()0f x f x -+=恒成立B .(0,1)m ∃∈,使得方程|()|f x m =有两个不等实数根C .12,x x R ∀∈,若12x x ≠,则一定有12()()f x f x ≠D .(1,)k ∃∈+∞,使得函数()()g x f x kx =-在R 上有三个零点6.定义在R 上的函数()f x 的图象关于点3(,0)4-成中心对称,对任意的实数x 都有3()()2f x f x =-+且(1)1,f -=(0)2f =-,则(1)(2)(3)...(2010)f f f f ++++=( )A .2-B .1-C .0D .1二、填空题(本题共7小题,每小题9分,共计63分)7 .已知1cos 3α=,1cos()3αβ+=-,且,(0,)2παβ∈,则cos()αβ-= .8.设点P 是曲线32333x y x x =---上的一个动点,则以点P 为切点的切线中,斜率取得最小值时的切线方程是9.已知数列{a n },a 1=1,a n =a n-1+a n-2+…+a 1( 2≥n ),则该数列的前8项和为 .10.若椭圆+22a x )0(122>>=b a by 的左、右焦点分别为1F 、2F ,线段12F F 被抛物线bx y 22=的焦点分成5:3两段,则此椭圆的离心率为_____________11. 向量(1,0),(1,1)OA OB == ,O 为坐标原点,动点(,)P x y 满足0102OP OA OP OB ⎧≤⋅≤⎪⎨≤⋅≤⎪⎩, 则点(,)Q x y y +构成图形的面积为 .12.在数列{}n a 中,12a =,11(*)n n a a n N +=-∈ ,设n S 为数列{}n a 的前n 项和,则2008200920102S S S -+= .13.设()f x 是定义在R 上的函数,若(2007)2007f =,且对任意x ∈R ,满足:(2)()32x f x f x +-≤⋅,(6)()632x f x f x +-≥⋅,则(2009)f 的个位数字是 .三、解答题:(本题共3小题,共计51分)14、(15分)设1F 、2F 分别是椭圆22154x y +=的左、右焦点. (Ⅰ)若P 是该椭圆上的一个动点,求21PF PF ⋅的最大值和最小值;(Ⅱ)是否存在过点A (5,0)的直线l 与椭圆交于不同的两点C 、D ,使得|F 2C|=|F 2D|?若存在,求直线l 的方程;若不存在,请说明理由.15. (18分)已知函数()ln()x f x e a =+,(a 为常数)是实数集R 上的奇函数,函数()()sin g x f x x λ=+是区间[]1,1-上的减函数.(1) 求a 的值;(2) 若2()1g x t t λ≤++在[1,1]x ∈-恒成立,求t 的取值范围; (3) 讨论关于x 的方程2ln 2()xx ex m f x =-+的根的个数.2009-2010学年度高二数学竞赛(理科)答案一、选择题 每题6分,总分36分AADBDC 6、解析:本题考查了函数的对称、奇偶性、周期性,综合性较强,函数()f x 关于点3(,0)4-对称,则有3()()2f x f x =---,又3()()2f x f x =-+,33()()22f x f x ∴+=--()y f x ∴=的图像关于y 轴对称;又 3()()2f x f x =-+,有3()()[(3)](3)2f x f x f x f x =-+=--+=+,∴ ()f x 是周期为3的偶函数.(1)(1)1,(2)(23)(1)1,(3)(0)2f f f f f f f ∴=-==-=-===-,(1)(2)(3)0f f f ∴++=,(1)(2)(3)(2009)(2010)0f f f f f ∴+++⋅⋅⋅++=,选C.二、填空题,每题9分,总分63分。
江西省赣州市六校2013-2014学年高二上学期期末联考数学(理)试题 含答案

2013-2014学年度第一学期期末联考高二数学试题(理科)本试卷分为第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共150分,考试用时120分钟第Ⅰ卷(选择题,共50分) 一、选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,有且只有一项是符合题目要求的. 1.下列说法中,正确的是:( )A .命题“若b a >,则122->b a ”的否命题为“若b a >,则122-≤ba ”B .命题“存在R x ∈,使得012<++x x ”的否定是:“任意R x ∈,都有012>++x x ” C .若命题“非p ”与命题“p 或q ”都是真命题,那么命题q 一定是真命题D .命题“若022=+b a ,则0=ab ”的逆命题是真命题2.抛物线24x y =的焦点坐标为( )A .)0,1(B .)0,1(-C .)161,0(-D .)161,0( 3.从甲、乙两个城市分别随机抽取6台自动售货机,对其销售额进行统计,统计数据用茎叶图表示(如图所示),设甲、乙两组数据的平均数分别为x 甲,x 乙,方差分别为m 甲,m 乙,则( )A .x x <甲乙,m 甲>m 乙B .x x <甲乙,m 甲<m 乙C .x x >甲乙,m 甲>m 乙D .x x >甲乙,m 甲<m 乙4.设γβα,,为两两不重合的平面,n m l ,,为两两不重合的直线,给出下列四个命题:(1)若γβγα⊥⊥,,则βα//;(2)若m ≠⊂α ,n ≠⊂α,ββ//,//n m ,则βα//;(3)若βα//,l ≠⊂α,则β//l ;(4)若l =βα ,m =γβ ,n =αγ ,γ//l ,则n m //. 其中正确的命题是( )A 、(1)(3)B 、(2)(3)C 、(2)(4)D 、(3)(4) 5.已知椭圆)0(12222>>n m ny m x =+和双曲线)0,0(12222>>b a b y a x =-有相同的焦点21,F F ,P 是两曲线的一个交点,则21PF PF ⋅的值是( ) A 、a m - B 、)(21a m - C 、22a m - D 、a m - 6.给出右图所示的算法流程图,若输出的值为15,则判断框中的条件是( )A .5<nB .5≥nC .4<nD .4≥n328328625568321乙甲7.如图,设四面体ABCD 各棱长均相等,F E ,分别为AD AC ,中点,则BEF ∆在该四面体的面ABC 上的射影是下图中的( )A B C D8.“过点)1,0(的直线l 与双曲线3122=-y x 有且仅有一个公共点”是“直线l 的斜率k 的值为2±”的( )A .充分必要条件B .充分但不必要条件C .必要但不充分条件D .既不充分也不必要条件9.如图所示22⨯方格,在每一个方格中填入一个数字,数字可以是4,3,2,1中的任何一个,允许重复..,则填入A 方格的数字大于D 方格的数字的概率为( ) A .21 B .41 C .43 D .8310.如图,在棱长为1的正方体1111D C B A ABCD -的对角线1AC 上任取一点P ,以A 为球心,AP 为半径作一个球.设x AP =,记该球面与正方体表面的交线的长度和为)(x f ,则函数)(x f 的图象最有可能的是( )A .B .C .D .第Ⅱ卷(非选择题 共100分)二、填空题:本大题共5小题,每小题5分,共25分,答案填写在答题卷上. 11.已知)3,1,1(),2,1,1(--==且)//()(k -+,则=k12.某校为了了解高三学生的身体状况,抽取了100名女生,测量其体重.将所得的数据整理后,画出了如图所示的频率分布直方图,则所抽取的女生中体重在kg 50~45的人数是 13. 已知直线1+-=x y与椭圆)0(12222>>=+b a b y a x 相交于B A ,两点,且线段AB 的中点在直线02=-y x 上,则此椭圆的离心率为_______14.如图,在长方形ABCD 中,E BC AB ,1,2==为DC 的中点,F 为线段EC (端点除外)上一动点,现将AFD ∆沿AF 折起,使平面⊥ABD 平面ABCF .在平面ABD 内过点D 作K AB DK ,⊥为垂足,设t AK =,则t 的取值范围是________DC BA15.已知⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧⎪⎩⎪⎨⎧-≤≥=240),(x y y y x M ,直线m mx y 2+=和曲线24x y -=有两个不同的交点,他们围成的平面区域为N ,向区域M 上随机投以点A ,点A 落在N 内的概率为)(N p ,若]1,22[)(ππ-∈N p ,则实数m 的取值范围是:三、解答题(本大题共6小题,共75分.解答应写出文字说明,证明过程或演算步骤) 16. (本题满分12分)已知离心率为22的椭圆1:2222=+b y a x C (0>>b a ) 过点)1,6(M(1)求椭圆C 的方程;(2)过点)0,1(作斜率为2直线l 与椭圆相交于B A ,两点,求||AB 的长. 17.(本题满分12分)在直三棱柱111C B A ABC -中,N M AA BC AB ABC ,,2,9010====∠分别是111,BC C A的中点.(1)求证://MN 平面11ABB A ;(2)求多面体B C B M 11-的体积.18. (本题满分12分)某校在一次趣味运动会的颁奖仪式上,高一、高二、高三各代表队人数分别为120人、120人、n 人.为了活跃气氛,大会组委会在颁奖过程中穿插抽 奖活动,并用分层抽样的方法从三个代表队中共抽取20人 在前排就坐,其中高二代表队有6人. (1)求n 的值;(2)把在前排就坐的高二代表队6人分别记为f e d c b a ,,,,,,现随机从中抽取2人上台抽奖,求a 和b 至少有一人上台抽奖的概率;(3)抽奖活动的规则是:代表通过操作按键使电脑自动产生两个]1,0[之间的均匀随机数y x ,,并按如右所示的程序框图执行.若电脑显示“中奖”,则该代表中奖;若电脑显示“谢谢”,则不中奖,求该代表中奖的概率.N M111C B A C BA "谢谢PFEDCBA 19. (本题满分12分)已知命题:p “存在021)1(2,2≤+-+∈x m x R x ”,命题q :“曲线182:2221=++m y m x C 表示焦点在x 轴上的椭圆”,命题:s “曲线11:222=--+-t m y t m x C 表示双曲线” (1)若“p 且q ”是真命题,求m 的取值范围; (2)若q 是s 的必要不充分条件,求t 的取值范围。
四川省成都市2022-2023学年高二上学期1月期末考试理科数学试题及答案

高二年级理科数学试题考试时间120分钟,满分150分注意事项:1.答题前,考生务必在答题卡上将自己的学校、姓名、班级、准考证号用0.5毫米黑色签字笔填写清楚,考生考试条形码由监考老师粘贴在答题卡上的“条形码粘贴处”。
2.选择题使用2B 铅笔填涂在答题卡上对应题目标号的位置上,如需改动,用橡皮擦擦干净后再填涂其它答案;非选择题用0.5毫米黑色签字笔在答题卡的对应区域内作答,超出答题区域答题的答案无效;在草稿纸上、试卷上答题无效。
3.考试结束后由监考老师将答题卡收回。
一、选择题:本题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.过点(0,2)-,且与已知直线0x y +=垂直的直线方程为 A .20x y +-= B .20x y --= C .20x y ++=D .20x y -+=2.若一个圆的标准方程为221)4x y +(-=,则此圆的圆心与半径分别是 A .1,0)4(-; B .1,0)2(; C .0,1)4(-;D .0,1)2(;3.将某选手的得分去掉1个最高分,去掉1个最低分,剩余分数的平均分为91,现场作的分数的茎叶图后来有1个数据模糊,无法辨认,在图中以x 表示,则x = A .2 B .3 C .4D .54.某校为了了解高二学生的身高情况,打算在高二年级12个班中抽取3个班,再按每个班男女生比例抽取样本,正确的抽样方法是 A .简单随机抽样 B .先用分层抽样,再用随机数表法 C .分层抽样D .先用抽签法,再用分层抽样 5.若x ∈R ,则“44x -<<”是“22x x <”的 A .充分不必要条件 B .必要不充分条件 C .充要条件D .既不充分也不必要条件6.已知命题*1:2p x x x∀∈+R ,…,则p ⌝为 A .*00012x x x ∃∈+R ,… B .*00012x x x ∃∈+<R , C .*00012x x x ∃∉+<R ,D .12x x x∀∈+<R , 7.下列命题正确的是A .若0a b <<,则11a b<B .若ac bc >,则a b >C .若a b >,c d >,则a c b d ->-D .若22ac bc >,则a b >8.已知双曲线的上、下焦点分别为120,5)0,5)F F ((-,,P 是双曲线上一点且满足126||PF ||PF ||-=,则双曲线的标准方程为A .221169x y -=B .221916x y -=C .221169y x -=D .221916y x -=9.已知O e 的圆心是坐标原点O 0y --=截得的弦长为6,则O e 的方程为A .224x y +=B .228x y +=C .2212x y +=D .22216x y +=10.如图所示程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”.执行该程序框图,若输入的a b ,分别为39,27,则输出的a = A .1 B .3 C .5D .711.若两个正实数x y ,满足311x y+=,则3x y +的最小值为A .6B .9C .12D .1512.直线l 过抛物线220)y px p =(>的焦点F ,且交抛物线于P ,Q 两点,由P ,Q 分别向准线引垂线PR ,QS ,垂足分别为R ,S ,如果2|4|PF |QF |==,,M 为RS 的中点,则|MF |=A .BC .D .2二、填空题:本题共4小题,每小题5分,共20分。
通辽市甘旗卡二中2012——2013学年度上学期期末考试高二理科数学试卷

通辽市甘旗卡二中2012——2013学年度上学期期末考试高二数学(理科)试题命题人:国瑞敏本试卷分为第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共150分,考试时间120分钟。
注意:1.答卷前,将姓名、考号填在答题卡的密封线内。
2.答案必须写在答题卡上,在试题卷上答题无效。
一、选择题:(本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的)1.如果直线x +2y -1=0和y =kx 互相平行,则实数k 的值为( ).A .2B .21C .-2D .-212.半径为R 的半圆卷成一个圆锥,则它的体积为( ).A3R B3R C3R D3R3.一个正方体的顶点都在球面上,它的棱长为2cm ,则球的表面积是( ). A.28cm π B.212cm πC.216cmπD.220cmπ4.某市高三数学调研考试中,对90分以上(含90分)的 成绩进行统计,其频率分布直方图如图所示, 若130~140分数段的人数为90,那么 90~100分数段的人数为( ). A .630 B .720 C .810 D .9005.过点(1,3)且与原点距离为1的直线有 ( ).A.3条B. 2条C. 1条D. 0条6.已知点M (4,2)与N (2,4)关于直线l 对称,则直线l 的方程为( ). A .06=++y x B .06=-+y x C .0=+y x D .0=-y x7.把21化为二进制数,则此数为( ).A .10011(2)B .10110(2)C .10101(2)D .11001(2)8.从五件正品,一件次品中随机取出两件,则取出的两件产品中恰好是一件正品,一件 次品的概率是().A. 1B.21 C. 31 D. 32 9.用秦九韶算法求n 次多项式0111)(a x a x a x a x f n n n n ++++=-- ,当0x x =时, 求)(0x f 需要算乘方、乘法、加法的次数分别为( ). A.n n n n ,,2)1(+B.n,2n,nC. 0,2n,nD. 0,n,n10.圆(x -1)2+(y -1)2=2被x 轴截得的弦长等于( ).A .1B .23C .2D .311.在如图所示的算法流程图中,输出S 的值为( ). A.11 B.12C.13 D.1512.若过定点)0,1(-M 且斜率为k 的直线与圆05422=-++y x x在第一象限内的部分有交点,则k 的取值范围是( ). A .50<<k B. 05<<-kC .130<<k D. 50<<k通辽市甘旗卡二中2012——2013学年度上学期期末考试高二数学(理科)试题答题卡一、 选择题(每小题5分,共60分)第Ⅱ卷(非选择题:共90分)二、填空题:(共4个小题,每小题5分,共20分.请将正确答案填在题中在横线上) 13.图中的三视图表示的实物为_____________.14. 过点()2,4A ,且在两坐标轴上截距相等的直线方程是_________________.15.已知03=-+y x ,则22)1()2(++-y x 的最小值等于.16.若连续掷两次骰子,第一次掷得的点数为m ,第二次掷得的点数为n ,则点(,)P m n 落在圆x 2+y 2=16内的概率是.三、解答题:(共6小题,共70分.解答应写出文字说明、证明过程或演算步骤) 17.(本小题满分10分)求直线012=--y x 被圆01222=--+y y x 所截得的弦长.18.(本小题满分12分)已知直线l 经过点(0,-2),其倾斜角是60°. (1)求直线l 的方程;(2)求直线l 与两坐标轴围成三角形的面积.19.(本小题满分12分)甲盒中有红,黑,白三种颜色的球各3个,乙盒子中有黄,黑,白, 三种颜色的球各2个,从两个盒子中各取1个球,求取出的两个球是不同颜色的概率.班级: 姓名: 考号: 密 封 线13题图20.(本小题满分12分)在正方ABCD A B C D E F BB CD -11111中,、分别是、的中点 (1)证明:AD D F ⊥1; (2)求AE D F 与1所成的角; (3)证明:面面AED A FD ⊥11.21.(本小题满分12分)已知两圆04026,010102222=--++=--+y x y x y x y x ,求(1)它们的公共弦所在直线的方程;(2)公共弦长.22.(本小题满分12分)已知半径为5的圆C 的圆心在x 轴上,圆心的横坐标是整数,且与直线4x +3y -29=0相切. (1)求圆C 的方程;(2)设直线ax -y +5=0与圆C 相交于A ,B 两点,求实数a 的取值范围; (3)在(2)的条件下,是否存在实数a ,使得过点P (-2,4)的直线l 垂直平分AB ? 若存在,求出实数a 的值;若不存在,请说明理由.高二数学理科科试题答案一、 选择题:1~12:DABC BDCC DCBA 二、 13. 圆锥 14. y=21x 或x+y=615. 92三、 解答题:17.解:圆心为(0,1),则圆心到直线012=--y x. 18.解:(1)因为直线l 的倾斜角的大小为60°,故其斜率为tan 60°=3,又直线l 经过点(0,-2),所以其方程为3x -y -2=0.(2)由直线l 的方程知它在x 轴、y 轴上的截距分别是32,-2,所以直线l 与两坐标轴围成三角形的面积S =21·32·2=332.19.解:(1)设A =“取出的两球是相同颜色”,B =“取出的两球是不同颜色”,则事件A 的概率为: P (A )=692323⨯⨯⨯+=92.由于事件A 与事件B 是对立事件,所以事件B 的概率为:P (B )=1-P (A )=1-92=97. 20.解:(1)是正方体1AC F D AD DC F D DC AD 1111,,⊥∴⊂⊥∴面又面(2)中点是,,连结中点取CD F FG G A G AB ,1∴GF AD //又A D AD 11//所成角是直角与即直线的中点是所成的角与是则设是平行四边形F D AE HA A GAH A GA ABE Rt AG A Rt BB E F D AE AHA HAE G A F D G A A GFD D A GF 1111111111111190////︒=∠∴∠=∠∴∆≅∆∴∠=∴∴∴ (3) AD D F ⊥11(中已证)()1111111,,,,FD A AED FD A F D AED F D A AE AD F D AE 面面面又面又⊥∴⊂⊥∴=⊥21.解:(1)2210100,x y x y +--=①;2262400x y x y ++--=②;②-①得:250x y +-=为公共弦所在直线的方程; (2=22.解:(1)设圆心为M (m ,0)(m ∈Z ).由于圆与直线4x +3y -29=0相切,且半径为5,所以,5294-m =5,即|4m -29|=25. 因为m 为整数,故m =1.故所求的圆的方程是(x -1)2+y 2=25.(2)直线ax -y +5=0即y =ax +5.代入圆的方程,消去y 整理,得 (a 2+1)x 2+2(5a -1)x +1=0.由于直线ax -y +5=0交圆于A ,B 两点,故△=4(5a -1)2-4(a 2+1)>0,即12a 2-5a >0,解得a <0,或a >125. 所以实数a 的取值范围是(-∞,0)∪(125,+∞). (3)设符合条件的实数a 存在,由(2)得a ≠0,则直线l 的斜率为-a 1,l 的方程为y =-a1(x+2)+4,即x +ay +2-4a =0.由于l 垂直平分弦AB ,故圆心M (1,0)必在l 上.所以1+0+2-4a =0,解得a =43.由于43∈(125,+∞),故存在实数a =43,使得过点 P (-2,4)的直线l 垂直平分弦AB .。
