第一章质点力学基础.ppt
合集下载
大学物理质点力学第一章 质点运动学 PPT

方向:
cosa
=
x r
cosβ=
y r
cosγ=
z r
路程:质点所经路径得总长度。
三、速度
描述位置矢量随时间变化快慢得物理量
1、平均速度
在移质为点r由)A,到单B的位过时程间中内(的所平用均时位间移为称为t该,质所点发在生该的过位
程中的平均速度。
v
=
Δ Δ
r t
=
Δx Δt
i
+ΔΔ
y t
j
+
Δ Δ
0
Δx
Δ t —割线斜率(平均速度)
dx —切线斜率(瞬时速度) dt
x~t图
t tt
1
2
2、 v ~ t 图
v ~ t图
割线斜率:
Δv Δt = a
v v2
切线斜率:
dv dt
=a
v1
v ~ t 图线下得面积(位移):
0 t1
t2
x2
dt dx x2 x1 x
t1
x1
t2 t
3、 a ~ t 图
=
dθ
dt
B
Δθ A
θ
0
x
(3)、角加速度
β =ΔΔωt
β
=
lim
Δt
Δω
0Δ t
=ddωt
=ddθt2 2
(4)、匀变速率圆周运动
0
t
1 2
t2
0 t
2
2 0
2
(5)、线量与角量得关系
Δ s = rΔθ
lim Δ s
Δt 0Δ t
=
lim
Δt 0
r
Δθ
第1章-质点运动学
为了描述速 度随时间
z A.
(t )
.B
的变化情况,定义:质点
的平均加速度为
(t t )
O
a t
y
24
x
质点的(瞬时)加速度定义为:
d d r a lim 2 t 0 t dt dt
2
即:质点在某时刻或某位置的(瞬时)加速度等于
速度矢量 对时间的一阶导数,或等于矢径 r 对时
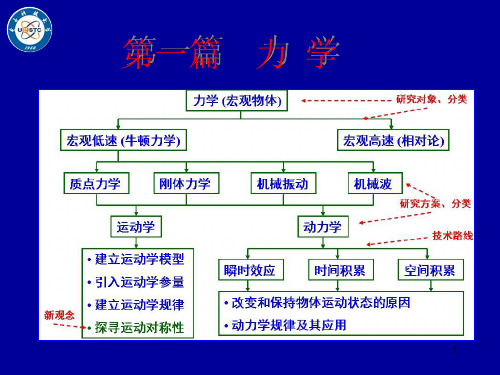
第一篇 力 学
1
内容提要
第一章 运动学 第二章 质点动力学(牛顿运动定律) 第三章 刚体力学
第四章 振动学基础
第五章 第六章 波动学基础
狭义相对论
2
第1章 质点运动学
§1-1 参考系、坐标系和理想模型
运动的可认知性——绝对运动与相对静止的辩证统一
案例讨论:关于物质运动属性的两种哲学论断 赫拉克利特:“人不能两次踏进同一条河流”
y
y
位置矢量 r 的大小(即质点P到原点o的距离)为
2 2 2 r r x y z
方向余弦: cos=x/r, cos=y/r, cos=z/r 式中 , , 取小于180°的值。
z
r
P(x,y,z)
z
C
cos2 + cos2 + cos2 =1
x
A
运动方程
—— 轨道方程。
11
消去时间t得:x2+y2=62
§1-3 位移 速 度
一.位移和路程
如图所示,质点沿曲线C运动。时刻t在A点,时 刻t+t在B点。 从起点A到终点B的有向线 段AB=r,称为质点在时间t内 的位移。 而A到B的路径长度S为 路程。
z A.
(t )
.B
的变化情况,定义:质点
的平均加速度为
(t t )
O
a t
y
24
x
质点的(瞬时)加速度定义为:
d d r a lim 2 t 0 t dt dt
2
即:质点在某时刻或某位置的(瞬时)加速度等于
速度矢量 对时间的一阶导数,或等于矢径 r 对时
第一篇 力 学
1
内容提要
第一章 运动学 第二章 质点动力学(牛顿运动定律) 第三章 刚体力学
第四章 振动学基础
第五章 第六章 波动学基础
狭义相对论
2
第1章 质点运动学
§1-1 参考系、坐标系和理想模型
运动的可认知性——绝对运动与相对静止的辩证统一
案例讨论:关于物质运动属性的两种哲学论断 赫拉克利特:“人不能两次踏进同一条河流”
y
y
位置矢量 r 的大小(即质点P到原点o的距离)为
2 2 2 r r x y z
方向余弦: cos=x/r, cos=y/r, cos=z/r 式中 , , 取小于180°的值。
z
r
P(x,y,z)
z
C
cos2 + cos2 + cos2 =1
x
A
运动方程
—— 轨道方程。
11
消去时间t得:x2+y2=62
§1-3 位移 速 度
一.位移和路程
如图所示,质点沿曲线C运动。时刻t在A点,时 刻t+t在B点。 从起点A到终点B的有向线 段AB=r,称为质点在时间t内 的位移。 而A到B的路径长度S为 路程。
高一物理必修一第一章第一节:质点、参考系和坐标系(48张PPT)

(3)质点的条件
①物体的形状、大小可忽略时,一般可以看作质点 例如:研究地球的公转 抛出去的手榴弹在空中的运动
②平动的物体一般可以看作质点 例如:平直公路上行驶的汽车, 分析:车身上各部分的运动情况相同,当我们把汽车作为 一个整体来研究它的运动的时候,就可以把汽车当作质点。
③物体只做转动时,不能看做质点 例如:乒乓球在空中只做旋转运 动时
注意
坐标系是在参考系的基础上抽象出来的概念,是 抽象化的参考系。
(2)坐标系的构成要素
原点 单位长度 正方向
数字 物理量的符号 单位
直线坐标系
(3)坐标系的种类
①一维坐标(直线坐标系) 描述物体在一条直线上运动,即物体做一维运动时,可以以 这条直线为 x 轴,在直线上规定原点、正方向和单位长度,建立 直线坐标系。如图所示,若某一物体运动到A点,此时它的位置坐 标 xA=3m,若它运动到B点,则此时它的坐标 xB=-2m(“-” 表示沿 x 轴负方向)。
练习1
问题思考:
送瘟神
绿水青山枉自多 千村薜荔人遗矢 坐地日行八万里 牛郎欲问瘟神事
毛泽东
华佗无奈小虫何 万户萧疏鬼唱歌 巡天遥看一千河 一样悲欢逐逝波
我看见某位同学坐在位子上,一动不动,毛主席却说他 “坐地日行八万里”,这是怎么回事?
运动是绝对的 静止是相对的
练一练
一般来说,可以把撑杆跳高运动分为如下几个阶段:助跑、 撑杆起跳、越过横杆。在下列几种情况下运动员能否看作质点, 从中体会质点模型的建立过程。
(1)质点的定义
我们在处理这些问题时,常常不考虑物体各部分的差 异,把物体简化成没有大小、形状的点,或者说用一个有 质量的点来代替物体。
名词解释
用来代替 物体的有质量的点叫做质点。 实际物体运动的描述 质点运动的描述
《大学物理教学课件》第1章 质点运动学

足右手定则:沿质点转动方向右
旋大拇指指向。
平均角加速度:β Δω Δt
角加速度:β
lim
t 0
Δω Δt
dω dt
d 2
dt 2
单位:rad/s2,
y
B
s
A
RO
x
29
匀变速圆周运动的基本公式
0 t
0
0t
1 2
t 2
2 02 2 ( 0 )
圆周运动线量和角量的关系:
与匀变速直线运动计 算公式有对应关系:
4
§1.2 质点运动的描述
1.2.1 位置矢量 运动方程
1.位置矢量(位矢)
从原点O向质点P所在位置画一矢
量来表示质点位置。
r称为位置矢量,简称位矢。
位矢 用坐标值表示为: r xi yj zk
z
xo
x
i , j , k表示沿x,y,z轴的单位矢量。
位矢的大小:r | r| x2 y2 z2
质点运动时在空间所经历的实际路径叫做运动轨道, 相应的曲线方程称为轨道方程。
在运动方程中,消去t即得轨道方程:f(x,y,z)=0。
6
1.2.2 位移 路程
z A
1.位移
t时刻,A点位矢为
r1
t+Δt时刻在B点位矢为 r2
r B
r1
r2
o
y
x
在t 时间内,位矢的变化量(即A到B的有向线
段)称为位移。
y
B
s
A
RO
x
角位置 :质点所在的矢径与x 轴的夹角。
运动方程: (t)
角位移: 质点从A到B矢径转过的角度 。
规定: 逆时针转向为正 顺时针转向为负
第1章-质点运动学

述
位移
rrrBArxBxBAii
rA
yA
yB
j j
y
yB A r
r y A A
rB
B
yB yA
(xB xA)i ( yB yA) j
xi yj
o
xA
xB x
xB xA
若质点r 在 (三x维B 空x间A中)i运动( yB
yA)
j
(zB
z A )k
位移的大小为 r x2 y2 z2
23
1-2 求解运动学问题举例
例3 有 一个球体在某液体中竖直下落, 其初速度
为 v0 10 j , 它的加速度为 a 1.0v j. 问:(1)经
过多少时间后可以认为小球已停止运动, (2)此球体
在停止运动前经历的路程有多长?
解:由加速度定义
v dv 1.0
t
dt
,
v v0
0
a dv 1.0v dt
v v2
位矢量
t
0,
t 0
0,
tv
rv
a
dv dt
v2 r
en
2ren
法向单 位矢量
vB
r
o
en
v
vB
vA et r
vA
31
1-3 圆周运动
三alitlami tm 变00速litdmdv圆vvvt0tt周nt运vtavt动dvdttrev2ttleeit切mntv向a0nn加aaevn速tntneen度t 和法向v加2v速tove度2vnrevtv1vn1
一 圆周运动的角速度和角加速度
角坐标 (t)
角速度 (t) d (t)
dt
速率
位移
rrrBArxBxBAii
rA
yA
yB
j j
y
yB A r
r y A A
rB
B
yB yA
(xB xA)i ( yB yA) j
xi yj
o
xA
xB x
xB xA
若质点r 在 (三x维B 空x间A中)i运动( yB
yA)
j
(zB
z A )k
位移的大小为 r x2 y2 z2
23
1-2 求解运动学问题举例
例3 有 一个球体在某液体中竖直下落, 其初速度
为 v0 10 j , 它的加速度为 a 1.0v j. 问:(1)经
过多少时间后可以认为小球已停止运动, (2)此球体
在停止运动前经历的路程有多长?
解:由加速度定义
v dv 1.0
t
dt
,
v v0
0
a dv 1.0v dt
v v2
位矢量
t
0,
t 0
0,
tv
rv
a
dv dt
v2 r
en
2ren
法向单 位矢量
vB
r
o
en
v
vB
vA et r
vA
31
1-3 圆周运动
三alitlami tm 变00速litdmdv圆vvvt0tt周nt运vtavt动dvdttrev2ttleeit切mntv向a0nn加aaevn速tntneen度t 和法向v加2v速tove度2vnrevtv1vn1
一 圆周运动的角速度和角加速度
角坐标 (t)
角速度 (t) d (t)
dt
速率
理论力学(周衍柏)第一章质点力学

(1)矢量形式的运动学方程
rr(t)
理论力学:Theoretical mechanics 当质点运动时r是时间t的单值连续函数。此方程常用来 进行理论推导。它的特点是概念清晰,是矢量法分析质点 运动的基础。
(2)直角坐标形式的运动学方程
x x(t)
y
y (t)
z z ( t )
这是常用的运动学方程,尤其当质点的轨迹未知时。它是 代数方程,虽然依赖于坐标系,但是运算容易。
说明: ① 参照物不同,对同一个物体运动的描述结果可能不同;
② 观察者是站在参照系的观察点上; ③ 不特别说明都以地球为参照系。
2. 坐标系
理论力学:Theoretical mechanics 为了定量研究的空间位置,就必须在参考系上建立坐标 系。参照系确定后,在参照系上选择适宜的坐标系,便于 用教学方式描述质点在空间的相对位置(方法)。
ji
解: 确定动系和静系 静系:河岸 动系:河流 研究对象:小船
理论力学:Theoretical mechanics
:0 牵连速度, : 绝对速度, :相 对 速度
ji
由:
0
0
c2i
r d
dt
j
c1 cosi c1 sin
j
i
选取极坐标, 得
理论力学:Theoretical mechanics
0:人行走速度, : 风速(相对于地), :风 相对于人的速
度 由:
得: 理论力学:Theoretical mechanics
得: 解得:
y
2
2
理论力学:Theoretical mechanics
因此:x 4,y 4
风速: x2y2 4 2km/h
第一章 质点运动学

16
物理学
已知:x(t ) 1.0t 2.0,y(t ) 0.25t 2 2.0, 解 (1) 由题意可得
dx dy vx 1.0, vy 0.5t dt dt t 3s 时速度为 v 1.0i 1.5 j
速度 v 与
x 轴之间的夹角
第一章 质点运动学
第一章 质点运动学
14
物理学
讨论 一运动质点在某瞬 y 时位于矢径 r ( x, y ) 的 y 端点处,其速度大小为
dr ( A) dt dr ( C) dt
注意
dr (B) dt
r (t )
x
o
x
dx 2 dy 2 ( D) ( ) ( ) dt dt
dr dr dt dt
1.5 0 arctan 56.3 1.0
17
物理学
x(t ) 1.0t 2.0, (2)运动方程 2 y(t ) 0.25t 2.0,
消去参数 t 可得轨迹方程为
y 0.25x x 3.0
2
轨迹图 t 4s
y/m
6 2
t 4s
t 2s 4
-6 -4 -2 0
dx B v A v x i i vi dt l dy vB v y j j o dt 2 2 2 x y l dx dy 两边求导得 2 x 2y 0 dt dt
第一章 质点运动学
解
y
A
v
x
20
物理学
dy x dx y 即 dt y dt B x dx vB j y dt dx o v dt vB vtan j
物理学
已知:x(t ) 1.0t 2.0,y(t ) 0.25t 2 2.0, 解 (1) 由题意可得
dx dy vx 1.0, vy 0.5t dt dt t 3s 时速度为 v 1.0i 1.5 j
速度 v 与
x 轴之间的夹角
第一章 质点运动学
第一章 质点运动学
14
物理学
讨论 一运动质点在某瞬 y 时位于矢径 r ( x, y ) 的 y 端点处,其速度大小为
dr ( A) dt dr ( C) dt
注意
dr (B) dt
r (t )
x
o
x
dx 2 dy 2 ( D) ( ) ( ) dt dt
dr dr dt dt
1.5 0 arctan 56.3 1.0
17
物理学
x(t ) 1.0t 2.0, (2)运动方程 2 y(t ) 0.25t 2.0,
消去参数 t 可得轨迹方程为
y 0.25x x 3.0
2
轨迹图 t 4s
y/m
6 2
t 4s
t 2s 4
-6 -4 -2 0
dx B v A v x i i vi dt l dy vB v y j j o dt 2 2 2 x y l dx dy 两边求导得 2 x 2y 0 dt dt
第一章 质点运动学
解
y
A
v
x
20
物理学
dy x dx y 即 dt y dt B x dx vB j y dt dx o v dt vB vtan j
《物理基础》第1章 质点力学

加速度为
这一分加速度叫切向加速度,表示质点速率变化的快慢。 还可以得到
例1—3 P8
1.2.3 一般曲线运动
质点运动学中最一般的运动为曲线运动,可以表示为
例1—4 P10
1.3 牛顿运动定律及其应用
1.3.1 牛顿第一定律
牛顿第一定律:任何物体都将保持静止或匀速直线运动的状态,直到其他物体所作的 力迫使它改变这种状态为止。
2.变力的功
变力对物体做的功为
例1—15 P22
1.5.2 保守力的功
1.重力的功
此式表明,重力对物体所做的功只与物体的始末位置有关,与物体的运动路径无关。
2.弹性力的功
此式表明,弹性力对物体所做的功只与物体的始末位置有关,与物体的运动路径无关。
3.万有引力的功
此式表明,万有引力作的功业只与始末位置有关,而与路径无关。
1.3.4 力学中常见的几种作用力
1.万有引力
2.弹性力
因变形而产生的恢复力称为弹性力。
3.摩擦力
滑动摩擦力的大小与正压力成正比,即
1.3.5 牛顿定律的应用
例1—5 P14 例1—6 P15 例1—7 P16
1.4 动量 动量守恒定律
1.4.1 质点的动量定理
这表明,作用在质点系上的合外力在某段时间内的冲量等于质点系在同一时间内动量 的增量。
1.4.3 动量守恒定律
例1—11 例1—12 例1—13 例1—14
P19 P20 P20 P21
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
- k 0 ( mg - kv - F ) 0 dt
ln( mg - kv - F ) v - kt
0
m
v
mg
-
F
(1 -
- kt
em
)
k
第三节 动量定理与守恒定律
一 冲量与动量定理
能量和动量是最基本的物理量。它们的守恒定律是自然 界中的基本规律,适用范围远远超出了牛顿力学。
力的时间积累(冲量)引起动量的变化
v0
m0
t ( 2v0 m)1 2 6.90 s b
思考: 在 6.90s 的时间里, 汽车行进了多长的路程 ?
例2
质量为m的小球,在水中受的浮力为常力F,当
它从静止开始沉降时,受到水的粘滞阻力为f=kv(k为
常数),证明小球在水中竖直沉降的速度v与时间t的
关系为
v
mg
-
F
- kt
(1- e m
dp
Fdt
或
dI Fdt
质点动量的元增量等于它获得的元冲量。
质点动量定理 (积分形式)
t
I
F
t0
dt
P
-
P0
P
质点动量的增量等于它获得的冲量。
二 、质点系的动量定理
1 质点系
由N个质点构成的系统 i, j 1,2, , N
◆内力和外力
内力: fij - f ji
外力: fi , fj
第一章 质点力学
▪ 质点力学基础 ▪ 牛顿运动定律 ▪ 动量定理与守恒定律 ▪ 功和能 机械能守恒定律
❖代表人物:牛顿
恩格斯说:牛顿由于发 现了万有引力定律而创 立了天文学,由于进行 光的分解而创立了科学 的光学,由于创立了二 项式定理和无限理论而 创立了科学的数学,由 于认识了力学的本性而 创立了科学的力学.
速度改变量为
Δvr vr (t Δt) - vr (t)
则定义质点的 z 平均加速度为
a Δv Δt
y
v(t)
P1
P2
r (t)
O
r (t Δt)
v(t Δt)
x
v(t ) Δv
v(t Δt)
瞬时加速度( instantaneous acceleration) : 平均加速度在t趋于零时的极限,即
即速率的大小为质点所走过路程的时间变化率
采用分量形式,速度可以表示为:
v
dx dt
i
dy dt
j
dz dt
k
vxi
vy
j
vzk
其中 vx,vy,vz分别表示速度矢量在三个坐标 轴上的分量.在直角坐标系中,速度的大小为
v
v
2 x
v2y
v2z
加速度
设质点在 t 和 t+t
时vr刻(t的), v速r (t度分Δt别),为
中的守恒量及相应的守恒条件.
第一节 质点力学基础
一、物理学理想模型
单位与量纲
物理学中,为了方便描述各物理量,常常选 择一些物理量作为基本量. 在国际单位制中,力学基本量及其单位: 长度(m),质量(kg),时间(s).
❖ 导出量:由基本量导出的量,如速度、 力、加速度等.
❖ 量纲式:表示一个物理量的单位与基本 量单位关系的式子.三个力学基本量的量 纲分别为L, M,T.
❖矢量的加法:两矢量 和仍为一矢量,即
C AB
❖矢量的减法:C
A
(-B)
矢量的加减法服从平行四边形法则和三角 形法则.
平行四边形法则和三角形法则
A
D A (-B)
-B
B
C AB
A
C AB
B
❖ 矢量的乘法:标积(点积)和矢积(叉积)
矢的投量影的与标矢积量(点B积大)小—的矢乘量积A,即在矢量 B上
◆解题时常用分量形式
关于质量的概念:
质量m是物体惯性大小的量度。
惯性质量:牛顿第二定律中的质量常被称为惯性质量
引力质量:
F
-G
m1m2 r2
r0
式中 m1、m2 被称为引力质量
经典力学中不区分引力质量和惯性质量
三、牛顿第三定律
两个物体之间对各自对方的相互作用总是相等 的,而且指向相反的方向。
i , j, k 分别表示沿三个坐标轴正向的单位矢量.
质点运动过程中,其位置随时间的改变可
以表示为
x x(t)
y
y(t)
或
z z(t)
r (t) x(t)i y(t) j z(t)k
位移
质点在一段时间内 位置的改变称为它
在这段时间内的位 移,记作 Δr ,大小
标志着在这段时间 内质点位置移动的 多少,方向表示质 点的位置移动方向. 图中s表示路程. z
温度、能量、质量; 矢量(vector):既有大小又有方向且只有一个方
向的物理量,如速度、加速度;
质点:任何物体都有一定的大小和形状, 但当物体的大小和形状在所描写的运动中 所起的作用可以忽略不计时,我们就把它 看作是一个只有质量而没有大小和形状的 点,称为质点.
二、参考系与坐标系
坐标系:描述一个物体的运动需要另一个物体作为 参考,这个被选定的参考物体称为参考系.
说明 ◆反映了物体的惯性,又叫做惯性定律
◆给出了力的概念,提出了力是改变物体 运动状态的原因
如物体在一参考系中不受其它物体作用,而 保持静止或匀速直线运动,这个参考系就称为惯 性参考系.
相对惯性系做匀速直线运动的参考系也是惯性系
二、牛顿第二定律
“动量”的定义:物体的质量与其速度的乘积
p mv
根据叉积运算定义,可以得到如下结果: A B -B A
四、质点的运动
运动描述
位置矢量
空间一质点 P 的位置可以用三个坐标
x,y,z 来确定,也可以用从原点O到Pr点的
有向r 线段 表示, 称 为位置矢量.
在直角坐标系中,
r
可以表示为
r xi yj zk
其r 中r xr,y,z,分别表示 rr在三个坐标轴上的分量,
A B ABcos
A
当两矢量同向时,点积结 果数值最大;当两矢量 反向时,点积结果数值最 小;当两矢量垂直时,点 积结果为0.
B
矢等于量的C=矢A积Bs(in叉积,方)—向—垂结直果于仍矢为量一A与矢B量构,大成的小
平面,并服从右手螺旋法则,即
C AB
当两个矢量平行时,叉积结果为零;当两 个矢量垂直时,叉积结果最大.
)
k
F
式中t为从沉降开始计算的时间 证明:取坐标,作受力图。
根据牛顿第二定律,有
mg - kv - F ma m dv dt
f
a x
mg
mg - kv - F ma m dv dt
初始条件:t=0 时 v=0
v
dv
t
0 ( mg - kv - F ) m 0 dt
m v d( mg - kv - F ) t
本节从牛顿力学出发给出动量的定义,推导动量守恒定
律,并讨论它在牛顿力学中的应用。
动量
p mv 单位:千克·米/秒( kg·m/s)
说明
★矢量、瞬时量和相对量 ★描述运动状态的参量
牛顿第二定律质点的动量定理:
F
dp
Fdt
dp
dt
将力的时间积累称为冲量 用I
表示I
t2
Fdt
t1
质点动量定理
(微分形式)
◆过程中包括的质点不变
fi
mi
ri
f ij
f ji
o 惯性系rj
mj fj
2 质点系的动量定理
第 i 个质点受系统内其它 质点作用的合力:Fi内
第 i 个质点受系统外部作
用的合力:Fi外Βιβλιοθήκη 第 i 个质点的动量:Pi
对第 i 个质点应用牛顿第二定律:
F合
Fi内
Fi外=
d
(Pi ) dt
对于整个质点系:
一般方法
第 一 类
第 二 类
已知 及
例如 或
时的 和
求得
求
解题的基本思路
1)确定研究对象,分析其运动,进行受力分析; (隔离物体,分析力,画受力图)
2)取坐标系; 3)列方程(一般用分量式, 用文字符号列方程式);
4)利用其它的约束条件列补充方程; 5)先用文字符号求解,后带入数据计算结果.
例1 设有一质量为m = 2500kg 的汽车, 在平直的高
牛 顿 (1643-1727) 英 国 伟大的物理学家、数学 家、天文学家,经典力 学理论的集大成者,建 立了著名的万有引力定 律和牛顿运动三定律.
❖力学的内容:
➢研究物体的运动轨道及其动力学因素; ➢研究物体间的相互作用以及作用过程
中物体运动量的交换和变化规律; ➢寻求物体运动过程中或相互作用过程
用动量描述运动比用速度更普遍和深刻
定律内容:物体在合外力作用下,其动量随时间的
变化F率v ,d等(于mvv作) 用d在m 物vv体m上dvv的合m外dvv力。mav
dt
dt
dt dt
F
dp dt
m ddvt
ma
分量式:
Fx Fy
max ma y
Fz
maz
说明
◆F 为合力
◆矢量关系
◆此关系是瞬时关系 ◆适用于质点的运动
Δt
瞬时速度(instantaneous velocity) :平均 速度的极限,即
v lim Δr dr Δt0 Δt dt
速率(speed) :速度的大小,即
v v lim
Δr
dr
Δt0 Δt dt
ln( mg - kv - F ) v - kt
0
m
v
mg
-
F
(1 -
- kt
em
)
k
第三节 动量定理与守恒定律
一 冲量与动量定理
能量和动量是最基本的物理量。它们的守恒定律是自然 界中的基本规律,适用范围远远超出了牛顿力学。
力的时间积累(冲量)引起动量的变化
v0
m0
t ( 2v0 m)1 2 6.90 s b
思考: 在 6.90s 的时间里, 汽车行进了多长的路程 ?
例2
质量为m的小球,在水中受的浮力为常力F,当
它从静止开始沉降时,受到水的粘滞阻力为f=kv(k为
常数),证明小球在水中竖直沉降的速度v与时间t的
关系为
v
mg
-
F
- kt
(1- e m
dp
Fdt
或
dI Fdt
质点动量的元增量等于它获得的元冲量。
质点动量定理 (积分形式)
t
I
F
t0
dt
P
-
P0
P
质点动量的增量等于它获得的冲量。
二 、质点系的动量定理
1 质点系
由N个质点构成的系统 i, j 1,2, , N
◆内力和外力
内力: fij - f ji
外力: fi , fj
第一章 质点力学
▪ 质点力学基础 ▪ 牛顿运动定律 ▪ 动量定理与守恒定律 ▪ 功和能 机械能守恒定律
❖代表人物:牛顿
恩格斯说:牛顿由于发 现了万有引力定律而创 立了天文学,由于进行 光的分解而创立了科学 的光学,由于创立了二 项式定理和无限理论而 创立了科学的数学,由 于认识了力学的本性而 创立了科学的力学.
速度改变量为
Δvr vr (t Δt) - vr (t)
则定义质点的 z 平均加速度为
a Δv Δt
y
v(t)
P1
P2
r (t)
O
r (t Δt)
v(t Δt)
x
v(t ) Δv
v(t Δt)
瞬时加速度( instantaneous acceleration) : 平均加速度在t趋于零时的极限,即
即速率的大小为质点所走过路程的时间变化率
采用分量形式,速度可以表示为:
v
dx dt
i
dy dt
j
dz dt
k
vxi
vy
j
vzk
其中 vx,vy,vz分别表示速度矢量在三个坐标 轴上的分量.在直角坐标系中,速度的大小为
v
v
2 x
v2y
v2z
加速度
设质点在 t 和 t+t
时vr刻(t的), v速r (t度分Δt别),为
中的守恒量及相应的守恒条件.
第一节 质点力学基础
一、物理学理想模型
单位与量纲
物理学中,为了方便描述各物理量,常常选 择一些物理量作为基本量. 在国际单位制中,力学基本量及其单位: 长度(m),质量(kg),时间(s).
❖ 导出量:由基本量导出的量,如速度、 力、加速度等.
❖ 量纲式:表示一个物理量的单位与基本 量单位关系的式子.三个力学基本量的量 纲分别为L, M,T.
❖矢量的加法:两矢量 和仍为一矢量,即
C AB
❖矢量的减法:C
A
(-B)
矢量的加减法服从平行四边形法则和三角 形法则.
平行四边形法则和三角形法则
A
D A (-B)
-B
B
C AB
A
C AB
B
❖ 矢量的乘法:标积(点积)和矢积(叉积)
矢的投量影的与标矢积量(点B积大)小—的矢乘量积A,即在矢量 B上
◆解题时常用分量形式
关于质量的概念:
质量m是物体惯性大小的量度。
惯性质量:牛顿第二定律中的质量常被称为惯性质量
引力质量:
F
-G
m1m2 r2
r0
式中 m1、m2 被称为引力质量
经典力学中不区分引力质量和惯性质量
三、牛顿第三定律
两个物体之间对各自对方的相互作用总是相等 的,而且指向相反的方向。
i , j, k 分别表示沿三个坐标轴正向的单位矢量.
质点运动过程中,其位置随时间的改变可
以表示为
x x(t)
y
y(t)
或
z z(t)
r (t) x(t)i y(t) j z(t)k
位移
质点在一段时间内 位置的改变称为它
在这段时间内的位 移,记作 Δr ,大小
标志着在这段时间 内质点位置移动的 多少,方向表示质 点的位置移动方向. 图中s表示路程. z
温度、能量、质量; 矢量(vector):既有大小又有方向且只有一个方
向的物理量,如速度、加速度;
质点:任何物体都有一定的大小和形状, 但当物体的大小和形状在所描写的运动中 所起的作用可以忽略不计时,我们就把它 看作是一个只有质量而没有大小和形状的 点,称为质点.
二、参考系与坐标系
坐标系:描述一个物体的运动需要另一个物体作为 参考,这个被选定的参考物体称为参考系.
说明 ◆反映了物体的惯性,又叫做惯性定律
◆给出了力的概念,提出了力是改变物体 运动状态的原因
如物体在一参考系中不受其它物体作用,而 保持静止或匀速直线运动,这个参考系就称为惯 性参考系.
相对惯性系做匀速直线运动的参考系也是惯性系
二、牛顿第二定律
“动量”的定义:物体的质量与其速度的乘积
p mv
根据叉积运算定义,可以得到如下结果: A B -B A
四、质点的运动
运动描述
位置矢量
空间一质点 P 的位置可以用三个坐标
x,y,z 来确定,也可以用从原点O到Pr点的
有向r 线段 表示, 称 为位置矢量.
在直角坐标系中,
r
可以表示为
r xi yj zk
其r 中r xr,y,z,分别表示 rr在三个坐标轴上的分量,
A B ABcos
A
当两矢量同向时,点积结 果数值最大;当两矢量 反向时,点积结果数值最 小;当两矢量垂直时,点 积结果为0.
B
矢等于量的C=矢A积Bs(in叉积,方)—向—垂结直果于仍矢为量一A与矢B量构,大成的小
平面,并服从右手螺旋法则,即
C AB
当两个矢量平行时,叉积结果为零;当两 个矢量垂直时,叉积结果最大.
)
k
F
式中t为从沉降开始计算的时间 证明:取坐标,作受力图。
根据牛顿第二定律,有
mg - kv - F ma m dv dt
f
a x
mg
mg - kv - F ma m dv dt
初始条件:t=0 时 v=0
v
dv
t
0 ( mg - kv - F ) m 0 dt
m v d( mg - kv - F ) t
本节从牛顿力学出发给出动量的定义,推导动量守恒定
律,并讨论它在牛顿力学中的应用。
动量
p mv 单位:千克·米/秒( kg·m/s)
说明
★矢量、瞬时量和相对量 ★描述运动状态的参量
牛顿第二定律质点的动量定理:
F
dp
Fdt
dp
dt
将力的时间积累称为冲量 用I
表示I
t2
Fdt
t1
质点动量定理
(微分形式)
◆过程中包括的质点不变
fi
mi
ri
f ij
f ji
o 惯性系rj
mj fj
2 质点系的动量定理
第 i 个质点受系统内其它 质点作用的合力:Fi内
第 i 个质点受系统外部作
用的合力:Fi外Βιβλιοθήκη 第 i 个质点的动量:Pi
对第 i 个质点应用牛顿第二定律:
F合
Fi内
Fi外=
d
(Pi ) dt
对于整个质点系:
一般方法
第 一 类
第 二 类
已知 及
例如 或
时的 和
求得
求
解题的基本思路
1)确定研究对象,分析其运动,进行受力分析; (隔离物体,分析力,画受力图)
2)取坐标系; 3)列方程(一般用分量式, 用文字符号列方程式);
4)利用其它的约束条件列补充方程; 5)先用文字符号求解,后带入数据计算结果.
例1 设有一质量为m = 2500kg 的汽车, 在平直的高
牛 顿 (1643-1727) 英 国 伟大的物理学家、数学 家、天文学家,经典力 学理论的集大成者,建 立了著名的万有引力定 律和牛顿运动三定律.
❖力学的内容:
➢研究物体的运动轨道及其动力学因素; ➢研究物体间的相互作用以及作用过程
中物体运动量的交换和变化规律; ➢寻求物体运动过程中或相互作用过程
用动量描述运动比用速度更普遍和深刻
定律内容:物体在合外力作用下,其动量随时间的
变化F率v ,d等(于mvv作) 用d在m 物vv体m上dvv的合m外dvv力。mav
dt
dt
dt dt
F
dp dt
m ddvt
ma
分量式:
Fx Fy
max ma y
Fz
maz
说明
◆F 为合力
◆矢量关系
◆此关系是瞬时关系 ◆适用于质点的运动
Δt
瞬时速度(instantaneous velocity) :平均 速度的极限,即
v lim Δr dr Δt0 Δt dt
速率(speed) :速度的大小,即
v v lim
Δr
dr
Δt0 Δt dt
