电磁场实验讲义书
《电磁场 电磁波》 讲义
《电磁场电磁波》讲义一、什么是电磁场在我们生活的这个世界里，电磁场是一种无处不在却又常常被我们忽略的存在。
简单来说，电磁场是由带电粒子的运动产生的一种物理场。
想象一下，一个电子在空间中移动，它的运动会形成电流，而这个电流就会产生磁场。
反过来，如果一个磁场发生变化，又会在周围的空间中产生电场。
电场和磁场就这样相互关联、相互作用，共同构成了电磁场。
电磁场的特性可以用一些物理量来描述。
比如电场强度，它表示电场的强弱和方向；还有磁感应强度，用来衡量磁场的强弱和方向。
二、电磁场的基本规律谈到电磁场，就不得不提到麦克斯韦方程组。
这组方程就像是电磁场世界的“宪法”，规定了电磁场的行为。
麦克斯韦方程组包含四个方程，分别描述了电场的高斯定律、磁场的高斯定律、法拉第电磁感应定律以及安培麦克斯韦定律。
电场的高斯定律告诉我们，通过一个闭合曲面的电通量等于这个闭合曲面所包围的电荷量除以真空介电常数。
这就好像是说，电荷是电场的“源头”，电荷的多少决定了电场的“流量”。
磁场的高斯定律则指出，通过任何一个闭合曲面的磁通量总是为零。
这意味着磁场没有“源头”和“尾闾”，磁力线总是闭合的。
法拉第电磁感应定律表明，当穿过一个闭合回路的磁通量发生变化时，会在回路中产生感应电动势。
这是电磁感应现象的基础，也是发电机工作的原理。
安培麦克斯韦定律说明了电流和变化的电场都能产生磁场。
三、电磁波的产生当电磁场发生变化时，就会产生电磁波。
比如，一个振荡的电荷或者电流会在其周围产生不断变化的电磁场，这些变化的电磁场向空间传播，就形成了电磁波。
电磁波的产生需要有一个能够产生交变电磁场的源。
常见的例子有天线，它通过电流的快速变化来发射电磁波。
四、电磁波的特性电磁波具有很多独特的特性。
首先是它的波动性，电磁波和其他波一样，具有波长、频率和波速等特征。
波长和频率之间存在着反比关系，波速则等于光速。
电磁波在真空中的传播速度是恒定的，约为 3×10^8 米每秒。
第5章-电磁场讲稿剖析
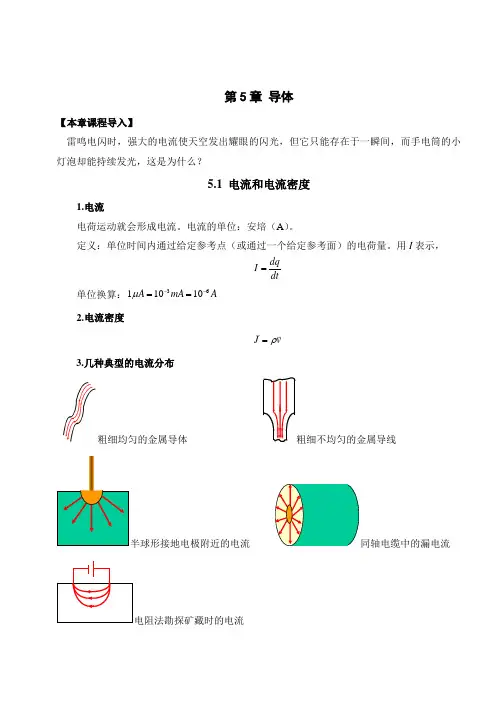
第5章 导体【本章课程导入】雷鸣电闪时，强大的电流使天空发出耀眼的闪光，但它只能存在于一瞬间，而手电筒的小灯泡却能持续发光，这是为什么？5.1 电流和电流密度1.电流电荷运动就会形成电流。
电流的单位：安培（A ）。
定义：单位时间内通过给定参考点（或通过一个给定参考面）的电荷量。
用I 表示，dqI dt=单位换算：3611010A mA A μ--== 2.电流密度J v ρ=3.几种典型的电流分布粗细均匀的金属导体 粗细不均匀的金属导线4.电流强度与电流密度的关系在导体中任取一截面元dS ，设该处电荷密度为ρ，运动速度为v 。
在dt 时间内通过截面元的电荷量为d d d d ()d d d d q V v t S v S t J S t ρρρ==⋅=⋅=⋅在dt 时间内通过某有限截面的电荷量为d d d SI t J S t =⋅⎰⎰电流强度与电流密度的关系为d SI J S =⋅⎰⎰电流强度就是电流密度穿过某截面的通量。
5.2 电流连续性电荷守恒定律：在孤立系统中，总电荷量保持不变。
在有电荷流动的导体内做任一闭合曲面S ，d t 时间内通过S 向外净流出的电荷量应等于同一段时间内S 内电荷量的减少。
d d d Sq J S t -=⋅⎰⎰即d d d SqJ S t⋅=-⎰⎰上式是电荷守恒定律的数学表述，又称电流连续性方程。
电流连续性方程的物理意义：如果闭合曲面S 内有正电荷积累起来，则流入S 面内的电荷量多于流出的电荷量；反之，如果S 面内的正电荷减少，则流出的电荷量多于流入的电荷量。
如果用Q i 来表示闭合面内的电荷，那么电荷的减少率是/i dQ dt -，且电荷守恒原理要求如果利用散度定理把面积分变换为体积分，就可以得到它的微分或点形式：由此可以得到，电流连续性方程的微分或点形式为：()J tυρ∂∇=-∂ 5.3 金属导体1900年特鲁德（P.Drude ）首先提出用金属中自由电子的运动来解释金属导电性问题，以后洛伦兹进一步发展了特鲁德的概念，建立了金属的经典电子理论。
电磁场讲义
1.2.2 Vector
a physical quantity having a magnitude as well as a direction
forቤተ መጻሕፍቲ ባይዱe F
velocity v
electric field intensity E
1. Graphical representation of a vector
Ax By − Ay Bx = Cz
1.2 Scalar and Vector Quantities
1.2.1 Scalar
a physical quantity that can be completely described by its magnitude mass ( m ), time ( t ), work ( W ), electric charge ( q )
A vector quantity is depicted by a line segment. The magnitude of the vector is represented by the length of the line segment. The direction of the vector is indicated by an arrow.
(3) If the dot product of two nonzero vectors is zero, the two vectors
are orthogonal. (θ = π/2 )
∵ Zero vector is thought to be orthogonal to any vector.
Electromagnetic Field
Guilin University of Electronic Technology
电磁场与电磁波实验指导书(参考)
电磁场与电磁波实验指导书目录实验一电磁波感应器的设计与制作实验二电磁波传播特性实验实验三电磁波的极化实验实验四天线方向图测量实验实验一电磁波感应器的设计与制作一、预习要求1、什么是法拉第电磁感应定律？2、什么是电偶极子？3、了解线天线基本结构及其特性。
二、实验目的1、认识时变电磁场，理解电磁感应的原理和作用。
2、通过电磁感应装置的设计，初步了解天线的特性及基本结构。
3、理解电磁波辐射原理。
三、实验原理随时间变化的电场要在空间产生磁场，同样，随时间变化的磁场也要在空间产生电场。
电场和磁场构成了统一的电磁场的两个不可分割的部分。
能够辐射电磁波的装置称为天线，用功率信号发生器作为发射源，通过发射天线产生电磁波。
图1 电磁感应装置如果将另一付天线置于电磁波中，就能在天线体上感生高频电流，我们可以称之为接收天线，接收天线离发射天线越近，电磁波功率越强，感应电动势越大。
如果用小功率的白炽灯泡接入天线馈电点，能量足够时就可使白炽灯发光。
接收天线和白炽灯构成一个完整的电磁感应装置，如图1所示。
电偶极子是一种基本的辐射单元，它是一段长度远小于波长的直线电流元，线上的电流均匀同相，一个作时谐振荡的电流元可以辐射电磁波，故又称为元天线，元天线是最基本的天线。
电磁感应装置的接收天线可采用多种天线形式，相对而言性能优良，但又容易制作，成本低廉的有半波天线、环形天线、螺旋天线等，如图2所示。
图2 接收天线本实验重点介绍其中的一种─—半波天线。
半波天线又称半波振子，是对称天线的一种最简单的模式。
对称天线（或称对称振子）可以看成是由一段末端开路的双线传输线形成的。
这种天线是最通用的天线型式之一，又称为偶极子天线。
而半波天线是对称天线中应用最为广泛的一种天线，它具有结构简单和馈电方便等优点。
半波振子因其一臂长度为/4λ，全长为半波长而得名。
其辐射场可由两根单线驻波天线的辐射场相加得到，于是可得半波振子（/L λ=4）的远区场强有以下关系式：()cos(cos )sin I I E f r rθπθθ==60602 式中，()f θ为方向性函数，对称振子归一化方向性函数为：()()maxcos(cos )sin f F f θθπθθ==2 其中max f 是()f θ的最大值。
大学物理电磁场第3章讲义教材
zˆ4(a20Iaz22)3/2
2
0
d'
B(z)2(a20Iaz22)3/2 z
3.2 真空中的静磁场基本方程
1. 磁通连续性定理
定义穿过磁场中给定曲面S 的磁感应强度B 的通量为磁通：
BdS 单位 韦伯Wb
S
若S面为闭合曲面
ΦBdS0
磁通连续 性定理
上页 下页
ΦBdS0
注意
① 磁通连续性原理也称磁场的高斯定理，表明磁力线是无头
Bdl 2B0I
l
得到
B
0I 2
e
323
I’ II 3 2 2-- 2 22 2 I 3 2 3 2-- 22 2
lBdl2B 0I3 2 3 2--22 2
得到
B
0I 2
32 -2 32 -22
e
同轴电缆的磁场分布
上页 下页
4.真空中的磁场方程
B (r)40 VJR 2R ˆd V '
磁矢位
注意 1 A是从矢量恒等式得出，是引入的辅助计算 量，无明确的物理意义；
2 A适用于整个磁场区域；
③因
mBdSAdS Stokes’ A dl
S
S
l
m Adl
l
A的单位 Wb/m （韦伯/米）
④ 恒定磁场中A满足库仑规范
A0
2 . 磁矢位 A 的求解
应用磁矢位A求解恒定磁场问题也可以分为 场源问题和边值问题。
③ 洛仑兹力垂直于电荷运动方向，只改变电荷运动方向， 对电荷不做功，而库仑力改变电荷运动速度做功。
上页 下页
安培力定律
真空中
描述两个电流回路之间相互作用力的规律。
l1
《电磁场和电磁波》 讲义
《电磁场和电磁波》讲义一、什么是电磁场在我们生活的这个世界里，电磁场无处不在。
从你手中的手机发出的信号，到照亮房间的灯光，再到地球上的闪电，都与电磁场有着密切的关系。
那么，究竟什么是电磁场呢？简单来说，电磁场是由带电粒子的运动产生的一种物理场。
电荷的存在会在其周围产生电场，而当电荷运动起来，比如电流在导线中流动时，就会产生磁场。
电场和磁场总是相互关联、相互依存的，它们共同构成了电磁场。
想象一下，一个静止的电荷会在周围空间产生一个静电场，这个电场的强度会随着距离电荷的远近而变化。
当这个电荷开始运动，比如在导线中形成电流时，就会产生一个磁场，这个磁场的方向可以通过右手定则来判断。
电磁场具有能量和动量，它能够传递电磁力，对处于其中的带电粒子产生作用。
电磁场的性质和行为可以用麦克斯韦方程组来描述，这是一组非常重要的数学方程，它们统一了电学和磁学的现象。
二、电磁波的产生既然电磁场是由带电粒子的运动产生的，那么电磁波又是如何产生的呢？当一个带电粒子加速运动时，它周围的电磁场就会发生变化。
这种变化的电磁场会以波的形式向周围空间传播，这就是电磁波。
举个例子，一个电子在天线中来回振动，就会产生变化的电流。
这个变化的电流会导致周围的电磁场不断变化，从而产生电磁波并向外辐射。
电磁波的频率取决于带电粒子振动的频率。
电磁波的产生需要一个源，比如天线、振荡器等。
这些源能够提供能量，使得电磁场不断变化从而产生电磁波。
同时，电磁波的产生还需要一个传播介质，在真空中电磁波同样可以传播，这是因为真空中存在着电磁场的相互作用。
三、电磁波的特性电磁波具有许多独特的特性，这些特性使得它在现代科技中有着广泛的应用。
首先，电磁波是横波，这意味着它的电场和磁场的振动方向与波的传播方向垂直。
电磁波的电场和磁场在空间和时间上相互垂直，并且它们的振幅和相位之间存在着一定的关系。
其次，电磁波的传播速度是恒定的，在真空中，电磁波的传播速度约为 3×10^8 米/秒，这个速度通常被称为光速。
《电磁场和电磁波》 讲义
《电磁场和电磁波》讲义一、引言在我们的日常生活中，电磁场和电磁波无处不在。
从手机通信到微波炉加热食物，从无线电广播到卫星导航，电磁场和电磁波的应用已经深入到我们生活的方方面面。
那么，什么是电磁场和电磁波？它们是如何产生、传播和相互作用的？这就是我们在本讲义中要探讨的内容。
二、电磁场的基本概念电磁场是由电荷和电流产生的一种物理场。
电场是由电荷产生的，它描述了电荷之间的相互作用力；磁场是由电流产生的，它描述了电流之间以及电流与磁铁之间的相互作用力。
当电荷和电流随时间变化时，电场和磁场也会随之变化，并且相互关联，形成了电磁场。
电场的强度用电场强度 E 来表示，单位是伏特每米（V/m）。
电场强度的方向是正电荷在该点所受电场力的方向。
磁场的强度用磁感应强度 B 来表示，单位是特斯拉（T）。
磁感应强度的方向可以用右手螺旋定则来确定。
三、电磁波的产生电磁波是由时变的电场和磁场相互激发而产生的。
当电荷做加速运动或者电流随时间变化时，就会产生电磁波。
例如，一个振荡的电荷会在周围空间产生交变的电场和磁场，从而形成电磁波向远处传播。
最常见的电磁波产生方式是通过天线。
天线中的电流在来回振荡时，会向周围空间辐射电磁波。
不同频率的振荡电流会产生不同频率的电磁波。
四、电磁波的传播电磁波在真空中以光速传播，速度约为3×10^8 米每秒。
在介质中，电磁波的传播速度会变慢，并且与介质的性质有关。
电磁波的传播不需要介质，可以在真空中传播。
这与机械波（如声波）需要介质来传播是不同的。
电磁波在传播过程中，电场和磁场相互垂直，并且都垂直于电磁波的传播方向，形成了横波。
电磁波具有波动性和粒子性。
从波动性的角度来看，电磁波具有波长、频率和波速等特征。
波长是相邻两个波峰或波谷之间的距离，频率是单位时间内电磁波振动的次数，波速等于波长乘以频率。
从粒子性的角度来看，电磁波可以看作是由一个个光子组成的，光子具有能量和动量。
五、电磁波的频谱电磁波的频谱非常广泛，按照频率从低到高可以分为无线电波、微波、红外线、可见光、紫外线、X 射线和伽马射线等。
电磁场与电磁波实验讲义
电磁场与电磁波实验讲义（试用）实验一、电磁波的反射特性研究一、实验目的1、研究电磁波在良导体表面的反射;2、熟悉微波分光仪DH962B的使用方法。
二、实验原理如上图所示,,我们用一块金属板作为障碍物来研究当电磁波以某一入射角投射到此金属板上所遵循的反射定律,即反射线在入射线和通过入射点的法线所决定的平面上,反射线和入射线分居在法线两侧,反射角等于入射角(如上图所示,θr =θi)。
三、实验装置(1)四、实验内容和步骤1、熟悉微波分光仪的结构、仪器的连接和系统调整:在微波分光仪的底座上有两个支臂,其中一个为固定支臂,另一个支臂则可绕中心轴旋转(带固定螺钉),发射喇叭天线和信号源安装在固定支臂上,接收喇叭天线和微安表安装在旋转支臂上。
微波分光仪底座中央有一带角度刻度线的园形工作平台。
仪器连接时,两喇叭天线的口面应正对,它们各自的轴线应在同一条直线上,两个臂的位置指针应分别指向工作平台的900刻度处。
按信号源的操作规程打开电源,调节衰减器使微安表有一适当的读数(满量程的三分之二及以上,这样可以减小读数误差对测试结果的影响)。
将带支座的金属反射板放在园形工作平台上(注意:金属反射板的平面应与支座下面的小园盘上的某一对刻度线一致),在将带支座的金属反射板放在园形工(2)作平台上时,应注意两点:(1)使小园盘的刻度线(与金属板平面一致的一对刻度线)与工作平台上相应900刻度的一对刻度线一致,这时工作平台上的00刻度线就与金属反射板的法线方向一致;(2)利用工作平台上的固定螺钉将金属反射板的支座固定。
2、测量入射角和反射角:转动工作平台,使固定臂的指针指在某一角度处,该角度数就是入射角,然后转动旋转臂使微安表的读数达到最大,此时旋转臂上的指针所指的刻度就是反射角。
如果此时微安表的指示太大或太小,可调节信号源的衰减器,使微安表的指示有一适当值。
做此项实验时,入射角最好取300至650之间,因为入射角太大接收喇叭天线有可能直接接收到入射波。
电磁场讲义.ppt
第一章 矢量分析
❖ 场：物理量数值的无穷集合表示一种场。例 温度场 T r,t 与空间 r 、时间 t 有关。
场重要属性：占有空间。
• 静态场：与时间无关.
• 动态场或时变场：与空间和时间有关。
• 标量场：只需用标量函数描绘的场。例：T、t、、。
• 矢量场：需要物理矢量描绘的场。例：力场 F ，流速场 v 。
无线电远距离传播。 1894年 无线电报 1906年 无线电广播 1911年 导航 1916年 无线电话
6 2020/10/6 Jin Jie
前言
1921年 短波通信 1923年 传真 1929年 电视 1933年 微波通信 1935年 雷达 近代：无线电遥测、遥控、卫星通信、光纤通信、移动 通信等。
❖ 学习时抓概念，掌握公式、定理，灵活运用，独立完成习 题；注意总结与归纳。做课堂笔记。
四、参考书
•电磁场理论基础 牛中奇著 电子工业出版社
•电磁场理论基础 陈 重著 北京理工大学
•电磁场与波
冯恩信著 西安交通大学
•电磁场与电磁波 郭辉萍著 西安电子科技大学
•电磁学专题研究 陈秉乾著 高教出版社
•电磁场与电磁波教学指导书 赵家升等著 高教出版社
(直角坐标系)
矢量场强处场线稠密；弱处场线稀疏。 场线上的切线方向代表该处矢量场的方向。
14 2020/10/6 Jin Jie
第一章 矢量分析
1.2 矢量与矢量场的不变特性 （指与坐标系关系）
(1)空间点的曲线坐标与坐标系
空间中任一点与有序数 的曲线坐标。
一一对应，则称
坐标曲线相互正交，且符合右手定则，即
8 2020/10/6 Jin Jie
第一章 矢量分析
电磁场实验指导书
电磁场实验讲义实验一 二线输电线静电场的造型 一、试验目的：1.学习两维电场模拟的原理与方法。
2.通过测量等位线及绘制电力线，学习电场图形的描绘方法。
二、实验原理（见教材静电模拟一节） 三、实验内容及步骤1、 将方格纸和导电纸的相对位置固定好，定好方格纸的坐标原点及x 轴y 轴。
2、连接线路，调节电源电压为9V ，依次测绘对电源负极电位分别为1V 、2V 、3V 、4V 、4.5V 、5V 、6V 、7V 、8V 时的各等位线。
四 实验原理1. 两导线电轴之间的电场是平行平面场;2. 电力线与等位线正交, 由于两线输电线的等位线方程为22222)12(2)11(-=+-+-K bK y b K K x所以得电力线方程为:2222)(c b c y x +=++3. 利用静电比拟原理, 使用电流线模拟电力线. 五、实验设备1.模拟试验台一套（导电纸半径为90mm ，电极半径为6.5mm ，电极几何中心连线构成的弦对应的圆心角为120）直流稳压电源一台; 数字万用表一只六、总结报告要求1.在实验用的方格纸上描绘等位线。
2.根据实验测得的等位线，描绘电力线，并与理论计算所得的电力线进行比较。
3.根据实验结果，试分析主要是哪些因素影响本实验精度？你认为这些因素是否可以解决。
实验二 接地电阻的研究 一、试验目的：1.学习用模拟实验的方法研究场的问题。
2.研究接地电阻与接地器的形状、大小以及埋入深度的关系。
3.观察接地器周围导电媒质表面上电位的分布。
二、原理与说明1.接地电阻指电流由接地装置流入大地再经大地向远处扩散时所遇到的电阻。
接地电阻主要是接地体到无限远处的大地的电阻，而接地线和接地体本身的电阻一般可以忽略。
对于半球埋地的接地器的电阻，可以用镜像法求解。
对于整个球埋入地下，而地面的影响又不可以忽略时，也可以用镜像法近似求解。
实际工作中，会遇到一些问题，它们既难通过实验获得满意的解答，又不便于实地测量，这类问题可以用“模拟法”研究。
第5章电磁场讲义.
进入每单位长度内导体的功率。
同轴线
25
解：（1）理想导体的情况下，电场和磁场只存在于内外导体 之间的理想介质中，导体表面电场无切向分量，只有电场的径向分 量。利用高斯定理和安培环路定理，容易求得内外导体之间的电场 和磁场分别为
同轴线中的电场、磁场和坡印廷矢量（理想导体情况）
14
2.麦克斯韦方程的物理意义
HJD t
EB t
B0
DV
第一方程，表明传导电流和变化的 电场都能产生磁场
第二方程，表明变化的磁 场产生电场
第三方程表明磁场是无源 场，磁感线总是闭合曲线
麦克斯韦第四方程，表 明电荷产生电场
15
3.时变电磁场的边界条件
两种不同媒质的分界面上各场量所满足的方程称为边界条件。
22
坡印廷定理各项物理意义
V E，H
,,
积分形式： (E H) dS d (1 E D 1 H B) dV E J dV
S
dt V 2
2
V
其中： d (1 E D 1 H B) dV —— 单位时间内体积V 中所增加
dt V 2
2
的电磁能量。
E J dV —— 单位时间内电场对体积V中的电流所做的功；
第五章 时变电磁场
静电场：由静止的且其电量不随时间变化的电荷所产磁场：由恒定电流所产生的磁场称为恒定磁场；
恒定磁场与时间无关，仅是空间位置的函数。
静电场和恒定磁场都不随时间变化，统称为静态场。
静态场的突出特点：电场和磁场各自独立，即：在静电场 的区域中可以没有恒定磁场，反之亦然。
U
E e ln(b a) ,
H
《电磁场和电磁波》 讲义
《电磁场和电磁波》讲义一、什么是电磁场在我们生活的世界中，电磁场是一种无处不在但又常常被我们忽视的存在。
简单来说，电磁场是由带电物体产生的一种物理场。
当电荷静止时，会产生静电场；当电荷运动时，就会产生磁场。
而当电荷的运动状态发生变化时，电场和磁场也会相互影响、相互作用，从而形成了电磁场。
想象一下，一个电子在空间中移动，它的周围就会产生一个变化的电场，同时这个变化的电场又会产生一个磁场，如此循环往复，就形成了电磁场。
电磁场具有能量和动量，它能够传递电磁力。
我们日常使用的各种电器设备，比如手机、电视、电脑等，都是通过电磁场来实现信号的传输和能量的传递。
二、电磁波的产生既然有了电磁场，那么电磁波又是怎么产生的呢？电磁波的产生通常是由于电荷的加速运动。
比如，在一个天线中，电流迅速地变化，导致电荷加速运动，从而产生了电磁波。
电磁波的产生过程可以类比为在池塘中扔一块石头，产生的涟漪会向四周扩散。
电荷的加速运动就像石头入水，产生的电磁波就像扩散的涟漪。
不同的电荷加速运动方式会产生不同频率和波长的电磁波。
从无线电波到微波，从红外线到可见光，从紫外线到 X 射线和伽马射线，它们都是电磁波的不同表现形式。
三、电磁波的性质电磁波具有一些重要的性质。
首先，电磁波是横波，这意味着它的电场和磁场振动方向与波的传播方向垂直。
其次，电磁波在真空中的传播速度是恒定的，大约为3×10⁸米/秒，这个速度被称为光速。
电磁波的频率和波长之间存在着一个简单的关系：速度等于频率乘以波长。
这意味着，频率越高，波长就越短；频率越低，波长就越长。
另外，电磁波具有能量，其能量大小与电磁波的频率有关，频率越高，能量越大。
四、电磁波的应用电磁波在我们的生活中有着广泛的应用。
无线电广播和电视就是利用无线电波来传输声音和图像信号。
手机通信则依靠微波频段的电磁波。
红外线在遥控器、夜视仪等设备中发挥着重要作用。
可见光让我们能够看到这个五彩斑斓的世界。
实验讲义：电子在电磁场中运动规律的研究
电子在电磁场中运动规律的研究【实验目的】1．了解带电粒子在电磁场中的运动规律，电子束的电偏转、电聚焦、磁偏转、磁聚焦的原理；2．学习测量电子荷质比的一种方法。
【实验原理】1． 示波管的简单介绍： 示波管如图1所示示波管包括有：（1）一个电子枪，它发射电子，把电子加速到一定速度，并聚焦成电子束； （2）一个由两对金属板组成的偏转系统；（3）一个在管子末端的荧光屏，用来显示电子束的轰击点。
所有部件全都密封在一个抽成真空的玻璃外壳里，目的是为了避免电子与气体分子碰撞而引起电子束散射。
接通电源后，灯丝发热，阴极发射电子。
栅极加上相对于阴极的负电压，它有两个作用：①一方面调节栅极电压的大小控制阴极发射电子的强度，所以栅极也叫控制极；②另一方面栅极电压和第一阳极电压构成一定的空间电位分布，使得由阴极发射的电子束在栅极附近形成一个交叉点。
第一阳极和第二阳极的作用一方面构成聚焦电场，使得经过第一交叉点又发散了的电子在聚焦场作用下又会聚起来；另一方面使电子加速，电子以高速打在荧光屏上，屏上的荧光物质在高速电子轰击下发出荧光，荧光屏上的发光亮度取决于到达荧光屏的电子数目和速度，改变栅压及加速电压的大小都可控制光点的亮度。
水平偏转板和垂直偏转板是互相垂直的平行板，偏转板上加以不同的电压，用来控制荧光屏上亮点的位置。
2．电子的加速和电偏转：为了描述电子的运动，我们选用了一个直角坐标系，其z 轴沿示波管管轴，x 轴是示波管正面所在平面上的水平线，y 轴是示波管正面所在平面上的竖直线。
从阴极发射出来通过电子枪各个小孔的一个电子，它在从阳极2A 射出时在z 方向上具有速度Z v ；Z v 的值取决于K 和2A 之间的电位差C B 2V V V +=（图2）。
电子从K 移动到2A ，位能降低了2V e ∙；因此，如果电子逸出阴极时的初始动能可以忽略不计，那么它从2A 射出时的动能2z v m 21∙ 就由下式确定：22z V e v m 21∙=∙ （1） 此后，电子再通过偏转板之间的空间。
《电磁场和电磁波》 讲义
《电磁场和电磁波》讲义一、什么是电磁场在我们生活的世界中，电磁场是一种无处不在但又常常被我们忽略的存在。
简单来说，电磁场就是由带电粒子的运动所产生的一种物理场。
想象一下，当一个电子在空间中移动时，它的周围就会产生一个电场。
这个电场会对周围的其他带电粒子产生力的作用。
与此同时，如果这个电子在移动的过程中还在不断地改变速度，那么就会产生磁场。
电场和磁场就像是一对好兄弟，它们总是同时出现，相互关联，并且相互影响。
这种相互作用的结果就是我们所说的电磁场。
电磁场的强度和方向可以用数学上的向量来描述。
电场强度用 E 表示，磁场强度用 B 表示。
它们的大小和方向会随着带电粒子的运动状态以及空间位置的变化而变化。
二、电磁场的特性电磁场具有一些非常重要的特性。
首先，电磁场可以在空间中传播。
这就像我们扔一块石头到水里，会产生一圈圈的水波向外扩散一样，电磁场也能以电磁波的形式在空间中传播能量和信息。
其次，电磁场遵循一定的规律。
比如，库仑定律描述了两个静止点电荷之间的电场力作用；安培定律则描述了电流与磁场之间的关系。
再者，电磁场具有能量。
当电磁场发生变化时，能量会在电场和磁场之间相互转换。
这也是电磁波能够传播的一个重要原因。
三、电磁波的产生电磁波的产生通常需要一个源，比如一个加速运动的电荷或者一个变化的电流。
以天线为例，当电流在天线中快速变化时，就会产生迅速变化的电磁场，并向周围空间发射出去，形成电磁波。
另外，原子内部的电子在不同能级之间跃迁时，也会释放出电磁波。
这种电磁波的频率和能量与电子跃迁的能级差有关。
四、电磁波的性质电磁波具有波动性和粒子性双重性质。
从波动性的角度来看，电磁波和其他波一样，具有波长、频率、振幅等特征。
波长是相邻两个波峰或波谷之间的距离；频率则是单位时间内波振动的次数；振幅表示波的能量大小。
电磁波的频率范围非常广泛，从极低频率的无线电波到高频率的伽马射线。
不同频率的电磁波在性质和应用上有着很大的差异。
电磁学实验讲义(总)
实验一 亥姆霍兹线圈磁场测定一、实验概述亥姆霍兹线圈磁场测定仪是综合性大学和工科院校物理实验教学大纲重要实验之一。
该实验可以学习和掌握弱磁场测量方法，证明磁场迭加原理，根据教学要求描绘磁场分布等。
传统的亥姆霍兹线圈磁场测量实验，一般用探测线圈配以指针交流电压表测量磁感应强度。
由于线圈体积大，指针式交流电压表等级低等原因，测量的误差较大。
近年来，在科研和工业中，集成霍耳传感器由于体积小，测量准确度高，易于移动和定位，所以被广泛应用于磁场测量。
例如：A SS 95型集成霍耳传感器就是一种高灵敏度的优质磁场传感器，它的体积小〔面积4mm 3mm ⨯，厚2mm 〕，其内部具有放大器和剩余电压补偿电路，采用此集成霍耳传感器〔配直流数字电压表〕制成的高灵敏度毫特计，可以准确测量0 2.000mT ～的磁感应强度，其分辨率可达6110T -⨯。
因此，用它探测载流线圈及亥姆霍兹线圈的磁场，准确度比用探测线圈高得多。
用高灵敏度集成霍耳传感器测量53110T 210T --⨯⨯～弱交、直流磁场的方法已在科研与工业中广泛应用。
本仪器采用先进的95A 型集成霍耳传感器作探测器，用直流电压表测量传感器输出电压，探测亥姆霍兹线圈产生的磁场，测量准确度比探测线圈优越得多，仪器装置固定件牢靠，实验内容丰富。
二、实验原理1.根据毕奥—萨伐尔定律，载流线圈在轴线〔通过圆心并与线圈平面垂直的直线〕上某点的磁感应强度为：I N x R R B ⋅+⋅=2/32220)(2μ 〔1〕式中0μ为真空磁导率，R 为线圈的平均半径，x 为圆心到该点的距离，N 为线圈匝数，I 为通过线圈的电流强度。
因此，圆心处的磁感应强度0B 为：I N RB ⋅=200μ 〔2〕轴线外的磁场分布计算公式较为复杂，这里简略。
2.亥姆霍兹线圈是一对彼此平行且连通的共轴圆形线圈，两线圈内的电流方向一致，大小相同，线圈之间的距离d 正好等于圆形线圈的半径R 。
这种线圈的特点是能在其公共轴线中点附近产生较广的均匀磁场区，所以在生产和科研中有较大的使用价值，也常用于弱磁场的计量标准。
2020年电磁场讲义2
即： J s v
5
第二章 电磁场中的基本物理量和
12/11/2019 Jin Jie
基本实验定律
特点： a、 I J sl J sl sin
sin n n sin n l e j
I J sl n
le j
2 r3
r
l
cos
1 r
(l cos )
e
l sin
r
e
E
r
q
4 0
l cos
1 r2
1 r2
l cos
e e
q
4
0
l
cos
2 r3
r
1 r2
l
( p
r) ex
ey x
y
ez
z
（ px
x
py y
pz z)
ex px ey py ez pz
p
1 r3
3 r4
er
3r r5
1 3( p r) p
E
r
4
0
r5
r
r
3
E
r
2
l
r
0
er
R1
23 12/11/2019 Jin Jie
《电磁场和电磁波》 讲义
《电磁场和电磁波》讲义一、什么是电磁场在我们生活的这个世界里，电磁场是一种看不见、摸不着，但却无处不在的“神秘力量”。
简单来说，电磁场就是由带电物体产生的一种物理场。
当电荷静止时，它只产生电场；而当电荷运动时，就会同时产生电场和磁场。
电场和磁场相互关联、相互作用，形成了电磁场。
想象一下，一个带电荷的小球，它周围的空间就存在着电场。
如果这个小球开始移动，那么它就像一个奔跑的运动员，在身后留下了磁场的“足迹”。
电场的强度可以用电场强度这个物理量来描述，它告诉我们电场对电荷的作用力有多大。
而磁场的强度则用磁感应强度来表示，反映了磁场对运动电荷或电流的作用能力。
二、电磁波的产生既然有了电磁场，那么电磁波又是怎么来的呢？当带电粒子加速运动时，它产生的电磁场就会发生变化。
这种变化的电磁场会在空间中传播出去，就形成了电磁波。
比如说，一个电子在天线中来回振荡，就会不断地产生变化的电磁场，从而发射出电磁波。
电磁波的产生需要有一个源，这个源可以是一个振荡的电路、一个原子的跃迁，甚至是宇宙中的天体活动。
三、电磁波的特性电磁波具有很多独特的特性。
首先，电磁波是横波，也就是说它的振动方向与传播方向垂直。
这就像一根绳子上下抖动，而波却沿着水平方向传播一样。
其次，电磁波在真空中的传播速度是恒定的，约为3×10^8 米每秒，这个速度被称为光速。
电磁波的频率和波长是两个重要的参数。
频率是指电磁波在单位时间内振动的次数，而波长则是电磁波在一个周期内传播的距离。
它们之间存在着一个简单的关系：速度＝频率×波长。
不同频率的电磁波具有不同的性质和用途。
例如，无线电波可以用于通信和广播，微波可以用于加热食物，红外线可以用于遥控和热成像，可见光让我们看到五彩斑斓的世界，紫外线可以杀菌消毒，X 射线可以用于医学成像，伽马射线则在核物理和天文学中有重要应用。
四、电磁波的传播电磁波可以在不同的介质中传播，包括真空、空气、水、玻璃等等。
电磁场实验讲义-书
《电磁场》实验指导书电子信息工程实验室目录实验1 电磁波参量的研究 (1)实验2 电磁波极化的研究 (11)实验3 电磁波反射与折射的研究 (5)实验4 均匀无耗媒质参量的研究 (18)实验1 电磁波参量的研究1． 实验目的：（1）在学习均匀平面电磁波特性的基础上，观察电磁波传播特性如、和互相垂直。
（2）熟悉并利用相干波原理，测定自由空间内电磁波波长λ，并确定电磁波的相位常数β和波速ν。
（3）了解电磁波的其他参量，如波阻抗η等。
2.实验仪器：（1） AT1123型3cm 固态源1台 （2） DH926B 型电磁 波综合测试仪1套 （3） XF-01选频放大器1台 （4） PX-16型频率计 3.实验原理两束等幅、同频率的均匀平面电磁波，在自由空间内以相同（或相反）方向传播时，由于初始相位不同，它们相互干涉的结果，在传播路径上，形成驻波分布。
我们正是利用相干波原理，通过测定驻波场节点的分布，求得自由空间电磁波波长λ的值，再由λπβ2=（1-1）βπλυ2f == （1-2）得到电磁波的主要参数：β、ν等我们用图1.1来说明自由空间内电磁波波长λ值的测试原理。
设入射波为:βγj 0i i e E E -=。
当入射波以入射角θ1向介质板斜投射时，在分界面上产生反射波E γ和折射波E i 。
设入射波为垂直极化波，用R ┴表示介质板的反射系数，用0T ⊥和ε⊥T 表示由空气进入介质板和由介质板进入空气的折射系数。
另外，可动板r2P 和固定板r1P 都是金属板，其电场反射系数为-1，在一次近似的条件下，接受喇叭r3P 处的相干波分别为：1j i 0r1e E T T R E φε-⊥⊥⊥-= ()1r3r11L L L ββφ=+= 2j i 0r2e E T T R E φε-⊥⊥⊥-= ()()r1r3r3r22L L L L L ++=+=∆ββφ其中，12L L L -=∆又因L 1是固定值，L 2则随可动板位移L ∆而变化。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
《电磁场》实验指导书电子信息工程实验室目录实验1 电磁波参量的研究 (1)实验3 电磁波极化的研究 (5)实验4 均匀无耗媒质参量的研究 (12)实验1 电磁波参量的研究1． 实验目的：（1）在学习均匀平面电磁波特性的基础上，观察电磁波传播特性如、和S 互相垂直。
（2）熟悉并利用相干波原理，测定自由空间内电磁波波长λ，并确定电磁波的相位常数β和波速ν。
（3）了解电磁波的其他参量，如波阻抗η等。
2.实验仪器：（1） AT1123型3cm 固态源1台 （2） DH926B 型电磁 波综合测试仪1套 （3） XF-01选频放大器1台 （4） PX-16型频率计 3.实验原理两束等幅、同频率的均匀平面电磁波，在自由空间内以相同（或相反）方向传播时，由于初始相位不同，它们相互干涉的结果，在传播路径上，形成驻波分布。
我们正是利用相干波原理，通过测定驻波场节点的分布，求得自由空间电磁波波长λ的值，再由λπβ2=（1-1）βπλυ2f == （1-2）得到电磁波的主要参数：β、ν等我们用图1.1来说明自由空间内电磁波波长λ值的测试原理。
设入射波为:βγj 0i i e E E -=。
当入射波以入射角θ1向介质板斜投射时，在分界面上产生反射波E γ和折射波E i 。
设入射波为垂直极化波，用R ┴表示介质板的反射系数，用0T ⊥和ε⊥T 表示由空气进入介质板和由介质板进入空气的折射系数。
另外，可动板r2P 和固定板r1P 都是金属板，其电场反射系数为-1，在一次近似的条件下，接受喇叭r3P 处的相干波分别为：1j i 0r1e E T T R E φε-⊥⊥⊥-= ()1r3r11L L L ββφ=+= 2j i 0r2e E T T R E φε-⊥⊥⊥-= ()()r1r3r3r22L L L L L ++=+=∆ββφ其中，12L L L -=∆又因L 1是固定值，L 2则随可动板位移L ∆而变化。
当r2P 移动L ∆值时，使r3P 具有最大输出指示时，则有r1E 和r2E 为同相叠加；当r2P 移动L ∆值，使r3P 具有零值输出指示时，必有r1E 和r2E 反相。
故可采用改变r2P 的位置，使r3P 输出最大或零指示重复出现。
从而测出电磁波的波长λ和相位常数β。
下面用数学式来表达测定波长的关系式。
在r3P 处的相干波合成 ()21j j i 0r2r1r e e E T T R E E E φφε--⊥⊥⊥+-=+=或写成 ⎪⎭⎫⎝⎛+-⊥⊥⊥⎪⎭⎫ ⎝⎛-=2j 21i 0r 21e 2-cos E T T 2R E φφεφφ 式中L 21∆βφφφ∆=-=为测准入值，一般采用r3P 零指示办法，即02cos =⎪⎭⎫⎝⎛φ或()212n 2πφ∆+= n =0.1.2…..这里n 表示相干波合成驻波场的波节点（0E r =）处。
同时，除n =0以外的n 值，又表示相干波合成驻波的半波长数。
将n =0时0E r =的驻波节点作为参考位置0l ，又因λ∆λπφ∆2= ，故()L 212n ∆λππ=+或()λ∆1n L 2+=有上式可知，只要确定驻波节点位置及波节数，就可方便地确定λ值。
相干波r1E 与r2E 的分布如图1．2所示，图中n =0的节点处0l 作为第一个波节点，对其他n 值则有n =1,()λ∆=-=01l l L 2,对应第二个波节点，或第一个半波长数。
n =2, ()λ∆=-=12l l L 2,对应第三个波节点，或第二个半波长数。
n =3, ()λ∆=-=23l l L 2,对应第四个波节点，或第三个半波长数。
n =n ，()λ∆=-=1-n n l l L 2,对应第n +1个波节点，或第n 个半波长数。
把以上各项相加，取波长数的平均值得()λn l l 20n =-即()n l l 20n -=λ02()n l l nλ-=把上式代入式（1-1）就可得到被测电磁波的参量λ、β、υ等值。
事实上，可动板移动时，不可能出现无限多个驻波节点。
测试时，一般取n =4已足够，它表示在5个波节点距离内，（4l -0l ）相应于4个半波长。
从而测得该距离内波长平均值。
从理论上讲，n 值越大，测出λ值的精度应越高。
由于r3P 所测得的合成驻波场，处于进区场分布的范围内，因此，r2P 的移动，不仅影响驻波节点位置均匀分布，而且驻波幅度也有起伏。
3.实验内容（1） 了解并熟悉电磁波综合测试仪的工作特点，使用方法，特别要熟悉与掌握利用相干波原理测试电磁场波长的方法。
（2） 了解3cm 固态源的使用方法和正确操作。
（3） 仪器工作正常后，观察电磁波E 、H和S 三者符合右手螺旋规则，向r3P 传播的波应有：y E y E ˆ= ，x H x -H ˆ= ，μηy 2x E z H z H E S ˆˆ==⨯=（4） 测λ值。
移动可动板r2P ，并测出n l 值。
根据测出的0l 与n l 及n 值，计算λ、β、υ值。
（5） 用PX-16频率计测出信号源工作波长（00f c=λ），并与被测电磁波的波长λ进行比较。
把相关测试数据的波长填入表1-1中。
（6） 改变仪器波长，等间距的选取4个频率点进行测量，记录实验数据同表1-1，并与理论值进行比较。
（7） 稍微改变半投射板角度使其偏离45 °（40 °或50 °），重新完成步骤4，并记录数据。
表1-14.实验报告内容与要求 （1） 实验目的 （2） 实验基本原理 （3） 实验数据表（4） 比较信号源工作波长（00f c=λ）与自由空间波长λ之间的差别，分析原因。
（5） 思考题，用相干波测电磁波波长时，图1-1中的介质板放置位置若转090，将出现什么现象？这是能否测准λ值？为什么？实验3 电磁波极化的研究1. 实验目的（1） 研究线极化波、圆极化波、椭圆极化波的形成和特点。
（2） 了解线极化波、圆极化波和椭圆极化波特性参数的测试方法 2. 实验仪器（1）DH926B 型电磁波综合测试仪，测极化用的金属丝栅附件一套 （2）AT1123型3cm 固态信号源一台 （3）一只或XF-01型选频放大器一台 3. 实验原理与说明电磁波极化是指波在无限大均包媒质中传播时，在空间某点位置上电场强度矢量E 随时间变化的规律。
当E末端总在一直线上周期变化时，称为线极化波，当E 末端的轨迹是圆（或椭圆）时，称为圆极化波；若圆轨道运动与波前进方向符合右手螺旋规则时，则称为右旋（或左旋）圆极化波，无论是线、圆或椭圆极化波都可由两个同频率的正交场线极化波组合而成。
设两同频率正交场线极化波为()x x j xm x e E E φβ--= （2-1） ()yx j ym y eE E φβ--= （2-2）1）组成线极化波如图所示，式（2-1）和式（2-1）中，当0y x =-φφ,()ym xm ym xm E E E E ≠±=或时，两个波在空间叠加()φβ-z -j m y x e E E y E x E =+= 式中ym xm m E y E x E +=合成场矢量E 的方向与x 轴夹角不变，即：=⎪⎪⎭⎫⎝⎛±=⎪⎪⎭⎫ ⎝⎛±=xm ym x y E E arctg E E arctg θ常数 若xmym E E 的值不同，则θ为不同的定值，从而获得合成场矢量末端沿直线轨迹周期变化的极化波。
若0E ym =则θ=0这时线极化波为在空间某点的场，且仅在x 轴方向上周期变化。
同理，线极化波也可以分成为频率相同、场相垂直的两个线极化波。
2）组成圆极化波根据式（2-1）和（2-2），若m ym xm E E E ==，及20y x πφφ-==,,这时合成波可写成：()z -j m y x e y j -x E E y E x E β=+=合成场E与x 轴的夹角（在z 0处）为()000x y z -t z -t c o s 2z -t c o s a r c t g E E a r c t g βωβωπβωθ=⎪⎪⎪⎪⎭⎫ ⎝⎛⎪⎭⎫⎝⎛+=⎪⎪⎭⎫ ⎝⎛= 当z=z θ时，θ随时间向正值增大，合成场矢量末端按右手螺旋规则作圆周运动，故称为右旋圆极化波，如图所示同理，可得左旋圆极化波()z -j m e y j x E E β+= 和()0x y z -t E E arctg βωθ-=⎪⎪⎭⎫ ⎝⎛=这里有m ym xm E E E ==,及0x =φ,2y πφ=,2y x πφφ-=-随时间增加E矢量末端运动轨迹符合左手螺旋定则，故称左旋极化波，如图所示（3）组成椭圆极化波 当式（2-1）和式（2-2）所表示的两个线极化波，幅度不等，相位差仍为±π/2时，可得椭圆长短轴分别在x 轴和y 轴的椭圆极化波。
如ym xm E E >，0x =φ,2y πφ=,则可得到左旋椭圆极化波。
当然，椭圆极化波可由两个同频率幅度不等的左，右旋圆极化波组成。
如图所示，若将式（3-1）和式（3-2）改写为()()()x x z j xm2xm1z j xm x e E E e E E φβφβ----+==()()()y y z j ym2ym1z j ym y eE E e E E φβφβ----+== 因0x =φ,2y πφ-=，及ym xm E E >，m1ym1xm1E E E ==，m2ym2xm2E E E ==，因而两个线极化波合成场波为()()zj m2z j m1z j ym z j xm e E y j x e E y j x e E y j e E x E ββββ----++-=-=ˆˆˆˆˆˆ12ˆˆˆˆˆˆ()()j z j z j z j xm ym m m E xEe jxE E x jy E e x jy E e βββ----=-=-++ 由上式可见，两个线极化波合成的椭圆极化波，也可以看成两个幅度不等的右旋和左旋极化波合成而得。
图3.4是实现各种极化波的装置。
金属丝栅P r1和P r2的功能，是分别反射⊥1r E 和//2r E 的波。
两反射波在接受喇叭P r3内实现相加的过程如图所示。
根据图中条件得11j 1m z j i 1e E e T'T R E E φβ-⊥-⊥⊥⊥⊥⊥=-= 22j 2m z j i 2r e E e T'T R E E φβ--=-=////////////为使辐射喇叭同时产生⊥i E 与//i E 两个入射波，只需将P r0转动一个角度α，使入射场i E 分成同频率的两个正交场αsin E E i i =, αcos E E i i =如图 3.5所示，当图中α=45o 时，⊥i E =//i E ，但这并不意味着2m//1m E E =⊥，其理由是//R R ≠⊥，可见，要实现幅度相等，必须有如下等式//////''T T R cos E T T R sin E i i αα=⊥⊥⊥在介质εr 和投射角θi 确定后，调整α角，即可实现两个线极化波幅度相等的要求，作为相位条件，当改变P r2的位置为l 0使z 2-z 1=±λ/4,即可实现221πφφ±=-。