一种改进的多属性模型压缩算法

合集下载

模型压缩的步骤和流程(Ⅰ)

模型压缩是指通过一系列技术手段，将原有的大规模模型精简为适用于特定场景或设备的小规模模型。

在人工智能领域，模型压缩是非常重要的话题，因为大规模模型往往需要庞大的计算资源和存储空间，不利于在一些资源受限的设备上部署和运行。

本文将从模型压缩的步骤和流程出发，简要介绍模型压缩的相关知识。

首先，模型压缩的步骤可以分为几个关键环节：选择模型、剪枝、量化、蒸馏和微调。

选择模型是指在开始压缩之前，需要明确选定要压缩的原始模型。

剪枝是指通过去除模型中一些冗余的连接或参数，来减小模型的规模。

量化是指将模型中的参数从浮点数转换为定点数或低精度浮点数，以减小模型的存储空间和计算复杂度。

蒸馏是指通过训练一个小模型来近似一个大模型，以达到压缩模型的目的。

微调是指在压缩后的模型上进行一定的调整和优化，以保证模型的性能。

其次，模型压缩的流程一般包括以下几个步骤：首先是数据收集和准备阶段，这一阶段需要收集并准备用于训练和评估模型的数据集。

然后是模型选择和设计阶段，需要选择适合目标任务的模型，并设计相应的压缩策略。

接着是模型训练和评估阶段，这一阶段需要使用准备好的数据集对模型进行训练和评估。

最后是模型压缩和部署阶段，需要对训练好的模型进行压缩，并将压缩后的模型部署到目标设备上。

除了以上的步骤和流程外，模型压缩还涉及到一些关键技术和方法。

例如，剪枝技术有很多种，包括结构剪枝、参数剪枝、通道剪枝等。

量化技术也有很多种，包括对称量化、非对称量化、混合精度量化等。

蒸馏技术也有不同的实现方式，包括知识蒸馏、数据蒸馏、模型蒸馏等。

这些技术和方法在模型压缩的过程中起着至关重要的作用。

总的来说，模型压缩是一个重要且复杂的任务，它涉及到多个步骤和环节，需要综合运用多种技术和方法。

对于人工智能领域的研究者和从业者来说，掌握模型压缩的步骤和流程，了解相关的技术和方法，对于进行模型压缩工作是非常有帮助的。

希望本文对大家有所启发，也希望人工智能领域的研究者和从业者们能够在模型压缩的道路上不断探索和创新，为推动人工智能技术的发展做出更大的贡献。

模型压缩方法

模型压缩方法
模型压缩是指通过降低模型的复杂度和参数量，减小模型的存储和计算资源需求，提高模型的运行效率。

模型压缩方法通常可以分为以下几种：
1. 剪枝：剪枝是一种常见的模型压缩方法，它通过删除一些冗余的连接或神经元来减小模型的规模。

剪枝可以分为结构剪枝和权重剪枝两种方式，其中结构剪枝主要删除冗余的神经元或层，权重剪枝则是删除小于预定义阈值的权重值。

2. 量化：量化是通过降低变量的精度来减少模型大小和计算量。

通常使用的量化方法包括二值化、定点化和浮点数量化等方式。

3. 分组卷积：分组卷积是通过将输入和输出通道分组来降低计算量和参数量。

通常使用的分组卷积方式包括基于深度可分离卷积的分组卷积和基于通道划分的分组卷积。

4. 知识蒸馏：知识蒸馏是通过将一个大型模型的知识传递给一个小型模型来减少模型大小和计算量。

通常使用的知识蒸馏方法包括基于软标签的知识蒸馏和基于模型输出的知识蒸馏。

5. 神经网络压缩：神经网络压缩是一种基于自编码器或变分自编码器的神经网络模型压缩方法。

它通过将模型参数用较少的参数来表示，从而达到压缩模型的目的。

6. 低秩分解：低秩分解是一种通过将卷积层和全连接层的权重分
解成小型的矩阵来减少参数数量的方法。

常见的低秩分解方式包括SVD分解、CP分解和TT分解等。

无损数据压缩算法的历史

⽆损数据压缩算法的历史引⾔有两种基本的压缩算法: 有损和⽆损。

有损压缩算法通过移除在保真情形下须要⼤量的数据去存储的⼩细节，从⽽使⽂件变⼩。

在有损压缩⾥，因某些必要数据的移除。

恢复原⽂件是不可能的。

有损压缩主要⽤来存储图像和⾳频⽂件。

同⼀时候通过移除数据能够达到⼀个⽐較⾼的压缩率，只是本⽂不讨论有损压缩。

⽆损压缩，也使⽂件变⼩，但相应的解压缩功能能够精确的恢复原⽂件，不丢失不论什么数据。

⽆损数据压缩被⼴泛的应⽤于计算机领域，从节省你个⼈电脑的空间。

到通过web发送数据。

使⽤Secure Shell交流，查看PNG或GIF图⽚。

⽆损压缩算法可⾏的基本原理是，随意⼀个⾮随机⽂件都含有反复数据。

这些反复数据能够通过⽤来确定字符或短语出现概率的统计建模技术来压缩。

统计模型能够⽤来为特定的字符或者短语⽣成代码，基于它们出现的频率，配置最短的代码给最经常使⽤的数据。

这些技术包含熵编码(entropy encoding)，游程编码(run-length encoding)，以及字典压缩。

运⽤这些技术以及其他技术，⼀个8-bit长度的字符或者字符串能够⽤⾮常少的bit来表⽰，从⽽⼤量的反复数据被移除。

历史直到20世纪70年代，数据压缩才在计算机领域開始扮演重要⾓⾊。

那时互联⽹变得更加流⾏，Lempel-Ziv算法被发明出来，但压缩算法在计算机领域之外有着更悠久的历史。

发明于1838年的Morse code。

是最早的数据压缩实例，为英语中最经常使⽤的字母⽐⽅"e"和"t"分配更短的Morse code。

之后。

随着⼤型机的兴起，Claude Shannon和Robert Fano发明了Shannon-Fano编码算法。

他们的算法基于符号(symbol)出现的概率来给符号分配编码(code)。

⼀个符号出现的概率⼤⼩与相应的编码成反⽐，从⽽⽤更短的⽅式来表⽰符号。

两年后，David Huffman在MIT学习信息理论并上了⼀门Robert Fano⽼师的课，Fano给班级的同学两个选项，写⼀篇学期论⽂或者參加期末考试。

一种改进的自动机压缩算法在深度包检测中的应用

的运算空间。
１深度包检测技术
当前日复杂的安全威胁中，很多恶意行为都隐藏在数据包中，可能充斥着蠕虫病毒、垃圾邮件、益漏洞利用等恶意代码，在
各种电子商务程序的Ｗｅ数据中也可能夹带着后门和木马程序在网络中传递。所以，网络应用和网络威胁都高速增长的今天，ｂ在仅仅依照数据包网络层信息的安全检测技术，已经无法满足信息安全的要求。
２传统算法存在的问题
图１深度包检测
传统的基于自动机的深度包检测算法，将给定的正则表达式集合中的所有正则表达式构造成一个ＤＡＦ。理论上，此方法可
以达到最好的运算时间。然而多个正则表达式对应一个ＤＡ的状态数要远远大于一个正则表达式对应一个ＤＡ状态数的总和。ＦＦ
引入了ＤＡ膨胀率之后我们就可以正式进入我们的算法。Ｆ
本算法的目的是在有限运算空间内尽快的增大ＤＦＡ的运算速度。即，在允许的内存范围内，尽量把多个正则表达式组合
针对这种问题，本文提出了一种构造最优ＤＦＡ状态数压缩法，该算法保证在有限的运算空间下，时间复杂度最小。ＤＦＡ所占据的运算空间的大小，取决于状态的数量和每个状态的转换的数量的乘积。为了表述方便，面运算空间（下内存）
同的状态来区分歧义，从而状态数增多。图１中，ＲＥ、ＲＥ２３和Ｒ４的识别能力依次变强且都存在歧义匹配，其ＤＡ状ＥＦ态数依次增多。我们引用一个ＤＡ膨胀率的概念，用来表述ＮＡ转化ＦＦ
情况下系统会使用虚拟内存作为补充，但是虚拟内存是操作系

模型压缩：量化、剪枝和蒸馏

模型压缩：量化、剪枝和蒸馏导读：近年来，BERT 系列模型成了应用最广的预训练语言模型，随着模型性能的提升，其参数规模不断增大，推理速度也急剧提升，导致原始模型必须部署在高端的GPU 显卡上，甚至部分模型需要多块显卡才能正常运行。

在移动智能终端品类越发多样的时代，为了让预训练语言模型可以顺利部署在算力和存储空间都受限的移动终端，对预训练语言模型的压缩是必不可少的。

本文将介绍针对BERT（以Transformer Block 堆叠而成的深度模型）的压缩方法。

01BERT模型分析想要深度压缩BERT，必须对模型各部分有更为深入的了解，前面的章节已经详细介绍过Transformer 和BERT 的结构，此处不再解释各模块的具体功能。

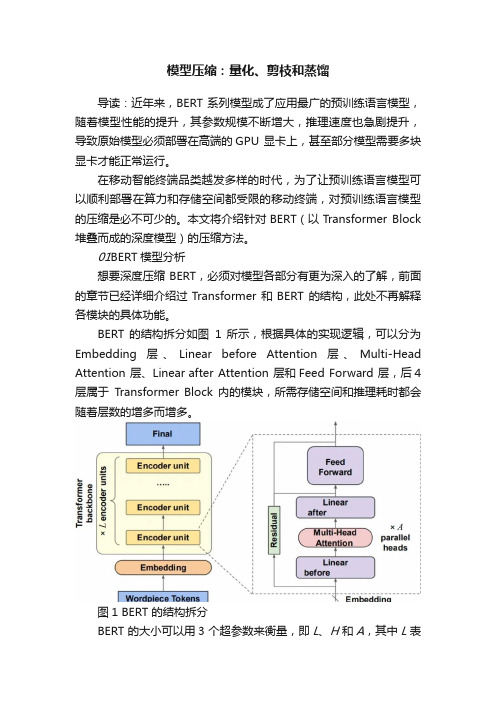
BERT 的结构拆分如图1 所示，根据具体的实现逻辑，可以分为Embedding 层、Linear before Attention 层、Multi-Head Attention 层、Linear after Attention 层和Feed Forward 层，后4 层属于Transformer Block 内的模块，所需存储空间和推理耗时都会随着层数的增多而增多。

图1 BERT 的结构拆分BERT 的大小可以用3 个超参数来衡量，即L、H和A，其中L表示Transformer Block 的层数，H表示隐层向量的维数（等于Embedding 层输出向量的维数），A 表示Self-Attention 层的头数。

通过这3 个超参数，可以基本知晓BERT 的各模块大小，L 和H 决定了模型的宽度和深度，A决定了模型Attention 的多样性。

以为例分析3 个超参数，其中L为12，H为768，A为12，模型各层所占存储空间和算力，如图2所示。

图2 BERTBASE 各层所占存储空间和算力显然，在数据存储空间方面，Feed Forward 层占据了约一半的空间，Embedding层和Linear before Attention 层分别占据约四分之一的空间，而最核心的Multi-Head Attention 层几乎不占存储空间，这里所谓的存储空间可以等效为模型参数的数量。

一种改进的压缩频繁模式挖掘算法

基金项目：四川省教育厅科研资助项目（ ¨ＺＢ２１９）．
作者简介：赖
性，该集合中最长的模式被称为闭频繁模式．Ｓ中的其他模式均为该最长的模式的子集，具有这个性质的
模式被认为能代表ｓ集合所有的频繁模式．该算法在一定程度上缩小了频繁模式挖掘结果集合的规模，但
①
收稿日期：２０１３— ０１ —１３
如果模式Ｘ的支持度的大小超过了用户事先设置的最小支持度ｍｉｎ — ｓｕｐ的大小，那么模式Ｘ就是频繁模式．频繁模式有个属性，即如果模式Ｘ是频繁模式，那么组成它的项构成的任意子集形成的模式ｙ也是频
２０１３年７月
Ｊｕ１．２０１３
文章编号００９３— ０７
一
种改进的压缩频繁模式挖掘算法①
赖娟，金澎，洪艳伟
１．乐山师范学院智能信息处理及应用实验室，四ＪｌＩ乐山６１４０００；２．乐山师范学院计算机科学学院，四川乐山６１４０００
来，国内一些学者也在该领域有了初步进展ｌ＿４］．早在１９９３年Ａｇｒａｗａｌ等ｌ９］就提出了该问题，频繁模式挖掘通常是基于一个事务集合Ｄ一｛ｔｌ，ｔｌ，… ，
ｔｎ｝，其中事务ｔｊ是构成事务集合Ｄ的一个项的集合，Ｊ∈ ［１， ” ］．项的集合一｛以，２， …，｝，其中模

一种改进的无线多媒体传感器网络分布式图像压缩算法

ｐｅｓｏＳｍｕａｉｎｒｓｌｓｄｍｏｔａｅｔａｈｅＩｒｓｉｎ．ｉｌｔｏｅｕｔｅｎｓｒｔｈｔｔＣＤＰｌｏｉｈｃｎｉａｇｒｔｍａｍｐｒｖｈｎｒｙｂｌｎｅａｈｅｗｏｋｏｅｔｅｅｅｇａａｃｎｄｔｅｎｔｒ
近年来，重叠变换技术在ＷＭＳｓ图像压缩中的应Ｎ用受到越来越多的关注，文献『 — ］出的图像如７８提压缩算法均通过节点间共享任务处理进程来解决单个节点计算、储能力以及能量受限的问题。存
像压缩效率的关键。
（ＩＡ）ａｐｏｅｇｏｐｅｓｎａｇｒｈａｅｎｉ－ｌｓｒｉｒｕｅｒｃｓｉｇＩＤ）ｓｒｐｓｄｉＤＣ，ｎｉｒｖｄｉｅｃｍｒｓｏｌｉｍｂｓｄｏｃｕｔｓｉｔｐｏｅｓ（ＣＰｉｐｏｏｅｍｍａｉｏｔｎｅｄｔｂｄｎｎ
案如图１所示。
较高，法往往需要将多级小波变换的计算量分布算到多个节点中去完成，而平衡节点能耗．分布式从但处理需要节点间进行数据交换．在一定程度上增这
加了节点能耗，因此如何设计一个有效的分布式处理机制是这类算法需要着重考虑的问题。文献［２提出了一种典型的无线多媒体传感器网络分１］
ｒｓｕｃ — ｏｓｒｉｅＭＳｔｉｈｎｄｅｅｓｔｅｏｒｅｃｎｔａｎｄＷＮｓｗｉｈｇｏｓｄｎｉｈｙ．

模型压缩的方法

模型压缩的方法
模型压缩指对于深度神经网络进行优化，减少其所需的计算资源和存储空间，使之能够在有限的硬件设备上运行和部署。

常用的模型压缩方法包括：
1. 参数下降：通过去除模型中冗余和不必要的参数，减少模型的大小和复杂度，较少计算量和存储光盘使用。

2. 知识蒸馏：将一个较为复杂的大模型所学习到的知识，通过训练一个较为简单的小模型来迁移，从而使得小型模型在满足一定精度要求的同时具有更高的计算效率。

3. 剪枝：通过去除一定数量的无用连接，来降低网络中的参数量和计算量。

剪枝方法包括结构剪枝、按照通道剪枝和按照元素剪枝等。

4. 量化：将网络中的参数和激活值从浮点数转换为定点数和整数，从而减少存储和计算量。

量化主要包括定点量化和二值量化。

5. 分享权重：将多个子网络的权重共享，从而减少网络的参数量和计算量。

以上是常见的模型压缩方法。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

关键词：型简化；次方拟合；模二多属性；进网格渐中图分类号：Ｐ１Ｔ３文献标识码：Ａ文章编号：６３６９２１）４０３－４１７－２Ｘ（０２０－０７０
ＡｎＩｐｒｖｄＳｕｆｃｉｐｉｃｔｏｇｒｔｍｏｅｒａｅＳｍｌｆａｉｎＡｌｏｉｈｍｉｗｉｈｕｔ— ｔｉｅｔＭｌｉ— ｒｂｕｔｓＡｔ
ｔａｈｅａｇｒｔｍｏｌｖｒｏｏｅｓｏｔｏｎｓａｄｂｅｉｅｒｄｃｄｂｔｒｉｔｇａｉｎｏｓｓｅｃｏｈｔｔｅｎｗｏｈｌｉｃｕｄｏｅｃｍｅｔｓｈｒｃｍｉｇｎｓｄｓｐｏｕｅｅｔｎｅｒｌｙａｄｃｎｉｔｎｙｃｍｐｒｎｔｒｄ－ｈｅｔａｇｗｉｔｉｉｈａｔｎｌａｇｒｔｍｓｉａｌｏｉｏｈ．
１背景介绍
随着各际模型简化中的效果，现其在应用中存在一定发
的不足；主要体现在拟合的新生成点的几何坐标可能存在较大的视觉误差，这个问题将在第三节进行详细
ＦＮＧＱｎＮｕ－ｉｇＬｉ－ｉＥｉ，ＩＧｉｑａ，ＵＯＪｎｘｎｎａ
（ｎｔｕｅｏｏＩｓｔｔｆｍｍａｄＡｕｏｔｎＰＡＵｉｒｉｆＳｉｎｅ＆Ｔｃｎｌｇ，ｎｉｇ２００，ｈｎ）ｉＣｎｔｍａｏ。ＬｎｖｓｙｏｃｃｉｅｔｅｅｈｏｏｙＮａｊ１０７Ｃｉａｎ
冯钦，桂强，倪罗健欣
（解放军Ｘ＿大学指挥自动化学院，苏南京２００）ｚ－江１０７
摘
要：传统的压缩算法在实际模型Ｌ应用时经常出现“ 洞 ” 面重叠等问题，过在．、ｏｊ．ｄ、ｍｘ等模型实例上空和通ｘ．ｂ、３ｓ．ａ
Ｋｅｒｓｓｒａｅｓｌｃｔｎ；ｕｄｃｅｒｒｍｅｒｃ；ｌ－ｔｂｔｓｐｏｒｓｉｅｍｅｈｙｗｏｄ：ｕｃｉｉａｉｑａｒｒｏｔｓｍｕｔａｔｕｅ；ｒｇｅｓｖｓｆｍｐｆｉｏｉｉｉｉｒ
第２２卷
第４期
计算机技术与发展
Ｃ０ＭＰＥＲＥＣＨＮＯＩＵＦＴＯＧＹＡＮＤＤＥＶＥＬＭＥＮＴＯＰ
２１０２年４月
Ｖ０．２Ｎ．１２ｏ４Ａｐｒ．２２０１
一
种改进的多属性模型压缩算法
Ａｂｓｒｃ：ｐｙｎｒｄｔｎｌａｇｒｈｉｅｌｍｏｅｓｏｔｎｌａｓｔｏｒｂｅｕｈａａｅｖｒａｓａｄ“ｈｌｓ．ｏｎｉＳｔａｔＡｐｌｉｇｔａｉｏａｏｔｍｎｒａｄｌｆｄｏｓｍｅｐｏｌｍｓｓｃｓｆｃｓｏｅｌｐｎｉｌｉｅｅｏｅ ” ＦｕｄｔｓＷａｈｂｃｕｅｏｏｅｇｏｔｃｌｉｌｒｐｉｔｉｈｏｔｎｒｓｔｄｉｏｇｐｓｔｎｕｎｉｌｃｔｎｈｎｐｏｏｅａｎｗｌｏｅａｓｆｔｓｅｍｅｒａｌｓｍｉｏｎｓｗｈｃｆｅｅｕｌｎｗｒｎｏｉｏｓｄｒｇｓｍｐｉａｏ．Ｔｅｒｐｓｅａｇ — ｈｉｙａｅｉｉｉｆｉｒｍ．ｉｇｒｔｍｅｒｈｓｇｏｔｃｌｙｓｍｉａｏｎｓｂｅｗａｆｐｒｉｏｉｇｓａｅｗｉｃｏａｙｔｅｔｅｕｌｅｈｓｓｏｉｈｔｈＴｓａｏｈｌｉｓａｃｅｅｍｅｒａｌｉｌｐｉｔｙｔｙｏａｔｉｎｎｐｃｔｏｔｎｒｒｅ，ｎｐｔａｍｐａｅｎｉｒｈｔｈｈｌｈｓｅｔｏｅｇｏｍｅｒｃｌｉｌｏｎｓａｄｍａｎａｎｔｅｒｇｏｔｉｏｔｕｔｕｎｉｌｃｔｎｆｏｓｍｅｓａｅｉｓＥｐｒｎｓｓｏｄｔｉａｌｓｍｉａｐｉｔｎｉｔｉｈｉｅｍｅｒｃｎｎｉｄｒｇｓｍｐｉａｉｒｍｏｔｔｇｅ．ｘｅｍｅｔｈｗｅｙｒｃｉｙｉｉｆｏｒｉ
实验发现，出现Ｌ述题的主要原因在于几何相似点，些点在压缩过程中出现了偏差。文中提出了～种改进的压缩算１这
法，法首先利用八叉树切分空间确定几何相似点，后针对几何相似点采用一系列策略，它们在压缩过程中仍然保该算然使持良好的几何连续性。对比实验表明，法不仅能克服传统算法出现的问题，能更好地保持模型的整体性与连贯性。该算还