2-3 方差分析
方差分析(包括三因素)讲解

2、CLASS 变量表;
CLASS必须的MODEL之前。
3、MODEL 因变量表=效应;
输出因变量均数,对主效应均数间的检
4、MEANS 效应[/选择项];
验。
5、ALPHA=p 显著性水平(缺省值为0.05)
是指因变量与自变量效应,模型如下:
1、主效应模型 MODEL y=a b c; (a b c是主效应,y是因变量)
计判断,得出结论。
5
方差分析的基本思想:把全部数据关于总均值的离差平方和 分解成几部分,每一部分表示某因素诸水平交互作用所产生 的效应,将各部分均方与误差均方相比较,从而确认或否认 某些因素或交互作用的重要性。
用公式概括为:
各因素引起
由个体差异 引起(误差)
总变异=组间变异+组内变异
种类:常用方差分析法有以下4种 1、完全随机设计资料的方差分析(单因素方差分析) 2、随机区组设计资料的方差分析(二因素方差分析) 3、拉丁方设计资料的方差分析(三因素方差分析) 4、R*C析因设计资料的方差分析(有交互因素方差分析)
3
第一节 概述
因素(因子)—— 可以控制的试验条件 因素的水平 —— 因素所处的状态或等级 单(双)因素方差分析——讨论一个(两个) 因素对试验结果有没有显著影响。
4
例如:某厂对某种晴棉漂白工艺中酸液浓度(g/k)进 行试验,以观察酸液浓度对汗布冲击强力有无显著影 响。
冲击强力 序号
1
浓度
2 3 4 56
计算出F值:
QA
4217.3
(3 1) 2 28.38
QE
1114.7
(3(6 1))
5
15
列表:
方差来源 因素A 试验误差 总误差
方差分析_精品文档

方差分析_精品文档方差分析(Analysis of Variance,简称ANOVA)是一种用于比较两个或更多个群体均值是否存在显著差异的统计方法。
它是一种非参数统计方法,适用于正态分布的数据,可以帮助我们理解不同因素对于观测变量的影响程度以及它们之间是否存在交互作用。
方差分析的基本原理是将总体方差拆分为组内方差和组间方差。
组间方差表示了不同群体之间的差异,组内方差则表示了同一群体内的个体差异。
通过比较组间方差与组内方差的大小,判断不同群体均值是否存在显著差异。
方差分析可以分为单因素方差分析和多因素方差分析。
单因素方差分析主要用于比较一个因素(或处理)对观测变量的影响,例如比较不同药物对于治疗效果的影响;而多因素方差分析则可以同时考虑多个因素的影响,并探究它们之间是否存在交互作用。
方差分析的基本步骤如下:1.建立假设:根据实际问题,建立相应的原假设(H0)和备择假设(H1)。
原假设通常是认为各组均值相等,备择假设则是认为各组均值不全相等。
2.收集数据:根据实验设计,对不同处理组进行观测,获取相应的数据。
3.计算统计量:计算组间方差和组内方差,进行方差分析,得到统计量(F值)。
4.判断显著性:根据计算出的F值和自由度,查找F分布表,计算出P值(显著性水平)。
5.做出结论:根据P值,结合原假设和备择假设,判断不同群体均值是否存在显著差异。
方差分析的优点在于可以同时比较多个群体均值,减少了多次独立t 检验的错误率。
此外,方差分析也可以用于研究不同因素的交互作用,帮助我们更全面地理解数据。
然而,方差分析也有一些限制。
首先,方差分析要求数据满足正态分布假设,如果数据不满足正态分布,则结果可能不准确。
其次,方差分析对样本量要求较高,特别是对于多因素方差分析,需要足够的样本量才能得到可靠的结果。
最后,方差分析只能告诉我们群体均值是否存在显著差异,而不能确定具体差异的大小,这需要通过其他统计方法进行进一步分析。
方差分析(ANOVA)简介

方差分析(ANOVA)简介方差分析(Analysis of Variance,简称ANOVA)是一种统计方法,用于比较两个或多个样本均值之间的差异是否显著。
它是通过分析样本之间的方差来判断均值是否存在差异。
ANOVA广泛应用于实验设计、医学研究、社会科学等领域,是一种重要的统计工具。
一、方差分析的基本原理方差分析的基本原理是通过比较组内变异和组间变异的大小来判断样本均值之间的差异是否显著。
组内变异是指同一组内个体之间的差异,组间变异是指不同组之间的差异。
如果组间变异显著大于组内变异,就可以认为样本均值之间存在显著差异。
二、方差分析的假设方差分析的假设包括以下几个方面:1. 观测值是独立的。
2. 观测值是正态分布的。
3. 各组的方差是相等的。
三、方差分析的步骤方差分析的步骤主要包括以下几个方面:1. 确定研究问题和目标。
2. 收集数据并进行数据清洗。
3. 计算组内平方和、组间平方和和总平方和。
4. 计算均方和。
5. 计算F值。
6. 进行显著性检验。
四、方差分析的类型根据研究设计的不同,方差分析可以分为单因素方差分析和多因素方差分析。
1. 单因素方差分析:适用于只有一个自变量的情况,用于比较不同水平下的均值差异。
2. 多因素方差分析:适用于有两个或两个以上自变量的情况,用于比较不同因素和不同水平下的均值差异。
五、方差分析的应用方差分析广泛应用于各个领域,包括实验设计、医学研究、社会科学等。
它可以用于比较不同治疗方法的疗效、不同教学方法的效果、不同产品的质量等。
六、方差分析的优缺点方差分析的优点包括:1. 可以同时比较多个样本均值之间的差异。
2. 可以通过显著性检验来判断差异是否显著。
3. 可以通过计算效应量来评估差异的大小。
方差分析的缺点包括:1. 对数据的正态性和方差齐性有一定要求。
2. 只能用于比较均值差异,不能用于比较其他统计指标的差异。
七、总结方差分析是一种重要的统计方法,通过比较组内变异和组间变异的大小来判断样本均值之间的差异是否显著。
方差分析的原理

方差分析的原理方差分析(ANOVA)是一种统计方法,用于比较三个或三个以上组的均值是否相等。
它是一种用于检验组间差异是否显著的方法,通常用于实验设计和数据分析中。
方差分析的原理基于对组间差异和组内差异的分解,通过比较组间变异和组内变异的大小来判断组间均值是否有显著差异。
方差分析的原理可以通过以下步骤来解释,首先,假设我们有多个组,每个组都有一定的样本量和均值。
我们想要知道这些组的均值是否有显著差异。
方差分析的原理就是通过计算组间变异和组内变异来判断这一点。
具体来说,方差分析的原理包括以下几个步骤:1. 计算组内变异,首先,我们计算每个组内观察值与该组均值的偏差平方和。
这个偏差平方和反映了每个组内观察值与该组均值之间的差异程度。
2. 计算组间变异,然后,我们计算每个组均值与总体均值的偏差平方和。
这个偏差平方和反映了每个组均值与总体均值之间的差异程度。
3. 比较组间变异和组内变异,接下来,我们比较组间变异和组内变异的大小。
如果组间变异显著大于组内变异,说明组间均值存在显著差异;反之,如果组间变异远小于组内变异,说明组间均值之间没有显著差异。
4. 判断显著性,最后,我们通过F检验或t检验来判断组间均值是否有显著差异。
如果F值或t值大于一定的临界值,我们就可以拒绝原假设,认为组间均值存在显著差异;反之,如果F值或t值小于临界值,我们就不能拒绝原假设,认为组间均值之间没有显著差异。
方差分析的原理是基于对组间差异和组内差异的分解,通过比较组间变异和组内变异的大小来判断组间均值是否有显著差异。
它是一种常用的统计方法,可以帮助研究者判断不同组之间的差异是否显著,对于实验设计和数据分析具有重要意义。
通过深入理解方差分析的原理,我们可以更好地应用这一方法,从而更准确地进行数据分析和实验设计。
高中数学选修2-3知识点

高中数学选修2-3知识点高中数学选修2-3知识点第一章:计数原理1.分类加法计数原理:完成一件事情,有N类方法,第一类方法有M1种不同的方法,第二类方法有M2种不同的方法,以此类推,第N类方法有MN种不同的方法。
那么完成这件事情共有M1+M2+。
+MN种不同的方法。
2.分步乘法计数原理:完成一件事情需要分成N个步骤,第一步有m1种不同的方法,第二步有M2种不同的方法,以此类推,第N步有MN种不同的方法。
那么完成这件事情共有XXX种不同的方法。
3.排列:从n个不同的元素中任取m(m≤n)个元素,按照一定顺序排成一列,叫做从n个不同元素中取出m个元素的一个排列。
4.排列数:从n个不同元素中取出m(m≤n)个元素排成一列,称为从n个不同元素中取出m个元素的m个排列。
从n个不同元素中取出m个元素的一个排列数,用符号An表示。
An=m!/(n-m)!(m≤n,n,m∈N)。
5.公式:A(n+m)=An+Am*m!(m≤n,n,m∈N);An=m*(m-1)*。
*(n-m+1)=n!/(n-m)。
6.组合:从n个不同的元素中任取m(m≤n)个元素并成一组,叫做从n个不同元素中取出m个元素的一个组合。
7.公式:C(m,n)=C(n,n-m)=m!/[(n-m)!*m!];C(m,n)=C(n-1,m-1)+C(n-1,m);C(n,m)=C(n-1,m-1)*(n-m+1)/m。
8.二项式定理:(a+b)^n=C(n,0)*a^n*b^0+C(n,1)*a^(n-1)*b^1+。
+C(n,n)*a^0*b^n。
9.二项式通项公式展开式的通项公式:T=C(n,r)*a^(n-r)*b^r (r=0,1.n),其中C(n,r)为二项式系数。
10.二项式系数Cn:C(n,r)=C(n,n-r)=n!/(r!(n-r)!),其中r为从n个元素中取出的元素个数。
11.杨辉三角:杨辉三角是一种数学图形,由二项式系数构成,XXX的数为C(n,0),C(n,1)。
Excel数据处理之三 方差分析
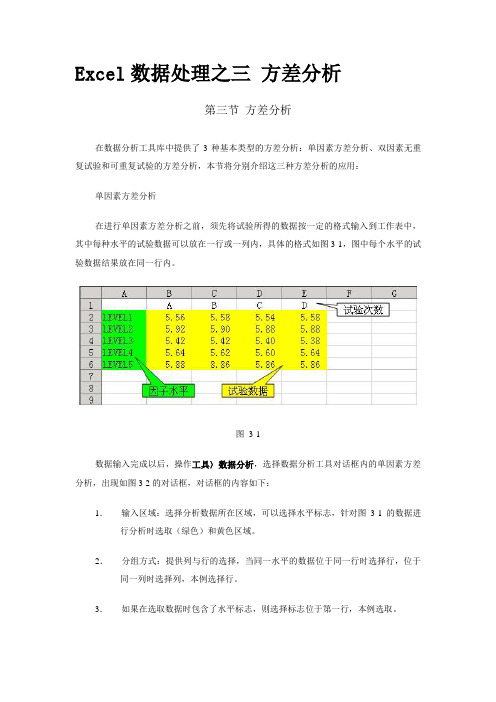
第三节方差分析
在数据分析工具库中提供了3种基本类型的方差分析:单因素方差分析、双因素无重复试验和可重复试验的方差分析,本节将分别介绍这三种方差分析的应用:
单因素方差分析
在进行单因素方差分析之前,须先将试验所得的数据按一定的格式输入到工作表中,其中每种水平的试验数据可以放在一行或一列内,具体的格式如图3-1,图中每个水平的试验数据结果放在同一行内。
图3-4
数据输入完成以后,操作工具〉数据分析,选择数据分析工具库中的双因素无重复方差分析,出现如图3-5的对话框,对话框的内容如下:
1.输入区域:选择数据所在区域,可以包含因素水平标志。
2.果数据输入时选择了因素水平标志,请选择标志按钮。
3.显著性水平α:根据实际情况输入,一般选择0.05。
4.输出选项:按需要选择分析结果存储的位置。
1.输入区域:选取图4-1数据表中的绿色和黄色区域,表示标志与数据。
2.分组方式:根据数据输入的方式选择逐行或逐列,此例选择逐列。
3.由于数据选择时包含了标志,所以要勾选标志位于第一行。
4.根据需要选择输出的位置。
图4-2
将信息按图4-2输入对话框后,选择确定,输出结果如图4-3所示。
图4-3
协方差分析
图3-5
分析图3-4中的数据,对话框如图3-5输入,分析结果输出如图3-6:
图3-6
双因素可重复方差分析
双因素可重复方差分析与双因素无重复方差分析数据输入的区别在于对重复试验数据的处理,如图3-7所示,就是将重复试验的数据叠加起来。
图3-7
数据输入完成以后,操作工具〉数据分析,选择数据分析工具库中的双因素可重复方差分析,出现如图3-8的对话框,对话框的内容基本与双因素无重复方差分析相同,区别在于每一样本的行数选项,在此输入重复试验的次数即可。
三因素方差分析的原理及应用

三因素方差分析的原理及应用1. 引言方差分析(Analysis of Variance,简称ANOVA)是一种统计分析方法,用于比较并确定一个因变量在不同组之间的均值是否存在显著差异。
在实际应用中,我们常常会遇到多个因素对结果的影响,这时可以使用三因素方差分析来研究它们之间的关系。
2. 三因素方差分析的原理三因素方差分析是将样本数据通过方差分解的方式,将总方差分解为三个部分,每个部分都与三个因素相关。
其中,总方差表示整体样本数据的变异程度,组内方差表示同一因素下各组数据之间的差异,而组间方差则表示不同因素间各组数据之间的差异。
三因素方差分析的统计模型可以表示为:$$ Y_{ijk} = \\mu + \\alpha_i + \\beta_j + \\gamma_k + \\epsilon_{ijk} $$其中,Y ijk表示第 i 个水平,第 j 个重复次数,第 k 个处理等 $\\mu$ 为总均值,$\\alpha_i$ 为第 i 个因素(水平)的影响效应,$\\beta_j$ 为第 j 个因素的影响效应,$\\gamma_k$ 为第 k 个因素的影响效应,$\\epsilon_{ijk}$ 为随机误差项。
3. 三因素方差分析的步骤具体进行三因素方差分析时,可以按照以下步骤进行:3.1 数据收集收集实验所需的样本数据,包括三个因素的取值和测量结果。
3.2 数据预处理对收集到的数据进行清洗、筛选和去除异常值等预处理操作,以保证数据的可靠性和准确性。
3.3 建立方差分析模型基于收集到的数据,建立三因素方差分析的统计模型,包括计算总平均值、组内平均值和组间平均值。
3.4 计算各因素的影响通过计算组内方差和组间方差,以及各因素的均方差来评估各因素的影响程度。
3.5 进行显著性检验采用适当的统计方法,比如 F 检验、t 检验等,对三因素方差分析的结果进行显著性检验,判断各因素的影响是否具有统计学意义。
3.6 结果解释和应用根据显著性检验的结果,解读各因素对结果的影响情况,并将其应用于实际问题中。
两差异法和三差异法公式

两差异法和三差异法公式两差异法和三差异法是在实证研究中常用的一种研究设计方法,用于评估某一干预措施对研究对象产生的影响。
这两种方法在研究中广泛应用于医学、教育、心理学等领域,帮助研究者了解干预措施的效果和推论因果关系。
一、两差异法两差异法(Two-group pretest-posttest design)是一种常用的实验设计方法。
该设计包括两组,即实验组和对照组,每组都要进行前测和后测。
实验组接受干预措施,而对照组则不接受干预,两组在实验开始前的特征一般应保持一致。
两差异法的公式如下:D1 = Y1t - Y1cD2 = Y2t - Y2c其中,D1表示实验组前测与后测变量的差异;D2表示对照组前测与后测变量的差异;Y1t和Y2t分别是实验组和对照组的后测得分;Y1c和Y2c分别是实验组和对照组的前测得分。
两差异法常用的推论统计方法是独立样本t检验或相关样本t检验,通过对D1和D2进行比较,用以评估干预措施的效果。
二、三差异法三差异法(Three-group pretest-posttest design)是一种扩展的实验设计方法,相比于两差异法,增加了一个比较组。
三差异法的设计包括实验组、对照组和比较组,每组都要进行前测和后测。
三差异法的公式如下:D1 = Y1t - Y1cD2 = Y2t - Y2cD3 = Y3t - Y3c其中,D1表示实验组前测与后测变量的差异;D2表示对照组前测与后测变量的差异;D3表示比较组前测与后测变量的差异;Y1t、Y2t和Y3t分别是实验组、对照组和比较组的后测得分;Y1c、Y2c和Y3c分别是实验组、对照组和比较组的前测得分。
三差异法常用的推论统计方法是方差分析(ANOVA),通过对D1、D2和D3进行比较,用以评估干预措施的效果,并进行组间比较。
总结起来,两差异法和三差异法是实证研究中常用的研究设计方法。
两者的差异在于研究组数的不同,通过对照组和比较组的设计,可以在一定程度上控制实验效应的干扰,并通过对差异进行比较来评估干预措施的效果。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
TRIZ创新理论教学研究中心 8
常州工程职业技术学院
单因子方差分析的案例
统计 > 方差分析 > 单因子(未堆叠存放)
TRIZ创新理论教学研究中心 9
常州工程职业技术学院
单因子方差分析的案例
TRIZ创新理论教学研究中心 10
常州工程职业技术学院
单因子方差分析的案例
先直观地判断出B除草剂 的效果是最好的
不同品牌的彩电在各地区的销售量数据 品牌 (因素A) A1 A2 A3 A4 销售地区(因素B) B1 365 345 358 288 B2 350 368 323 280 B3 343 363 353 298 B4 340 330 343 260 B5 323 333 308 298
常州工程职业技术学院
TRIZ创新理论教学研究中心 14
常州工程职业技术学院
课后练习
4-2.MPJ
一所工厂试验了4种不同的草莓防腐剂。冷藏6个月 后,检查草莓变色程度,并分成10个等级,其中10级为 最差。 四组数据中第一组数据为对照组,其它三组数据 来自使用了新设计的防腐剂使草莓变色的程度。 请确定 其中任何一组是否与其它组相同(=0.05)。 你得出的结论是什么?
TRIZ创新理论教学研究中心 4
常州工程职业技术学院
方差分析所涉及的参数
%SS贡献度(R-Sq):
是计算每个变异来源对总变异的影响量,若该值 ≥85%,则说明是影响结果的重要原因。
TRIZ创新理论教学研究中心 5
常州工程职业技术学院
目 录
第1部分 单因子方差分析
第2部分 双因子方差分析
TRIZ创新理论教学研究中心 6
TRIZ创新理论教学研究中心 18
常州工程职业技术学院
无交互作用的双因子方差分析案例
统计 > 方差分析 > 双因子
TRIZ创新理论教学研究中心 19
常州工程职业技术学院
无交互作用的双因子方差分析案例
TRIZ创新理论教学研究中心 20
常州工程职业技术学院
无交互作用的双因子方差分析案例
P值>0.05, H0成立,即 残差符合正 态分布
注意事项
执行残差分 析以检验误 差假设
单因子 方差分 析
方差分析的基本方法
6、验证误差假设是否 成立 (残差分析)? 7、用 p-值诠释因子的 影响 (p < ) 8、计算因子及误差项 的 % SS 9、用得出的结论诠释 实际问题
1、描述实际问题 2、描叙虚无假设H0 3、描述对立假设H1 4、验证模型假设 是否成立? 5、建立ANOVA表
TRIZ创新理论教学研究中心 21
常州工程职业技术学院
无交互作用的双因子方差分析案例
从图上很难看 出因素A和B对 其结果的影响 程度
TRIZ创新理论教学研究中心 22
常州工程职业技术学院
无交互作用的双因子方差分析案例
?
TRIZ创新理论教学研究中心 23
常州工程职业技术学院
无交互作用的双因子方差分析案例
在DOE的语言中,该实验设计是单因子3水平实验
TRIZ创新理论教学研究中心 7 常州工程职业技术学院
单因子方差分析的案例
4-1.MPJ
打开一个空白Minitab表格,分别在C1、C2和C3列输入 上述数据(格式为数字格式)。保存文件名为4-1.MPJ。 H0:使用两种除草剂的桃树苗处理不影响其生长率 H1:至少有一种除草剂与未除草对照组不同并且影响 桃树苗的生长率
TRIZ创新理论教学研究中心 17
无交互作用的双因子方差分析案例
打开一个空白Minitab表格,在C1列输入表中数据(格 式为数字格式) ,在C2 列输入品牌号,在C3列输入销售 地区号 。保存文件名为4-3.MPJ。 H0:彩电的品牌和销售地区均不影响其销售量 H1:上述至少有一种因素影响了彩电的销售量
在DOE的语言中,该实验设计是单因子4水平实验
TRIZ创新理论教学研究中心 15 常州工程职业技术学院
目 录
第1部分 单因子方差分析
第2部分 双因子方差分析
TRIZ创新理论教学研究中心 16
常州工程职业技术学院
无交互作用的双因子方差分析案例
4-3.MPJ
有4个品牌的彩电在5个地区销售,为分析彩电的品牌(因 素A)和销售地区(因素B)对销售量是否有影响,对每个品 牌在各地区的销售量记录在下表内。请分析因素A和因素B对 彩电的销售量是否具有显著影响。
P值<0.05,H1成立,即品牌对 销售量有显著影响 P值>0.05,H0成立,即销售地 区对销售量没有显著影响
彩电销售量的变异83.94%是可因不同品牌而引起的原因来解释的
TRIZ创新理论教学研究中心 24
常州工程职业技术学院
有交互作用的双因子方差分析案例
如某些合金,当分别加入金属A或金属B时,其 性能变化不大,但是同时在加入A和B之后,合金的 性能变化显得非常显著,则金属A和B之间对合金的 性能存在交互作用。 此时我们可把交互作用作为一个新的因素来处 理。至于要研究3因素及以上多因素的问题,宜使用 DOE(实验设计)。
第二章 数据分析
第3节 方差分析
1
方差分析(ANOVA)
如:考察温度对某一化工产品的产率是否存在显著影响。
应变量 不连续 不连续 卡方检定 (列联表分析) 比例检析
相关性分析 回归分析
TRIZ创新理论教学研究中心 2
常州工程职业技术学院
方差分析(ANOVA)
TRIZ创新理论教学研究中心 25
常州工程职业技术学院
26
ANOVA
是一种检定多个样本平均数之间差异的方法 是平均值检定中二样本 t-检定的延伸 也是分析 DOE的基础 类型 假 设
1、每一个样本都是独立随机样本 2、每一个样本通过常态检定 3、误差假设:
各误差值间相互独立,没有任何趋 势、模式、或明显的畸点;各误差值 服从常态分配。
TRIZ创新理论教学研究中心 3 常州工程职业技术学院
TRIZ创新理论教学研究中心 11
常州工程职业技术学院
单因子方差分析的案例
P值>0.05,H0成立,即残差符 合正态分布 若P值≤0.05,则H1成立,说明 因子之间有交互作用,此时应 采用实验设计法来解决。
残差图可用来确定所选统计模型的适用性 TRIZ创新理论教学研究中心 常州工程职业技术学院
12
单因子方差分析的案例
?
TRIZ创新理论教学研究中心 13
常州工程职业技术学院
单因子方差分析的案例
P值<0.05,拒绝H0,则H1成立 桃树苗生长高度的变异83.66%是可用不同除草剂处理来解释的
置信区间无一重合, 说明A、B和不实施除 草剂对树苗的生长高 度所造成的影响都不 一样 用B除草剂处理过的桃树苗长势最好
常州工程职业技术学院
单因子方差分析的案例
想要测试两种除草剂的性能,以确定在桃树周围 清除杂草是否有助于桃树树苗的生长,保留第三组未 施用除草剂的桃树当作对照组。随机挑选了18棵树苗 做试验,每组随机分配6棵树苗。在研究结束时, 每棵 树苗的生长高度均以厘米单位记录下来( = 0.05 )。
对照組 除草剂A 除草剂B 66 85 91 67 85 93 74 76 88 73 82 87 75 79 90 64 86 86
