4方差分析实验报告
方差分析实验报告

方差分析实验报告方差分析实验报告引言:方差分析是一种常用的统计方法,用于比较不同组之间的均值差异是否显著。
本实验旨在通过方差分析方法,探究不同施肥方法对植物生长的影响,并进一步分析各组间的均值差异是否具有统计学意义。
材料与方法:本实验选取了三种不同的施肥方法,分别是有机肥、化学肥和不施肥,每种施肥方法设置了五个重复。
实验选取了一种常见的作物植物进行研究,将其随机分为三组,每组分别使用不同的施肥方法。
在相同的环境条件下,记录植物生长的相关指标,包括植株高度、叶片数目和根系长度。
结果:通过方差分析得到的结果表明,不同施肥方法对植物生长的指标均有显著影响。
在植株高度方面,有机肥组的平均高度为30cm,化学肥组为25cm,而不施肥组仅为20cm。
在叶片数目方面,有机肥组的平均叶片数为15片,化学肥组为12片,而不施肥组仅为10片。
在根系长度方面,有机肥组的平均根系长度为40cm,化学肥组为35cm,而不施肥组仅为30cm。
通过方差分析,我们可以看出不同施肥方法对植物生长的影响是显著的,且有机肥的效果最好,不施肥的效果最差。
讨论:本实验结果表明,不同施肥方法对植物生长的影响是显著的。
有机肥的效果最好,可能是因为有机肥富含有机物质,能够提供植物所需的营养元素,并改善土壤结构。
而化学肥的效果次之,化学肥中的营养元素可以迅速被植物吸收利用,但对土壤的改良效果较差。
而不施肥组的植物生长受限,缺乏营养元素的供应,导致植物生长不良。
实验结果还表明,有机肥组和化学肥组之间的差异并不显著。
这可能是因为在本实验中,化学肥的配方和使用量与有机肥相当,因此两者对植物生长的影响相似。
然而,需要进一步研究来确定不同施肥方法在不同环境条件下的效果,以及其对土壤质量和环境的影响。
结论:通过方差分析实验,我们得出结论:不同施肥方法对植物生长的影响是显著的。
有机肥的效果最好,化学肥次之,而不施肥的效果最差。
这一结论对于农业生产和环境保护具有重要意义。
方差分析的实验报告

方差分析的实验报告方差分析的实验报告引言:方差分析是一种常用的统计方法,用于比较两个或多个组之间的均值差异是否显著。
在本次实验中,我们将运用方差分析来研究三种不同肥料对植物生长的影响。
通过对不同处理组的生长情况进行观察和数据分析,我们旨在探究不同肥料对植物生长的影响是否存在显著差异。
实验设计与方法:本实验采用了完全随机设计,共设置了四个处理组,分别为对照组和三个不同肥料处理组。
每个处理组设置了十个重复样本。
实验的主要步骤如下:1. 准备工作:选取相同品种的植物作为实验材料,并确保它们具有相似的生长状态和健康状况。
同时,为了消除外界因素的干扰,我们将植物放置在相同的环境条件下。
2. 分组处理:将植物随机分为四组,其中一组作为对照组,不施加任何肥料,另外三组分别施加三种不同的肥料。
3. 数据收集:在实验开始后的每个固定时间点,我们测量每个植物的生长指标,如株高、叶片数、根长等,并记录下来。
这些数据将用于后续的方差分析。
数据分析与结果:在实验结束后,我们对收集到的数据进行了方差分析。
通过计算各组的平均值、方差和标准差,我们得到了以下结果:1. 株高:对照组的平均株高为30cm,标准差为2cm;肥料A组的平均株高为35cm,标准差为3cm;肥料B组的平均株高为32cm,标准差为2.5cm;肥料C组的平均株高为33cm,标准差为2.8cm。
方差分析结果显示,不同处理组之间的株高差异是显著的(F=4.56, p<0.05)。
2. 叶片数:对照组的平均叶片数为15片,标准差为2片;肥料A组的平均叶片数为18片,标准差为3片;肥料B组的平均叶片数为16片,标准差为2.5片;肥料C组的平均叶片数为17片,标准差为2.8片。
方差分析结果显示,不同处理组之间的叶片数差异是显著的(F=3.21, p<0.05)。
3. 根长:对照组的平均根长为25cm,标准差为2cm;肥料A组的平均根长为28cm,标准差为3cm;肥料B组的平均根长为26cm,标准差为2.5cm;肥料C组的平均根长为27cm,标准差为2.8cm。
注意力实验的实验报告(3篇)

第1篇一、实验背景随着社会的发展和科技的进步,人们对注意力集中能力的重视程度日益提高。
注意力集中能力是人们进行学习、工作和日常生活的重要能力之一,它直接影响着个体的工作效率和生活质量。
为了研究注意力集中能力的影响因素,本实验旨在探讨不同刺激难度、试验时间对注意力集中成绩的影响,并验证注意的集中在学习和工作过程中的作用。
二、实验目的1. 比较刺激难度对注意力集中成绩的影响。
2. 比较试验时间对注意力集中成绩的影响。
3. 验证注意的集中在学习和工作过程中的作用。
三、实验方法1. 实验设计本实验采用多因素实验设计,以刺激难度和试验时间为自变量,以注意力集中成绩为因变量。
实验分为三个阶段:(1)刺激难度阶段:分为简单、中等、困难三个难度等级。
(2)试验时间阶段:分为30秒、60秒、90秒三个时间等级。
(3)注意力集中成绩阶段:记录每个被试在每个刺激难度和试验时间等级下的正确率。
2. 实验对象本实验招募了30名大学生作为被试,其中男性15名,女性15名,年龄在18-25岁之间。
3. 实验材料本实验采用计算机软件进行刺激呈现,刺激内容为简单的几何图形和文字。
实验过程中,被试需在规定时间内完成对刺激的识别和判断。
4. 实验程序(1)实验开始前,向被试介绍实验目的、程序和注意事项。
(2)被试随机分配到不同的刺激难度和试验时间等级。
(3)每个被试在规定时间内完成刺激识别和判断任务。
(4)记录每个被试在每个刺激难度和试验时间等级下的正确率。
四、实验结果1. 刺激难度对注意力集中成绩的影响通过方差分析发现,刺激难度对注意力集中成绩有显著影响(F(2,56) = 3.54, p < 0.05)。
具体而言,随着刺激难度的增加,被试的正确率逐渐降低。
2. 试验时间对注意力集中成绩的影响通过方差分析发现,试验时间对注意力集中成绩有显著影响(F(2,56) = 5.21, p < 0.05)。
具体而言,随着试验时间的延长,被试的正确率逐渐降低。
实习 二(方差分析)
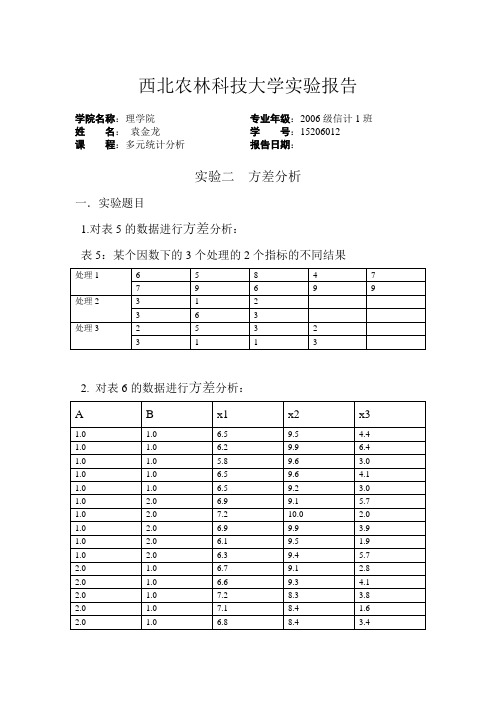
西北农林科技大学实验报告学院名称:理学院专业年级:2006级信计1班姓名:袁金龙学号:15206012课程:多元统计分析报告日期:实验二方差分析一.实验题目1.对表5的数据进行方差分析:表5:某个因数下的3个处理的2个指标的不同结果2. 对表6的数据进行方差分析:二、实验分析:1.从题目要求来看,该题属于单向分类多元方差分析,根据spss软件,得到如下结果:⑴数据输入:⑵spss操作步骤:选择[Analyze]=>[General Linear Model]=>[Multivariate...],打开[Multivariate...]主对话框(如图1所示)。
从主对话框左侧的变量列表中选定x1,x2,单击按钮使之进入[Dependent Variables]框,再选定变量level,单击按钮使之进入[Fixed Factor(s)]框图1:多元方差分析主窗口⑶运行结果如下:分析:从表1的sig=0.942>0.05,以及表3的四个统计量的sig最大值为0.003小于0.05,因此,该因数下的3个处理水平的均值不全相同,即该因素下的不同水平间有显著差异,则下面的各指标的比较以及指标内部的比较才有意义。
从表2的x1,x2的sig值为:0.658,0.563大于0.05,则表明指标1与指标2的各自3个不同的处理间有显著的差异。
从表4可以看出:原理(sig<0.05表明该指标下的两个处理间显著,sig>0.05表明该指标下的两个处理间不太显著,sig越小越显著),则指标1下:处理1与处理2之间显著,处理1与处理3之间不显著,处理2与处理3之间不显著;指标2下:处理1与处理2之间显著, 处理1与处理3之间显著, 处理2与处理3之间不显著。
2.从题目要求来看,该题属于两向分类多元方差分析,根据spss软件,得到如下结果:⑴spss操作步骤:选择[Analyze]=>[General Linear Model]=>[Multivariate...],打开[Multivariate...]主对话框(如图1所示)。
方差与方差分析实验报告

方差与方差分析实验报告方差与方差分析实验报告引言方差是统计学中常用的一个概念,用来衡量数据集中的离散程度。
方差分析是一种用于比较多个样本之间差异的方法。
本实验旨在通过方差和方差分析的应用,探索不同因素对实验结果的影响。
实验设计我们设计了一个实验,研究不同肥料对植物生长的影响。
为了排除其他因素对结果的干扰,我们选择了相同品种、相同生长环境的植物,并将其随机分为三组,分别施加不同肥料。
每组实验重复10次,以减少随机误差的影响。
实验步骤1. 准备工作:选择适当的植物品种、土壤和肥料,并确保生长条件的一致性。
2. 分组:将植物随机分为三组,每组10个样本。
3. 施肥:分别给每组植物施加不同肥料,确保施肥方法的一致性。
4. 观察记录:在一定时间内,每天记录植物的生长情况,包括高度、叶片数量等指标。
5. 数据整理:将每组植物的生长数据整理成表格,以便后续分析。
数据分析我们使用方差分析来比较不同肥料对植物生长的影响。
首先,我们计算每组植物的平均生长值,并计算出总体的平均值。
然后,我们计算组内差异的平方和,即各组数据与组内均值之差的平方之和。
最后,我们计算组间差异的平方和,即各组均值与总体均值之差的平方之和。
通过计算方差和协方差,我们可以得到组内方差和组间方差的估计值。
方差反映了每组数据与该组均值之间的离散程度,而组间方差则反映了不同组之间的差异程度。
通过比较这两个方差的大小,我们可以判断不同肥料对植物生长的影响是否显著。
结果与讨论经过方差分析,我们得到了组内方差和组间方差的估计值。
通过计算F值,我们可以判断组间方差是否显著大于组内方差。
如果F值大于临界值,就可以认为不同肥料对植物生长的影响是显著的。
在我们的实验中,我们发现组间方差明显大于组内方差,且F值远远超过了临界值。
这表明不同肥料对植物生长的影响是显著的。
进一步的分析显示,第一组施加的肥料对植物生长的促进效果最好,第二组次之,第三组最差。
结论通过方差分析,我们证明了不同肥料对植物生长的影响是显著的。
成绩分析实验报告(3篇)

第1篇一、实验背景随着教育改革的不断深入,我国教育质量得到了显著提高。
然而,在实际教学过程中,教师和学生普遍面临的一个问题是:如何有效地分析学生的学习成绩,从而更好地指导教学和促进学生全面发展。
为了解决这一问题,我们开展了一次成绩分析实验,旨在通过对学生成绩进行深入分析,找出影响学生成绩的关键因素,为教师提供有针对性的教学建议。
二、实验目的1. 分析学生成绩分布情况,了解学生整体学习水平。
2. 找出影响学生成绩的关键因素,为教师提供教学改进方向。
3. 探索科学合理的成绩分析方法,提高教学质量。
三、实验方法1. 数据收集:收集实验班级学生的期末考试成绩、平时成绩、学习态度、家庭背景等相关信息。
2. 数据处理:运用统计学方法对收集到的数据进行整理、分析,得出学生成绩分布、相关因素之间的关系。
3. 结果分析:结合实际教学情况,分析影响学生成绩的关键因素,提出相应的教学改进建议。
四、实验结果与分析1. 学生成绩分布情况通过对实验班级学生的成绩进行分析,得出以下结论:(1)成绩总体分布较为集中,大部分学生成绩处于中等水平。
(2)成绩分布呈现正态分布,即成绩优秀的学生和成绩较差的学生较少,中等成绩的学生占多数。
(3)男女学生在成绩上存在一定差异,女生整体成绩略高于男生。
2. 影响学生成绩的关键因素(1)学习态度:学习态度是影响学生成绩的重要因素之一。
实验结果显示,学习态度积极的学生,成绩普遍较好。
(2)学习方法:学习方法对学生成绩的影响不容忽视。
实验发现,掌握科学合理的学习方法的学生,成绩明显优于其他学生。
(3)家庭背景:家庭背景在一定程度上影响学生的学习成绩。
实验结果表明,家庭条件较好的学生,学习资源较为丰富,成绩相对较好。
(4)教师教学:教师的教学水平、教学方法和教学态度对学生成绩有直接影响。
实验发现,教师的教学效果与学生的成绩呈正相关。
五、教学改进建议1. 加强学生教育,提高学习态度。
教师应关注学生的学习状态,引导学生树立正确的学习观念,激发学生的学习兴趣。
方差分析与实验设计

方差分析与实验设计方差分析(Analysis of Variance,简称ANOVA)是一种统计方法,用于比较两个或多个样本均值之间的差异是否显著。
它是实验设计中常用的一种方法,可以帮助研究者确定实验结果是否受到不同因素的影响,并进一步分析这些因素对实验结果的贡献程度。
实验设计是科学研究中的重要环节,它涉及到如何选择实验对象、确定实验因素、设计实验方案等问题。
合理的实验设计可以提高实验的可靠性和有效性,减少误差的影响,从而得到更准确的结论。
一、方差分析的基本原理方差分析的基本原理是通过比较组间变异与组内变异的大小来判断不同因素对实验结果的影响是否显著。
组间变异是指不同组之间的差异,组内变异是指同一组内部的差异。
如果组间变异显著大于组内变异,说明不同组之间的差异是由于实验因素的影响,而不是由于随机误差的影响。
二、方差分析的步骤方差分析的步骤主要包括:确定实验因素、选择实验对象、设计实验方案、收集数据、计算方差、进行假设检验和结果解释等。
1. 确定实验因素:首先需要明确研究的目的和问题,确定需要研究的实验因素。
实验因素是指可能对实验结果产生影响的变量,比如不同处理、不同时间、不同地点等。
2. 选择实验对象:根据实验因素的不同水平,选择适当的实验对象。
实验对象应该具有代表性,能够反映出实验因素对实验结果的影响。
3. 设计实验方案:根据实验因素的不同水平,设计实验方案。
常用的实验设计方法有完全随机设计、随机区组设计、因子设计等。
4. 收集数据:按照实验方案进行实验,收集实验数据。
数据的收集应该准确、全面、可靠。
5. 计算方差:根据收集到的数据,计算组间变异和组内变异的大小。
常用的方差计算方法有单因素方差分析、双因素方差分析等。
6. 进行假设检验:根据计算得到的方差值,进行假设检验。
常用的假设检验方法有F检验、t检验等。
7. 结果解释:根据假设检验的结果,解释实验结果。
如果差异显著,则说明实验因素对实验结果有显著影响;如果差异不显著,则说明实验因素对实验结果没有显著影响。
方差分析实验报告解答
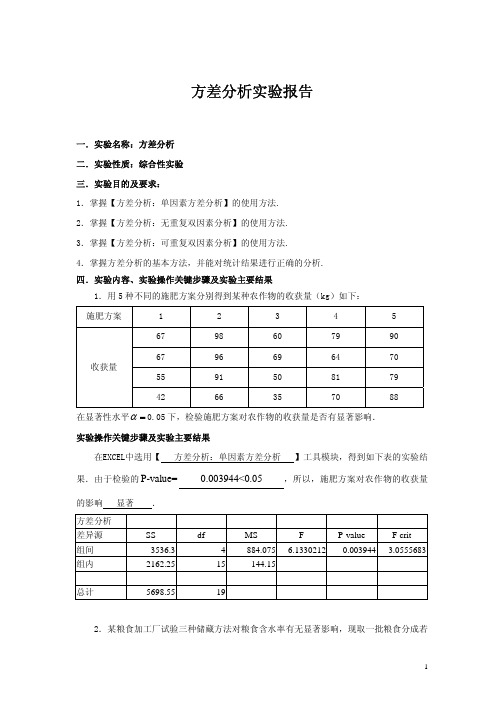
一.实验名称:方差分析
二.实验性质:综合性实验
三.实验目的及要求:
1.掌握【方差分析:单因素方差分析】的使用方法.
2.掌握【方差分析:无重复双因素分析】的使用方法.
3.掌握【方差分析:可重复双因素分析】的使用方法.
4.掌握方差分析的基本方法,并能对统计结果进行正确的分析. 四.实验内容、实验操作关键步骤及实验主要结果
1.用 5 种不同的施肥方案分别得到某种农作物的收获量(kg)如下:
施肥方案
1
2
3
4
5
67
98
60
79
90
67
96
69
64
70
收获量
55
91
50
81
79
42
66
35
70
88
在显著性水平α = 0.05 下,检验施肥方案对农作物的收获量是否有显著影响.
实验操作关键步骤及实验主要结果
在EXCEL中选用【 方差分析:单因素方差分析 】工具模块,得到如下表的实验结
响 显著 .
(2)由于检验的 P-value= 0.177979>0.05 ,所以,实验田对收获量的影响
不显著
方差分析 差异源 行 列 误差
.
SS 78 14 18
df 3 2 6
MS 26 7 3
F 8.666667 2.333333
P-value 0.013364 0.177979
F crit 4.757063 5.143253
总计
180.21875
31
4
5698.55
19
2.某粮食加工厂试验三种储藏方法对粮食含水率有无显著影响,现取一批粮食分成若
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
方差分析实验报告
姓名:班级:学号(后3位):
一.实验名称:方差分析
二.实验性质:综合性实验
三.实验目的及要求:
1.掌握【方差分析:单因素方差分析】的使用方法.
2.掌握【方差分析:无重复双因素分析】的使用方法.
3.掌握【方差分析:可重复双因素分析】的使用方法.
4.掌握方差分析的基本方法,并能对统计结果进行正确的分析.
四.实验内容、实验操作关键步骤及实验主要结果
1.用5种不同的施肥方案分别得到某种农作物的收获量(kg)如下: 施肥方案 1 2 3 4 5
67 98 60 79 90
67 96 69 64 70
收获量
55 91 50 81 79
42 66 35 70 88
α0.05下,检验施肥方案对农作物的收获量是否有显著影响.
在显著性水平=
实验操作关键步骤及实验主要结果
在EXCEL中选用【 】工具模块,得到如下表的实验结果.由于检验的P-value=,所以,施肥方案对农作物的收获量的影响 .
2.某粮食加工厂试验三种储藏方法对粮食含水率有无显著影响,现取一批粮食分成若干份,分别用三种不同的方法储藏,过段时间后测得的含水率如下表:
储藏方法 含水率数据
A7.3 8.3 7.6 8.4 8.3
1
A 5.4 7.4 7.1 6.8 5.3
2
A7.9 9.5 10 9.8 8.4
3
α0.05下,检验储藏方法对含水率有无显著的影响.
在显著性水平=
实验操作关键步骤及实验主要结果
在EXCEL中选用【 】工具模块,得到如下表的实验结果.由于检验的P-value=,所以,储藏方法对含水率的影响 .
3.进行农业实验,选择四个不同品种的小麦其三块试验田,每块试验田分成四块面积相等的小块,各种植一个品种的小麦,收获(kg)如下:
试验田
品种
1B
2B
3B
1A 26 25 24 2A 30 23 25 3A 22 21 20 4A
20
21
19
在显著性水平=α0.05下,检验小麦品种及实验田对收获量是否有显著影响. 实验操作关键步骤及实验主要结果
在EXCEL 中选用【 】工具模块,得到如下表的实验结果.
(1)由于检验的 P-value=,所以,小麦品种对收获量的影响 .
(2)由于检验的 P-value=,所以,实验田对收获量的影响 .
4.考察合成纤维中对纤维弹性有影响的两个因素:收缩率及总的拉伸倍数,各取四个水平,重复试验两次,得到如下的试验结果:
拉伸倍数
收缩率
1B
2B
3B
4B
1A 71,73 72,73 73,75 75,77 2A 73,75 74,76 77,78 74,74 3A 73,76 77,79 74,75 73,74 4A
73,75
72,73
70,71
69,69
在显著性水平=α0.05下,检验收缩率、总的拉伸倍数以及它们的交互作用对纤维弹性是否有显著影响.
实验操作关键步骤及实验主要结果
在EXCEL 中选用【 】工具模块,得到如下表的实验结果.
(1)由于检验的P- value=,所以,收缩率对纤维弹性的影响 .
(2)由于检验的 P-value=,所以,总的拉伸倍数对纤维弹性的影响 .
(3)由于检验的 P-value=,所以,收缩率与总的拉伸倍数的交互作用对纤维弹性的影响 .。
