组合图形(长方形,正方形,梯形,平行四边形)图题
五年级组合图形的面积精选32题
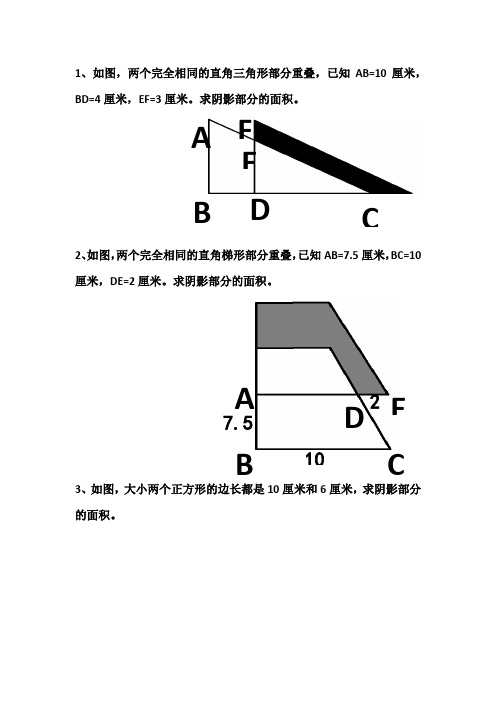
1、如图,两个完全相同的直角三角形部分重叠,已知AB=10厘米,BD=4厘米,EF=3厘米。
求阴影部分的面积。
2、如图,两个完全相同的直角梯形部分重叠,已知AB=7.5厘米,BC=10厘米,DE=2厘米。
求阴影部分的面积。
3、如图,大小两个正方形的边长都是10厘米和6厘米,求阴影部分的面积。
ABCDEFADEBC107.524、如图,大小两个正方形的边长都是10厘米和6厘米,求阴影部分的面积。
5、如图,由长方形ABCD 和直角梯形BEFC 组成,其中阴影部分的面积是36.5平方厘米,CD 是5厘米。
求长方形ABCD 的面积。
6、如图,平行四边形ABCD 的底BC 长12厘米,线段EF 长8.3厘米,求图中阴影部分的面积总和是多少平方厘米?ABCDEFABCDFEG7、如图,梯形上底长5.4厘米,下底长8.6厘米,高长4厘米,求三角形甲的面积比三角形乙的面积小多少平方厘米?8、如图,ABCD 是长方形,AB=8厘米,BC=6厘米,三角形ABF 的面积比三角形DEF 的面积大12平方厘米,求DE 长多少厘米?9、如图,平行四边形ABCD 的底BC 长10厘米,直角三角形FBC 的直角边FC 长8厘米。
已知阴影部分的总面积比三角形EFG 的面积大10平方厘米。
求EF 的长度。
甲乙ABCDEF8681010、如图,△ABC 和△DCB 都是直角三角形,已知AB=3.4厘米,BC=7.2厘米,且甲比乙的面积大3.6平方厘米,求CD 的长。
11、如图,CA=AB=4厘米,三角形ABE 的面积比三角形CDE 的面积小2平方厘米,求CD 的长。
12、如图,甲的面积比乙的面积大36平方厘米,已知AB 长8厘米,BC 长12厘米,CD 长6厘米,求DE 的长。
ABCD甲乙7.23.4ABCDE4ABCDE 甲乙812613、如图,D 是AC 的中点,E 、F 是BC 边上的三等分点,已知阴影部分的面积为20平方厘米,求三角形ABC 的面积。
五年级数学重点图形题

组合图形的面积1.组合图形:是由几种基本图形(三角形、平行四边形、正方形、梯形、圆)组合而成的较复杂的平面图形。
2.求组合图形的面积就是对组合图形进行分割或添补转化为我们学过的三角形、平行四边形、梯形、圆的面积来求解。
包含知识点组合图形的面积 ,平行四边形的面积 ,正方形、长方形的周长121.在边长是40cm的正方形木板上锯下一个最大的圆,圆的面积是_____cm2,剩下的边料是_____cm2.122.如图:长方形ABCD的面积为55平方厘米,三角形ABQ的面积为5平方厘米,三角形APD的面积为11平方厘米,那么中间三角形的面积是_____平方厘米.123.124. 如图所示,正方形的面积为5平方厘米,圆的面积是_____平方厘米.125.如图,在长方形ABCD中,△EAG的面积是13平方厘米,四边形EHFD的面积是49平方厘米,△FKC的面积是35平方厘米.求图中阴影部分的面积.126. 求图形阴影部分的周长和面积.(单位:cm)127. 求如图组合图形的面积(单位:厘米).你能想出几种方法.128. 如图,三角形ABC面积是30平方厘米,D、E分别是AC、AB 边上的中点,三角形BOC面积是三角形ABC面积的,三角形BOE 面积是_____平方厘米.129.(1)小船的面积大约有_____平方厘米;画出小船图向左平移8格后的图形.(2)画出图1的另一半,使它成为一个轴对称图形.(3)图2向_____平移了_____格.130. 求图形中阴影部分的面积(单位:m)132. 如图,ABCD是直角梯形,其中AD=12厘米,AB=8厘米,BC=15厘米,且△ADE、四边形DEBF、△CDF的面积相等.△EDF(阴影部分)的面积是多少平方厘米?133. 计算图中涂色部分的面积.(单位:厘米)134. 图中,有四条线段的长度已经知道,还有两个角是直角,那么四边形ABCD(阴影部分)的面积是多少(单位:厘米)?135. 甲、乙为正方形,计算阴影部分面积(单位:厘米).136. 如图,三个等圆的周长都是18.84厘米,求阴影部分的面积.(用最简便的方法解)137.求组合图形的面积.(单位:m)138. 求阴影部分的面积.(单位:厘米)139.140.如图为一面墙,这面墙每平方米需要60块砖,砌这面墙需要_____块砖.141. ABCD为任意四边形,其中AE=AB,BF=BC,CG=CD,DH=DA,连结E、F、G、H.求四边形EFGH的面积是四边形ABCD的面积的_____(如图).142. 求如图阴影部分的面积.单位:厘米.143.同学们去秋游,在路上他们看到了很多如图所示的指示牌,你能求出它的面积吗?144.已知△ABC的面积是32平方厘米,求阴影部分的面积.145.李大爷家有一块菜地.(形装如图,单位米)左边的长方形地里种的是圆白菜,右边的梯形地里种的是茄子.(1)每棵圆白菜占地0.15平方米,一共可以种多少棵?(2)茄子地一共有多少平方米?(3)你还能提出什么问题?并解答?146.如图,长方形ABCD的面积是120平方厘米,E是BC边的三等分点,F是DC边的二等分点.求阴影部分的面积.147. 堆一个雪人大约需要清扫10.5平方米的积雪.图中阴影部分的积雪能堆多少雪人呢?148. 求下面图形阴影部分的面积.(单位:厘米)149. 求出阴影部分的周长和面积.(单位:厘米)150.已知正方形ABCD的面积为160cm2,E、F分别为边BC、DC 的中点,求阴影三角形的面积.。
《组合图形的面积》 优秀课件 (共31张PPT)

思考题:计算下面图形的面 积,你能想出不同的解法吗?
单位:米
6 10
5
12 S = S梯形 + S长方形
=(10+5)×6÷2+6×5
思考题:计算下面图形的面 积,你能想出不同的解法吗?
单位:米
6 10
5
12 S = S三角形 + S长方形
=5×6÷2+12×5
思考题:计算下面图形的面 积,你能想出不同的解法吗?
要计算下图的面积,你认为哪种方法是对 的?为什么?(单位:厘米)
8
5
向下
10 ①10×8-5×4
②8×5+5×4
4
③(8+4)×5÷2+(10+5)×4÷2
8
10 ①10×8-5×4
5 4
8
5
10 5
4
②8×5+5×4
③(8+4)×5÷2+(10+5)×4÷2
8
5
45
10
4
这是我们少先队的中队旗,怎样算 出它的面积。(你能想出不同的方法 吗?)
15、最终你相信什么就能成为什么。因为世界上最可怕的二个词,一个叫执着,一个叫认真,认真的人改变自己,执着的人改变命运。只要在路上,就没有到不了的地方。 16、你若坚持,定会发光,时间是所向披靡的武器,它能集腋成裘,也能聚沙成塔,将人生的不可能都变成可能。 17、人生,就要活得漂亮,走得铿锵。自己不奋斗,终归是摆设。无论你是谁,宁可做拼搏的失败者
答:它的面积是30平方米。
例4 右图表示的是一间房子
侧面墙的形状。它的面积是 多少平方米?
2米
5 米
5×2÷2+5×5÷2×2 =5+25 =30(平方米)5米Biblioteka 答:它的面积是30平方米。
冀教版四年级数学下册期末《认识平行四边形、梯形和组合图形》专项精选试卷 附答案

冀教版四年级数学下册6.认识平行四边形、梯形和组合图形一、填空。
(每空2分,共26分)1.一个四边形,如果有两组对边分别平行,那么这个四边形是( ),只有一组对边平行的四边形是( )。
2.如图,平行四边形ABCD中,CD边上的高为( ) 厘米,BC边上的高为( )厘米。
3.四边形ABCD为平行四边形。
(1)∠C=( ),∠D=( )。
(2)平行四边形ABCD的周长为( )厘米。
4.观察下面的图形,四边形①一定是( ),四边形②可能是( ),也可能是( )。
5.两个完全相同的直角梯形可以拼成的四边形是( )、( )、( )。
二、选择。
(每小题4分,共16分)1.一个梯形中最多有( )个直角。
A.0B.1C.2D.32.平行四边形有( )条高。
A.1B. 2C.4D.无数3.工人叔叔把一块长方形木头锯掉了一块,下面图形中( )是锯掉的那块。
4.把一个平行四边形任意分割成两个梯形,这两个梯形的( )总相等。
A.高B.周长C.面积D.以上均不对三、按要求做题。
(共18分)1.画出下面图形指定底边上的高。
(9分)2.在下面图形中分别画出一条线段,按要求分一分。
(9分)四、解决问题。
(共40分)1.一个平行四边形的一条边长15厘米,它的邻边比它短3厘米,这个平行四边形的周长是多少厘米?(8分)2.动物园有一块平行四边形的区域(如图),相邻两条边的长分别是 50米、30米。
工作人员将这块区域的周围用围栏围上,然后用围栏将这块区域分成一块三角形的区域和一块等腰梯形的区域,分别用来饲养不同的鸟类。
工作人员共用了多少米的围栏?(8分)3.一个梯形的上底是15厘米,如果将这个梯形的上底向一端延长6厘米,那么这个梯形就变成了一个正方形,这个梯形的下底和高分别是多少厘米? (提示:可以先画示意图再解答哦!)(8分)4.装修师傅准备在一楼的楼梯台阶上涂油漆(如图),涂油漆的面积是多少平方米?(8分)5.如图所示,这是步行街最西边一个门市的地基平面图,请你画一画,分一分,并求出地基的周长和面积各是多少。
苏教版五年级上册数学组合图形专项试卷(共9页)

苏教版五年级上册数学组合图形专项试卷(共9页)-本页仅作为预览文档封面,使用时请删除本页-五年级数学(上册):《组合图形的面积》试题1、求图形的面积(单位:厘米)2、校园里有两块花圃(如图),你能计算出它们的面积吗(单位:m)3、下图直角梯形的面积是49平方分米,求阴影部分的面积。
4、图中梯形中空白部分是5、阴影部分面积是40平方米,求空白部分面积。
(单位:米)6、如图,平行四边形面积240平方厘米,求阴影部分面积。
7、下图ABCD是梯形,它的面积是140平方厘米,已知AB=15厘米,DC=5厘米。
求阴影部分的面积。
8、求下图阴影部分的面积(单位:厘米)9、求梯形的面积。
(单位:厘米)10、如图,已知梯形ABCD的面积为平方厘米,BE长7厘米,EC长4厘米,求平行四边形ABED的面积。
多边形的面积应用题【例1】一个长方形长是18厘米宽是长的一半多2厘米;求这个长方形面积和周长分别是多少?【例2】一个长方形是由两个大小相等的正方形拼成的正方形的边长是4厘米求这个长方形的面积是多少?【例3】一个正方形纸条周长是64厘米把这个正方形对折变成两个大小相同的长方形求这两个【例4】用篱笆围成一个梯形养鸡场(如图),其中一边利用房屋墙壁。
已知篱笆长80m,求养鸡场的占地面积。
【例5】一个梯形的下底的长是上底的3倍,把上底延长8厘米,组成一个面积是288平方厘米的平行四边形。
原来梯形的面积是多少平方厘米?【例6】有一块青菜地,中间是有两个小池塘,如右图,平均每平方米菜地能生产出8千克的青【例7】在上面的梯形中,剪去一最大的三角形,剩下的面积是多少,有几种剪法6cm5cm8cm巩固练习1、一个梯形,下底长14厘米,高12厘米,如果下底减少6厘米,它就成为一个平行四边形。
梯形的面积是多少?2、有一块平行四边形的麦田,底275米,高60米,共收小麦吨。
这块麦田有多少公顷平均每公顷收小麦多少吨3、一堆水泥电线杆堆成一个梯形,最上层有4根,最下层有12根,一共有5层,2堆这样的电线杆一共有多少根?4、刘店乡有一块长方形的牧地,长是宽的2倍,一辆汽车以每小时36千米的速度绕牧场一周需要小时,这个牧场的面积是多少平方千米?5、一个三角形的底长3米,如果底延长1米,那么三角形的面积就增加平方米,原来三角形的面积是多少平方米?五、计算下面各图的面积。
北师大版五年级数学上册期末复习专题组合图形的面积练习(含答案)

北师大版五年级数学上册期末复习专题组合图形的面积【知识点归纳】 方法:①“割法”:观察图形,把图形进行分割成容易求得的图形,再进行相加减.②“补法”:观察图形,给图形补上一部分,形成一个容易求得的图形,再进行相加减. ③“割补结合”:观察图形,把图形分割,再进行移补,形成一个容易求得的图形. 【典例分析】例1:求图中阴影部分的面积.(单位:厘米)分析:根据图所示,可把组合图形分成一个直角梯形和一个41圆,阴影部分的面积等于梯形的面积减去41圆的面积再加上41圆的面积减去三角形面积的差,列式解答即可得到答案. 解:[(5+8+5)×5÷2-41×3.14×52]+(41×3.14×52-5×5÷2), =[18×5÷2-0.785×25]+(0.785×25-25÷2), =[90÷2-19.625]+(19.625-12.5), =[45-19.625]+7.125, =25.375+7.125,=32.5(平方厘米);答:阴影部分的面积为32.5平方厘米.点评:此题主要考查的是梯形的面积公式(上底+下底)×高÷2、三角形的面积公式底×高÷2和圆的面积公式S=πr 2的应用.同步测试一.选择题(共10小题)1.已知长方形和正方形的面积相等,阴影部分A和B的面积不相等是()A.B.C.D.2.如图是一个直角梯形,图中阴影部分面积是100平方厘米,空白部分面积是()平方厘米.A.140 B.120 C.100 D.703.如图中阴影部分的面积是60平方厘米,空白部分的面积是()平方厘米.A.12 B.30 C.60 D.无法判断4.下面三个完全一样的直角梯形中,阴影部分的面积()A.甲最大B.乙最大C.丙最大D.一样大5.在图的平行四边形中,E、F把AB边分成了相等的三段,平行四边形的面积是48平方厘米,阴影三角形的面积是()A.8平方厘米B.12平方厘米C.16平方厘米D.24平方厘米6.如图,平行四边形的面积是24cm2,则阴影部分的面积是()A.2cm2B.4cm2C.10cm2D.12cm27.两个完全一样的正方形,如果①号图形阴影部分的面积是10平方厘米,那么②号图形阴影部分的面积是()平方厘米.A.30 B.25 C.20 D.108.下面两个是完全一样的平行四边形,涂色部分的面积()A.甲大B.乙大C.一样大9.如图中,阴影部分面积与三角形()的面积相等.A.BCD B.BFC C.BCE10.比较下面两个图形,说法正确的是()A.甲、乙的面积相等,周长也相等B.甲、乙的面积相等,但甲的周长长C.甲、乙的周长相等,但乙的面积大D.甲、乙的面积相等,它们周长不一定相等二.填空题(共8小题)11.如图(单位:dm),半圆是长方形内最大的半圆,则这个长方形的面积是dm2.12.如图的面积是平方厘米.13.如果用1厘米表示如图小方格的边长,那么阴影部分的面积是平方厘米.14.如图,平行四边形的面积是20cm2,那么三角形的高是cm,面积是cm2.15.图中四边形的面积是平方厘米.16.如图,阴影部分是面积是平方厘米.(π取3.14)17.某正方形园地是由边长为1的四个小正方形组成的,现要在园地上建一个花坛(阴影部分)使花坛面积是园地面积的一半,以下图中设计不合要求的是.18.如图是一块长方形ABCD的场地,长AB=102m,宽AD=51m,从A、B两处入口的中路宽都为1m,两小路汇合处路宽为2m,其余部分种植草坪,则草坪面积为.(A)5050m2(B)4900m2(C)5000m2(D)4998m2三.判断题(共5小题)19.图中阴影部分的面积比半圆大..(判断对错)20.如图所示,梯形的上底长等于下底长的一半,空白面积也等于阴影部分面积的一半.(判断对错)21.图中阴影部分的面积为24cm2.(判断对错)22.如图中阴影部分的面积是14平方厘米.(判断对错)23.计算组合图形的面积时,可以把组合图形分成几个简单的图形,然后再进行计算..(判断对错)四.计算题(共2小题)24.求阴影部分的面积.(单位:cm)25.计算下面图形的面积.五.解答题(共3小题)26.下面是一个菜园的平面图,算一算这个菜园的面积是多少平方米.27.如图,在平行四边形ABCD中,BC长10厘米,直角三角形BCE的直角边EC长8厘米,已知两块阴影部分的面积和比三角形EFG的面积大10平方厘米,求CF的长.28.李大爷家有一块菜地.(形状如图,单位米)长方形地里种的是圆白菜,右边的梯形地里种的是茄子.(1)每棵圆白菜占地0.15平方米,一共可以种几棵?(2)茄子地一共有多少平方米?参考答案与试题解析一.选择题(共10小题)1.【分析】我们通过对每个选项给出的图形计算可知,A选项中阴影部分A的面积等于正方形的面积的,B的面积等于长方形面积的,而长方形和正方形的面积相等;所以阴影部分A和B的面积;选项B阴影部分A和B的面积分别等于长方形的面积和正方形的面积减去空白的正方形的面积,所以相等;选项C阴影部分A等于长方形的面积减去大的空白部分长方形的面积,B的面积得出正方形减去空白部分小长方形的面积,所以不相等.选项D阴影部分A和B的面积分别等于长方形的面积和正方形的面积减去空白的三角形的面积,所以相等;据此解答.解:A选项中阴影部分A的面积等于正方形的面积的,B的面积等于长方形面积的,而长方形和正方形的面积相等;所以阴影部分A和B的面积;选项B阴影部分A和B的面积分别等于长方形的面积和正方形的面积减去空白的正方形的面积,所以相等;选项C阴影部分A等于长方形的面积减去大的空白部分长方形的面积,B的面积得出正方形减去空白部分小长方形的面积,所以不相等.选项D阴影部分A和B的面积分别等于长方形的面积和正方形的面积减去空白的三角形的面积,所以相等;故选:C.【点评】本题考查了学生的观察能力,考查了学生灵活解决问题的能力.2.【分析】空白三角形、阴影三角形,以及梯形的高相等,根据三角形的面积=底×高÷2可知,先用阴影三角形的面积乘上2,再除以它的底20厘米,即可求出它的高,再用空白三角形的底乘上高,再除以2,即可求出空白部分的面积.解:100÷20×2=5×2=10(厘米)14×10÷2=140÷2=70(平方厘米)答:空白部分的面积是70平方厘米.故选:D.【点评】本题考查了三角形的面积公式,三角形的面积=底×高÷2,关键是得出两个三角形的高相等.3.【分析】先利用三角形的面积公式S=ah÷2计算出三角形的高,也就等于知道了空白部分的高,从而利用三角形的面积公式进行解答即可.解:60×2÷20=120÷20=6(厘米)10×6÷2=30(平方厘米)答:空白部分的面积是30平方厘米.故选:B.【点评】此题主要考查三角形的面积公式的灵活应用.4.【分析】这几个直角梯形中,阴影部分总面积都是以梯形的下底为底,以梯形的高为高的三角形的面积,由此即可判断它们面积的大小.解:三图中,阴影部分总面积都是以梯形的下底为底,以梯形的高为高的三角形的面积,因为三个梯形完全相同,由此可得:阴影部分的面积都相等.故选:D.【点评】此题主要考查等底等高的三角形面积都相等,据图即可以作出判断.5.【分析】根据图得出阴影部分的三角形,与平行四边形的等高,底是平行四边形底的,又三角形的面积是与它底等高平行四边形面积的一半,所以三角形的面积是平行四边形面积的×=,然后解答即可.解:因为E、F把AB边分成了相等的三段,所以阴影部分三角形的底是平行四边形底的,所以三角形的面积是平行四边形面积的×=,阴影三角形的面积是48×=8(平方厘米).答:阴影三角形的面积是8平方厘米.故选:A.【点评】本题关键理解以三角形的面积是与它底等高平行四边形面积的一半.6.【分析】首先根据平行四边形的面积公式:s=ah,那么a=s÷h,已知平行四边形的面积和高求出平行四边形的底,然后用平行四边形的底减去5就是阴影部分三角形的底,然后根据三角形的面积公式:s=ah÷2,把数据代入公式解答.解:24÷4=6(厘米),(6﹣5)×4÷2=1×4÷2=2(平方厘米),答:阴影部分的面积是2平方厘米.故选:A.【点评】此题主要考查平行四边形的面积公式、三角形的面积公式的灵活运用,关键是熟记公式.7.【分析】由正方形的特征可知,①号图中阴影部分的面积等于正方形面积的,因此正方形的面积就等于图①中阴影部分面积的4倍,已知①号图形阴影部分的面积是10平方厘米,用10乘上4即可得到正方形的面积;而②号图中阴影部分的面积是正方形面积的,因此再用正方形的面积乘上即可得到②号图形阴影部分的面积,据此解答.解:由分析知②号图形阴影部分的面积是:10×4×=40×=20(平方厘米);答:②号图形阴影部分的面积是20平方厘米.故选:C.【点评】解决本题的关键是明确各个图中阴影部分的面积和正方形的面积之间的数量关系.8.【分析】甲图中阴影部分的面积可以看作与平行四边形等底等高的三角形,三角形的面积是平行四边形的面积的一半,乙图中的阴影部分面积也可以看作与平行四边形等底等高的三角形,三角形的面积是平行四边形的面积的一半,平行四边形又是完全一样,所以阴影部分的三角形的面积也是一样据此判断.解:甲图中阴影部分的面积和乙图中的阴影部分面积都可以看作与平行四边形等底等高的三角形,平行四边形的面积一样,它们的面积也一样大.故选:C.【点评】此题主要考查等底等高的三角形面积相等及平行四边形的特点.据图即可以作出判断.9.【分析】三角形的面积S=ah,只要是三角形的底和高相等,则它们的面积相等,据此即可得解.解:由图意可知:图中3个三角形的底是相等的,要想面积与阴影部分的三角形面积相等,那么如果高与阴影部分的三角形的高相等即可;再根据平行线间的距离相等,所以△BCE的面积与阴影部分的面积相等.故选:C.【点评】解答此题的主要依据是:等底等高的三角形的面积相等.10.【分析】由图形可知,甲的面积小于长方形面积的一半,乙的面积大于长方形面积的一半,所以乙的面积大于甲的面积;因为甲的周长=长方形的两条邻边的和+中间的曲线的长,乙的周长=长方形的两条邻边和+中间的曲线的长,进行解答继而得出结论.解:因为甲的面积小于长方形面积的一半,乙的面积大于长方形面积的一半,所以甲的面积小于乙的面积;甲的周长=长方形的两条邻边的和+中间的曲线的长,乙的周长=长方形的两条邻边的和+中间的曲线的长,所以甲的周长等于乙的周长;故选:C.【点评】解答此题应根据长方形的特征,并结合周长的计算方法进行解答.二.填空题(共8小题)11.【分析】观察图形可知,长方形的长等于圆的直径是8分米,宽是半圆的半径是8÷2=4分米,据此利用长方形的面积=长×宽计算即可解答问题.解:8÷2=4(分米)8×4=32(平方分米)答:这个长方形的面积是32平方分米.故答案为:32.【点评】掌握长方形内的半圆的特征得出长方形的长与宽的值,是解决本题的关键.12.【分析】根据图示,这个组合图形可以看作由一个梯形和一个长方形拼成的图形,利用长方形和梯形面积公式求解即可.解:如图:该图形可看作一个梯形和一个长方形拼成的图形,其面积为:(12+16)×(10﹣5)÷2+16×5=28×5÷2+80=70+80=150(平方厘米)答:这个图形的面积为150平方厘米.故答案为:150平方厘米.【点评】此题主要考查的是梯形的面积公式:(上底+下底)×高÷2、长方形面积公式:长×宽的应用.13.【分析】右边图形中阴影部分的面积=最上面一行中的2个方格的面积+下面图形中的长方形的面积﹣1个方格的面积,据此即可求解.解:2+4×5﹣1=2+20﹣1=21(平方厘米)答:阴影部分的面积是21平方厘米.故答案为:21.【点评】解答此题的关键是:看利用小方格的边长计算简单还是利用小正方形的面积计算简单,要灵活应对.14.【分析】根据平行四边形的面积变形公式h=S÷a,可求平行四边形的高,根据三角形面积公式S=ah可求三角形的面积;依此即可求解.解:高:20÷5=4(厘米)三角形的面积:3×4÷2=12÷2=6(平方厘米)故答案为:4,6.【点评】本题考查了学生求平行四边形、三角形面积的知识,关键是求出平行四边形的高.15.【分析】根据图意可把这个不规则的四边形,看作是2个直角三角形面积的和来进行解答,然后再根据三角形的面积公式进行计算.解:11×6÷2=66÷2=33(平方厘米)答:这个四边形的面积是33平方厘米.故答案为:33.【点评】本题属于求组合图形面积的问题,这种类型的题目主要明确组合图形是由哪些基本的图形构成的,然后看是求几种图形的面积和还是求面积差,然后根据面积公式解答即可.16.【分析】观察图示可知,阴影部分的面积=梯形面积﹣圆面积的,代入数据,解答即可.解:(4+10)×4÷2﹣3.14×42×=28﹣12.56=15.44(平方厘米)答:阴影部分是面积是15.44平方厘米.故答案为:15.44.【点评】本题属于求组合图形面积的问题,这种类型的题目主要明确组合图形是由哪些基本的图形构成的,然后看是求几种图形的面积和还是求面积差,然后根据面积公式解答即可.17.【分析】运用面积公式、割补法求阴影部分面积,再与题目的要求比较.解:花坛面积为4m2,一半为2m2,A、阴影部分面积为2×2÷2=2(m2)B、阴影部分面积为1×1+1×1÷2+1×2÷2=2.5(m2)不符合要求;C、阴影部分面积为1×1÷2×4=2(m2)D、把图中上面两个扇形移下来,刚回拼成两个小正方形,面积为2m2;故答案为:B.【点评】本题考查了阴影部分图形面积的计算方法,即规则图形用面积公式求,不规则图形用割补法求解.18.【分析】本题要看图解答.从图中可以看出剩余部分的草坪正好可以拼成一个长方形,然后根据题意求出长和宽,最后可求出面积.解:由图可知:矩形ABCD中去掉小路后,草坪正好可以拼成一个新的矩形,且它的长为:(102﹣2)米,宽为(51﹣1)米.所以草坪的面积=长×宽=(102﹣2)×(51﹣1)=100×50=5000(米2).故答案为:C.【点评】此题考查了生活中的平移,根据图形得出草坪正好可以拼成一个长方形是解题关键.三.判断题(共5小题)19.【分析】分别计算出阴影部分和半圆的面积,再判断.解:设正方形的边长为a,则:阴影部分面积=πa2﹣=a2;半圆的面积为:π×═a2;所以阴影部分面积等于半圆的面积,原说法错误.故答案为:错误.【点评】解决本题的关键是计算出组合图形中相关部分的面积,再比较.20.【分析】分别运用梯形的面积公式和三角形的面积公式进行列式比较就可做出判断.解:设梯形的上底为a,高为h,则下底为2a;梯形的面积=(a+2a)×h÷2=3ah÷2=ah;空白三角形的面积=a×h÷2=ah;则阴影部分的面积=梯形的面积﹣空白三角形的面积=ah﹣ah=ah;由此可以看出:空白面积等于阴影部分面积的一半.故此题是正确的.故答案为:√.【点评】此题主要考查三角形和梯形的面积公式.21.【分析】观察图形可知,可把右侧阴影部分割补到左侧对称的位置,如下图所示:会发现阴影部分是一个上底为4cm、下底为8cm,高为4cm的梯形,利用梯形的面积公式代入数据计算即可.解:由分析知,阴影部分的面积等于上图所示梯形的面积,梯形的上底为:8﹣8÷2=8﹣4=4(cm),高为:8÷2=4(cm),所以面积为:(4+8)×4÷2=12×4÷2=48÷2=24(cm2);答:图中阴影部分的面积为24cm2.所以题干说法正确.故答案为:√.【点评】本题考查了求组合图形的面积,组合图形的面积一般都是转化为规则图形的面积的和或差,再利用规则图形的面积公式进行计算.22.【分析】把这个图形分成三部分计算,上面是底4厘米、高2厘米的三角形,中间是上底2厘米、下底4厘米、高1厘米的梯形,下面是长与宽分别是3厘米、2厘米的长方形,据此计算出它们的面积,再加起来即可判断.解:4×2÷2+(2+4)×1÷2+2×3=4+3+6=13(平方厘米)答:阴影部分的面积是13平方厘米.故答案为:×.【点评】此题考查了不规则图形的周长与面积的计算方法,一般都是转化到规则图形中利用面积公式计算解答.23.【分析】根据组合图形的面积的计算方法可知:计算组合图形的面积时,可以把组合图形分成几个简单的图形,然后再利用规则图形的面积公式进行计算,据此即可判断.解:计算组合图形的面积时,可以把组合图形分成几个简单的图形,然后再根据简单图形的计算公式进行计算.故答案为:√.【点评】此题考查组合图形的面积的计算方法:关键是把组合图形的面积转化为我们学过的图形的面积,再利用相应的面积公式与基本的数量关系解决问题.四.计算题(共2小题)24.【分析】(1)通过旋转平移把阴影部分转化为一个半圆,根据圆的面积公式:S=πr2,把数据代入公式解答.(2)阴影部分的面积等于圆的面积减去正方形的面积,根据圆的面积公式:S=πr2,三角形的面积公式:S=ah÷2,把数据代入公式解答.解:(1)3.14×42÷2=3.14×16÷2=50.24÷2=25.12(平方厘米);答:阴影部分的面积是25.12平方厘米.(2)3.14×(10÷2)2﹣10×(10÷2)÷2×2=3.14×25﹣10×5÷2×2=78.5﹣50=28.5(平方厘米);答:阴影部分的面积是28.5平方厘米.【点评】解答求阴影部分的面积关键是观察分析图形是由哪几部分组成的,是各部分的面积和、还是求各部分的面积差,再根据相应的面积公式解答.25.【分析】组合图形的面积等于底为35米,高为12米的三角形面积加上底为50米,高为33米的平行四边形的面积;根据三角形和梯形面积公式解答即可.解:33×50+35×12÷2=1650+210=1860(平方米)答:图形的面积是1860平方米.【点评】本题属于求组合图形面积的问题,这种类型的题目主要明确组合图形是由哪些基本的图形构成的,然后看是求几种图形的面积和还是求面积差,然后根据面积公式解答即可.五.解答题(共3小题)26.【分析】本题可用长80米、宽40米的长方形面积减去边长10米的正方形面积求出菜园的面积,长方形面积=长×宽,正方形面积=边长×边长.解:80×40﹣10×10=3200﹣100=3100(平方米)答:这个菜园的面积是3100平方米.【点评】本题主要考查了学生利用长方形的面积公式解题的能力,找出正确的计算组合图形的面积的方法是解题关键.27.【分析】根据题意:如图,已知两块阴影部分的面积和比三角形EFG的面积大10平方厘米,则三角形EFG的面积+10平方厘米+梯形BCFG的面积=平行四边形ABCD的面积,又因为三角形EFG的面积+梯形BCFG的面积=三角形BCF的面积,所以三角形BCF的面积+10平方厘米=平行四边形ABCD的面积;CF是平行四边形的高,根据平行四边形的面积=底×高,则高CF=平行四边形的面积÷底即可.解:(10×8÷2+10)÷10=(40+10)÷10=50÷10=5(厘米)答:CF长5厘米.【点评】解决此题的关键用直角三角形的面积+10平方厘米代替平行四边形的面积,根据面积公式求出CF.28.【分析】(1)先利用长方形的面积公式S=ab计算出圆白菜地的面积,再用它的面积除以每棵圆白菜的占地面积,即可得解;(2)依据梯形的面积公式S=(a+b)×h÷2,代入数据即可求解.解:(1)8×4.5÷0.15=36÷0.15=240(棵)答:一共可以种240棵.(2)(4.8+10.5﹣4.5)×(8﹣2)÷2=10.8×6÷2=32.4(平方米)答:茄子地一共有32.4平方米.【点评】此题主要考查长方形和梯形的面积公式的灵活应用.。
(完整版)五年级组合图形面积练习题

(完整版)五年级组合图形⾯积练习题姓名1图形名称⾯积公式(⽂字) ⾯积公式(字母) 长⽅形正⽅形平⾏四边形三⾓形梯形2、求下⾯图形的⾯积。
(单位:cm )154、计算下⾯图形中阴影部分的⾯积。
30dm12dm 5m25dm 5m3m2010643482 1032 20125、求下列阴影部分的⾯积。
①②已知S平=48dm2,求S阴。
③已知:阴影部分的⾯积为24 ④求S阴。
平⽅厘⽶,求梯形的⾯积。
6、求下⾯各图形的⾯积。
(单位:分⽶)13cm16cm8dm3dm12cm7cm4dm8dm7、“实践操作”显⾝⼿:10分⼀、已知右⾯的两个正⽅形边长分别为6分⽶和4分⽶,求图中阴影部分的⾯积。
⼆、右图是两个相同的直⾓三⾓形叠在⼀起,求阴影部分的⾯积。
(单位:厘⽶)三、如图,这个长⽅形的长是9厘⽶,宽是8厘⽶,A 和B 是宽的中点,求长⽅形内阴影部分的⾯积。
四、在右图中,三⾓形EDF 的⾯积⽐三⾓形ABE 的⾯积⼤6平⽅厘⽶,已知长⽅形ABDC 的长和宽分别为6厘⽶、4厘⽶,DF 的长是多少厘⽶?16cm12cm14cm 24m10m8m1、求下⾯图形中阴影部分的⾯积。
2、求下⾯图形的⾯积。
五、右图是⼀块长⽅形公园绿地,绿地长24⽶,宽16⽶,中间有⼀条宽为2⽶的道路,求草地(阴影部分)的⾯积。
六、如图,三⾓形ABC的⾯积是24平⽅厘⽶,且DC=2AD,E、F分别是AF、BC的中点,那么阴影部分的⾯积是多少?七、如图,三⾓形ABC的⾯积是90平⽅厘⽶,EF平⾏于BC,AB=3AE,那么三⾓形甲、⼄、丙的⾯积各是多少平⽅厘⽶?⼋、如图长⽅形,长18厘⽶,宽12厘⽶,AE、AF两条线段把长⽅形⾯积三等分,求三⾓形AEF的⾯积。
九如图,ABCD是⼀个长12厘⽶,宽5厘⽶的长⽅形,求阴影部分三⾓形ACE的⾯积。
⼗已知正⽅形甲的边长是8厘⽶,正⽅形⼄的⾯积是36平⽅厘⽶,那么图中阴影部分的⾯积是多少?。
【小升初专项训练】01 组合图形的计数

第1讲组合图形的计数第一关【知识点】1.组合图形的概念:圆,三角形,正多边形,梯形,平行四边形为基本图形其余的为组合图形,可以用辅助线分解为基本图.2.组合图形的计数实质上就是分类数图形,解决方法是:(1)合理进行分类.(2)利用排列组合的有关公式进行每一个类的数量计算.(3)将所有的类的数量进行相加.(4)仔细检查,防止遗漏.【例1】图中有多少个三角形?【答案】3【例2】数一数,图中一共有多少个三角形?【答案】13【例3】数一数,图中一共有多少个三角形?【答案】27【例4】数一数,图中一共有多少个三角形?【答案】48【例5】数一数,图中一共有多少个三角形?【答案】9【例6】数一数,图中一共有多少个三角形?【答案】8【例7】数一数,图中一共有多少个三角形?【答案】8【例8】数一数,图中一共有多少个三角形?【答案】20;24;24【例9】数一数,图中一共有多少个三角形?【答案】35【例10】数一数,图中一共有多少个三角形?【答案】67【例11】数一数,图中一共有多少个三角形?【答案】11【例12】数一数,图中一共有多少个三角形?【答案】40【例13】图中,有多少个三角形?【答案】16【例14】数一数,图中一共有多少个三角形?【答案】8【例15】数一数,图中一共有多少个三角形?【答案】13【例16】数一数,图中一共有多少个三角形?【答案】12【例17】数一数,图中一共有多少个三角形?【答案】11【例18】数一数,图中一共有多少个三角形?【答案】20【例19】数一数,图中一共有多少个三角形?【答案】12【例20】如图中有多少个三角形?【答案】27【例21】如图中有多少个三角形?【答案】17【例22】如图中有多少个三角形?【答案】10【例23】数一数,图中有多少个三角形?【答案】27【例24】图中有多少个三角形?【答案】14【例25】图中有多少个三角形?【答案】11【例26】数一数,图中共有多少个三角形?【答案】15【例27】如图是一些等腰直角三角形组成的图形,图中一共有多少个三角形?【答案】23【例28】如图中,一共有多少个三角板?【答案】12【例29】如图中共能数出多少个三角形?【答案】24【例30】如图中共能数出多少个三角形?【答案】24【例31】在△ABC中,D1、D2、D3为AB边的内分点,E1、E2、E3为AC边的内分点,那么图中有 多少个三角形?【答案】64【例32】如图中共能数出多少个三角形?【答案】11【例33】如图中,共有多少个三角形?【答案】10【例34】数一数,图中共有多少个三角形?【答案】10【例35】数一数,图中共有多少个三角形?【答案】12【例36】数一数,图中共有多少个三角形?【答案】16【例37】数一数,图中共有多少个三角形?【答案】18【例38】数一数,图中共有多少个三角形?【答案】30【例39】数一数,图中共有多少个三角形?【答案】28【例40】如图中,一共有多少个三角形?【答案】32【例41】如图中,一共有多少个三角形?【答案】72【例42】如图中,一共有多少个三角形?【答案】22【例43】图中共有多少个三角形?【答案】60【例44】下图中共有多少个三角形?【答案】8【例45】下图中共有多少个三角形?【答案】24【例46】下图中共有多少个三角形?【答案】34【例47】下图中共有多少个三角形?【答案】35【例48】下图中共有多少个三角形?【答案】16【例49】下图中共有多少个三角形?【答案】30【例50】下图中共有多少个三角形?【答案】22【例51】下图中共有多少个三角形?【答案】62【例52】下图中共有多少个三角形?【答案】10【例53】下图中共有多少个三角形?【答案】35【例54】下图中共有多少个三角形?【答案】32【例55】下图“七角星”中共有多少个三角形?【答案】35【例56】下图中共有多少个三角形?【答案】20【例57】下图中共有多少个三角形?【答案】40【例58】如图,图中3个大三角形都是等边三角形,则图中共有多少个三角形?【答案】30【例59】如图中有多少个三角形?【答案】76【例60】如图中有多少个三角形?【答案】76【例61】如图中,包含“”的三角形有多少个?【答案】4【例62】如图,数一数其中共有多少个包含“☆”的三角形?【答案】8【例63】如图是由18个大小相同的小正三角形拼成的四边形.其中某些相邻的小正三角形可以拼成较大的正三角形若干个.那么,图中包含“*”号的大、小正三角形一共有多少个?【答案】6【例64】如图,图中包含“★”的大、小三角形共有多少个?【答案】12【例65】数一数如图中共有多少个包含“﹡”号的三角形?【答案】6【例66】图中,共有多少个直角三角形?【答案】16【例67】图中,共有多少个等边三角形?【答案】14【例68】数一数,图中一共有多少个正三角形?【答案】44【例69】如图,四边形ABCD与CEFG是边长相等的正方形,且B、C、G在一条直线上,则图中有多少个等腰直角三角形?【答案】22【例70】如图,连接一个正六边形的各顶点,问图中共有多少个等腰三角形(包括等边三角形)?【答案】38【例71】圆周上有8个点,把它们两两相连,若任意三条线都不交于一点,那么图中顶点全在圆内的三角形共有多少个?【答案】56【例72】如图,有这样的两条线,请问从这5个点中任选三个点可以构成多少个不同的三角形?【答案】8【例73】木板上钉有五颗钉子(如图所示,排成两行),用橡皮筋可以套出多少个三角形?【答案】9【例74】如图,木板上有10根钉子,任意相邻的两根钉子距离都相等,以这些钉子为顶点,用橡皮筋可套出多少个正三角形?【答案】13【例75】以平面上4个点为端点连接线段,形成的图形中最多可以有多少个三角形?【答案】8【例76】平面上有四个点,任意三个点都不在﹣条直线上.以这四个点为端点连接六条线段,在所组成的图形中用它们作顶点可以组成多少个三角形?【答案】4【例77】以平面上任意4个点为顶点的三角形中,钝角三角形最多有多少个?【答案】4【例78】从图中两个正方形的7个顶点中选出3个点作为顶点构成三角形,一共可以构成多少个不同的三角形?【答案】32【例79】如图由5个大小相同的正方形构成.以图中12个点为顶点的三角形共有多少个?【答案】200【例80】长方形内有2017个点,连同长方形的4个顶点在内,共有2021个点,任意3个点都不在同一条直线上,以这2021个点中的某三点为顶点,可作出多少个互不重叠的三角形?【答案】4036【例81】如图,是由9个点组成的点阵,那么以图中3个点为顶点的直角三角形有多少个?【答案】44【例82】如图有12个点,相邻两个点之间的距离是1厘米,这些点为顶点可以连成多少个面积为3平方厘米的三角形?【答案】26【例83】如图是由四个边长为1的小正方形组织的图形,图中共有9个格点(格点即为小正方形的顶点).如果以这些格点为顶点,那么一共可组成多少个等腰三角形?【答案】36【例84】如图是由32个面积为1的等边三角形组成的一个大的平行四边形,这个大的平行四边形内部及边上共有25个交叉点.以这些交叉点为顶点,可以连成多少个等边三角形?【答案】28【例85】在一个圆周上均匀分布10个点,以这些点为顶点,可以画出多少个不同的钝角三角形?(补充知识:由直径和圆周上的一点构成的三角形一定是直角三角形,其中直径的边所对的角是直角,所以如果圆周上三点在同一段半圆周上,则这三点构成钝角三角形)【答案】60【例86】用9个钉子钉成相互间隔为l厘米的正方阵(如图).如果用一根橡皮筋将适当的三个钉子连结起来就得到一个三角形,这样得到的三角形中,面积等于1平方厘米的三角形有多少个?【答案】32【例87】如图由4个正六边形组成,每个面积是6,以这4个正六边形的顶点为顶点,可以连接面积为4的等边三角形有多少个?【答案】8【例88】如图,大三角形由9个形状、大小相同的等边三角形组成,共有10个顶点,以这些顶点为顶点构成的三角形中,面积与阴影部分面积相等的三角形共有多少个?【答案】36【例89】如图,一小正方形的边为边向小正方形外作四个正方形,再依次连接几个定点,若图中阴影三角形的面积是S,则面积为2S的三角形有_______个,面积为8S的正方形有_______个【答案】20;1【例90】如图由九个边长为1厘米的正方形组成,在如图中面积为0.5平方厘米的三角形有_______个.面积为1平方厘米的三角形有_______个,面积为1.5平方厘米的三角形有_______个,面积最大的三角形的面积是_______平方厘米.【答案】5;11;2;2.5【例91】在图中填上2条直线,最多能数出多少个三角形?【答案】10【例92】今有甲、乙两个大小相同的正三角形,各画出了一条两边中点的连线,如图,甲、乙位置左右对称,但甲、乙内部所画线段的位置不对称,从图中所示的位置开始,甲向右水平移动,直至两个三角形重叠后在离开.在移动过程中的每个位置,甲与乙所组成的图形中都有若干个三角形,那么三角形个数最多的位置,图形中有多少个三角形?【答案】11【例93】如图,在正方形的内部放入1个点,就可以把原来的正方形分成了4个小三角形;在正方形的内部放入2个点,就可以把原来的正方形分成了6个小三角形.那么如果在正方形的内部放入10个点,最多能把原来的正方形分成了多少个小三角形?【答案】22【例94】在一张三角形纸内任作2009个互不重合的点(所有的点都不在三角形的任意一条边上),以这2009个点和三角形纸的3个顶点为顶点的三角形,最多能剪出多少个?【答案】4019【例95】在三角形ABC中,D是BC的中点,图中面积相等的三角形共有多少对?【答案】6第二关【知识点】【例96】图中一共能数出多少正方形?【答案】26【例97】图中一共能数出多少正方形?【答案】55【例98】图中一共能数出多少正方形?【答案】26【例99】图中一共能数出多少正方形?【答案】23【例100】图中一共能数出多少正方形?【答案】14【例101】.将4×4的大正方形切割为16个1×1的小正方形,擦去其中的两条线段,得到如图所示图形.则图中一共有多少个正方形?【答案】22【例102】图中一共能数出多少正方形?【答案】20【例103】图中一共能数出多少正方形?【答案】13【例104】图中一共能数出多少正方形?【答案】17【例105】图中一共能数出多少正方形?【答案】35【例106】图中一共能数出多少正方形?【答案】46【例107】图中一共能数出多少正方形?【答案】10【例108】图中一共能数出多少正方形?【答案】14【例109】图中共有多少个正方形?【答案】17【例110】数一数,图中共有多少个正方形?【答案】23【例111】数一数,图中共有多少个正方形?【答案】18【例112】数一数,图中共有多少个正方形?【答案】11【例113】数一数,图中共有多少个正方形?【答案】20【例114】数一数,图中共有多少个正方形?【答案】15【例115】数一数,图中共有多少个正方形?【答案】28【例116】如图由相同的正方形和相同的等腰直角三角形构成,求正方形的个数。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
长方形你、正方形、梯形、平行四边形图题 练习一1、求下面图形的面积(单位:m )。
你能想出几种方法。
102、求下面图形的面积。
(单位:cm )153、计算下面图形中阴影部分的面积。
30dm12dm 5m1530 402010643482 1032 20123m25dm 5m4、图中的甲和乙都是正方形,求阴影部分的面积。
(单位:厘米)5、计算下图的面积。
(单位:厘米)6、如图,已知四条线段的长分别是:AB=2厘米,CE=6厘米,CD=5厘米,AF=4厘米,并且有两个直角。
求四边形ABCD的面积。
7、下图是两个相同的直角三角形叠在一起,求阴影部分的面积。
(单位:分米)8、下图是一块长方形草地,长方形的长是16,宽是10,中间有两条道路,一条是长方形,一条是平行四边形,那么,有草部分(阴影部分)的面积有多大?(单位:米)长方形你、正方形、梯形、平行四边形图题练习二1、求图中阴影部分的面积。
2、求图中阴影部分的面积。
3、下图的长方形中,三角形ADE与四边形DEBF和三角形CDF的面积分别相等,求三角形DEF的面积。
4、平等四边形ABCD的边BC长10厘米,直角三角形BCE的直角边EC长8厘米,已知阴影部分的面积比三角形EFG的面积大10平方厘米,求CF的长。
5、图中三角形的高为4,面积为16;长方形的宽为6,长方形的面积是三角形面积的多少倍?6、如图,长方形的长是8,宽是6,A和B是宽的中点,求长方形内阴影部分的面积。
7、如图,BC长为5,求画斜线的两个三角形的面积之和。
8、下图是两个一样的直角三角形重叠在一起,按照图上标出的数,计算阴影部分的面积。
9、下图是一块长方形草地,长方形长为16,宽为12,中间有一条宽为2的道路,求草地(阴影部分)的面积。
长方形你、正方形、梯形、平行四边形图题练习三1、一个正方形,如果它的边长增加5厘米,那么,所成的正方形比原来正方形的面积多95平方厘米。
原来的正方形的面积是多少平方厘米?2、下图中由9个小长方形组成的一个大长方形。
按图中的编号,1号、2号、3号、4号、5号长方形的面积依次为1平方厘米、2平方厘米、3平方厘米、4平方厘米、5平方厘米。
求6号长方形的面积。
3、下图中三角形ABC为等边三角形,D为AB边上的中点。
已知三角形BDE的面积为5平方厘米。
求等边三角形ABC的面积。
4、下图中长方形的长为12厘米,宽为6厘米。
把它的长3等分,宽2等分,然后在长方形内任取一点,把这一点与分点及顶点连结(如图)。
求图中阴影部分的面积。
5、在等腰三角形ABC中,AB的长度是AC的2倍,如果这个等腰三角形中的周长是200厘米,那么,BC长多少厘米?6、一个梯形,它的下底是上底的2倍。
如果上底延长7厘米,就形成一个面积是42平方厘米的平行四边形。
这个梯形的面积是多少平方厘米?7、一个直角梯形的周长是48厘米,两底之和是两腰之和的4倍,一条腰的长度是另一条腰的1.5倍。
还应这个梯形的面积。
8、一个长方形,如果长增加2厘米,宽增加5厘米,那么,面积增加60平方厘米,这时恰好成为一个正方形。
原来长方形的面积是多少平方厘米?9、把一块边长为9.5分米的正方形钢板切割成两条直角边分别为4.5分米的直角三角形小钢板,最多可以切割成多少块?长方形你、正方形、梯形、平行四边形图题练习四1、有四个完全一样的直角三角形,它们的两条直角边分别是7厘米、5厘米。
把它们拼成下左图图的正方形,求大、小两个正方形的面积。
2、下图中,大、小两个正方形对应边的距离均为1厘米。
已知两个正方形之间部分的面积是20平方厘米,求小正方形的面积。
第2题3.求下图中阴影部分的面积。
(单位:厘米)4.上右图中,长方形的周长是多少厘米?(单位:厘米)5.下图中,甲三角形的面积比乙三角形的面积大多少平方厘米?(单位:厘米)6.求图中阴影部分的面积。
(单位:厘米)7.如图,在腰长为10厘米,面积为34平方厘米的等腰三角形的底边上任意取一点,设这个点到两腰的垂线段分别长a厘米和b厘米,那么,a+b的长度是多少厘米?8.一个正方形,面积为18.75平方厘米。
在正方形内有两条平行于对角的线段把正方形分成3等份(如图)。
图中线段AB、CD各长多少厘米?9.如图,在梯形ABCD中,BO的长度等于DO长度的2倍,阴影部分的面积是4平方分米。
求梯形ABCD的面积。
长方形你、正方形、梯形、平行四边形图题练习五1、求面积(单位:厘米)(1)(2)(3)2、如图,已知长方形ABCD的面积是72平方厘米,AC=6厘米,CE=4厘米。
求:三角形BED的面积。
3、如图,正方形ABCE的边长是18厘米,FC=2EF,求三角形FCD的面积。
4、如图,AD=20厘米,AB=12厘米,BC=10厘米,求梯形ABCD的面积。
5、如图,已知:CD=20厘米,AC=10厘米,求:阴影部分的面积。
6、如图,已知:AB=3.5cm,CD=3.2cm,BC=4.48cm,AE垂直于BC,CD垂直于AB,求:AE的长度。
7、如图,已知:四边形ABCD的面积使203平方厘米,DE垂直于AB,∠DBE=45°,ED=14cm。
求:梯形AECD的面积。
8、如图,已知等腰三角形ABC的面积是36平方厘米,D是AC中点,AE是高。
求:三角形DEC的面积。
9、如图,已知:三角形ACD的面积是1400平方厘米,AB=20厘米,CD=56厘米,求:三角形ADB的面积。
长方形你、正方形、梯形、平行四边形图题练习六1、如图,AB=20厘米,AC=18厘米,HD=8厘米,求阴影部分的面积。
2、如图,已知:AE=EF=FC=10厘米,AB垂直于BC,AB=24厘米,BC=24厘米,求三角形EBF的面积。
3、如图,大正方形的边长是8厘米,小正方形的边长是4厘米,求阴影部分的面积。
4、如图,正方形的周长是60厘米,DF=2FC,求三角形DFE的面积。
5、如图,平行四边形中,一组平行线之间的距离是8厘米,它的面积是多少平方厘米?周长是多少厘米?6、求图中平行四边形的面积。
(单位:厘米)7、如图,求阴影部分的面积。
(单位:厘米)8、如图,求阴影部分的面积。
(单位:厘米)9、如图,长方形ABCD中,AE=DE,DF=FC,EG是GF的2倍,AB=6厘米,BC=10厘米。
求阴影部分的面积。
长方形你、正方形、梯形、平行四边形图题练习七1、如图,长方形AECD中,AD=10厘米,CD=12厘米,三角形CFB的面积是24平方厘米。
求阴影部分的面积。
2、如图,正方形ABCD中,BD分成三等份,没等份长是1厘米,AF平行EC。
求正方形ABCD的面积。
3、如图,AB=3厘米,DC=1.8厘米,求阴影部分的面积。
4、如图,三角形ABC的面积是16平方厘米,它的面积是平行四边形CDEF的2倍,求三角形BEF的面积。
5、如图,正方形ABCD的周长是48厘米,AE=2ED,CD=3DF,求阴影部分的面积。
6、如图,AECD是平行四边形,DC=6厘米,AB=10厘米,四边形AEFD的面积比三角形EFD的面积多12平方厘米。
求三角形ABD的面积。
7、如图,长方形长和宽分别为30厘米和20厘米,A面积比B面积小360平方厘米,求A的面积。
8、长方形ABCD中,AD=10厘米,CD=12厘米,S△CFB=24平方厘米,求阴影部分的面积。
9、如图,正方形ABCD的边长是5厘米,CG是2厘米,求梯形EDGF的面积。
长方形你、正方形、梯形、平行四边形图题练习八1、如图,梯形ABCD的面积是45平方厘米,AC=AD,AC=10厘米,AF=2厘米,求阴影部分的面积。
2、如图,DC是BD长度的2倍,三角形ABC的面积是48平方厘米,AE=11厘米,AC =16厘米。
求阴影部分的面积。
3、如图,阴影部分的面积是30平方厘米,AB是15厘米,求空白部分的面积。
4、如图,两个相交正方形的边长都是6厘米,求阴影部分的面积。
5、如图,平行四边形中DC=8厘米,CD上的高是4厘米,三角形ABF的面积比三角形FCE的面积大10平方厘米。
求阴影部分的面积。
6、如图,阴影部分的面积是6平方厘米,求梯形ABCD的面积。
7、如图,梯形面积是三角形面积的4倍,求梯形另一底边的长(单位:厘米)。
8、如图,平行四边形BCEF中,阴影部分的面积比三角形ADH的面积大12平方厘米,BC=8厘米,AC=7厘米,求HC的长度。
9、一个长方形和一个正方形的周长相等。
已知长方形的长是66厘米,宽是34厘米,求正方形的边长是多少厘米?长方形你、正方形、梯形、平行四边形图题练习九1、一个等腰三角形的面积是6.8平方厘米,底边上的高是3.4厘米,它的底长是多少?2、如图,阴影部分的面积是64平方厘米,求AB的长度。
3、如图,求AD的长度。
(单位:厘米)4、如图,梯形的面积是45平方分米,高6分米,阴影部分的面积是5平方分米,求OA 的长度。
5、如图,梯形的面积为120平方厘米,求阴影部分图形中CD的长度。
6、一个梯形的面积是216平方厘米,中位线长18厘米,已知这个梯形的下底是高的2倍,它的上底是多少?7、如图,已知梯形ABCE的面积是60平方厘米,求AD的长度。
8、如图等腰三角形CED的面积是48平方厘米,BC=2BD,BC=8厘米,A是ED的中点。
求阴影三角形ABC中BC上的高是多少厘米?9、一个长方形如果宽不变,长增加1米,面积就增加3平方米,如果长不变,宽增加1米,面积就增加4平方米。
这个长方形原来的面积时多少平方米?10、用一根铁丝围成一个长是20厘米,宽是8厘米的长方形。
如果再把这根铁丝围成最大的正方形,这个正方形的面积是多少平方厘米?长方形你、正方形、梯形、平行四边形图题练习十1、一个正方形,一边截去10厘米,另一边截去9厘米,剩下的长方形的面积比原来正方形的面积少480平方厘米,原来正方形的面积是多少平方厘米?2、一个长方形宽不变,长增加1米,面积就增加4平方米,如果长不变,宽增加1米,面积就增加8平方米。
这个长方形原来的面积时多少平方米?3、生产队造一个长方形的饲养场,长方形的一条长是利用原来的旧墙,其余三面砌新墙48米。
若长是宽的2倍,那么饲养场的面积是多少平方米?4、一个正方形的边长缩短2厘米,剩下的正方形面积减少48平方厘米,求原来正方形的面积。
5、一个梯形的中位线长10厘米,如果它的上底增加3厘米,下底和高都不变,它的面积就增加7.5平方厘米,求原来梯形的面积。
6、一个梯形的下底是上底的1.2倍,如果把上底延长3厘米,就成了一个平行四边形,面积比原来增加了24平方厘米,求原来梯形的面积。
7、一个长方形,如果宽增加2分米,那么面积就增加10平方分米,这时恰好成一个正方形,求原长方形的面积。
8、把正方形一边减去4厘米,它的对边增加11厘米,这个正方形就变成一个梯形。
