控制系统仿真与CAD 实验报告
控制系统CAD实验报告
控制系统CAD实验报告一、实验目的1. 掌握如何使用Matlab进行系统的根轨迹分析。
2. 掌握如何使用Matlab进行系统的稳定性分析。
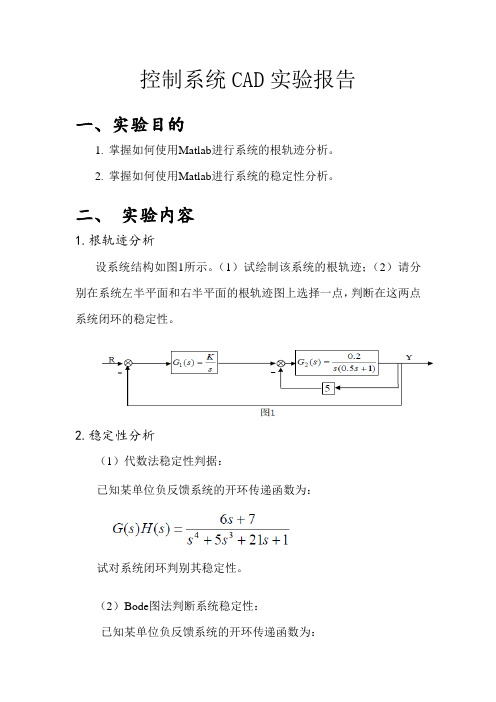
二、实验内容1.根轨迹分析设系统结构如图1所示。
（1）试绘制该系统的根轨迹；（2）请分别在系统左半平面和右半平面的根轨迹图上选择一点，判断在这两点系统闭环的稳定性。
2.稳定性分析（1）代数法稳定性判据：已知某单位负反馈系统的开环传递函数为：试对系统闭环判别其稳定性。
（2）Bode图法判断系统稳定性：已知某单位负反馈系统的开环传递函数为：试绘制系统的Bode图和Nyquist曲线，分别用两种方法判断闭环系统的稳定性，并求出系统的频域性能指标w，γ与时域性能指标σ%、s t。
c三、预习报告1.根轨迹分析g1=tf(1,[1 0])g2=tf(0.2,[0.5 1 0])sys=g1*g2+5*g2rlocus(sys)Gridnyquist(G)2.稳定性分析(1)G=tf([6 7],[1 5 0 27 8]) %闭环环传递函数den=[1 5 0 27 8]p=roots(den)i=find(real(p)>=0)n=length(i)if(n>0) disp('系统不稳定，不稳定根个数为：')nelse disp('系统稳定')end四、上机实验结果1.根轨迹分析2.稳定性分析（1）代数法稳定性判据：Transfer function:6 s + 7----------------------s^4 + 5 s^3 + 27 s + 8den =1 5 0 27 8p =-5.76950.5307 + 2.1137i0.5307 - 2.1137i-0.2920i =23n = 2系统不稳定，不稳定根个数为：n =2（2）Transfer function:0.3 s + 1------------------s^3 + 12 s^2 + 5 s Gm = Inf Pm = 69.1650 Wcg =InfWcp =0.1842五、实验总结对知识的掌握不足，对知识点理解错误。
控制系统仿真与CAD 实验报告
《控制系统仿真与CAD》实验课程报告一、实验教学目标与基本要求上机实验是本课程重要的实践教学环节。
实验的目的不仅仅是验证理论知识，更重要的是通过上机加强学生的实验手段与实践技能，掌握应用MATLAB/Simulink 求解控制问题的方法，培养学生分析问题、解决问题、应用知识的能力和创新精神，全面提高学生的综合素质。
通过对MATLAB/Simulink进行求解，基本掌握常见控制问题的求解方法与命令调用，更深入地认识和了解MATLAB语言的强大的计算功能与其在控制领域的应用优势。
上机实验最终以书面报告的形式提交，作为期末成绩的考核内容。
二、题目及解答第一部分：MATLAB 必备基础知识、控制系统模型与转换、线性控制系统的计算机辅助分析1.>>f=inline('[-x(2)-x(3);x(1)+a*x(2);b+(x(1)-c)*x(3)]','t','x','flag','a','b','c');[t,x]=ode45(f,[0,100],[0;0;0],[],0.2,0.2,5.7);plot3(x(:, 1),x(:,2),x(:,3)),grid,figure,plot(x(:,1),x(:,2)),grid2.>>y=@(x)x(1)^2-2*x(1)+x(2);ff=optimset;rgeScale='off';ff.TolFun= 1e-30;ff.TolX=1e-15;ff.TolCon=1e-20;x0=[1;1;1];xm=[0;0;0];xM=[];A=[]; B=[];Aeq=[];Beq=[];[x,f,c,d]=fmincon(y,x0,A,B,Aeq,Beq,xm,xM,@wzhfc1,f f)Warning: Options LargeScale = 'off' and Algorithm ='trust-region-reflective' conflict.Ignoring Algorithm and running active-set algorithm. To runtrust-region-reflective, setLargeScale = 'on'. To run active-set without this warning, use Algorithm = 'active-set'.> In fmincon at 456Local minimum possible. Constraints satisfied.fmincon stopped because the size of the current search direction is less thantwice the selected value of the step size tolerance and constraints are satisfied to within the selected value of the constraint tolerance.<stopping criteria details>Active inequalities (to within options.TolCon = 1e-20):lower upper ineqlin ineqnonlin2x =1.00001.0000f =-1.0000c =4d =iterations: 5funcCount: 20lssteplength: 1stepsize: 3.9638e-26algorithm: 'medium-scale: SQP, Quasi-Newton, line-search' firstorderopt: 7.4506e-09constrviolation: 0message: [1x766 char]3.(a) >> s=tf('s');G=(s^3+4*s+2)/(s^3*(s^2+2)*((s^2+1)^3+2*s+5)) G =s^3 + 4 s + 2------------------------------------------------------s^11 + 5 s^9 + 9 s^7 + 2 s^6 + 12 s^5 + 4 s^4 + 12 s^3Continuous-time transfer function.(b)>> z=tf('z',0.1);H=(z^2+0.568)/((z-1)*(z^2-0.2*z+0.99))H =z^2 + 0.568-----------------------------z^3 - 1.2 z^2 + 1.19 z - 0.99Sample time: 0.1 secondsDiscrete-time transfer function.4.>> A=[0 1 0;0 0 1;-15 -4 -13];B=[0 0 2]';C=[1 00];D=0;G=ss(A,B,C,D),Gs=tf(G),Gz=zpk(G)G =a =x1 x2 x3x1 0 1 0x2 0 0 1x3 -15 -4 -13b =u1x1 0x2 0x3 2c =x1 x2 x3y1 1 0 0d =u1y1 0Continuous-time state-space model. Gs =2-----------------------s^3 + 13 s^2 + 4 s + 15Continuous-time transfer function. Gz =2---------------------------------(s+12.78) (s^2 + 0.2212s + 1.174)Continuous-time zero/pole/gain model.5.设采样周期为0.01s>> z=tf('z',0.01);H=(z+2)/(z^2+z+0.16)H =z + 2--------------z^2 + z + 0.16Sample time: 0.01 secondsDiscrete-time transfer function.6.>> syms J Kp Ki s;G=(s+1)/(J*s^2+2*s+5);Gc=(Kp*s+Ki)/s;GG=feedback(G*Gc,1)GG =((Ki + Kp*s)*(s + 1))/(J*s^3 + (Kp + 2)*s^2 + (Ki + Kp + 5)*s + Ki) 7.(a)>>s=tf('s');G=(211.87*s+317.64)/((s+20)*(s+94.34)*(s+0.1684));Gc=( 169.6*s+400)/(s*(s+4));H=1/(0.01*s+1);GG=feedback(G*Gc,H),Gd=ss(GG),G z=zpk(GG)GG =359.3 s^3 + 3.732e04 s^2 + 1.399e05 s + 127056----------------------------------------------------------------0.01 s^6 + 2.185 s^5 + 142.1 s^4 + 2444 s^3 + 4.389e04 s^2 + 1.399e05 s + 127056Continuous-time transfer function.Gd =a =x1 x2 x3 x4 x5 x6 x1 -218.5 -111.1 -29.83 -16.74 -6.671 -3.029 x2 128 0 0 0 0 0 x3 0 64 0 0 0 0 x4 0 0 32 0 0 0 x5 0 0 0 8 0 0 x6 0 0 0 0 2 0b =u1x1 4x2 0x3 0x4 0x5 0x6 0c =x1 x2 x3 x4 x5 x6 y1 0 0 1.097 3.559 1.668 0.7573d =u1y1 0Continuous-time state-space model.Gz =35933.152 (s+100) (s+2.358) (s+1.499)----------------------------------------------------------------------(s^2 + 3.667s + 3.501) (s^2 + 11.73s + 339.1) (s^2 + 203.1s + 1.07e04) Continuous-time zero/pole/gain model.(b)设采样周期为0.1s>>z=tf('z',0.1);G=(35786.7*z^2+108444*z^3)/((1+4*z)*(1+20*z)*(1+74.04 *z));Gc=z/(1-z);H=z/(0.5-z);GG=feedback(G*Gc,H),Gd=ss(GG),Gz=zpk(GG) GG =-108444 z^5 + 1.844e04 z^4 + 1.789e04 z^3----------------------------------------------------------------1.144e05 z^5 +2.876e04 z^4 + 274.2 z^3 + 782.4 z^2 + 47.52 z + 0.5Sample time: 0.1 secondsDiscrete-time transfer function.Gd =a =x1 x2 x3 x4 x5x1 -0.2515 -0.00959 -0.1095 -0.05318 -0.01791x2 0.25 0 0 0 0x3 0 0.25 0 0 0x4 0 0 0.125 0 0x5 0 0 0 0.03125 0b =u1x1 1x2 0x3 0x4 0x5 0c =x1 x2 x3 x4 x5y1 0.3996 0.6349 0.1038 0.05043 0.01698d =u1y1 -0.9482Sample time: 0.1 secondsDiscrete-time state-space model.Gz =-0.94821 z^3 (z-0.5) (z+0.33)---------------------------------------------------------- (z+0.3035) (z+0.04438) (z+0.01355) (z^2 - 0.11z + 0.02396) Sample time: 0.1 secondsDiscrete-time zero/pole/gain model.8.>>s=tf('s');g1=1/(s+1);g2=s/(s^2+2);g3=1/s^2;g4=(4*s+2)/(s+1)^2;g5=50 ;g6=(s^2+2)/(s^3+14);G1=feedback(g1*g2,g4);G2=feedback(g3,g5);GG=3*fe edback(G1*G2,g6)GG =3 s^6 + 6 s^5 + 3 s^4 + 42 s^3 + 84 s^2 + 42 s---------------------------------------------------------------------------s^10 + 3 s^9 + 55 s^8 + 175 s^7 + 300 s^6 + 1323 s^5 + 2656 s^4 + 3715 s^3 + 7732 s^2 + 5602 s + 1400Continuous-time transfer function.>>s=tf('s');T0=0.01;T1=0.1;T2=1;G=(s+1)^2*(s^2+2*s+400)/((s+5)^2*(s^2 +3*s+100)*(s^2+3*s+2500));Gd1=c2d(G,T0),Gd2=c2d(G,T1),Gd3=c2d(G,T2),s tep(G),figure,step(Gd1),figure,step(Gd2),figure,step(Gd3)Gd1 =4.716e-05 z^5 - 0.0001396 z^4 + 9.596e-05 z^3 + 8.18e-05 z^2 - 0.0001289 z + 4.355e-05----------------------------------------------------------------z^6 - 5.592 z^5 + 13.26 z^4 - 17.06 z^3 + 12.58 z^2 - 5.032 z + 0.8521Sample time: 0.01 secondsDiscrete-time transfer function.Gd2 =0.0003982 z^5 - 0.0003919 z^4 - 0.000336 z^3 + 0.0007842 z^2 - 0.000766 z + 0.0003214----------------------------------------------------------------z^6 - 2.644 z^5 + 4.044 z^4 - 3.94 z^3 + 2.549 z^2 - 1.056 z + 0.2019Sample time: 0.1 secondsDiscrete-time transfer function.Gd3 =8.625e-05 z^5 - 4.48e-05 z^4 + 6.545e-06 z^3 + 1.211e -05 z^2 - 3.299e-06 z + 1.011e-07---------------------------------------------------------------z^6 - 0.0419 z^5 - 0.07092 z^4 - 0.0004549 z^3 + 0.002495 z^2 - 3.347e-05 z + 1.125e-07Sample time: 1 secondsDiscrete-time transfer function.10.(a)>> G=tf(1,[1 2 1 2]);eig(G),pzmap(G) ans =-2.0000-0.0000 + 1.0000i-0.0000 - 1.0000i系统为临界稳定。
“控制系统数字仿真与CAD”实验指导书.
写，均要求用标准Ａ４纸进行撰写，单栏排版，单面打印，并左侧装订，以便于报告最终的批阅与存档，（对于存在“逻辑混乱” 、“文字不清” 、“作图潦草” 、“排版混乱”等问题的报告，将予以退回重新撰写）。
封页：（参考最后一页的“封页”格式）正文：（小四字体）仿真实验题目 1、 2、 3、 4、 5、五、思考题 1．在系统启动过程的第 2 阶段中，理想的电流特性为：实际值小于给定/设定值，试说明为何？引言原理/建模设计/分析/论述仿真实验/结果分析结论（思考题解答） 2．动态性能中，电流/转速特性的“超调量”与理论值是否有偏差？；如有偏差，试给出分析/解释。
3．在“双闭环直流电动机调速系统”中，电流调节器与速度调节器的输出都要设置“限幅” ，试说明：你是如何选取限幅值的？ 4．假设系统中的励磁电压减小/增加，试说明：系统转速将可能怎样变化？参考文献： [1] 张晓华主编《控制系统数字仿真与 CAD》第 3 版机械工业出版社 2009 [2] 张晓华主编《系统建模与仿真》清华大学出版社 2006 [3] 陈伯时主编《电力拖动自动控制系统》第 3 版机械工业出版社 2008 25
“控制系统数字仿真与CAD” 仿真实验报告姓班学名：级：号：联系电话： Email: 提交日期： 26。
控制系统仿真与CAD
《控制系统仿真与CAD》——控制系统建模、分析、设计与仿真一、摘要本结课论文为设计两个控制器，分别为最小拍无波纹和最小拍有波纹控制器。
通过这次实践可以进一步对所学的《控制系统仿真与CAD》有进一步的了解，并对Matlab软件的操作有一定程度的熟悉，为以后的学习或工作做根底。
MATLAB是矩阵实验室〔Matrix Laboratory〕的简称，是美国MathWorks公司出品的商业数学软件，用于算法开发、数据可视化、数据分析以与数值计算的高级技术计算语言和交互式环境，主要包括MATLAB和Simulink两大局部。
关键字：Matlab；控制系统仿真与CAD；建模；仿真二、课程设计的内容1、求被控对象传递函数G(s)的MATLAB描述。
输入：num=conv([968],conv([1 2],[1 9]));den=conv([1 0 0],conv([1 1],conv([1 4],[1 8])));T=0.05;sys=tf(num,den)显示结果：Transfer function:968 s^2 + 10648 s + 17424------------------------------s^5 + 13 s^4 + 44 s^3 + 32 s^22、求被控对象脉冲传递函数G(z)。
输入：Gz=c2d(Gs,0.02,'zoh')显示结果：ransfer function:------------------------------------------------------------------3、转换G(z)为零极点增益模型并按z-1形式排列。
输入：[z,p,k]=zpkdata(Gz)Gz=zpk(z,p,k,T,'variable','z^-1')显示结果：z = [4x1 double]p = [5x1 double]Zero/pole/gain:0.001132 z^-1 (1+3.605z^-1) (1-0.9802z^-1) (1-0.8869z^-1) (1+0.2586z^-1) ------------------------------------------------------------------------ (1-z^-1)^2 (1-0.9608z^-1) (1-0.9048z^-1) (1-0.8694z^-1)4、确定误差脉冲传递函数Ge(z)形式,满足单位加速度信号输入时闭环稳态误差为零和实际闭环系统稳定的要求。
控制系统仿真与CAD-实验报告
《控制系统仿真与CAD》实验课程报告一、实验教学目标与基本要求上机实验是本课程重要的实践教学环节。
实验的目的不仅仅是验证理论知识，更重要的是通过上机加强学生的实验手段与实践技能，掌握应用MATLAB/Simulink 求解控制问题的方法，培养学生分析问题、解决问题、应用知识的能力和创新精神，全面提高学生的综合素质。
通过对MATLAB/Simulink进行求解，基本掌握常见控制问题的求解方法与命令调用，更深入地认识和了解MATLAB语言的强大的计算功能与其在控制领域的应用优势。
上机实验最终以书面报告的形式提交，作为期末成绩的考核内容。
二、题目及解答第一部分：MATLAB 必备基础知识、控制系统模型与转换、线性控制系统的计算机辅助分析1.>>f=inline('[-x(2)-x(3);x(1)+a*x(2);b+(x(1)-c)*x(3)]','t','x','flag','a','b','c');[t,x]=ode45( f,[0,100],[0;0;0],[],0.2,0.2,5.7);plot3(x(:,1),x(:,2),x(:,3)),grid,figure,plot(x(:,1),x(:,2)), grid2.>>y=@(x)x(1)^2-2*x(1)+x(2);ff=optimset;rgeScale='off';ff.TolFun=1e-30;ff.Tol X=1e-15;ff.TolCon=1e-20;x0=[1;1;1];xm=[0;0;0];xM=[];A=[];B=[];Aeq=[];Beq=[];[ x,f,c,d]=fmincon(y,x0,A,B,Aeq,Beq,xm,xM,@wzhfc1,ff)Warning: Options LargeScale = 'off' and Algorithm ='trust-region-reflective' conflict.Ignoring Algorithm and running active-set algorithm. To runtrust-region-reflective, setLargeScale = 'on'. To run active-set without this warning, useAlgorithm = 'active-set'.> In fmincon at 456Local minimum possible. Constraints satisfied.fmincon stopped because the size of the current search direction is less thantwice the selected value of the step size tolerance and constraints aresatisfied to within the selected value of the constraint tolerance.<stopping criteria details>Active inequalities (to within options.TolCon = 1e-20):lower upper ineqlin ineqnonlin2x =1.00001.0000f =-1.0000c =4d =iterations: 5funcCount: 20lssteplength: 1stepsize: 3.9638e-26algorithm: 'medium-scale: SQP, Quasi-Newton, line-search'firstorderopt: 7.4506e-09constrviolation: 0message: [1x766 char]3.(a) >> s=tf('s');G=(s^3+4*s+2)/(s^3*(s^2+2)*((s^2+1)^3+2*s+5))G =s^3 + 4 s + 2------------------------------------------------------s^11 + 5 s^9 + 9 s^7 + 2 s^6 + 12 s^5 + 4 s^4 + 12 s^3Continuous-time transfer function.(b)>> z=tf('z',0.1);H=(z^2+0.568)/((z-1)*(z^2-0.2*z+0.99))H =z^2 + 0.568-----------------------------z^3 - 1.2 z^2 + 1.19 z - 0.99Sample time: 0.1 secondsDiscrete-time transfer function.4.>> A=[0 1 0;0 0 1;-15 -4 -13];B=[0 0 2]';C=[1 00];D=0;G=ss(A,B,C,D),Gs=tf(G),Gz=zpk(G)G =a =x1 x2 x3x1 0 1 0x2 0 0 1x3 -15 -4 -13b =u1x1 0x2 0x3 2c =x1 x2 x3y1 1 0 0d =u1y1 0Continuous-time state-space model.Gs =2-----------------------s^3 + 13 s^2 + 4 s + 15 Continuous-time transfer function.Gz =2---------------------------------(s+12.78) (s^2 + 0.2212s + 1.174) Continuous-time zero/pole/gain model.5.设采样周期为0.01s>> z=tf('z',0.01);H=(z+2)/(z^2+z+0.16) H =z + 2--------------z^2 + z + 0.16Sample time: 0.01 secondsDiscrete-time transfer function.6.>> syms J Kp Ki s;G=(s+1)/(J*s^2+2*s+5);Gc=(Kp*s+Ki)/s;GG=feedback(G*Gc,1) GG =((Ki + Kp*s)*(s + 1))/(J*s^3 + (Kp + 2)*s^2 + (Ki + Kp + 5)*s + Ki)7.(a)>>s=tf('s');G=(211.87*s+317.64)/((s+20)*(s+94.34)*(s+0.1684));Gc=(169.6*s+400)/(s*(s+4));H=1/(0.01*s+1);GG=feedback(G*Gc,H),Gd=ss(GG),Gz=zpk(GG)GG =359.3 s^3 + 3.732e04 s^2 + 1.399e05 s + 127056----------------------------------------------------------------0.01 s^6 + 2.185 s^5 + 142.1 s^4 + 2444 s^3 + 4.389e04 s^2 + 1.399e05 s + 127056Continuous-time transfer function.Gd =a =x1 x2 x3 x4 x5 x6x1 -218.5 -111.1 -29.83 -16.74 -6.671 -3.029x2 128 0 0 0 0 0x3 0 64 0 0 0 0x4 0 0 32 0 0 0x5 0 0 0 8 0 0x6 0 0 0 0 2 0b =u1x1 4x2 0x3 0x4 0x5 0x6 0c =x1 x2 x3 x4 x5 x6y1 0 0 1.097 3.559 1.668 0.7573d =u1y1 0Continuous-time state-space model.Gz =35933.152 (s+100) (s+2.358) (s+1.499)----------------------------------------------------------------------(s^2 + 3.667s + 3.501) (s^2 + 11.73s + 339.1) (s^2 + 203.1s + 1.07e04) Continuous-time zero/pole/gain model.(b)设采样周期为0.1s>>z=tf('z',0.1);G=(35786.7*z^2+108444*z^3)/((1+4*z)*(1+20*z)*(1+74.04*z));Gc= z/(1-z);H=z/(0.5-z);GG=feedback(G*Gc,H),Gd=ss(GG),Gz=zpk(GG)GG =-108444 z^5 + 1.844e04 z^4 + 1.789e04 z^3----------------------------------------------------------------1.144e05 z^5 +2.876e04 z^4 + 274.2 z^3 + 782.4 z^2 + 47.52 z + 0.5Sample time: 0.1 secondsDiscrete-time transfer function.Gd =a =x1 x2 x3 x4 x5 x1 -0.2515 -0.00959 -0.1095 -0.05318 -0.01791x2 0.25 0 0 0 0x3 0 0.25 0 0 0x4 0 0 0.125 0 0x5 0 0 0 0.03125 0b =u1x1 1x2 0x3 0x4 0x5 0c =x1 x2 x3 x4 x5y1 0.3996 0.6349 0.1038 0.05043 0.01698d =u1y1 -0.9482Sample time: 0.1 secondsDiscrete-time state-space model.Gz =-0.94821 z^3 (z-0.5) (z+0.33)----------------------------------------------------------(z+0.3035) (z+0.04438) (z+0.01355) (z^2 - 0.11z + 0.02396)Sample time: 0.1 secondsDiscrete-time zero/pole/gain model.8.>>s=tf('s');g1=1/(s+1);g2=s/(s^2+2);g3=1/s^2;g4=(4*s+2)/(s+1)^2;g5=50;g6=(s^2+2) /(s^3+14);G1=feedback(g1*g2,g4);G2=feedback(g3,g5);GG=3*feedback(G1*G2,g6) GG =3 s^6 + 6 s^5 + 3 s^4 + 42 s^3 + 84 s^2 + 42 s---------------------------------------------------------------------------s^10 + 3 s^9 + 55 s^8 + 175 s^7 + 300 s^6 + 1323 s^5 + 2656 s^4 + 3715 s^3 + 7732 s^2 + 5602 s + 1400Continuous-time transfer function.9.>>s=tf('s');T0=0.01;T1=0.1;T2=1;G=(s+1)^2*(s^2+2*s+400)/((s+5)^2*(s^2+3*s+100 )*(s^2+3*s+2500));Gd1=c2d(G,T0),Gd2=c2d(G,T1),Gd3=c2d(G,T2),step(G),figure,st ep(Gd1),figure,step(Gd2),figure,step(Gd3)Gd1 =4.716e-05 z^5 - 0.0001396 z^4 + 9.596e-05 z^3 + 8.18e-05 z^2 - 0.0001289 z + 4.355e-05----------------------------------------------------------------z^6 - 5.592 z^5 + 13.26 z^4 - 17.06 z^3 + 12.58 z^2 - 5.032 z + 0.8521Sample time: 0.01 secondsDiscrete-time transfer function.Gd2 =0.0003982 z^5 - 0.0003919 z^4 - 0.000336 z^3 + 0.0007842 z^2 - 0.000766 z + 0.0003214----------------------------------------------------------------z^6 - 2.644 z^5 + 4.044 z^4 - 3.94 z^3 + 2.549 z^2 - 1.056 z + 0.2019Sample time: 0.1 secondsDiscrete-time transfer function.Gd3 =8.625e-05 z^5 - 4.48e-05 z^4 + 6.545e-06 z^3 + 1.211e -05 z^2 - 3.299e-06 z + 1.011e-07---------------------------------------------------------------z^6 - 0.0419 z^5 - 0.07092 z^4 - 0.0004549 z^3 + 0.002495 z^2 - 3.347e-05 z + 1.125e-07Sample time: 1 secondsDiscrete-time transfer function.10.(a)>> G=tf(1,[1 2 1 2]);eig(G),pzmap(G) ans =-2.0000-0.0000 + 1.0000i-0.0000 - 1.0000i系统为临界稳定。
控制系统仿真与CAD课程设计报告
控制系统仿真与CAD 课程设计学院：物流工程学院专业：测控技术与仪器班级：测控102姓名：杨红霞学号：201010233037指导教师：兰莹完成日期：2013年7月4日目的和任务配合《控制系统仿真与CAD》课程的理论教学，通过课程设计教学环节，使学生掌握当前流行的演算式MATLAB语言的基本知识，学会运用MATLAB语言进行控制系统仿真和辅助设计的基本技能，有效地提高学生实验动手能力。
一、基本要求：1、利用MATLAB提供的基本工具，灵活地编制和开发程序，开创新的应用；2、熟练地掌握各种模型之间的转换，系统的时域、频域分析及根轨迹绘制；3、熟练运用SIMULINK对系统进行仿真；4、掌握PID控制器参数的设计。
二、设计要求1、编制相应的程序，并绘制相应的曲线；2、对设计结果进行分析；3、撰写和打印设计报告（包括程序、结果分析、仿真结构框图、结果曲线）。
三、设计课题设计一：二阶弹簧—阻尼系统的PID控制器设计及其参数整定考虑弹簧－阻尼系统如图1所示，其被控对象为二阶环节，传递函数G(S)如下，参数为M=1kg，b=2N.s/m，k=25N/m，F（S）=1。
设计要求：（1）控制器为P控制器时，改变比例系数大小，分析其对系统性能的影响并绘制相应曲线。
（2）控制器为PI控制器时，改变积分时间常数大小，分析其对系统性能的影响并绘制相应曲线。
(例如当kp=50时，改变积分时间常数)（3）设计PID控制器，选定合适的控制器参数，使闭环系统阶跃响应曲线的超调量σ%<20%，过渡过程时间Ts<2s, 并绘制相应曲线。
图1 弹簧－阻尼系统示意图弹簧－阻尼系统的微分方程和传递函数为：F kx x b xM =++ 25211)()()(22++=++==s s k bs Ms s F s X s G图2 闭环控制系统结构图附：P 控制器的传递函数为：()P P G s K =PI 控制器的传递函数为：11()PI P I G s K T s=+⋅ PID 控制器的传递函数为：11()PID P D I G s K T s T s=+⋅+⋅(一)设计P控制器，改变比例系数大小，分析其对系统性能的影响并绘制相应曲线。
控制系统仿真及CAD实验报告(研2021)2
控制系统仿真及CAD实验报告(研2021)2控制系统仿真及CAD试题（研2021）一、（20分）试论述系统仿真的目的、意义、分类及应用与发展概况。
解：系统仿真的目的：在分析系统各要素性质及其相互关系的基础上，建立能描述系统结构或行为过程的、且具有一定逻辑关系或数量关系的仿真模型，据此进行试验或定量分析，以获得正确决策所需的各种信息。
系统仿真的意义：由于仿真技术经济、安全、快捷的优点以及其特殊的用途，例如优化设计和预测功能，使得其在工程设计、理论研究、产品开发等方面具有重要意义。
系统仿真的分类：1、按模型分类。
当仿真实验所采用的模型是物理模型时，称之为物理仿真；是数学模型是，称之为数学仿真。
2、按计算机类型分类。
（1）模拟仿真。
采用数学模型在模拟计算机上进行的实验研究称之为模拟仿真。
（2）数字仿真。
采用数学模型在数字计算机上进行的实验研究称之为数字仿真。
（3）混合仿真。
将模拟仿真与数字仿真结合起来的混合仿真实验系统，简称混合仿真。
（4）全数字仿真。
对象的模拟也用一台计算机来实现，用软件来实现对象各种机理的模型。
（5）分布式数字仿真。
数字仿真系统将所研究的问题分布成若干个子系统，分别在主站与各分站的计算机上同时进行。
系统仿真的应用：现代仿真技术经过近50年的发展与完善，已经在各行业做出卓越贡献，同时也充分体现出其在科技发展与社会进步中的重要作用。
仿真技术广泛应用在航空与航天工业、电力工业、原子能工业、石油、化工及冶金工业中。
仿真技术还广泛应用在医学、社会学、宏观经济与商业策略的研究等非工程领域中。
系统仿真的发展概况：（1）在硬件方面，基于多CPU并行处理技术的全数字仿真系统将有效提高系统仿真的速度，从而使仿真系统“实时性”得到进一步的加强。
（2）随着网络技术的不断完善与提高，分布式数字仿真系统将为人们广泛采用，从而达到“投资少、效果好”的目的。
（3）在应用软件方面，直接面向用户的高效能的数字仿真软件不断推陈出新，各种专家系统与智能化技术奖更深入的应用于仿真软件开发中，使得在人―机界面、结果输出、综合评判等方面达到更理想的境界。
控制系统仿真实验报告书
一、实验目的1. 掌握控制系统仿真的基本原理和方法；2. 熟练运用MATLAB/Simulink软件进行控制系统建模与仿真；3. 分析控制系统性能，优化控制策略。
二、实验内容1. 建立控制系统模型2. 进行仿真实验3. 分析仿真结果4. 优化控制策略三、实验环境1. 操作系统：Windows 102. 软件环境：MATLAB R2020a、Simulink3. 硬件环境：个人电脑一台四、实验过程1. 建立控制系统模型以一个典型的PID控制系统为例，建立其Simulink模型。
首先，创建一个新的Simulink模型，然后添加以下模块：（1）输入模块：添加一个阶跃信号源，表示系统的输入信号；（2）被控对象：添加一个传递函数模块，表示系统的被控对象；（3）控制器：添加一个PID控制器模块，表示系统的控制器；（4）输出模块：添加一个示波器模块，用于观察系统的输出信号。
2. 进行仿真实验（1）设置仿真参数：在仿真参数设置对话框中，设置仿真时间、步长等参数；（2）运行仿真：点击“开始仿真”按钮，运行仿真实验；（3）观察仿真结果：在示波器模块中，观察系统的输出信号，分析系统性能。
3. 分析仿真结果根据仿真结果，分析以下内容：（1）系统稳定性：通过观察系统的输出信号，判断系统是否稳定；（2）响应速度：分析系统对输入信号的响应速度，评估系统的快速性；（3）超调量：分析系统超调量，评估系统的平稳性；（4）调节时间：分析系统调节时间，评估系统的动态性能。
4. 优化控制策略根据仿真结果，对PID控制器的参数进行调整，以优化系统性能。
调整方法如下：（1）调整比例系数Kp：增大Kp，提高系统的快速性，但可能导致超调量增大；（2）调整积分系数Ki：增大Ki，提高系统的平稳性，但可能导致调节时间延长；（3）调整微分系数Kd：增大Kd，提高系统的快速性，但可能导致系统稳定性下降。
五、实验结果与分析1. 系统稳定性：经过仿真实验，发现该PID控制系统在调整参数后，具有良好的稳定性。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
《控制系统仿真与CAD》实验课程报告一、实验教学目标与基本要求上机实验是本课程重要的实践教学环节。
实验的目的不仅仅是验证理论知识，更重要的是通过上机加强学生的实验手段与实践技能，掌握应用MATLAB/Simulink 求解控制问题的方法，培养学生分析问题、解决问题、应用知识的能力和创新精神，全面提高学生的综合素质。
通过对MATLAB/Simulink进行求解，基本掌握常见控制问题的求解方法与命令调用，更深入地认识和了解MATLAB语言的强大的计算功能与其在控制领域的应用优势。
上机实验最终以书面报告的形式提交，作为期末成绩的考核内容。
二、题目及解答第一部分：MATLAB 必备基础知识、控制系统模型与转换、线性控制系统的计算机辅助分析1.>>f=inline('[-x(2)-x(3);x(1)+a*x(2);b+(x(1)-c)*x(3)]','t','x','flag','a','b','c');[t,x]=ode45( f,[0,100],[0;0;0],[],0.2,0.2,5.7);plot3(x(:,1),x(:,2),x(:,3)),grid,figure,plot(x(:,1),x(:,2)), grid2.>>y=@(x)x(1)^2-2*x(1)+x(2);ff=optimset;rgeScale='off';ff.TolFun=1e-30;ff.Tol X=1e-15;ff.TolCon=1e-20;x0=[1;1;1];xm=[0;0;0];xM=[];A=[];B=[];Aeq=[];Beq=[];[ x,f,c,d]=fmincon(y,x0,A,B,Aeq,Beq,xm,xM,@wzhfc1,ff)Warning: Options LargeScale = 'off' and Algorithm ='trust-region-reflective' conflict.Ignoring Algorithm and running active-set algorithm. To runtrust-region-reflective, setLargeScale = 'on'. To run active-set without this warning, useAlgorithm = 'active-set'.> In fmincon at 456Local minimum possible. Constraints satisfied.fmincon stopped because the size of the current search direction is less thantwice the selected value of the step size tolerance and constraints aresatisfied to within the selected value of the constraint tolerance.<stopping criteria details>Active inequalities (to within options.TolCon = 1e-20):lower upper ineqlin ineqnonlin2x =1.00001.0000f =-1.0000c =4d =iterations: 5funcCount: 20lssteplength: 1stepsize: 3.9638e-26algorithm: 'medium-scale: SQP, Quasi-Newton, line-search'firstorderopt: 7.4506e-09constrviolation: 0message: [1x766 char]3.(a) >> s=tf('s');G=(s^3+4*s+2)/(s^3*(s^2+2)*((s^2+1)^3+2*s+5))G =s^3 + 4 s + 2------------------------------------------------------s^11 + 5 s^9 + 9 s^7 + 2 s^6 + 12 s^5 + 4 s^4 + 12 s^3Continuous-time transfer function.(b)>> z=tf('z',0.1);H=(z^2+0.568)/((z-1)*(z^2-0.2*z+0.99))H =z^2 + 0.568-----------------------------z^3 - 1.2 z^2 + 1.19 z - 0.99Sample time: 0.1 secondsDiscrete-time transfer function.4.>> A=[0 1 0;0 0 1;-15 -4 -13];B=[0 0 2]';C=[1 00];D=0;G=ss(A,B,C,D),Gs=tf(G),Gz=zpk(G)G =a =x1 x2 x3x1 0 1 0x2 0 0 1x3 -15 -4 -13b =u1x1 0x2 0x3 2c =x1 x2 x3y1 1 0 0d =u1y1 0Continuous-time state-space model.Gs =2-----------------------s^3 + 13 s^2 + 4 s + 15 Continuous-time transfer function.Gz =2---------------------------------(s+12.78) (s^2 + 0.2212s + 1.174) Continuous-time zero/pole/gain model.5.设采样周期为0.01s>> z=tf('z',0.01);H=(z+2)/(z^2+z+0.16) H =z + 2--------------z^2 + z + 0.16Sample time: 0.01 secondsDiscrete-time transfer function.6.>> syms J Kp Ki s;G=(s+1)/(J*s^2+2*s+5);Gc=(Kp*s+Ki)/s;GG=feedback(G*Gc,1) GG =((Ki + Kp*s)*(s + 1))/(J*s^3 + (Kp + 2)*s^2 + (Ki + Kp + 5)*s + Ki)7.(a)>>s=tf('s');G=(211.87*s+317.64)/((s+20)*(s+94.34)*(s+0.1684));Gc=(169.6*s+400)/(s*(s+4));H=1/(0.01*s+1);GG=feedback(G*Gc,H),Gd=ss(GG),Gz=zpk(GG)GG =359.3 s^3 + 3.732e04 s^2 + 1.399e05 s + 127056----------------------------------------------------------------0.01 s^6 + 2.185 s^5 + 142.1 s^4 + 2444 s^3 + 4.389e04 s^2 + 1.399e05 s + 127056Continuous-time transfer function.Gd =a =x1 x2 x3 x4 x5 x6x1 -218.5 -111.1 -29.83 -16.74 -6.671 -3.029x2 128 0 0 0 0 0x3 0 64 0 0 0 0x4 0 0 32 0 0 0x5 0 0 0 8 0 0x6 0 0 0 0 2 0b =u1x1 4x2 0x3 0x4 0x5 0x6 0c =x1 x2 x3 x4 x5 x6y1 0 0 1.097 3.559 1.668 0.7573d =u1y1 0Continuous-time state-space model.Gz =35933.152 (s+100) (s+2.358) (s+1.499)----------------------------------------------------------------------(s^2 + 3.667s + 3.501) (s^2 + 11.73s + 339.1) (s^2 + 203.1s + 1.07e04) Continuous-time zero/pole/gain model.(b)设采样周期为0.1s>>z=tf('z',0.1);G=(35786.7*z^2+108444*z^3)/((1+4*z)*(1+20*z)*(1+74.04*z));Gc= z/(1-z);H=z/(0.5-z);GG=feedback(G*Gc,H),Gd=ss(GG),Gz=zpk(GG)GG =-108444 z^5 + 1.844e04 z^4 + 1.789e04 z^3----------------------------------------------------------------1.144e05 z^5 +2.876e04 z^4 + 274.2 z^3 + 782.4 z^2 + 47.52 z + 0.5Sample time: 0.1 secondsDiscrete-time transfer function.Gd =a =x1 x2 x3 x4 x5 x1 -0.2515 -0.00959 -0.1095 -0.05318 -0.01791x2 0.25 0 0 0 0x3 0 0.25 0 0 0x4 0 0 0.125 0 0x5 0 0 0 0.03125 0b =u1x1 1x2 0x3 0x4 0x5 0c =x1 x2 x3 x4 x5y1 0.3996 0.6349 0.1038 0.05043 0.01698d =u1y1 -0.9482Sample time: 0.1 secondsDiscrete-time state-space model.Gz =-0.94821 z^3 (z-0.5) (z+0.33)----------------------------------------------------------(z+0.3035) (z+0.04438) (z+0.01355) (z^2 - 0.11z + 0.02396)Sample time: 0.1 secondsDiscrete-time zero/pole/gain model.8.>>s=tf('s');g1=1/(s+1);g2=s/(s^2+2);g3=1/s^2;g4=(4*s+2)/(s+1)^2;g5=50;g6=(s^2+2) /(s^3+14);G1=feedback(g1*g2,g4);G2=feedback(g3,g5);GG=3*feedback(G1*G2,g6) GG =3 s^6 + 6 s^5 + 3 s^4 + 42 s^3 + 84 s^2 + 42 s---------------------------------------------------------------------------s^10 + 3 s^9 + 55 s^8 + 175 s^7 + 300 s^6 + 1323 s^5 + 2656 s^4 + 3715 s^3 + 7732 s^2 + 5602 s + 1400Continuous-time transfer function.9.>>s=tf('s');T0=0.01;T1=0.1;T2=1;G=(s+1)^2*(s^2+2*s+400)/((s+5)^2*(s^2+3*s+100 )*(s^2+3*s+2500));Gd1=c2d(G,T0),Gd2=c2d(G,T1),Gd3=c2d(G,T2),step(G),figure,st ep(Gd1),figure,step(Gd2),figure,step(Gd3)Gd1 =4.716e-05 z^5 - 0.0001396 z^4 + 9.596e-05 z^3 + 8.18e-05 z^2 - 0.0001289 z + 4.355e-05----------------------------------------------------------------z^6 - 5.592 z^5 + 13.26 z^4 - 17.06 z^3 + 12.58 z^2 - 5.032 z + 0.8521Sample time: 0.01 secondsDiscrete-time transfer function.Gd2 =0.0003982 z^5 - 0.0003919 z^4 - 0.000336 z^3 + 0.0007842 z^2 - 0.000766 z + 0.0003214----------------------------------------------------------------z^6 - 2.644 z^5 + 4.044 z^4 - 3.94 z^3 + 2.549 z^2 - 1.056 z + 0.2019Sample time: 0.1 secondsDiscrete-time transfer function.Gd3 =8.625e-05 z^5 - 4.48e-05 z^4 + 6.545e-06 z^3 + 1.211e -05 z^2 - 3.299e-06 z + 1.011e-07---------------------------------------------------------------z^6 - 0.0419 z^5 - 0.07092 z^4 - 0.0004549 z^3 + 0.002495 z^2 - 3.347e-05 z + 1.125e-07Sample time: 1 secondsDiscrete-time transfer function.10.(a)>> G=tf(1,[1 2 1 2]);eig(G),pzmap(G) ans =-2.0000-0.0000 + 1.0000i-0.0000 - 1.0000i系统为临界稳定。