河南省洛阳市2017届高三上学期期中考试数学(理)试题.doc
河南省洛阳市2017届高三上学期期中考试数学(理)试题.docx

【考试时间:2016年10月13日15:00~17:00】洛阳市2016—2017学年高中三年级期中考试数 学 试 卷(理)本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择),考生作答时,须将答案答答题卡上,在本试卷、草稿纸上答题无效。
满分150分,考试时间120分钟。
第Ⅰ卷(选择题,共60分注意事项:1.必须使用2B 铅笔在答题卡上将所选答案对应的标号涂黑. 2.考试结束后,将本试题卷和答题卡一并交回。
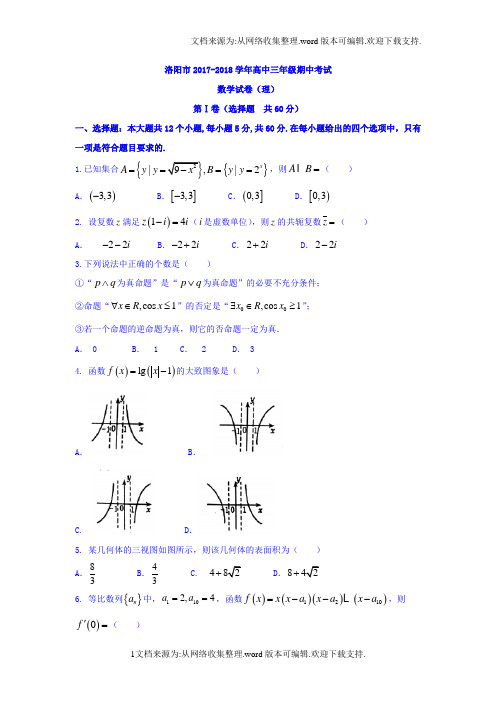
一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.集合{}Z x x x A ∈=,<<3log 12,{}95<x x B ≤=,则=⋂B A ( ) A .),5[2e B.]7,5[ C .}7,6,5{ D .}8,7,6,5{2.复数i i++12的共扼复数是( ) A .i 2123+- B .i 2123-- C.i 2123- D .i 2123+3.设n m ,是两条不同的直线,βα,是两个不同的平面,下列命题是真命题的是( ) A .若α//m ,β//m ,则βα// B .若α//m ,βα//,则β//m C .若α⊂m ,β⊥m ,则βα⊥ D .若α⊂m ,βα⊥,则β⊥m 4.函数)42cos(ln π+=x y 的一个单调递减区间是( )A .)8,85(ππ--B .)8,83(ππ--C .)8,8(ππ--D .)83,8(ππ-5.O 为△ABC 内一点,且02=++OC OB OA ,AC t AD =,若D O B ,,三点共线,则t 的值为( ) A .41B .31C .21 D.32 6.一个几何体的三视图都是边长为1的正方形,如图,则该几何体的体积是( )A .121 B .31 C .42 D.21 7.由2,1,===x xy x y 及x 轴所围成的平面图形的面积是( ) A .12ln + B .2ln 2- C .212ln - D.212ln +8.直角△ABC 中,∠C =90°,D 在BC 上,CD =2DB ,tan ∠BAD =51,则BAC ∠sin =( ) A .22 B .23 C .13133 D.22或13133 9.已知函数)(x f 是R 上的奇函数,且满足)()2(x f x f -=+,当]1,0[∈x 时,x x f =)(,则方程182)(+-=x x x f 在 ),0(+∞解的个数是( )A .3B .4C .5 D.6 10.已知数列n S 为等比数列{}n a 的前n 项和,14,2248==S S ,则=2016S ( ) A .22252- B .22253- C .221008- D.222016-11.已知三棱锥ABC P -中,1===AC PB PA ,⊥PA 面ABC ,∠BAC =32π,则三棱锥ABC P -的外接球的表面积为( )A .π3B .π4C .π5 D.π8 12.定义在R 上的函数)(x f 满足:x e x x f x f ∙=-')()(,且21)0(=f ,则)()(x f x f '的最大值为( )A .0B .21C .1 D.2第Ⅱ卷(非选择题,共90分)注意事项:必须使用0.5毫米黑色墨迹签字笔在答题卡题目所指示的答题区域内作答。
河南省洛阳市高三数学上学期期中试题 理(含解析)

洛阳市2014-2015学年高中三年级期中考试数学试卷(理A)【试卷综析】本试卷是高三理科试卷,以基础知识为载体,以基本能力测试为主导,重视学生科学素养的考查.知识考查注重基础、兼顾覆盖面.试题重点考查:集合、、复数、导数、圆锥曲线、函数的性质、立体几何,三选一等;考查学生解决实际问题的综合能力,是份比较好的试卷.第I卷(选择题,共60分)注意事项:1.答卷前,考生务必将自己的姓名,考号填写在答题卷上.2.考试结束,将答题卷交回.【题文】一、选择题:本大题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
【题文】1.则M N=A.[)1,0-B.(]21--,C.(]01,D.(0,2)【知识点】集合及其运算A1【答案解析】C x2-2x<0⇔0<x<2,则集合M={x|0<x<2},|x|≤1⇔-1≤x≤1,则集合N={x|-1≤x≤1},则M∩N={x|0<x≤1}=(0,1]故答案为C【思路点拨】解x2-2x<0可得集合M={x|0<x<2},解|x|<1可得集合N,由交集的定义,分析可得答案.【题文】2.则a b+=A.7B.-7C.1D.-1【知识点】复数的基本概念与运算L4【答案解析】B:∵,且(2=a+bi,∴34ab=-⎧⎨=-⎩.则a+b=-7.故答案为:B.【思路点拨】利用复数代数形式的乘除运算化简等式左边,然后利用复数相等的条件求得a,b的值,则a+b可求.【题文】3.设等差数列{}na的前n项和为nS,若6718a a=-,则12=SA.18B.54C.72D.108 【知识点】等差数列及等差数列前n项和D2【答案解析】D ∵等差数列{an}的前n项和为Sn,a6=18-a7,∴a1+a12)=6(a6+a7)=6×18=108.故选:D.【思路点拨】利用等差数列的通项公式和前n 项和公式求解.【题文】4.为【知识点】双曲线及其几何性质H6【答案解析】A∴(2b )2=(2a )•(2c )∴b2=ac 又∵b2=c2-a2∴c2-a2=ac ∴e2-e-1=0∴e >1∴A .【思路点拨】由实轴长、虚轴长、焦距成等比数列可得b2=ac 再结合b2=c2-a2可得c2-a2=ac 即e2-e-1=0则可求出e 【题文】5.已知向量()20OB =,,向量()22OC =,,(2CA =cos 量OA与向量OB 的夹角的取值范围是【知识点】单元综合F4【答案解析】B 由题知点A 在以C (2,2∴如图示,OD ,OE为圆的切线,在△COD 中,,所以∠A 在D 处时,则OA OB与夹角最小为当A 在E 处时,则OA OB与夹角最大为∴OA OB 与夹角的取值范围是∴故答案为B【思路点拨】由题知点A 在以C (2,2)为圆心,结合来解题,由图来分析其夹角的最大最小值点.【题文】6.执行右边的程序框图,若输出的S 是127,则判断框内应该是A.5n ≤B.6n ≤C.7n ≤D.8n ≤【知识点】算法与程序框图L1【答案解析】B 第一次循环,S=1+2=3,n=2,满足条件, 第二次循环,S=3+22=7,n=3,满足条件, 第三次循环,S=7+23=15,n=4,满足条件, 第四次循环,S=15+24=31,n=5,满足条件, 第五次循环,S=31+25=63,n=6,此时满足条件,第六次循环,S=63+26=127,n=7,此时不满足条件输出S ,所以判断框的条件为n≤6? 故选B .【思路点拨】分析程序中各变量、各语句的作用,再根据流程图,可得该程序的作用是计算S=1+2+22+…+2n 的值,利用S=127,求出满足条件的n ,并确定循环的条件,据此即可得到答案.【题文】7.p 是q 的A.充分不必要 条件B.必要不充分条件C.充要条件D.既不充分也不必要条件【知识点】充分条件、必要条件A2【答案解析】AP :-2≤x≤-1,-2≤x≤p 是q 的充分不必要条件,故选A .【思路点拨】由题设知:命题p :-2≤x≤-1,命题q :-2≤x≤由此得到p 是q 的充分不必要条件,【题文】8.已知x,y 都是区间内任取的一个实数 ,则使得sin y x ≤的概率是【知识点】几何概型K3【答案解析】C 此题为几何概型,事件A的度量为函数y=sinx的图象在内与x轴围成的图形的面积,即,则事件A的概率为A【思路点拨】根据几何概型的概率公式,结合积分的应用求出对应的面积即可得到结论.【题文】9.2,则该展开式中常数项为A.-40B.40C.-20D.20 【知识点】二项式定理J3【答案解析】B 令x=1则有1+a=2,得a=1,故二项式为故其常数项为-22×C53+23C52=40故答案为B【思路点拨】由于二项式展开式中各项的系数的和为2,故可以令x=1,建立起a的方程,解出a的值来,然后再由规律求出常数项.【题文】10.若()2cos()(0)f x x mωϕω=++>对任意实数tm的值等于A.-3或1B.-1或3C.3±D.1±【知识点】三角函数的图象与性质C3【答案解析】A 因为f(x)=2cos(ωx+φ)+m,对任意实数t都有,所以函数的对称轴是,所以-1=±2+m,所以m=1或-3.故答案为:A.【思路点拨】通过,判断函数的对称轴,就是函数取得最值的x值,结合,即可求出m的值.【题文】11.过抛物线24y x=的焦点F的直线交抛物线于A,B两点,点O则AOB的面积为【知识点】抛物线及其几何性质H7【答案解析】C 设∠AFx=θ(0<θ<π)及|BF|=m,∵|AF|=3,∴点A到准线l:x=-1的距离为3∴2+3cosθ=3∴cosθm=2+mcos(π-θ)∴AOB的面积为θ【思路点拨】设∠AFx=θ(0<θ<π,利用AF|=3,可得点A到准线l:x=-1的距离为3,从而cosθ|BF|,|AB|,由此可求AOB的面积.【题文】12.设()f x是定义在R上的函数,其导函数为()f x',若()()1f x f x'+>,(0)=2015f,则不等式()2014x xe f x e>+(其中e为自然对数的底数)的解集为A.()2014+∞,B.()()02014-∞+∞,,C.()()00-∞+∞,,D.()0+∞,【知识点】导数的应用B12【答案解析】D 设g(x)=exf(x)-ex,(x∈R),则g(x)=exf(x)+exf′(x)-ex=ex[f(x)+f′(x)-1],∵f(x)+f′(x)>1,∴f(x)+f′(x)-1>0,∴g′(x)>0,∴y=g(x)在定义域上单调递增,∵exf(x)>ex+2014,∴g(x)>2014,又∵g(0)=e0f(0)-e0=2015-1=2014,∴g(x)>g(0),∴x>0故选:D.【思路点拨】构造函数g(x)=exf(x)-ex,(x∈R),研究g(x)的单调性,结合原函数的性质和函数值即可求解.第II卷(非选择题,共90分)【题文】二、填空题:本大题共4小题,每小题5分,共20分.【题文】13.若等比数列{}na满足243520,40a a a a+=+=,则57a a+=_________. 【知识点】等比数列及等比数列前n项和D3【答案解析】160 设等比数列的公比为q,∵a2+a4=20,a3+a5=40,∴a1q+a1q3=20,a1q2+a1q4=40,解得a1=q=2∴an=a1qn-1=2n,∴a5+a7=160,故答案为:160.【思路点拨】设出等比数列的首项和公比,由已知列方程组求出首项和公比,即可求出a5+a7.【题文】14.已知实数x,y满足1,21,.yy xx y m≥⎧⎪≤-⎨⎪+≤⎩,如果目标函数z x y=-的最小值是-1,则实数m等于____.【知识点】简单的线性规划问题E5【答案解析】3 作出不等式组对应的平面区域如图:由目标函数z=x-y的最小值是-1,得y=x-z,即当z=-1时,函数为y=x+1,此时对应的平面区域在直线y=x+1的下方,由121y xy x=+⎧⎨=-⎩,解得23xy=⎧⎨=⎩,即A(2,3),同时A也在直线x+y=m上,即m=2+3=5,即直线方程为x+y=5,平移直线y=x-z,当直线y=x-z经过点B时,直线y=x-z的截距最小,此时z最大.由51x yy+=⎧⎨=⎩,解得41xy=⎧⎨=⎩,即B(4,1),此时zmax=x-y=4-1=3,故答案为:3.【思路点拨】作出不等式组对应的平面区域,利用目标函数z=x-y的最小值是-1,确定m 的取值,然后利用数形结合即可得到目标函数的最大值.【题文】15.如图,网格纸的小正方形的边长是1,在其上用粗线画出了某多面体的三视图,则这个多面体的表面积为_____________.【知识点】空间几何体的三视图和直观图G2由题意可知三视图复原的几何体是底面为边长为2的正方形,一条侧棱垂直底面正方形的顶点的四棱锥,并且棱锥的高为2,所以几何体的体积为:【思路点拨】三视图复原的几何体是四棱锥,利用几何体的数据求解几何体的体积即可.【题文】16._________.【知识点】基本不等式E6【答案解析】分子分母同除2x 得到【思路点拨】利用基本不等式,求出函数f(x)的最大值与最小值,即可得出结论.【题文】三、解答题:本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.【题文】17.(本小题满分12分)在ABC中,角A,B,C所对应的边分别为a,b,c,且角A满足(1,求ABC的面积;(2【知识点】单元综合C9【答案解析】(1(1Aπ<<…………2分在ABC 中,由余弦定理得解得:b=4,(b=-2舍去). ………4分ABCS=………6分(2)原式22sin cos()sin cos()sin cos()333R CA C A C A C πππ==+++……9分33cos()cos()323C C ππ++ (12)分【思路点拨】利用余弦定理求出边进而求面积,用三角形边角之间关系求出最后结果。
河南省洛阳市2017-2018学年高三期中考试理数试题Word版含答案
洛阳市2017-2018学年高中三年级期中考试数学试卷(理) 第Ⅰ卷(选择题 共60分)一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合{}{}2|9,|2x A y y x B y y ==-==,则A B =I ( ) A .()3,3- B .[]3,3- C .(]0,3 D .[)0,32. 设复数z 满足()14z i i -=(i 是虚数单位),则z 的共轭复数z =( ) A . 22i -- B .22i -+ C .22i + D .22i -3.下列说法中正确的个数是( )①“p q ∧为真命题”是“p q ∨为真命题”的必要不充分条件; ②命题“,cos 1x R x ∀∈≤”的否定是“00,cos 1x R x ∃∈≥”; ③若一个命题的逆命题为真,则它的否命题一定为真. A . 0 B . 1 C . 2 D . 3 4. 函数()()lg 1f x x =-的大致图象是( )A .B .C. D .5. 某几何体的三视图如图所示,则该几何体的表面积为( ) A .83 B .43C. 482+.842+ 6. 等比数列{}n a 中,1102,4a a ==,函数()()()()1210f x x x a x a x a =---L ,则()0f '=( )A .62B .92 C. 122 D .152 7. 将函数sin cos 22y x x ϕϕ⎛⎫⎛⎫=++ ⎪ ⎪⎝⎭⎝⎭的图象沿x 轴向左平移8π个单位后,得到一个偶函数的图象,则ϕ的取值不可能是( )A . 34π-B .4π- C. 4πD .54π 8. 向量,a b r r 均为非零向量,()()2,2a b a b a b -⊥-⊥r r r r r r ,则,a b r r的夹角为( )A .3π B . 2πC. 23π D .56π9. 已知数列{}n a的首项11=0,1n n a a a +=+,则20a =( ) A .99 B .101 C. 399 D .40110.在三棱锥S ABC -中,底面ABC ∆是直角三角形,其斜边4,AB SC =⊥平面ABC ,且3SC =,则此三棱锥的外接球的表面积为( ) A .25π B .20π C. 16π D .13π11.已知函数()124,041,0x x f x x x x -⎧>⎪=⎨--+≤⎪⎩,若关于x 的方程()()2220f x af x a -++=有8个不等的实数根,则实数a 的取值范围是 ( ) A .181,7⎛⎫ ⎪⎝⎭ B .91,4⎛⎫ ⎪⎝⎭C. 182,7⎛⎫ ⎪⎝⎭ D .92,4⎛⎫⎪⎝⎭ 12. 用[]x 表示不超过x 的最大整数(如[][]2,12,3,54=-=-).数列{}n a 满足()()*114,113n n n a a a a n N +=-=-∈,若12111n n S a a a =+++L ,则[]n S 的所有可能值的个数为( )A . 4B . 3 C. 2 D .1第Ⅱ卷(非选择题,共90分)二、填空题:本大题共4小题,每小题5分,满分20分,将答案填在答题纸上13.设变量x y 、满足约束条件:222y xx y x ≥⎧⎪+≤⎨⎪≥-⎩,则22z x y =+的最大值是 .14.若定义在[)1,-+∞上的函数()21143,1x f x x x x -≤≤=-+>⎪⎩,则()31f x dx -=⎰ .15.设x y 、均为正数,且1111212x y +=++,则xy 的最小值为 . 16.已知函数()f x 是定义在R 上的偶函数,其导函数为()f x ',且当0x <时,()()20f x xf x '+<,则不等式()()()22017201710x f x f ----<的解集为 .三、解答题 :本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.17.已知向量(()sin ,,1,cos a x b x ==r r.(1)若a b ⊥r r,求tan 2x 的值;(2)令()f x a b =r rg ,把函数()f x 的图象上每一点的横坐标都缩小为原来的一半(纵坐标不变),再把所有图象沿x 轴向左平移3π个单位,得到函数()y g x =的图象,求函数()y g x =的单调增区间及图象的对称中心.18.已知数列{}n a 满足()1112,21n n n n a a a na n a ++=+=+,设n nn b a =. (1)求证:数列{}1n b -为等比数列,并求{}n a 的通项公式; (2)设1n nc b =,数列{}n c 的前n 项和为n S ,求证:2n S n <+. 19.在ABC ∆中,,,a b c 分别是角,,A B C 的对边,且()2cos cos tan tan 11A C A C -=. (1)求B 的大小;(2)若D 为AC 的中点,且1BD =,求ABC ∆面积的最大值.20. 已知函数()()2x f x x mx n e =++,其导函数()y f x '=的两个零点为-3和0. (1)求曲线()y f x =在点()()1,1f 处的切线方程; (2)求函数()f x 的单调区间;(3)求函数()f x 在区间[]2,2-上的最值.21. 如图,四棱锥P ABCD -中,底面ABCD 为梯形,PD ⊥底面ABCD ,//,,1,AB CD AD CD AD AB BC ⊥===(1)求证:平面PBD ⊥平面PBC ;(2)设H 为CD 上一点,满足23CH HD =u u u r u u u r,若直线PC 与平面PBD 所成的角的正切值为H PB C --的余弦值. 22. 已知函数()()22ln f x x x mx m R =+-∈.(1)若()f x 在其定义域内单调递增,求实数m 的取值范围; (2)若1752m <<,且()f x 有两个极值点()1212,x x x x <,求()()12f x f x -取值范围. 试卷答案一、选择题1-5:CABBD 6-10: DBACA 11、12:CB 二、填空题 13. 8 14. 423π-15. 9216. {}|20162018x x x <>或 三、解答题17.(1)∵(()sin ,1,cos 0a b x x ==r rg g ,即sin 0x x =,∴tan x =∴22tan tan 21tan xx x==-. (2)由(1)得()2sin 3f x x π⎛⎫=- ⎪⎝⎭,从而()2sin 23g x x π⎛⎫=+⎪⎝⎭. 解222232k x k πππππ-≤+≤+得()51212k x k k Z ππππ-≤≤+∈, ∴()g x 的单调增区间是()5,1212k k k Z ππππ⎡⎤-+∈⎢⎥⎣⎦, 由23x k ππ+=得()126x k k Z ππ=-∈,即函数()y g x =图象的对称中心为()1,026k k Z ππ⎛⎫-∈⎪⎝⎭.18.(1)由已知易得0n a ≠,由()1121n n n n a a na n a +++=+, 得()1211n n n n a a +++=,即121n n b b +=+; ∴()11112n n b b +-=-, 又111112n b a -=-=-, ∴{}1n b -是以12-为首项,以12为公比的等比数列. 从而11111222n nn b -⎛⎫⎛⎫⎛⎫-=-=- ⎪ ⎪⎪⎝⎭⎝⎭⎝⎭g ,即112nn n a ⎛⎫=- ⎪⎝⎭,整理得221n n n n a =-g ,即数列{}n a 的通项公式为221nn n n a =-g .(2)∵112nn b ⎛⎫=- ⎪⎝⎭,∴12112121112n n n n n c ===+--⎛⎫- ⎪⎝⎭, ∴23012111111111212121212222n n n S n n -=+++++≤+++++----L L , 11222n n n -=+-<+.19.(1)由()2cos cos tan tan 11A C A C -=,得sin sin 2cos cos 11cos cos A C A C A C ⎛⎫-= ⎪⎝⎭,∴()2sin sin cos cos 1A C A C -=,∴()1cos 2A C +=-, ∴1cos 2B =, 又0B π<<,∴3B π=.(2)在ABD ∆中由余弦定理得22121cos 22b b c ADB ⎛⎫=+-∠ ⎪⎝⎭g g ,在CBD ∆中由余弦定理得22121cos 22b b a CDB ⎛⎫=+-∠ ⎪⎝⎭g g ,二式相加得222222cos 2222b ac ac Ba c +-+=+=+, 整理得224a c ac +=-, ∵222a c ac +≥,∴43ac ≤,所以ABC ∆的面积114sin 223S ac B =≤=g .当且仅当3a c ==时“=”成立,∴ABC ∆面积的最大值为3. 20.(1)∵()()2x f x x mx n e =++,∴()()()()()2222x x xf x x m e x mx n e x m x m n e '⎡⎤=++++=++++⎣⎦,由()()3000f f '-=⎧⎪⎨'=⎪⎩知()()93200m m n m n ⎧-+++=⎨+=⎩,解得11m n =⎧⎨=-⎩,从而()()21x f x x x e =+-,∴()()23x f x x x e '=+, 所以()1f e =,∴()14f e '=,曲线()y f x =在点()()1,1f 处的切线方程为()41y e e x -=-, 即43y ex e =-.(2)由于0x e >,当x 变化时,()(),f x f x '的变化情况如下表:故()f x 的单调增区间是(),3-∞-,()0,+∞,单调减区间是()3,0-, (3)由于()225f e =,()()201,2f f e -=--=,所以函数()f x 在区间[]2,2-上的最大值为25e ,最小值为-1. 21.(1)由,//,1AD CD AB CD AD AB ⊥==,可得BD =又4BC BDC π=∠=,∴BC BD ⊥,从而2CD =,∵PD ⊥底面ABCD ,∴BC PD ⊥.∵PD BD D =I ,∴BC ⊥平面PBD ,所以平面PBD ⊥平面PBC . (2)由(1)可知BPC ∠为PC 与底面PBD 所成的角.所以tan BPC ∠=,所以1PB PD ==, 又23CH HD =uuu r uuu r ,及2CD =,可得64,55CH DH ==,以D 点为坐标原点,,,DA DC DP 分别,,x y z 轴建立空间直角坐标系, 则()()()41,1,0,0,0,1,0,2,0,0,,05B PC H ⎛⎫ ⎪⎝⎭.设平面HPB 的法向量为(),,n x y z =r,则由00n HP n PB ⎧=⎪⎨=⎪⎩r uu u r g r uu r g 得4050y z x y z ⎧-+=⎪⎨⎪+-=⎩,取()1,5,4n =--r ,同理平面PBC 的法向量为()1,1,2m =u r.所以cos ,m n m n m n==u r ru r r g u r r又二面角H PB C --为锐角, 所以二面角H PB C --余弦值为7. 22.(1)()f x 的定义域为()0+∞,,()f x 在定义域内单调递增,()220f x x m x '=+-≥,即22m x x≤+在()0+∞,上恒成立, 由于224x x+≥,所以4m ≤,实数m 的取值范围是(],4-∞. (2)由(1)知()22222x mx f x x m x x -+'=+-=,当1752m <<时()f x 有两个极值点,此时1202mx x +=>,121x x =, ∴1201x x <<<, 因为1111725,2m x x ⎛⎫⎛⎫=+∈⎪ ⎪⎝⎭⎝⎭,解得11142x <<,由于211x x =,于是()()()()22121112222ln 2ln f x f x x mx x x mx x -=-+--+ ()()()222121212112112ln ln 4ln x x m x x x x x x x =---+-=-+, 令()2214ln h x x x x =-+,则()()223210x h x x --'=<, ∴()h x 在1142⎛⎫⎪⎝⎭,上单调递减,()1124h h x h ⎛⎫⎛⎫<< ⎪ ⎪⎝⎭⎝⎭, 即()()()()121141ln 2161ln 2416f x f x --<-<--, 故()()12f x f x -的取值范围为15255ln 216ln 2416⎛⎫-⎪⎝⎭-4,.。
河南省洛阳市2017届高三上学期期中考试数学理试卷Word版含解析

洛阳市2016—2017学年高中三年级期中考试数 学 试 卷(理)一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.集合{}Z x x x A ∈=,<<3log 12,{}95<x x B ≤=,则=⋂B A ( )A .),5[2e B.]7,5[ C .}7,6,5{ D .}8,7,6,5{ 2.复数ii ++12的共扼复数是( ) A .i 2123+- B .i 2123-- C.i 2123- D .i 2123+ 3.设n m ,是两条不同的直线,βα,是两个不同的平面,下列命题是真命题的是( )A .若α//m ,β//m ,则βα//B .若α//m ,βα//,则β//mC .若α⊂m ,β⊥m ,则βα⊥D .若α⊂m ,βα⊥,则β⊥m4.函数)42cos(ln π+=x y 的一个单调递减区间是( ) A .)8,85(ππ-- B .)8,83(ππ-- C .)8,8(ππ-- D .)83,8(ππ- 5.O 为△ABC 内一点,且02=++,t =,若D O B ,,三点共线,则t 的值为( )A .41B .31C .21 D.32 6.一个几何体的三视图都是边长为1的正方形,如图,则该几何体的体积是( )A .121B .31 C .42 D.21 7.由2,1,===x xy x y 及x 轴所围成的平面图形的面积是( ) A .12ln + B .2ln 2- C .212ln - D.212ln + 8.直角△ABC 中,∠C =90°,D 在BC 上,CD =2DB ,tan ∠BAD =51,则BAC ∠sin =( )A .22B .23C .13133 D.22或13133 9.已知函数)(x f 是R 上的奇函数,且满足)()2(x f x f -=+,当]1,0[∈x 时,x x f =)(,则方程182)(+-=x x x f 在),0(+∞解的个数是( ) A .3 B .4 C .5 D.610.已知数列n S 为等比数列{}n a 的前n 项和,14,2248==S S ,则=2016S ( )A .22252-B .22253-C .221008- D.222016-11.已知三棱锥ABC P -中,1===AC PB PA ,⊥PA 面ABC ,∠BAC =32π,则三棱锥ABC P -的外接球的表面积为( )A .π3B .π4C .π5 D.π812.定义在R 上的函数)(x f 满足:x e x x f x f ∙=-')()(,且21)0(=f ,则)()(x f x f '的最大值为( )A .0B .21 C .1 D.2第Ⅱ卷(非选择题,共90分)二、填空题:本大题共4小题,每小题5分,共20分.13.若21cos sin cos sin =+-αααα,则α2tan 的值为 . 14.等差数列{}n a 中,n S 为其前n 项和,若105=a ,305=S ,则20163211...111S S S S ++++= .15.等腰△ABC 中,底边BC =23,-,则△ABC 的面积为 . 16.b a ,为正数,给出下列命题:①若122=-b a ,则1<b a -;②若111=-a b ,则1<b a -; ③1=-b a e e ,则1<b a -; ④若1ln ln =-b a ,则1<b a -.其中真命题的有 .三、解答题:本大题共6小题,共70分.解答应写出文字说明,证明过程或演算步骤.17.(本小题满分10分)数列{}n a 中, 11=a ,11++=-n n n n a a a a ,*∈N n .(1)求数列{}n a 的通项公式;(2)n S 为{}n a 的前n 项和,n b =n n S S -2,求n b 的最小值.18.(本小题满分12分) 函数))2,2(0)(sin(ππϕωϕω-∈+=,>x y 的一条对称轴为3π=x ,一个对称中心为)0,127(π,在区间]3,0[π上单调. (1)求ϕω,的值; (2)用描点法作出)sin(ϕω+=x y 在],0[π上的图像.19.(本小题满分12分)锐角△ABC 中,其内角A 、B 满足:B B ocsA cos 3sin 2-=.(1)求角C 的大小;(2)D 为AB 的中点,CD =1,求△ABC 面积的最大值.20.(本小题满分12分)函数x e x x f ∙=)(.(1)求)(x f 的极值;(2)x x x f k +≥⨯221)(在),1[+∞-上恒成立,求k 值的集合.21.(本小题满分12分)等腰△ABC 中,AC =BC =5,AB =2,E 、F 分别为AC 、BC 的中点,将△EFC 沿EF 折起,使得C 到P ,得到四棱锥P —ABFE ,且AP =BP =3.(1)求证:平面EFP ⊥平面ABFE ;(2)求二面角B-AP-E 的大小.22.(本小题满分12分)已知函数xk x x f -=ln )(有两个零点1x 、2x . (1)求k 的取值范围;(2)求证:ex x 221>+.2016-2017学年河南省洛阳市高三(上)期中数学试卷(理科)参考答案与试题解析一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.(5分)(2016秋•洛阳期中)集合A={x|1<log2x<3,x∈Z},B={x|5≤x<9},则A∩B=()A. C.{5,6,7} D.{5,6,7,8}【考点】交集及其运算.【专题】对应思想;定义法;集合.【分析】化简集合A,再求A∩B的值.【解答】解:集合A={x|1<log2x<3,x∈Z}={x|2<x<8,x∈Z}={3,4,5,6,7},B={x|5≤x<9},∴A∩B={5,6,7}.故选:C.【点评】本题考查了集合的化简与运算问题,是基础题目.2.(5分)(2016秋•洛阳期中)复数的共扼复数是()A.﹣+i B.﹣﹣i C.﹣i D.+i【考点】复数代数形式的乘除运算.【专题】转化思想;数系的扩充和复数.【分析】利用复数的运算法则、共轭复数的定义即可得出.【解答】解:复数==的共扼复数是+i.故选:D.【点评】本题考查了复数的运算法则、共轭复数的定义,考查了推理能力与计算能力,属于基础题.3.(5分)(2016秋•洛阳期中)设m ,n 是两条不同的直线,α,β是两个不同的平面,下列命题是真命题的是( )A .若m ∥α,m ∥β,则α∥βB .若m ∥α,α∥β,则m ∥βC .若α⊂m ,β⊥m ,则βα⊥D .若α⊂m ,βα⊥,则β⊥m【考点】空间中直线与平面之间的位置关系.【专题】计算题;转化思想;综合法;空间位置关系与距离.【分析】在A 中,α与β相交或平行;在B 中,m ∥β或m ⊂β;在C 中,由面面垂直的判定定理得α⊥β;在D 中,m ⊥与β相交、平行或m ⊂β.【解答】解:由m ,n 是两条不同的直线,α,β是两个不同的平面,知:在A 中,若m ∥α,m ∥β,则α与β相交或平行,故A 错误;在B 中,若m ∥α,α∥β,则m ∥β或m ⊂β,故B 错误;在C 中,若α⊂m ,m ⊥β,则由面面垂直的判定定理得α⊥β,故C 正确;在D 中,若α⊂m ,α⊥β,则m ⊥与β相交、平行或m ⊂β,故D 错误.故选:C .【点评】本题考查命题真假的判断,是基础题,解题时要认真审题,注意空间中线线、线面、面面间的位置关系的合理运用.4.(5分)(2016秋•洛阳期中)函数y=lncos (2x+)的一个单调递减区间是( ) A .(﹣,﹣) B .(﹣,﹣) C .(﹣,﹣) D .(﹣,)【考点】复合函数的单调性.【专题】函数思想;转化法;函数的性质及应用.【分析】先求出函数的定义域,结合复合函数单调性的关系进行求解即可.【解答】解:设t=cos (2x+),则lnt 在定义域上为增函数, 要求函数y=lncos (2x+)的一个单调递减区间, 即求函数函数t=cos (2x+)的一个单调递减区间,同时t=cos (2x+)>0, 即2k π≤2x+<2k π+,k ∈Z , 即k π﹣≤x <k π+,k ∈Z ,当k=0时,﹣≤x<,即函数的一个单调递减区间为(﹣,﹣),故选:C【点评】本题主要考查函数单调区间的求解,利用复合函数单调性之间的关系以及对数函数和三角函数的性质是解决本题的关键.5.(5分)(2016秋•洛阳期中)O为△ABC内一点,且2++=,=t,若B,O,D三点共线,则t的值为()A.B.C.D.【考点】平行向量与共线向量.【专题】数形结合;转化思想;平面向量及应用.【分析】以OB,OC为邻边作平行四边形OBFC,连接OF与 BC相交于点E,E为BC的中点.2++=,可得=﹣2==2,因此点O是直线AE的中点.可得B,O,D三点共线,=t,∴点D是BO与AC的交点.过点O作OM∥BC交AC于点M,点M为AC 的中点.利用平行线的性质即可得出.【解答】解:以OB,OC为邻边作平行四边形OBFC,连接OF与 BC相交于点E,E为BC的中点.∵2++=,∴=﹣2==2,∴点O是直线AE的中点.∵B,O,D三点共线,=t,∴点D是BO与AC的交点.过点O作OM∥BC交AC于点M,则点M为AC的中点.则OM=EC=BC,∴=,∴,∴AD=AM=AC,=t,∴t=.故选:B.【点评】本题考查了向量三角形法则、平行线的性质定理、向量共线定理三角形中位线定理,考查了推理能力与计算能力,属于难题.6.(5分)(2016秋•洛阳期中)一个几何体的三视图都是边长为1的正方形,如图,则该几何体的体积是()A.B.C.D.【考点】由三视图求面积、体积.【专题】数形结合;转化思想;空间位置关系与距离.【分析】把三视图还原成原图如图:是一个棱长为1的正方体切去了四个小三棱锥.【解答】解:把三视图还原成原图如图:是一个棱长为1的正方体切去了四个小三棱锥.∴V=1﹣=.故选:B.【点评】本题考查了正方体与四棱锥的三视图、体积计算公式,考查了推理能力与计算能力,属于中档题.7.(5分)(2016秋•洛阳期中)由y=x,y=,x=2及x轴所围成的平面图形的面积是()A.ln2+1 B.2﹣ln2 C.ln2﹣D.ln2+【考点】定积分在求面积中的应用.【专题】计算题;转化思想;综合法;导数的概念及应用.【分析】利用定积分的几何意义,首先表示平面图形,然后计算定积分.【解答】解:由题意,由y=x,y=,x=2及x轴所围成的平面图形如图,其面积是;故选:D.【点评】本题考查了定积分的应用;关键是将曲边梯形的面积正确利用定积分表示,然后正确计算.8.(5分)(2016秋•洛阳期中)直角△ABC中,∠C=90°,D在BC上,CD=2DB,tan∠BAD=,则sin∠BAC=()A.B.C.D.或【考点】正弦定理.【专题】计算题;转化思想;数形结合法;解三角形.【分析】设DE=k,BD=x,CD=2x,BC=3x,先在Rt△ADE中,由tan∠BAD=,得出AE=5k,AD=k,在Rt△BDE中,由勾股定理求出BE,于是AB=AE+BE=5k+,然后根据AC的长度不变得出AD2﹣CD2=AB2﹣BC2,即26k2﹣4x2=(5k+)2﹣9x2,解方程求出x=k,或x=k,然后在Rt△ABC中利用正弦函数的定义即可求解.【解答】解:设DE=k,BD=x,CD=2x,BC=3x.∵在Rt△ADE中,∠AED=90°,tan∠BAD==,∴AE=5DE=5k,∴AD==k.∵在Rt△BDE中,∠BED=90°,∴BE==,∴AB=AE+BE=5k+.∵∠C=90°,∴AD2﹣CD2=AB2﹣BC2,即26k2﹣4x2=(5k+)2﹣9x2,解得k2=x2,或x2,即x=k,或x=k,经检验,x=k,或x=k是原方程的解,∴BC=3k,或k,AB=AE+BE=5k+=6k,或,∴sin∠BAC==,或.【点评】本题考查了解直角三角形,勾股定理,锐角三角函数的定义,设DE=k,BD=CD=x,利用勾股定理列出方程26k2﹣4x2=(5k+)2﹣9x2是解题的关键,本题也考查了解无理方程的能力,考查了转化思想和数形结合思想,计算量较大,属于难题.9.(5分)(2016秋•洛阳期中)已知函数f(x)是R上的奇函数,且满足f(x+2)=﹣f(x),当x∈时,f(x)=x,则方程f(x)=在(0,+∞)解的个数是()A.3 B.4 C.5 D.6【考点】函数奇偶性的性质.【专题】综合题;数形结合;综合法;函数的性质及应用.【分析】确定f(x)是以4为周期的周期函数,关于直线x=1对称,作出相应函数的图象,即可得出结论.【解答】解:∵f(x+2)=﹣f(x),∴f(x+4)=﹣f(x+2)=f(x).∴f(x)是以4为周期的周期函数.∵f(x+2)=﹣f(x)=f(﹣x),∴函数关于直线x=1对称,在(0,+∞)上函数y=f(x)与y=的图象如图所示,交点有4个,∴方程f(x)=在(0,+∞)解的个数是4,故选B.【点评】本题考查函数的奇偶性、对称性、周期性,考查数形结合的数学思想,属于中档题.10.(5分)(2016秋•洛阳期中)已知数列S n为等比数列{a n}的前n项和,S8=2,S24=14,则S2016=()A.2252﹣2 B.2253﹣2 C.21008﹣2 D.22016﹣2【考点】等比数列的前n项和.【专题】计算题;转化思想;整体思想;等差数列与等比数列.【分析】由S n为等比数列{a n}的前n项和,由前n项和公式求得a1和q的数量关系,然后再来解答问题.【解答】解:∵数列S n为等比数列{a n}的前n项和,S8=2,S24=14,∴=2,①=14,②由②÷①得到:q8=2或q8=﹣3(舍去),∴=2,则a1=2(q﹣1),∴S2016===2253﹣2.故选:B.【点评】本题考查了等边数量的前n项和,熟练掌握等比数列的性质是解题的关键,注意:本题中不需要求得首项和公比的具体数值.11.(5分)(2016秋•洛阳期中)已知三棱锥P﹣ABC中,PA=AB=AC=1,PA⊥面ABC,∠BAC=,则三棱锥P﹣ABC的外接球的表面积为()A.3πB.4πC.5πD.8π【考点】球内接多面体.【专题】综合题;方程思想;综合法;立体几何.【分析】求出BC,可得△ABC外接圆的半径,进而可得三棱锥P﹣ABC的外接球的半径,即可求出三棱锥P﹣ABC的外接球的表面积.【解答】解:△ABC中,BC==.设△ABC外接圆的半径为r,则2r=,∴r=1,∴三棱锥P﹣ABC的外接球的半径为=,∴三棱锥P﹣ABC的外接球的表面积为=5π.故选:C.【点评】本题考查三棱锥P﹣ABC的外接球的表面积,考查学生的计算能力,确定三棱锥P﹣ABC的外接球的半径是关键.12.(5分)(2016秋•洛阳期中)定义在R上的函数f(x)满足:f′(x)﹣f(x)=x•e x,且f(0)=,则的最大值为()A.0 B.C.1 D.2【考点】导数的运算.【专题】综合题;函数思想;综合法;导数的概念及应用.【分析】先构造函数,F(x)=,根据题意求出f(x)的解析式,即可得到=,再根据根的判别式即可求出最大值.【解答】解:令F(x)=,则F′(x)===x,则F(x)=x2+c,∴f(x)=e x(x2+c),∵f(0)=,∴c=,∴f(x)=e x(x2+),∴f′(x)=e x(x2+)+x•e x,∴=,设y=,则yx2+y=x2+2x+1,∴(1﹣y)x2+2x+(1﹣y)=0,当y=1时,x=0,当y≠1时,要使方程有解,则△=4﹣4(1﹣y)2≥0,解得0≤y≤2,故y的最大值为2,故的最大值为2,故选:D.【点评】本题考查了导数和函数的关系以及函数的值域问题,关键是构造函数和利用根的判别式求函数的值域,属于中档题.二、填空题:本大题共4小题,每小题5分,共20分.13.(5分)(2016秋•洛阳期中)若=,则tan2α的值为﹣.【考点】同角三角函数基本关系的运用.【专题】转化思想;综合法;三角函数的求值.【分析】利用同角三角函数的基本关系求得tanα的值,再利用二倍角的正切公式求得tan2α的值.【解答】解:若==,则tanα=3,∴tan2α===﹣,故答案为:﹣.【点评】本题主要考查同角三角函数的基本关系,二倍角的正切公式的应用,属于基础题.14.(5分)(2016秋•洛阳期中)等差数列{a n}中,S n为其前n项和,若a5=10,S5=30,则+++…+= .【考点】数列的求和;等差数列的前n项和.【专题】方程思想;转化思想;等差数列与等比数列.【分析】设等差数列{a n}的公差为d,由a5=10,S5=30,可得,解得a1,d.可得S n,再利用“裂项求和”方法即可得出.【解答】解:设等差数列{a n}的公差为d,∵a5=10,S5=30,∴,解得a1=d=2.∴S n==n(n+1),∴==.则+++…+=++…+=1﹣=.故答案为:.【点评】本题考查了等比数列与等差数列的通项公式、“裂项求和”方法,考查了推理能力与计算能力,属于中档题.15.(5分)(2016秋•洛阳期中)等腰△ABC中,底边BC=2,|﹣t|的最小值为||,则△ABC的面积为.【考点】平面向量数量积的运算.【专题】转化思想;综合法;平面向量及应用.【分析】由题意可得BC边上的高为||,利用直角三角形中的边角关系求得∠C=30°=∠B,可得∠A=120°,AB=AC,利用余弦定理求得AB=AC的值,可得△ABC的面积•AB•AC•sin120° 的值.【解答】解:等腰△ABC中,底边BC=2,|﹣t|的最小值为||,则△ABC的面积故BC边上的高为||,故有sin∠C==,∴∠C=30°=∠B,∴∠A=120°,AB=AC,∴=AB2+AC2﹣2AB•AC•cos120°,∴AB=AC=2,∴△ABC的面积为•AB•AC•sin120°=,故答案为:.【点评】本题主要考查两个向量的数量积的运算,直角三角形中的边角关系,余弦定理,属于中档题.16.(5分)(2016秋•洛阳期中)a,b为正数,给出下列命题:①若a2﹣b2=1,则a﹣b<1;②若﹣=1,则a﹣b<1;③e a﹣e b=1,则a﹣b<1;④若lna﹣lnb=1,则a﹣b<1.期中真命题的有①③.【考点】不等式的基本性质.【专题】综合题;转化思想;综合法;不等式.【分析】不正确的结论,列举反例,正确的结论,进行严密的证明,即可得出结论.【解答】解:①中,a,b中至少有一个大于等于1,则a+b>1,由a2﹣b2=(a+b)(a﹣b)=1,所以a﹣b<1,故①正确.②中﹣==1,只需a﹣b=ab即可,取a=2,b=满足上式但a﹣b=>1,故②错;③构造函数y=x﹣e x,x>0,y′=1﹣e x<0,函数单调递减,∵e a﹣e b=1,∴a>b,∴a﹣e a<b﹣e b,∴a﹣b<e a﹣e b=1,故③正确;④若lna﹣lnb=1,则a=e,b=1,a﹣b=e﹣1>1,故④不正确.故答案为:①③.【点评】本题考查不等式的性质、导数的应用等基础知识,意在考查学生分析问题解决问题的能力、推理能力、运用转化与化归思想的能力.三、解答题:本大题共6小题,共70分.解答应写出文字说明,证明过程或演算步骤. 17.(10分)(2016秋•洛阳期中)数列{a n}中,a1=1,a n﹣a n+1=a n a n+1,n∈N*.(1)求数列{a n}的通项公式;(2)S n为{a n}的前n项和,b n=S2n﹣S n,求b n的最小值.【考点】数列的求和;数列递推式.【专题】方程思想;转化思想;等差数列与等比数列.【分析】(1)由a1=1,a n﹣a n+1=a n a n+1,n∈N*.可得=1,利用等差数列的通项公式即可得出.(2)由(1)可得:b n=S2n﹣S n=+…+.再利用数列的单调性即可得出.【解答】解:(1)∵a1=1,a n﹣a n+1=a n a n+1,n∈N*.∴=1,∴数列是等差数列,公差为1,首项为1.∴=1+(n﹣1)=n,可得a n=.(2)由(1)可得:S n=1++…+.∴b n=S2n﹣S n=+…+.∴b n+1﹣b n=+…+++﹣(+…+)=+﹣=﹣>0,∴数列{b n}单调递增,∴b n的最小值为b1=.【点评】本题考查了等差数列的通项公式与求和公式、数列的单调性,考查了推理能力与计算能力,属于中档题.18.(12分)(2016秋•洛阳期中)函数y=﹣sin(ωx+φ)(ω>0,φ∈(﹣,))的一条对称轴为x=,一个对称中心为(,0),在区间上单调.(1)求ω,φ的值;(2)用描点法作出y=sin(ωx+φ)在上的图象.【考点】五点法作函数y=Asin(ωx+φ)的图象;正弦函数的图象.【专题】综合题;转化思想;数形结合法;三角函数的图像与性质.【分析】(1)由条件利用三角形函数的周期,对称轴,对称中心,即可ω,φ.(2)用五点法作函数y=Asin(ωx+φ)在一个周期上的图象.【解答】解:(1)由题意得:,即,解得又ω>0,k∈Z,所以ω=2,x=为对称轴,2×+φ=kπ+,所以φ=kπ﹣,又φ∈(﹣,),∴φ=﹣,(2)由(1)可知f(x)=sin(2x﹣),由x∈,所以2x﹣∈,列表:﹣﹣画图:【点评】本题主要考查三角函数的周期,用五点法作函数y=Asin(ωx+φ)的图象,属于中档题.19.(12分)(2016秋•洛阳期中)锐角△ABC中,其内角A、B满足:2cosA=sinB﹣cosB.(1)求角C的大小;(2)D为AB的中点,CD=1,求△ABC面积的最大值.【考点】正弦定理;三角函数的化简求值.【专题】计算题;转化思想;数形结合法;解三角形.【分析】(1)由已知利用特殊角的三角函数值,两角差的正弦函数公式可得cosA=cos(﹣B),结合A,B为锐角,利用三角形内角和定理可求C的值.(2)设∠ACD=α,延长CD到E,使CD=DE,则AEBC为平行四边形,在△ACE中,由正弦定理可得a=4sinα,b=4sin(﹣α),利用三角形面积公式,三角函数恒等变换的应用化简可得S△ABC=2sin(2α+)﹣,利用正弦函数的性质可求△ABC面积的最大值.【解答】(本题满分为12分)解:(1)∵2cosA+cosB=sinB,可得:cosA=sinB﹣cosB=cos(﹣B),…2分又∵A,B为锐角,∴0,<﹣B<,∴A=﹣B,A+B=,可得:C=π﹣=.…5分(2)设∠ACD=α,延长CD到E,使CD=DE,则AEBC为平行四边形,在△ACE中,AC=b,AE=BC=α,CE=2,∠CAE=,∠AEC=﹣α,由正弦定理可得:==,所以,a=4sinα,b=4sin(﹣α),…7分S△ABC=absin∠ABC=sin=4sinα•sin(﹣α)=2sinαcosα﹣2sin2α=sin2α+cos2α﹣=2sin(2α+)﹣,…11分当α=时,△ABC的面积取得最大值,最大值为2﹣.…12分【点评】本题主要考查了特殊角的三角函数值,两角差的正弦函数公式,三角形内角和定理,正弦定理,三角形面积公式,三角函数恒等变换的应用,正弦函数的性质在解三角形中的综合应用,考查了转化思想和数形结合思想,综合性较强,属于中档题.20.(12分)(2016秋•洛阳期中)函数f(x)=x•e x.(1)求f(x)的极值;(2)k×f(x)≥x2+x在递减,φ(x)≥φ(0)=1,故k≤1,综上,k=1,故k∈{1}.【点评】本题考查了函数的单调性、最值问题,考查导数的应用以及转化思想,是一道中档题.21.(12分)(2016秋•洛阳期中)等腰△ABC中,AC=BC=,AB=2,E、F分别为AC、BC的中点,将△EFC沿EF折起,使得C到P,得到四棱锥P﹣ABFE,且AP=BP=.(1)求证:平面EFP⊥平面ABFE;(2)求二面角B﹣AP﹣E的大小.【考点】二面角的平面角及求法;平面与平面垂直的判定.【专题】转化思想;运动思想;空间角;立体几何.【分析】(1)用分析法找思路,用综合法证明.取EF中点O,连接OP、OC.等腰三角形CEF 中有CO⊥EF,即OP⊥EF.根据两平面垂直的性质定理,平面PEF和平面ABFE的交线是EF,且PO⊥EF,分析得PO⊥平面ABFE.故只需根据题中条件证出PO⊥平面ABFE,即可利用面面垂直的判定定理证得平面EFP⊥平面ABFE.(2)根据第一问分析空间位置关系,可建立空间直角坐标线求得平面ABP和平面AEP的法向量的所成角,利用向量角和二面角关系,确定二面角大小.【解答】解:(1)证明:在△ABC中,D为AB中点,O为EF中点.由AC=BC=,AB=2.∵E、F分别为AC、BC的中点,∴EF为中位线,得CO=OD=1,CO⊥EF∴四棱锥P﹣ABFE中,PO⊥EF,…2分∵OD⊥AB,AD=OD=1,∴AO=,又AP=,OP=1,∴四棱锥P﹣ABFE中,有AP2=AO2+OP2,即OP⊥AO,…4分又AO∩EF=O,EF、AO⊂平面ABFE,∴OP⊥平面ABFE,…5分又OP⊂平面EFP,∴平面EFP⊥平面ABFE.…6分(2)由(1)知OD,OF,OP两两垂直,以O为原点,建立空间直角坐标系(如图):则A(1,﹣1,0),B(1,1,0),E(0,,0),P(0,0,1)…7分∴,,设,分别为平面AEP、平面ABP的一个法向量,则⇒取x=1,得y=2,z=﹣1∴.…9分同理可得,…11分由于=0,所以二面角B﹣AP﹣E为90°.…12分【点评】证面面垂直,找对线面垂直是解决问题的关键,求二面角转化为向量角是解决问题方向.考查了空间位置关系,用勾股定理确定垂直关系,求二面角大小的空间向量法,平面法向量的求解方法.考查了折叠问题的运动思想,空间想象能力,分析问题解决问题的能力,化归与转化的能力.属于中档题.22.(12分)(2016秋•洛阳期中)已知函数f(x)=lnx﹣有两个零点x1、x2.(1)求k的取值范围;(2)求证:x1+x2>.【考点】利用导数研究函数的单调性;函数零点的判定定理.【专题】函数思想;综合法;函数的性质及应用.【分析】(1)问题转化为函数g(x)=xlnx的图象与直线y=k有2个交点,求出g(x)的单调性,画出函数图象,从而求出k的范围即可;(2)设x1<x2,根据函数的单调性得到x2,﹣x1∈(,+∞),g(x)在(,+∞)递增,从而证出结论即可.【解答】解:(1)函数f(x)=lnx﹣有2个零点,即函数g(x)=xlnx的图象与直线y=k有2个交点,g′(x)=lnx+1,令g′(x)>0,解得:x>,令g′(x)<0,解得:0<x<,∴g(x)在(0,)递减,在(,+∞)递增,x=是极小值点,g()=﹣,又x→0时,g(x)→0,x→+∞时,g(x)→+∞,g(1)=0,g(x)的大致图象如图示:;由图象得:﹣<k<0,(2)证明:不妨设x1<x2,由(1)得:0<x1<<x2<1,令h(x)=g(x)﹣g(﹣x)=xlnx﹣(﹣x)ln(﹣x),h′(x)=ln,当0<x<时,h′(x)<0,h(x)在(0,)递减,h()=0,∴h(x1)>0,即g(x1)>g(﹣x1),g(x2)>g(﹣x1),x2,﹣x1∈(,+∞),g(x)在(,+∞)递增,∴x2>﹣x1,故x1+x2>.【点评】本题考查了函数的单调性、极值问题,考查导数的应用以及函数零点问题,是一道中档题.。
高三数学上学期期中试题理(含解析)

洛阳市2017—2018学年高中三年级期中考试数学试卷(理)一、选择题:本大题共12个小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的、1、已知集合,,则( )A、 B、C。
D。
【答案】C【解析】因为, ,因此因为,因此 ,,选C、2。
设复数满足(是虚数单位),则的共轭复数( )A、 B、C。
D、【答案】A【解析】,,,故选A。
3、下列说法中正确的个数是( )①“为真命题”是“为真命题”的必要不充分条件;②命题“,”的否命题是“,”;③若一个命题的逆命题为真,则它的否命题一定为真、A、0 B、 1 C、 2 D、 3【答案】B【解析】关于①,若“” 为真命题,则都为真命题,“”为真命题,若为真命题,只需为真命题或为真命题,“”不一定为真命题,因此“为真命题”是“为真命题”的充分不必要条件,故①错误;关于②,命题“,”的否定是“”, 故②错误;关于③,因为逆命题与否命题互为逆否命题,因此③正确,即正确命题的个数为,故选B、4、函数的大致图象是( )A、B、C、 D、【答案】B【解析】首先函数为偶函数,图象关于轴对称,排除C、D,当时,,图象就是把的图象向右平移1个单位,可见选B、5。
某几何体的三视图如图所示,则该几何体的表面积为( )A。
B、 C。
D。
【答案】D【解析】由三视图知,该几何体是一个一条侧棱与底面垂直,底面是边长为的正方形的四棱锥,其中两个侧面面积为,两个侧面面积为,底面积为,因此表面积为,故选D、6、等比数列中,,,函数,则( )A、 B、 C。
D、【答案】D【解析】试题分析:因为函数,,则、故选C、考点:导数的运算、7、将函数的图象沿轴向左平移个单位后,得到一个偶函数的图象,则的取值不估计是( )A、 B、C。
D、【答案】B【解析】,将函数的图象向左平移个单位后得到,,为偶函数,,,当时,的取值分别为 , ,的取值不估计是,故选B、8。
向量,均为非零向量,,,则,的夹角为( )A、 B。
洛阳市高三期中考试数学理

洛阳市2016—2017学年高中三年级期中考试数 学 试 卷(理)本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择),考生作答时,须将答案答答题卡上,在本试卷、草稿纸上答题无效。
满分150分,考试时间120分钟。
第Ⅰ卷(选择题,共60分)注意事项:1.必须使用2B 铅笔在答题卡上将所选答案对应的标号涂黑. 2.考试结束后,将本试题卷和答题卡一并交回。
一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.集合,,则( ) {}Z x x x A ∈=,<<3log 12{}95<x x B ≤==⋂B A A . B. C . D .),5[2e ]7,5[}7,6,5{}8,7,6,5{2.复数的共扼复数是( ) ii++12 A . B . C. D .i 2123+-i 2123--i 2123-i 2123+3.设是两条不同的直线,是两个不同的平面,下列命题是真命题的是( ) n m ,βα, A .若,,则 B .若,,则 α//m β//m βα//α//m βα//β//m C .若,,则 D .若,,则 α⊂m β⊥m βα⊥α⊂m βα⊥β⊥m 4.函数的一个单调递减区间是( ))42cos(ln π+=x y A . B . C . D . 8,85(ππ--8,83(ππ--8,8(ππ--)83,8(ππ-5.为△ABC 内一点,且,,若三点共线,则O 02=++OC OB OA AC t AD =D O B ,,t 的值为( ) A .B .C . D. 413121326.一个几何体的三视图都是边长为1的正方形,如图,则该几何体的体积是() A .B .C . D. 1213142217.由及轴所围成的平面图形的面积是( ) 2,1,===x xy x y x A . B . C . D.12ln +2ln 2-212ln -212ln +8.直角△ABC 中,∠C =90°,D 在BC 上,CD =2DB ,tan ∠BAD =,则=51BAC ∠sin ( )A .B .C . D.或22231313322 131339.已知函数是上的奇函数,且满足,当时,)(x f R )()2(x f x f -=+]1,0[∈x x x f =)(,则方程在182)(+-=x x x f 解的个数是( )),0(+∞ A .3 B .4 C .5 D.6 10.已知数列为等比数列的前项和,,则( ) n S {}n a n 14,2248==S S =2016S A . B . C . D.22252-22253-221008-222016-11.已知三棱锥中,,面,∠BAC =,则三ABC P -1===AC PB PA ⊥PA ABC 32π棱锥的外接球的表ABC P -面积为( )A .B .C . D. π3π4π5π812.定义在上的函数满足:,且,则的最R )(x f xe x xf x f ∙=-')()(21)0(=f )()(x f x f '大值为( )A .0B .C .1 D.2 21第Ⅱ卷(非选择题,共90分)注意事项:必须使用0.5毫米黑色墨迹签字笔在答题卡题目所指示的答题区域内作答。
河南省洛阳市2017届高三第三次统一考试(5月)数学(理)试题 Word版含答案

洛阳市2016-2017学年高中三年级第三次统一考试数学试卷(理)本试卷分第1卷(选择题)和第Ⅱ卷(非选择题)两部分:共150分.考试时间120分钟.第Ⅰ卷(选择题,共60分)注意事项:1.答卷前,考生务必将自己的姓名、考号填写在答题卡上. 2.考试结束,将答题卡交回.一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1·已知复数2z =(其中i 为虚数单位),则z =( ) A .1B .-iC .-1D .i2.已知集合22194x y M x ⎧⎫⎪⎪=+=⎨⎬⎪⎪⎩⎭,132x y N y ⎧⎫=+=⎨⎬⎩⎭,M ∩N =( )A .∅B .{(3,0),(0,2)}C .[一2,2]D .[一3,3]3.已知a 、b ∈R ,则“ab =1”是“直线“ax +y -l =0和直线x +by -1=0平行”的( ) A .充分不必要条件 B .充要条件 C .必要不充分条件 D .既不充分又不必要条件4.利用如图算法在平面直角坐标系上打印一系列点,则打印的点在圆x 2+y 2=25内的个数为( ) A .2B .3C .4D .55.已知数列{}n a 为等差数列,且201620180a a +=⎰,则2017a 的值为( )A .2π B .2π C .2πD .π6.祖冲之之子祖暅是找国南北朝时代伟大的科学家,他在实践的基础上提出了体积计算的原理:“幂势既同,则积不容异”.意思是,如果两个等高的几何体在同高处截得的截面面积恒等,那么这两个几何体的体积相等.此即祖咂原理,利用这个原理求球的体积时,需要构造一个满足条件的几何体,已知该几何体三视图如图所示,用一个与该几何体的下底面平行相距为h (0<h <2)的平面截该几何体,则截面面积为( )A .4πB .2h πC .()22h π-D .()24h π-7.已知随机变量()1,1ZN ,其正态分布密度曲线如图所示,若向正方形OABC 中随机投掷10000个点,则落入阴影部分的点的个数的估计值为( )A .6038B .6587C .7028D .7539附:若()2,ZN μσ,则:()0.6826;P Z μσμσ-<≤+=()220.9544;P Z μσμσ-<≤+=()330.9974;P Z μσμσ-<≤+=8.已知实数x ,y 满足若目标函数Z =ax +y 的最大值为39a +,最小值为33a -,则实数a 的取值范围是( ) A A .{}11a a -≤≤B .{}1a a ≤-C .{}11a a a ≤-≥或D .{}1a a ≥9.若空间中四个不重合的平面1234,,,αααα满足122334,,αααααα⊥⊥⊥,则下列结论一定正确的是( ) A .14αα⊥B .14ααC .14αα与既不垂直也不平行D .14αα与的位置关系不确定10.设()52501252x a a x a x a x -=++++,则2413++a a a a 的值为( ) A .6160-B .122121-C .34-D .90121-11.已知点A 足抛物线24x y =的对称轴与准线的交点,点B 为抛物线的焦点,P 在抛物线上且满足PA m PB =,当m 取最大值时,点P 恰好在以A ,B 为焦点的双曲线上,则双曲线的离心率为( ) A1B.12C.12D112.已知函数()()()()22132228122=x x x f x e x x x -⎧--≤⎪⎨⎪-+->⎩,若在区间(1,)∞上存在()2n n ≥个不同的数123,,,,n x x x x ,使得()()()1212n nf x f x f x x x x ==成立,则n 的取值集合是( ) A .{2,3,4,5}B .{2,3}C .{2,3,5}D .{2,3,4}第Ⅱ卷(非选择题,共90分)二、填空题:本大题共4个小题,每小题5分,共20分.13.已知1=a ,2b =,a 与b 的夹角为120°,0a b c ++=,则a 与c 的夹角为 .14.等比数列{}n a 的前n 项和为n S ,()12=n n S b a ---则ab= . 15.已知直三棱柱ABC -A 1B 1C 1中,AB =3,AC =4,AB ⊥AC ,AA 1=2,则该三棱柱内切球的表面积与外接球的表面积的和为 . 16.已知函数()22f x x =+,点O 为坐标原点,点()()()*,n A n f n n N ∈,向量i =(0,1),n θ是向量n OA 与i 的夹角,则使得312123cos cos cos cos sin sin sin sin nnt θθθθθθθθ++++<恒成立的实数t 的最小值为.三、解答题:本大题共6个小题,共70分,解答应写出必要的文字说明、证明过程或演算 步骤. 17.(本小题满分12分) 已知函数())()cos cos =f x xx x m m R -+∈,将()y f x =的图象向左平移6π个单位后得到g (x )的图象,且y =g (x )在区间,43ππ⎡⎤⎢⎥⎣⎦. (1)求m 的值;(2)在锐角△ABC 中,若122C g ⎛⎫=- ⎪⎝⎭sin A +cos B 的取值范围.18.(本小题满分12分)如图,在直三棱柱ABC -A 1B 1C 1中,∠BAC =90°,AB =AC =AA 1=2,E 是BC 中点. (1)求证:A 1B //平面AEC 1;(2)在棱AA 1上存在一点M ,满足B 1M ⊥C 1E ,求平面MEC 1与平面ABB 1A 1所成锐二面角的余弦值.19.(本小题满分12分)某市为了了解全民健身运动开展的效果,选择甲、乙两个相似的小区作对比,一年前在甲小区利用体育彩票基金建设了健身广场,一年后分别在两小区采用简单随机抽样的方法抽取20人作为样本,进行身体综合素质测试,测试得分分数的茎叶图(其中十位为茎,个们为叶)如图:(1)求甲小区和乙小区的中位数;(2)身体综合素质测试成绩在60分以上(含60)的人称为“身体综合素质良好”,否则称为“身体综合素质一般”。
河南省洛阳市高三数学上学期期中试题 文

洛阳市2017——2018学年高中三年级期中考试数学试卷(文科)第Ⅰ卷(选择题)一、选择题:本大题共12小题,每小题5分,共60分.在每个小题给出的四个选项中,有且只有一项符合题目要求.1.设全集{}|15U x N x =∈-<<,集合{}1,3A =,则集合U C A 的子集的个数为A.16B. 8C. 7D.42.已知复数12,z z 在复平面内对应的点分别为()()1,1,2,1-,则21z z = A. 1322i + B. 1322i -+ C. 1322i - D.1322i -- 3.设m R ∈,则"2"m =是“1,,4m 成等比数列”的A.充分不必要条件B.必要不充分条件C. 充要条件D.既不充分也不必要条件4.已知函数()[][]2,0,1,0,1x f x x x ⎧∈⎪=⎨∉⎪⎩,若()()2f f x =,则x 取值集合为 A.∅ B. []0,1 C. {}2 D.{}[]20,15.设,a b 是不同的直线,,αβ是两个不同的平面,则下列四个命题中错误的是A.若,,a b a b αα⊥⊥⊄,则//b αB.若,//,a a βα⊥,则αβ⊥C. 若αβ⊥,,a β⊥,则//a αD. 若,,a b a b αβ⊥⊥⊥,则a β⊥6.设等差数列{}n a 满足3835a a =,且10,n a S >为其前n 项和,则数列{}n S 的最大项为A. 15SB. 16SC. 29SD.30S7. 等比数列{}n a 中,1102,4a a ==,函数()()()()1210f x x x a x a x a =---,则()0f '=A. 62B. 92C. 122D. 1528.已知函数()sin 0,1y a b x b b =+>≠的图象如图所示,那么函数()log b y x a =+的图象可能是9.某几何体的三视图如图所示,图中小正方形的边长为1,则该几何体的体积为A. 60B. 48C. 24D. 2010.已知函数()()sin cos sin f x x x x =+,则下列说法不正确的是A. 函数()f x 的最小正周期为πB.()f x 在37,88ππ⎡⎤⎢⎥⎣⎦上单调递减 C.()f x 的图象关于直线8x π=-对称 D.将函数()f x 的图象向右平移8π个单位,再向下平移12个单位长度后会得到一个奇函数的图象11.在平面直角坐标系xoy 中,已知点()()()2,3,3,2,1,1A B C ,点(),P x y 在ABC ∆三边围成的区域内(包含边界),设(),OP mAB nCA m n R =+∈,则2m n +的最大值为A. -1B. 1C. 2D. 312.已知定义在1,ππ⎡⎤⎢⎥⎣⎦上的函数()f x 满足()1f x f x ⎛⎫= ⎪⎝⎭,且当[]1,x π∈时,()ln f x x =,若函数()()g x f x ax =-在1,ππ⎡⎤⎢⎥⎣⎦上有唯一的零点,则实数a 的取值范围是 A. 1,ln e ππ⎛⎤ ⎥⎝⎦ B. {}ln ,ln 0ππππ⎛⎤ ⎥⎝⎦C. []0,ln ππD.{}1,ln 0e ππ⎛⎤ ⎥⎝⎦二、填空题:本大题共4小题,每小题5分,共20分.13.已知()()2,2,1,0a b =-=,若向量c 与a b λ+共线,则λ= .14.若函数()212xx k f x k -=+⋅在定义域上为奇函数,则实数k = .15.已知()11sin 22f x x ⎛⎫=+- ⎪⎝⎭,数列{}n a 满足()()12101n n a f f f f f n n n -⎛⎫⎛⎫⎛⎫=+++++ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭,则2017a = . 16.已知菱形ABCD 边长为2,60A=将ABD ∆沿对角线BD 翻折成四面体ABCD ,当四面体ABCD的体积最大时,它的外接球的表面积为 .三、解答题:本大题共6小题,共70分.解答应写出必要的文字说明或推理、验算过程.17.(本题满分10分)设函数()21cos sin .22f x x x x π⎛⎫=+- ⎪⎝⎭ (1)求()f x 的单调递减区间;(2)当,34x ππ⎡⎤∈-⎢⎥⎣⎦时,求()f x 的最值.18.(本题满分12分) 已知公差不为0的等差数列{}n a 的前三项的和为6,且248,,a a a 成等比数列.(1)求数列{}n a 的通项公式;(2)设11n n n b a a +=,数列{}n b 的前n 项和为n S ,求使1415n S <的n 的最大值.19.(本题满分12分)在ABC ∆中,角,,A B C 的对边分别为,,a b c ,已知()()2,,cos ,cos m c b a n A C =-=,且.m n ⊥(1)求角A 的大小;(2)若3a b c =+=,求ABC ∆的面积.20.(本题满分12分)已知函数()()32,,.f x x ax bx c a b c R =+++∈(1)若函数()f x 在1x =-和2x =处取得极值,求,a b 的值;(2)在(1)的条件下,当[]2,3x ∈-时,()2f x c >恒成立,求c 的取值范围.21.(本题满分12分)如图,在四棱锥P ABCD -中,底面ABCD 为直角梯形,60,ADC ADP ∠=∆是边长为2的等边三角形,Q 为AD 的中点,M 是棱PC 的中点,1,BC CD PB ===(1)求证:平面PAD ⊥平面ABCD ;(2)求三棱锥B PQM -的体积.22.(本题满分10分)已知函数()f x 为偶函数,当0x ≥时,()x f x ae =且曲线()y f x =在点()()1,1f 处的切线方程为20ebx y a -+-=(1)求,a b 的值;(2)若存在实数m ,对任意的[]()1,1x k k ∈>,都有()2f x m ex +≤,求整数k 的最小值.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
【考试时间:2016年10月13日15:00~17:00】
洛阳市2016—2017学年高中三年级期中考试
数 学 试 卷(理)
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择),考生作答时,须将答案答答题卡上,在本试卷、草稿纸上答题无效。
满分150分,考试时间120分钟。
第Ⅰ卷(选择题,共60分
注意事项:
1.必须使用2B 铅笔在答题卡上将所选答案对应的标号涂黑. 2.考试结束后,将本试题卷和答题卡一并交回。
一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.集合{}
Z x x x A ∈=,<<3log 12,{}
95<x x B ≤=,则=⋂B A ( ) A .),5[2e B.]7,5[ C .}7,6,5{ D .}8,7,6,5{
2.复数
i i
++12的共扼复数是( ) A .i 2123+- B .i 2123-- C.i 2123- D .i 2
1
23+
3.设n m ,是两条不同的直线,βα,是两个不同的平面,下列命题是真命题的是( ) A .若α//m ,β//m ,则βα// B .若α//m ,βα//,则β//m C .若α⊂m ,β⊥m ,则βα⊥ D .若α⊂m ,βα⊥,则β⊥m 4.函数)4
2cos(ln π
+=x y 的一个单调递减区间是( )
A .)8,85(ππ--
B .)8,83(ππ--
C .)8,8(ππ--
D .)8
3,8(π
π-
5.O 为△ABC 内一点,且02=++OC OB OA ,AC t AD =,若D O B ,,三点共线,则t 的值为( ) A .41
B .31
C .2
1 D.
3
2 6.一个几何体的三视图都是边长为1的正方形,如图,则该几何体的体积是( ) A .
121 B .31 C .4
2
D.21 7.由2,1
,==
=x x
y x y 及x 轴所围成的平面图形的面积是( )
A .12ln +
B .2ln 2-
C .212ln -
D.2
12ln +
8.直角△ABC 中,∠C =90°,D 在BC 上,CD =2DB ,tan ∠BAD =
5
1
,则BAC ∠sin =( ) A .
22 B .23 C .13133 D.22或13
133 9.已知函数)(x f 是R 上的奇函数,且满足)()2(x f x f -=+,当]1,0[∈x 时,x x f =)(,则方程1
8
2)(+-=
x x x f 在 ),0(+∞解的个数是( )
A .3
B .4
C .5 D.6 10.已知数列n S 为等比数列{}n a 的前n 项和,14,2248==S S ,则=2016S ( ) A .22
252
- B .22253- C .221008- D.222016-
11.已知三棱锥ABC P -中,1===AC PB PA ,⊥PA 面ABC ,∠BAC =3
2π
,则三棱锥ABC P -的外接球的表
面积为( )
A .π3
B .π4
C .π5 D.π8 12.定义在R 上的函数)(x f 满足:x e x x f x f ∙=-')()(,且21
)0(=f ,则)
()(x f x f '的最大值为( )
A .0
B .2
1
C .1 D.2
第Ⅱ卷(非选择题,共90分)
注意事项:
必须使用0.5毫米黑色墨迹签字笔在答题卡题目所指示的答题区域内作答。
作图题可先用铅笔绘出,确认无误后再用0.5毫米黑色墨迹签字笔绘清楚。
答在答题卷、草稿纸上无效。
二、填空题:本大题共4小题,每小题5分,共20分. 13.若
2
1
cos sin cos sin =+-αααα,则α2tan 的值为.
14.等差数列{}n a 中,n S 为其前n 项和,若105=a ,305=S ,则2016
3211
...111S S S S ++++=.
15.等腰△ABC 中,底边BC =2
3,
,则△ABC 的面积为. 16.b a ,为正数,给出下列命题:①若122=-b a ,则1<b a -;②若11
1=-a
b ,则1<
b a -;③1=-b a e e ,则1<
b a -; ④若1ln ln =-b a ,则1<
b a -.期中真命题的有.
三、解答题:本大题共6小题,共70分.解答应写出文字说明,证明过程或演算步骤. 17.(本小题满分10分)
数列{}n a 中, 11=a ,11++=-n n n n a a a a ,*
∈N n .
(1)求数列{}n a 的通项公式;
(2)n S 为{}n a 的前n 项和,n b =n n S S -2,求n b 的最小值.
18.(本小题满分12分)
函数))2,2(0)(sin(π
πϕωϕω-
∈+=,>x y 的一条对称轴为3
π
=x ,一个对称中心为)0,127(
π,在区间]3,0[π
上单调. (1)求ϕω,的值; (2)用描点法作出)sin(ϕω+=x y 在],0[π上的图像.
19.(本小题满分12分) 锐角△ABC 中,其内角A 、B 满足:B B ocsA cos 3sin 2-=.
(1)求角C 的大小;
(2)D 为AB 的中点,CD =1,求△ABC 面积的最大值.
20.(本小题满分12分) 函数x e x x f ∙=)(.
(1)求)(x f 的极值; (2)x x x f k +≥⨯2
2
1)(在),1[+∞-上恒成立,求k 值的集合.
21.(本小题满分12分)
等腰△ABC 中,AC =BC =5,AB =2,E 、F 分别为AC 、BC 的中点,将△EFC 沿EF 折起,使得C 到P ,得到四棱锥P —ABFE ,且AP =BP =3.
(1)求证:平面EFP ⊥平面ABFE ; (2)求二面角B-AP-E 的大小.
22.(本小题满分12分) 已知函数x
k
x x f -
=ln )(有两个零点1x 、2x . (1)求k 的取值范围; (2)求证:e
x x 221>+.
洛阳市2016—2017学年高中三年级期中考试
理科数学参考答案及评分标准2016.10
第Ⅰ卷(60分)
第Ⅱ卷(90分)
二、填空题:4×5′=20′
13.43-
14.2017
2016 15.3 16.①③ 三、解答题: 12′×5+10′=70′
17.解:(1)由条件可知: 0≠n a ,11+-=-n n n n a a a a 可得
11
11=-+n
n a a , 数列⎭
⎬⎫
⎩⎨⎧n a 1为公差为1的等差数列 .
.....3分
n n a a n =⨯-+=1)1(1
11
, 故n
a n 1
=
. ......5分 (2)n n n S S b n n n 21...21112+++++=-=, 2
21
121...3121121++++++++=-=++n n n n S S b n n n ,
所以{}n b 为递增数列, ......9分
1b 为最小的项,2
1
1=
b . ......10分 18.解:(1)由题意得:
⎩⎨
⎧+=≤⇒⎪⎪⎩⎪⎪⎨⎧=⨯+≥⇒⎪⎪⎩⎪⎪⎨⎧-=+≥24344
12331274123
21k k T k T ωωπ
ωππωππππ. 又Z k ∈,>0ω,所以2=ω. ......3分
32π=
x 为对称轴,232ππϕπ+=+⨯k ,所以6
π
πϕ-=k ,。
