盲均衡算法及仿真
分数间隔盲均衡与盲辨识算法的研究的开题报告

分数间隔盲均衡与盲辨识算法的研究的开题报告(注:以下是该研究开题报告的示范,具体内容和格式可根据实际情况进行修改)一、选题背景和意义现代通信技术日新月异,有效的频率利用和信道均衡是通信系统性能提高的重要手段之一。
分数间隔盲均衡和盲辨识算法是其中较为重要的研究方向之一,在数字通信领域、调制解调领域等都有广泛的应用。
对于分数间隔盲均衡算法,其主要目的是将混沌的传输信号进行分段分析,然后利用线性均衡方法进行频率补偿。
而在盲辨识方面,主要是无法控制信道的前提下,通过识别信号特征来消除其干扰。
目前,针对上述两种算法的研究还存在一些问题和挑战,比如如何更有效的利用若干种算法结合优化信道均衡的性能,如何在实际环境下应用和改进算法等。
因此,对于这一领域的深入研究仍具有很大的理论和应用价值。
二、研究内容和方法本研究主要围绕分数间隔盲均衡和盲辨识两种算法展开。
具体研究内容包括:1. 基于分数间隔盲均衡算法的频率补偿技术研究2. 基于线性均衡算法的分数间隔盲均衡优化研究3. 结合多种盲辨识算法的信道均衡方法研究4. 基于实际环境的算法应用和性能测试研究方法主要包括实验研究和理论分析两方面。
实验研究采用Matlab和C++等工具,通过模拟或实际测试来验证不同算法在均衡过程中的性能和效果,并针对算法进行数据分析和优化。
同时,对于关键的理论问题进行分析和推导,为算法的改进和优化提供理论依据。
三、预期成果和意义本研究的预期成果包括:1. 提出一种高效的基于分数间隔盲均衡算法的频率补偿方法,改进传统线性均衡算法的性能2. 提出一种基于线性均衡算法的分数间隔盲均衡优化方法,使其在实际应用中更为实用和稳定3. 探索多种盲辨识算法的结合方法,提升信道均衡的性能4. 在理论和实践上都对分数间隔盲均衡和盲辨识算法进行深入分析和研究,对相关领域的理论和应用发展做出贡献本研究的意义在于推进当前数字通信和调制解调领域的技术发展,提高通信系统的性能和效率,以及为相关领域的理论研究提供重要参考和支持。
一种面向测试的载波频偏盲同步算法及仿真

文章编号 :1007-1423 (2014 )26-0034-04
DOI :10.3969/j.issn.1007-1423.2014.26.007
一种面向测试的载波频偏盲同步算法及仿真
刘健
( 广东电网公司电力科学研究院 , 广州 510080 )
摘要要求: 字数在120-150字,并附 上英文翻译。
(a ) 中数字下变频 DDC 模块输出的基带 I/Q 信号 。 将系 统 的 分 析 带 宽 设 置 为 5MHz , 等 效 采 样 率 设 置 为
6.4MHz。 滑动帧数 M 设置为 32, 频偏估计误差阈值 姿f
设置为 20KHz , 对 64QAM 信号进行 1024 点 FFT 变换 , 仿真结果如图 4 所示 。 图中的横线表示了载波频偏估 计时的信号功率电平阈值 L , 图 4 (a ) 为 64QAM 信号未 平均的实时频谱 , 带内信号频谱幅度快速抖动 , 将会在 载波频偏盲估计中引入较大误差 。 图 4 (b ) 为经 32 帧频 谱滑动平均后的 256QAM 信号实时频谱 , 消除了信号 频谱上的随机噪声 , 估计精度将大大提高 。
趲 趦
现代计算机
2014.09 中
研究与开发
画图要求: 请在visio中绘 制
图
* #+
"#$% !
图 1 典型测试 解调整 体 框图
& ' ( )
幅度在 DFT 变换的带宽内进行比较得到载波大频偏的 估计值 , 最后根据得到的估计值改变 NCO 的输入端控 制信号 , 使 NCO 的输出与输入两路的 I 、Q 两路信号分 别进行混频 , 这样就补偿了接收信号中的频率偏差 。
以通信分析仪器的接收信号与发送信号之间不可避免 地存在一个较大的频率偏差 , 该偏差的存在会严重影 响到接收机对接收信号进行有效的同步处理 , 所以必 须进行大载波频偏的盲估计 , 使得到修正的信号载波 频偏小于后级载波同步和定时同步算法的最大容许 值 。 目前常用的无线通信分析设备中针对载波大频偏 的校正估计和补偿主要采用一种基于快速傅里叶变换 (FFT ) 的载波频偏盲估计算法 。 该算法通过 FFT 得到 信号频率谱 , 并据此对偏差进行修正 , 其精度取决于
基于正交小波变换的变步长盲均衡算法研究

0 引 言
在现代通信 系统 中, 克服 多径 衰落和信道失 真引起
的码 间干扰 (S) II最有 效 的手 段是存 接收机 中采用 均衡 技术 , 传统 的均衡 技术是采用发送 周期性 训练序列 的 自
表明 , 出的新算法明显地提高了收敛速度 , 提 同时减小 了
剩余误差 。
1 指数形变步长 常数模 盲均衡 算法
I h r p s d lo i m,t e a ib e t p sz d a n h r o o a v lt r n fr a e i to u e i t h T CMA. n t e p o o e ag rt h h v r l a se — ie i e s a d t e o t g n l wa ee t so m r n r d c d n o e W —V h a t S mu ai n e u t i l t r s l w t u d n a e a o si c a n l n iae h t h p o o e ag rt m a n t n y h fse c n e g n e o s i h n e v tr c u t c h n e i d c t t a t e r p s d lo i h s o o l t e a tr o v r e c h rt s b t as h e s r sd a e r r wh c c mp r d wi h s f CMA a d ae u lo t e l s e i u ro i h o a e t t o e o h n VC MA.
基于模糊神经网络控制的变步长盲均衡算法

( o e e o noma o n ier g T iu n U i ri fT c n l y T i a 3 0 4 C l g fIfr t n E gn ei , a a nv sy o e h oo , a u n 0 0 2 ) l i n y e t g y
维普资讯
基于模糊神经 网络控制的变步长盲均衡算法
张 晓琴 白 煜 张彬彬 张立毅 王华 查
( 太原 理 工 大学信 息工程 学院 , 太原 0 02 ) 30 4
E— i: i n r iac m mala s e@sn . l o o
摘 耍
文章提 出了一种新的模糊神 经网络 (N F zy N ua e ok 控制 的变步长盲均衡 算法, F N:uz erlN t r) w 利用模糊神 经网络
t i a e , e tu t r o NN o t l r s d sg e sae q ain 0e ie a e c s u cin i r p s d n h s p p r t sr cu e f F c n r l i e in d,tt e u t s % gv n, n w o t n to s p o e a d h o e o f o
速 度 和 跟踪 速度 慢f 因此 , 文 采用 模 糊 神 经 网 络控 制器 。 1 l 。 本 利 用 人类 的经 验 知 识 构 造 模 糊 规 则 , 从误 差 信 号 中提 取 信 息 实 现
式 中 。 ( ) 单 位 冲 激 响 应 , 一 整 数 时 延 , 在 信 道 均 8n 为 k为 这
基于MMMA的双模式变步长盲均衡算法

(.C lg f l bmain a sa U i rt,H biQn u n d o0 6 0 ,C ia2 Deat n f Eet ncE gneig an nSfw r 1 oeeo n r t .Y nh n nv sy ee ih a g a 6 0 4 hn ;. p r to l r i n ier ,H ia o ae l J o ei me co n t Vct n lTc nclC lg,Han n Qog a 5 10 ,C ia oai a eh i oee o a l ia in h i 74 0 hn )
1 算 法描 述
11 常见 的盲均衡算法 . 设 a n 是原 始发送序 列 , ( ) () h 1 是信道 的冲激响应 , 2 v n 是信 道 中加性 噪声 , n 是经 信道加噪后 的信号 , () ( ) w( ) n 是采用抽头延迟线模 型的线 性均衡 器 , ( ) y n 是均衡 后 的信号 ,( ) P 凡 代表迭代误差 。 在C MA中 , 误差 函数定义为
第3 (第 6 ) 0 年 3 1 总 3 期 1 1 卷 期 3
Ta s tn rn miig& r e igi t e in c v
传 输与 攫 收 _
均衡器权向量的迭代过程为
W ( +1 n ) =W () () () n n 一 n nY () () 8
() 1
E1(I ( n) a )
Y() n=W “n () () n
() 2 () 3
相位偏转 问题 , 而且 在收敛速度和剩余误差 方面也 有很 多改进 。上述文献 中提 的方法都是采用 固定步长 , 文
献[】 4提 了V — MA D — M 方法 , 固定 步长为变 S MC + D L S 改
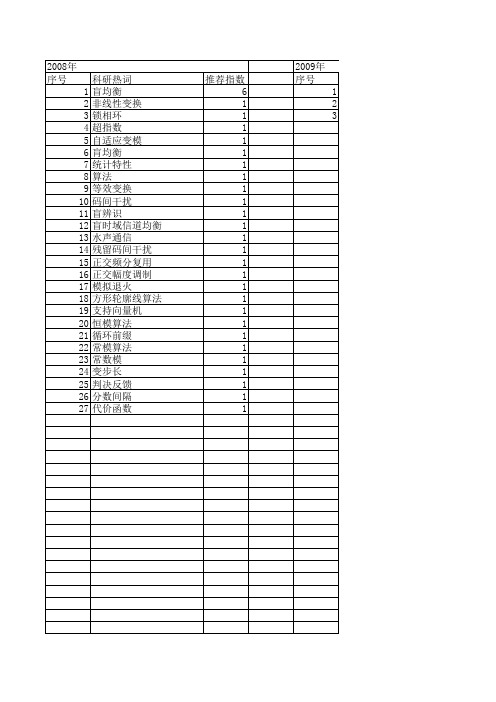
【计算机仿真】_盲均衡_期刊发文热词逐年推荐_20140723
推荐指数 3 1 1 1 1 1 1 1 1
2012年 序号 1 2 3 4 5 6 7 8
2012年 科研热词 盲均衡 水声信道 遗传算法 神经网络 码间干扰 水声通信 常数模 分数间隔 推荐指数 3 2 1 1 1 1 1 1
2013年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14
推荐指数 6 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
2009年 序号 1 2 3
2009年 科研热词 过采样 盲辨识 盲均衡 推荐指数 1 1 1
2011年 序号 1 2 3 4 5 6 7 8 9
科研热词 盲均衡 遗传算法 神经网络 收敛速度 后验概率 同相关状态 双模常模算法 卡尔曼滤波 代价函数
科研热词 盲均衡 水声信道 遗传算法 蚁群优化 自适应软约束常模算法 码间干扰 水声通信 正交幅度调制信号 正交小波变换 果蝇算法 常模盲均衡算法 双模式 动量粒子群优化 代价函数
推荐指数 4 2 1 1 1 1 1 1 1 1 1 1 1 1
2014年 序号 1 2 3 4
科研热词 遗传算法 水声信道 时变 多途环境
2008年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27
科研热词 盲均衡 非线性变换 锁相环 超指数 自适应变模 肓均衡 统计特性 算法 等效变换 码间干扰 盲辨识 盲时域信道均衡 水声通信 残留码间干扰 正交频分复用 正交幅度调制 模拟退火 方形轮廓线算法 支持向量机 恒模算法 循环前缀 常模算法 常数模 变步长 判决反馈 分数间隔 代价函数
几种盲均衡算法的比较及仿真研究
摘 要 :以新 兴 的 盲 均衡 技 术 为 理 论 基 础 , 些 盲 均 衡 算 法相 继提 出。 本 文 以 高 阶 的 Q M 信 号 作 为 输 入 信 号 , 对 常 一 A 针
模算 法、 多模 算 法 、 权 多模 算 法存 在 的缺 陷 , 终 引入 一 种 性 能优 越 的加 入 动 量项 的加 权 多模 算 法 。 通 过 计 算 机 的 加 最 仿 真 实验 首 次 对 这 些 算 法进 行 依 次 比较 , 所得 实验 结 果 表 明加 入 动 量 项 的 加 权 多模 盲 均 衡 算 法在 信 道 均 衡 上 的 性 能 明 显 优 于 前 面 几 种 算 法 , 具 有 更 快 的 收 敛 速 度 和 更 小 的稳 态误 差 , 此 具 有 实 用 价 值 。 它 因
在无 线 通信 领 域 , 通信 信 道 通 常 是 时 变 、 径 、 落 的 , 多 衰 会 使 接 收 到 的 信 号 存 在 严 重 的 码 间 干 扰 ( I。目前 信 道 均衡 【 I ) S 捌
Ab t a t e e a l d e u l ai n ag r h r n r d c d b s d o h sn l d e u l ai n tc n lg . h i h sr c:S v r lb i q ai t lo t ms a e i t u e a e n t e r i g b i q a i t e h oo yT e h g — n z o i o i n z o
关 键 词 :盲 均衡 ;收 敛 速 度 ;稳 态误 差 ;加 权 ;动 量
中 图 分 类 号 : N 1 T 9l
文献标识码 : A
文 章 编 号 :1 7 — 2 6 2 1 ) 1 0 6 — 4 6 4 6 3 (0 2 0 — 0 3 0
盲均衡1
也就是说,盲均衡器的目的就是要使其 传输函数和信道传输函数的关系应满足式 实现传递函数,也就是设计均衡器的抽头 系数。
算法
• 由于盲均衡器是在自适应均衡器的基础上 发展起来的,其算法基本上同自适应均衡 算法类似,只是没有训练信号而已。在自 适应均衡器中最常用的用的算法主要有最 小均方(LMS)算法和递归最小二乘(RLS)算 法。 • 衡量算法收敛性能的指标主要有收敛速度、 稳态剩余误差(算法收敛后的剩余误差包 含两方面,理论误差和超量均方误差), 误码特性等。
• 在盲均衡器中,因无训练序列,x(n)是未知 的,一般用发送序列的估计值
盲均衡原理
• 盲均衡技术是一种不借助于训练序列,仅 利用接收序列本身的先验信息来均衡信道 特性,使其输出序列尽量逼近发送序列的 新兴自适应均衡技术,它能有效地补偿信 道的非理想特性,克服码间干扰,减小误 码率,提高通信质量。
若不考虑噪声的影响,则有下式成立:
盲均衡的目的就是将
作为x(n)的最佳估计值,因此要求
• 即y(n)是由x(n)与h(n)卷积而成,要从y(n)中 恢复出x(n),意味着要解出卷积因子h(n), 这样的过 • 程叫做去卷积或逆解卷积。当y(n)和x(n)均 为已知时,解决这个问题并不困难,均衡 器工作于训练模式 • 就属于这种情况。当只有y(n)为已知,三个 参数中有两个是未知时,问题就比较困难 了,这类问题的能止常工作的条什是输入信号的眼图预先张 丌到一定程度(判决结果的错误率极低),以保证均衡器可靠地收敛。 如果这个条什不满足,就要由发送端发送一个接收端己知的i)il练序列 • 对均衡器进行训练,使均衡器达到收敛。因此训练过程也被称为均衡 器的学习过程,通常情}兑对,二通信 • 系统而言是一个必要的阶段1“。 • 由于训练序列的存在,不传递有效信息,占用了大量的带宽,降低了 通信系统的效率, • 由于信道上的强干扰和其他因素的影响,可能导致均衡器发散,必然 会频繁地发送训练序列,影响系统的工作。 • 某些情况只有发送通道没有反相请求通道,训练序列无法使用,一些 情况不可能发送训练序列,如信息截获,侦察系统
改进狼群算法优化的小波常模盲均衡算法
安徽科技学院学报,2019,33(5):65〜70Journal of Anhui Science and Technology University改进狼群算法优化的小波常模盲均衡算法郑亚强(淮南联合大学机电系,安徽淮南232001)摘要:针对常模盲均衡算法中因代价函数优化问题带来的收敛速度慢、稳态误差大等问题,本文提出一种新的盲均衡算法,即改进狼群算法优化的小波常模盲均衡算法。
该算法改进了基本狼群算法的更新机制,提高狼群算法的全局寻优性能,将改进后的狼群算法代替传统的梯度思想最小化盲均衡算法中的代价 函数,获取盲均衡器的最优初始权向量。
仿真实验结果证明,新算法均衡效果更好,且收敛速度更快,稳态误差更小,星座图更加清晰。
关键词:狼群算法;常模算法;盲均衡&、波变换;最优权向量中图分类号:T N911.5 文献标志码:A文章编号=1673-8772(2019)05-0065-06开放科学(资源服务)标识码(O S I D):D O I:10. 19608/ki. 1673 — 8772.2017.0711 An Orthogonal Wavelet Transform Weighted Constant Modulus Blind Equalization Algorithm Based on Improved Wolf Pack AlgorithmZ H E N G Y a q i a n g(Electrical and Mechanical Department,Huainan Union University,Huainan 232001,China)Abstract:For the problem of slow convergence and large steady-state error cau optimization problem in the wavelet norm blind equalization algorithm.In this paper,a n e w blind equalization algorithm,orthogonal wavelet transform weighted constant modulus blind equalization algorithm based on improved wolf pack algorithm i s proposed.T h e n e w algorithm improves the update mechanismof the basic wolf group algorithm and improves the global optimization performance of the wolf group algorithm.T h e improved wolf group algorithm replaces t he traditional gradient idea function in the blind equalization algorithm,and obtains the optimal i n i t i a l weight vector of qualizer.A s the simulation results have s h o w n,the n e w algorithm has better equalization effect,faster convergence,smaller steady-state error,and clearer constellation m a p.Key words:Wolf pack algorithm;Constant modulus algorithm;Blind equalization;Wavelet transform;Optimal weight vector盲均衡是解决无线通信系统因多径传输形成码间干扰的有效方法之一,可大大节约带宽。
基于余弦代价函数的双模盲均衡算法
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
基于最小差错概率的变步长盲均衡算法及仿真The Simulation of Blind Equalization algorithm based on Minimum ErrorProbability of Variable Step Size郑华电气信息工程学院,北方民族大学,宁夏银川,750021摘 要:本文在分析了李道本、陈少霞提出的基于最小差错概率盲均衡算法的基础上,用牛顿梯度变步长实现了基于最小差错概率新的盲均衡,仿真结果表明 ,与固定步长的盲均衡算法相比,该算法收敛速度快,均方误差小,在均衡技术的应用方面有一定的实用价值。
关键词:盲均衡算法; 变步长; 错误概率;仿真Zheng HuaCollege of electrical and Information Engineering ,Beifang Ethnic University ,Ningxia Yinchuan ,750021Abstract: This paper analyzes minimum error probability blind equalization algorithm proposed by Daoben Li. Anew minimum error probability blind equalization based on Newton gradient steepest ascent variable step size algorithm is proposed compared . Computer simulations demonstrate the proposed algorithm accomplisher faster convergence and steady smaller MSE than fixed step size algorithm. It is used valuable in engineering.Key words :Blind equalization algorithm ;Variable step size ;Error Probability ;Simulation1.引言均衡技术的发展和应用极大地提高了通信系统的性能,但随着数字通信技术向宽带、高速、大容量方向的发展,自适应均衡技术日益暴露出其不足和缺陷,而盲均衡技术有效地克服了自适应均衡的缺陷。
本文针对目前盲均衡技术研究领域的一种主要算法——最小错误概率盲均衡算法进行研究,提出一种运算量小,收敛性好,实用性强的变步长盲均衡算法,并从理论上对其进行了分析。
基于最小错误概率的盲均衡器是在自适应均衡器的基础上发展起来的,其显著特点是不增加计算的复杂度,保持了传统自适应均衡器的简单性,易于实现。
其算法的基本原理是先建立一个代价函数,该代价函数可以保证在错误概率最小的同时,使总的信道响应最大限度地逼近所期望的信道特性。
2.最小错误概率的盲均衡原理基于最小错误概率(MEP 所示[1]。
假定输入信号为一平稳的随机序列()()()()[]T L n x n x n x n 11+--=,,, X ,传输信道的冲激响应为()()()()[]T L n h n h n h n 110-=,,, H ,均衡器的权值系数为()()()()[]T L n w n w n w n 110-=,,, W ,L 为均衡器的长度,均衡器的输入为()()()()[]T L n y n y n y n 11+--=,,, Y 。
由于输入信号一般为零均值信号,假设其功率为A ,由于输入信号一般为零均值信号,假设其功率为A ,则()[]0=n x E∧()()[]()()1100+-=⎪⎩⎪⎨⎧≠==L n m n m n m n n A m x n x E ,,,,当当 δ (1)同时,由于噪声是独立于输入信号的高斯白序列(方差2σ),则()[]0=n n E ,()()[]()()⎪⎩⎪⎨⎧+-=≠==11002L n m n m n m n n m n n n E ,,,,当当 δσ (2)根据信号传输理论可得()()()()n n n n n T +=X H Y (3)()()()()()n n n n n x T T W Y Y W ==~ (4)系统的总冲激响应用()n S 表示,即()()()()[]T L n s n s n s n 110-=,,, S ,且()()()n n n s T i H W =。
盲均衡技术就是希望在()n X 未知情况下,仅通过对()n x ~、()n Y 的观测以及对()n W 的适当调整,使()n x ˆ尽可能逼近输入序列,即使()n S 尽量向理想冲激响应()n S '逼近。
()n S '中只有一个非零元素,即符合置零条件[2]。
3.最小错误概率的变步长LMS 盲均衡算法在均衡前,重要的是选择一个既合理又便于数学处理的代价函数。
在数字通信中,差错概率p 是最重要的性能测度,因此选择一个代价函数是p 的凸函数,且最小代价点min p 处是最终目标。
本文选用李道本、陈少霞[3]提出的判决导引盲均衡代价函数:()()()[](){}()()()()()⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧--+--=∑∑*22ˆˆ1l T l T l s l n x n n E l s n n l n x E A n J W Y W Y (5) 牛顿梯度权值迭代公式为()()()()()n n J n n n n W W W W ∂∂-=∇-=+μμ1. (6) 根据式(5)得()()()[]()()[]v n p n l n p n n J R W b R a R W --⎥⎥⎦⎤⎢⎢⎣⎡-+=∂∂∑12212 (7) 式中,()()[]n n E T *=Y Y R a ,()()[]()()[]n l n x E n l n x E A T Y Y R b --=**2ˆˆ1,()()(){}n l n x E l s A l v Y R -⎪⎭⎫ ⎝⎛+=∑**ˆ11。
代入式(6),得到基于最小错误概率的牛顿梯度权值迭代公式为()()()⎥⎦⎤⎢⎣⎡---+-=+v n P n H b n P a n n R W R R W W ))(1(]2))(1([21μ (8) 4.基于最小错误概率的变步长牛顿梯度盲均衡算法收敛速度、跟踪能力和稳态剩余误差是衡量均衡算法优劣的三个主要指标。
步长因子μ对算法收敛过程有很大影响。
μ值越大,算法收敛速度越快,但稳态剩余误差较大。
μ值减小,可以减小稳态剩余误差,提高算法的收敛精度,但将降低算法的收敛速度和跟踪速度。
因此,固定步长算法在收敛速度、跟踪速度与收敛精度之间对步长因子的要求是相互矛盾的 [4] ,因此选择变步长的牛顿梯度算法。
在一般的变步长LMS 算法中,控制步长更新的都是误差)(n e ,而实际系统中)(n e 是被噪声污染的,加之LMS 算法缺少平均操作的固有缺陷,这样当接近最佳权时,权值仍有较大的波动,因此,有较大的失调。
为了克服上述缺点,可以利用当前误差与上一步误差的自相关估计来控制步长更新。
这样做的好处是在更新步长)(n μ时,消除了不相关噪声序列的干扰。
具体做法是[5])1()()1()1()(--+-=n e n e n p n q ββ(9)式中,)(n q 为)1()(-n e n e 的自相关时间均值估计,则步长的更新公式为)(2)()1(n q n n γαμμ+=+ (10) 其中,1>α,10<<β,0>γ。
这种算法目的是保证当算法远离最佳值时具有较大()n μ,随着接近最佳值, ()n μ也逐渐减小,即使在噪声环境中也是如此。
这种算法是通过使用)1()(-n e n e 自相关估计来控制步长更新,成功地达到了步长更新。
在更新()n μ中使用)(n q 具有两个优点:(l )自相关误差通常是接近最佳值的较好的衡量标准;(2)在更新()n μ时,排除了不相关噪声序列的影响。
在自适应初始阶段,自相关估计误差()n q 2较大,导致较大的步长()n μ,当我们接近最佳值时,自相关误差()n q 2接近于零,导致一个较小的步长。
由于较大的初始()n μ值,产生了快速收敛,同时由于后期()n μ较小,导致在最佳值附近产生较小的失调,即使有噪声存在也是如此。
这种算法根据)1()(-n e n e 自相关的时间均值估计的平方来调节步长。
因此该算法能有效地接近最佳权系数值,且不受不相关噪声干扰。
3.计算机仿真输入序列采用4PAM 和8PAM 信号,信噪比为20dB ,信道采用典型电话信道[6]和普通最小相位信道[7],其传输函数为典型的电话信道()76543211016.0016.0049.0218.0854.0024.0009.0005.0---------+-+-+=z z z z z z z z H (11)普通最小相位信道()2125.08.01--++=z z z H (12)图2到图5分别给出了4PAM ,8PAM 信号在典型电话信道和普通最小相位信道中变步长牛顿梯度算法和固定步长算法的收敛曲线。
图2 4PAM 信号通过典型的电话信道时两种算法收敛曲线的比较图3 8PAM 信号通过典型的电话信道时两种算法收敛曲线的比较5.结论由理论分析和计算机仿真表明,本论文提出的牛顿梯度变步长盲均衡算法具有良好的收敛性能,收敛速度加快,稳态剩余误差减小。
参考文献:[1] 李道本,陈少霞.快速最小差错概率盲均衡算法[J].电子学报,1995,(4):17~20.[2] 成磊,葛临东.变步长LMS 算法性能比较与仿真[J].信息工程大学学报,2003,4(4):70~73.[3] 蒋明峰,郑小林.彭承琳.一种新的变步长LMS 自适应算法及其在自适应噪声对消中的应用.信号处理,2001,17::282~286.[4] 白煜.基于模糊神经网络理论盲均衡算法的研究[D].太原:太原理工大学硕士学位论文,2005.[5] 张智星,孙春在,水谷英二(日).神经-模糊和软计算[M].西安:西安交通大学出版社,2000.[6] Andreas F.Molisch .Wideband wireless digital communications[M].Beijing :Publishing House of Electronics Industry ,2002.[7] Haykin. Adaptive Filter Theory (4th Edition)(M). 北京: 电子工业出版社,2002图4 4PAM 信号通过普通最小相位信道时两种算法收敛曲线的比较 图5 8PAM 信号通过普通最小相位信道时两种算法收敛曲线的比较。
