静力学-计算题
静力学习题
静力学习题一. 填空题(40分,每题4分。
请将简要答案填入划线内)1.图示系统只受F 作用而平衡。
欲使A支座约束力的作用线与AB 成︒30角,则斜面的倾角θ 应为 。
2.物A 重100kN ,物B 重25kN ,A 物与地面的静摩擦因数为0.2,滑轮处摩擦不计。
则物体A 与地面间的摩擦力为 。
3.正六面体三边长分别为4,4,23(单位m );沿AB 联线方向作用了一个力F (单位kN ),其大小为F ,则该力对x 轴的力矩为 ;对z 轴的力矩为 。
4.在图示桁架中,已知F 、a ,则:杆1内力之大小为 ;杆2内力之大小为 ;杆3内力之大小为 。
5.图示结构受矩为M =10m kN ⋅的力偶作用。
若a =1m ,各杆自重不计。
则固定铰支座D 的约束力的大小为 。
一.填空题(40分,每题4分。
请将简要答案填入划线内)1.杆AB 以铰链A 及弯杆BC 支持,杆AB上作用一力偶,其力偶矩大小为M ,不计各杆自重,则A 支座反力的大小为 。
2.若F =50kN ,P =10kN ,墙与物体间的静摩擦因数f s =0.3,则摩擦力为 。
3.已知一正方体,各边长为a ,沿对角线BH 作用一力F ,则该力在x 1轴上的投影为 ,对z 轴的矩为 。
4.图示简支桁架,已知力F 1、F 2和长度a 。
则杆1内力的大小为 ;杆2内力的大小为 ;杆3内力的大小为 。
二.填空题(40分,每题4分。
请将简要答案填入划线内)1.平面系统受力偶矩为m kN 10⋅=M 的力偶作用,不计各杆自重,则A 支座反力的大小为为 kN 。
2.物A ,B 分别重P1=1kN ,P 2=0.5kN ,A 与B以及A 与地面间的摩擦因数均为f s =0.2,A ,B通过滑轮C 用一绳连接,滑轮处摩擦不计。
今在A 物块上作用一水平力F ,则能拉动物体A时该力应大于 。
3.图示悬臂桁架中,内力为零的杆有 。
4.一重为P ,边长为a 的均质正方形薄板与另一重为2P 的均质三角形薄板焊接成一梯形板,在A 点悬挂。
静力学计算题答案

静力学计算题答案(总28页)--本页仅作为文档封面,使用时请直接删除即可----内页可以根据需求调整合适字体及大小--静力学和运动学计算题1 如图所示结构中各杆的重力均不计,D ,C 处为光滑接触,已知:P = 50 kN ,试求铰链B ,E 对杆DE 的约束力。
解:取整体为研究对象: 0=∑x F ,F Hx = 00=∑y F ,F D - P - F Hy = 0 ∑=0)(F M D,P · 70 - F Hy · 250 = 0, F Hy = 14 kN ,F D = 64 kN取ECH 为研究对象:∑=0)(F M E,F C · 100 - F Hy · 200 = 0,F C = 28 kN取ABC 为研究对象:∑=0)(F M A,F By · 90 - F C · 220 = 0,F By = kN0=∑y F ,F sin+ F By -F C -P = 0,F = 16 kN 0=∑x F , F cos α + F Bx = 0,F Bx = kN取DE 为研究对象:0=∑x F ,2Ex F - F'Bx = 0, 2Ex F = F'Bx = F Bx = - kN0=∑y F ,F D - F'By + 2Ey F = 0,2Ey F = kN2 如图所示结构由直杆AB ,CD 及折杆BHE 组成。
已知:P = 48 kN ,L 1 = 2 m , L 2 =3 m ,r = m ,各杆及滑轮绳索重量均不计。
求A ,D ,E 处的约束力。
解:取整体为研究对象:∑=0)(F M A,3F E - P + = 0,F E = 32 kN 0=∑x F ,F Ax = 0,0=∑y F ,F Ay = P - F E = 16 kN ,取COD 为研究对象:∑=0)(F M C,F Dy L 2 + Pr - P (21L 2 + r ) = 0,F Dy = 24 kN取BHE 为研究对象:∑=0)(F M B,- F'Dx L 1 - F'Dy L 2 + F E L 2 = 0,D y D y F F =' F'Dx = 12 kN3 不计重力的三直杆用铰连接如图所示,重物M的重力为P ,由系在销钉D并绕过GC杆C端不计直径的小滑轮,再绕过定滑轮O 的绳系住。
重修班静力学复习题答案

重修班静力学复习题一、 是非判断题(10分)1.若两个力的力矢量相等,12F F =r r ,则两个力等效。
(×) (若两个力偶的力偶矩矢相等,12M M =r r,则两个力偶等效)(√)2.根据力的可传性原理,可以将构架ABC 上的作用在AB 杆的力F 移至AC 杆图示位置。
2. 图中圆盘处于平衡状态,说明力偶M 与力F 等效。
(×)3. 空间中三个力构成一平衡力系,此三力必共面。
(√)4. 空间任意力系向某一点O 简化,主矢为零,则主矩与简化中心无关。
(√)5. 空间任意力系总可以用二个力来平衡。
(√)6. 力与轴共面则力对轴的矩为零。
(√)7. 空间平行力系不可能简化为力螺旋。
(√) 二 选择题(15分)1不经计算,可直接判断出图示桁架结构的零杆数目为 C 个。
A 2; B 3;C 4;D 5期未试题A :(6分)图示简支桁架,已知力P 、Q ,长度a ,刚杆1,2,3的内力分别为=1T ( 0 ),=2T ( -P ),=3T ( 0 )。
期未试题B (6分) 图示悬臂桁架受到大小均为F 的三个力作用,则杆1内力大小为( 0),杆2内力大小为( -F ),杆3内力大小为( 0 )。
2 物块重力大小为5kN G =,与水平面间的摩擦角为020f ϕ=,今用与铅垂线成025角的力F 推动物块,若5kN F G ==,则物块 A 。
A 保持静止;B 处于临界状态;C 向右加速滑动;D 向右匀速滑动期未试题:2 物块重力大小为5kN G =,与水平面间的摩擦角为030f ϕ=,今用与铅垂线成050角的力F 推动物块,若5kN F G ==,则物块( A )。
补考试题:物块重力大小为5kN G =,与水平面间的摩擦角为030f ϕ=,今用与铅垂线成065角的力F 推动物块,若5kN FG ==,则物块( C )。
3在正方体的一个侧面,沿AB 方向作用一集中力F , 则该力对坐标轴的力矩大小为 D 。
静力学习题

第一章静力学基础一、是非题1.力有两种作用效果,即力可以使物体的运动状态发生变化,也可以使物体发生变形。
()2.在理论力学中只研究力的外效应。
()3.两端用光滑铰链连接的构件是二力构件。
()4.作用在一个刚体上的任意两个力成平衡的必要与充分条件是:两个力的作用线相同,大小相等,方向相反。
()5.作用于刚体的力可沿其作用线移动而不改变其对刚体的运动效应。
()6.三力平衡定理指出:三力汇交于一点,则这三个力必然互相平衡。
()7.平面汇交力系平衡时,力多边形各力应首尾相接,但在作图时力的顺序可以不同。
()8.约束力的方向总是与约束所能阻止的被约束物体的运动方向一致的。
()二、选择题和2,沿同一直线但方向相反。
1.若作用在A点的两个大小不等的力则其合力可以表示为。
①1-2;②2-1;③1+2;2.作用在一个刚体上的两个力A、B,满足A=-B的条件,则该二力可能是。
①作用力和反作用力或一对平衡的力;②一对平衡的力或一个力偶。
③一对平衡的力或一个力和一个力偶;④作用力和反作用力或一个力偶。
3.三力平衡定理是。
①共面不平行的三个力互相平衡必汇交于一点;②共面三力若平衡,必汇交于一点;③三力汇交于一点,则这三个力必互相平衡。
、2、3、4为作用于刚体上的平面共点力系,其力矢4.已知关系如图所示为平行四边形,由此。
①力系可合成为一个力偶;②力系可合成为一个力;③力系简化为一个力和一个力偶;④力系的合力为零,力系平衡。
5.在下述原理、法则、定理中,只适用于刚体的有。
①二力平衡原理;②力的平行四边形法则;③加减平衡力系原理;④力的可传性原理;⑤作用与反作用定理。
三、填空题1.二力平衡和作用反作用定律中的两个力,都是等值、反向、共线的,所不同的是。
2.已知力沿直线AB作用,其中一个分力的作用与AB成30°角,若欲使另一个分力的大小在所有分力中为最小,则此二分力间的夹角为度。
3.作用在刚体上的两个力等效的条件是。
静力学试题及答案

静力学试题及答案一、选择题1. 在一个平衡的物体上,作用的重力和支持该物体的力的相对位置关系是:A. 重力和支持力的作用线重合B. 重力和支持力的作用线不重合答案:A2. 下列哪个不是满足平衡条件的必要条件:A. 物体受到合力为零的作用B. 物体受到合力矩为零的作用C. 物体所受合力与其自重相等反向答案:B3. 下列哪个条件不是平衡杆的平衡条件:A. 杆上所有质点的合外力为零B. 杆上所有质点的合力矩为零C. 杆上所有质点的合重力为零答案:C4. 若在一根水平杆上放置两个等质量物体,物体A在杆的左端,物体B在杆的右端,下列哪个位置组合是平衡位置:A. A在杆的中点,B在杆的左端B. A在杆的中点,B在杆的右端C. A、B均在杆的两端答案:B5. 下列哪个条件不是平衡力夹具的平衡条件:A. 物体受到合力为零的作用B. 力夹具上所有质点的合力为零C. 力夹具上所有质点的合力矩为零答案:A二、填空题1. 物体所受重力与支持力方向相反,其合力为______。
答案:零2. 物体所受重力矩与支持力矩之间的关系为______。
答案:相等且反向3. 在平衡位置,物体所受合力矩等于______。
答案:零4. 平衡力夹具上所有质点所受力矩之和等于______。
答案:零三、计算题1. 质量为10 kg的物体悬挂在离支点2 m处的杆上,求支持力的大小。
答案:由于平衡条件下物体所受合力为零,支持力的大小等于物体的重力大小,即支持力=mg=10 kg × 9.8 m/s²= 98 N。
2. 在一个长度为6 m的水平杆上有两个距离杆左端为1 m和5 m处的质量分别为4 kg和6 kg的物体,求物体B对杆的支持力和物体A对杆的支持力。
答案:物体B对杆的支持力为FB=6 kg × 9.8 m/s²= 58.8 N;物体A 对杆的支持力为FA=4 kg × 9.8 m/s²= 39.2 N。
静力学计算题
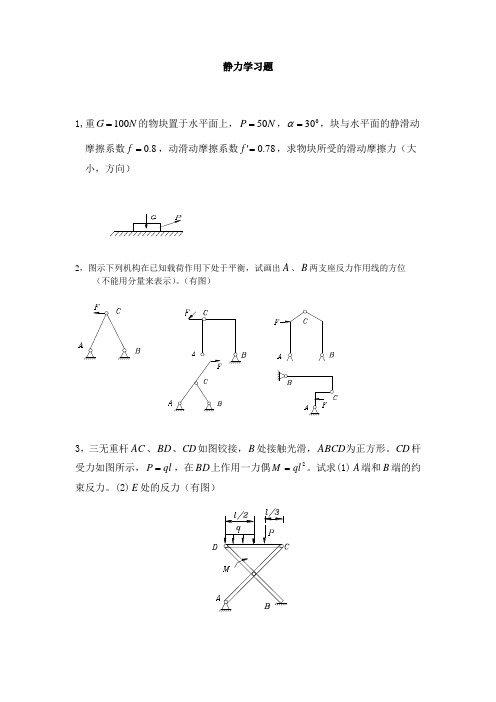
静力学习题1,重N G 100=的物块置于水平面上,N P 50=,030=α,块与水平面的静滑动摩擦系数8.0=f ,动滑动摩擦系数78.0'=f ,求物块所受的滑动摩擦力(大小,方向)2,图示下列机构在已知载荷作用下处于平衡,试画出A 、B 两支座反力作用线的方位(不能用分量来表示)。
(有图)3,三无重杆AC 、BD 、CD 如图铰接,B 处接触光滑,ABCD 为正方形。
CD 杆受力如图所示,ql P =,在BD 上作用一力偶2ql M =。
试求(1)A 端和B 端的约束反力。
(2)E 处的反力(有图)4,如图所示,ABCD 呈正方形,外载荷为P ,求杆AC 的内力。
(下图)5,试分别画出如图所示物体系中每个物体的受力图。
(下左图)6,图所示m a 2=,受有载荷kN P 6=,m kN q /6=,m kN m ⋅=8,试求各铰链处的约束反力。
(上右图)7,均质杆在A 、B 两点分别与矩形光滑接触,并在图示情况下平衡。
AD 杆长为_______ 。
(图1)8,如图所示,物体A 重为N P 100=放在与水平面成030=α的粗糙斜面上,物体A 与斜面间的静滑动摩擦系数为1=f ,则摩擦力的大小为__ 。
(图2)图1) (图2)9,正方形ABCD ,边长m a 2=,受如图所示平面力系作用。
已知:m kN q /1=,kN F F F F 24321====。
试求力系的合成结果,并画在图上。
10,分别画出如图所示物体系中每个物体的受力图。
11,构如图示,已知m L 4=,m kN q /6=,m kN M ⋅=8,试求(1)A 、B 处约束反力。
(2)CD 杆的内力。
静力学模拟试题及答案

静力学模拟试题及答案一、选择题1. 静力学中,力的平衡状态是指:A. 物体静止不动B. 物体速度为零C. 物体加速度为零D. 物体受力为零答案:C2. 以下哪项不是静力学中的基本概念?A. 力B. 力矩C. 动量D. 平衡答案:C二、填空题1. 根据牛顿第一定律,物体在不受外力作用时,将保持________状态。
答案:静止或匀速直线运动2. 在静力学中,当物体受到多个力作用时,若这些力的合力为零,则物体处于________状态。
答案:平衡三、简答题1. 解释什么是静力学中的二力平衡,并给出一个生活中的例子。
答案:二力平衡是指两个大小相等、方向相反、作用在同一直线上的力作用在物体上,使得物体保持静止或匀速直线运动的状态。
例如,当一个人站在水平地面上时,其受到的重力和地面的支持力就是一对二力平衡的例子。
2. 描述力矩的三要素,并说明它们是如何影响力矩的大小和方向的。
答案:力矩的三要素包括力的大小、力臂的长度以及力的作用点。
力的大小越大,力臂越长,力矩就越大;力臂长度固定时,力的作用点越远离旋转轴,力矩也越大。
力矩的方向遵循右手定则,即当力的方向从旋转轴指向力的作用点时,拇指指向的方向即为力矩的方向。
四、计算题1. 一个质量为10kg的物体,受到一个水平向右的力F=20N,求物体的加速度。
答案:根据牛顿第二定律,F=ma,所以a=F/m=20N/10kg=2m/s²。
2. 一个杠杆长2m,一端固定,另一端受到一个垂直向下的力G=100N,求杠杆的力臂长度。
答案:由于杠杆平衡,力臂长度等于杠杆长度的一半,即1m。
五、论述题1. 论述静力学在工程学中的应用,并给出至少两个具体的例子。
答案:静力学在工程学中有着广泛的应用,例如:- 在建筑设计中,通过静力学分析可以确定建筑物结构的稳定性和承载能力,确保建筑物的安全。
- 在机械设计中,通过计算零件的受力情况,可以设计出既满足功能需求又具有足够强度的机械结构。
静力学30个例题

的约束力。
l 2 l 2 F1 F AX F AY
F1
45
A
l 2
C
B
FBC
D
解:研究对象: ACB 杆 1. 受力分析:易知 CD 是二力杆,所以点 C 受力如图 2. 列平衡方程求解: 3. 研究对象: ACB 杆 4. 受力分析:易知 CD 是二力杆,所以点 C 受力如图 5. 列平衡方程求解: (1) 基本方程:
M z ( F ) F y x Fx y 0
2.计算力 F 对坐标轴 x,y,z 之矩。 先计算力 F 对点 O 之力矩矢 M o ( F ) ,为此写出力 F 和矢径 r 的解析式:
F 42.4i 56.6 j 70.7k , r OB 5k (m)
iy
iz
解得 例 7
FDA FCA 869 N
FBA 1950 N
力 F 作用于支架上的点 C,如图所示,设 F 100 N ,试求力 F 分别对点
A,B 之矩。
A
B
3m
C
60
F
解: 因为求力 F 对 A、B 两点的力臂比较麻烦,故利用合力矩定理求解。
M A ( F ) M A ( Fx ) M A ( Fy ) 2 F sin 60 3F cos 60 23 N m M B ( F ) M B ( Fx ) M B ( Fy ) 0 3F cos 60 150 N m
y F1
A B
F4
y
D C
2
45
A
Fx MB Fy
1
D B Cx
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
五、计算题1、如图所示,在由四根杆铰接而成的结构中,HK 杆为水平杆,竖直载荷P 和尺寸a 、b 均为已知,各杆自重均不计。
当结构处于平衡时,求载荷P 的作用点与B 点之间的水平距离x 的值。
解:注意到: 杆HK 为“二力杆”。
以“整 体”为研究对象,受力分析如“图(i )”所示。
()∑=0F M A : ()04=+⋅-⋅b x P b F D , 得P b bx F D ⋅+=4∑=0yF : 0=-+P F F D Ay , 得P b xb F P F D Ay ⋅-=-=43∑=0xF:0=+Ax F , 得 0=Ax F再以“AB 杆”为研究对象,受力分析如“图(ii )”所示。
由 ③ 可知,此时A 处的约束力只有AyF 。
()∑=0F M B:2=⋅-⋅b F a F Ay HK , 得Ay HK F a bF 2=将 ② 代入, 得P a xb F HK ⋅-=83再以“CD 杆”为研究对象,受力分析如“图(iii )”所示。
()∑=0F M C: 03=⋅-⋅a F b F HK D , 得D HK F a b F 3=第三题图将 ① 代入, 得P a xb F HK ⋅+=12由 ④、⑤ ,得 Pa xb P a x b ⋅+=⋅-1283解得bx 57=2杆AC 、BC 在C 处铰接,另一端均与墙面铰接,如图所示,F1和F2作用在销钉C 上,F1=445 N ,F2=535 N ,不计杆重,试求两杆所受的力。
解:(1) 取节点C 为研究对象,画受力图,注意AC 、BC 都为二力杆,A DF 图(ii )AF 图(iii )F 1F(2) 列平衡方程:12140 sin 600530 cos6005207 164 oy ACo x BC AC AC BC FF F F F F F F F N F N =⨯+-==⨯--=∴==∑∑AC 与BC 两杆均受拉。
3.水平力F 作用在刚架的B 点,如图所示。
如不计刚架重量,试求支座A 和D 处的约束力。
解:(1) 取整体ABCD 为研究对象,受力分析如图,画封闭的力三角形:(2)2111.1222D A D D A F F FF F BC AB AC F F F F F =====∴===4. 在简支梁AB 的中点C 作用一个倾斜45o 的力F ,力的大小等于20KN ,如图所示。
若梁的自重不计,试求两支座的约束力。
解:(1) 研究AB ,受力分析并画受力图:(2) 画封闭的力三角形:相似关系:B A F F FCDE cde CD CE ED ∆≈∆∴==几何尺寸:11 22CE BD CD ED =====求出约束反力:12010 22010.4 45arctan 18.4B A o oCE F F kNCDED F F kNCDCECD α=⨯=⨯==⨯===-=4.如图所示结构由两弯杆ABC 和DE 构成。
构件重量不计,图中的长度单位为cm 。
已知F=200 N ,试求支座A 和E 的约束力。
解:(1) 取DE 为研究对象,DE 为二力杆;FD = FEFF BF A dce(2) 取ABC 为研究对象,受力分析并画受力图;画封闭的力三角形:'15166.7 23A D E F F F F N===⨯=5.在四连杆机构ABCD 的铰链B 和C 上分别作用有力F1和F2,机构在图示位置平衡。
试求平衡时力F1和F2的大小之间的关系。
解:(1)取铰链B 为研究对象,AB 、BC 均为二力杆,画受力图和封闭力三角形;1=(2) 取铰链C 为研究对象,BC 、CD 均为二力杆,画受力图和封闭力三角形;22cos302o CB F F F ==由前二式可得:12122210.61 1.634BC CB F F F F F or F F ==∴===FA FC6.铆接薄板在孔心A 、B 和C 处受三力作用,如图所示。
N 1001=F ,沿铅直方向;N503=F ,沿水平方向,并通过A ;N 502=F ,力的作用线也通过点A ,尺寸如图。
求此力系的合力。
(来自试题22) 解:1、几何法求解作力多边形abcd ,其封闭边ad 即确定了合力FR 的大小和方向。
根据图(a)的几何关系,得223221R )53()54(⋅++⋅+=F F F F F 22)535050()5450100(⋅++⋅+==161 N)54arccos(),(R211R F F F ⋅+=∠F F4429.7429)1615450100arccos('︒=︒=⋅+=2、解析法求解建立直角坐标系xy ,如图(b)所示。
N 805350505321=⋅+==⋅+=∑F F F x N16114080)()(2222R =+=∑+∑=y x F F F N 14054501005421=⋅+=⋅+=∑F F F y7.物体重W=20kN ,用绳子挂在支架的滑轮B 上,绳子的另一端接在铰车D上,如图所示。
转动铰车,物体便能升起。
设滑轮的大小、AB 与CB 杆自重及摩擦略去不计,A 、B 、C 三处均为铰链连接。
当物体处于平衡状态时,试求拉杆AB 和支杆CB 所受的力。
(来自试题22)解:取支架、滑轮及重物为研究对象,画受力图,如图(a)所示。
选取直角坐标系Bxy ,建立平衡方程030sin 30cos ,0T =︒-︒--=∑F F F F BC AB x 030cos 30sin ,0T =-︒-︒--=∑W F F F BC y由于FT=W=20kN ,将FT 、W 代入方程(1),(2)得kN 6.54=AB F (拉力) kN 6.74-=BC F (压力)7.在图示刚架的点B 作用一水平F ,刚架重量略去不计。
求支座A 、D 的反力FA 和FD 。
解:取刚架为研究对象画受力图,根据三力平衡汇交定理,支座A 的约束反力FA 必通过C 点,方向如图(a)所示。
选取直角坐标系Cxy ,建立平衡方程52 ,0=⋅-=∑A x F F F(1)51 ,0=⋅-=∑A D y F F F (2)解方程组(1)、(2),得F F F A 12.125==,F F D 5.0=8. 图示液压夹紧机构中,D 为固定铰链,B 、C 、E 为活动铰链。
已知力F ,机构平衡时角度如图,求此时工件H 所受的压紧力。
解:(一)研究对象:B ;受力图(a)方程:αsin 0FF F BC y ==∑(受压)(二)研究对象:C ; 受力图(b)由图(b)知,CDBC F F ⊥')290cos( ,0=-︒-=∑αCE BC x F F Fα2sin BCCE F F =(三)研究对象: E : 受力图(c)αα2N sin 2cos ' , 0FF F F CE H y ===∑即:工件所受的压紧力α2N sin 2FF H =9. 铰链四杆机构CABD 的CD 边固定,在铰链A 、B 处有力F1、F2作用,如图所示。
该机构在图示位置平衡,杆重略去不计。
求力F1与F2的关系。
解:1.取节点A 为研究对象,其受力如图(a)所示。
取坐标系Axy ,列平衡方程45cos ,01=+︒=∑F F F AB x11245cos F F F AB -=︒-=(压力)2.取节点B 为研究对象,其受力如图(b)所示。
取坐标系Bxy ,列平衡方程30cos ,02=︒--=∑F F F AB x1112 1.633622/3230cos F F F F F AB ==--=︒-=故61.021=F F10.图示一拔桩装置装置,AB 、ED 、DB 、CB 均为绳,r a d 1.0=θ,DB 水平,AB 铅垂。
力图2-4N F 800=,求绳AB 作用于桩上的力。
解:1、 以D 点为研究对象N F F F F N F F F F DB DE DB x DE DE y 80000cos80000sin 0==-∑===-=∑θθ2、 以B 点为研究对象N BAF BAF BC F F N BCF BDF BC F F y x 800000cos 0 800000sin 0==-∑===-=∑θθ10.物体重P=20kN ,用绳子挂在支架的滑轮B 上,绳子的另一端接在绞D 上,如图所示。
转动绞,物体便能升起。
设滑轮的大小、AB 与CB 杆自重及摩擦略去不计,A ,B ,C 三处均为铰链连接。
当物体处于平衡状态时,求拉杆AB 和支杆CB 所受的力。
(来自试题23)解:以B 结点为研究对象BAF B BDF BCF DBF FDDEF 图2-5PBAF BCF TF B11.如图结构,已知kN F 8.1=,其他物体的自重不计,试求铰链A 的约束反力和杆BC 所受的力。
12.如图所示,三铰拱桥又左右两拱铰接而成,在BC 作用一主动力。
忽略各拱的自重,分别画出拱AC 、BC 的受力图。
解:(1)选AC 拱为研究对象,画分离体,AC 杆为二力杆。
受力如图 (2)选BC 拱为研究对象,画出分析体,三力汇交原理。
F F NB030sin 30cos 0030cos 30sin 0=---∑==---∑=οοοοTF BC F BA F F P T F BC F F x y N BAF N BC F 64.5464.74=-=(b)(c)13已知梁AB 上作用一力偶,力偶矩为M ,梁长为l ,梁重不计。
求在图a ,b ,c 三种情况下,支座A 和B 的约束力解:(a) 受力分析,画受力图;A 、B 处的约束力组成一个力偶;列平衡方程:0 0 B B A B M M F l M F lM F F l=⨯-==∴==∑(b) 受力分析,画受力图;A 、B 处的约束力组成一个力偶;列平衡方程:0 0 B B A B M M Fl M F lM F F l=⨯-==∴==∑(a)(c) 受力分析,画受力图;A 、B 处的约束力组成一个力偶;列平衡方程:0 cos 0 cos cos B B A B M M F l M F l M F F l θθθ=⨯⨯-==∴==∑14在题图所示结构中二曲杆自重不计,曲杆ABM ,试求A 和C 点处的约束力。
解:(1) 取BC 为研究对象,受力分析,BC为二力杆,画受力图;B CF F =(2) 取AB 为研究对象,受力分析,A 、B 的约束力组成一个力偶,画受力图;()''030 0.35420.354B B AC M M F a a M F a MF F a=⨯+-===∴==∑15. 齿轮箱的两个轴上作用的力偶如题图所示,它们的力偶矩的大小分别为M1=500 Nm ,M2 =125 Nm 。
