(完整版)初二数学全等三角形专题难题
初二数学(八年级)全等三角形重难点题型 考点

特训强化专题01 全等三角形重难点题型梳理汇总【举一反三】
【考点1 利用全等三角形的性质求角】
【方法点拨】全等三角形的性质:(1)全等三角形的对应边相等、对应角相等;(2)全等三角形的周长相等、面积相等;(3)全等三角形的对应边上的对应中线、角平分线、高线分别相等。
【例1】(2019春•临安区期中)如图,△ACB≌△A′CB′,∠ACB=70°,∠ACB′=100°,则∠BCA′的度数为()
A.30°B.35°C.40°D.50°
【变式1-1】(2018秋•绍兴期末)如图,△ABC≌△EDC,BC⊥CD,点A,D,E在同一条直线上,∠ACB =20°,则∠ADC的度数是()
A.55°B.60°C.65°D.70°
【变式1-2】(2018秋•厦门期末)如图,点F,C在BE上,△ABC≌△DEF,AB和DE,AC和DF是对应边,AC,DF交于点M,则∠AMF等于()
A.2∠B B.2∠ACB C.∠A+∠D D.∠B+∠ACB
【变式1-3】(2018秋•桐梓县校级期中)如图,△ABC≌△A′B′C,∠ACB=90°,∠B=50°,点B′在线段AB上,AC,A′B′交于点O,则∠COA′的度数是()
A.50°B.60°C.70°D.80°。
(完整版)初二数学全等三角形专题难题

、如图,点M为正三角形ABD的边AB所在直线上的任意一点(点B除外),作60DMN,射线MN与DBA∠
N,DM与MN有怎样的数量关系?
、已知:如图,ABCD是正方形,∠FAD=∠FAE. 求证:BE+DF=AE.
、如图所示,ABC是边长为1的正三角形,BDC是顶角为120的等腰三角形,以D为顶点作一个60的MDN,
、在等边ABC的两边AB,AC所在直线上分别有两点MND,,为ABC外一点,且60MDN,120BDC,
CD,探究:当点MN,分别爱直线ABAC,上移动时,BMBNMN,,之间的数量关系.
MN,在边ABAC,上,且DMDN时,BMNCMN,,之间的数量关系式_________;
MN,在边ABAC,上,且DMDN时,猜想(1)问的结论还成立吗?写出你的猜想并加
BMNMDCBA
3) 如图,在四边形ABCD中,ABAD,180BADC,EF,分别是边BCCD,延长线上的点,
1
EAFBAD, (1)中的结论是否仍然成立?若成立,请证明;若不成立,请写出它们之间的数量
、如图,已知⑴ABC是等边三角形,E是AC延长线上一点,选择一点D,使得⑴CDE是等边三角形,如果M是
AD的中点,N是线段BE的中点,
、如图,ABC的边BC在直线l上,ACBC,且ACBC;EFP的边FP也在直线l上,边EF与边AC重合,
EFFP.
在图1中,请你通过观察、测量,猜想并写出AB与AP所满足的数量关系和位置关系;
将EFP沿直线l向左平移到图2的位置时,EP交AC于点Q,连结AP,BQ.猜想并写出BQ与AP
将EFP沿直线l向左平移到图3的位置时,EP的延长线交AC的延线于点Q,连结AP,BQ.你
(完整)八年级数学全等三角形复习题及答案
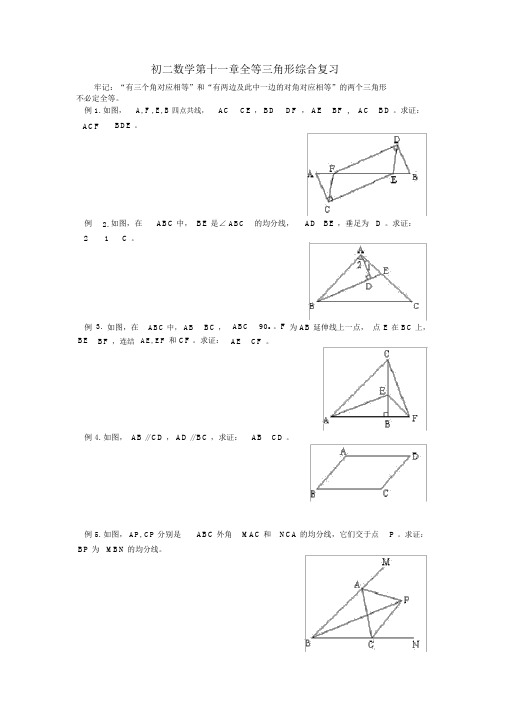
初二数学第十一章全等三角形综合复习牢记:“有三个角对应相等”和“有两边及此中一边的对角对应相等”的两个三角形不必定全等。
例 1. 如图,A, F , E, B 四点共线,AC CE , BD DF, AE BF,AC BD 。
求证:ACF BDE 。
例 2.如图,在ABC 中, BE 是∠ABC的均分线,AD BE ,垂足为 D 。
求证:21 C 。
例3.如图,在ABC 中, AB BC ,ABC90o。
F为 AB 延伸线上一点,点E 在 BC 上,BE BF,连结AE, EF和 CF 。
求证:AE CF。
例 4. 如图,AB // CD,AD // BC,求证:AB CD 。
例 5. 如图, AP, CP 分别是ABC 外角MAC 和NCA 的均分线,它们交于点P 。
求证:BP 为MBN 的均分线。
例 6. 如图,D是ABC 的边 BC 上的点,且 CD AB , ADB BAD , AE 是ABD 的。
中线。
求证:AC2AE例7.如图,在ABC 中, AB AC ,1 2 , P 为 AD 上任意一点。
求证:AB AC PB PC 。
同步练习一、选择题:1.能使两个直角三角形全等的条件是()A. 两直角边对应相等B. 一锐角对应相等C. 两锐角对应相等D. 斜边相等2.依据以下条件,能画出独一ABC 的是()oA.AB3, BC 4 , CA8B.AB 4 , BC3, A 30C.C60o, B45o,AB4D.C90o,AB63.如图,已知12, AC AD ,增添以下条件:① AB AE ;② BC ED ;③C D ;④B E 。
此中能使ABC AED 的条件有()A. 4 个B. 3 个C. 2 个D. 1 个()4. 如图,1 2 ,C D ,AC , BD交于E 点,以下不正确的选项是A.DAE CBEB.CE DEC.DEA 不全等于CBED.EAB 是等腰三角形5. 如图,已知AB CD , BC AD ,B23o,则D等于()A. 67oB.46oC. 23oD. 没法确立二、填空题:6. 如图,在ABC 中, C 90o,ABC 的平分线 BD 交 AC 于点 D ,且CD : AD 2:3 , AC10cm ,则点 D 到 AB 的距离等于__________cm;7. 如图,已知AB DC,AD BC ,E, F是 BD 上的两点,且 BE DF ,若AEB 100o, ADB 30o,则BCF ____________;BC , BD为折痕,则CBD的大小为8.将一张正方形纸片按如图的方式折叠,_________;9.如图,在等腰 Rt ABC 中, C 90o,AC BC,AD均分BAC 交 BC 于 D ,DE AB 于 E ,若 AB 10 ,则BDE 的周长等于____________;10. 如图,点 D , E, F , B在同一条直线上,AB // CD ,AE // CF,且AE CF,若BD10 , BF 2 ,则EF___________;三、解答题:11. 如图,交于 Q 点。
初二数学全等三角形难题

1、三角形ABC,角A=60°,∠B、∠C的角平分线BE与CD交与点O求:OE=OD.在BC上取点G,使得BD=BG因为∠A=60°所以∠BOC=120°因为∠DOB=∠EOC(对顶角)所以∠DOB=∠EOC=60°(360-120)/2尤SAS得△DBO≌△BOG所以DO=G0 ∠DOB=∠GOB=60°所以∠GOC=∠BOG=60°再由ASA得△OGC≌△OEC所以OG=OE因为OD=OG所以OE=OD2、已知在△ABC中,∠A=90°,AB=AC,AE⊥BD于E,∠ADB=∠CDF,延长AE交BC于F,求证:D为AC的中点作D关于BC的对称点G连接FG、CG由于角ADB=角BAF 所以角FDC=角BAF而角B=角C=45°所以角AFB=180°-角B-角BAF=180°-角C-角CDF=角DFG所以角AFD+角DFG=角AFD+角DFC+角AFB=180°所以A、F、G共线又因为角CAG=角ABD角ACG=2*45°=90°=角BAD所以三角形BAD全等于三角形ACG所以CG=AD又CG=DC所以AD=DC3.已知三角形ABC中,AD为BC边的中线,E为AC上一点,BE与AD交于F,若AE=EF,求证:AC=BF延长AD到M使DM=AD,连BM,CM∵AD=DM,BD=CD∴ABMC为平行四边形(对角线互相平分)∴AC‖BM,AC=BM(等于那个最后再用到)∴∠DAC=∠DMB(∠DAC即∠EAF,∠DMB即∠BMF下面用到)(内错角相等)……①在三角形AEF中,∵AE=EF∴∠EAF=∠EFA (等腰三角形)……②又∵∠EFA=∠BFM(对顶角相等)……③由①②③,得∠EAF=∠EFA=∠BFM=∠BMF在三角形BFM中,∵∠BFM=∠BMF∴三角形BFM为等腰三角形,边BF=BM由前面证得的AC=BM,得AC=BF4.已知三角形ABC,AD为BC边上的中线,E为AC上一点,AD、BE交于点F,且AE=EF,请问BF=AC吗?延长AD并过B点作AC的平行线,相交于G点则AC//BG,AE=EF,可得BF=BG在三角形BDG和三角形CDA中BD=CD,<ADC=<GDB,<DBG=<ACD,两三角形全等所以AC=BG=BF5、在△ABC中,∠ACB是直角,∠B= 60°,AD、CE分别是∠BAC、∠BCA 的平分线,AD、CE相交于点F。
初二全等三角形难题压轴题

全等三角形难题易错点剖析一、错用三角对应相等说明全等例1如图,∠CAB=∠DBA,∠C=∠D,E为AC和BD的交点.△ADB与△BCA全等吗?说说理由.错解:△ADB≌△BCA.因为∠C=∠D,∠CAB=∠DBA,∠DAB=CBA,所以△CBE≌△DAE(AAA).分析:两个三角形全等是对的,但说明的理由不正确.三个角对应相等不能作为三角形全等的识别方法.因为三个角对应相等的两个三角形不一定全等.正解:△CBE≌△DAE.因为∠CAB=∠DBA,∠C=∠D,AB=BA(公共边),所以△CAB≌△DBA(AAS).二、错用两边及一角对应相等说明全等例2如图,已知△ABC中,AB=AC,D,E分别是AB,AC的中点,且CD=BE,△ADC与△AEB全等吗?说说理由.错解:△ADC≌△AEB.因为AB=AC,BE=CD,∠BAE=∠CAD,所以△ADC≌△AEB(SSA).分析:错解在把SSA作为三角形全等的识别方法,实际上,SSA不能作为三角形全等的识别条件.因为两边及一边对角相等的两个三角形不一定全等.正解:△ADC≌△AEB.因为AB=AC,D,E为AB,AC的中点,所以AD=AE.在△ADC和△AEB中,因为AB=AC,AD=AE,CD=BE,所以△ADC≌△AEB(SSS).三、错用部分当整体说明全等例3如图,已知AB=AC,BD=CE,试说明△ABE与△ACD全等的理由.错解:因为AB=AC,所以∠B=∠C,在△ABE和△ACD中,因为AB=AC,∠B=∠C,AD=CE,所以△ABE≌△ACD(SAS).分析:错解在把三角形边上的一部分当作说明的条件,这不符合三角形全等的识别方法.正解:△ABE与△ACD全等.因为AB=AC,所以∠B=∠C,因为BD=CE,所以BD+DE=CE+DE,即BE=CD.在△ABE和△ACD中,因为AB=AC,B=C,BE=CD,所以△ABC≌△ACF(SAS).四、错用减法运算说明全等例4如图,已知AC,BD相交于点O,∠A=∠B,∠1=∠2,AD=BC.试说明△AOD≌△BOC.错解:在△ADC和△BCD中,因为∠A=∠B,∠2=∠1,DC=CD,所以△ADC≌△BCD(AAS),所以△ADC-△DEC=△BCD-△DEC,即△A0D≌△B0C.分析:错解在将等式的性质盲目地用到三角形全等中,实际上,三角形全等是不能根据等式的性质说明的.正解:在△ADO和△BCD中,∠A=∠B,∠AOD=∠BOC,AD=BC,所以△AOD≌△BOC(AAS).。
完整版)全等三角形难题题型归类及解析

完整版)全等三角形难题题型归类及解析1.在三角形ABC中,AD是角BAC的平分线,AE=AC,DE=2cm,BD=3cm,求BC的长度。
为了解决这个问题,我们可以利用角平分线的轴对称性,构造全等三角形ADE和ABC。
因为AE=AC,所以三角形ADE和三角形ABC的两边分别相等,因此它们是全等的。
根据全等三角形的性质,∠DAE=∠CAB,∠AED=∠ACB。
又因为AD是角BAC的平分线,所以∠DAE=∠EAC,因此∠CAB=2∠EAC。
设BC=x,则根据正弦定理可得:3/x=sin(2EAC)/sin(EAC),化简后得到x=6.2.在三角形ABC中,BD是角ABC的平分线,AB=BC,P在BD上,PM⊥AD于M,PN⊥CD于N,求解PM与PN 的关系。
首先,我们可以利用角平分线的性质,构造等腰三角形ABD和CBD。
因为AB=BC,所以三角形ABD和三角形CBD的两边分别相等,因此它们是全等的。
根据全等三角形的性质,∠BDA=∠BDC,∠ADB=∠CDB。
又因为BD是角ABC的平分线,所以∠ADB=∠BDC,因此∠BDA=∠CDB。
因此,三角形APM和三角形CPN是全等的。
因为全等三角形的对应边相等,所以PM=PN。
3.在三角形OAB中,P是角OAB的平分线上的一点,PC⊥OA于C,∠OAP+∠OBP=180°,OC=4cm,求解AO+BO的值。
我们可以利用角平分线的轴对称性,构造全等三角形OAC和OBC。
因为∠OAP+∠OBP=180°,所以∠AOP=∠BOP=90°。
因此,三角形OAP和三角形OBP是直角三角形。
设AO=x,BO=y,则根据勾股定理可得:x^2+PC^2=OP^2,y^2+PC^2=OP^2.又因为OC=4cm,所以PC=2cm。
将PC代入上面的两个式子中,得到x^2+y^2=OP^2-4.又因为三角形OAC和三角形OBC是全等的,所以x=y,因此2x^2=OP^2-4,即OP^2=2x^2+4.因此,AO+BO=2x=2√((OP^2-4)/2)=2√(2x^2)=2√(2y^2)=2√(2x^2+4)/2=2√(OP^2)/2=OP√2=2√6.4.在三角形ABC中,E在边AC上,且∠XXX∠ABC。
八年级数学三角形全等(倍长中线)(人教版)(专题)(含答案)

C.AF+FC<AB D.AF=AB+CF
答案:B
解题思路:
平行夹中点,考虑延长证全等,
延长AE交DF的延长线于点M,
延长之后证全等.
如图,延长AE交DF的延长线于点M.
∵E为BC的中点
∴BE=CE
∵AB∥CD
∴∠1=∠M
在△ABE和△MCE中
∴△ABE≌△MCE(AAS)
结合已知条件可知10-8 <CE<10+8,
所以2 <AB<18.
故选A.
试题难度:三颗星知识点:略
4.已知,在△ABC中,AB=5,中线AD=7,则边AC的取值范围是( )
A.1<AC<29 B.9<AC<19
C.5<AC<19 D.4<AC<24
答案:B
解题思路:
解:如图,延长AD到点E,使DE=AD,连接CE.
1.因为AD为△ABC的中线,考虑________________________________(辅助线叙述);
2.进而利用全等三角形的判定_________,证明_______≌_______;
3.由全等可得________________;
4.观察图形,2AD放在△_______中,利用三角形的三边关系,可得2<5.以上空缺处依次所填最恰当的是( )<5.
A.①延长AD到F,使DF=AD;
②SAS,△BDF,△CDA;
③∠DBF=∠C
④ABF
B.①延长AD到F,使DF=AD,连接BF;
②SAS,△BDF,△CDA;
③FB=AC
八年级数学全等三角形解答题10道题专题难点训练

八年级数学全等三角形解做题10道题专题难点练习学校:姓外班级:考号:一、解做题1.:A8=AC, BE=CD.(1)如图1,求证:ZB=ZC:(2)如图2,连接AO,不添加任何辅助线,直接写出图中所有的全等三角形.2.如图,点A, F, E, D 在一条直线上,AB=CD, AF=DE, ZBAE=ZCDF,求证:BE=CF.3.在四边形A3.中,E为BC边中点、.己知:如图,假设AE平分NBA.,NAEO=90., 点F为AD上一点,AF=AB.求证:(1) △ABE/AFE: (2) AD=AB+CD,C5.如下图,点B、F、C、E在同一条直线上,AB〃DF, AC〃DE, AC=DE, FC与BE相等吗?请说明理由.6.如图,点B、E、C、F在同一条直线上,BE=CF, AB=DE, AC=DF.求证:AB//DE.7.如图:AE=DE, BE=CE, AC和BD相交于点E,求证:AB=DC8.:如图,A8=AC, AD=AE. Z1 = Z2.求证:AABD^AACE.9.如图,aABC.〔1〕尺规作图:作NBAC的角平分线交BC于点D,作NABC的角平分线交AC于点£,且AD、BE交于点0 〔保存作图痕迹〕〔2〕连接.C,假设AB=6, BC=4, AC=8, 求S&mo - ^J^ACO -^^BCO的比值.A10.如图,:A3_L5C于3,AC于G, DF人BC于D, BC = DF,那么线段AC与线段EF有什么数量关系?参考答案1.(1)详见解析;(2)图中的全等三角形有△ABOgZVICE, AAEO^AADO. △BEOQXCDO,△A3.t△AC.,理由详见解析【解析】【分析】(1)求出AE=AD,根据SAS推出△ABDg/kACE,根据全等三角形的性质即可得出;(2)根据全等三角形的性质和判定得出即可.【详解】证实:(1) VAB=AC t BE=CD,,AB-BE=AC-CD,即AE=AD,在^ABD和^ACE中,AD = AE</A = N A , AB = ACAAABD^AACE (SAS),/.ZB = ZC:(2)图中的全等三角形有△ABDg/kACE, A AEO^AADO, A BEO^ACDO,△ABO^AACO,理由是::在△ ABO和△ ACO中,ZB = ZC<Z EAO = ZDAO , AO = AOAAABO^AACO (AAS):由(1)知:△ABDgZkACE;V^E A AEO和△ ADO 中,AE = AD/EAO = ZDAO , AO = AOAAAEO^AADO (SAS):V^A BEO^I A CDO中,NEOB = ZDOC<Z B = ZC , BE = CD此题考查了全等三角形的判定定理和性质定理,能灵活运用全等三角形的判定和性质定理进行推理是解此题的关键,注意牢固掌握全等三角形的判定定理和性质定理.2.见解析【解析】【分析】首先根据AF=Q上可以求出A£ = O匕再结合条件即可证实A ABE三△OCF,从而得到BE = CF.【详解】证实:•・・Af = OE:.AF+FE = DE+FE即AE = OF在△ABE和△OCT7中'AB = CDNBAE = ZCDFAE = DF・•. ^ABE三A DCF(SAS)BE = CF【点睛】此题主要考查全等三角形的判定和性质,根据线段的和差关系找出全等条件是求解此题的关键.3.(1)详见解析;(2)详见解析【解析】【分析】(1)根据AE平分NBAD,可以得到NBAE=NFAE.然后根据SAS即可得到△ABEgAFE:(2)根据(1)中的结论,可以得到EB=EF, NAEB=NAEF,再根据NAED=90.,可以得至l]NDEC=NDEF,然后根据点E为BC的中点,即可得至lJEC=EF,再根据SAS即可得到△ ECD^AEFD,从而可以得到DF=DC,然后即可证实结论成立.(1)证实:•••AE 平分N84.,:./BAE=/FAE,在和△AFE中,AB = AF</BAE=NFAE , AE = AE:.AABE^AAFE (SAS):(2)证实:由(1)知,△ABEgAAFE,:.EB=EF, ZAEB=ZAEF.<ZBEC= 180% NAED=90.,A ZAEB+ZDEC=9O\ NAEF+/DEF=9..,:./DEC= /DEF,<.•点七为3.的中点,;.EB=EC,:.EF=EC9在△EC.和△EFQ中,EC = EF<Z DEC=ZDEF , ED = ED:•△ECDWAEFD (SAS),:.DC=DF,9:AD=AF+DF, AB=AF,:.AD=AB+CD.【点睛】此题考查全等三角形的判定与性质、角平分线的性质,解题关键是明确题意,利用数形结合的思想解答.4.详见解析【分析】利用HL证实RtAABD^RtACBD nJ^ZADB=ZCDB,进而证实结论.【详解】证实:V ZA = ZC=90°,在RtAABD 和RtACBD 中,AB=BC, BD=BD,.,.RtAABD^RtACBD (HL),:.NADB=NCDB,・・.8.平分/ABC.【点睛】此题主要考查全等三角形的判定与性质,证实「△ABD/Rt^CBD是解题的关键.5.相等;理由见解析【解析】试题分析:AAS证实A ABC^A DEF,即可得证.试题解析:相等;理由如下:V AB\\DF,AC\\DE,ZB = NF, ZACB = /FED,在A A3c和尸中/B = /F{ZACB =/FEDAC = DE,..△ABC@ A DEF,BC = EF.BC-EC = EF-EC,即5E = CE6.见解析【解析】证实它们所在的三角形全等即可.根据等式的性质可得BC=EF.运用SSS证实AABC与△DEF 全等.【详解】解:证实:*/ BE=CF, ,BC=EF,在AABC与4DEF中, rAB = DE< AC = DF , BC = EF.,.△ABC^ADEF (SSS), .*.ZABC=ZDEF, ,AB〃DE.【点睛】此题考查了全等三角形的性质和判定.全等三角形的判定定理有SAS, ASA, A AS, SSS, 全等三角形的对应角相等.7.见详解.【解析】【分析】【详解】由SAS可得△ABEg4DCE,即可得出AB=CD.VAE=DE, BE=CE, ZAEB=ZCED (对顶角相等), .,.△ABE^ADCE (SAS), .\AB=CD.8.证实见解析.【解析】【分析】首先得出NEAC=NBAD,进而利用全等三角形的判定方法(SAS)得出即可. 【详解】证实:VZ1=Z2,:.ZEAC=ZBAD,在△D48和△E4C中,AB = AC< /BAD=/EAC ,AD = AE:.AABD^AACE〔SAS〕:【点睛】此题主要考查了全等三角形的判定,正确应用全等三角形的判定方法是解题关键.9.〔1〕见解析:〔2〕 3: 2: 4【解析】【分析】〔1〕依据题干要求作出图形即可;〔2〕根据角平分线的性质可得AABO中AB边上的高和AACO中AC边上的高以及△BCO中BC边上的高相等,从而得到的比值等于AB: AC: BC.【详解】解:〔1〕如图,即为所作图形:〔2〕・.・AO平分NBAC, BE平分NABC,・・.OC平分NACB,・♦.点O到AB、BC和AC的距离相等,即AABO中AB边上的高和△ACO中AC边上的高以及△BCO中BC边上的高相等, VAB=6, BC=4, AC=8,, S4mo :5幺.:=AB: AC: BC=6: 4: 8=3: 2: 4.此题考查了尺规作图,角平分线的性质,解题的关键是根据角平分线的性质得到三角形的高相等.10.AC=EF,理由见解析【解析】【分析】只要证实△ABCgZ\EDF,即可解决问题.【详解】解:结论:AC=EF.理由如下,VABIBC^B, EFJ_AC 于G, DFJ_BC 于D,:.Z ABC= ZEDF= ZCGE=90°,ZC+ZCEF=90°,NF+NCEF=90.,,NC=NF,在AABC与AEDF中,AABC = ZEDF< BC = DF ,ZC=ZFAAABC^AEDF,AAC=EF.【点睛】此题考查全等三角形的判定和性质,同角的余角相等等知识,解题的关键是熟练掌握全等三角形的判定和性质,属于中考常考题型.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
初二数学全等三角形专题(难题) 1、在等边ABC ∆的两边AB ,AC 所在直线上分别有两点M N D ,,为ABC ∆外一点,且60MDN ∠=︒,120BDC ∠=︒,
BD CD =,探究:当点M N ,
分别爱直线AB AC ,上移动时,BM BN MN ,,之间的数量关系.
⑴如图①,当点M N ,在边AB AC ,上,且DM DN =时,BM NC MN ,,之间的数量关系式_________; ⑵如图②,当点M N ,在边AB AC ,上,且DM DN ≠时,猜想(1)问的结论还成立吗?写出你的猜想并加以证明;
2、如图,ABC ∆的边BC 在直线l 上,AC BC ⊥,且AC BC =;EFP ∆的边FP 也在直线l 上,边EF 与边AC 重合,且EF FP =.
⑴ 在图1中,请你通过观察、测量,猜想并写出AB 与AP 所满足的数量关系和位置关系;
⑵ 将EFP ∆沿直线l 向左平移到图2的位置时,EP 交AC 于点Q ,连结AP ,BQ .猜想并写出BQ 与AP 所满足的数量关系和位置关系,请证明你的猜想;
⑶ 将EFP ∆沿直线l 向左平移到图3的位置时,EP 的延长线交AC 的延长线于点Q ,连结AP ,BQ .你认为⑵中所猜想的BQ 与AP 的数量关系和位置关系还成立吗?若成立,给出证明;若不成立,请说明理由.
3、已知,在ABC ∆中,ACB ∠为锐角,D 是射线BC 上一动点(D 与C 不重合),以AD 为一边向右侧作等边ADE ∆(C 与E 不重合),连接CE .
⑴ 若ABC ∆为等边三角形,当点D 在线段BC 上时(如图1所示),则直线BD 与直线CE 所夹锐角为 度;
⑴ 若ABC ∆为等边三角形,当点D 在线段BC 的延长线上时(如图2所示),你在⑴中得到的结论是否仍然成立?请说明理由;
⑴ 若ABC ∆不是等边三角形,且BC AC >(如图3所示).试探究当点D 在线段BC 上时,你在⑴中得到的结论是否仍然成立?若成立,请说明理由;若不成立,请指出当ACB ∠满足什么条件时,能使⑴中的结论成立,并说明理由.
3、(1)如图,在四边形ABCD 中,90AB AD B D =∠=∠=︒,,E F 、分别是边BC CD 、上的点,
且1
2
EAF =BAD ∠∠.求证:EF BE FD =+;
图①
M N
D
C
B
A
图②
M
N
D C
B
A
图⑴
l
P
C (F )
B A (E )
图⑵
Q ←
l
P
F
E C B A
图⑶
←
Q
A
E
B C
F P
l
图1
F
E
D C B A
图2
B C D F A
E
图3
B C
F
A
(2) 如图在四边形ABCD 中,180AB AD B+D =∠∠=︒,,E F 、分别是边BC CD 、上的点,且
1
2
EAF BAD ∠=∠, (1)中的结论是否仍然成立?不用证明.
(3) 如图,在四边形ABCD 中,AB AD =,180B ADC ∠+∠=︒,E F ,分别是边BC CD ,延长线上的点,
且1
2
EAF BAD ∠=∠, (1)中的结论是否仍然成立?若成立,请证明;若不成立,请写出它们之间的数量
关系,并证明.
4、如图,已知⑴ABC 是等边三角形,E 是AC 延长线上一点,选择一点D ,使得⑴CDE 是等边三角形,如果M 是线段AD 的中点,N 是线段BE 的中点, 求证:⑴CMN 是等边三角形.
(根据⑴ACD ⑴⑴BCE ,得出AD=BE ,AM=BN ;又⑴AMC ⑴⑴BNC ,可得CM=CN ,⑴ACM=⑴BCN ,证明⑴NCM=⑴ACB=60°即可证明⑴CMN 是等边三角形;)
E
F
D
C
B
A
E
F
D C
B
A
E
F
D
C
B
A
外角的平分线交于点N,DM与MN有怎样的数量关系?
点M、N分别在AB、AC上,求AMN
∆的周长.
B
M
N
M C
B
A。
