全等三角形练习题含答案
全等三角形习题精选(含答案)
全等三角形习题精选(含答案)1.在图中，已知△ABC≌△ADE，BC的延长线过点E，∠ACB=∠AED=105°，∠CAD=10°，∠B=50°，求∠DEF的度数。
2.在图中，已知△AOB中，∠B=30°，将△AOB绕点O 顺时针旋转52°，得到△A′OB′，边A′B′与边OB交于点C（A′不在OB上），则∠A′CO的度数为多少？3.在图中，已知△ABC中，∠A=90°，D、E分别是AC、BC上的点，若△AADB≌△EDB≌△EDC，则∠C的度数是多少？4.在图中，把△ABC绕点C顺时针旋转35°，得到△A′B′C，A′B′交AC于点D，若∠A′DC=90°，则∠A=？5.已知，如图所示，AB=AC，AD⊥BC于D，且AB+AC+BC=50cm，而AB+BD+AD=40cm，则AD的长度是多少？6.在图中，Rt△ABC中，∠BAC=90°，AB=AC，分别过点B、C作过点A的垂线BC、CE，垂足分别为D、E，若BD=3，CE=2，则DE的长度是多少？7.在图中，AD是△XXX的角平分线，DE⊥AB，DF⊥AC，垂足分别是E、F，连接EF，交AD于G，需要证明AD与EF垂直。
8.在图中，△ABC中，AD为∠BAC的角平分线，DE⊥XXX于E，DF⊥AC于F，△ABC的面积是28cm，AB=20cm，AC=8cm，求DE的长度。
9.已知，如图所示：AB=AE，∠B=∠E，∠BAC=∠EAD，∠XXX∠DAF，需要证明AF⊥CD。
10.在图中，已知AD=BD，AD⊥BC于D，BE⊥AC于E，AD与BE相交于点H，需要判断BH是否等于AC，并解释原因。
11.在图中，已知AD为△ABC的高，E为AC上一点，BE交AD于F，且有ABF=AC，FD=CD，需要证明BE⊥AC。
12.在图中，△DAC、△EBC均是等边三角形，AF、BD分别与CD、CE交于点M、N，需要证明：（1）AE=BD（2）CM=CN（3）△CMN为等边三角形（4）MN∥BC。
全等三角形证明经典40题(含答案)
1.已知：AB=4,AC=2,D 是BC 中点,AD 是整数,求AD 的长.解：延伸AD 到E,使AD=DE ∵D 是BC 中点 ∴BD=DC在△ACD 和△BDE 中 AD=DE∠BDE=∠ADC BD=DC∴△ACD≌△BDE ∴AC=BE=2 ∵在△ABE 中 AB-BE ＜AE ＜AB+BE ∵AB=4即4-2＜2AD ＜4+2 1＜AD ＜3 ∴AD=22.已知：BC=ED,∠B=∠E,∠C=∠D,F 是CD 中点,求证：∠1=∠2证实：衔接BF 和EFADBC∵ BC=ED,CF=DF,∠BCF=∠EDF∴ 三角形BCF 全等于三角形EDF(边角边) ∴ BF=EF,∠CBF=∠DEF 衔接BE在三角形BEF 中,BF=EF ∴∠EBF=∠BEF. ∵∠ABC=∠AED. ∴∠ABE=∠AEB. ∴ AB=AE.在三角形ABF 和三角形AEF 中 AB=AE,BF=EF,∠ABF=∠ABE+∠EBF=∠AEB+∠BEF=∠AEF ∴三角形ABF和三角形AEF全等.∴∠BAF=∠EAF (∠1=∠2).3.已知：∠1=∠2,CD=DE,EF//AB,求证：EF=AC过C 作CG∥EF 交AD 的延伸线于点G CG∥EF,可得,∠EFD＝CGD DE ＝DC ∠FDE＝∠GDC（对顶角）BA CDF2 1 E∴△EFD≌△CGDEF＝CG ∠CGD＝∠EFD 又,EF∥AB ∴,∠EFD＝∠1∠1=∠2∴∠CGD＝∠2∴△AGC为等腰三角形, AC＝CG 又EF＝CG ∴EF＝AC4.已知：AD等分∠BAC,AC=AB+BD,求证：∠B=2∠CA证实：延伸AB取点E,使AE＝AC,衔接DE∵AD等分∠BAC∴∠EAD＝∠C AD∵AE＝AC,AD＝AD∴△AED≌△ACD （SAS）∴∠E＝∠C∵AC＝AB+BD∴AE＝AB+BD∵AE＝AB+BE∴BD＝BE∴∠BDE＝∠E∵∠ABC＝∠E+∠BDE∴∠ABC＝2∠E∴∠ABC＝2∠C5.已知：AC等分∠BAD,CE⊥AB,∠B+∠D=180°,求证：AE=AD+BE证实：在AE上取F,使EF＝EB,衔接CF∵CE⊥AB∴∠CEB＝∠CEF＝90°∵EB＝EF,CE＝CE,∴△CEB≌△CEF(SAS)∴∠B＝∠CFE∵∠B＋∠D＝180°,∠CFE＋∠CFA＝180°∴∠D＝∠CFA∵AC等分∠BAD∴∠DAC＝∠FAC∵AC＝AC∴△ADC≌△AFC（SAS）∴AD＝AF∴AE＝AF＋FE＝AD＋BE6. 如图,四边形ABCD中,AB∥DC,BE.CE分离等分∠ABC.∠BCD,且点E在AD上.求证：BC=AB+DC.在BC上截取BF=AB,衔接EF∵BE等分∠ABC∴∠ABE=∠FBE又∵BE=BE∴⊿ABE≌⊿FBE（SAS）∴∠A=∠BFE∵AB//CD∴∠A+∠D=180º∵∠BFE+∠CFE=180º∴∠D=∠CFE又∵∠DCE=∠FCE , CE等分∠BCD ,CE=CE∴⊿DCE≌⊿FCE（AAS）∴CD=CF∴BC=BF+CF=AB+CD7.已知：AB=CD,∠A=∠D,求证：∠B=∠C证实：设线段AB,CD地点的直线交于E,则：△AED是等腰三角形.∴AE=DE而AB=CD∴BE=CE∴△BEC是等腰三角形∴∠B=∠C.8.P是∠BAC等分线AD上一点,AC>AB,求证：PC-PB<AC-AB在AC上取点E, 使AE＝AB. ∵A E＝ABAP＝AP∠EAP＝∠BAE,∴△EAP≌△BAP∴PE＝PB. PC＜EC＋PE ∴PC＜（AC－AE）＋PB ∴PC－PB＜AC－AB.9.已知∠ABC=3∠C,∠1=∠2,BE⊥AE,求证：AC-AB=2BE证实：延伸BE交AC于点F,可证△ABE≌△AFE∴∠ABE=∠AFE,AB=AF,BE=FE∴AC –AB =FC,FB=2BE∵∠ABC=3∠C∴∠ABE+∠FBC=3∠C∴∠AFB+∠FBC=3∠C∵∠AFB=∠C+∠FBC∴∠C+∠FBC+∠FBC=3∠C∴∠FBC=2∠C即∠FBC=∠C∴FB=FC∴AC-AB=FB=2BE10．如图,在△ABC中,BD=DC,∠1=∠2,求证：AD⊥BC．解：延伸AD至BC于点E, ∵BD=DC ∴△BDC是等腰三角形∴∠DBC=∠DCB又∵∠1=∠2 ∴∠DBC+∠1=∠DCB+∠2即∠ABC=∠ACB ∴△ABC是等腰三角形∴AB=AC在△ABD和△ACD中｛AB=AC ∠1=∠2BD=DC∴△ABD和△ACD是全等三角形（边角边）∴∠BAD=∠CAD∴AE是△ABC的中垂线∴AE⊥BC∴AD⊥BC11．如图,OM等分∠POQ,MA⊥OP,MB⊥OQ,A.B为垂足,AB交OM于点N．求证：∠OAB=∠OBA证实：∵OM等分∠POQ∴∠POM＝∠QOM∵MA⊥OP,MB⊥OQ∴∠MAO＝∠MBO＝90∵OM＝OM∴△AOM≌△BOM （AAS）∴OA＝OB∵ON＝ON∴△AON≌△BON （SAS）∴∠OAB=∠OBA,∠ONA=∠ONB∵∠ONA+∠ONB＝180∴∠ONA＝∠ONB＝90∴OM⊥AB12.如图,已知AD∥BC,∠PAB的等分线与∠CBA的等分线订交于E,CE的连线交AP于D．求证：AD+BC=AB．做BE的延伸线,与AP订交于F点,∵PA//BC∴∠PAB+∠CBA=180°,又∵,AE,BE均为∠PAB和∠CBA的角等分线∴∠EAB+∠EBA=90°∴∠AEB=90°,EAB为直角三角形在三角形ABF中,AE⊥BF,且AE为∠FAB的角等分线∴三角形FAB为等腰三角形,AB=AF,BE=EF在三角形DEF与三角形BEC中,∠EBC=∠DFE,且BE=EF,∠DEF=∠CEB,∴三角形DEF与三角形BEC为全等三角形,∴DF=BC∴AB=AF=AD+DF=AD+BC13.如图,△ABC中,AD是∠CAB的等分线,且AB=AC+CD,求证：∠C=2∠B延伸AC到 E 使AE=AC 衔接 ED∵ AB=AC+CD∴ CD=CE 可得∠B=∠E△CDE为等腰∠ACB=2∠B14．已知：如图,DC∥AB,且DC=AE,E为AB的中点,（1）求证：△AED≌△EBC．（2）不雅看图前,在不添帮助线的情形下,除△EBC外,请再写出两个与△AED的面积相等的三角形．（直接写出成果,不请求证实）：证实：∵DC∥AB∴∠CDE＝∠AED∵DE＝DE,DC＝AE∴△AED≌△EDC∵E为AB中点∴AE＝BE∴BE＝DC∵DC∥AB∴∠DCE＝∠BEC∵CE＝CE∴△EBC≌△EDC∴△AED≌△EBC15.如图,△ABC中,∠BAC=90度,AB=AC,BD是∠ABC的等分线,BD 的延伸线垂直于过C点的直线于E,直线CE交BA的延伸线于F．求证：BD=2CE．证实：∵∠CEB=∠CAB=90°∴ABCE四点共元∵∠ABE=∠CBE∴AE=CE∴∠ECA=∠EAC取线段BD的中点G,衔接AG,则：AG=BG=DG∴∠GAB=∠ABG而：∠ECA=∠GBA (同弧上的圆周角相等）∴∠ECA=∠EAC=∠GBA=∠GAB而：AC=AB∴△AEC≌△AGB∴EC=BG=DG∴BE=2CE16.如图：DF=CE,AD=BC,∠D=∠C.求证：△AED≌△BFC.证实：∵DF=CE,∴DF-EF=CE-EF,即DE=CF,在△AED和△BFC中,∵ AD=BC, ∠D=∠C ,DE=CF ∴△AED≌△BFC（SAS）17.如图：AE.BC交于点M,F点在AM上,BE∥CF,BE=CF.求证：AM是△ABC的中线.证实：∵BE‖CF∴∠E=∠CFM,∠EBM=∠FCM∵BE=CF∴△BEM≌△CFM∴AM是△ABC的中线.18.如图：在△ABC中,BA=BC,D是AC的中点.求证：BD⊥AC.∵△ABD和△BCD的三条边都相等∴△ABD=△BCD∴∠ADB=∠CD∴∠ADB=∠CDB=90°∴BD⊥AC19.AB=AC,DB=DC,F是AD的延伸线上的一点.求证：BF=CF在△ABD与△ACD中AB=ACBD=DCAD=AD∴△ABD≌△ACD∴∠ADB=∠ADC∴∠BDF=∠FDC在△BDF与△FDC中BD=DC∠BDF=∠FDCDF=DF∴△FBD≌△FCD∴BF=FC20.如图：AB=CD,AE=DF,CE=FB.求证：AF=DE.AE=DF,CE=FBCE+EF=EF+FB∴△ABE=△CDF∵∠DCB=∠ABFAB=DC BF=CE△ABF=△CDE∴AF=DE21.公园里有一条“Z”字形道路ABCD,如图所示,个中AB∥CD,在AB,CD,BC三段路旁各有一只小石凳E,F,M,且BE＝CF,M在BC的中点,试解释三只石凳E,F,M正好在一条直线上.证实：衔接EF ∵AB∥CD∴∠B=∠C∵M是BC中点∴BM=CM在△BEM和△CFM中BE=CF∠B=∠CBM=CM∴△BEM≌△CFM（SAS）22．已知：点 A.F.E.C 在统一条直线上, AF ＝CE,BE∥DF,BE＝DF ．求证：△ABE≌△CDF．∵AF=CE,FE=EF.∴AE=CF.∵DF//BE,∴∠AEB=∠CFD（两直线平行,内错角相等）∵BE=DF∴：△ABE≌△CDF（SAS ）23.已知：如图所示,AB ＝AD,BC ＝DC,E.F 分离是DC.BC 的中点,求证： AE ＝AF.衔接BD;∵AB=ADBC=D∴∠ADB=∠ABD∠CDB=∠ABD;两角相加,∠ADC=∠ABC;∵BC=DCE \F 是中点∴DE=BF; ∵AB=ADDE=BF ∠ADC=∠ABC ∴AE=AF.24．如图,在四边形ABCD 中,E 是AC 上的一点,∠1=∠2,∠3=∠4,求证: ∠5=∠6．证实：在△ADC,△ABC 中∵AC=AC,∠BAC=∠DAC,∠BCA=∠DCA ∴△ADC≌△ABC（两角加一边） ∵AB=AD,BC=CD 在△DEC 与△BEC 中∠BCA=∠DCA,CE=CE,BC=CD ∴△DEC≌△BEC（双方夹一角） ∴∠DEC=∠BEC25．已知AB∥DE,BC∥EF,D,C 在AF 上,且AD ＝CF,求证：△ABC≌△DEF． ∵AD=DF ∴AC =DF ∵AB//DE ∴∠A=∠EDF 又∵BC//EF∴∠F=∠BCA∴△ABC≌△DEF（ASA ）26．已知：如图,AB=AC,BD AC,CE AB,垂足分离为D.E,BD.CE 订交于点F,求证：BE=CD ．证实：ACDEF∵BD⊥AC∴∠BDC=90°∵CE⊥AB∴∠BEC=90°∴∠BDC=∠BEC=90°∵AB=AC∴∠DCB=∠EBC∴BC=BC∴Rt△BDC≌Rt△BEC（AAS) ∴BE=CD27.如图,在△AB C中,AD为∠BAC的等分线,DE⊥AB于E,DF⊥AC于F.求证：DE=DF．证实：∵AD是∠BAC的等分线∴∠EAD=∠FAD∵DE⊥AB,DF⊥AC∴∠BFD=∠CFD=90°∴∠AED与∠AFD=90°在△AED与△AFD中∠EAD=∠FAD AD=AD∠AED=∠AFD∴△AED≌△AFD（AAS ） ∴AE=AF在△AEO 与△AFO 中 ∠EAO=∠FAO AO=AO AE=AF∴△AEO≌△AFO （SAS ）∴∠AOE=∠AOF=90° ∴AD⊥EF28.已知：如图, AC BC 于 C , DE AC 于 E , AD AB 于 A , BC=AE ．若AB=5 ,求AD 的长？∵AD⊥AB ∴∠BAC=∠ADE 又∵AC⊥BC 于C,DE⊥AC 于 E 依据三角形角度之和等于180度∴∠ABC=∠DAED CBAE∵BC=AE,△ABC≌△DAE（ASA）∴AD=AB=529．如图：AB=AC,ME⊥AB,MF⊥AC,垂足分离为 E.F,ME=MF.求证：MB=MC证实：∵AB=AC∴∠B=∠C∵ME⊥AB,MF⊥AC∴∠BEM=∠CFM=90°在△BME和△CMF中∵∠B=∠C ∠BEM=∠CFM=90° ME=MF∴△BME≌△CMF（AAS）∴MB=MC．30．在△ABC中,,,直线经由点,且于,于.(1)当直线绕点扭转到图1的地位时,求证：①≌;②;(2)当直线绕点扭转到图2的地位时,（1）中的结论还成立吗？若成立,请给出证实;若不成立,解释来由.（1）①∵∠ADC=∠ACB=∠BEC=90°,∴∠CAD+∠ACD=90°,∠BCE+∠CBE=90°,∠ACD+∠BCE=90°．∴∠CAD=∠BCE． ∵AC=BC,∴△ADC≌△CEB． ②∵△ADC≌△CEB, ∴CE=AD,CD=BE． ∴DE=CE+CD=AD+BE．（2）∵∠ADC=∠CEB=∠ACB=90°, ∴∠ACD=∠CBE． 又∵AC=BC,∴△ACD≌△CBE． ∴CE=AD,CD=BE． ∴DE=CE﹣CD=AD ﹣BE31．如图所示,已知AE⊥AB,AF⊥AC,AE=AB,AF=AC.求证：（1）EC=BF;（2）EC⊥BF（1）∵AE⊥AB,AF⊥AC, ∴∠BAE=∠CAF=90°,∴∠BAE+∠BAC=∠CAF+∠BAC, 即∠EAC=∠BAF,AE BM CF在△ABF和△AEC中,∵AE=AB,∠EAC=∠BAF,AF=AC,∴△ABF≌△AEC（SAS）,∴EC=BF;（2）如图,依据（1）,△ABF≌△AEC,∴∠AEC=∠ABF,∵AE⊥AB,∴∠BAE=90°,∴∠AEC+∠ADE=90°,∵∠ADE=∠BDM（对顶角相等）,∴∠ABF+∠BDM=90°,在△BDM中,∠BMD=180°-∠ABF-∠BDM=180°-90°=90°,∴EC⊥BF．32．如图：BE⊥AC,CF⊥AB,BM=AC,CN=AB.求证：（1）AM=AN;（2）AM⊥AN.证实：（1）∵BE⊥AC,CF⊥AB∴∠ABM+∠BAC=90°,∠ACN+∠BAC=90°∴∠ABM=∠ACN∵BM=AC,CN=AB∴△ABM≌△NAC∴AM=AN（2）∵△ABM≌△NAC∴∠BAM=∠N∵∠N+∠BAN=90°∴∠BAM+∠BAN=90°即∠MAN=90°∴AM⊥AN33．如图,已知∠A=∠D,AB=DE,AF=CD,BC=EF.求证:BC∥EF在△ABF和△CDE中,AB=DE∠A=∠DAF=CD∴△ABF≡△CDE（边角边）∴FB=CE在四边形BCEF中FB=CEBC=EF∴四边形BCEF是平行四边形∴BC‖EF34．如图,已知AC∥BD,EA.EB分离等分∠CAB和∠DBA,CD过点E,则AB与AC+BD相等吗？请解释来由在AB上取点N ,使得AN=AC∵∠CAE=∠EAN∴AE为公共, ∴△CAE≌△EAN∴∠ANE=∠ACE又∵AC平行BD∴∠ACE+∠BDE=180而∠ANE+∠ENB=180∴∠ENB=∠BDE∠NBE=∠EBN∵BE为公共边∴△EBN≌△EBD∴BD=BN∴AB=AN+BN=AC+BD35.如图,已知: AD是BC上的中线 ,且DF=DE．求证:BE∥CF．证实：∵AD是△ABC的中线BD=CD ∵DF=DE（已知）∠BDE=∠FDC ∴△BDE≌△FDC 则∠EBD=∠FCD ∴BE∥CF（内错角相等,两直线平行）.36.已知：如图,AB＝CD,DE⊥AC,BF⊥AC,E,F是垂足,．求证：．证实：∵DE⊥AC,BF⊥AC∴∠CED=∠AFB=90º又∵AB=CD,BF=DE∴Rt⊿ABF≌Rt⊿CDE（HL ）∴AF=CE∠BAF=∠DCE∴AB//CD37.如图,已知∠1=∠2,∠3=∠4,求证：AB=CD ∵,∠3=∠4∴OB=OC在△AOB 和△DOC 中∠1=∠2OB=OC∠AOB=∠DOC△AOB≌△DOC∴AO=DO AO+OC=DO+OB AC=DB在△ACB 和△DBC 中AC=DB A D ECBF,∠3=∠4BC=CB△ACB≌△DBC∴AB=CD38.如图,已知AC⊥AB,DB⊥AB,AC ＝BE,AE ＝BD,试猜测线段CE 与DE 的大小与地位关系,并证实你的结论.CE>DE.当∠AEB 越小,则DE 越小.证实：过D 作AE 平行线与AC 交于F,衔接FB由已知前提知AFDE 为平行四边形,ABEC 为矩形 ,且△DFB 为等腰三角形.RT△BAE 中,∠AEB 为锐角,即∠AEB<90°∵DF//AE ∴∠FDB=∠AEB<90°△DFB 中 ∠DFB=∠DBF=(180°-∠FDB)/2>45°RT△AFB 中,∠FBA=90°-∠DBF <45°∠AFB=90°-∠FBA>45°∴AB>AF∵AB=CE AF=DE∴CE>DE 39.(10分)如图,已知AB ＝DC,AC ＝DB,BE ＝CE,求证：AE ＝DE. ∵AB=DC,AC=DB,BC=BC∴△ABC≌△DCB,A CE D B A B E CD∴∠ABC=∠DCB又∵BE=CE,AB=DC∴△ABE≌△DCE∴AE=DE40．如图9所示,△ABC 是等腰直角三角形,∠ACB＝90°,AD 是BC 边上的中线,过C 作AD 的垂线,交AB 于点E,交AD 于点F,求证：∠ADC＝∠BDE．作CG ⊥AB,交AD 于H, 则∠ACH=45º,∠BCH=45º∵∠CAH=90º-∠CDA, ∠BCE=90º-∠CDA ∴∠CAH=∠BCE又∵AC=CB, ∠ACH=∠B=45º∴△ACH≌△CBE, ∴CH=BE 又∵∠DCH=∠B=45º, CD=DB∴△CFD≌△BED∴∠ADC=∠BDE AB CD E F图9。
全等三角形基础练习题及答案
全等三角形基础练习题及答案一、选择题1. △ABC和△A.△ABC≌△C. △ABC≌△2. 如图，已知AB＝CD，AD＝BC，则下列结论中错误的是A.AB∥DCB.∠B＝∠DC.∠A＝∠CD.AB＝BC 中，若AB＝，BC＝，AC＝ .则B. △ABC≌△ D. △ABC≌△3. 下列判断正确的是A.两个等边三角形全等B.三个对应角相等的两个三角形全等C.腰长对应相等的两个等腰三角形全等D.直角三角形与锐角三角形不全等4. 如图，AB、CD、EF相交于O，且被O点平分，DF ＝CE，BF＝AE，则图中全等三角形的对数共有A. 1对B.对C.对D.对5. 如图，将两根钢条，的中点O连在一起，使，可以绕着点O自由的转动，就做成了一个测量工件，则理由是的长等于内槽宽AB，那么判定△OAB≌△A.边角边B.角边角C.边边边D.角角边6. 如图，已知AB⊥BD于B，ED⊥BD于D，AB＝CD，BC＝ED，以下结论不正确的是A.EC⊥ACB.EC＝ACC.ED ＋AB ＝DBD.DC ＝CB二、填空题7. 如图，AB＝CD，AC＝DB，∠ABD＝25°，∠AOB＝82°，则∠DCB＝_________.8. 如图，在四边形ABCD中，对角线AC、BD互相平分，则图中全等三角形共有_____对.9. 如图，在△ABC和△EFD中，AD＝FC，AB＝FE，当添加条件_______时，就可得△ABC≌△EFD10. 如图，AC＝AD，CB＝DB，∠2＝30°，∠3＝26°，则∠CBE＝_______.11. 如图，点D在AB上，点E在AC上，CD与BE相交于点O，且AD＝AE，AB＝AC，若∠B ＝20°，则∠C＝______． 12. 已知，如图，AB＝CD，AC＝BD，则△ABC≌______，△ADC≌ ______.三、解答题13. 已知：如图，四边形ABCD中，对角线AC、BD相交于O，∠ADC＝∠BCD，AD＝BC，求证：CO＝DO．14. 已知：如图，AB∥CD，AB＝CD．求证：AD∥BC．分析：要证AD∥BC，只要证∠______＝∠______，又需证______≌______．证明：∵ AB∥CD ，∴ ∠______＝∠______ ，在△______和△______中，∴ Δ______≌Δ______ ．∴ ∠______＝∠______ ．∴ ______∥______．15. 如图，已知AB＝DC，AC＝DB，BE＝CE求证：AE ＝DE.答案与解析一.选择题1. B；注意对应顶点写在相应的位置.2. D；连接AC或BD证全等.3. D；4. C；△DOF≌△COE，△BOF≌△AOE，△DOB≌△COA.5. A；将两根钢条再由对顶角相等可证.6. D；△ABC≌△EDC，∠ECD＋∠ACB＝∠CAB＋∠ACB＝90°，所以EC⊥AC，ED ＋AB ＝BC＋CD＝DB.，的中点O连在一起，说明OA＝，OB＝，二.填空题7. 66°；可由SSS证明△ABC≌△DCB，∠OBC＝∠OCB＝∠ABC＝25°＋41°＝66°.8. 4；，所以∠DCB＝△AOD≌△COB，△AOB≌△COD，△ABD≌△CDB，△ABC≌△CDA.9. BC＝ED；10.56°；∠CBE＝26°＋30°＝56°.11.20°；△ABE≌△ACD12.△DCB，△DAB；注意对应顶点写在相应的位置上.三.解答题13.证明：在△ADC与△BCD中，14.3，4；ABD，CDB；已知；1，2；两直线平行，内错角相等；ABD，CDB；AB，CD，已知；全等三角形 one 姓名一．填空题1．如图,△ABC≌△DBC,且∠A和∠D,∠ABC和∠DBC 是对应角,其对应边:_______.2．如图,△ABD≌△ACE,且∠BAD和∠CAE,∠ABD和∠ACE,∠ADB和∠AEC是对应角,则对应边_________．. 已知:如图,△ABC≌△FED,且BC=DE.则∠A=__________,A D=_______．. 如图,△ABD≌△ACE,则AB的对应边是_________,∠BAD的对应角是______．5. 已知:如图,△ABE≌△ACD,∠B=∠C,则∠AEB=_______,AE=________．6．已知：如图, AC⊥BC于C , DE⊥AC于E , AD⊥AB 于 A , BC=AE．若AB=, 则AD=___________．．已知：△ABC≌△A’B’C’，△A’B’C’的周长为12cm，则△ABC 的周长为 .8．如图, 已知：∠1=∠, ∠3=∠, 要证BD=CD , 需先证△AEB≌△A EC , 根据是_________再证△BDE≌△______ , 根据是__________．AC’A’AACBC9．如图，∠1=∠2，由AAS判定△ABD≌△ACD，则需添加的条件是____________.10．如图，在平面上将△ABC绕B点旋转到△A’BC’的位置时，AA’∥BC，∠ABC=70°，则∠CBC’为________度.二．选择题11、下列条件中，不能判定三角形全等的是 A.三条边对应相等 B.两边和一角对应相等C.两角的其中一角的对边对应相等D.两角和它们的夹边对应相等12. 如果两个三角形全等,则不正确的是A.它们的最小角相等B.它们的对应外角相等C.它们是直角三角形D.它们的最长边相等13. 如图,已知:△ABE≌△ACD,∠1=∠2,∠B=∠C,不正确的等式是A.AB=ACB.∠BAE=∠CAD C.BE=DC D.AD=DE14. 图中全等的三角形是A.Ⅰ和ⅡB.Ⅱ和ⅣC.Ⅱ和ⅢD.Ⅰ和Ⅲ15. 下列说法中不正确的是 A.全等三角形的对应高相等 B.全等三角形的面积相等 C.全等三角形的周长相等D.周长相等的两个三角形全等16. AD=AE , AB=AC , BE、CD交于F , 则图中相等的角共有A.5对B.4对C.3对D.2对CADO17．如图,OA=OB,OC=OD, ∠O=60°, ∠C=25°则∠BED 的度数是A.70°B.5°C.5°D. 以上都不对18. 已知:如图,△ABC≌△DEF,AC∥DF,BC∥EF.则不正确的等式是A.AC=DFB.AD=BEC.DF=EFD.BC=EF19．如图, ∠A=∠D , OA=OD , ∠DOC=50°, 求∠DBC的度数为A.50°B.30°C.45°D.25°20. 如图, ∠ABC=∠DCB=70°, ∠ABD=40°, AB=DC , 则∠BAC=A.70°B.80°C.100°D.90° 三．解答题21. 已知:如图, 四边形ABCD中, AB∥CD , AD∥BC．求证：△ABD≌△CDB.22. 如图,有一池塘,要测池塘两端A、B的距离,可先在平地上取一个可以直接到达A和B的点C,连结AC并延长到D,使CD=CA.连结BC并延长到E,使EC=CB,连结DE,量出DE的长,就是A、B的距离.写出你的证明．23. 已知:如图,点B,E,C,F在同一直线上,AB∥DE,且AB=DE,BE=CF.求证:AC∥DF．24. 如图,已知: AD是BC上的中线 ,且DF=DE．求证:BE∥CF．25.如图, 已知：AB⊥BC于B , EF⊥AC于G , DF⊥BC 于D , BC=DF．求证：AC=EF．BEDCAGF全等三角形 two一.填空题：1.如图1，AD⊥BC，D为BC的中点，则△ABD≌_________.图1图24. 如图4，△ABC≌△AED，若AB?AE，?1?27?，则?2? .5.如图5，已知AB∥CD，AD∥BC，E.F是BD上两点，且BF＝DE，则图中共有对全等三角形.图56.如图6，四边形ABCD的对角线相交于O点，且有AB∥DC，AD∥BC，则图中有＿＿＿对全等三角形..“全等三角形对应角相等”的条件是 .8.如图8，AE＝AF，AB＝AC，∠A＝60°，∠B＝24°，则∠BOC＝__________.图9图8图6A9.若△ABC≌△A′B′C′，AD和A′D′分别是对应边BC和B′C′的高，则△ABD≌△A′B′D′，理由是_______________.10.在Rt△ABC中，∠C＝90°，∠A.∠B的平分线相交于O，则∠AOB＝_________. 二.选择题：11.如图9，△ABC≌△BAD，A和B.C和D分别是对应顶点，若AB＝6cm，AC＝4cm，BC＝5cm，则AD的长为A.4cmB.5cmC.6cmD.以上都不对 12.下列说法正确的是 A.周长相等的两个三角形全等B.有两边和其中一边的对角对应相等的两个三角形全等C.面积相等的两个三角形全等D.有两角和其中一角的对边对应相等的两个三角形全等13.在△ABC中，∠B＝∠C，与△ABC全等的三角形有一个角是100°，那么在△ABC中与这100°角对应相等的角是A.∠AB.∠BC.∠CD.∠B或∠C 14.下列条件中，能判定△ABC≌△DEF的是 A.AB＝DE，BC＝ED，∠A＝∠D B.∠A＝∠D，∠C＝∠F，AC＝EF C.∠B＝∠E，∠A＝∠D，AC＝EF D.∠B＝∠E，∠A＝∠D，AB＝DE15.AD是△ABC中BC边上的中线，若AB＝4，AC＝6，则AD的取值范围是 A.AD＞1B.AD＜5C.1＜AD＜ D.2＜AD＜10 16.下列命题正确的是 A.两条直角边对应相等的两个直角三角形全等； B.一条边和一个锐角对应相等的两个直角三角形全等C.有两边和其中一边的对角对应相等的两个三角形全等D.有两条边对应相等的两个直角三角形全等17.如图10.△ABC中，AB＝AC，BD⊥AC于D，CE⊥AB 于E，BD和CE交于点O，AO的延长线交BC于F，则图中全等直角三角形的对数为A.3对B.4对C.5对D.6对OBD图 11CA图10全等三角形测试题一、选择题 1．下列命题中真命题的个数有⑴形状相同的两个三角形是全等形；⑵在两个三角形中，相等的角是对应角，相等的边是对应边；⑶全等三角形对应边上的高、中线及对应角平分线分别相等， A、3个 B、2个 C、1个D、0个2．如图,已知△ABC的六个元素,则下面甲、乙、丙三个三角形中和△ABC全等的图形是 A．甲和乙Ｂ．乙和丙Ｃ．只有乙Ｄ．只有丙3．在⊿ABC和⊿A′B′C′中，AB=A′B′，∠A=∠A′，若证⊿ABC≌⊿A′B′C′还要从下列条件中补选一个，错误的选法是A. ∠B=∠B′B. ∠C=∠C′C. BC=B′C′D. AC=A′C′4．P是∠AOB平分线上一点，CD⊥OP于F，并分别交OA、OB于CD，则CD_____P点到∠AOB两边距离之和．A．小于B．大于 C．等于D．不能确定两直角三角形全等的是6．有以下条件：①一锐角与一边对应相等；②两边对应相等；③两锐角对应相等。
全等三角形证明题及答案15道
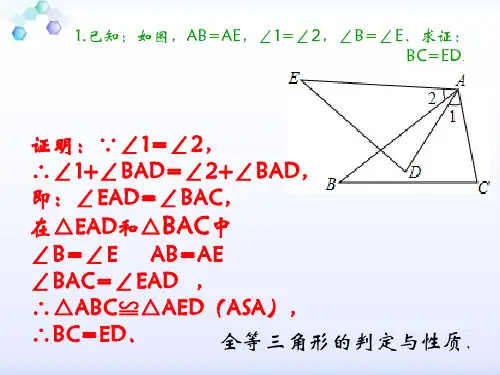
证明：∵∠1=∠2，
∴∠1+∠BAD=∠2+∠BAD，
即：∠EAD=∠BAC，
在△EAD和△BAC中
∠B=∠E AB=AE
∠BAC=∠EAD ，
∴△ABC≌△AED（ASA），
∴BC=ED．
全等三角形的判定与性质．
如图，E、F是四边形ABCD的对角线BD上的两点，AE∥CF， AE=CF，BE=DF．求证：△ADE≌△CBF．
∴△BCF≌△CBD（ASA）． 全等三角形的判定．
如图，在△ABC中，D是BC的中点，DE⊥AB， DF⊥AC，垂足分别是E，F，BE=CF． 求证：AD是△ABC的角平分线．
证明：∵DE⊥AB，DF⊥AC， ∴Rt△BDE=Rt△DCF=90°． BD=DC BE=CF ， ∴Rt△BDE≌Rt△DCF（HL）， ∴DE=DF， 又∵DE⊥AB，DF⊥AC， ∴AD是角平分线．
直角三角形全等的判定
如图，△ABC中，∠ABC=∠BAC=45°，点 P在AB上，AD⊥CP，BE⊥CP，垂足分别为D， E，已知DC=2，求BE的长．
∵∠ABC=∠BAC=45° ∴∠ACB=90°，AC=BC ∵∠DAC+∠ACD=90°，∠BCE+∠ACD=90° ∴∠DAC=∠BCE 又∵∠ADC=∠CEB ∴△ACD≌△CEB ∴BE=CD=2．
：∵AC平分∠BAD， ∴∠BAC=∠DAC， 在△ABC和△ADC 中， AB=AD ∠BAC=∠DAC AC=AC ， ∴Fra bibliotekABC≌△ADC．
全等三角形的判定．
9.如图，已知点E，C在线段BF上，BE=CF， AB∥DE，∠ACB=∠F．求证：△ABC≌△DEF．
全等三角形证明经典50题(含答案)
全等三角形证明经典50题(含答案)1. 已知：AB=4，AC=2，D 是BC 中点，AD 是整数，求AD解：延长AD 到E,使AD=DE∵D 是BC 中点∴BD=DC在△ACD 和△BDE 中AD=DE∠BDE=∠ADCBD=DC∴△ACD ≌△BDE∴AC=BE=2∵在△ABE 中AB-BE ＜AE ＜AB+BE∵AB=4即4-2＜2AD ＜4+21＜AD ＜3∴AD=22. 已知：D 是AB 中点，∠ACB=90°，求证：12CD AB延长CD 与P ，使D 为CP 中点。
连接AP,BP∵DP=DC,DA=DB∴ACBP 为平行四边形又∠ACB=90∴平行四边形ACBP 为矩形AD BC∴AB=CP=1/2AB3. 已知：BC=DE ，∠B=∠E ，∠C=∠D ，F 是CD 中点，求证：∠1=∠2证明：连接BF 和EF∵ BC=ED,CF=DF,∠BCF=∠EDF∴ 三角形BCF 全等于三角形EDF(边角边)∴ BF=EF,∠CBF=∠DEF连接BE在三角形BEF 中,BF=EF∴ ∠EBF=∠BEF 。
∵ ∠ABC=∠AED 。
∴ ∠ABE=∠AEB 。
∴ AB=AE 。
在三角形ABF 和三角形AEF 中AB=AE,BF=EF,∠ABF=∠ABE+∠EBF=∠AEB+∠BEF=∠AEF∴ 三角形ABF 和三角形AEF 全等。
∴ ∠BAF=∠EAF (∠1=∠2)。
4. 已知：∠1=∠2，CD=DE ，EF//AB ，求证：EF=AC过C 作CG ∥EF 交AD 的延长线于点GCG ∥EF ，可得，∠EFD ＝CGDDE ＝DC∠FDE ＝∠GDC （对顶角）B ACDF21 E∴△EFD≌△CGDEF＝CG∠CGD＝∠EFD又，EF∥AB∴，∠EFD＝∠1∠1=∠2∴∠CGD＝∠2∴△AGC为等腰三角形，AC＝CG又EF＝CG∴EF＝AC5.已知：AD平分∠BAC，AC=AB+BD，求证：∠B=2∠CA证明：延长AB取点E，使AE＝AC，连接DE∵AD平分∠BAC∴∠EAD＝∠CAD∵AE＝AC，AD＝AD∴△AED≌△ACD （SAS）∴∠E＝∠C∵AC＝AB+BD∴AE＝AB+BD∵AE＝AB+BE∴BD＝BE∴∠BDE＝∠E∵∠ABC＝∠E+∠BDE∴∠ABC＝2∠E∴∠ABC＝2∠C6. 已知：AC 平分∠BAD ，CE ⊥AB ，∠B+∠D=180°，求证：AE=AD+BE证明：在AE 上取F ，使EF ＝EB ，连接CF∵CE ⊥AB∴∠CEB ＝∠CEF ＝90°∵EB ＝EF ，CE ＝CE ，∴△CEB ≌△CEF∴∠B ＝∠CFE∵∠B ＋∠D ＝180°，∠CFE ＋∠CFA ＝180°∴∠D ＝∠CFA∵AC 平分∠BAD∴∠DAC ＝∠FAC∵AC ＝AC∴△ADC ≌△AFC （SAS ）∴AD ＝AF∴AE ＝AF ＋FE ＝AD ＋BE7. 已知：AB=4，AC=2，D 是BC 中点，AD 是整数，求AD解：延长AD 到E,使AD=DE∵D 是BC 中点∴BD=DC在△ACD 和△BDE 中AD BCAD=DE∠BDE=∠ADCBD=DC∴△ACD≌△BDE∴AC=BE=2∵在△ABE中AB-BE＜AE＜AB+BE ∵AB=4即4-2＜2AD＜4+21＜AD＜3∴AD=28.已知：D是AB中点，∠ACB=90°，求证：12 CD AB9. 已知：BC=DE ，∠B=∠E ，∠C=∠D ，F 是CD 中点，求证：∠1=∠2证明：连接BF 和EF 。
用“HL”证直角三角形全等同步练习含答案
用“HL ”证直角三角形全等同步练习含答案基础题基础题知识点1 1 用“用“用“HL HL HL”判定两个三角形全等”判定两个三角形全等”判定两个三角形全等1．如图，∠．如图，∠A A ＝∠D＝＝∠D＝909090°，°，°，AC AC AC＝＝DB DB，则△ABC≌△DCB ，则△ABC≌△DCB 的理由是（的理由是（ ） A ．HL HL B ．ASA C ．AAS D ．SAS2．下列判定两个直角三角形全等的方法中，不正确的是（．下列判定两个直角三角形全等的方法中，不正确的是（ ） A ．两条直角边分别对应相等．两条直角边分别对应相等 B ．斜边和一锐角分别对应相等．斜边和一锐角分别对应相等 C ．斜边和一条直角边分别对应相等．斜边和一条直角边分别对应相等 D ．两个三角形的面积相等．两个三角形的面积相等3．如图所示，△．如图所示，△ABC ABC 中，中，AD AD AD⊥⊥BC 于D ，再添加一个条件，再添加一个条件____________________________________________________________，可使△ABD≌△ACD.，可使△ABD≌△ACD.，可使△ABD≌△ACD.4．如图，小明和小芳以相同的速度分别同时从A ，B 出发，小明沿AC 行走，小芳沿BD 行走，并同时到达C 、D ，若CB⊥AB，CB⊥AB，DA DA DA⊥⊥AB AB，则，则CB 与DA 相等吗？为什么？21世纪教育网版权所有5．已知AD⊥BE，垂足C 是BE 的中点，的中点，AB AB AB＝＝DE DE，请说明，请说明AB∥DE 的理由．的理由．6．如图，∠．如图，∠ACB ACB ACB＝∠CFE＝＝∠CFE＝＝∠CFE＝909090°，°，°，AB AB AB＝＝DE DE，，BC BC＝＝EF EF，求证：，求证：，求证：AD AD AD＝＝CF.知识点2 2 直角三角形全等判定方法的选用直角三角形全等判定方法的选用直角三角形全等判定方法的选用7．在Rt Rt△△ABC 和Rt Rt△△A ′B ′C ′中，∠′中，∠C C ＝∠C′＝＝∠C′＝909090°，如图，那么下列各条件中，不能使°，如图，那么下列各条件中，不能使Rt Rt△△ABC ABC≌≌Rt △A ′B ′C ′的是（′的是（）21教育网A ．AB AB＝A′B′＝＝A′B′＝＝A′B′＝55，BC BC＝B′C′＝＝B′C′＝＝B′C′＝3 3 B ．AB AB＝B′C′＝＝B′C′＝＝B′C′＝55，∠，∠A A ＝∠B′＝＝∠B′＝404040°° C ．AC AC＝A′C′＝＝A′C′＝＝A′C′＝55，BC BC＝B′C′＝＝B′C′＝＝B′C′＝3 3D ．AC AC＝A′C′＝＝A′C′＝＝A′C′＝55，∠，∠A A ＝∠A′＝＝∠A′＝404040°°8．如图，在△．如图，在△ABC ABC 中，点D 是BC 的中点，的中点，DE DE DE⊥⊥AB 于点E ，DF DF⊥⊥AC 于点F ，BE BE＝＝CF.(1)(1)图中有几对全等的三角形？请一一列出；图中有几对全等的三角形？请一一列出；图中有几对全等的三角形？请一一列出；(2)(2)选择一对你认为全等的三角形说明理由．选择一对你认为全等的三角形说明理由．选择一对你认为全等的三角形说明理由． 中档题中档题9．如图，在Rt Rt△△ABC 中，∠中，∠BAC BAC BAC＝＝9090°，°，°，DE DE DE⊥⊥BC BC，，AC AC＝＝6，EC EC＝＝6，∠，∠ACB ACB ACB＝＝6060°，则∠ACD °，则∠ACD 的度数为（的度数为（）A ．4545°°B ．3030°°C ．2020°°D ．1515°°1010．如图，在直角三角形．如图，在直角三角形ABC 中，∠中，∠C C ＝9090°，一条线段°，一条线段PQ PQ＝＝AB AB，点，点P ，Q 两点分别在AC 和AC 的垂线AX 上移动，当AP AP＝＝________________时，才能使△ABC≌△QPA.时，才能使△ABC≌△1111．如图，已知方格纸中是．如图，已知方格纸中是4个相同的正方形，则∠1＋∠3＝个相同的正方形，则∠1＋∠3＝________________________．．1212．如图，已知．如图，已知AE AE＝＝DE DE，，AB AB⊥⊥BC BC，，DC DC⊥⊥BC BC，且，且AB AB＝＝EC.EC.求证：求证：求证：BC BC BC＝＝AB AB＋＋DC.1313．如图所示，已知．如图所示，已知AB AB＝＝CD CD，，DE DE⊥⊥AC 于E ，BF BF⊥⊥AC 于F ，且BF BF＝＝DE DE，求证：AB∥CD.，求证：AB∥CD.，求证：AB∥CD.1414．如图，已知．如图，已知AD AD，，AF 分别是两个钝角△ABC 和△ABE 的高，如果AD AD＝＝AF AF，，AC AC＝＝AE.AE.求证：求证：求证：BC BC BC＝＝BE.综合题综合题1515．已知：点．已知：点O 到△ABC 的两边AB AB，，AC 所在直线的距离相等，且OB OB＝＝OC.(1)(1)如图如图1，若点O 在边BC 上，求证：∠ABO＝∠ACO；上，求证：∠ABO＝∠ACO；(2)(2)如图如图2，若点O 在△ABC 的内部，求证：∠ABO＝∠ACO.的内部，求证：∠ABO＝∠ACO.参考答案参考答案1．A A 2.D 2.D 2.D 3.3.3.答案不唯一，如答案不唯一，如AB AB＝＝AC AC，或，或BD BD＝＝CD 等 4.CB 4.CB＝＝DA.DA.理由：由题意易知理由：由题意易知AC AC＝＝BD. ∵CB⊥AB，∵CB⊥AB，DA DA DA⊥⊥AB AB，， ∴∠∴∠DAB DAB DAB＝∠CBA＝＝∠CBA＝＝∠CBA＝909090°°.在Rt Rt△△DAB 与Rt Rt△△CBA 中，îïíïìBD BD＝＝AC AC，，AB AB＝＝BA BA，， ∴Rt Rt△△DAB DAB≌≌Rt Rt△△CBA(HL)CBA(HL)．． ∴DA＝∴DA＝CB. CB. CB. 5.∵C 是BE 的中点，的中点， ∴BC BC＝＝CE .∵AD⊥BE，.∵AD⊥BE，∴∠∴∠ACB ACB ACB＝∠DCE＝＝∠DCE＝＝∠DCE＝909090°°.在Rt Rt△△ACB 与Rt Rt△△DCE 中，îïíïìAB AB＝＝DE DE，，BC BC＝＝EC EC，，∴Rt Rt△△ACB ACB≌≌Rt Rt△△DCE(HL)DCE(HL)．． ∴∠B＝∠E.∴∠B＝∠E. ∴AB∥DE.∴AB∥DE.6.6.证明：∵∠ACB＝∠CFE＝证明：∵∠ACB＝∠CFE＝证明：∵∠ACB＝∠CFE＝909090°，°，°， ∴∠∴∠ACB ACB ACB＝∠DFE＝＝∠DFE＝＝∠DFE＝909090°°.在Rt Rt△△ACB 和RtRt△△DFE 中，îïíïìAB AB＝＝DE DE，，BC BC＝＝EF EF，，∴Rt Rt△△ACB ACB≌≌Rt Rt△△DFE(HL)DFE(HL)．． ∴AC＝∴AC＝DF. DF.∴AC－∴AC－AF AF AF＝＝DF DF－－AF AF，即，即AD AD＝＝CF. CF. 7.B8．(1)△BDE≌△CDF，△．(1)△BDE≌△CDF，△AED AED AED≌△≌△≌△AFD AFD AFD，△，△，△ABD ABD ABD≌△≌△≌△ACD. ACD. (2)∵DE⊥AB，(2)∵DE⊥AB，DF DF DF⊥⊥AC AC，， ∴△∴△BDE BDE 和△CDF 是直角三角形．是直角三角形． ∵D 是BC 的中点，的中点，∴BD BD＝＝CD. 又∵BE＝又∵BE＝CF CF CF，，∴Rt Rt△△BDE BDE≌≌Rt Rt△△CDF(HL)CDF(HL)．． 9.B 10．CB CB 11.9011.9011.90°° 12.12.证明：∵AB⊥BC，证明：∵AB⊥BC，证明：∵AB⊥BC，DC DC DC⊥⊥BC BC，， ∴∠∴∠B B ＝∠C＝＝∠C＝909090°°.在Rt Rt△△ABE 和Rt Rt△△ECD 中，îïíïìAE AE＝＝ED ED，，AB AB＝＝EC EC，， ∴Rt Rt△△ABE ABE≌≌Rt Rt△△ECD. ∴BE BE＝＝CD. ∵BC＝∵BC＝BE BE BE＋＋EC EC，， ∴BC BC＝＝AB AB＋＋DC. DC.13.13.证明：∵DE⊥AC，证明：∵DE⊥AC，证明：∵DE⊥AC，BF BF BF⊥⊥AC AC，， ∴∠∴∠AFB AFB AFB＝∠CED＝＝∠CED＝＝∠CED＝909090°°.在Rt Rt△△ABF 和Rt Rt△△CDE 中，îïíïìAB AB＝＝CD CD，，BF BF＝＝DE DE，， ∴Rt Rt△△ABF ABF≌≌Rt Rt△△CDE(HL)CDE(HL)．． ∴∠∴∠BAF BAF BAF＝∠DCE.＝∠DCE.＝∠DCE. ∴AB∥CD.∴AB∥CD.14.14.证明：∵证明：∵证明：∵AD AD AD，，AF 分别是两个钝角△ABC 和△ABE 的高，的高， ∴∠∴∠ADB ADB ADB＝∠AFB＝＝∠AFB＝＝∠AFB＝909090°°. ∵AB AB＝＝AB AB，，AD AD＝＝AF AF，， ∴Rt Rt△△ABD ABD≌≌Rt Rt△△ABF. ∴DB DB＝＝FB.∵AC＝∵AC＝AE AE AE，，AD AD＝＝AF AF，， ∴Rt Rt△△ADC ADC≌≌Rt Rt△△AFE. ∴DC DC＝＝FE.∴DB－∴DB－DC DC DC＝＝FB FB－－FE FE，即，即BC BC＝＝BE. BE.15.15.证明：证明：证明：(1)(1)(1)过点过点O 作OE⊥AB 于E ，作OF⊥AC 于F ，则∠BEO＝∠CFO＝，则∠BEO＝∠CFO＝909090°°. 又∵OB＝又∵OB＝OC OC OC，，OE OE＝＝OF OF，，∴Rt Rt△△BOE BOE≌≌Rt Rt△△COF(HL)COF(HL)．． ∴∠ABO＝∠ACO.∴∠ABO＝∠ACO.(2)(2)过点过点O 分别作OE⊥AB，OE⊥AB，OF OF OF⊥⊥AC AC，，E ，F 分别是垂足，则∠BEO＝∠CFO＝分别是垂足，则∠BEO＝∠CFO＝909090°°. 又∵OB＝又∵OB＝OC OC OC，，OE OE＝＝OF OF，， ∴Rt Rt△△OEB OEB≌≌Rt Rt△△OFC.∴∠∴∠EBO EBO EBO＝∠FCO，即∠ABO＝∠ACO.＝∠FCO，即∠ABO＝∠ACO.＝∠FCO，即∠ABO＝∠ACO.。
全等三角形证明50题(含答案)
全等三角形证明经典50题(含答案)1. 已知：AB=4，AC=2，D 是BC 中点，AD 是整数，求AD解：延长AD 到E,使AD=DE ∵D 是BC 中点 ∴BD=DC 在△ACD 和△BDE 中 AD=DE ∠BDE=∠ADC BD=DC ∴△ACD ≌△BDE ∴AC=BE=2 ∵在△ABE 中 AB-BE ＜AE ＜AB+BE ∵AB=4即4-2＜2AD ＜4+2 1＜AD ＜3 ∴AD=2ADBC2. 已知：D 是AB 中点，∠ACB=90°，求证：12CD AB延长CD 与P ，使D 为CP 中点。
连接AP ,BP ∵DP=DC,DA=DB ∴ACBP 为平行四边形 又∠ACB=90∴平行四边形ACBP 为矩形 ∴AB=CP=1/2AB3. 已知：BC=DE ，∠B=∠E ，∠C=∠D ，F 是CD 中点，求证：∠1=∠2证明：连接BF 和EF ∵ BC=ED,CF=DF,∠BCF=∠EDF∴ 三角形BCF 全等于三角形EDF(边角边) ∴ BF=EF,∠CBF=∠DEF连接BE在三角形BEF 中,BF=EF ∴ ∠EBF=∠BEF 。
∵ ∠ABC=∠AED 。
∴ ∠ABE=∠AEB 。
∴ AB=AE 。
在三角形ABF 和三角形AEF 中 AB=AE,BF=EF,∠ABF=∠ABE+∠EBF=∠AEB+∠BEF=∠AEF ∴ 三角形ABF 和三角形AEF 全等。
∴ ∠BAF=∠EAF (∠1=∠2)。
4. 已知：∠1=∠2，CD=DE ，EF//AB ，求证：EF=AC过C 作CG ∥EF 交AD 的延长线于点G CG ∥EF ，可得，∠EFD ＝CGD DE ＝DC∠FDE ＝∠GDC （对顶角）BA CDF2 1 EEF＝CG∠CGD＝∠EFD又，EF∥AB∴，∠EFD＝∠1∠1=∠2∴∠CGD＝∠2∴△AGC为等腰三角形，AC＝CG又EF＝CG∴EF＝AC5.已知：AD平分∠BAC，AC=AB+BD，求证：∠B=2∠CA证明：延长AB取点E，使AE＝AC，连接DE∵AD平分∠BAC∵AE＝AC，AD＝AD∴△AED≌△ACD （SAS）∴∠E＝∠C∵AC＝AB+BD∴AE＝AB+BD∵AE＝AB+BE∴BD＝BE∴∠BDE＝∠E∵∠ABC＝∠E+∠BDE∴∠ABC＝2∠E∴∠ABC＝2∠C6.已知：AC平分∠BAD，CE⊥AB，∠B+∠D=180°，求证：AE=AD+BE证明：在AE 上取F ，使EF ＝EB ，连接CF ∵CE ⊥AB∴∠CEB ＝∠CEF ＝90° ∵EB ＝EF ，CE ＝CE ， ∴△CEB ≌△CEF ∴∠B ＝∠CFE∵∠B ＋∠D ＝180°，∠CFE ＋∠CFA ＝180° ∴∠D ＝∠CFA ∵AC 平分∠BAD ∴∠DAC ＝∠FAC ∵AC ＝AC∴△ADC ≌△AFC （SAS ） ∴AD ＝AF∴AE ＝AF ＋FE ＝AD ＋BE7. 已知：AB=4，AC=2，D 是BC 中点，AD 是整数，求AD解：延长AD 到E,使AD=DEADB C∵D 是BC 中点 ∴BD=DC在△ACD 和△BDE 中 AD=DE ∠BDE=∠ADC BD=DC ∴△ACD ≌△BDE ∴AC=BE=2 ∵在△ABE 中 AB-BE ＜AE ＜AB+BE ∵AB=4即4-2＜2AD ＜4+2 1＜AD ＜3 ∴AD=28. 已知：D 是AB 中点，∠ACB=90°，求证：12CD AB解：延长AD到E,使AD=DE∵D是BC中点∴BD=DC在△ACD和△BDE中AD=DE∠BDE=∠ADCBD=DC∴△ACD≌△BDE∴AC=BE=2∵在△ABE中AB-BE＜AE＜AB+BE∵AB=4即4-2＜2AD＜4+21＜AD＜3∴AD=29.已知：BC=DE，∠B=∠E，∠C=∠D，F是CD中点，求证：∠1=∠2证明：连接BF和EF。
全等三角形证明经典40题(含答案)
1. 已知：AB=4，AC=2，D 是BC 中点，AD 是整数，求AD 的长.解：延长AD 到E,使AD=DE∵D 是BC 中点∴BD=DC在△ACD 和△BDE 中AD=DE∠BDE=∠ADCBD=DC∴△ACD ≌△BDE∴AC=BE=2∵在△ABE 中AB-BE ＜AE ＜AB+BE∵AB=4即4-2＜2AD ＜4+21＜AD ＜3∴AD=22. 已知：BC=ED ，∠B=∠E ，∠C=∠D ，F 是CD 中点，求证：∠1=∠2证明：连接BF 和EF∵ BC=ED,CF=DF,∠BCF=∠EDF∴ 三角形BCF 全等于三角形EDF(边角边)∴ BF=EF,∠CBF=∠DEF连接BE在三角形BEF 中,BF=EF∴ ∠EBF=∠BEF 。
∵ ∠ABC=∠AED 。
∴ ∠ABE=∠AEB 。
∴ AB=AE 。
在三角形ABF 和三角形AEF 中AB=AE,BF=EF,∠ABF=∠ABE+∠EBF=∠AEB+∠BEF=∠AEF∴ 三角形ABF 和三角形AEF 全等。
∴ ∠BAF=∠EAF (∠1=∠2)。
AD B C3. 已知：∠1=∠2，CD=DE ，EF//AB ，求证：EF=AC过C 作CG∥EF 交AD 的延长线于点GCG∥EF，可得，∠EFD＝CGDDE ＝DC∠FDE＝∠GDC（对顶角）∴△EFD≌△CGDEF ＝CG∠CGD＝∠EFD又，EF∥AB∴，∠EFD＝∠1∠1=∠2∴∠CGD＝∠2∴△AGC 为等腰三角形，AC ＝CG又 EF ＝CG∴EF ＝AC4. 已知：AD 平分∠BAC ，AC=AB+BD ，求证：∠B=2∠ C证明：延长AB 取点E ，使AE ＝AC ，连接DE∵AD 平分∠BAC∴∠EAD ＝∠CAD∵AE ＝AC ，AD ＝AD∴△AED ≌△ACD （SAS ）∴∠E ＝∠C∵AC ＝AB+BD∴AE ＝AB+BD∵AE ＝AB+BE∴BD ＝BE∴∠BDE ＝∠EBACDF21 E A∵∠ABC＝∠E+∠BDE∴∠ABC＝2∠E∴∠ABC＝2∠C5.已知：AC平分∠BAD，CE⊥AB，∠B+∠D=180°，求证：AE=AD+BE证明：在AE上取F，使EF＝EB，连接CF∵CE⊥AB∴∠CEB＝∠CEF＝90°∵EB＝EF，CE＝CE，∴△CEB≌△CEF(SAS)∴∠B＝∠CFE∵∠B＋∠D＝180°，∠CFE＋∠CFA＝180°∴∠D＝∠CFA∵AC平分∠BAD∴∠DAC＝∠FAC∵AC＝AC∴△ADC≌△AFC（SAS）∴AD＝AF∴AE＝AF＋FE＝AD＋BE6. 如图，四边形ABCD中，AB∥DC，BE、CE分别平分∠ABC、∠BCD，且点E在AD上。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
1 / 16 七年级全等测试 •选择题（共3小题） 1. 如图，EB交 AC于 M，交 FC于 D, AB交 FC于 N,/ E=Z F=90° / B=Z C, AE=AF,给出下列结论：①/ 1 = /2;②BE=CF③厶ACN^AABM:④CD=DN 其 中正确的结论有（ ）
A. 4个B. 3个C. 2个D. 1个 2. 如图，△ ABC为等边三角形，D、E分别是AC、BC上的点，且AD=CE AE与 BD相交于点P，BF丄AE于点F.若BP=4则PF的长（ ）
A. 2 B. 3 C. 1 D. 2 二 3. 如图，OA=OC OB=OD且 0A丄OB, OCX OD,下列结论：①△ AOD^A COB ②CD=AB③/ CDA=Z ABC; 其中正确的结论是（ ）
D A.①② B.①②③ C•①③ D.②③ 二.解答题（共11小题） 4. 如图，四边形 ABCD中，对角线AC BD交于点O, AB=AC点E是BD上 点，且 AE=AD / EAD=Z BAC 2 / 16
（1）求证：/ ABD=/ ACD3 / 16
(2)若/ ACB=65，求/ BDC的度数. B C 5. (1)如图①，在四边形 ABCD中，AB// DC, E是BC的中点，若 AE是/ BAD 的平分线，试探究AB, AD，DC之间的等量关系，证明你的结论； (2)如图②，在四边形 ABCD中，AB// DC, AF与DC的延长线交于点F, E是 BC的中点，若AE是/BAF的平分线，试探究AB，AF, CF之间的等量关系，证 明你的结论.
6 .已知：在△ ABC中，AB=AC D为AC的中点，DE丄AB, DF丄BC,垂足分别为 点E, F,且DE=DF求证：△ ABC是等边三角形.
7. 已知，在△ ABC中，/ A=90°, AB=AC点D为BC的中点. (1) 如图①，若点E、F分别为AB、AC上的点，且DE丄DF,求证：BE=AF (2) 若点E、F分别为AB、CA延长线上的点，且 DE丄DF,那么BE=AF吗？请 利用图②说明理由.
圍① 图
图圏4 / 16
8. 如图，在RtA ABC,/ ACB=90, AC=BC分别过A、B作直线I的垂线，垂足 分别为M、N. (1) 求证：△ AMC^^ CNB (2) 若 AM=3，BN=5,求 AB的长. B
9. 已知，如图，在等腰直角三角形中，/ C=90°, D是AB的中点，DE± DF,点 E、F 在 AC BC上，求证：DE=DF
10. 如图，OC是/MON内的一条射线，P为OC上一点，PAI OM，PB丄ON， 垂足分别为A，B，PA=PB连接AB, AB与OP交于点E. (1)求证：△ OPA^A OPB
11. 如图，△ ABC和厶ADE分别是以BC, DE为底边且顶角相等的等腰三角形, 点D在线段BC上, AF平分DE交BC于点F,连接BE, EF. (1) CD与BE相等？若相等，请证明；若不相等，请说明理由； (2) 若/ BAC=90,求证：BF2+CD?=FD2. 5 / 16
B F D C 12 .如图，OC是/AOB的角平分线，P是OC上一点，PD丄OA, PEL OB,垂足 分别为D, E. F是OC上另一点，连接DF, EF.
13.如图，OP平分/ AOB, PELOA于E，PFLOB于F,点M在OA上，点N在 OB 上，且 PM=PN.求证：EM=FN.
B 14.如图，△ ABC中，D为BC边上一点，BEL AD的延长线于E, CFL AD于F, BE=CF求证：D为BC的中点.
答案 一.选择题（共3小题） 1. 如图，EB交 AC于 M，交 FC于 D, AB交 FC于 N,/ E=Z F=90° / B=Z C, AE=AF给出下列结论：①/ 1 = /2;②BE=CF③厶ACN^AABM:④CD=DN 其 中正确的结论有（ ） £ 6 / 16
A. 4个B. 3个C. 2个D. 1个 【解答】 解：I/ E=Z F=90°, / B=Z C, AE=AF •••△ ABE^A ACF ••• BE=CF / BAE/ CAF / BAE- / BAC=Z CAF- / BAC •••/ 仁/ 2
△ ABE^A ACF
•••/ B=/ C, AB=AC
又/ BACK CAB △ ACN^A ABM. ④CD=DN不能证明成立，3个结论对. 故选：B. 2. 如图，△ ABC为等边三角形，D、E分别是AC、BC上的点，且AD=CE AE与 BD相交于点P，BF丄AE于点F.若BP=4则PF的长（ ）
A. 2 B. 3 C. 1 D. 2 二 【解答】解：•••△ ABC是等边三角形, ••• AB=AC •••/ BACK C.
在厶ABD和厶CAE中， fAB=AC ZBAD^ZC, 7 / 16
AD=CE •••△ ABD^A CAE( SAS .
•••/ ABD=Z CAE
•••/ APD=Z ABF+Z PAB=/ BAC=60. •••/ BPF=/ APD=60. •••Z BFP=90, Z BPF=60, •••Z PBF=30.
故选：A. 3. 如图，OA=OC OB=OD且 OA丄OB, OCX OD,下列结论：①△ AOD^A COB ②CD=AB③Z CDA=Z ABC; 其中正确的结论是（ ）
D A.①② B.①②③ C•①③ D.②③
【解答】 解：• OAX OB, OCX OD, • Z AOB=Z COD=9O.
• Z AOB^Z AOC=Z COD+Z AOC, 即Z COBZ AOD. 在厶AOB和厶COD中， rAO=CO 弋 ZACB=ZC0D, i BO二DO • △ AOB^A COD ( SAS,
• AB=CD Z ABO=Z CDO. 在厶AOD和厶COB中 'AO=CO ZWD-ZCOB, HOBO •••△ AOD^A COB( SAS
•••/ CBOK ADO, 8 / 16
•••/ ABO- / CBOK CDO-Z ADO, 即/ ABC=/ CDA 综上所述，①②③都是正确的. 故选：B. 二•解答题(共11小题) 4•如图，四边形 ABCD中，对角线AC BD交于点O, AB=AC点E是BD上 点，且 AE=AD / EAD=/ BAC (1) 求证：/ ABD=/ ACD (2) 若/ ACB=65，求/ BDC的度数.
【解答】 证明：(1)v/ BAC=/ EAD •••/ BAC- / EAC/ EAD- / EAC 即：/ BAE=/ CAD rAB=AC 在厶 ABEft^ ACD中・ ZBAE=ZCAD
tAE=AD
•••△ ABE^A ACD •••/ ABD=/ ACD (2)v/ BOC是厶ABO和ADCO的外角
•••/ BOC=/ ABD+/BAC, / BOC=/ ACD+/ BDC •••/ ABD+/BAC=/ ACD+/ BDC •••/ ABD=/ ACD 9 / 16
:丄 BACK BDC ACB=65, AB=AC •••/ ABC2 ACB=65
•••/ BAC=180-Z ABC- / ACB=180 -65° - 65°=50°
•••/ BDC=/ BAC=50. 5. (1)如图①，在四边形 ABCD中，AB// DC, E是BC的中点，若 AE是/ BAD 的平分线，试探究AB, AD, DC之间的等量关系，证明你的结论； (2)如图②，在四边形 ABCD中，AB// DC, AF与DC的延长线交于点F, E是 BC的中点，若AE是/BAF的平分线，试探究AB, AF, CF之间的等量关系，证
【解答】解：(1)证明：延长AE交DC的延长线于点F, ••• E是BC的中点, ••• CE=BE ••• AB// DC, •••/ BAE=/ F, rZBAE=ZF 在厶 AEBft^ FEC中，Z拡B二ZFEC, tBE=CE
•••△ AEB^A FEC ••• AB=FC ••• AE是/ BAD的平分线,
•••/ BAE=/ EAD,
明你的结10 / 16
••• AB// CD, •••/ BAEK F, •••/ EADH F, ••• AD=DF, ••• AD=DF=DCCF=D(+AB,
••• E是BC的中点， ••• CE=BE ••• AB// DC, •••/ BAEK G, rZBAE=ZG 在厶 AEBft^ GEC中，，/拯B二ZGEC, 艇HE
••• AB=GC ••• AE是/ BAF的平分线, •••/ BAGN FAG ••• AB// CD, •••/ BAGN G, •••/ FAG=/ G, ••• FA=FG ••• AB=CG=AfCF,
6. 已知：在△ ABC中,AB=AC D为AC的中点,DE丄AB , DF丄BC,垂足分别为 点E , F,且DE=DF求证：△ ABC是等边三角形.
(2)如图②，延长AE交DF的延长线于点 G
,