线面垂直,面面垂直
线面、面面平行和垂直的八大定理

线面、面面平行和垂直的八大定理一、线面平行。
1、判定定理:平面外一条直线与平面内一条直线平行,那么这条直线与这个平面平行。
符合表示:βββ////ababa⇒⎪⎭⎪⎬⎫⊂⊄2、性质定理:如果一条直线与平面平行,经过这条直线的平面和这个平面相交,那么这条直线和交线平行。
符号表示:babaaa////⇒⎪⎪⎭⎪⎪⎬⎫=⊂⊄βαβαα二、面面平行。
1、判定定理:如果一个平面内有两条相交直线分别平行于另一个平面内的两条相交直线,那么这两个平面平行。
符号表示:βα//////⇒⎪⎪⎪⎭⎪⎪⎪⎬⎫==NnmMbaambn2、性质定理:如果两个平面平行同时与第三个平面相交,那它们的交线平行。
符号表示:dldl////⇒⎪⎭⎪⎬⎫==γβγαβα(更加实用的性质:一个平面内的任一直线平行另一平面)三、线面垂直。
1、判定定理:如果一条直线与一个平面内的两条相交直线都垂直,那么这条直线垂直这个平面。
符号表示: α⊥⇒⎪⎪⎪⎪⎭⎪⎪⎪⎪⎬⎫=⊥⊥a M c b b a c a $:三垂线定理:(经常考到这种逻辑)在平面内的一条直线,如果它和这个平面的一条斜线的射影垂直,那么它也和这条斜线垂直。
符号表示:PA a A oA a po oA a ⊥⇒⎪⎪⎭⎪⎪⎬⎫=⊥⊥⊂⊂ααα2、性质定理:垂直同一平面的两条直线互相平行。
(更加实用的性质是:一个平面的垂线垂直于该平面内任一直线。
)四、面面垂直。
1、判定定理:经过一个平面的垂线的平面与该平面垂直。
βααβ⊥⇒⊂⊥a a ,2、性质定理:已知两个平面垂直,在一个平面内垂直于交线的直线垂直于另一个平面。
βαβαβα⊥⇒⊥⊂=⋂⊥a b a a b ,,,。
怎么由面面垂直证明线面垂直

怎么由面面垂直证明线面垂直
因为已知面面垂直,所以这俩个面上的任何一条线都相互垂直,只要证明一条线垂直于一个平面,并且这条线属于垂直于这个平面的另一个平面的线,那么这条线就垂直与那个面。
直线与平面垂直定义:如果一条直线与一个平面内的任意一条直线都垂直,就说这条直线与此平面互相垂直。
延伸阅读
出生证明怎么办
1、首先办理出生证明所需要的流程和资料。
办理出生证明需要注意以下几点。
3、办理出生证明需要注意:新生儿姓名和地址确定后不能更改,切记!
4、第6版和第5版最大的区别是哪里呢?主要是出生医学证明(第六版)将出生医学证明(第五版)封底“_____国家卫生和计划生育委员会监制”字样更改为“_____国家卫生健康委员会监制”。
5、新版出生证明在增加了防伪功能的基础上,更进一步地提供了一些信息,可谓是更加良心了。
6、不知道你是否还记得以前的出生证明,它长这样!
如何快速拿到离职证明
如何顺利拿到离职证明
方法/步骤1按公司离职流程填写离职单,办理离职手序。
2各流程完结,相关部门人员都签完字,离职交接完毕并签字。
确保无遗留问题。
3拿离职单以及工作交接单到人力资源部,找负责办理离职手续的主管开具离职证明。
没有工作证明怎么申请信用卡
如果没有工作证明,但是每个月都在缴税的话,那还是有可能申请到信用卡的。
银行官网申请申请条件:
1、年满十八周岁;
2、有稳定的还款能力。
提交证明:
2、工作证明或收入证明;
4、完税证明或自己名下房产车辆;
5、其他银行信用卡等。
线面垂直与面面垂

1.如图,若PA=PB=PC,则O 是 △ABC的外心.
2.如图,若PA,PB,PC两两垂 直,则O 是△ABC的垂心.
P
C
A O P B
3.如图,若点P到三边的距离 相等(即PD=PE=PF),则O是 △ABC的内心.
C D A O E
F B
例1.已知,如图,四面体A-BCD中,
A B C D , A D B C , H 为 B C D的 垂 心 。
D H A
C
B
四、小结
1、两个平面垂直定义:A
B
D
β
E
2、两个平面垂直的判定定理: 如果一个平面经过了另一个平面的一条垂线, 那么这两个平面互相垂直 3、两个平面垂直的性质定理: 如果两个平面垂直,那么在一个平面内垂直 于它们交线的直线垂直于另一个平面
课堂检测
1. 下列命题中正确的是( C ) (A)平面α和β分别过两条互相垂直的直 线,则α⊥β (B)若平面α内的一条直线垂直于平面β 内的两条平行直线,则α⊥β (C)若平面α内的一条直线垂直于平面β 内的两条相交直线,则α⊥β (D)若平面α内的一条直线垂直于平面β 内的无数条直线,则α⊥β
AD 面 ABC
1
(1) 求 证 : A D B C 1
C1
( 2 )求 证 : 面 A D C 1 面 B D C1.
BC C1D
1
BC 1
AD
1
C
B
O A
BC 1 面 ADC
D
课时作业参考答案
十一:DABC
13 5
①③
a
3
十二:DCDD③⑤ ②⑤
6
O
如图所示:已知四棱锥P-ABCD的底面为等腰 梯形,AB//CD,AC⊥BD,垂足为H,PH是四棱 锥高。 (1)证明:平面PAC ⊥平面PBD (2)若AB= 6 ,APB ADB 60 0 ,求四棱锥P P ABCD的体积。
线面、面面平行和垂直的八大定理

线面、面面平行和垂直的八大定理一、线面平行。
1、判定定理:平面外一条直线与平面内一条直线平行,那么这条直线与这个平ab a //面平行。
符合表示:a// b2、性质定理:如果一条直线与平面平行,经过这条直线的平面和这个平面相交,那么这条直线和交线平行。
符号表示:aa//a // bab二、面面平行。
1、判定定理:如果一个平面内有两条相交直线分别平行于另一个平面内的两条相交直线,那么这两个平面平行。
n // b m // aa b M //mnN符号表示:2、性质定理:如果两个平面平行同时与第三个平面相交,那它们的交线平行。
//符号表示:l l// d (更加实用的性质:一个平d面内的任一直线平行另一平面)三、线面垂直。
1、判定定理:如果一条直线与一个平面内的两条相交直线都垂直,那么这条直a c线垂直这个平面。
符号表示: a b ab c M$:三垂线定理:(经常考到这种逻辑)在平面内的一条直线,如果它和这个平面的一条斜线的射影垂直,那么它也和这条斜线垂直aoApoa oA A2、性质定理:垂直同一平面的两条直线互相平行。
(更加实用的性质是:一个平 面的垂线垂直于该平面内任一直线。
)四、面面垂直。
1、 判定定理:经过一个平面的垂线的平面与该平面垂直。
a , a2、 性质定理:已知两个平面垂直,在一个平面内垂直于交线的直线垂直于另一 个平面。
, b, a ,a b a 符号表示:a PA。
线面、面面平行和垂直的八大定理

线面、面面平行和垂直的八大定理一、线面平行。
1、判定定理:平面外一条直线与平面内一条直线平行,那么这条直线与这个平面平行。
符合表示: βββ////a b a b a ⇒⎪⎭⎪⎬⎫⊂⊄2、性质定理:如果一条直线与平面平行,经过这条直线的平面和这个平面相交,那么这条直线和交线平行。
符号表示:b a b a a a ////⇒⎪⎪⎭⎪⎪⎬⎫=⊂⊄βαβαα二、面面平行。
1、判定定理:如果一个平面内有两条相交直线分别平行于另一个平面内的两条相交直线,那么这两个平面平行。
符号表示: βα//////⇒⎪⎪⎪⎭⎪⎪⎪⎬⎫==N n m M b a a m b n 2、性质定理:如果两个平面平行同时与第三个平面相交,那它们的交线平行。
符号表示: d l d l ////⇒⎪⎭⎪⎬⎫==γβγαβα (更加实用的性质:一个平面内的任一直线平行另一平面)三、线面垂直。
1、判定定理:如果一条直线与一个平面内的两条相交直线都垂直,那么这条直线垂直这个平面。
符号表示: α⊥⇒⎪⎪⎪⎪⎭⎪⎪⎪⎪⎬⎫=⊥⊥a M c b b a c a $:三垂线定理:(经常考到这种逻辑)在平面内的一条直线,如果它和这个平面的一条斜线的射影垂直,那么它也和这条斜线垂直。
符号表示:PA a A oA a po oA a ⊥⇒⎪⎪⎭⎪⎪⎬⎫=⊥⊥⊂⊂ααα2、性质定理:垂直同一平面的两条直线互相平行。
(更加实用的性质是:一个平面的垂线垂直于该平面内任一直线。
)四、面面垂直。
1、判定定理:经过一个平面的垂线的平面与该平面垂直。
βααβ⊥⇒⊂⊥a a ,2、性质定理:已知两个平面垂直,在一个平面内垂直于交线的直线垂直于另一个平面。
βαβαβα⊥⇒⊥⊂=⋂⊥a b a a b ,,,。
线面垂直与面面垂直的判定与性质

立体几何之垂直关系【知识要点】空间中的垂直关系如果一条直线与平面内的两条相交直线垂直,则这条直线与这个平面垂直.如果一个平面过另一个平面的一条垂线,则两个平面互相垂直. 如果两个平面互相垂直,那么在一个平面内垂直于它们交线的直线垂直于另一个平面.解决空间问题的重要思想方法:等价转化——化空间问题为平面问题.空间平行、垂直关系证明的基本思想方法——转化与联系,如图所示.题型1 平移证明线线垂直 例1 如图,在四棱锥ABCD P -中,N M AD BC AB AD BC BC AB ,.2,1,,===⊥分别为DC PD ,的中点,求证:AC MN ⊥例2 底面ABCD 是正方形,Q G BE PD PD BE ,,2,=‖分别为AP AB ,的中点,求证:CG QE ⊥例3 如图,在正方形1111D C B A ABCD -中,M 为1CC 的中点,F E ,分别为11,D A CD 的中点,AC 交BD 于点O ,求证:OM EF ⊥题型2 线面垂直判定例1 如图,在三棱锥ABC P -中,PAB ∆是等边三角形。
①若ABC ∆是等边三角形,证明:PC AB ⊥②若 90=∠=∠PBC PAC ,证明:PC AB ⊥例 2 已知四棱台1111D C B A ABCD -的上下底面边长分别是2和4的正方形,41=AA 且ABCD AA 底面⊥1,点P 为1DD 的中点,求证:PBC AB 面⊥1例3 如图,在三棱柱111C B A ABC -中,AC AB BAC ==∠,90,1A 在底面ABC 的射影为BC 的中点,D 为11C B 的中点。
证明:⊥D A 1平面BC A 1题型3 线面垂直性质证明线线垂直例1 如图,在三棱柱111C B A ABC -中,侧棱垂直于底面,D AA AC ACB ,21,901==∠ 是棱1AA 的中点,求证:BD DC ⊥1例2 已知正方形ABCD 所在平面与正方形ABEF 所在平面互相垂直,M 为AC 上一点,N 为BF 上一点,且FN AM =。
线面、面面平行和垂直的八大定理

线面、面面平行和垂直的八大定理一、线面平行。
1、判定定理:平面外一条直线与平面内一条直线平行,那么这条直线与这个平面平行。
符合表示: βββ////a b a b a ⇒⎪⎭⎪⎬⎫⊂⊄2、性质定理:如果一条直线与平面平行,经过这条直线的平面和这个平面相交,那么这条直线和交线平行。
符号表示:b a b a a a ////⇒⎪⎪⎭⎪⎪⎬⎫=⊂⊄βαβααI 二、面面平行。
1、判定定理:如果一个平面内有两条相交直线分别平行于另一个平面内的两条相交直线,那么这两个平面平行。
符号表示: βα//////⇒⎪⎪⎪⎭⎪⎪⎪⎬⎫==N n m M b a a m b n I I 2、性质定理:如果两个平面平行同时与第三个平面相交,那它们的交线平行。
符号表示: d l d l ////⇒⎪⎭⎪⎬⎫==γβγαβαI I (更加实用的性质:一个平面内的任一直线平行另一平面)三、线面垂直。
1、判定定理:如果一条直线与一个平面内的两条相交直线都垂直,那么这条直线垂直这个平面。
符号表示: α⊥⇒⎪⎪⎪⎪⎭⎪⎪⎪⎪⎬⎫=⊥⊥a M c b b a c a I $:三垂线定理:(经常考到这种逻辑)在平面内的一条直线,如果它和这个平面的一条斜线的射影垂直,那么它也和这条斜线垂直。
符号表示:PA a A oA a po oA a ⊥⇒⎪⎪⎭⎪⎪⎬⎫=⊥⊥⊂⊂ααα2、性质定理:垂直同一平面的两条直线互相平行。
(更加实用的性质是:一个平面的垂线垂直于该平面内任一直线。
)四、面面垂直。
1、判定定理:经过一个平面的垂线的平面与该平面垂直。
βααβ⊥⇒⊂⊥a a ,2、性质定理:已知两个平面垂直,在一个平面内垂直于交线的直线垂直于另一个平面。
βαβαβα⊥⇒⊥⊂=⋂⊥a b a a b ,,,尽管人智慧有其局限,爱智慧却并不因此就属于徒劳。
智慧果实似乎是否定性:理论上——“我知道我一无所知”;实践上——“我需要我一无所需”。
然而,达到了这个境界,在谦虚和淡泊哲人胸中,智慧痛苦和快乐业已消融为了一种和谐宁静了。
线面垂直面面垂直
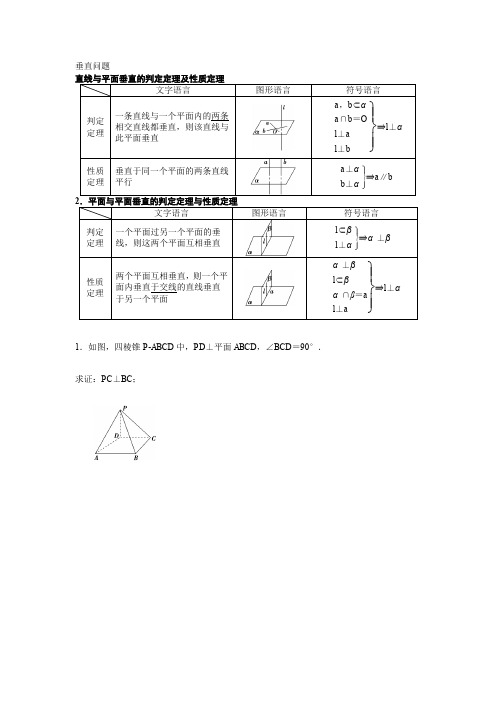
垂直问题文字语言图形语言符号语言判定定理一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直⎭⎪⎬⎪⎫a,b⊂αa∩b=Ol⊥al⊥b⇒l⊥α性质定理垂直于同一个平面的两条直线平行⎭⎪⎬⎪⎫a⊥αb⊥α⇒a∥b2.平面与平面垂直的判定定理与性质定理文字语言图形语言符号语言判定定理一个平面过另一个平面的垂线,则这两个平面互相垂直⎭⎪⎬⎪⎫l⊂βl⊥α⇒α⊥β性质定理两个平面互相垂直,则一个平面内垂直于交线的直线垂直于另一个平面⎭⎪⎬⎪⎫α⊥βl⊂βα∩β=al⊥a⇒l⊥α1.如图,四棱锥P-ABCD中,PD⊥平面ABCD,∠BCD=90°.求证:PC⊥BC;2.如图,在四棱锥P-ABCD中,P A⊥底面ABCD,AB⊥AD,AC⊥CD,∠ABC=60°,P A=AB=BC,E是PC的中点.求证:(1)CD⊥AE;(2)AE⊥平面PCD.3.如图,在直四棱柱ABCD–A1B1C1D1中,AB∥CD,AD⊥AB,AB=2,AD=2,E为CD 上一点,DE=1,EC=3.证明:BE⊥平面BB1C1C4.(2014·高考江苏卷) 如图,在三棱锥P-ABC中,D,E,F分别为棱PC,AC,AB的中点.已知P A⊥AC,P A=6,BC=8,DF=5.求证:平面BDE⊥平面ABC.5.如图,已知正方形ABCD中AC与BD交于点O,将正方形ABCD沿对角线BD折起,得到三棱锥A-BCD.求证:平面AOC⊥平面BCD;。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
线面垂直,面面垂直一、教学大纲要求:(1)使学生掌握直线和平面垂直的定义及判定定理;(2)使学生掌握判定直线和平面垂直的方法;(3)使学生正确理解和掌握“二面角”、“二面角的平面角”及“直二面角”、“两个平面互相垂直”的概念;(4)使学生掌握两个平面垂直的判定定理及其简单的应用;(5)使学生掌握直线与平面垂直,平面与平面垂直的性质定理;(6)能运用性质定理解决一些简单问题;(7)了解直线与平面、平面与平面垂直的判定定理和性质定理间的相互联系二、教学重点、难点直线与平面垂直的定义和判定定理的探究。
平面与平面垂直的判定;如何度量二面角的大小。
两个性质定理的证明三、预习提示:线面垂直的判定与性质线面角面面垂直的判定与性质二面角四、定理内容:1:线面垂直判定定理:一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直强调“两条”、“相交”缺一不可,并结合前面“检验旗杆与地面垂直”问题再进行确认。
简记法:线线垂直线面垂直这里指出要判断一条直线与一个平面是否垂直,取决于在这个平面内能否找到两条相交直线和已知直线垂直,这充分体现了“直线与平面垂直”与“直线与直线垂直”相互转化的数学思想,(即是把空间问题转化成了平面问题)大家回过头来看一下,这个定理我们只是通过动手实验和直观感知来说明而已,还没有经过严谨的证明,这里我们不深究,请有兴趣的同学下课后自己去思考如何严格证明这个定理,当做选做作业。
例1:AB为⊙O的直径,C为圆周上一点,PA⊥面ABC,求证:BC⊥面PAC。
(见课本65页)练习1正方体ABCD-A1B1C1D1中,M为C1D1中点.(1)求证:AC1⊥平面A1BD.解: (1)连AC,∵C1C⊥平面ABCD,∴C1C⊥BD.又AC⊥BD,∴AC1⊥BD.同理AC1⊥A1B∵A1B∩BD=B.∴AC1⊥平面A1BD.2:线面垂直的定义应用给出定义:如果直线l 与平面α内的任意一条直线都垂直,我们就说直线l 与平面α互相垂直,记作:l ⊥α. 直线l 叫做平面α的垂线,平面α叫做直线l 的垂面.直线与平面垂直时,它们唯一的公共点P 叫做垂足。
师:学习这个定义我们要注意的是什么呢?(关键点是什么?) 关键点是:(1)任意 (2)都垂直例1已知:⊿ABC 中∠ABC=900,SA ⊥平面ABC ,E 、F 分别为点A 在SC 、SB 上的射影求证:SC ⊥EFSABCE F证明∴AB ⊥BC SA ⊥BC∵∠ABC=900,SA ⊥平面ABC∴BC ⊥平面SAB BC ⊥AF ∵F 为点A 在SB 上的射影∴AF ⊥SB∴AF ⊥平面SBC∵E 为点A 在SC 上的射影AE ⊥SC∴SC ⊥EF例2:如图,PA ⊥平面ABC ,∆ABC 中,∠ABC=90° 则图中Rt ∆的个数是A 、4B 、3C 、2D 、1( )练习如图,P 是△ABC 所在平面外一点,P A =PB ,CB ⊥平面P AB ,M 是PC 的中点,N 是AB 上的点,AN =3NB ,(1)求证:MN ⊥AB ; (2)当∠APB =90°,BC =2,AB =4时,求MN 的长。
3:线面垂直的性质定理:垂直于同一个平面的两条直线平行4:线面角:斜线与平面所成的角就是斜线与它在平面内的射影的夹角。
求斜线与平面所成的角关键是找到斜线在平面内的射影,即确定过斜线上一点向平面所作垂线的垂足,这时经常要用面面垂直来确定垂足的位置。
若垂足的位置难以确定,可考虑用其它方法求出斜线上一点到平面的距离。
例3:.如图在正方体AC 1中, (1) 求BC 1与平面ACC 1A 1所成的角; (2) 求A 1B 1与平面A 1C 1B所成的角.备课说明:求直线与平面所成角的关键是找直线在 此平面上的射影,为此必须在这条直线上找一点作平面的垂线. 作垂线的方法常采用:①利用平面垂直的性质找平面的垂线.②点的射影在面内的特殊 位置. sin α=sin ∠OC 1B=1BC OB =21.解:(1)设所求的角为α,先证BD ⊥平面ACC 1A 1,则故α=30o .(2)△A 1BC 1是正三角形,且A 1B 1=B 1C 1=BB 1. ∴棱锥B 1-A 1BC 1是正三棱锥.过B 1作B 1H ⊥平面A 1BC 1,连A 1H, ∠B 1A 1H 是直线A 1B 1与平面A 1C 1B 所成的角.设A 1B 1=a 则A 1B =a 2得A 1H =a 36.故cos ∠ADC 1D 1A 1B 1CBB 1A 1H=111B A H A =36.所求角为36arccos练习:设线段AB=a ,AB 在平面α内,CA ⊥α,BD 与α成30ο角,BD ⊥AB,C 、D 在α同侧,CA=BD=b .求: (1)CD 的长;(2)CD 与平面α所成角正弦值.解:(1)作DD '⊥α于D ',连接AD ',BD '.CA ⊥α,∴CA ∥'.四边形CAD 'D 是直角梯形,∠CAD '=∠D D 'A =90ο,AB α⊂,AB ⊥DD '.又AB ⊥BD,∴AB ⊥平面BDD ',BD '⊂平面BDD '.∴AB ⊥BD '.∵∠DBD '是BD 与α所成的角,∴∠DBD '=30ο,BD =b ,DD '=2b,BD '=23b .在△ABD '中,AB=a ,BD '=23b ,∠ABD '=90ο,∴AD '=22'BDAB +=4322b a +.在CAD 'D 中,CD=222'2')(b a D D AC AD +=-+.(2)作D 'C '∥DC 交CA 于C ',∠C 'D 'A 是CD 与α所成的角,sin ∠C 'D 'A=22'2''ba b D C AC +=.5:面面垂直的判定定理:6:面面垂直的性质定理:两个平面垂直,则一个平面内垂直于交线的直线与另一个平面垂直。
例2、已知直角三角形ABC 中, AB=AC=a ,AD 是斜边BC 上的 高,以AD 为折痕使角BDC 成 直角。
(如图) ABCD求证:1)平面ABD 垂直平面BDC 平面ACD 垂直平面BDCC例2、如图,已知平面α与平面β垂直,在他们的交线上取线段AB=4,AC ,CD 分别在平面和平面内,它们都垂直于直线AB ,并且AC=3cm ,BD=12cm,求CD 长。
αβCADBαβ7:二面角定义:3、二面角的平面角:在二面角的棱上任取一点O ,以点O 为垂足,在两个半平面内分别做垂直于棱的射线,则射线所组成的叫做二面角的平面角。
思想:将空间二面角转化为平面角来求解。
αβABO步骤:1)在两个半平面内作棱的垂线,且交于一点。
2)找角3)求角(利用三角形)4)还原1)角的大小与O 的位置有关吗?为什么?2)二面角的范围应该是什么?二面角的平面角是多少度,就说二面角是多少度。
平面角是直角的二面角是直二面角。
A 定义法即在二面角的棱上找一点,在二面角的两个面内分别作垂直于棱的射线即得二面角的平面角.定义法是“众法之源”,万变不离其宗,“树高千尺,叶落归根”,求二面角的一切方法盖源出定义这个“根”! 例1、正方体ABCD-A 1B 1C 1D 1中,二面角A 1-BD-C 1的余弦值为变式:正方体ABCD-A 1B 1C 1D 1中,求二面角A-BD-C 1的正切值。
例2、如图,正三角形ABC 的边长为3,过其中心G 作BC 边的平行线,分别交AB 、AC 于1B 、1C . 将11AB C ∆沿11B C 折起到111A B C ∆的位置,使点1A 在平面11BB C C 上的射影恰是线段BC 的中点M . 试求二面角111A B C M --的大小.B 三垂线法这是最典型也是最常用的方法,当然此法仍扎“根”于二面角平面角的定义. 此法最基本的一个模型为:如图1,设锐二面角βα--l ,过面α内一点P 作PA ⊥α于A ,作AB ⊥l 于B ,连接PB ,由三垂线定理得PB ⊥l ,则∠PBA 为二面角βα--l 的平面角,故称此法为三垂线法.练习:矩形ABCD 的两边AB=3,AD=4,PA ⊥平面ABCD ,且PA=,则二面角A-BD-P 的度数为(A )度A 30B 45C 60D 90五 本节小结六 课后练习1、从平面外一点引平面的垂线和若干条斜线,且这些斜线与平面所成的角都相等,则_C __。
485 A图1αβPBlA .斜足一定是正多边形的顶点B .垂足是斜足所组成的多边形的内切圆圆心C .垂足是斜足所组成的多边形的外接圆圆心D .垂足是斜足所组成的多边形的垂心2、互不重合的三个平面将空间分成____D __。
A .四部分B .四或八部分C .四、六或八部分D .四、六、七或八部分3、设l 为平面α外一直线,则“l 不垂直于α”是“l 不垂直于α内某一直线”的__A ___。
A .必要不充分条件 B .充分不必要条件C .充要条件D .非充分也不必要条件4、若一直线一有两点到一个平面的距离都等于1,则该直线与这个平面的位置关系是__D _。
A .直线在平面内 B .直线平行平面C .直线与平面相交D .直线与平面相交或平行5、若a 、b 、c 为直线,α为平面,则下列命题中正确的是___B ___。
A .b //a //b ,//a ⇒αα B .b //a b ,a ⇒α⊥α⊥ C .b //a c b ,c a ⇒⊥⊥D .b //a //b ,a ⇒αα⊂6、将菱形ABCD 沿对角线BD 折成空间四边形D 'ABC ,使此空间四边形的对角线'AC 的长等于菱形ABCD 的对角线AC 长的一半,则二面角A BD 'C --的度数为___C ___。
A .︒30B .︒45C .︒60D .︒907、在同一平面内射影等长的两斜线段_____C _。
A .若有公共端点时必等长 B .等长时必有公共端点C .平行时必等长D .等长时必平行8、直线a 、b 为异面直线,则下列四个命题中正确的个数为___B ___。
①过空间任一点可作一平面和a 、b 都平行; ②过直线a 有且只有一个平面与b 平行; ③有且只有一条直线和a 、b 都垂直; ④过空间任一点可作一条直线和a 、b 都相交。
A .0B .1C .2D .3。
