惯性矩抵抗矩面积矩
惯性矩、抵抗矩、面积矩共19页

56、极端的法规,就是极端的不公。 ——西 塞罗 57、法律一旦成为人们的需要,人们 就不再 配享受 自由了 。—— 毕达哥 拉斯 58、法律规定的惩罚不是为了私人的 利益, 而是为 了公共 的利益 ;一部 分靠有 害的强 制,一 部分靠 榜样的 效力。 ——格 老秀斯 59、假如没有法律他们会更快乐的话 ,那么 法律作 为一件 无用之 物法。— —西塞 罗
谢谢
11、越是没有本领的就越加自命不凡。——邓拓 12、越是无能的人,越喜欢挑剔别人的错儿。——爱尔兰 13、知人者智,自知者明。胜人者有力,自胜者强。——老子 14、意志坚强的人能把世界放在手中像泥块一样任意揉捏。——歌德 15、最具挑战性的挑战莫过于提升自我。——迈克尔·F·斯特利
最新惯性矩总结(含常用惯性矩公式)

惯性矩是一个物理量,通常被用作描述一个物体抵抗扭动,扭转的能力。
惯性矩的国际单位为(m^4)。
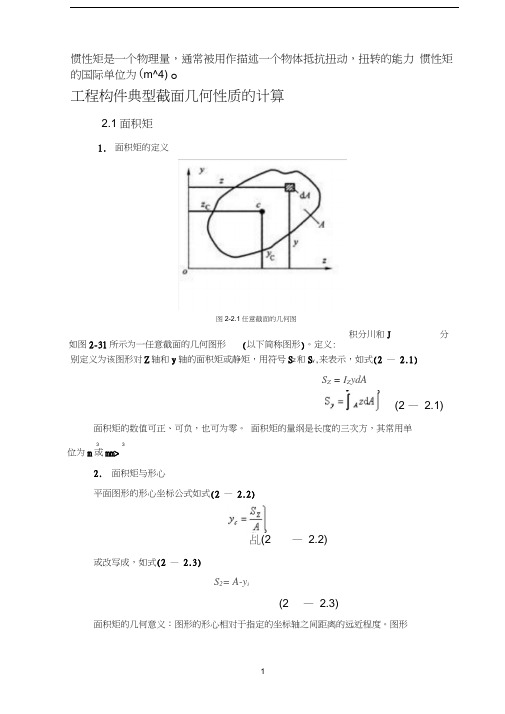
工程构件典型截面几何性质的计算2.1面积矩1.面积矩的定义图2-2.1任意截面的几何图形如图2-31所示为一任意截面的几何图形(以下简称图形)。
定义:积分和分别定义为该图形对z轴和y轴的面积矩或静矩,用符号S z和S y,来表示,如式(2—2.1)(2—2.1)面积矩的数值可正、可负,也可为零。
面积矩的量纲是长度的三次方,其常用单位为m3或mm3。
2.面积矩与形心平面图形的形心坐标公式如式(2—2.2)(2—2.2)或改写成,如式(2—2.3)(2—2.3)面积矩的几何意义:图形的形心相对于指定的坐标轴之间距离的远近程度。
图形形心相对于某一坐标距离愈远,对该轴的面积矩绝对值愈大。
图形对通过其形心的轴的面积矩等于零;反之,图形对某一轴的面积矩等于零,该轴一定通过图形形心。
3.组合截面面积矩和形心的计算组合截面对某一轴的面积矩等于其各简单图形对该轴面积矩的代数和。
如式(2—2.4)(2—2.4)式中,A和y i、z i分别代表各简单图形的面积和形心坐标。
组合平面图形的形心位置由式(2—2.5)确定。
(2—2.5)2.2极惯性矩、惯性矩和惯性积1.极惯性矩任意平面图形如图2-31所示,其面积为A。
定义:积分称为图形对O点的极惯性矩,用符号I P,表示,如式(2—2.6)(2—2.6)极惯性矩是相对于指定的点而言的,即同一图形对不同的点的极惯性矩一般是不同的。
极惯性矩恒为正,其量纲是长度的4次方,常用单位为m4或mm4。
(1)圆截面对其圆心的极惯性矩,如式(2—7)(2—2.7)(2)对于外径为D、内径为d的空心圆截面对圆心的极惯性矩,如式(2—2.8)(2—2.8)式中,d/D为空心圆截面内、外径的比值。
2.惯性矩在如图6-1所示中,定义积分,如式(2—2.9)(2—2.9)称为图形对z轴和y轴的惯性矩。
惯性矩是对一定的轴而言的,同一图形对不同的轴的惯性矩一般不同。
截面的几何性质面积矩惯性矩惯性积平行移轴公式

1
HOHAI UNIVERSITY
2
HOHAI UNIVERSITY
例1 求如图矩形Sz和Sy
解:Sz
ydA
A
ah
ybdy
a
bh(a h) 2
A yC
同样地
Sy
bh(d
b) 2
A
zC
z b/2 b/2 a
y h/2
h/2
dy
y
d
3
HOHAI UNIVERSITY
解: A1 15050mm 2 A2 18050mm 2
150
A3 250 50mm 2
50
C1
yC1 255mm yC2 140mm
5c0
C2
yC3 25mm zC1 zC2 zC3 0
50
C3
z
yC
A1
yC1 A2 yC2 A1 A2 A3
A3
yC 3
250
y
15050 255 18050140 25050 25 mm 15050 18050 25050
i=1
同理
n
Iz =∑ Izi
i=1
n
Iyz =∑ Iyzi
i=1
12
HOHAI UNIVERSITY
例5 图示矩形中,挖去两个直径为d 的圆形,求余下 图形对z轴的惯性矩。
b/2 b/2
z
Iz
1 bh3 12
5 d 4
32y13HOHAI UNIVERSITY
14
HOHAI UNIVERSITY
作业题 求图示工字形截面对z轴的惯性矩。
b d
z
15
极惯性矩、惯性矩、惯性积

§ 8-2 极惯性矩 惯性矩 惯性积
y
定义: 定义:
dA y ρ x 0
截面对 o 点的极惯性矩为
x
截面对 x ,y 轴的惯性矩分别为
Iy Ix
= ∫ A x dA
2
3
y
Iy
=
hb 12
dy h C y x
b
例 2 -其圆心 O 的 极惯性矩为 y
Iρ =
πd 32
4
I x + I y = Iρ
Ix = Iy
4
x
所以
Ix = Iy =
πd 64
�
dx dx x y dA y
惯性积一定等于零 .
截面对 x , y 轴的惯性半俓为
iy =
Iy , A
ix =
Ix A
例2_1 解:
轴的惯性矩. 求矩形截面对其对称轴 x , y 轴的惯性矩.
dA = b dy
2 h 2 h 2 2 3
I x = ∫A y dA
2
bh = ∫A y dA = ∫ by dy = Ix 12
= ∫ A y dA
2
因为
ρ = x +y
2 2
y
2
dA y ρ x 0
x
所以
Iρ = Ix + Iy
截面对 x , y 轴的惯性积为
Ixy = ∫ A xydA
惯性矩的数值恒为正,惯性积则可能为正值,负值, 惯性矩的数值恒为正,惯性积则可能为正值,负值, 也可能等于零. 也可能等于零. 若 x , y 两坐标轴中有一个为 截面的对称轴, 则截面对 x , y 轴的 截面的对称轴,
惯性矩

惯性矩惯性矩是一个物理量,通常被用作述一个物体抵抗扭动,扭转的能力。
惯性矩的国际单位为千克乘以平方米(kg·m2)。
面积元素dA与其至y轴或z轴距离平方的乘积z^2dA或y^2dA,分别称为该面积元素对于y轴或z轴的惯性矩或截面二次轴矩。
Z轴的惯性矩:IX=∫Ay^2dAY轴的惯性矩:IY=∫Az^2dA截面对任意一对互相垂直轴的惯性矩之和,等于截面对该二轴交点的极惯性矩。
惯性矩计算公式:矩形:b*h^3/12三角形:b*h^3/36圆形:π*d^4/64环形:π*D^4*(1-α^4)/64;α=d/D^3表示3次静矩静矩(面积X面内轴一次)把微元面积与各微元至截面上指定轴线距离乘积的积分称为截面的对指定轴的静矩Sx=ydA。
静矩就是面积矩,是构件的一个重要的截面特性,是截面或截面上某一部分的面积乘以此面积的型心到整个截面的型心轴之间的距离得来的,是用来计算应力的。
注意:惯性矩是乘以距离的二次方,静矩是乘以距离的一次方,惯性矩和面积矩(静矩)是有区别的。
截面惯性矩截面惯性矩(I=截面面积X截面轴向长度的二次方)截面惯性矩:the area moment of inertiacharacterized an object's ability to resist bending and is required to calculate displacement.截面各微元面积与各微元至截面某一指定轴线距离二次方乘积的积分Ix= y^2dF.截面极惯性矩截面极惯性矩(Ip=面积X垂直轴二次)。
扭转惯性矩Ip: the torsional moment of inertia极惯性矩:the polar moment of inertia截面各微元面积与各微元至某一指定截面距离二次方乘积的积分Ip=P↑2dF。
a quantity to predict an object's ability to resist torsion, to calculate the angular displacement of an object subjected to a torque.相互关系截面惯性矩和极惯性矩的关系截面对任意一对互相垂直轴的惯性矩之和,等于截面对该二轴交点的极惯性矩Ip=Iy+Iz。
[精品]惯性矩
![[精品]惯性矩](https://img.taocdn.com/s3/m/e44b76c3b8f3f90f76c66137ee06eff9aef84930.png)
惯性矩是一个物理量,通常被用作述一个物体抵抗扭动,扭转的能力。
惯性矩的国际单位为千克乘以平方米(kg·m2)。
面积元素dA与其至y轴或z轴距离平方的乘积z^2dA或y^2dA,分别称为该面积元素对于y轴或z轴的惯性矩或截面二次轴矩。
Z轴的惯性矩:IX=∫Ay^2dAY轴的惯性矩:IY=∫Az^2dA截面对任意一对互相垂直轴的惯性矩之和,等于截面对该二轴交点的极惯性矩。
惯性矩计算公式:矩形:b*h^3/12三角形:b*h^3/36圆形:π*d^4/64环形:π*D^4*(1-α^4)/64;α=d/D^3表示3次静矩静矩(面积X面内轴一次)把微元面积与各微元至截面上指定轴线距离乘积的积分称为截面的对指定轴的静矩Sx=ydA。
静矩就是面积矩,是构件的一个重要的截面特性,是截面或截面上某一部分的面积乘以此面积的型心到整个截面的型心轴之间的距离得来的,是用来计算应力的。
注意:惯性矩是乘以距离的二次方,静矩是乘以距离的一次方,惯性矩和面积矩(静矩)是有区别的。
截面惯性矩截面惯性矩(I=截面面积X截面轴向长度的二次方)截面惯性矩:the area moment of inertiacharacterized an object's ability to resist bending and is required to calculate displacement.截面各微元面积与各微元至截面某一指定轴线距离二次方乘积的积分Ix=y^2dF.截面极惯性矩截面极惯性矩(Ip=面积X垂直轴二次)。
扭转惯性矩Ip: the torsional moment of inertia极惯性矩:the polar moment of inertia截面各微元面积与各微元至某一指定截面距离二次方乘积的积分Ip=P↑2dF。
a quantity to predict an object's ability to resist torsion, to calculate the angular displacement of an object subjected to a torque.相互关系截面惯性矩和极惯性矩的关系截面对任意一对互相垂直轴的惯性矩之和,等于截面对该二轴交点的极惯性矩Ip=Iy+Iz。
史上最全的常用截面几何特性计算公式

史上最全的常用截面几何特性计算公式构件截面的几何性质,如静力矩、形心、轴向惯性矩、极惯性矩、惯性积和主惯性轴位置等,对构件的承载能力有影响,常用于分析构件的弯曲、扭转和剪切。
1.静态力矩:也称为面积力矩或静态表面力矩。
截面对轴线的静力矩等于每个微区的积分乘以整个截面上微区到轴线的距离。
静力矩可以是正的,也可以是负的。
它的维数是长度的三次方。
静力矩的力学意义是:如果有均布载荷作用在截面上,其值表示为单位面积的量,则该载荷在某一轴上的合成力矩等于分布载荷乘以该轴的静力矩。
2、形心:又称面积中心或面积重心,是截面上具有如下性质的点:截面对通过此点任一个轴的静矩等于零。
如果将截面看成一均质等厚板,则截面的形心就是板面的重心。
形心坐标xo、yo的计算公式为:3、惯性矩:反映截面抗弯特性的一个量,简称惯性矩。
截面对某个轴的轴惯性矩等于截面上各微面积乘微面积到轴的距离的平方在整个截面上的积分。
下图所示的面积为A的截面对x、y轴的轴惯性矩分别为:转动惯量总是正的,量纲是长度的四次方。
构件的抗弯能力与轴的惯性矩成正比。
一些典型截面的轴惯性矩可在专业手册中找到。
例如,平行四边形对中心线的惯性矩为4、极惯性矩:反映截面抗扭特性的一个量。
截面对某个点的极惯性矩等于截面上各微面积乘微面积到该点距离的平方在整个截面上的积分。
下图所示面积为A的截面对某点O的极惯性矩为:极惯性矩永远是正的,量纲是长度的四次方。
构件的抗扭能力与惯性矩成正比。
圆形截面相对于其中心的惯性矩为5、惯性积:截面对于两个正交坐标轴的惯性积等于截面上各个微面积乘微面积到两个坐标轴的距离在整个截面上的积分。
面积为A的截面对两个正交坐标轴x、y的惯性积为:惯性积的量纲是长度的四次方。
截面位于坐标系的一、三象限,Ixy为正,位于二、四象限则为负。
6.主惯性轴:使截面惯性积为零的一对正交坐标轴称为截面主惯性轴,简称主轴。
截面对主惯性轴的惯性矩称为主惯性矩。
若两条主惯性轴的交点为质心,则这两条轴称为质心主惯性轴(或称主质心惯性轴)。
惯性矩总结(含常用惯性矩公式).docx
惯性矩是一个物理量,通常被用作描述一个物体抵抗扭动,扭转的能力惯性矩的国际单位为(m^4) O工程构件典型截面几何性质的计算2.1面积矩1.面积矩的定义别定义为该图形对Z轴和y轴的面积矩或静矩,用符号S Z和S y,来表示,如式(2 —2.1)面积矩的数值可正、可负,也可为零。
面积矩的量纲是长度的三次方,其常用单3 3位为m或mm>2.面积矩与形心平面图形的形心坐标公式如式(2 —2.2)乩(2 — 2.2)或改写成,如式(2 —2.3)S2= A-y i(2 —2.3)面积矩的几何意义:图形的形心相对于指定的坐标轴之间距离的远近程度。
图形如图2-31所示为一任意截面的几何图形(以下简称图形)。
定义:积分川和J 分(2 —2.1)图2-2.1任意截面的几何图形S Z= I Z ydA形心相对于某一坐标距离愈远,对该轴的面积矩绝对值愈大。
图形对通过其形心的轴的面积矩等于零;反之,图形对某一轴的面积矩等于零, 该轴一定通过图形形心。
3 •组合截面面积矩和形心的计算组合截面对某一轴的面积矩等于其各简单图形对该轴面积矩的代数和。
如式 (2 — 2.4)Σ¾ =Σj ⅛z J (2 — 2.4)式中,A 和y i 、Z i 分别代表各简单图形的面积和形心坐标。
组合平面图形的形心位 置由式(2 — 2.5)确定2.2极惯性矩、惯性矩和惯性积1 •极惯性矩任意平面图形如图2-31所示,其面积为A 。
定义:积分丨「’川称为图形对O 点的 极惯性矩,用符号I P ,表示,如式(2 — 2.6)'[ 」(2 — 2.6)极惯性矩是相对于指定的点而言的,即同一图形对不同的点的极惯性矩一般是不同的。
极惯性矩恒为正,其量纲是长度的4次方,常用单位为m 4或mr ⅛(1)圆截面对其圆心的极惯性矩,如式(2 — 7)IP- 32 (2 — 2.7)(2)对于外径为D 内径为d 的空心圆截面对圆心的极惯性矩,如式(2 — 2.8)_(1 —況)P 32(2 — 2.8)式中,:二d/D 为空心圆截面内、外径的比值。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
A
A
二、形心:(等厚均质板的质心与形心重
合。 )
¯x
x dm m
m
质心 :
y dm
¯y m
m
等厚 均质
等厚 均质
x trd AtrA
A
xd A A
A
Sy A
y trd AtrA
A
yd A
A
A
Sx A
等于形心坐标
累加式:x y
xi Ai
A (正负面积法公 ) yi Ai
A
¯x y¯
Sy Ax Ai xi Sx Ay Ai yi
例 I-1-1 是确定下图的形心。
解 : 组合图形,用正负面积法解之。
C2 C1
y
1、用正面积法求解,图形分割及坐标如
C1(0,0) 图(a)
C2(-35,60)
x
x xiAi x1A1x2A2
、建立坐标系。
Байду номын сангаас
、计算面积和面积矩
、求形心位置。
x
Sy A
y
Sx A
xi Ai A yi Ai A
、建立形心坐标系;求:Iyc , Ixc , Ixcyc ,
、求形心主轴方向
——
0 tg20
2Ixcyc Ixc Iyc
、求形心主惯性矩 IIx y0 0ccIxc 2Iyc(Ixc 2Iyc)2Ix 2cy
xy
x
Ix
Iy
IP 2
d4
64
IAB Ixd2A6 d44 d 445 6d44
§6-4 惯性矩和惯性积的转轴定理* 截面的主惯性轴和主惯性矩
一、 惯性矩和惯性积的转轴定理y 1
x1
y1
x1
x y1 1
xco s ysin xsi n yco s
惯性矩抵抗 矩面积矩
§6-1 面积矩与形心位置
一、面积(对轴)矩:(于力矩类似)是面积与它到轴的距离
之积。
maxN A ma;x
M n; GPI
maxM W nP max
dSx dAy
dSy dAx
S x dS x ydA
A
A
S y dS y xdA
三、惯性积:面积与其到两轴距离之积。
A
I xy xydA
A
!如果 x 或 y 是对称轴,则,Ix y =0
§6-3 惯性矩和惯性积的平行移轴定理
一、平行移轴定理:(与转动惯量的平行移轴定理类似)
yc
C a
b
\ I I b 2A x xc
以形心为原点,建立与原坐标轴平行 的坐标轴如图
I x I c 矩 x I c 圆 x I c 矩 x A 矩 y 2 [ I 圆 x 1 A 圆 ( 0 . 5 d y ) 2 ]
1 . 5 d ( 2 d ) 3 3 d 2 ( 0 . 1d ) 7 2 [d 7 4 d 2 ( 0 . 5 d 0 . 1d ) 7 2 ] 0 7 . 6 d 4 8
12
64 4
Iyc I矩 x cI圆 x c(1 .5 d 1 )3 2 2 d6 d4 40 .5d 1 4 3
Ixcy c 0\xcyc轴 便 是 形 Ix心 c、 Iyc便 主是 轴形 心 主 惯
I I abA
点
xy xcyc
必
I I (a b)2A P Pc
须 为
形
心
y
例6-3-1 求图示圆对其切线AB的惯性矩.
解 :求解此题有两种方法:一是安
定义直接积分;二是用平行移轴
d
x
定理等知识求。
O
建立形心坐标如图,求图形对形心轴
的惯性矩。
B
I
d
4
I
I
圆 2 I
P 32
例6-4-1 在矩形内挖去一与上边 解 : 、建立坐标系如图。
内切的圆,求图形的形心主轴。
(b=1.5dy)
yc
x
xi A
、求形心位置。
Ai 0 0 A
O
x1
x
xc
y
yi Ai A
d d 2
2 3d 2
4
d 2
0.177d
4
、建立形心坐标系;求:Iyc , Ixc ,Ixcyc
2、形心主轴和形心主惯性矩:主轴过形心时,称其为形心主轴。 平面图形对形心主轴之惯性矩,称为形心主惯性矩
2I
tg 2
xcyc
0
I I
xc yc
形心主惯性矩:
I
x
c0
I xc
I y c±
I y c0
2
I I
( x c y c) 2 I 2
2
xcyc
3、求截面形心主惯性矩的方法
A
A1A2
5(7 011) 02.0 3 128 0 07 0110
图(b)
§6-2 惯性矩、惯性积、极惯性矩
一、惯性矩:(与转动惯量类似)是面积与它到轴的距离的平方 之积。
I x y 2 dA
A
I y x 2 dA
A
二、极惯性矩:是面积对极点的二次矩。 IP r2dAIxIy
A
A1A2
3 51 0110 2.0 3 1 0118 0 010
图(a)
6 01 0110
y
3.4 7
1 0118 0 010
y
负面积
CC 11 C 2
2、用负面积法求解,图形分割及坐标 如图(b)
x
C1(0,0) C2(5,5)
x xiAi x1A1x2A2
xc
SxcAyc0
x a xc
y
b
yc
I x y 2d A A( y c b ) 2d A
A
( yc2 2byc b2)d A
A
Ix
c
2b
Sx
c
b 2A
\ I I b 2A x xc
注
意
I I a 2A
!
y yc
C
I I
I I
I x y ( x y c o s 2 I sin 2 )
x1
2
2
xy
Iy1Ix 2Iy(Ix 2Iyco s2Ixysin2) Ix1y1 (Ix 2Iysin2Ixycos2)
Ix1Iy1 IxIy
二、截面的形心主惯性轴和形心主惯性矩
1、主惯性轴和主惯性矩:坐标旋转到= 0 时;恰好有
Ix 0y 0 (Ix 2Iysi2n 0 Ixc y o 20s ) 0
与 0 对应的旋转轴x 0 y 0 称为主惯性轴;平面图形对主轴 之惯性矩主惯性矩。
tg20
2Ixcyc Ixc Iyc
主惯 I Ix y性 0 0Ix 2 矩 Iy: (Ix 2Iy)2Ix 2y
