高斯烟羽模型
高斯烟羽模型

模型假设:1、 坐标系高斯模型的坐标系如图2.1所示,原点为排放点(若为高架源,原点为排放点在地面的投影),x 轴正向为风速方向,y 轴在水平面上垂直于x 轴,正向在x 轴的左侧,z 轴垂直于水平面xoy ,向上为正向。
在此坐标系下烟流中心线或烟流中心线在xoy 面的投影与x 轴重合。
2、模型假设(1)污染物的浓度在y 、z 轴上的分布是高斯分布(正态分布)的;(2)污染源的源强是连续且均匀的,初始时刻云团内部的浓度、温度呈均匀分布;(3)扩散过程中不考虑云团内部温度的变化,忽略热传递、热对流及热辐射;(4)泄漏气体是理想气体,遵守理想气体状态方程;(5)在水平方向,大气扩散系数呈各向同性;(6)取x 轴为平均风速方向,整个扩散过程中风速的大小、方向保持不变,不随地点、时间变化而变化;(7)地面对泄漏气体起全反射作用,不发生吸收或吸附作用;(8)整个过程中,泄漏气体不发生沉降、分解,不发生任何化学反应等。
3、模型公式推导由正态分布假设可以导出下风向任意一点X (x,y,z )处泄漏气体浓度的函数为:22)(),,(bz ay e e x A z y x X --=(1)由概率统计理论可以写出方差的表达式为:⎪⎪⎪⎩⎪⎪⎪⎨⎧==⎰⎰⎰⎰∞∞∞∞00220022Xdz Xdz z Xdy Xdy y z yσσ (2) 由假设可以写出源强的积分公式:⎰⎰∞∞-∞∞-=uXdydz Q (3)式中:y σ、z σ为泄漏气体在y 、z 方向分布的标准差,单位为 m ;X (x,y,z )为任一点处泄漏气体的浓度,单位为 kg/m 3;u 为平均风速,单位为 m/s ;Q 为源强(即泄漏速度),单位为 kg/s ;将(1)式代入(2)式,积分可得:⎪⎪⎩⎪⎪⎨⎧==222121z y b a σσ (4)将(1)式和(4)式代入(3)式,积分可得:zy u Q x A σσπ2=)( (5) 再将(4)式和(5)式代入(1)式,可得:⎥⎥⎦⎤⎢⎢⎣⎡⎪⎪⎭⎫ ⎝⎛+-=222222exp 2,,z y z y z y u Q z y x X σσσσπ)( (6) 上式为无界空间连续点源扩散的高斯模型公式,然而在实际中,由于地面的存在,烟羽的扩散是有界的。
高斯烟羽模型课件

温度和湿度影响大气稳定度和湍流强 度,进而影响污染物的扩散。这些数 据可以通过气象观测站获取。
排放参数的估算方法
源强
源强表示污染物的排放速率。根据工厂或设施的工艺流程、设备运行状况等因素进行估算。
排放高度
排放高度决定了烟羽在垂直方向上的扩散范围。根据工厂或设施的建筑高度、排放设备的位置等因素进行估算。
案例一:城市空气质量预测
总结词:动态模拟
详细描述:高斯烟羽模型能够模拟城市空气质量的动态变化过程,揭示不同气象条件和地形地貌对空气质量的影响。
案例一:城市空气质量预测
总结词
可视化展示
详细描述
通过可视化技术,高斯烟羽模型能够将预测结果以直观的方式呈现出来,便于分析和理 解。
案例二:工业区污染物扩散模拟
特点
高斯烟羽模型适用于污染物在大气中扩散的情况,特别是对 于低空污染物的扩散,如工厂排放、汽车尾气等。该模型能 够考虑气象条件、地形等因素对污染物扩散的影响,提供较 为准确的预测结果。
模型的应用领域
环境评估
高斯烟羽模型广泛应用于环境评 估领域,用于评估工厂、交通工 具等污染源对周围环境的影响, 为环境管理和污染控制提供依据。
z
垂直距离,表示烟 羽扩散的垂直方向 上的距离。
公式的应用场景
高斯烟羽模型适用于描述烟羽 在大气中的扩散情况,特别是
在稳定气象条件下。
该模型广泛应用于环境科学、 大气污染控制等领域,用于 预测烟羽的扩散范围、浓度 分布等。
通过高斯烟羽模型,可以评估 烟羽对周围环境和居民的影响,
为制定相应的污染控制措施提 供科学依据。
03
高斯烟羽模型的参数估算
扩散参数的估算方法
扩散系数
高斯烟羽模型
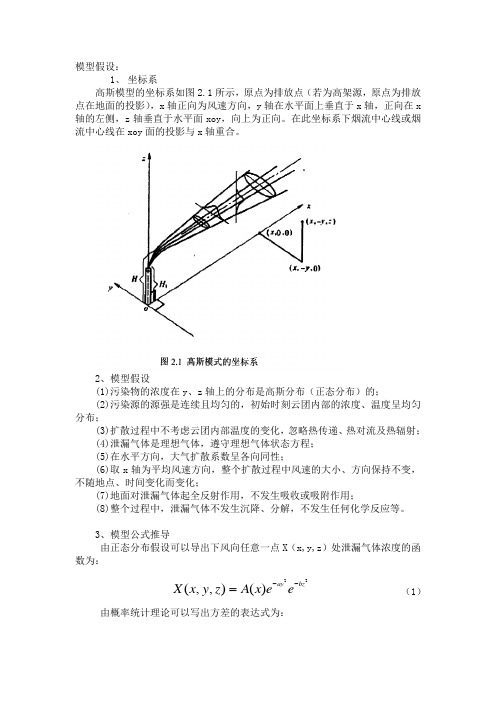
模型假设:1、 坐标系高斯模型的坐标系如图2.1所示,原点为排放点(若为高架源,原点为排放点在地面的投影),x 轴正向为风速方向,y 轴在水平面上垂直于x 轴,正向在x 轴的左侧,z 轴垂直于水平面xoy ,向上为正向。
在此坐标系下烟流中心线或烟流中心线在xoy 面的投影与x 轴重合。
2、模型假设(1)污染物的浓度在y 、z 轴上的分布是高斯分布(正态分布)的;(2)污染源的源强是连续且均匀的,初始时刻云团内部的浓度、温度呈均匀分布;(3)扩散过程中不考虑云团内部温度的变化,忽略热传递、热对流及热辐射; (4)泄漏气体是理想气体,遵守理想气体状态方程; (5)在水平方向,大气扩散系数呈各向同性;(6)取x 轴为平均风速方向,整个扩散过程中风速的大小、方向保持不变,不随地点、时间变化而变化;(7)地面对泄漏气体起全反射作用,不发生吸收或吸附作用;(8)整个过程中,泄漏气体不发生沉降、分解,不发生任何化学反应等。
3、模型公式推导由正态分布假设可以导出下风向任意一点X (x,y,z )处泄漏气体浓度的函数为:22(,,)()aybzX x y z A x ee--= (1)由概率统计理论可以写出方差的表达式为:22022y z y XdyXdyz Xdz Xdzσσ∞∞∞∞==⎧⎪⎪⎪⎨⎪⎪⎪⎩⎰⎰⎰⎰(2) 由假设可以写出源强的积分公式:⎰⎰∞∞-∞∞-=uXdydz Q (3)式中:y σ、z σ为泄漏气体在y 、z 方向分布的标准差,单位为 m ;X (x,y,z )为任一点处泄漏气体的浓度,单位为 kg/m 3;u 为平均风速,单位为 m/s ;Q 为源强(即泄漏速度),单位为 kg/s ;将(1)式代入(2)式,积分可得:221212y za b σσ==⎧⎪⎪⎨⎪⎪⎩ (4)将(1)式和(4)式代入(3)式,积分可得:zy u Qx A σσπ2=)( (5)再将(4)式和(5)式代入(1)式,可得:⎥⎥⎦⎤⎢⎢⎣⎡⎪⎪⎭⎫ ⎝⎛+-=222222exp 2,,z y z y zy u Qz y x X σσσσπ)( (6) 上式为无界空间连续点源扩散的高斯模型公式,然而在实际中,由于地面的存在,烟羽的扩散是有界的。
基于高斯烟羽模型的铁路气体类危险货物泄漏扩散研究

Logistics Sci-Tech No.8, 2018物流科技2018年第8期•交通运输!文章编号:1002-3100 (2018) 08-0109-05Research on Leakage and Diffusion of Gas Dangerous Goods Based on Gaussian Plume Model李丹,杨睿,宋辉(兰州交通大学交通运输学院,甘肃兰州730070)L I D an,Y A N G R u i,SONG H u i(School o f Traffic and Transportation,Lanzhou Jiaotong U n ive rsity,Lanzhou730070, C hina)摘要:铁路运输的危险货物中,气体类危险货物占有较大的比重。
故文章针对易燃气体在铁路运输过程中的泄漏事故,以丙烷气体为例,运用高斯烟羽模型,通过m a tla b模 拟出在不同大气状况下,单个泄漏源和多个泄漏源的气体平面扩散范围和扩散高度,分析了大气稳定度对于气体在扩散半径、扩散高度以及浓度方面的影响。
最后得出结论,随着 大气状况从极不稳定到稳定,易燃气体的扩散半径逐渐扩大,扩散高度逐渐降低,因此,大气状况越稳定越有利于易燃气体在平面内的扩散,并且大气状况越稳定,沿水平方向的气体浓度下降越快。
关键词:高斯烟羽模型;易燃气体运输;m a tla b仿真中图分类号:F530 文献标识码:AAbstract:A m on g the dangerous goods transported by ra il,gas dangerous goods occu py a large p ro p o rtio n.T h ere fore,in view o f the leakage a ccid e n t o f flam m able gas d u rin g the ra ilw a y tra n sp o rta tio n,ta k in g propane gas as an exa m ple,G aussian plum e m odel is used to sim ula te the gas d iffu s io n range of single and m u ltip le leakage sources u n d e r d iffe re n t atm ospheric c o n d itio n s b y m a tla b.W ith the h e ig h t o f d iffu s io n,the e ffe c t of atm ospheric s ta b ility on the d iffu s io n ra d iu s,d iffu s io n h e ig h t,and con ce n tra tio n o f the gas was analyzed.F in a lly,it is con clu d e d th a t as the atm ospheric co n d itio n s change fro m extrem e ly unstable to stable,the d iffu s io n ra dius of flam m able gases g ra d u a lly expands and the d iffu s io n h e ig h t g ra d u a lly d ecreases.T h ere fore,the more stable the atm ospheric c o n d itio n s, the more con ducive to the d iffu s io n of flam m able gases in the p la n e,and the atm osphere The m ore stable the s itu a tio n,the faster the con centration of gas in the h o rizonta l d ire c tio n drops.Key words:G aussian plum e m o d e l;fla m m a b le gas tra n sp o rt; m atlab s im u la tio n随着化工行业的持续发展,化工气体的用量也在持续增长,而铁路承载了相当一部分的气体运输量。
高斯烟羽模式公式

高斯烟羽模式
高斯烟羽模式是计算释入大气中的气载污染物下风向浓度的应用最广的方法。
此模式假定烟羽中污染物浓度在水平方向和垂直方向都遵循高斯分布。
对于在恒定气象条件(指风向、风速、大气稳定度不随时间而改变)高架点源的连续排放,在考虑了烟羽在地面的全反射后,下风向任一点的污染物浓度C (x ,y ,z )由下式给出:
][2),,(2z 22z 2y 22)(2)(2σσσzyσπσσHe z He z y e e e u z y x C +----+=
式中 C (x ,y ,z )—— 下风某点(x ,y ,z )处的空气中污染物浓度,g/m 3。
x —— 下风向距离,m ;
y —— 横截风向距离,m ;
Q —— 气载污染物源强,即释放率,g/s ;
U —— 排放高度处的平均风速,m/s ;
He —— 有效排放高度;m 。
σy ,σz —— 水平方向和垂直方向扩散参数,m ,它们是下风距离x 急大气稳
定度的函数:
下风地面处(z = 0)的污染物浓度则为:
y 2z 222z y σσσσπy H e e u Q C --=。
云团扩散模型

1 云团扩散模型根据物质泄漏后所形成的气云的物理性质的不同,可以将描述气云扩散的模型分为非重气云模型和重气云模型两种[5-13]。
非重气云模型高斯模型是一种常用的非重气扩散模型,高斯烟羽(Plume model)模型又称高架点连续点源扩散模型,适用于连续源的扩散,即连续源或泄放时间大于或等于扩散时间的扩散。
高斯烟团(Puff model)模型适用于短时间泄漏的扩散,即泄放时间相对于扩散时间比较短的情形,如突发性泄放等。
若假设气体云内空间上的分布为高斯分布,则地面地处风向的烟团浓度分布算式为式中,c(x,y,H)——点(x,y,H)处浓度值,mg/m3;Q——源强,即单位时问的排放量,mg/s;u——环境平均风速,m/s;σx,σy,σz——扩散参数;H——源高(烟团高度),m;x——下方向到泄漏原点的距离,m;y,z——侧风方向、垂直向上方向离泄漏原点的距离,m。
高斯模式的实际应用效果很大程度上依赖于如何给定模式中的一些参数,尤其要注意源强、扩散参数等的确定。
源强与污染物的物理化学属性、扩散方式、释放点的地理环境等有关。
扩散参数表征大气边界层内湍流扩散的强弱,是高斯模式的一项重要数据。
高斯扩散模式所描述的扩散过程(实质上也包含了在实际应用中对高斯模式的一些限制)主要有:1)下垫面平坦、开阔、性质均匀,平均流场稳定,不考虑风场的切变。
2)扩散过程中,污染物本身是被动、保守的,即污染物和空气无相对运动,且扩散过程中污染物无损失、无转化,污染物在地面被反射。
3)扩散在同一温度层结中发生,平均风速大于 m/s。
4)适用范围一般小于10~20 km。
重气云模型由于重气本身的特殊性,在重气扩散领域也有大量基于不同理论的模型。
鉴于重气扩散与中性或浮性气体扩散有着明显的区别,目前国内外已开发大量的不同复杂程度的重气扩散模型,如箱模型、相似模型、LTA-HGDM模型、CFD模型等。
箱(BOX)模型箱模型是指假定浓度、温度和其他场,在任何下风横截面处为矩形分布等简单形状,这里的矩形分布是指在某些空间范围内场是均匀的,而在其他地方为零。
基于高斯烟羽模型的放射性气体的扩散

关于核电站泄漏放射性气体扩散的预估模型摘要由于核泄漏导致放射性气体扩散对经济和人身造成巨大损失的报道在国内外屡见不鲜,本文中日本福岛核泄漏事件更加使我们认识到对放射性气体扩散进行合理性的预估从而为以后类似于此的突发性事件作积极有效的补救措施的重要性。
对于问题一我们运用了点源烟羽扩散模型,用抛物型二阶偏微分方程解出理想状态下的不同时刻、不同地点的浓度表达式:222432 (,,,)(4)x y zktQC x y z t ektπ++-=。
此模型是建立在以泄漏点为圆心的一个无界球形区域内的。
为了使模型更符合实际情况,能够被应用于现实生活中,我们在泄漏源有效高度的确定和考虑地面反射与吸收作用下对此模型进行了修正,最终得到问题一浓度的确定公式(14)(,,,)C x y z t的表达式。
对于问题二,我们采用高位连续点源烟羽扩散模式,其扩散服从正态分布,并根据概率论的相关知识通过数学公式推导,得到理想状态下的高斯模型,由泄漏源有效高度,地面反射等因素的影响对其进行修正,又由于重力干沉积,雨洗湿沉积以及核衰变等因素对源强的影响,对高斯烟羽模型再次进行修正,最终得到泄漏源周边浓度变化情况即公式(32),在风速为k m/s的条件下浓度为(,,,)C x y z H。
对于问题三,我们在第二问建立的模型的基础上,引入时间变量rt和t,和扩散速度变量s,在风速和扩散速度的共同影响下,可分别求出上风向和下风向浓度预估模型即公式(40)和(41)。
对于问题四,本文参阅整理大量气象、地理、新闻资料,选择我国东海岸典型地域---山东半岛和美国西海岸典型地域---加利福尼亚州作为研究对象,综合考虑对应海域平均风速及风向、地理距离、海水对放射性物质扩散的部分反射系数等因素,并通过计算机模拟,预测出放射性核物质将经过6天到达我国东海岸,且131I浓度预测值为:0.1053mBq m-⋅,,经过6.8天到达美国西海岸,且氙-133浓度的预测值几乎为零,与实际情况比较吻合。
高斯烟羽模型

模型假设:1、坐标系高斯模型的坐标系如图2.1所示,原点为排放点(若为高架源,原点为排放点在地面的投影),x轴正向为风速方向,y轴在水平面上垂直于x轴,正向在x轴的左侧,z轴垂直于x轴重时间变化而变化;(7)地面对泄漏气体起全反射作用,不发生吸收或吸附作用;(8)整个过程中,泄漏气体不发生沉降、分解,不发生任何化学反应等。
3、模型公式推导由正态分布假设可以导出下风向任意一点X (x,y,z )处泄漏气体浓度的函数为:22)(),,(bz ay e e x A z y x X --= (1)由概率统计理论可以写出方差的表达式为:⎧∞2⎪⎪⎩⎪⎪⎨⎧==222121z y b a σσ (4)将(1)式和(4)式代入(3)式,积分可得:zy u Q x A σσπ2=)( (5) 再将(4)式和(5)式代入(1)式,可得:⎤⎡⎫⎛22一部分P 其中,像源的贡献为:))(21exp()21exp(2,,22222zy z y H z y u Q z y x X σσσσπ+--=)( (8) 则该处的实际浓度为:)()()(z y x X z y x X z y x X ,,,,,,21+= (9) 由以上条件公式可得到高架连续点源扩散的高斯烟羽模型公式为:)])(1exp())(1[exp()21exp(2,,,,222222yz y H z H z y u Q H t z y x X σσσπ+-+--⨯-=)( (10)为y σ为水s ;H m 。
其中,X (x,y,0)为下风向x 米、横向y 米处的地面扩散气体浓度,单位为kg/m 3;若令y=0,则可以得到下风向中心线上的浓度分布。
4、泄漏源有效高度(烟云抬升高度的计算):以上式中的泄漏源有效高度是指泄漏气体形成的气云基本上变成水平状的时候气云中心的离地高度。
实际上,泄漏源有效高度就等于泄漏源几何高度加泄漏烟云抬升高度。
影响烟云抬升高度的因素有很多,主要包括:泄漏气体的初始速度和方向、初始温度、泄漏口直径、环境风速及风速岁高度的变化率、环境温度及大气稳定度。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Most probable wind direction
6
Simple Model #2:
Conc at 2 =
( wind speed)(area of disk 2 )
Mass emission rate
[Gaussian distribution function ]
µg µg/sec [ ] = − 3 2 m (m/sec )( m )
*Pollutant is well mixed and confined within the cone *Pollutant is continuously swept thru the cone by the wind
2 1
3
mass/time passing point 1
=
mass/time passing thru disk area 2 C1 > C 2 > C 3
1
Instantaneous Plume Shape
Time-averaged Plume Shape
Describing Plume Concentrations
wind
Fig 4 -3, p.44 in Martin et al
2
Tim’s Simple Plume Model
h
x
Simplified Steady-State Plume Model
“Eddy” Diffusion
Consider two enclosed air volumes separated by a wall
(arrows represent eddy motions; balls represent pollutant molecules)
Size of eddies > size of pollutant molecules
8
The rate of pollutant molecules crossing plane AA depends upon the concentration difference between the two sides. Specifically, this rate =K δc/δx ,where K is termed an “eddy diffusivity” with units of m2 /sec. The magnitude of K depends upon the magnitude of the eddy motions.
“Advection-Diffusion” Equation
∂C ∂C ∂ ∂C ∂ ∂C + other losses = −u + K + K due to ∂t ∂x ∂y y ∂y ∂z z ∂z deposition and
chemical reactions = 0 for steadystate models “Advection”, i.e., transport by the mean wind, u Effect of turbulent “diffusion”, i.e., exchange of polluted air parcel with surrounding air parcels. If the surrounding air is cleaner, δC/δz & δC/δy are negative. K is the “eddy diffusivity” and represents the intensity of turbulent motions and varies with stability
Source: Slade et al “Meteorology and Atomic Energy, 1968”
5
unstable
neutral
stable
More Detailed Plume Model
Mass is not uniformly distributed within the cone’s volume
* Constant wind speed with height (u does not depend on z) * Constant eddy diffusivity (K does not depend on y or z)
Define:
ó2 z =
2 Kz x u
ó2 y =
2 Ky x u
A similar result is obtained in the y direction. Given that the net rate of change in the volume [ = V(δc/δt)] is the change in all three directions , we obtain an overall expression in terms of x, y and z.
7
z
y x dy dz dx
*Transport of mass in x direction depends on the average horizontal wind *Transport of mass in the y and z directions depends on turbulent motions
Pollutant molecules are moving around in random directions due to random eddy motions
Random eddy motions in pollution-free air
Now remove the wall between the enclosures
Mass emission rate “Effective” stack height, including rise of the hot plume near the source
Q C(x, y, z) = 2π u σyσz
Wind speed evaluated at “effective” release height
µg = µg/sec m 3 (m/sec)( m2 )
2 1
Disk shape depends upon stability category
More unstable and thus more pronounced vertical spreading
4
Perspective View of “Fanning” Plume in Very Stable Air Less vertical motion
Changes in z Direction via “ Turbulent Diffusion”:
Mass Flow Rate In = - A xy ∂ { K z C} ∂z [m 2 ][m-1 ][ µg m -3 ][m 2 sec-1 ]
Net Rate of Change =
∂ ∂ (K z C ) V ∂ z ∂z
Gaussian Plumes from “Point” Sources
• • • • • • • • • • Time averaged vs instantaneous plumes Simplified steady-state plume model “Eddy” diffusion, advection/diffusion equation Gaussian point source plume model Plume sigma values vs stability and distance Plume reflection Non-gaussian plumes Plume Rise; plume trajectories Buoyancy-induced dispersion Stack downwash
* Mass is conserved
∞
−∞
∫∫
∞
−∞
Cdydz = Q
[for x > 0]
{µg/sec }
Pollutant concentration as a function of downwind position (x,y,z)
Gausቤተ መጻሕፍቲ ባይዱian “Point” Source Plume Model:
=
mass/time passing thru disk area 3
Concentration vs. distance downwind depends upon cone shape
3
Simple Model #1:
Concentration of air at 2 = Mass emission rate (wind speed )(area of disk 2)
2 1 y
z x
X is the time-averaged wind direction, Y is the cross-wind direction, Z is the vertical dimension
Gaussian Plume Model
2 1
In order to derive an equation describing the distribution of mass within the plume, we must first consider the transport of mass within a small control volume
dx dy dz
V =Volume = dxdydz Axy = dxdy Ayz = dydz Axz = dxdz
Changes in x Direction:
