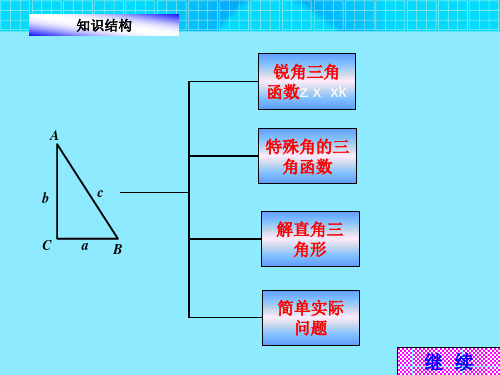
公开课锐角三角函数复习
锐角三角函数复习课课件

90度角
总结词
正弦值和余弦值不存在,正切值为无穷大
详细描述
在90度角时,正弦函数值和余弦函数值都不存在,因为无法定义与x轴的角度;正切函数值为无穷大 ,因为在直角三角形中,对边长度可以无限小而保持与斜边的比值不变。
03
锐角三角函数的图像与性质
正弦函数图像
总结词
正弦函数图像是一个周期函数,其图像在直角坐标系中呈波 浪形。
用三角函数来处理角度和旋转。
05
常见题型解析与解题技巧
选择题
• 题型特点:选择题通常考察学生对锐角三角函数基础知识的理 解和应用,题目会给出一些具体的数值或图形,要求选择正确 的答案。
选择题
排除法
根据题目给出的选项,逐一排除明显 错误的答案,缩小选择范围。
代入法
对于涉及数值计算的题目,可以将选 项中的数值代入题目中,通过计算验 证答案的正确性。
在研究磁场和电场时,我们经常需要使用锐 角三角函数来描述场的方向和强度。
日常生活中的问题
建筑和设计
在建筑设计、工程规划和土木工程中,锐角 三角函数用于计算角度、高度和距离等参数 ,以确保结构的稳定性和安全性。
游戏和娱乐
在许多游戏和娱乐活动中,锐角三角函数也 起着重要作用。例如,在制作动画、设计游 戏关卡或创建虚拟现实环境时,我们需要使
总结词
正弦值为0,余弦值和正切值不存在
详细描述
在0度角时,正弦函数值为0,表示射线与x轴重合;余弦函数值不存在,因为无 法定义与x轴的角度;正切函数值也不存在,因为没有对边形成直角三角形。
30度角
总结词
正弦值为0.5,余弦值为0.866,正切值为1/3
详细描述
在30度角时,正弦函数值为0.5,表示对边长度为斜边长度的一半;余弦函数值 为0.866,表示邻边长度为斜边长度的一半的平方根;正切函数值为1/3,表示对 边长度与邻边长度的比值。
初三锐角三角函数复习讲义

锐角三角函数:知识点一:锐角三角函数的定义: 一、 锐角三角函数定义:如图所示,在Rt △ABC 中,∠C=900, ∠A 、∠B 、∠C 的对边分别为a 、b 、c , 则∠A 的正弦可表示为:sinA ∠A 的余弦可表示为:cosA∠A 的正切可表示为:tanA ,它们称为∠A 的锐角三角函数①斜边)(sin =A =______,②斜边)(cos =A =______,③的邻边A A ∠=)(tan =______,【特别提醒:1、sinA 、cosA 、tanA 表示的是一个整体,是两条线段的比,没有单位,这些比值只与 有关,与直角三角形的 无关。
2、取值范围 <sinA< , <cosA< ,tanA> 例1. 锐角三角函数求值:在Rt △ABC 中,∠C =90°,若a =9,b =12,则c =______,sin A =______,cos A =______,tan A =______, sin B =______,cos B =______,tan B =______.典型例题:类型一:利用直角三角形求值1.已知:如图,Rt △TNM 中,∠TMN =90°,MR ⊥TN 于R 点,TN =4,MN =3.求:sin ∠TMR 、cos ∠TMR 、tan ∠TMR .2.已知:如图,⊙O 的半径OA =16cm ,OC ⊥AB 于C 点,⋅=∠43sin AOC 求:AB 及OC 的长.类型二. 利用角度转化求值:1.已知:如图,Rt △ABC 中,∠C =90°.D 是AC 边上一点,DE ⊥AB 于E 点.DE ∶AE =1∶2.求:sin B 、cos B 、tan B .2. 如图,直径为10的⊙A 经过点(05)C ,和点(00)O ,,与x 轴的正半轴交于点D ,B 是y 轴右侧圆弧上一点,则cos ∠OBC 的值为( ) A .12 B .32C .35D .455.如图,O ⊙是ABC △的外接圆,AD 是O ⊙的直径,若O ⊙的半径为32,2AC =,则sin B 的值是( )A .23 B .32 C .34 D .436. 如图4,沿AE 折叠矩形纸片ABCD ,使点D 落在BC 边的点F 处.已知8AB =,10BC =,AB=8,则tan EFC ∠的值为 ( )A.34 B.43C.35D.45A D ECB F7. 如图6,在等腰直角三角形ABC ∆中,90C ∠=︒,6AC =,D 为AC 上一点,若1tan 5DBA ∠= ,则AD 的长为( )A .2B .2C .1D .22D C B A Oyx第8题图类型三. 化斜三角形为直角三角形1. 如图,在△ABC 中,∠A=30°,∠B=45°,AC=23,求AB 的长.2.如图,在Rt △ABC 中,∠BAC=90°,点D 在BC 边上,且△ABD 是等边三角形.若AB=2,求△ABC 的周长.(结果保留根号)3. ABC 中,∠A =60°,AB =6 cm ,AC =4 cm ,则△ABC 的面积是 ( )A.23 cm 2B.43 cm 2C.63 cm 2D.12 cm 2类型四:利用网格构造直角三角形1.如图所示,△ABC 的顶点是正方形网格的格点,则sinA 的值为( ) A .12B .55 C .1010D .2552.如图,△ABC 的顶点都在方格纸的格点上,则sin A =_______. 3.如图,A 、B 、C 三点在正方形网络线的交点处,若将ABC ∆绕着点A 逆时针旋转得到''B AC ∆,则'tan B 的值为 ( )A.41 B. 31 C.21D. 14.正方形网格中,AOB ∠如图放置,则tan AOB ∠的值是( )A .55B.2 5 5 C.12D. 2 CB A ABO知识点二:特殊角的三角函数值当 时,正弦和正切值随着角度的增大而 余弦值随着角度的增大而例1.求下列各式的值.1.计算:︒-︒+︒30cos 245sin 60tan 22.计算:3-1+(2π-1)0-33tan30°-tan45°3.计算:030tan 2345sin 60cos 221⎪⎪⎭⎫ ⎝⎛︒-︒+︒+ 4.计算: tan 45sin 301cos 60︒+︒-︒例2.求适合下列条件的锐角α . (1)21cos =α (2)33tan =α (3)222sin =α (4)33)16cos(6=- α(5)已知α 为锐角,且3)30tan(0=+α,求αtan 的值(6)在ABC ∆中,0)22(sin 21cos 2=-+-B A ,B A ∠∠,都是锐角,求C ∠的度数.例3. 三角函数的增减性 1.已知∠A 为锐角,且sin A <21,那么∠A 的取值范围是 A. 0°< A < 30° B. 30°< A <60° C. 60°< A < 90° D. 30°< A < 90° 2. 已知A 为锐角,且030sin cos <A ,则 ( )A. 0°< A < 60°B. 30°< A < 60°C. 60°< A < 90°D. 30°< A < 90°锐角α30°45°60°sin αcos αtan α类型五:三角函数在几何中的应用1.已知:如图,在菱形ABCD 中,DE ⊥AB 于E ,BE =16cm ,⋅=1312sin A 求此菱形的周长.2.已知:如图,Rt △ABC 中,∠C =90°,3==BC AC ,作∠DAC =30°,AD 交CB 于D 点,求:(1)∠BAD ;(2)sin ∠BAD 、cos ∠BAD 和tan ∠BAD .3. 已知:如图△ABC 中,D 为BC 中点,且∠BAD =90°,31tan =∠B ,求:sin ∠CAD 、cos ∠CAD 、tan ∠CAD .4. 如图,在Rt △ABC 中,∠C=90°,53sin =B ,点D 在BC 边上,DC= AC = 6,求tan ∠BAD 的值.5.(本小题5分)如图,△ABC 中,∠A=30°,3tan 2B =,43AC =.求AB 的长.DCBAACB知识点三:解直角三角形:1.在解直角三角形的过程中,一般要用的主要关系如下(如图所示): 在Rt △ABC 中,∠C =90°,AC =b ,BC =a ,AB =c ,①三边之间的等量关系:________________________________.②两锐角之间的关系:__________________________________. ③边与角之间的关系:==B A cos sin ______;==B A sin cos _______;==BA tan 1tan _____;==B A tan tan 1______.④直角三角形中成比例的线段(如图所示).在Rt △ABC 中,∠C =90°,CD ⊥AB 于D .CD 2=_________;AC 2=_________; BC 2=_________;AC ·BC =_________.例1.在Rt △ABC 中,∠C =90°.(1)已知:32=a ,2=b ,求∠A 、∠B ,c ; (2)已知:32sin =A ,6=c ,求a 、b ;(3).已知:△ABC 中,∠A =30°,∠B =60°,AC =10cm .求AB 及BC 的长.类型六:解直角三角形的实际应用 仰角与俯角1.如图,从热气球C 处测得地面A 、B 两点的俯角分别是30°、45°,如果此时热气球C 处的高度CD 为100米,点A 、D 、B 在同一直线上,则AB 两点的距离是( ) A . 200米 B . 200米 C . 220米 D . 100()米 2. 在一次数学活动课上,海桂学校初三数学老师带领学生去测万泉河河宽,如图13所示,某学生在河东岸点A 处观测到河对岸水边有一点C ,测得C 在A 北偏西31︒的方向上,沿河岸向北前行20米到达B 处,测得C 在B 北偏西45︒的方向上,请你根据以上数据,帮助该同学计算出这条河的宽度.(参考数值:tan31°≈53,sin31°≈21)图13ABCD 45° 30°3 .如图,小聪用一块有一个锐角为30︒的直角三角板测量树高,已知小聪和树都与地面垂直,且相距33米,小聪身高AB 为1.7米,求这棵树的高度.A BCD E4.一数学兴趣小组为测量河对岸树AB 的高,在河岸边选择一点C ,从C 处测得树梢A 的仰角为45°,沿BC 方向后退10米到点D ,再次测得点A 的仰角为30°.求树高.(结果精确到0.1米.参考数据:2 1.414≈,3 1.732≈)5.超速行驶是引发交通事故的主要原因之一.上周末,小明和三位同学尝试用自己所学的知识检测车速.如图,观测点设在A 处,离益阳大道的距离(AC )为30米.这时,一辆小轿车由西向东匀速行驶,测得此车从B 处行驶到C 处所用的时间为8秒,∠BAC=75°. (1)求B 、C 两点的距离;(2)请判断此车是否超过了益阳大道60千米/小时的限制速度?(计算时距离精确到1米,参考数据:sin75°≈0.9659,cos75°≈0.2588,tan75°≈3.732,3≈1.732,60千米/小时≈16.7米/秒)坡度与坡角1.如图,某水库堤坝横断面迎水坡AB 的坡比是1:3,堤坝高BC=50m ,则应水坡面AB 的长度是( )A .100mB .1003mC .150mD .503m2.数学活动课上,老师和学生一起去测量学校升旗台上旗杆AB 的高度.如图,老师测得升旗台前斜坡FC 的坡比为i =1:10,学生小明站在离升旗台水平距离为35m (即CE =35m )处的C 点,测得旗杆顶端B 的仰角为α,已知tan α=37,升旗台高AF =1m ,小明身高CD =1.6m ,请帮小明计算出旗杆AB 的高度.3.如图,有两条公路OM ,ON 相交成30°角,沿公路OM 方向离O 点80米处有一所学校A ,当重型运输卡车P 沿道路ON 方向行驶时,在以P 为圆心、50米长为半径的圆形区域内部会受到卡车噪声的影响,且卡车P 与学校A 的距离越近噪声影响越大,若已知重型运输卡车P 沿道路ON 方向行驶的速度为18千米/时. (1)求对学校A 的噪声影响最大时,卡车P 与学校A 的距离;(2)求卡车P 沿道路ON 方向行驶一次给学校A 带来噪影响的时间.30°80米OMNAP4.如图是某儿童乐园为小朋友设计的滑梯平面图.已知BC =4米,AB =6米,中间平台宽度DE =1米,EN 、DM 、CB 为三根垂直于AB 的支柱,垂足分别为N 、M 、B ,∠EAB =31°,αABD CEF i FC =1:10DF ⊥BC 于F ,∠CDF =45°.求DM 和BC 的水平距离BM 的长度.(结果精确到0.1米,参考数据:sin31°≈0.52,cos31°≈0.86,tan31°≈0.60)5.如图,某幼儿园为了加强安全管理,决定将园内的滑滑板的倾角由45º降为30º,已知原滑滑板AB 的长为5米,点D 、B 、C 在同一水平地面上.(1)改善后滑滑板会加长多少?(精确到0.01)(2)若滑滑板的正前方能有3米长的空地就能保证安全,原滑滑板的前方有6米长的空地,像这样改造是否可行?说明理由。
中考复习13讲:锐角三角函数复习(组内公开课)

例题一、“三角函数的定义”的考 查: (1)在Rt△ABC中∠C=90 °, AC=40, BC=9,则∠ B的正弦值是__, 余弦值 是___,∠ A的正切值是___ (2)如果两条直角边分别都扩大2 倍,那么锐角的各三角函数值都( ) (A)扩大2倍;(B)缩小2倍; (C)不变;(D)不能确定
(1)当角度在0~90之间变化时, 正弦值和正切值随角度的增大而 增大
(2)当角度在0~90之间变化时, 余弦值随角度的增大而减小
例题分析:
(1)当锐角A>300时,cosA的值是(
1 ( A). 小于 2 3 C .小于 2 1 B .大于 2 3 D .大于 2
)
(2)下列判断中正确的是()
例、如图,在等腰直角三角形ABC中,
∠C=90°,AC=6,D是
AC上一点, 若tan∠DBA=1/ 5,
D
C
求AD的长。
A
E
B
点拨:解三角函数题目最关键的是要构造合适的直角三角形,把已知 1 角放在所构造的直角三角形中。本题已知tan∠DBA= 5 ,所以可 以过点D作DE⊥AB于E,把∠ DBA放于Rt△DBE中,然后根据正切函数的 定义,即可弄清DE与BE的长度关系,再结合等腰Rt△的性质,此题 就不难解答了。
二、本章专题讲解
(一)知识专题讲解 专题一:锐角三角函数的定义、公式、特殊角的三角函数值 专题概述:锐角三角函数的定义在解某些问题时可用 作一种基本的方法。要熟练掌握特殊锐角的三角函数 值,并理解常用的关系式:
sin cos 1 sin tan cos
2 2
tan tan 1( 900 ) sin A cos(90 A) cos B
锐角三角函数复习课件九年级中考复习

误的是( A )
A.sin B=
1
3
1
C.tan B=
2
B.sin C=
2 5
5
D.sin2B+sin2C=1
3
8.如图,点 A(x,4)在第一象限,OA 与 x 轴所夹的锐角为 α,cos α= ,
5
则 tan α 的值为( A
A.
4
3
B.
3
4
C.
5
4
)
D.
4
5
3
9.在 Rt△ABC 中,∠C=90°,若 sin A= ,则 cos B 的值是( B )
B
2- 3
2+ 3 2-
=23.类比这种方法,计算
tan
22.5°的
3
)
B. 2-1
C. 2
1
D.
2
14.在如图所示的网格中,小正方形的边长为1,点A,B,C,D都在
格点上,
AB与CD相交于点O,则∠AOC的正切值是( A )
A.
C.
2
3
3
5
3
B.
2
5
D.
3
(1)cos260°+sin260°=
1 ;
cos45°
(2)
-
tan 45°= 0 ;
sin45°
3
(3)1-2sin 30°cos 30°= 1- 2
.
练习题
1.在△ABC 中,∠A=105°,∠B=45°,tan C 的值是
3
3
.
2.在Rt△ABC中,∠C=90°,若△ABC的三边都缩小5倍,则sin
是( D )
公开课锐角三角函数复习课件

特殊角的三角函数值
• 0°、30°、45°、60°、90°等特殊角的三角函数值应熟练掌握, 包括sin、cos、tan、cot、sec、csc等函数。
02
锐角三角函数的图像与 性质
正弦函数的图像与性质
正弦函数的周期性和对称性
正弦函数是周期函数,具有轴对称性和中心对称性。
正弦函数的单调性
在每个周期内,正弦函数在一定区间内单调递增或递减。
正切函数的图像与性质
正切函数的定义域
正切函数只在直角三角形 中定义,表示对边与邻边 的比值。
正切函数的单调性
正切函数在每个区间内单 调递增,无周期性。
正切函数的值域
正切函数的值域为全体实 数,表示任意两个边的比 值。
三角函数图像的变换
平移变换
翻折变换
通过平移正弦、余弦、正切函数的图 像,可以得到其他三角函数图像。
根据数学模型,选择合适的三角 函数公式进行计算。
计算结果
根据选择的公式进行计算,得出 结果。
理解题意
首先需要仔细阅读题目,理解题 目的要求和所给条件,明确解题 的目标。
检验结果
最后需要对计算结果进行检验, 确保结果的正确性。经典Leabharlann 角三角函数综合题解析题型一
求角度问题
题型二
求边长问题
题型三
求面积问题
02
通过已知的边长和角度,利用三角函数可以求出其他边长或角
度,从而解决实际问题。
特殊角的三角函数值
03
对于一些特殊角,如30°、45°、60°等,其三角函数值是已知的
,这些值在解直角三角形时非常有用。
三角函数在实际问题中的应用
测量问题
在建筑、工程和地理测量等领域 ,经常需要使用三角函数来解决 实际问题,如计算距离、高度和
锐角三角函数复习.ppt
解得x=6
∴CD=6
A
B
C
D
例题解析
(2) BC=BD+CD=4+6=10=AD
在Rt△ACD中
在Rt△ABC中z x xk
问题2 要解一个直角三角形,除一个直角的已知元素外,还需要几个元素?为什么这些元素中至少要有一条边?试给出可以求解直角三角形的两个条件.
A
B
C
D
问题3 如果题中给出的图形不是直角三角形而是一个综合图形,我们用什么方法进行处理,就能把它转化为可以解的直角三角形?
问题4 你认为需要具备哪些知识、掌握哪些方法,就能较顺利地解决有关实际问题?请总结实际问题的一般步骤和注意点.
锐角三角 函数z x xk
特殊角的三 角函数
解直角三 角形
简单实际 问题
c
a
b
A
B
C
知识
特殊角的三 角函数
2
1
30°
1
1
45°
2
1
60°
30°+ 60°= 90°
返 回
解直角 三角形
∠A+ ∠ B=90°
a2+b2=c2
三角函数 关系式
计算器
由锐角求三角函数值
由三角函数值求锐角
返 回
简单实 际问题
数学模型
直角三角形
等腰梯形
组合图形
等腰三角形
构建
解
作高转化为直角三角形
解
返 回
问题1 已知:如同,在△ABC中,∠ACB=90°,CD⊥AB,垂足为D,AD=3,CD= ,怎样求sinA和cos∠BCD的值?怎样求∠B的正切值?
已知:如图,在△ABC中,∠C=90°,点D在BC上,BD=4,AD=BC,cos∠ADC= ,求:(1)DC的长;(2)sinB的值.
公开课-锐角三角函数复习

D
A
⑴正弦
1.锐角三角函数的定义 ⑵余弦
锐
⑶正切
角 2.30°、45°、60°特殊角的三角函数值
三
⑴定义
角
①三边间关系
函
3.解直角三角形
⑵解直角三角形的依据 ②锐角间关系
③边角间关系
数
⑶解直角三角形在实际问题中
的应用
达标检测
1.如图所示,边长为1的小正方形构成的 网上格,中则,∠A半E径D的为正1的切⊙值O等的于圆﹍心﹍12O﹍在。格点
(3)边角的关系:sin A a cos A b tan A a
c
c
b
归纳:只要知道其中的2个元素(至少有一个是边),
就可以求出其余3个未知元素.
四.解直角三角形的应用
1.仰角和俯角
在进行测量时, 从下向上看,视线与水平线的夹角叫做仰角; 从上往下看,视线与水平线的夹角叫做俯角.
视线
铅 直
仰角
3
例3.在Rt △ ABC中,∠C=90°,∠ A=30°,a=5, 求b、c的大小.
解: ∠B=90°- ∠ A=90°-30°=60°,
B
∵tanB=b/a,
∴b=a·tanB=5·tan60°= 5 3
5
∵ sinA=a/c,
30°
A
C
∴ c=a/sinA=5/sin30=5/(1/2)=10.
1
2
3
2
2
2
3
2
1
2
2
2
3
1
3
3
锐角的三角函数值有 何变化规律呢?
三.解直角三角形
1.什么叫解直角三角形?
由直角三角形中,除直角外的已知元素,求出所 有未知元素的过程,叫做解直角三角形.
锐角三角函数复习课件公开课

欢迎来到锐角三角函数复习课件公开课! 在本课程中,我们将回顾锐角三角 函数的基本概念,常见公式,性质和图像,解三角方程,以及一些实际应用。
锐角三角函数的基本概念
锐角三角函数是用于描述锐角三角形中角度和边长之间关系的函数。包括正弦、余弦和正切等函 数。
1 正弦函数
描述角的对边与斜边之间的关系。
总结和回顾
在本课程中,我们回顾了锐角三角函数的基本概念、常见公式、性质和图像。学习了如何利用锐角三角 函数求解三角方程,并了解了一些实际应用。希望你已经对锐角三角函数有了更深入的理解!
锐角三角函数在直角三角形的图像中不断变化,并呈现出一些特殊的性质。
单位圆
单位圆是用于可视化锐角三角 函数图像和特殊性质的工具。
正弦函数
正弦函数是一条波浪形曲线, 用于描述周期性变化。
余弦函数
余弦函数是一条类似正弦函数 的波浪形曲线,但相位差90度。
利用锐角三角函数求解三角方程
锐角三角函数可以用于解决涉及三角函数的方程,从而求得角度的值。
2 余弦函数
描述角的邻边与斜边之间的关系。
3 正切函数
描述角的对边与邻边之间的关系。
常见的锐角三角函数公式
锐角三角函数有一些常见的公式用于计算和简化角度的计算。
倍角和半角公式
• 正弦和余弦的倍角和半角公式。 • 正切的双角和半角公式。
和差公式
• 正弦和余弦的和差公式。 • 正切的和差公式。
锐角三角函数的性质和图像
1
方程转化
将方程转化为以三角函数为未知数的
方程求解
2
方程。
利用三角函数的运算特性和解方程的
方法求解得出角度的值。
3
验证解
